地震前兆观测资料易受多种因素干扰影响,包含人为作用、仪器故障、气象变化及诸多未知因素。因此,排查干扰因素成为识别地震前兆异常的必要工作。从实际曲线形态看,干扰与地震前兆形态相似,需充分分析现有观测资料,就近对比其他可用地震前兆资料,才可能对某些固体潮畸变和趋势变化做出准确判定(王梅等,2004;陈运泰,2009;王小平等,2010)。
目前重庆地区地震前兆观测台站观测项目较为单一,在出现异常变化时,对干扰引起的异常信息难以准确判定。本文以巴南石龙地震台钻孔应变某一时段观测资料异常变化为实例,逐步分析、识别钻孔应变干扰因素,排查地震前兆异常存在的可能性,为日后地震前兆观测资料异常判定提供参考。
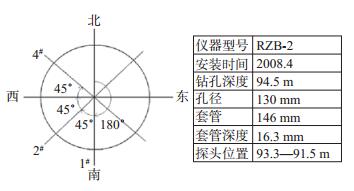
1 观测台概况重庆巴南钻孔台站地处四川盆地东部地台区中台拗川东南褶皱带,具有地叶升降幅度小、沉积建造厚度小等地台构造的一般特征。台站所处地质构造部位在莲石向斜与丰盛场背斜之间,岩石倾角约15°,侏罗纪上统遂宁组地层,主要岩性为色泥岩夹砂岩(丁仁杰等,2004)。台站应变钻孔井为2007年6月施工成井,井深94.5 m,钻孔探头深度91.5—93.3 m;架设RZB-2型压容四分量钻孔应变仪,于2008年8月正式观测,采用分钟值连续采样,应变灵敏度达10-8,4个分量探头观测元件方位角分别为NS、N45°E、EW、N45°W(图 1)。
|
图 1 巴南地震台钻孔应变元件与观测井布设参数 Fig.1 Four components and parameters of borehole strain at Banan Seismic Station |
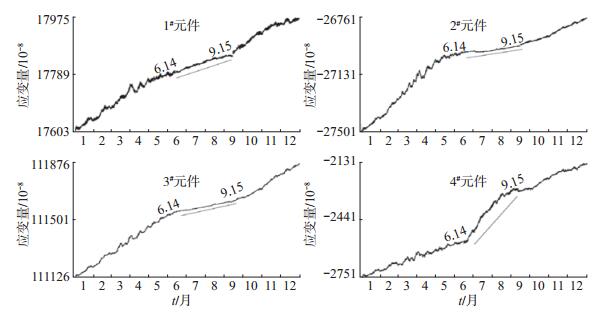
2010年以来巴南地震台钻孔应变观测曲线变化形态较为稳定,4个分量均呈现向上拉张的线性变化。2015年6月14日至9月15日钻孔应变各元件分量观测曲线出现与前期不同趋势的短临异常,其中:1#、2#、3#元件线性趋势减缓,上升速率变小;4#元件明显加速上升;4#元件变化幅度最大,应变量约3.06×10-6(图 2)。
|
图 2 2015年巴南钻孔应变月观测曲线 Fig.2 Monthly curves of Banan borehole strain record in 2015 |
(1) 观测系统自检分析。目前,RZB分量式钻孔应变仪实际监测数据是井孔径相对变化量。根据钻孔加衬模型(邱泽华等,2005;王勇等,2005),当探头与围岩耦合处于理想状态时,主应变ε1、ε2与钻孔分量θ方向的理论孔径相对变化可以表示为
| $S = {A_i}\left( {{\varepsilon _1} + {\varepsilon _2}} \right) + {B_i}\left( {{\varepsilon _1} - {\varepsilon _2}} \right)\cos 2\left( {\theta - \varphi } \right)$ | (1) |
其中:φ是ε1的方位角,Ai为第i个元件对(ε1 + ε2)的灵敏度系数,Bi为第i个元件对(ε1 -ε2)的灵敏度系数,Ai和Bi与套筒内径、套筒外径、围岩等效杨氏模量和泊松比、套筒材料杨氏模量和泊松比有关。
将2个相互垂直分量的孔径观测值相加,则有
| ${S_1} + {S_3} = {S_2} + {S_4} = 2{A_i}\left( {{\varepsilon _1} + {\varepsilon _2}} \right)$ | (2) |
式中,(ε1 + ε2)为主应变之和,即面应变。对钻孔观测数据采用式(2) 进行自检,得到2条变化形态基本一致的面应变值观测数据曲线,以此检验四分量钻孔应变观测值的真实性和可靠性。
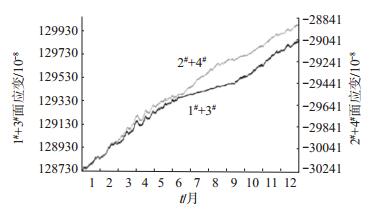
图 3为2015年巴南钻孔应变观测资料(1# + 3#)和(2# + 4#)元件的面应变自检观测数据对比曲线。将2015年数据按6—9月异常时段、1—5月异常出现前时段及10—12月异常数据恢复时段划分,分别对3个时段的面应变数据做相关系数分析,结果显示:① 在异常出现前后时段,(1# + 3#)和(2# + 4#)元件的面应变自检曲线变化幅度和趋势形态均比较一致,异常出现前的1—5月相关系数为0.94,异常恢复后的10—12月为0.92,可见2组数据相关性较好,观测资料真实可靠,监测系统工作正常;② 在6—9月异常时段内,面应变自检曲线相关性差,相关系数为0.36,(1# + 3#)元件观测曲线趋势向下压缩,(2# + 4#)元件观测曲线快速向上拉张,2条曲线相互交叉,可见该时段钻孔观测数据不太真实可靠(图 3)。
|
图 3 2015年巴南台钻孔面应变曲线 Fig.3 Curves of area strain of borehole strain at Banan Seismic Station |
(2) 固体潮汐与元件标定格值对比分析。本文以巴南钻孔应变观测曲线朔望时期的固体潮汐幅度为例,对6月14日异常前后4个元件观测数据的大潮幅度进行对比分析,结果显示:在异常变化期间1#、2#、3#元件潮汐幅度明显减小,每月朔望期间大潮潮汐幅度约为6月初数据正常时段的1/3—1/2;4#元件在异常时段固体潮汐幅度增大,约为正常时段的1.4倍(图 4)。

|
图 4 2015年6月巴南台钻孔应变固体潮汐幅度 Fig.4 Solid tidal amplitude of borehole strain at Banan Seismic Station in June, 2015 |
查看维护日志可知,此次异常时段发生在6月14日钻孔应变数采更换之后,故现场再次对钻孔元件的格值标定数据(以下简称格值)进行核查,发现巴南钻孔应变仪现场标定格值与数据库录入格值差别较大。其中:1#—3#元件现场标定格值变为数据库录入格值的30%—45%,4#元件现场标定格值变为入库格值的1.27倍。1#—4#元件格值变化幅度与上述固体潮汐变化幅度相似,详细数据见表 1。分析认为,2015年6月14日至9月15日巴南钻孔应变出现趋势变化的可能原因是,格值参数设置错误,造成数据潮汐幅度改变,从而改变观测数据线性趋势形态。
| 表 1 钻孔元件标定格值与固体潮汐比值 Tab.1 The ratio of calibration and solid tide of strain component |
通常RZB-2分量式钻孔应变观测数据与仪器格值等参数可简易表示为
| $D = \frac{F}{g} \times K + d$ | (3) |
式中,D为观测数据,F为应变测量值,g为标定格值,K为系统灵敏度参数,d为系统参数断点值。
由式(3) 可知,仪器观测输出数据与格值有关,当格值变大时,实际数据幅度变小,反之数据变大。异常时段观测数据Dy和校正后观测数据Dx可以表示为
| ${D_y} = \frac{F}{{{g_y}}} \times K + {d_y}$ | (4) |
| ${D_x} = \frac{F}{{{g_x}}} \times K + {d_x}$ | (5) |
其中,Dy、gy和dy为异常时段观测数据、格值和系统参数断点值,Dx、gx和dx为校正后观测数据、格值和系统参数断点值,F、K为同一时段应变测量值和系统参数,联合式(4)、式(5),得到校正后观测数据
| ${D_x} = \frac{{{g_y}}}{{{g_x}}}{D_y} + \left( {{d_x} - \frac{{{g_y}}}{{{g_x}}}{d_y}} \right)$ | (6) |
式中,gx、gy、dx、dy均为常数,即(dx-gydy/gx)可以看作常数C,则式(6) 可以简化为
| ${D_x} = \frac{{{g_y}}}{{{g_x}}}{D_y} + C$ | (7) |
将异常时段gy和校正后gx的格值代入式(7),即可以排除格值干扰,得到巴南地震台钻孔应变校正恢复后的观测数据。
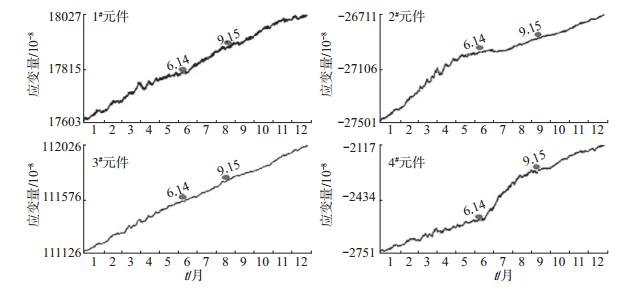
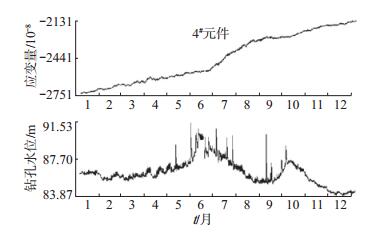
4 校正恢复数据分析根据上述格值干扰的物理机制分析,对巴南钻孔应变1#—4#元件观测数据进行格值校正,得到2015年校正后钻孔应变观测数据,见图 5。由图 5可见,6月14日至9月15日异常时段1#—3#元件观测数据恢复较好,3个元件的观测数据线性变化速率也基本恢复到异常变化异常前后的线性变化速率。4#元件观测数据恢复不太理想,仍持续加速拉张变化。分析认为,4#元件可能受当地钻孔井水位变化影响较大,在6—9月,钻孔水位快速下降,观测数据显示加速上升的同步响应(图 6)。
|
图 5 2015年巴南钻孔应变月观测格值校正曲线 Fig.5 Monthly curves of Banan borehole strain record after calibration correction in 2015 |
|
图 6 巴南台钻孔应变与水位对比 Fig.6 The comparison between borehole strain and water level at Banan Seismic Station |
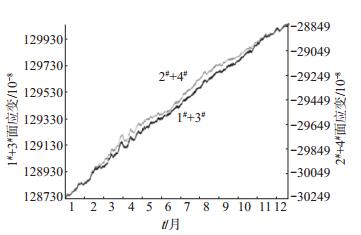
校正后的1#、3#元件应变值之和与2#、4#元件应变值之和的面应变自检分析曲线见图 7,可见:异常时段数据经校正后,观测曲线的线性趋势形态基本一致,相关系数达0.89(4#元件观测数据可能对相关性有一定影响),接近异常前后时段计算的面应变相关系数值;经校正后(1#+ 3#)和(2# + 4#)元件面应变量变化幅度基本一致,前者为1.41×10-6,后者为1.40×10-6。结果显示,异常时段观测数据经校正后真实可靠,错误格值经校正,数据曲线恢复正常变化形态(图 7)。
|
图 7 2015年巴南钻孔台面应变曲线 Fig.7 Curves of area strain of Banan borehole strain station after calibration correction |
(1) 本文以巴南台钻孔应变某一时段观测资料异常变化为例,指出观测仪器标定的格值是影响应变观测数据的重要参数,与固体潮汐变化幅度成反比例关系。格值变化也可能是改变钻孔应变曲线趋势形态的一种因素。即格值增大时,潮汐幅度变小,导致观测曲线形态压缩,抑制上升的线性趋势,出现上升变缓的趋势异常变化,如1#—3#元件。反之,格值设置变小,固体潮汐幅度变大,曲线出现形态拉张加速变化,如4#元件。
(2) 从巴南地震台钻孔格值与观测数据之间的物理机制入手,经格值校正后的曲线速率也基本恢复到非异常时段曲线速率,对面应变自检验证,认为恢复的数据较为真实可靠,达到较为理想的效果,可为钻孔应变异常干扰识别工作提供参考。
| 陈运泰. 地震预测:回顾与展望[J]. 中国科学D辑(地球科学), 2009, 39(12): 1633-1658. | |
| 丁仁杰, 李克昌. 重庆地震研究暨重庆1:50万地震构造图[M]. 北京: 地震出版社, 2004: 43. | |
| 邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122. | |
| 王梅, 李峰, 孔向阳, 等. 数字化形变观测干扰识别[J]. 大地测量与地球动力学, 2004, 24(1): 94-98. | |
| 王小平, 尹京苑, 陈军, 等. 上海形变固体潮资料干扰因素分析[J]. 大地测量与地球动力学, 2010, 30(Z2): 18-21. | |
| 王勇, 杨选辉, 刘福生, 等. 昌平台钻孔应变观测资料的可靠性研究[J]. 中国地震, 2005, 21(2): 291-294. |
 2017, Vol. 38
2017, Vol. 38
