2. 中国呼和浩特 010010 内蒙古自治区地震局
2. Earthquake Agency of Inner Mongolia Autonomous Region, Hohhot 010010, China
由于观测环境、气象、仪器、区域应力、地下介质和外空间等因素叠加影响,地震前兆观测数据曲线通常是1条由多种变化形态叠加在一起的复杂曲线,例如:多数地电阻率(简称地电)数据曲线具有长期变化、年变和脉冲等,地磁数据曲线具有典型的年变和日变形态等,形变数据曲线具有潮汐和长期零漂等(中国地震局监测预报司, 2008, 2010;戴勇等,2012;杨彦明等,2013)。从频率域角度来说,地震前兆数据信号包含多个谐波分量,对不同谐波分量频率等进行确定和分析,是地震前兆数据处理的核心环节。近年来数字信号处理技术日趋成熟,在地震前兆数据处理中的应用愈加广泛。当前地震前兆数据处理常用且理论较为成熟的方法主要有傅里叶变换方法(何友等,2010;司祯祯,2011;戴勇等,2012)和小波变换方法(衡彤,2003;郭彤颖等,2004;杨从杰等,2005;司祯祯,2011;戴勇等,2013)。其中傅里叶变换是纯频域分析方法,无法提供时域信息,且无法处理非平稳非线性信号;小波分析虽在时频两域具有表征信号局部特征的能力和多分辨率分析的特点,但小波基选取时的多样性和不可变更性限制了小波变换的适应能力,且小波基的有限长会造成信号的能量泄漏(刘庆敏等,2009)。考虑到上述2种变换在地震前兆数据处理中存在的弊端,尝试采用希尔伯特—黄变换方法处理地电阻率观测数据。
1 方法原理希尔伯特—黄变换(Hilbert-Huang Transform,简称HHT)方法是美国工程院院士Norden Huang等提出的一种全新的信号分析方法(Huang N E et al,1998, 2003;刘庆敏等,2009;王黎黎,2009;贾春花,2013)。希尔伯特—黄变换由经验模态分解(Empirical Mode Decomposition,简称EMD)和希尔伯特谱分析(Hilbert Spectrum Analysis,简称HAS)组成。
1.1 EMD分解过程经验模态分解是对信号进行非线性的自适应分解,得到不同固有模态函数(Intrinsic Mode Function,简称IMF),是希尔伯特—黄变换核心部分。为保证IMF是单分量函数,必须满足下列条件:① 极值点数和零交叉点数相同或最多相差一个;② 固有模态函数在任意点,由局部极值定义的包络的均值是零。
第2个条件很难满足,一般取近似。在此用Huang(2000)提出的近似条件,设(standard deviation)是连续2个分解结果的标准偏差,于是
| ${\rm{SD = }}\sum\limits_{t = 0}^T {\frac{{{{\left| {{h_{k - 1}}\left( t \right) - {h_k}\left( t \right)} \right|}^2}}}{{h_{k - 1}^2\left( t \right)}}} \le {\rm{constant}}$ | (1) |
其中,hk-1(t)、hk(t)分别表示第k次分解前后的信号;constant∈[0.2,0.3]。
EMD分解基本过程:对于任意给定信号x(t),将极大值点和极小值点分别用2条曲线拟合,使2条曲线间包含所有信号数据,从而得到x(t)的上下2条包络线。m(t)记作包络线的平均值,令h(t) = x(t)-m(t),则h(t)为一个近似的IMF。将h(t)作为新的x(t),重复以上操作,直到满足IMF的条件时,得到第1阶IMF分量,记作c1(t),即c1(t) = h(t),令r(t) = x(t) -c1(t),将r(t)作为新的x(t),重复以上步骤可依次得到第2阶IMF分量c2(t),第3阶IMF分量c3(t),…,最终得到分解式
| $x\left( t \right) = \sum\limits_{k = 1}^n {{c_k}\left( t \right) + r\left( t \right)} $ | (2) |
式中r(t)称为残余函数。
1.2 Hilbert变换对式(2) 中每个固有模态函数ck(t)作Hilbert变换,得
| $\overline {{c_k}} \left( t \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\int_{ - \infty }^\infty {\frac{{{c_k}\left( \tau \right)}}{{t - \tau }}} {\rm{d}}\tau $ | (3) |
构造解析信号
| ${Z_k}\left( t \right) = {c_k}\left( t \right) + j\overline {ck} \left( t \right) = {a_k}\left( t \right){{\rm{e}}^{j{\phi _k}t}}$ | (4) |
得到幅值函数
| ${a_k}\left( t \right) = \sqrt {c_k^2\left( t \right) + \overline {c_k^2} \left( t \right)} $ | (5) |
瞬时相位
| ${\phi _k}\left( t \right) = \arctan \frac{{\overline {{c_k}} \left( t \right)}}{{{c_k}\left( t \right)}}$ | (6) |
进一步可求出瞬时频率
| ${w_k}\left( t \right) = \frac{{{\rm{d}}{\phi _k}\left( t \right)}}{{{\rm{d}}t}}$ | (7) |
则信号可表示成
| $x\left( t \right) = {\mathop{\rm Re}\nolimits} \sum\limits_{k = 1}^n {{a_k}\left( t \right){{\rm{e}}^{j{\phi _k}t}}} = {\mathop{\rm Re}\nolimits} \sum\limits_{j = 1}^n {{a_k}\left( t \right){{\rm{e}}^{j\int {{w_k}\left( t \right){\rm{d}}t} }}} $ | (8) |
此处省略残量,Re表示取实部。由此可以绘制瞬时幅度、瞬时频率与时间的三维谱图,记作Hilbert谱H(t,ω)。
2 地电阻率数据分析选取具有典型性和代表性的大同地震台(以下简称大同台)、宝昌地震台(以下简称宝昌台)地电阻率月值数据和宝昌台地电阻率整点值数据进行希尔伯特—黄变换,观测数据变换前进行去突跳、去台阶和缺数等必要预处理。
2.1 大同台地电阻率数据分析大同台位于大同上皇庄村东北,自1982年开始地电阻率观测(山西省地震局,2006)。选取该台地电阻率EW、NW测道1994年1月至2012年10月月值数据作为研究对象,进行希尔伯特—黄变换,主要结果见图 1。
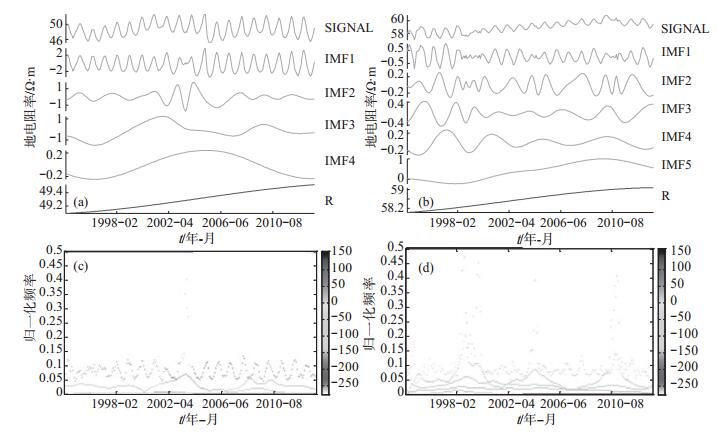
|
图 1 大同台地电阻率希尔伯特—黄变换结果 (a) EW测道EMD分解结果;(b) NW测道EMD分解结果;(c) EW测道Hilbert谱;(d) NW测道Hilbert谱 Fig.1 Hilbert -Huang transform results of earth resistivity recorded by Datong Seismic Station |
(1) 模态分析。图 1(a)和图 1(b)分别显示EW和NW测道经过EMD分解得到的结果,比较发现,二者趋势项R能量占各自信号总能量比例均超过90%,且显示出显著趋势上升的长期变化特征。二者之间也存在显著区别,EW测道分解结果为4个模态和1个趋势项,而NW测道则被分解为6个模态和1个趋势项。这是因为,NW测道的地电阻率变化形态相对于EW测道复杂,说明采用希尔伯特—黄变换方法进行EMD分解时获得的模态个数并不确定,不同测道数据曲线形态复杂度不同,其EMD分解结果不同,对于同一测道随着数据长度的变化EMD分解的结果也可能不同。但不论分解模态个数如何不同,主要模态分量或趋势项能准确反映原信号中的主要分量特征。
大同台地电阻率NW测道IMF1模态曲线(图 2)显示了周期为1年的谐波分量变化。由图 2可见,在1998—2000年、2004年、2010—2012年3个时期,地电阻率年变形态畸变,其他时段年变特征明显。查阅年变畸变阶段的观测记录,发现1999年1月更换观测仪器(开始使用ZD8A型地电仪)、2004年1月更换观测仪器(开始使用ZD8B数字地电阻率仪器),2次仪器更换与年变畸变时间吻合。分析认为,第3次年变畸变与“九五”“十五”的数据衔接在时间上吻合。
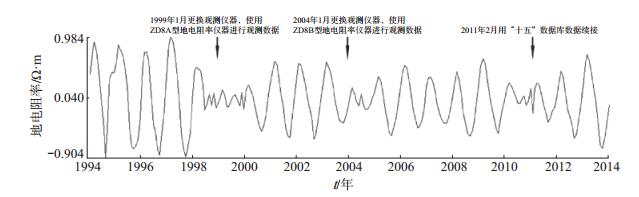
|
图 2 大同台地电阻率NW测道经验模态IMF1曲线 Fig.2 Empirical mode IMF1 curve of earth resistivity in NW-direction recorded by Datong Seismic Station |
(2) Hilbert谱分析。图 1(c)和图 1(d)分别显示大同台地电阻率EW和NW测道Hilbert谱,其中EW测道希尔伯特谱中高值分布集中,在归一化频率0.05—0.15区间内呈现类似余弦形态的变化规律;NW测道Hilbert谱中高值分布较为离散,在归一化频率0.05—0.15区间也呈现“余弦”变化形态,但规律性特征不如EW测道Hilbert谱明显。另外,在NW测道原始曲线不同变化形态过渡时段内,对应的Hilbert谱高幅值离散度大。
2.2 宝昌台地电阻率数据分析宝昌台位于内蒙古太仆寺旗,地貌为低山丘陵地带,覆盖层较浅。该台地电阻率自1980年投入观测(内蒙古自治区地震局,2006),对发生于晋冀蒙交界地区的地震,震前有不同程度的异常反应(高立新等,1999;戴勇等, 2009, 2013;徐锡泉等,2014)。选取宝昌台地电阻率NS测道1994年1月至2012年10月月值数据以及2013年3月整点值数据作为研究对象,进行希尔伯特—黄变换(图 3,图 4)。
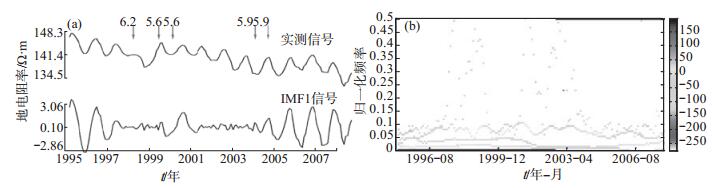
|
图 3 宝昌台地电阻率NS测道月值曲线及Hilbert谱 (a)月值曲线;(b) Hilbert谱 Fig.3 Monthly mean curves and Hilbert spectrum of earth resistivity in NS-direction recorded by Baochang Seismic Station |
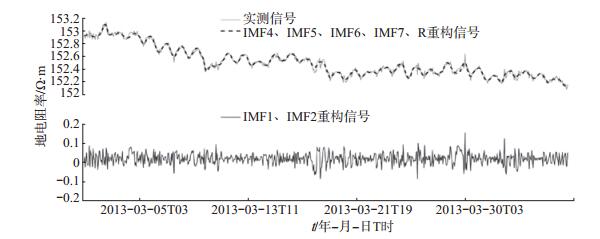
|
图 4 宝昌台地电阻率EW测道整点值数据曲线 Fig.4 Hourly value curves of earth resistivity in EW-direction recorded by Baochang Seismic Station |
月均值数据希尔伯特—黄变换分析。图 3显示宝昌台地电阻率NS测道月值曲线,以及经EMD分解后的IMF1分量曲线。1993—2007年宝昌台460 km范围内累计发生5次5.5级以上地震,在上述地震发生前或期间,该台地电阻率IMF1分量曲线出现的异常变化比同期原始曲线更加明显,见图 3(a)。图 3(b)为宝昌台地电阻率NS测道Hilbert谱,谱中高值由于噪声影响出现一定离散分布,但在归一化频率为0.05—0.15区间内仍呈现明显的“余弦”变化形态。由上述分析可知,采用希尔伯特—黄变换处理地电阻率月值数据,可以获得分辨率较好的频谱结果,同时有效提取地电阻率异常变化信息。
2.2.2整点值数据希尔伯特—黄变换分析。应用希尔伯特—黄变换,处理2013年3月宝昌台地电阻率NS测道整点值观测数据(采样率较高)。经EMD处理后,宝昌台地电阻率NS测道整点值曲线被分解为7个经验模态和1个趋势项。其中,IMF1和IMF2模态重构后获得的信号能够较好反映宝昌台地电阻率高频特征;IMF4、IMF5、IMF6、IMF7模态和趋势项重构后获得的信号,能清晰、客观地反映宝昌台地电存在显著日变形态,且重构信号并未使原始曲线形态失真,见图 4。地电阻率整点值数据重构结果客观说明:通过希尔伯特—黄变换的分解和重构,可实现提取高频和去除噪声的目的,在“去噪”方面具有高效和低失真的优点;宝昌台地电阻率具有规则的日变形态,戴勇等(2013)曾给出其产生原因,在此不再赘述。
3 结论与讨论(1) 希尔伯特—黄变换是继傅里叶变换和小波变换之后出现的第3种主要变换,其在谱分析时具有很好的应用效果。本文采用希尔伯特—黄变换相继对具有典型特征的大同台、宝昌台地电阻率数据进行处理,结果显示希尔伯特谱具有较高分辨率,能够清晰、精确地反映出谱值在时间、频率二维区域中的分布情况。地电阻率月均值对应的希尔伯特谱中,高幅值在归一化频率0.05—0.15区间内呈现“余弦”的变化形态。
(2) 利用希尔伯特—黄变换可有效挖掘地电阻率数据中丰富有效的信息,能有效提取由干扰或者地震孕育引起的异常变化,对于地电分析具有重要意义。另外,希尔伯特—黄变换在提取地电阻率高频信息以及去除噪声等方面效果较好,在未来地电数据处理中将具有广泛应用前景。
(3) 希尔伯特—黄变换虽具有能分析非线性非稳态信号、自适应强、无需选择窗口和谱分辨率高等众多优点,但也有其不足之处,例如:EMD筛选过程中迭代次数和终止准则的人为设置,造成EMD分解的原始信号中可能包含多余IMF模态分量。因此,今后在获得希尔伯特—黄变换结果时要结合实际情况进行分析,而不能仅就结果本身简单地进行讨论。
(4) 单点突跳等对希尔伯特—黄变换分析结果影响较大,可以说预处理工作进行的好坏直接影响结果的可信度。因此,今后在采用希尔伯特—黄变换方法处理数据前,要对原始数据进行细致、科学地预处理。
(5) 在采用希尔伯特—黄变换分析宝昌台地电阻率整点值数据时,获得所谓意外成果,即发现宝昌台地电阻率整点值曲线具有规则的日变形态。笔者初步统计全国其他台站地电阻率,发现大同、甘孜、新沂、代县、乌加河(新场地)等很多台站地电阻率整点值曲线均具有显著的日变现象,但不同台站间地电阻率日变特征略有不同。对于日变现象特征及产生原因,今后需做深入研究。
| 戴勇, 高立新, 高昌志, 等. 宝昌台地电阻率变化特征[J]. 地震研究, 2013, 36(3): 358-363. | |
| 戴勇, 高立新, 杨彦明, 等. 基于小波变换方法的包头台形变分析[J]. 华南地震, 2013, 33(4): 39-46. | |
| 戴勇, 高立新, 尹战军, 等. 基于快速傅里叶方法的地震前兆振幅谱分析[J]. 地震地磁观测与研究, 2012, 33(2): 51-58. | |
| 戴勇, 闫海滨, 丁风和, 等. 张北6.2级地震宝昌地震台地电异常特征及机制分析[J]. 地震地磁观测与研究, 2009, 30(1): 51-55. | |
| 高立新, 黄根喜, 阎海滨. 张北-尚义6.2级地震(1998-01-10) 前倾斜与地电阻率前兆异常[J]. 地壳形变与地震, 1999, 19(4): 88-90. | |
| 郭彤颖, 吴成东, 曲道奎. 小波变换理论应用进展[J]. 信息与控制, 2004, 33(1): 67-71. | |
| 衡彤. 小波分析及其应用研究[D]. 成都: 四川大学, 2003. | |
| 何友, 宋强, 熊伟. 基于傅里叶变换的航迹对准关联算法[J]. 航空学报, 2010, 31(2): 356-362. | |
| 贾春花. 希尔伯特-黄变换及其在信号处理中的应用研究[J]. 电力学报, 2013, 28(2): 148-151. | |
| 刘庆敏, 杨午阳, 李书平, 等. 希尔伯特-黄变换在地震资料处理中的应用[J]. 西北地震学报, 2009, 31(3): 211-216. | |
| 内蒙古自治区地震局. 内蒙古自治区地震监测志[M]. 呼和浩特: 内蒙古人民出版出版社, 2006. | |
| 山西省地震局. 山西省地震监测志[M]. 北京: 地震出版社, 2006. | |
| 司祯祯. 傅里叶变换与小波变换在信号去噪中的应用[J]. 电子设计工程, 2011, 19(4): 155-157. | |
| 王黎黎. 基于希尔伯特-黄变换的时频分析算法研究[D]. 西安电子科技大学, 2009. http://d.wanfangdata.com.cn/Thesis/Y1485577 | |
| 徐锡泉, 高昌志, 王亮. 内蒙古宝昌台地电阻率长期观测数据研究[J]. 地震工程学报, 2014, 36(2): 405-412. | |
| 杨从杰, 冯志生, 宋德伟, 等. 小波分析方法在提取井水位潮汐因子震前变化特征的初步应用[J]. 西北地震学报, 2005, 27(2): 163-167. | |
| 杨彦明, 张文韬, 张帆, 等. 内蒙古地震监测台网的建设与发展[J]. 高原地震, 2013, 25(2): 22-25. | |
| 中国地震局监测预报司. 地震电磁学理论基础与观测技术(使用本)[M]. 北京: 地震出版社, 2010. | |
| 中国地震局监测预报司. 地形变测量(使用本)[M]. 北京: 地震出版社, 2008. | |
| Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995. | |
| Huang N E, Wu M L C, Long S R. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2003, 459(2 037): 2317-2345. | |
| Potter R K, Kopp G, Green H C. Visible speech[M]. New York: Van Nostrand, 1947. |
 2017, Vol. 38
2017, Vol. 38

