2. 中国河北 056001 邯郸地震中心台;
3. 中国石家庄 050224 黄壁庄地震台
2. Handan Central Seismic Station, Hebei Province 056001, China;
3. Huangbizhuang Seismic Station, Shijiazhuang 050224, China
河北省永年地震台 (以下简称永年台) 建于1970年,地处太行山东麓山前丘陵地带,东邻太行山山前断裂,北依永年断裂,台基条件好,基底深,岩体完整且分布面积大。洞体岩性为燕山期火成岩,基墩用钢筋水泥浇筑而成,基墩及支撑墩周围均设有隔震槽 (马栋等,2014)。洞室密封效果较好,内装6道密封门,其中3道为船舱水密门,墙面做防潮处理,仪器本体用2层5 cm厚的聚乙烯泡沫板密封包装。2007年该台开始进行数字化形变观测,配备数字化DSQ水管倾斜仪和SSY-Ⅱ型伸缩仪,观测资料稳定可靠。2015年5月11日起,永年台伸缩仪EW分量出现加速拉张变化,截至6月23日,变化幅度约5.522×10-7,张性变化速率明显大于往年。虽然该测项年变形态与往年大致相同,但整体趋势转呈张性变化。因2014年2月8日永年地震台水管仪EW分量开始加速W倾,并确定为异常测项,在此基础上出现的伸缩仪异常现象需要密切关注。因此,需对该测项仪器工作状态、周围环境变化等开展详细调查研究工作,才能对此次异常变化性质做出准确可靠的判断。
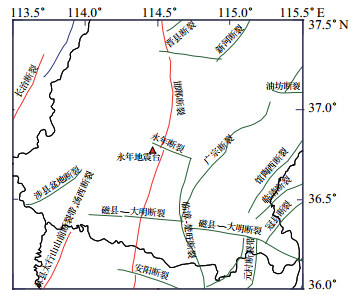
1 伸缩仪EW分量异常特征永年台位于邯郸市永年县永合会大队村西南,距县城6 km,台站周围地质构造复杂 (图 1),数字化形变观测数据自2007年起连续可靠。
|
图 1 永年地震台附近地质构造 Fig.1 The geological structure around Yongnian Seismic Station |
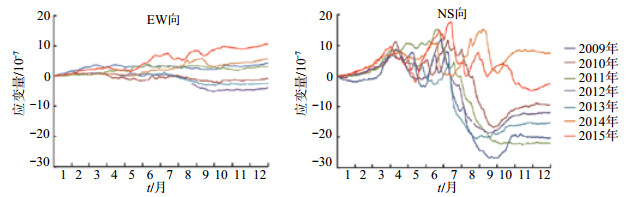
永年台伸缩仪EW分量2015年5月11日起出现张性变化 (图 2),年变形态与往年基本一致,但变化速率较快,变化幅度约5.522×10-7,加速张性变化明显。伸缩仪NS分量同期存在上升变化,与往年相比形态一致、速率略快,异常变化幅度没有EW分量明显 (图 3)。

|
图 2 永年伸缩仪2015年1-6月观测曲线 Fig.2 Extensometer observation curve at Yongnian Seismic Station from Jan. to June, 2015 |
|
图 3 永年伸缩仪2009-2015年EW、NS向年变对比 Fig.3 The change shape contrast chart of NS and EW components of the extensometer at Yongnian Seismic Station |
计算2009年-2015年永年台伸缩仪EW分量日均值变化速率,统计结果见表 1,结果显示:2009-2014年,每年5月1日至6月23日的EW分量平均变化速率6.079×10-9,最大变化速率为9.982×10-9;2015年5月1日至6月23日变化速率达2.4148×10-8,为往年平均变化速率4倍,最大变化速率2.4倍。将2009-2015年伸缩仪观测数据进行年变形态对比,可以直观发现,2015年5-6月伸缩仪观测数据变化速率明显高于往年同期水平 (图 3)。
| 表 1 伸缩仪EW分量变化速率统计 (单位10-10/d) Tab.1 Statistical table of change rate of EW component of the extensometer |
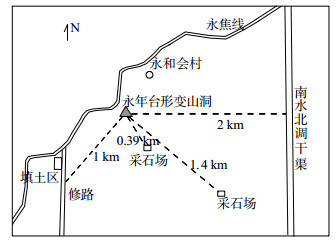
2015年5-6月永年台伸缩仪EW分量出现异常,可能与仪器工作状态、洞室环境、气象条件、外界环境干扰有关,由此认真开展异常排查核实工作。经现场核实,发现:① 2015年最近1次伸缩仪标定记录中格值变化范围符合形变前兆观测规范,仪器工作状态稳定;② 仪器观测室及仪器观测墩较干燥,无积水现象,仪器供电系统和数据采集系统工作正常;③ 2010年以来辅助洞温、气温、气压、降雨量观测数据均正常动态变化;④ 形变山洞周围存在采石场、南水北调干渠、山顶土地平整、修路工程等环境干扰源 (图 4)。
|
图 4 永年台形变山洞周围环境 Fig.4 Environment around deformation mountain cave at Yongnian Seismic Station |
基于以上核实结果,排除仪器自身、洞室环境及气象等因素对永年台伸缩仪观测数据的影响。对EW分量异常时段内形变观测数据进行时间相关性分析,发现修路工程与异常出现时间一致,需要进一步分析。
2.2 道路施工影响伸缩仪是高精度形变观测仪器,在观测点周围有效距离内,大型工程建设造成的荷载变化会对伸缩仪观测产生一定影响 (王梅等,2004;马栋等,2015)。环境调查发现,距山洞西南方向约1 km新修一条柏油公路,道路跨过一个长约200 m的大坑,以砂石填坑铺路,并用石头加固道路两边,土方量比较大。此工程施工时间集中在2015年5月初到6月,6月下旬完工,与伸缩仪EW分量异常时段基本吻合。
2.2.1 荷载变化新修道路长约2 100 m,宽约10 m,厚度约0.5 m;路上坑洞长约200 m,宽约20 m,深约20 m。2015年5-6月的修路工程土方量较大,造成的荷载影响比较明显,采用3个荷载模型,分别计算土石方荷载对永年伸缩仪EW向可能造成的应变变化量。
(1) 地表集中荷载模型。根据半无限空间均布荷载模型 (骆鸣津等,2008),利用圆柱坐标调和函数推导的地面负荷,建立面应力应变影响的理论模型,即
| $ {e_{rr}}(r,z) = \frac{P}{{4\pi \mu }}\left[ {\frac{{\lambda + 2\mu }}{{\lambda + \mu }}\frac{z}{{{{({r^2} + {z^2})}^{\frac{2}{3}}}}} - \frac{{3{z^2}}}{{{{({r^2} + {z^2})}^{\frac{5}{2}}}}}} \right] + \frac{P}{{4\pi \mu {r^2}}}\left[ { - \frac{\mu }{{\lambda + \mu }} + \frac{{\lambda + 2\mu }}{{\lambda + \mu }}\frac{z}{{{{({r^2} + {z^2})}^{\frac{1}{2}}}}} - \frac{{{z^3}}}{{{{({r^2} + {z^2})}^{\frac{3}{2}}}}}} \right] $ | (1) |
| $ {e_{zz}}(r,z) = \frac{P}{{4\pi \mu }}\frac{\mu }{{\mu (\lambda + \mu )}}\frac{z}{{{{({r^2} + {z^2})}^{\frac{3}{2}}}}} + \frac{P}{{4\pi \mu }}\frac{{3{z^2}}}{{{{({r^2} + {z^2})}^{\frac{5}{2}}}}} $ | (2) |
| $ {e_{\theta \theta }}(r, z) = \frac{P}{{4{\rm{\pi (}}\lambda + \mu {\rm{)}}}}\frac{1}{{{r^2}}} - \frac{P}{{4{\rm{\pi }}}}\frac{{\lambda + 2\mu }}{{\mu (\lambda + \mu)}}\frac{z}{{{r^2}}}\frac{1}{{{{({r^2} + {z^2})}^{\frac{1}{2}}}}} + \frac{P}{{4{\rm{\pi }}\mu }}\frac{{{z^3}}}{{{r^2}}}\frac{1}{{{{({r^2} + {z^2})}^{\frac{3}{2}}}}} $ | (3) |
式中,P为道路施工所用土石的重力;r为道路施工位置与永年伸缩仪仪器位置的水平距离;z为山洞垂直高差;拉梅常数λ = νE / [(1 + ν)(1-2ν)];剪切模量μ = E / [2(1 + ν)],其中E为岩石弹性模量,ν为岩石泊松系数。根据体应变与面应变的关系 (蒋骏,1994),荷载对钻孔体应变的影响为:b = 2/3[err(r, z)+ eθθ (r, z)]。
此次道路施工所用土石的重力P = (2100×10×0.5+200×20×20)×2.65×103×9.8(土密度取2.65×103 kg/m3)= 2.35×109 N,r约为1 000 m,z约为10 m,正长岩弹性模量E = 5×1010 Pa,泊松比ν = 0.25。带入上述模型,得到道路修建阶段荷载引起的应变量为b =1.43×10-10。
(2) 三维集中载荷模型 (邱泽华等,2004),即三维无限半空间边界上作用集中载荷的模型,忽略荷载变化的形状和面积,只重视荷载所受的重力变化。具体公式为
| $ u = \frac{{Fxy}}{{4{\rm{\pi }}G{R^3}}} - \frac{{Fx}}{{4{\rm{\pi }}(G + \lambda)R(R + Z)}} $ |
式中:u为x水平方向的位移,F为荷载变化的重力,λ和G为拉梅常数,道路施工位置与永年伸缩仪仪器位置的距离
导出水平方向应变
| $ \begin{array}{l} {e_x} = + \frac{{F{x^2}}}{{4{\rm{\pi }}({x^2} + {y^2} + {z^2}){{(z + \sqrt {{x^2} + {y^2} + {z^2}})}^2}(G + \lambda)}} - \frac{{3F{x^2}z}}{{4G{\rm{\pi }}{{({x^2} + {y^2} + {z^2})}^{5/2}}}} + \\ \;\;\;\;\;\;\;\;\;\frac{{Fz}}{{4G{\rm{\pi }}{{({x^2} + {y^2} + {z^2})}^{3/2}}}} + \frac{{F{x^2}}}{{4{\rm{\pi }}{{({x^2} + {y^2} + {z^2})}^{3/2}}{{(z + \sqrt {{x^2} + {y^2} + {z^2}})}^2}(G + \lambda)}} - \\ \;\;\;\;\;\;\;\;\;\frac{F}{{4{\rm{\pi }}{{({x^2} + {y^2} + {z^2})}^{1/2}}{{(z + \sqrt {{x^2} + {y^2} + {z^2}})}^2}(G + \lambda)}} \end{array} $ |
取y = 0,G = E / [2(1 + ν)],λ = νE / [(1 + ν)(1-2ν)],E = 5.0×1010 Pa,ν =0.25,F=2.35×109 N,R =1 000 m,其他参数与地表集中荷载模型参数一致,使用三维集中载荷模型计算,得到道路修建阶段荷载引起的应变量为ex=4.48×10-10。
(3) 三维有限线段载荷模型 (邱泽华等,2004)。利用集中载荷公式,在长为2a的线段上对所有点的影响进行积分,总应变为
| $ \begin{array}{l} {e_x} = - \frac{{3F{x^2}z}}{{4G{\rm{\pi }}{A^{5/2}}}} + \frac{{Fz}}{{4G{{\rm{\pi }}^{3/2}}}} + \frac{{F{x^2}}}{{4{\rm{\pi }}A{{(z + \sqrt A)}^2}(G + \lambda)}} + \frac{{F{x^2}}}{{4{\rm{\pi }}{A^{3/2}}(z + \sqrt A)(G + \lambda)}} - \\ \;\;\;\;\;\;\frac{F}{{4{\rm{\pi }}\sqrt A (z + \sqrt A)(G + \lambda)}} \end{array} $ |
式中:单位长度荷载所受的重力F=总荷载的重力/道路长度=2.35×109 N/2100 m,系数A = x2 + (y-y0)2 + z2。取道路的中点为原点,y=0,道路施工位置与永年伸缩仪仪器位置的水平距离x = 1 000 m,高差z =10 m,λ和G为拉梅常数。
使用三维有限线段载荷模型计算修路荷载应变量,所用其他参数与地表集中荷载模型一致,得到道路修建阶段荷载引起的应变量为2.08×10-9。
2.2.2 影响排除使用上述3个荷载模型计算得到道路施工的应变影响量分别为1.43×10-10、4.48×10-10、2.08×10-9。从应变影响量数值而言,3个模型计算结果虽有所不同,但量级在10-9-10-10,与永年伸缩仪EW向观测数据异常变化量5.522×10-7差距较大。即使考虑到模型的适用范围和模型自身误差、计算参数误差、仪器灵敏度及年变形态的差异性,理论值和实际变化值的量级差距仍较大,由此可以认为,道路施工荷载对伸缩仪EW向影响不大。
3 异常分析通过现场排查与核实,可以认为,永年台伸缩仪EW向观测数据异常与以上干扰因素无关,可能是永年地区地壳应力变化所致。
3.1 对比分析永年台配备伸缩仪和水管仪进行形变观测,在此对2种形变观测数据进行对比分析,以揭示伸缩仪EW向数据异常原因。选取永年台2008年1月-2015年10月形变观测数据,绘制时间序列图,见图 5,可见水管仪和伸缩仪观测曲线陆续出现趋势转折。统计2种测量曲线出现转折的时间,见表 2,可知,水管仪NS向2012年8月开始出现转折N倾的趋势变化,水管仪EW向、伸缩仪NS向和EW向2013年7-9月陆续出现折转,时间接近;从趋势变化性质看,永年测点形变测项伸缩仪呈EW向张性、NS向微张性变化,水管仪向NW方向倾斜。由图 5和表 2可见,永年台形变观测4个测项2012-2013年陆续出现转折,说明永年地区地壳应力变化是真实存在的,可靠性比较大。

|
图 5 永年台伸缩仪和水管仪观测曲线 (a) 永年伸缩仪观测曲线;(b) 永年水管仪观测曲线 Fig.5 Observation curves of extensometer and water tube tiltmeter at Yongnian Seismic Station |
| 表 2 永年伸缩仪和水管仪趋势转折统计 Tab.2 Trend turning statistics of extensometer and water tube tiltmeter at Yongnian |
通过将永年台伸缩仪和水管仪的观测数据进行对比分析,可以发现,2种观测手段在NS向、EW向先后出现趋势转折,且时间接近。这种趋势转折的同步性和成组特征说明,永年地区应力场调整使该区地壳运动出现新的趋势变化,即永年台测点附近地区转为张性变化,且向NW方向倾斜。永年伸缩仪EW向从2013年9月以来处于张性趋势变化阶段,此年尺度的张性变化已经形成EW向趋势变化的背景,而2015年5-6月出现的短期变化和该背景变化趋势一致,均为张性变化,在某种程度上说明,2015年5-6月应为此张性背景下的一个阶段。由此可知,2015年5-6月伸缩仪EW向快速张性变化可能是永年地区应力场调整结果。
4 结论通过对永年台伸缩仪观测系统、洞室环境、气象条件、周围环境变化情况等调查,对各种可能的影响因素进行一一排查,与伸缩仪EW分量异常时段内观测数据进行时间相关性分析,发现道路施工与异常出现时间一致。利用地表集中荷载模型、三维集中载荷模型和三维有限线段载荷模型,对路修建阶段荷载引起的应变量进行计算,发现应变量量级在10-9-10-10,与永年伸缩仪EW向观测数据异常变化量5.522×10-7差距较大,排除道路施工对伸缩仪EW向的影响。由此对永年台对比分析永年台伸缩仪和水管仪观测数据,发现二者在2012-2013年即出现近似同步的趋势转折变化。分析认为,永年台附近区域应力场进行调整,伸缩仪EW向在2013年起即具有张性变化背景,2015年5-6月出现的短期变化应为永年地区应力场调整的结果。对永年台周围环境变化需作进一步调查核实,以排除其他可能干扰因素,密切跟踪永年甚至河北省南部地区的地壳应力变化。
| 国家地震局科技监测司. 地震地形变观测技术[M]. 北京: 地震出版社, 1995: 423-430. | |
| 蒋骏, 张雁滨. 潮汐线应变组合观测的物理力学实质及其调和分析[J]. 地球物理学报, 1994, 37(Z2): 204-212. | |
| 骆鸣津, 池顺良, 马鸿钧. 地层绝对应力测量与钻孔应变测量[M]. 北京: 地震出版社, 2008: 170-177. | |
| 马栋, 陈建国, 张双凤, 袁国旭, 张冀东. 永年地震台水管加速N倾异常分析[J]. 地震地磁观测与研究, 2014, 35(Z2): 192-197. | |
| 马栋, 屈曼, 侯晓真, 张肖, 陈建国. 载荷对地形变观测干扰的数值模拟研究[J]. 国际地震动态, 2015, 09: 99 DOI:10.3969/j.issn.0253-4975.2015.09.099 | |
| 邱泽华. 倾斜观测载荷干扰源最小安静距离理论分析[J]. 地震, 2004, 24(4): 80-86. | |
| 王梅, 李峰, 孔向阳, 刘厚明. 数字化形变观测干扰识别[J]. 大地测量与地球动力学, 2004, 01: 94-98. |
 2017, Vol. 38
2017, Vol. 38