2. 中国河北 065201 防灾科技学院;
3. 中国北京 100081 中国地震局地球物理研究所;
4. 中国长春 130022 吉林省地震局
2. Institute of Disaster Prevention Science and Technology, Hebei Province 065201, China;
3. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
4. Earthquake Administration of Jilin Province, Changchun 130022, China
强震后地震趋势的快速判定对减轻地震灾害和顺利开展救援工作至关重要,可有效减轻地震灾害损失,有利于震区的社会安定。但是震后趋势的快速判定至今仍是一个没有解决的科学难题,只能根据地震活动性进行预判,对震后救灾提供指导意见。
目前,主要根据地震活动性,如:b值(吴忠良,2001)、h值(包秀敏,2013)、R值(马宏生等,2004)、U值、地震活动图像、地震活动增强和平静、震源机制、地震活动的太阴时特征等,进行震后趋势判定。前述b值、h值等判定方法利用强震发生后震区中小地震活动信息,需要一定时间的地震活动资料积累,一般是震后2—3天或更长时间的资料(陈学忠等,2003)。利用强震自身信息开展震后趋势判定研究,是震后趋势快速判定研究的一个方向(刘红桂等,2007)。
近年来,随着对地震监测投入力度的加大,地震监测数据成倍增长,中国地震台网取得丰富的地震观测数据产品,包括大量地震目录、震相及波形数据(梁珊珊等,2015)。这些数字地震资料成为地震活动性、震源机制、地球内部研究、地震监测及预报等的基本数据源。对大量地震数据进行处理、剔除干扰、基于数据挖掘方法寻找隐藏的知识和规律,可以从中发现许多潜在的、有价值的信息。其中,主震和余震之间的关联关系对于震后余震的快速判断具有一定理论意义和研究价值。
地震历史数据规模庞大,为了能快速挖掘主震和余震关联关系,本文采用基于最小二乘法的线性回归分析方法,在进行数据预处理的基础上,分析主震与最大余震震级之间以及主震视应力与最大余震震级之间的关系,结果表明,主震震级与最大余震震级之间有一定的线性关系,主震视应力和最大余震震级之间除走滑型地震存在一定的线性关系外,其他类型地震并没有什么明显的线性关系,不过视应力与最大余震震级的范围比较集中,为主震后余震的快速判定提供一定参考。
1 计算方法为了得到主震与最大余震之间的相关关系,采用回归分析方法进行分析,线性回归的主要思想是,通过线性方程y = a + bx表征给定的1组数据(xi,yi)的关系,其中(i = 1,2,…,m),关键是求出最佳参数a和参数b,本研究选取较为简单的最小二乘法进行求解,其基本思想是,调节参数使得实际值和计算值的差值平方和φ(a, b)最小,即
| $ \varphi \left({a, b} \right) = \sum\limits_{i = 1}^m {{{\left({a + b{x_i} - {y_i}} \right)}^2}} $ | (1) |
根据微积分极值理论,φ(a, b)达最小时,(a, b)满足以下条件
| $ \left\{ \begin{gathered} \frac{{\partial \varphi \left({a, b} \right)}}{{\partial a}} = 2\sum\limits_{i = 1}^m {\left({a + b{x_i} - {y_i}} \right) = 0} \hfill \\ 2\sum\limits_{i = 1}^m {\left({a + b{x_i} - {y_i}} \right){x_i} = 0} \hfill \\ \end{gathered} \right. $ | (2) |
进行求解,得
| $ a = \frac{{\sum\limits_{i = 1}^m {{y_i}} \sum\limits_{i = 1}^m {x_i^2} - \sum\limits_{i = 1}^m {{x_i}} \sum\limits_{i = 1}^m {{x_i}{y_i}} }}{{m\sum\limits_{i = 1}^m {x_i^2} - {{\left({\sum\limits_{i = 1}^m {{x_i}} } \right)}^2}}} $ | (3) |
| $ b = \frac{{m\sum\limits_{i = 1}^m {{x_i}{y_i}} - \sum\limits_{i = 1}^m {{x_i}} \sum\limits_{i = 1}^m {{y_i}} }}{{m\sum\limits_{i = 1}^m {x_i^2} - {{\left({\sum\limits_{i = 1}^m {{x_i}} } \right)}^2}}} $ | (4) |
将a、b值带入线性方程y=a+bx,即得到回归直线方程。
为了测定变量间的相关程度,需计算相关系数r、判定系数r2及估计标准误差Sxy。
(1)相关系数r。相关系数可以表示2个变量之间的相关程度,计算公式为
| $ r = \frac{{\sum\limits_{i = 1}^m {\left({{x_i} - \bar x} \right)\left({{y_i} - \bar y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^m {{{\left({{x_i} - \bar x} \right)}^2}} \sum\limits_{i = 1}^m {{{\left({{y_i} - \bar y} \right)}^2}} } }} = \frac{{\sum\limits_{i = 1}^m {{x_i}{y_i}} - m\bar x\bar y}}{{\sqrt {\left({\sum\limits_{i = 1}^m {x_i^2} - m{{\bar x}^2}} \right)\left({\sum\limits_{i = 1}^m {y_i^2} - m{{\bar y}^2}} \right)} }} $ | (5) |
如果r为正数,则表示变量x、y正相关,否则为负相关。如果
(2)判定系数r2是一个重要的判定指标,用于判定线性回归直线拟合程度。0≤r2≤1,r2越大说明回归函数拟合效果越好,变量之间的相关系性越强。
(3)估计标准误差Sxy是表征实际值与估计值之间相对偏离程度的指标,计算公式为
| $ {S_{xy}} = \sqrt {\frac{{\sum\limits_{i = 1}^m {{{\left({{y_i} - \bar y} \right)}^2}} }}{{m - 2}}} $ | (6) |
其中
选取美国国家地震信息中心(NEIC)的宽频带辐射能量目录和哈佛矩心矩张量(CMT)目录的地震目录数据,从中选择1970年1月1日—2009年9月30日发生在全球范围内5—10级地震信息。数据信息包括地震发生时间(YR, MO, DA, HR MN SEC)、经度(LONG)、纬度(LAT)、震级(MW)、震源深度(DEPTH)、地震能量指数(EX)等,地震目录格式见表 1。
| 表 1 NEIC地震目录格式 Tab.1 Example of earthquake data |
所选地震资料数据量大、时间性较强,且数据干扰多、空缺多、随机性强,具有很多不确定因素,为此开展数据清理工作。
能量是地震数据中的一个重要维度,很多地震实例未曾记录,需完成对地震能量的计算和补充。由已知地震实例的能量、震级,基于最小二乘法解矛盾方程的方法构造线性拟合函数,构造能量方程logE=a×M+b,并利用相关系数、判断系数分析方法和标准误差计算方法,对计算结果进行分析。要得到能量方程,需求得参数a、b。实验中,采用以下算法实现a、b的求解。
循环处理数据库中的每一行数据;
获取地震震级mm;
获取地震能量系数nm;
获取地震能量指数prc
if(mm!=0.0 & & nm!=0.0 & & prc!=0)
求得地震能量y=nm×10prc;
u21=u21+mm;
u22+=mm×mm;
c1=c1+log(y)/log(10);
c2=c2+mm×log(y)/log(10);
m=m+1;
计算参数a=(c1×u21-c2×m)/(u212-m×u22);
计算参数b=(c1×u22-c2×u21)/(m×u22-u212);
计算相关系数r1=a×sqrt(m×u22-u212)/sqrt(m×u22-c12);
计算判断系数r2=(m×b×c1+A×m×c2-c12)/(m×u22-c12);
计算估计标准误差Sxy=sqrt((u22-b×c1-a×c2)/(m-2));
计算a估计量Sa=Sxy/sqrt(u22-u212/m);
由以上算法,得到地震能量方程拟合结果,见表 2,可知:对于逆冲型、正断型、走滑型地震,r > 0.8,r2 > 0.6,且Sxy较小,表明计算结果相对准确。
| 表 2 地震能量方程拟合结果 Tab.2 Result of the energy equation |
根据不同要求对从地震目录数据中提取的地震序列进行分析,寻找主震与最大余震的相关性。
3.1 震级关系由于8—9级地震序列比较少,实验中只对6—7级和7—8级主震进行分析。为了挖掘主震震级和最大余震震级之间的相关关系,构造回归方程MWZ = a×MWY + b,其中MWZ和MWY分别表示主震震级和最大余震震级,基于最小二乘法,求得参数a、b的值以及对线性回归方程的校验信息,见表 3,并给出逆冲型、正断型和走滑型地震6—7级主震与最大余震震级关系图,见图 1。
| 表 3 主震与最大余震震级关系分析结果 Tab.3 The result of relation model between the magnitude of the principal earthquake and of largest aftershock |
|
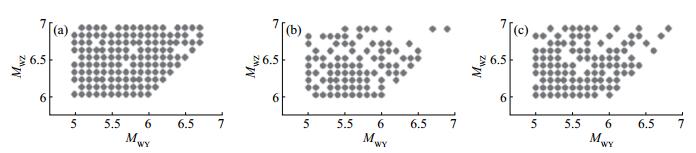
图 1 6—7级地震主震与最大余震级关系 (a)逆冲型地震;(b)正断型地震;(c)走滑型地震 Fig.1 Point diagram of relationship between the magnitude of the principal earthquake and of the largest aftershock |
由表 3和图 1可见:① 6—7级逆冲型主震与最大余震震级之间存在一定线性关系,r = 0.75,表征二者之间关系的线性回归方程为MWZ = 0.7×MWY + 2.3;② 6—7级正断型主震与最大余震震级之间存在一定线性关系,r = 0.83,可以通过线性回归方程MWZ = 0.8×MWY + 1.6表征二者关系;③ 6—7级走滑型主震与最大余震震级之间存在一定线性关系,r = 0.95,可以通过线性回归方程MWZ = 1×MWY + 0.4表征二者关系。
上述分析表明,对于6—7级地震,主震与最大余震震级之间存在一定线性关系,为震后余震快速判定提供了一定参考依据。
3.2 主震视应力与最大余震震级关系同理,建立线性回归方程Aapp = a×MWY + b,探究主震视应力与最大余震震级之间的关系,基于最小二乘法求解方程,并对结果进行校验,具体结果见表 4和图 2。
| 表 4 主震视应力与最大余震震级关系分析结果 Tab.4 The result of relation model between principal earthquake apparent stress and earthquake magnitude of the largest aftershock |
|
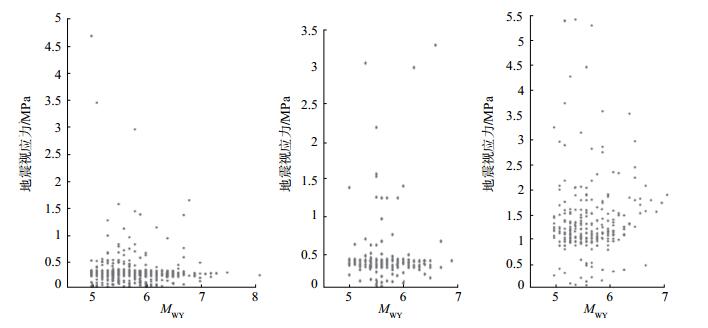
图 2 地震视应力与最大余震震级关系 Fig.2 Point diagram of relationship between earthquake apparent stress and the earthquake magnitude of the largest aftershock |
由表 4和图 2可知:① 对于逆冲型和正断型地震,主震视应力与最大余震震级之间不存在线性关系,不过在逆冲型地震视应力约0.2 MPa、正断型地震视应力约0.1 MPa时,最大余震震级一般5—6级;② 对于走滑型地震,r = 0.64,主震视应力与最大余震震级之间存在一定线性关系,可以用线性回归方程Aapp = 0.2×MWY表征二者关系。
通过以上对主震视应力与最大余震震级之间关系的分析可以看出,只有走滑型地震主震视应力与最大余震震级之间存在一定线性关系,但逆冲型、正断型、走滑型地震的主震视应力与最大余震的震级范围均比较集中,可以为震后余震的快速判定提供一定参考。
4 结论为了能够利用强震后观测数据预测发生余震的可能性,利用已有地震数据围绕主震和余震之间的相关关系展开分析。本研究采用基于最小二乘法的线性回归方法,挖掘主余震之间的关系,重点关注主震与最大余震震级以及主震视应力和最大余震震级之间的关系。结果表明,逆冲型、正断型、走滑型地震的主震震级与最大余震震级之间存在一定线性关系,而仅走滑型地震的主震视应力与最大余震震级之间除存在一定线性关系,逆冲型、正断型地震不存在明显的线性关系,但视应力与最大余震震级范围均比较集中。
| 包秀敏. 赫斯特指数H值在地震预测中的应用[J]. 地震地磁观测与研究, 2013, 34(Z1): 92-96. | |
| 陈学忠, 王小平, 王林瑛, 张天中. 地震视应力用于震后趋势快速判定的可能性[J]. 国际地震动态, 2003, 7: 1-4. DOI:10.3969/j.issn.0253-4975.2003.02.001 | |
| 刘红桂, 王培玲, 杨彩霞, 徐戈, 孙业军, 陈章立, 郑斯华. 地震视应力在地震预测中的应用[J]. 地震学报, 2007, 29(4): 437-445. | |
| 梁珊珊, 黄志斌. 中国地震台网观测数据统计[J]. 地震地磁观测与研究, 2015, 36(4): 41-46. | |
| 马宏生, 刘杰, 吴昊, 李杰飞. 基于R值评分的年度地震预报能力评价[J]. 地震, 2004, 24(2): 31-37. | |
| 王炜. 数据挖掘及其在地震预报中的应用前景[J]. 国际地震动态, 2005, 12: 1-13. DOI:10.3969/j.issn.0253-4975.2005.01.001 | |
| 吴忠良. 关于b值应用于地震趋势预测的讨论[J]. 地震学报, 2001, 23(5): 548-551. |
 2017, Vol. 38
2017, Vol. 38