2. 中国武汉 430000 长江三峡勘测研究院有限公司
2. Three Gorges Geotechnical Consultants Co., Ltd, Wuhan 430000, China
尾波Q值是描述介质非均匀性的量,与区域构造活动和地震活动性密切相关(Singh et al,1983;Jin et al,1985;韦士忠等,1987;李强等,2016;师海阔等,2016)。随着数字地震学的发展,地震学家对尾波Q值展开广泛研究,寻找中强震发震时间和地点的前兆信息,并取得显著成果。在区域分布上,有学者认为构造稳定地区Q值高,活跃地区Q值低(Singh S et al,1983;韦士忠等,1987),而也有一些震例表明,大震前震中区附近Q值较高(朱传镇等,1977),而易发生震群的地区Q值较(Suzuki et al,1972)。在中强震前后Q值随时间变化的研究上,有震例表明,Q值在主震前后有明显变化,具体表现为:主震前Q值升高(Sato H,1988;王伟君等,2004;钱晓东等,2004;陈靖等,2015;李强等,2016)和主震前Q值降低(啜永清等,2004)。
目前,应用广泛的尾波单次散射模型主要有Aki(Aki K et al,1975)和Sato(Sato,H 1977;Domfnguez T et al,1997)2种模型。其中,Aki单次回传散射模型假设震源点和台站在相同位置,且未考虑极化向量和能量在三分量上的分割;Sato各向同性单次散射模型将Aki模型普遍化、推广化(Sato H,1997),提出将震源点和台站分开,被认为是多次散射模型的一阶近似(Zeng Y et al,1991),在物理解释上,Sato模型与实际情况更为接近。本文选取2009年1月到2016年3月首都圈地震数字台网记录的唐山地区地震波形资料,利用Sato尾波单次散射模型,计算该区尾波Q值,并分析其时空分布特征。
1 方法原理根据Sato单次散射模型(Sato H,1977;Domfnguez T et al,1997),在一定频率下,尾波振幅与时间的函数关系表达式为
| $ F\left(t \right) = \lg \left[ {{{\left({{A_\text{c}}\left(t \right)/{A_{\text{S}}}} \right)}^2}{K^{ - 1}}\left(a \right)} \right] = C\left(f \right) - b\left({t - {t_{\text{S}}}} \right) $ | (1) |
式中,AS为S波最大振幅;tS为S波到时;为发震时刻起算的地震波流逝时间;K(a)为依赖于时间的传播因子,K(a) = 1/aln[(a + 1)/(a-1)],其中a = t/tS;Ac(t)为流逝时间t附近的尾波平均振幅,Ac(t) = (AT2 -An2)1/2,其中AT为所取时间窗内地震波平均振幅,An为P波到达前适当时段的地震波平均振幅,用以进行地震波的噪声矫正(Pulli,1984;李白基等,2004);C(f)为与频率f有关的因子,对于特定频率,可视为常数。式(1)中
| $ b = \left({20{\pi }f{\text{lge}}} \right)/Q $ | (2) |
对于不同频率点,拟合F(t)和(t-tS)的线性关系,求出斜率b,即可得到该频率点的Q值,即可拟合出Q(f)= Q0fη,Q0为f= 1 Hz时的Q值。
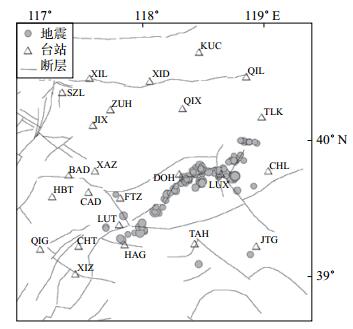
2 资料处理唐山及周边地区地震台站较多,选取24个地震台(分布相对均匀、记录质量较高)记录的2009年1月至2016年3月唐山地区ML 2.5以上地震进行研究,其中ML 4.0以上地震6次,具体参数见表 1。地震台站和震中分布见图 1。
| 表 1 2009年以来唐山地区ML 4.0以上地震的参数 Tab.1 The parameters of earthquakes above ML 4.0 in Tangshan region since 2009 |
|
图 1 所选地震及台站分布 Fig.1 The distribution of selected earthquakes and seismic stations |
采用在时间域求取尾波Q值的方法(朱新运等,2005),分析频段为4—18 Hz,间隔1 Hz,对原始波形进行带宽[0.7f,1.3f]的六阶Butterworth滤波器滤波。对滤波后的数据,从tS开始,取窗长2 s,步长0.5 s滑动计算各时间点平均振幅。背景噪声取P波初动前2 s的平均信号,当采样信号的能量密度小于
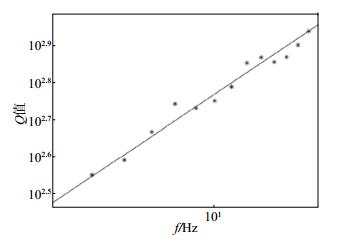
以2012年5月28日唐山ML5.1地震为例,按照以上步骤,拟合QIX台(迁西)尾波Q值随频率的变化曲线,见图 2。
|
图 2 ML 5.1地震尾波Q值拟合曲线 Fig.2 The fitting curve of coda Q of ML 5.1 earthquake |
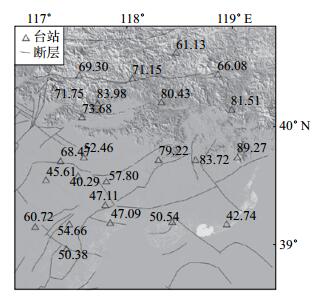
尾波Q值主要反映以震源和台站为焦点的椭球范围内介质的衰减特性(Pulli J J,1984)。1个台站记录的多个地震求出的Q值,可以反映该台站附近的介质衰减特征。本文首先对各台站进行多地震拟合,得到尾波Q值随频率的变化关系。各台站尾波Q0值见表 2,台站按照从北向南的顺序排列,尾波Q0值基本北高南低,具体空间分布见图 3,从图中明显可见,位于山区的台站尾波Q0值较高,位于沉积平原的台站Q0值较低,沿着震源区从东北向西南Q0值逐渐降低,在横向上存在明显差异,与马云生等(1995)和王勤彩等(2004)的研究结果一致。尾波Q0值的横向不均匀性与唐山地区地壳的10 km深度处P波速度表现一致(于湘伟等,2003;Huang J et al,2004)。
| 表 2 唐山地区各台站尾波Q0值(从北向南) Tab.2 The coda Q0 of various stations in Tangshan region(from north to south) |
|
图 3 唐山地区各台站尾波Q0值分布 Fig.3 The distribution of coda Q0 of various stations in Tangshan region |
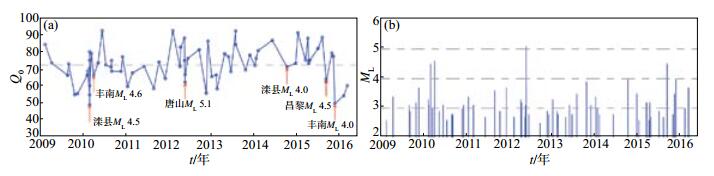
一个地震多台站求出的尾波Q值,反映了震源附近的介质因子特征,尾波Q值随时间的变化对研究孕震过程具有重要意义。本文对各地震进行多台站拟合,得到各地震的尾波Q值随频率的变化关系,值得注意的是,为保证数据的可靠性,对于单个地震,要求至少3个台站参与尾波Q值计算,否则舍弃。研究各地震的Q0值随时间的变化关系,见图 4,从图中可以看出,时间跨度较长的地震,2010年3月6日滦县ML 4.5、2012年5月28日唐山ML 5.1和2014年10月14日滦县ML 4.0地震,时间跨度均超过2年,这些地震前Q0值变化能较好的体现孕震过程,具体表现为,在震前较长时间内Q0值降低,一段时间内Q0值出现升高现象,再次降低后发震。时间跨度较短的地震,如:2010年4月9日丰南ML 4.6、2015年9月14日昌黎ML 4.5和2015年11月28日丰南ML 4.0地震前,Q0值未出现此变化过程,更多表现为升高—降低的趋势。
|
图 4 唐山地区Q0值演化及M—T关系 (a)Q0值时间演化;(b)相应M—T Fig.4 The map of Q0 value evolution and the M-T map |
有学者认为,大震前由于作用在孕震区的应力较强,可使地壳介质特别是韧性层破裂增加,相应的尾波Q值则会减小,但临近破裂时,由于持续增强的应力作用会导致裂隙闭合,介质压实,Q值反而增大(马宏生等,2005)。而大震后由于作用在地壳韧性层上的应力得到释放,介质破裂严重,所以反映其介质衰减特性的Q值减小(Sato H,1988;Hiramatsu Y et al,2000;王伟军等,2004)。因此,在孕震中期阶段,Q值可能表现为减小,但中短期阶段则为增大,本文研究的唐山地区Q0值的时间演化符合此特点。
进一步研究震源区Q值的区域分布,能更好认识中强震易发区域的Q值特征。唐山地区地震多发,为震源区Q值分布研究提供了有利条件。将各地震Q0值插值,给出Q0值区域分布,见图 5(a),从整体上看,Q0值沿震源区从东北向至西南向递减,与台站的Q0值区域分布一致。

|
图 5 震源区Q0值值空间分布 (a)震源区Q0值值空间分布;(b)5.1级地震前震源区Q0值值空间分布;(c)5.1级地震后震源区Q0值值空间分布 Fig.5 The spatial distribution of Q0value in the focal region |
研究时间段内,唐山地区发生的最大地震为2012年5月28日唐山ML 5.1地震,为精确研究唐山地区ML 4.0以上地震震源区域Q0值特征,以该地震为界,对此地震前后发生的地震Q0值进行插值,研究相应Q0值区域分布特征。唐山ML 5.1地震前后唐山发震区Q0值空间分布见图 5中(b)、(c)图,从图中可以看出,除发生在南部的2个ML 4.0以上地震周边无可用于计算的地震外,2012年5月28日唐山ML 5.1、2014年10月14日滦县ML 4.0和2015年9月14日昌黎ML 4.5地震均发生在高低值交界区偏高值一侧,而2010年3月6日滦县ML 4.5地震发生在相对低值地区,该地震前后发生多次中小地震,持续数天,属于震群中的最大地震。因此,对于唐山老震区这种小尺度区域,符合大震前震中区附近Q值较高,而易发生震群地区Q值较低的特点。
4 结论基于Sato单次散射模型,以固定尾波窗长,在时间域计算唐山地区尾波Q值,并研究其时空分布特征,得到以下结论:① 在大空间尺度上,唐山地区山区Q值较高,平原Q值较低,存在明显横向差异,与唐山地区地壳10 km深度的P波速度分布基本一致;② 在较长时间的孕震过程中,唐山地区Q值呈现降低—升高—降低—发震的变化过程,可为中强震的发生时间提供预测依据;③ 在小空间尺度上,中强震大部分发生在Q高低值交界区偏高值一侧,震群发生在Q值相对较低区域,可作为中强震发生地点的预测参考。
浙江省地震局朱新运高级工程师提供尾波Q值计算软件,河北省地震局监测网络中心提供地震波形资料,在此表示感谢。| 陈婧, 赵文舟. 利用Sato模型研究上海及邻近地区尾波Q值[J]. 地震地磁观测与研究, 2015, 36(1): 21-27. | |
| 啜永清, 张淑亮, 苏燕, 等. 大同地震序列的尾波Q值变化特征研究[J]. 地震, 2004, 24(2): 66-72. | |
| 李白基, 秦嘉政, 钱晓东, 等. 云南姚安地区的尾波衰减[J]. 地震学报, 2004, 26(1): 47-52. | |
| 李强, 李军, 袁丽文, 等. 福建仙游地震序列尾波Qc值特征[J]. 大地测量与地球动力学, 2016, 36(2): 184-188. | |
| 马宏生, 刘杰, 张国民, 等. 尾波Qc值随时间变化在地震预测中应用的研究[J]. 地震, 2005, 25(4): 39-48. | |
| 马云生, 张天中, 张焕生. 北京及其周围地区尾波Q值分布特征的研究[J]. 地震学报, 1995, 4: 448-458. | |
| 钱晓东, 李白基, 秦嘉政. 2001年云南施甸MS5.9地震余震序列尾波Qc值研究[J]. 地震地磁观测与研究, 2004, 25(1): 9-17. | |
| 师海阔, 曾宪伟, 田小慧, 等. 利用Sato模型研究宁夏及邻区尾波Q值分布特征[J]. 地震地磁观测与研究, 2016, 37(1): 22-29. | |
| 王伟君, 刘杰. 1999年岫岩地震序列尾波Qc的变化过程[J]. 地震, 2004, 24(4): 37-44. | |
| 王勤彩, 刁桂苓, 李雪英, 等. 唐山地区尾波Qc值研究[J]. 华北地震科学, 2006, 24(1): 13-16. | |
| 韦士忠, 辛书义, 徐臣芝. 京津唐张地区地壳Q值的分布与地震活动性的关系[J]. 地震, 1987, 6: 15-24. | |
| 于湘伟, 陈运泰, 王培德. 京津唐地区中上地壳三维P波速度结构[J]. 地震学报, 2003, 25(1): 1-14. | |
| 朱传镇, 傅昌洪, 容珍贵, 等. 海城地震前后微震震源参数与介质品质因子[J]. 地球物理学报, 1977, 3: 222-231. | |
| 朱新运, 杨钢宇, 张震峰. 基于Sato模型的近震S波尾波Q值求解及分析软件研制[J]. 地震地磁观测与研究, 2005, 26(3): 63-70. | |
| Aki K, Chouet B. Origin of coda waves:Source, attenuation, and scattering effects[J]. Journal of Geophysical Research Atmospheres, 1975, 80(23): 3322-3342. DOI:10.1029/JB080i023p03322 | |
| Domfnguez T, Rebollar C J, Fabriol H. Attenuation of Coda Waves at the Cerro Prieto Geothermal Field, Baja California, Mexico[J]. Bulletin of the Seismological Society of America, 1997, 87(5): 1368-1374. | |
| Hellweg M, Spudich P, Fletcher J B, et al. Stability of coda Q in the region of Parkfield, California:View from the U.S. Geological Survey Parkfield Dense Seismograph Array[J]. J Geophys Res, 1995, 100: 2089-2102. DOI:10.1029/94JB02888 | |
| Hiramatsu Y, Hayashi N, Furumoto M, et al. Temporal changes in coda Q-1 and b value due to the static stress change associated with the 1995 Hyogo-ken Nanbu earthquake[J]. Journal of Geophysical Research Atmospheres, 2000, 105(B3): 6141-6151. DOI:10.1029/1999JB900432 | |
| Huang J, Zhao D. Crustal heterogeneity and seismotectonics of the region around Beijing, China[J]. Tectonophysics, 2004, 385(1-4): 159-180. DOI:10.1016/j.tecto.2004.04.024 | |
| Jin A, Cao T, Keiiti A. Regional change of coda Q in the oceanic lithosphere[J]. Journal of Geophysical Research, 1985, 90(90): 8651-8660. | |
| Pulli J J. Attenuation of coda waves in New England[J]. Bulletin of the Seismological Society of America, 1984, 74(4): 1149-1166. | |
| Sato H. Energy propagation including scattering effects single isotropic scattering, approximation[J]. BSSA, 1977, 68: 923-948. | |
| Sato H. Temporal change in scattering and attenuation associated with the earthquake occurrence-A review of recent studies on coda waves[J]. Pure & Applied Geophysics, 1988, 126(126): 465-497. | |
| Singh S, Herrmann R B. Regionalization of crustal coda Q in the continental United States[J]. Journal of Geophysical Research Solid Earth, 1983, 88(B1): 527-538. DOI:10.1029/JB088iB01p00527 | |
| Suzuki, Sadaomi. Anomalous attenuation of P waves in the matsushiro earthquake swarm area[J]. Earth Planets & Space, 1972, 20(1): 1-21. | |
| Zeng Y, Su F, Aki K. Scattering wave energy propagation in a random isotropic scattering medium:1. Theory[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 1991, 96(B1): 607-619. DOI:10.1029/90JB02012 |
 2017, Vol. 38
2017, Vol. 38