2. 中国北京 100036 中国地震局地震预测研究所
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 10036, China
通过用高度可重复的人工可控震源向地下介质连续发射地震波信号,由地震台站的观测仪器记录地震波信号,分析处理地震波资料,开展对地下结构变化的主动监测,可获得地下介质的动态变化信息 (王洪体等,2009)。北京港震机电有限公司生产的精密可控震源 (CASS),是一种重复性高、可长时间连续运行、对环境影响小的绿色震源,是主动探测地下介质结构及变化的有利工具。由于精密可控震源对地输入作用力小,观测台站接收信号强度弱,如何利用精密可控震源激发高质量发射信号来保证探测的距离和精度,是主动地震探测面临的关键问题。
精密可控震源是一种旋转机械震源,根据其机械特性,选择合适的发射信号是提高可控震源探测分辨率的重要因素。由于线性扫描信号易于操作和实现,在已开展的河北沽源、四川芦山、广东河源等地多次可控震源探测试验中,均采用线性扫描信号进行野外数据采集 (王洪体等,2009;刘希康等,2013)。线性扫描信号的特点是,在所有频率处持续时间相同,由于震源作用力的特点,在低频部分能量明显不足,影响发射信号相关子波的分辨率 (陶知非,1995;张子三等,1998;陶知非,2001;林君,2004),可见单一的简单函数变频方式难以满足理想的发射信号设计要求。
高质量的发射信号应该适应探区探测目的和复杂地震地质条件的需要,使得信号频谱满足探区的频率响应特点,尽可能提高探测分辨能力。因此,发射信号的设计思路是,根据研究区域地质条件和地震信号频率衰减特性模拟出理想的扫描频谱,进而设计扫描信号波形。理想的扫描信号可以满足频谱要求,同时压制干扰波,提高了地层分辨力。不考虑地基耦合等因素,假定传播介质各向同性且无衰减特性,提出在能量均衡原则和信噪比最大原则下,分别设计精密可控震源扫描信号,并计算频谱和相关子波,对能量分布及分辨能力进行对比,分析可控震源扫描信号质量本身对探测效果的影响。
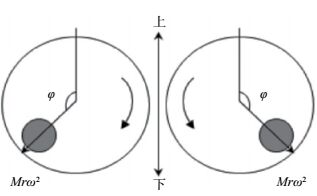
1 发射信号设计原则 1.1 发射信号作为一种旋转机械震源,精密可控震源中两个旋转质量体 (图 1) 对称旋转,产生的水平方向作用力相互抵消,垂直向作用力为单体作用力的2倍,震源产生的垂直方向作用力可表示为
| $F\left( t \right) = 2Mr\omega {\left( t \right)^2}\cos \left( {\varphi \left( t \right)} \right)$ | (1) |
|
图 1 精密可控震源旋转示意 Fig.1 Diagram of the rotation of CASS |
式中M为偏心旋转体质量,r为偏心旋转体的质心距,ω为旋转角频率,t为时间,φ为旋转质量体的瞬时相位,而ω是φ的时间微分。由式 (1) 可看出,精密可控震源产生的对地作用力是幅度与角频率的平方成正比的变频余弦信号 (王洪体等,2009)。由于地震观测系统记录资料是速度量,不考虑地基耦合等影响因素,只考虑波形,精密可控震源发射信号可以表示为
| $s\left( t \right) = B\omega \left( t \right)\sin \left( {\int_0^t {\omega \left( t \right){\rm{d}}t} } \right)$ | (2) |
在耦合不改变信号动态特性的情形下,B为与旋转体质量和质心距有关,而与ω(t) 无关的仅影响振幅的常量,为计算方便,在本文中设为1。发射信号的频谱、相关子波及相对发射能量均使用式 (2) 进行波形计算;不考虑地基耦合等因素,假定理想状态下发射信号能量均转换为地震波能量传入地下,无其他能量损耗,则相对发射能量使用式 (3) 计算
| $E = \int\limits_0^T {{s^2}\left( t \right){\rm{d}}t} $ | (3) |
其中T为发射信号持续时间。由式 (2) 可知,发射信号主要受旋转质量体质量、质心距、信号时间、频带宽度、频率—时间关系等因素影响。当旋转质量体质量、质心距、发射频带和发射时间一定时,根据式 (2) 可通过设计发射信号的角频率—时间关系,即ω(t) 来改善发射信号质量,也就是设计精密可控震源偏心质量体旋转的角频率—时间关系得到最佳震源发射信号。为计算方便,本文中均假定发射信号频带为4 — 10 Hz,发射时间为300 s。
1.2 能量均衡原则假设记录信号无噪声时,相关子波是脉冲函数时分辨能力最高,即在频率域表现为信号振幅谱为白色时分辨能力最高 (李庆忠,1993)。本文提出的能量均衡原则就是发射信号频带内各频率发射能量均衡,在频域表现为信号频谱平坦,有助于改善相关子波形态。因此仅考虑各频率能量分布,设A为 (2) 式中发射信号某频率处速度量的振幅,ΔT为发射时间,当ΔT无限小时,该时间段发射频率假设为固定频率,根据能量均衡原则,各频率发射能量应相等,即满足
| ${A^2}\Delta T \approx \Delta E$ | (4) |
ΔE为能量,发射信号各频率能量应近似等于ΔE,即ΔE为固定值,不随频率变化。结合式 (2),因此发射信号各角频率持续时间与振幅的平方成反比,只考虑速度波形,发射信号振幅与角速度成正比,因此各频率持续时间与角频率的平方成反比。通过在较低角频率处分配较长的持续时间,在较高频率处分配较少的发射时间,实现信号振幅谱平坦,保证各频率能量均衡提高。
1.3 信噪比最大原则假定传播介质各向同性且无衰减特性,同时与地基的耦合不改变信号的动态特性,可控震源发射信号传播过程中不损失能量,地震台站的观测波形可简化为发射信号加上噪声之和,因此观测信号相关子波不仅与发射信号的频带有关,还与噪声的频谱有关。Widess (1982) 定义有噪声的相关子波分辨能力为子波最大极值平方与子波加噪声的总能量之比。假设发射信号与噪声不相关,此时信号加噪声的总能量等于信号能量与噪声能量之和。定义有噪声时的分辨能力为
| $P = \frac{{{{\left[ {\int {S\left( f \right)\cos \theta \left( f \right){\rm{d}}f} } \right]}^2}}}{{\left[ {\int {{S^2}\left( f \right) + {N^2}\left( f \right)} } \right]{\rm{d}}f}}$ | (5) |
式中S(f) 为信号振幅谱,cosθ(f) 为信号的相位谱,N(f) 为噪声振幅谱。当噪声不存在时分辨能力最高;噪声越强,分辨能力越低。假设无噪声时的分辨能力用P0表示,则
| $P = \frac{{{P_0}}}{{1 + \frac{{\int {{N^2}\left( f \right){\rm{d}}f} }}{{\int {{S^2}\left( f \right){\rm{d}}f} }}}}$ | (6) |
即分辨能力由信噪比决定 (俞寿朋,1993)。定义信噪能量比
| ${\rm{SN}}{{\rm{R}}^2} = \frac{{\int {{S^2}\left( f \right){\rm{d}}f} }}{{\int {{N^2}\left( f \right){\rm{d}}f} }}$ | (7) |
则有
| $P = \frac{{{P_0}}}{{1 + \frac{1}{{{\rm{SN}}{{\rm{R}}^2}}}}}$ | (8) |
考虑到实际记录中包含噪声,振幅谱平坦的发射信号可能分辨率不是最高。噪声本身降低相关子波的分辨率,在相关子波不变的条件下,实际记录的信噪比越低,分辨能力越低。当信噪比为1时,由式 (5) 可以看出,分辨能力比在无噪声情况下降低一半。当观测点场地噪声强度大淹没相关子波主瓣峰值时,已无分辨力可言。分辨能力与相关子波形态有关,见图 2,相关子波主瓣宽度越窄,主旁瓣振幅比值越大,尾波振荡衰减越快,相关子波越容易辨识,分辨力越高 (物探局研究所震源室,1977)。在地震勘探工作中,当地震信号的信噪比低于1时,提高信噪比成为改善分辨能力的关键。假设信号中存在白噪声,由于白噪声在频带内均匀分布,白噪声的功率谱保持一定,因此式 (6) 中的噪声振幅谱N(f) 不变,信噪比的提高有赖于改善信号振幅谱S(f)。由于升频扫描信号角频率不断升高,只好通过调节各角频率发射持续时间来改善振幅谱S(f),改善相关子波形态,直至相关子波主旁瓣比值最大。在有噪声的情形下,信噪比越高分辨力越高,提高信噪比能够在一定程度上改善分辨能力。

|
图 2 扫描信号的相关子波 Fig.2 Correlative wavelet of the sweep signal |
图 3所示为精密可控震源发射信号设计的流程图。按照能量均衡原则或信噪比最大原则,计算1组时间、角频率的控制点,通过3次样条函数拟合内插计算扫描时间段内每个时间点的瞬时角频率,得到角频率—时间曲线,进而模拟合成发射信号,计算其频谱和相关子波,分析二者形态,如不符合要求,重新调整角频率—时间的控点值,重复上述过程,直至扫描信号频谱和相关子波满足要求,输出扫描信号 (崔仁胜等,2011)。

|
图 3 发射信号设计流程 Fig.3 Diagram of the signal designing |
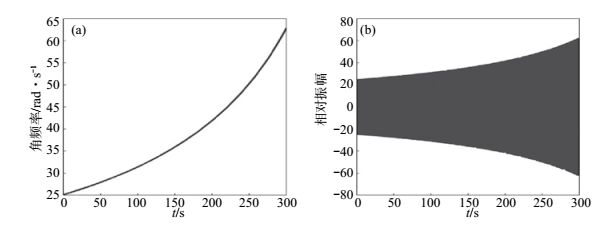
按照能量均衡原则,各频率持续时间与角频率成反比,计算得到1组角频率—时间离散控制点,通过3次样条函数插值拟合计算的离散控制点得到角频率—时间变化关系曲线,见图 4(a)。根据角频率—时间变化关系计算得到发射信号 (以下称为能量均衡拟合扫描信号),分别计算其相对发射能量、频谱和相关子波。
|
图 4 能量均衡拟合扫描信号角频率—时间曲线和理论发射信号 Fig.4 The angular frequency-time relationship and the transmitting signal of the designed signal based on energy balance principle |
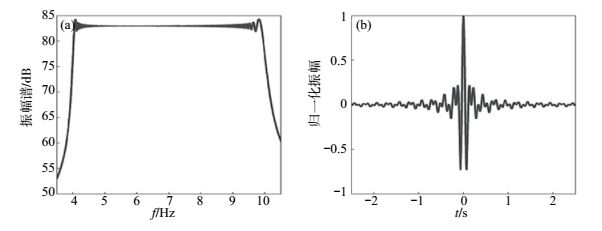
能量均衡拟合扫描信号波形的频谱和相关子波见图 5,由角频率—时间变化关系可以看出,在高频段扫描时间较短,而在低频段频率变化较慢扫描时间较长,通过较长的持续时间增加低频段能量,能量分布均衡最终表现在图 5(a),该信号的频谱平坦,频带范围外能量泄漏较少。各频率能量均衡带来了分辨率的提高,由5(b) 所示,相关子波主瓣宽度较窄,主瓣突出,振荡衰减较快,主旁瓣振幅比为4.549 6,计算其发射相对能量为2.3689×105。
|
图 5 能量均衡拟合扫描信号的频谱和相关子波 Fig.5 The spectrum and the correlative wavelet of the designed signal based on energy balance principle |
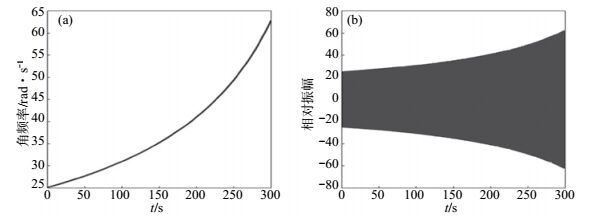
按照信噪比最大原则计算得到1组角频率—时间曲线的离散控制点,与能量均衡原则下得到的角频率—时间关系相比,低频部分分配了更长的持续时间。对离散角频率值经3次样条拟合得到角频率—时间变化曲线,见图 6(a),曲线的斜率不断增大,角频率越大分配的持续时间越少。图 6(b)为由角频率—时间变化曲线计算得到的理论发射信号 (以下简称为信噪比最大拟合扫描信号)。
|
图 6 信噪比最大拟合扫描信号角频率—时间曲线和理论发射信号 Fig.6 The angular frequency-time relationship and the transmitting signal of the designed signal based on maximum signal to noise ratio principle |
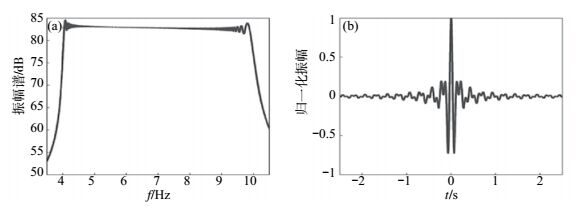
对扫描信号计算其频谱和相关子波,见图 7,由图 7(a)可以看出,低频能量多,高频段能量较少,频谱呈下降斜坡趋势,发射相对总能量为2.3044×105。其相关子波形态与能量均衡拟合扫描信号相关子波相似,主旁瓣振幅比为5.022 6,高于能量均衡拟合扫描信号,同时尾波振荡衰减较快。在有噪声存在的情况下追求信噪比最大增加了低频能量,使发射总能量有所减少,但在噪声强度大的观测环境中保持信噪比均衡,有助于检测信号和进一步改善分辨率。
|
图 7 信噪比最大拟合扫描信号的频谱和相关子波 Fig.7 The spectrum and the correlative wavelet of the designed signal based on maximum signal to noise ratio principle |
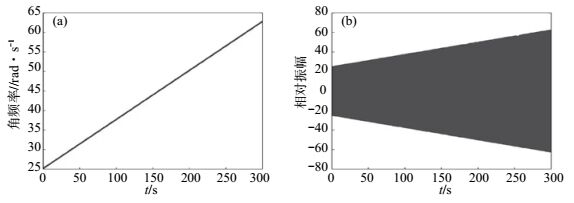
目前野外实验中常用的线性扫描信号频率变化与时间成正比,瞬时频率是时间的线性函数,所以角频率也是时间的线性函数。如图 8(a)所示为线性扫描信号的角频率—时间变化,图 8(b)为理论发射信号记录。由其理论发射信号计算得到相对发射能量为3.0793×105;分别计算其发射信号频谱和相关子波,见图 9。由图 9(a)可以看出,线性扫描信号在高频段能量分布较多,是因为线性扫描各频率持续时间相同,其能量主要和振幅的平方成正比,振幅与角频率成正比,因此频率越大能量分布越多;图 9(b)中相关子波旁瓣较高,主瓣和旁瓣的比为2.159 8。
|
图 8 线性扫描信号角频率—时间曲线和理论发射信号 Fig.8 The angular frequency-time relationship and the transmitting signal of the linear sweep signal |

|
图 9 线性扫描信号的频谱和相关子波 Fig.9 The spectrum and the correlative wavelet of the linear sweep signal |
与线性扫描信号相比,能量均衡拟合扫描信号和信噪比最大拟合扫描信号均损失部分发射能量来改善相关子波分辨力。其中能量均衡拟合扫描信号各频率能量均衡,振幅谱平坦,相关子波分辨率较高;信噪比最大拟合扫描信号在噪声存在情况下改善信噪比,使得相关子波主旁瓣比值最大,分辨力高,但能量分布不均,低频能量较多,发射相对总能量减少。表 1所示为3种扫描信号的相对发射能量和相关子波主旁瓣比值对比,线性扫描相对发射能量最大,相关子波主旁瓣比值最小;信噪比最大拟合扫描信号相对发射能量最小,相关子波主旁瓣比值最大。
| 表 1 3种扫描信号对比 Tab.1 The comparison of 3 kinds of signals |
图 10所示为不同扫描信号的角频率—时间变化关系对比,直线1为线性扫描信号的角频率—时间关系,曲线2为按能量均衡原则生成的拟合扫描信号的角频率—时间变化关系,曲线3为按信噪比最大原则生成的拟合扫描信号的角频率—时间变化关系。位于曲线2上方的扫描信号能量分布呈高频能量多、低频能量少现象,如:线性扫描;位于曲线2下方的扫描信号能量分布呈高频能量少、低频能量多现象,如:信噪比最大拟合扫描信号。角频率—时间曲线变化关系越靠近曲线2,扫描信号能量分布越均衡;角频率—时间曲线变化关系越靠近曲线3,扫描信号相关子波主旁瓣比值越大,分辨力越高。
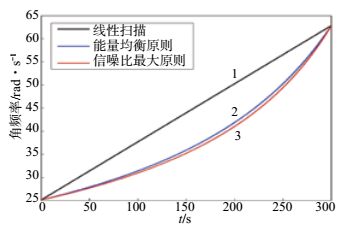
|
图 10 3种扫描信号角频率—时间关系对比 Fig.10 The comparison of angular frequency-time relationship about 3 kinds of signals |
地震探测中应根据研究区域实际情况设计合适的扫描信号,如观测台站距离较远,背景噪声强度较大,可按照信噪比最大原则来设计扫描信号,角频率—时间变化关系趋近于曲线3,有利于接收台站记录的信号检测;如探测距离较近,台站观测条件较好信噪比高,可选择能量均衡来设计扫描信号,角频率—时间变化关系趋近于曲线2;如信噪比和能量分布均需要考虑,角频率—时间变化关系应位于曲线2和曲线3之间。实际工作中如考虑研究区域的衰减特性,对衰减较多的频率补偿一定的能量,可根据给不同频率分配不同的时间,调整时间、角频率分布来生成满足条件的发射信号。通过自由分配各频率能量可灵活设计非线性扫描信号。
4 结束语综上所述,根据能量均衡原则和信噪比最大原则优化设计非线性扫描信号设计,可针对性的分配各频率持续扫描时间,角频率—时间拟合曲线的生成不受单一函数形式的约束,可以灵活设计发射信号的频谱,从而得到较好的相关子形态,提高探测分辨力,是一种有效的精密可控震源发射信号设计方法,对提高可控震源探测中的信号质量有一定参考意义。
本文在假定各向同性均匀介质中场地无衰减理想状态下探讨发射信号本身对探测结果的影响,理想状态下的发射信号设计忽略了地基耦合和能量损失等因素,具有一定局限性,实际工作中地基耦合、场地特性和传播路径均会对地震波信号产生影响,有待开展深入研究。高质量的精密可控震源发射信号有利于提高相关子波分辨能力,能够提高可控震源信号提取精度,对主动探测具有实际应用价值。
| 崔仁胜, 王洪体. 精密控制震源发射信号设计方法研究[J]. 地震地磁观测与研究, 2011, 32(2): 47-52. | |
| 李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993: 30-36. | |
| 林君. 电磁驱动可控震源地震勘探原理及应用[M]. 北京: 科学出版社, 2004: 58-65. | |
| 刘希康, 崔仁胜, 王洪体. 用Wigner-Hough变换检测精密可控震源信号[J]. 地震, 2013, 33(3): 33-42. | |
| 陶知非. 可控震源的现状与问题[J]. 石油物探装备, 1995, 5(1): 11-25. | |
| 陶知非. 可控震源扫描信号设计中一些问题的考虑[J]. 物探装备, 2001, 11(1): 9-15. | |
| 王洪体, 庄灿涛, 薛兵, 等. 精密主动地震监测[J]. 地球物理学报, 2009, 52(11): 1 808-1 815. | |
| 物探局研究所震源室. 可控震源的原理及工作方法[J]. 石油地球物理勘探, 1977, 21(4): 1-34. | |
| 俞寿朋. 高分辨率地震勘探[M]. 北京: 石油工业出版社, 1993: 23-28. | |
| 张贤达. 现代信号处理[M]. 清华大学出版社, 1995: 157-165. | |
| 张子三, 林君, 于生宝. 可控震源线性扫描的优化设计[J]. 石油仪器, 1998, 12(3): 1-5. | |
| Widess M A. Quantifying resolving power of seismic system[J]. Geophysics, 1982, 47: 1 160-1 173. DOI:10.1190/1.1441379 |
 2017, Vol. 38
2017, Vol. 38

