2. 中国郑州 450002 中国地震局地球物理勘探中心;
3. 中国四川 615000 中国西昌卫星发射中心
2. Geophysical Exploration Center, China Earthquake Administration, Zhengzhou 450002, China;
3. Xichang Satellite Launch Center, Sichuan Province 615000, China
PDS型地震仪是中国地震局地球物理勘探中心研制的一种一体化、低功耗、轻便数字地震仪,采用内置地震波拾振器、A/D模数转换、数据采集控制、GPS授时定位、CF卡数据存储以及内置锂电池供电的一体化设计,整机平均功率约70 mW,重量仅3 kg(包括内置电池)(原秦喜等,1999)。该地震仪适用于开展深地震宽角折/反射法探测等强流动性观测的野外地震数据采集工作,也可用于天然地震(地方震)监测。
PDS型数字地震仪采用24位A/D转换,32位ARM微处理器和CF卡作为数据存储媒介的基本硬件结构;拾振器采用三分量速度型磁电式低频检波器,标称自然频率为2.5 Hz;时间服务采用GPS授时同步与内部高精度实时时钟相结合的方法,内时钟的时基TCXO的稳定度为±5×10-7(-10℃— + 50℃);仪器有定时启动和连续记录两种工作方式,其中定时启动主要用于深地震宽角折/反射法探测,启动容量为1—32次(日、时、分),而连续记录可用于天然地震(地方震)监测(孙鸿等,2013)。
近年来,随着人工地震数据资料解释处理方法的发展,在读取震相走时信息的同时,往往还需要由地震波形数据推导计算地面运动的绝对位移值、速度值。因此,只有获得PDS型地震仪的传递函数,才能反向解算真实地面运动的动力学信息。本文拟利用超低频振动台频率特性测试和Matlab数值拟合方法,给出PDS地震仪拾振器的传递函数数学表达式。
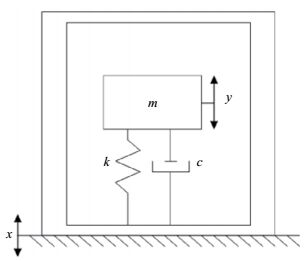
1 实验原理PDS型地震仪内置拾振器是一种磁电式振动速度传感器,用于检测地面的绝对运动。拾振器内部固定永久磁芯,当一个由弹簧片支撑的质量为m的线圈与磁芯产生相对运动时,线圈切割磁感线产生电压信号输出,且该输出电压数值与振动速度成正比(图 1)。为了确定PDS型地震仪拾振器传递函数的数学表达式形式,首选推导拾振器运行方程,再进行拉普拉斯变换,获得拾振器传递函数表达式的标准形式。
|
图 1 PDS型地震仪拾振器的力学模型 Fig.1 Mechanical model of geophone of PDS seismograph |
地震仪拾振器是一个由质量块和弹簧组成的典型二阶系统,力学模型可简化为一个惯性质量块m、弹性系数为k的弹簧和阻尼系数为c的阻尼器构成的单自由度系统(Yang Xueshan et al,2004)。如图 1所示,其运动方程为
| $m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + c\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}t}}-\frac{{{\rm{d}}x}}{{{\rm{d}}t}}} \right) + k\left( {y-x} \right) = F\left( t \right)$ | (1) |
式中,m为惯性体质量(即线圈);k为弹簧刚度;c为阻尼系数;y为惯性体的绝对位移;x为拾振器基座壳体的绝对位移;
传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换与激励(即输入)量的拉普拉斯变换之比。令F(t) = 0,ω02=k/m,其中ω0为特征角频率;2ξ0ω0=c/m,其中ξ0为阻尼比;yr = y-x,为质量块相对拾振器壳体的振动位移。则式(1)经拉氏变换为
| $H\left( s \right) = \frac{{{Y_r}\left( s \right)}}{{X\left( s \right)}} = \frac{{ - {s^2}}}{{{s^2} + 2{\xi _0}{\omega _0}s + \omega _0^2}}$ | (2) |
地震仪拾振器线圈切割磁力线,所产生的输出电压为
| ${u_0} = Bl \cdot \frac{{{\rm{d}}{y_r}}}{{{\rm{d}}t}}$ | (3) |
经拉普拉斯变换为
| ${U_0}\left( s \right) = Bl \cdot s \cdot {Y_r}\left( s \right) = {k_0}s{Y_r}\left( s \right)$ | (4) |
式中,B为磁场强度,l为切割磁力线的线圈长度,k0为拾振器灵敏度系数。
由式(2)和式(4)可得拾振器对地动位移的输出响应,为
| ${U_0}\left( s \right) = {k_0}H\left( s \right)sY\left( s \right) = \frac{{ - {k_0}{s^2}}}{{{s^2} + 2{\xi _0}{\omega _0}s + \omega _0^2}} \cdot sY\left( s \right)$ | (5) |
则拾振器对地动速度的传递函数为
| ${H_v}\left( s \right) = \frac{{ - {k_0}{s^2}}}{{{s^2} + 2{\xi _0}{\omega _0}s + \omega _0^2}}$ | (6) |
式(6)函数表达形式即为拾振器传递函数的目标函数形式,表征为一个典型的二阶高通滤波器。
2 实验方法 2.1 振动台频率特性标定测量PDS型地震仪内置垂直正交三分向拾振器,包括1个垂直向和2个水平向(南北向,东西向)。利用中国数字地震观测网络工程科学探测台阵系统地震计标准校准振动台系统,对拾振器在14个频点上进行正弦波灵敏度测试(戴仕贵等,2009)。为获取拾振器高精度的频率响应灵敏度数据,采取以下措施:① 确保拾振器与振动台测试平面刚性连接。制作固定卡座,防止振动测试过程中拾振器与测试平面产生滑移形成测量误差;② 最大程度减小连接引线对测量过程的影响。拾振器输出信号端采用0.05 mm漆包线作为信号输出导线,做到尽量减小连线牵引对测量精度的影响;③ 消除测量误差。随机选取20组拾振器并在每个频点上做5次标定测量,计算平均值,作为频响曲线拟合的原始数据。

|
图 2 超低频振动台 Fig.2 Ultra low-frequency vibration table |

|
图 3 拾振器灵敏度测试界面 Fig.3 Sensitivity testing GUI |
利用超低频地震计标准校准振动台系统,获取所测试拾振器分别在0.25 Hz、0.50 Hz、0.80 Hz、1.00 Hz、2.00 Hz、2.50 Hz、4.00 Hz、5.00 Hz、10.00 Hz、16.00 Hz、20.00 Hz、40.00 Hz、60.00 Hz、80.00 Hz共14个频点上的灵敏度数据。±据实际测量结果,剔除无效数据和粗大误差数据,求取各频率点上的灵敏度均值,见表 1、表 2。
| 表 1 拾振器幅值灵敏度标定数据 Tab.1 Sensitivity testing of amplitude data |
| 表 2 拾振器相位灵敏度标定数据 Tab.2 Sensitivity testing of phase data |
根据上文式 (6) 可知,拾振器传递函数的目标函数表征为一个典型的二阶高通滤波器。因此,选择标准二阶高通滤波器的传递函数作为拟合目标函数,表达式如下
| $H\left( s \right) = \frac{{{H_0}{s^2}}}{{{s^2} + \alpha {\omega _0}s + \omega _0^2}}$ | (7) |
该拟合过程采用非线性最小二乘法原理(周云耀,2005),利用Matlab Optimization Toolbox工具箱,使用非线性曲线拟合函数lsqcurvefit ()。首先,由拾振器的拟合目标传递函数表达式,令s = jω,可得拾振器频响特性曲线的数学表达式,即灵敏度幅频响应函数H(ω)。
| $H\left( \omega \right) = {H_0}\sqrt {{\omega ^4}/\left[ {{\omega ^4} + {\omega ^2}\omega _0^2\left( {{\alpha ^2} - 2} \right) + \omega _0^4} \right]} $ | (8) |
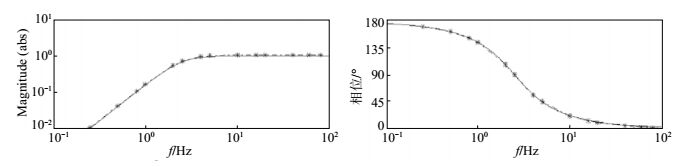
利用Matlab工具箱lsqcurvefit () 函数,求取H(ω) 中的拟合参数,即H0、α和ω0的参数值,其中ω0 = 2πf0。拟合结果见图 4,图中黑色实曲线为拟合理论曲线,原始数据曲线以灰色星点线所示,由图可知曲线拟合结果良好。
|
图 4 Matlab幅频特性拟合曲线 Fig.4 Matlab ftting curve |
利用上述方法,对PDS型地震仪拾振器做频率响应测试,考虑其工作频段为中低频,因此测试频点频率下限频率选择为0.25 Hz,上限频率为80 Hz。该方法仅考虑使用灵敏度测试的幅度数据,曲线拟合过程未考虑相位数据。由振动台相频测试特性决定,对相位数据做180°的校正。由图 4可知,相位拟合曲线与测量所得相位数值吻合。
利用Matlab工具箱中的lsqcurvefit () 函数,对拾振器频率特性数据进行最小二乘法拟合,可得拟合参数数值分别为:H0=-120.18,α =1.57和f0 = 2.52,则可得PDS地震仪拾振器传递函数为
| ${H_v}\left( s \right) = \frac{{ - 120.18{s^2}}}{{{s^2} + 24.85s + 250.45}}$ | (9) |
经对拾振器测试幅频特性数值与拟合的传递函数幅频特性理论值之间的误差计算得知,辨识结果在测试频段内的幅频特性绝对误差<0.5 dB,具有较高的辨识精度。
4 结论本文基于超低频振动台对PDS型地震仪拾振器的频率特性进行测试,提出一种利用拾振器幅频特性和Matlab数值拟合对拾振器传递函数辨识的方法,并给出PDS型地震仪拾振器传递函数的数学表达式。实验结果表明,利用该方法可以实现拾振器传递函数的辨识,并且可以达到幅频特性绝对误差<0.5 dB的辨识精度。±据所得拾振器传递函数,结合已知的A/D模数转换环节以及FIR滤波环节的传递特性,即可得到PDS地震仪完整的传递函数(刘瑞丰等,1995)。PDS型地震仪传递函数的取得,对人工地震数据挖掘和先进的人工地震数据资料解释处理方法的应用,将产生积极的促进作用。
| 戴仕贵, 谌亮, 康宏, 等. CMG-3ESPC宽频带地震计稳态标定和传递函数构建[J]. 四川地震, 2009, 132(2): 12-15. | |
| 刘瑞丰, 党京平, 方韶东, 等. 全球地震台网 (GSN) 数字地震仪的传递函数[J]. 地震地磁观测与研究, 1995, 16(5): 1-5. | |
| 孙鸿, 李从庆, 郭磊. PBS型32位宽频带流动地震仪[J]. 现代电子技术, 2013, 36(18): 121-124. DOI:10.3969/j.issn.1004-373X.2013.18.036 | |
| 原秦喜, 孙鸿, 戴鹏, 等. 人工地震测深和天然地震流动观测兼用的轻便数字地震仪系统[J]. 中国地震, 1999, 15(2): 159-166. | |
| 周云耀. 超宽与甚宽频带地震计阶跃标定的加权动态拟合法[J]. 大地测量与地球动力学, 2005, 25(1): 123-126. | |
| Yang Xueshan, Gao Feng, Hou Xingmin. Low-frequency characteristics extension for vibration sensors[J]. Earthquake Engineering and Engineering Vibartion, 2004, 3(1): 139-146. DOI:10.1007/BF02668859 |
 2017, Vol. 38
2017, Vol. 38