地震动地形效应已被众多研究证实,如Nguyen等 (2007)计算了不同地形的地震动放大效应后发现,地震动通常在山脊与坡顶处得到放大,且坡角越大,地震动放大效应越突出,但山谷处的地震动得到衰减。胡元鑫等 (2011)通过计算同样发现,不同地点的Z向速度分量波幅遵循峰顶、山脊得到放大或沟谷得到降低的模式,这说明与已有的二维概化模型计算结果相比,三维真实地形对地震动的影响比二维概化模型更为复杂。
近年,大量数值模拟方式 (如有限差分法、有限元法、谱元法) 被用于研究地震引起的强地面运动 (Olsen et al,1995, 1996;Wald and Graves 1998;Komatistch et al,2004)。然而,对于各向异性变化显著的低速沉积层盆地以及有显著地形变化的模型,利用有限差分进行模拟,在模型构建处理自由起伏边界的同时,在模拟地震波传播影响时 (Robertsson,1996;Tarras et al,2011) 会遇到实际困难。
本研究区域为首都圈地区,北面为燕山山脉,西面为太行山脉,地势轮廓西北高东南低,由西北山区向东南平原区呈台阶式倾斜下降,分别构成高山、丘陵、冲洪积扇、基岩残丘及平原。研究区内层状地形普遍发育,显现3个不同高度的层状地形面,由高而低依次为1 000 m左右、800-500 m和300-150 m (相当于上新世初的唐县期夷平面)。
为研究地形变化显著的沉积层盆地,使用谱元法 (SEM) 模拟首都圈区域的地震波传播过程。谱元法最早被用于流体动力学 (Patera,1984),而后Komatistich和Tromp (1999, 2002) 将SEM方法引入地震学。SEM方法被应用到多个地区的地震学研究,如:Komatistch等 (2004)利用SEM方法模拟Yorba Linda地震 (MW 4.2) 在洛杉矶盆地的传播及地面运动;Lee等 (2008, 2009) 则模拟了中国台北地震;Magnoni (2014)模拟了L'Aquila地震。以上研究表明,SEM模型对于模拟地震波传播及地面运动具有较高的准确性。
1 三维地震波场模拟谱元法算法谱元法是在传统有限元方法的基础上在每个单元内使用谱方法或者伪谱法,选取正交多项式为基作为插值基函数,从而提高插值精度和数值解的收敛速度。Komatistich和Tromp (1999, 2002) 给出了波动方程理论和利用谱元法数值模拟地震波传播的详细理论基础。
1.1 三维波动弹性动力方程弱形式图 1为SEM计算模型简图,图中Ω表示计算模型区域,Ω与Γ分别代表地表的自由边界和吸收边界,n为各边界向外的法向量,地震触发xs(位于Ω内任何地点)。则某单元体内三维波动的弹性动力方程为
| $\rho \left( x \right)\frac{{{\partial ^2}}}{{\partial {t^2}}}u\left( {x,t} \right) - \nabla \cdot \sigma \left( {x,t} \right) = f\left( {x,t} \right)$ | (1) |
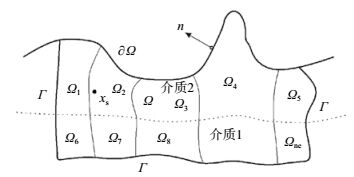
|
图 1 SEM计算模型 Fig.1 SEM computation model |
其中:ρ(x) 为质量场;μ (x, t) 为位移场;σ (x, t) 为应力场;f (x, t) 为震源项。式 (1) 两端同乘以测试矢量w (x),并在整个模型域内积分,得到
| $\int w \rho \left( x \right)\ddot u{\rm{d}}x - \int\limits_\mathit{\Omega } w \nabla \cdot \sigma {\rm{d}}x = \int\limits_\mathit{\Omega } w f{\rm{d}}x$ | (2) |
对式 (2) 左侧第2项在模型域内及边界处进行分部积分
| $\int w \rho \left( x \right)\ddot u{\rm{d}}x - \int\limits_\mathit{\Gamma } w \nabla \cdot \sigma {\rm{d}}x + \int\limits_\mathit{\Omega } w \nabla \cdot \sigma {\rm{d}}x = \int\limits_\mathit{\Omega } w f{\rm{d}}x$ | (3) |
自由边界∂Ω上σ∂Ω= 0,而在模型吸收边界Γ上可表示为
| $\int w \rho \left( x \right)\ddot u{\rm{d}}x - \int\limits_\mathit{\Gamma } w \nabla \rho v\dot u{\rm{d}}x + \int\limits_\mathit{\Omega } w \nabla \cdot \sigma {\rm{d}}x = \int\limits_\mathit{\Omega } w f{\rm{d}}x$ | (4) |
式 (4) 即为式 (1) 积分形式的弱形式,其中v为波速场,右端表示震源。
1.2 三维地震震源项计算震源通过矩张量Me进行描述,则式 (4) 右侧地震源项中f可表示为
| $f\left( {x,t} \right) = - {M_{\rm{e}}} \cdot \nabla \delta \left( {x - {x_{\rm{s}}}} \right)S\left( t \right)$ |
其中:S(t) 为震源时间函数;▽ δ(x-xs) 为震源的Dirac Delta分布。利用该分布的性质,式 (4) 右侧积分采用矩张量Me可表示为
| $\int\limits_\mathit{\Omega } w f{\rm{d}}x = {M_{\rm{e}}} \cdot \nabla w\left( {{x_{\rm{s}}}} \right)S\left( t \right)$ | (5) |
计算区域选定38°-41° N,116°-120° E,深度从地表至Moho面 (地下40 km),分为40层,垂直分辨率为每层1 km。地面至地下1 km为第三系沉积层界面,地下1-2 km为第四系沉积层界面,地下6 km为G界面,地下14 km为C2界面,地下20 km为C3界面,地下40 km为Moho面,每个分界面的起伏数据在SEM计算程序中设置。地质模型的水平向分辨率为336×336,分别在第三系沉积层和沉积层至G界面2次将模型网格数加倍。沿E、N向的谱单元数分别为336,Z向深度为40 km,共划分40个谱单元,模型中每个谱单元均含有125个GLL点,因此模型共有4 515 840个谱单元,地形采用etop1′的数据。模型沿深度方向上的参数P波、S波及品质因子Q综合参考了前人的研究成果 (孙若昧等,1996;宋松岩等,1997;李鼎容等,1979;赵金仁等,1999;刘昌铨,杨健,1982;高孟潭等,2002),首都圈区域各层介质参数见表 1。计算区域中震中及选取的记录台站分布见图 2。
| 表 1 模型计算参数 Tab.1 Computational parameters of model |
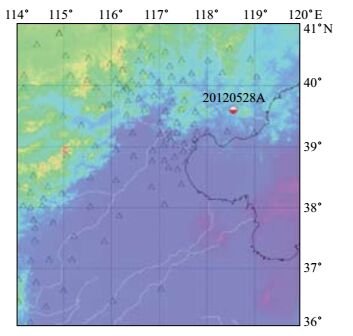
|
图 2 计算区域及台站分布 Fig.2 Computational area and station distribution |
选取研究区域内唐山地区发生的一个MS 4.7地震 (图 2),震源设定为点源,矩张量从CMT全球网站上获取,设定如下
| ${M_{\rm{e}}} = \left( {\begin{array}{*{20}{l}} {{M_{rr}}} & {{M_{r\theta }}} & {{M_{r\phi }}}\\ {{M_{r\theta }}} & {{M_{\theta \theta }}} & {{M_{\theta \phi }}}\\ {{M_{r\phi }}} & {{M_{\theta \phi }}} & {{M_{\phi \phi }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 4.210000{{\rm{e}}^{22}}} & { - 4.780000{{\rm{e}}^{22}}} & {4.470000{{\rm{e}}^{21}}}\\ { - 4.780000{{\rm{e}}^{22}}} & {1.670000{{\rm{e}}^{23}}} & { - 1.350000{{\rm{e}}^{22}}}\\ {4.470000{{\rm{e}}^{21}}} & { - 1.350000{{\rm{e}}^{22}}} & { - 1.250000{{\rm{e}}^{23}}} \end{array}} \right)$ |
计算使用的核心代码为SPECFEM3D的谱元法程序,考虑地形影响和介质衰减特性。设定计算50 000个时间步,步长0.001 s,可计算地震发生后50 s的地震波传播过程,采用4个节点18个进程进行计算,占用内存约40 G,耗时约12小时,数据可视化及后处理采用GMT绘图软件包。
3 计算结果 3.1 地震波传播模拟设定为验证某一模拟地震波传播过程是否可靠,需在给定震源设置下,对包含起伏地形的谱元法模型进行地震波传播模拟,将数值模拟中设置的虚拟台站波形记录与该位置的实际台站记录进行对比。本研究选取唐山地震台 (TST) 和八宝山地震台 (BBS) 的模拟波形记录和实际台站记录,对波形以[0.02-0.5 Hz]的频段进行带通滤波,对比结果见图 3。图中浅灰色实线为模拟合成波形记录,黑色实线为台站波形记录,可以看到,模拟结果与实际波形记录经过带通滤波后,波形较为吻合。
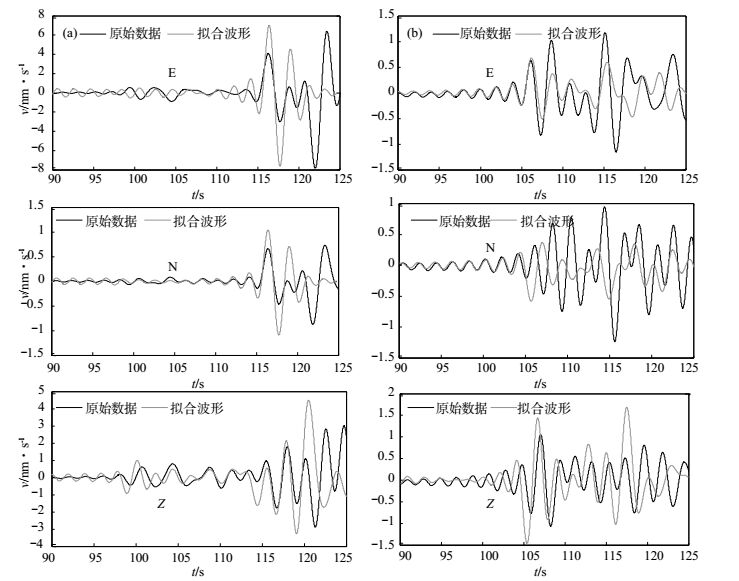
|
图 3 台站模拟波形记录与台站记录对比 (a) TST台站;(b) BBS台站 Fig.3 Three component velocity seismograms for stations |
模拟地震发生后50 s的地震波传播过程,此处选地震发生3 s、6 s、9 s、12 s后的波场三分量快照,见图 4。由图 4可见,3 s时初至P波到达,但幅度较弱,6 s时振幅较强的S波到达,12 s以后可见反射或转换面波到达;区内近环状波前形态较为明显,其中两个水平分量 (E和N分量) 的地形效应弱于垂直分量。

|
图 4 波场三分量快照 (a) E分量;(b) N分量;(c)Z分量 Fig.4 Snapshots of three components of wave feld |
模拟地震发生后50 s的地震波传播过程,此处选地震发生3 s、6 s、9 s、12 s后的波场三分量快照,见图 4。由图 4可见,3 s时初至P波到达,但幅度较弱,6 s时振幅较强的S波到达,12 s以后可见反射或转换面波到达;区内近环状波前形态较为明显,其中两个水平分量 (E和N分量) 的地形效应弱于垂直分量。
3.2 地形对波形影响Komatistch (2004)、Lee (2008, 2009)、胡元鑫等 (2011)众多研究表明,地形效应在地震波传播及地面运动时确实存在,并对准确重现地震波传播过程及地表运动有较大影响,他们强调,SEM方法可以在模型中考虑高分辨率的地形变化。一般来说,地形可以导致复杂的地震波传播现象 (包括地震波能量在山脊中的反射及散射),特别是峰值速度和加速度会在山顶沿着山脊被放大。本研究建立包含高分辨率地形和不含地形的2个模型,来模拟地形对峰值速度和加速度的影响。
首先模拟包含地形的模型地震波传播过程,并与实际台站记录进行对比。为研究地形影响,再次对唐山MS 4.7地震首都圈区域的山区进行模拟,横跨燕山山脉,沿40.5° N线,每隔0.25°设置一个台站,记录地震速度及加速度,对比2次模拟的速度及加速度结果,测试台站分布见图 5。

|
图 5 测试台站剖面 Fig.5 The profle of test stations |
首先对比包含地形模型和不含地形模型的Test10测试台站 (40.5° N,116.5° E) 的三方向速度分量[图 6(a)],由图可见,不同计算模型输出的三分量速度信号整体变化趋势相似,且二者在P波初至及P波震相拟合较好,说明前几秒的波形主要受破裂过程影响,当S波到达地表后,三分量速度均逐渐增大,Z向速度相比于水平向速度变化更为明显,尤其是地震尾波受地形影响较大。因此,本研究只对其他台站的Z分量进行对比,结果发现,位于山顶处的Test10、Test14、Test15测站,山谷处的Test11、Test12、Test13测站均存在S波抵达后真实地形波幅比平坦地形大的震相,表明这些地点的地震动信号得到放大;位于平原的XUS台站,模拟地震动信号相比于实际波形基本无变化。本文仅给出Test10-Test14测站的模型速度波形对比曲线,见图 6。
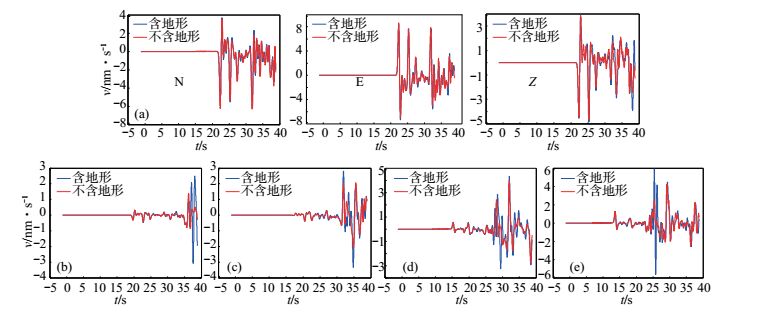
|
图 6 包含地形与不含地形的模型速度波形对比 (a) Test10测站三分量对比;(b) Test11测站Z分量对比;(c) Test12测站Z分量对比;(d) Test13测站Z分量对比;(e) Test14测站Z分量对比 Fig.6 The comparison of seismogram with and without topography |
地形对PGA的相对放大效应可通过下式表达
| ${\rm{A}}{{\rm{F}}_{{\rm{PGA}}}}{\rm{ = }}\frac{{{\rm{PG}}{{\rm{A}}_{\rm{T}}} - {\rm{PG}}{{\rm{A}}_{\rm{F}}}}}{{{\rm{PG}}{{\rm{A}}_{\rm{F}}}}} \times 100{\rm{\% }}$ |
其中:AFPGA为PGA的地形相对放大系数;PGAT为真实地形条件下的PGA分布;PGAF是无地形条件下PGA分布。对本研究设置的测试台站包含地形和不含地形的PGA记录,按式 (2) 计算PGA放大系数,结果见表 2。真实地形对PGA的相对放大系数约为-20.4%-174.6%,但并非总是峰顶、山脊得到放大或沟谷得到降低的模式,如:位于沟谷的Test11、Test12、Test13测站峰值加速度放大,而位于山顶的Test10测站峰值加速度降低,与高孟潭等 (2002)的结论存在差别。在复杂地形影响下,地形对PGA的相对放大效应也呈现复杂模式。
| 表 2 测试台站三分量加速度放大系数 Tab.2 Amplification coefficient of three acceleration components |
谱元法为高阶有限元方法,将高阶Lagrange多项式作为插值基函数,具有高计算精度与高计算收敛速度等特点,并能模拟复杂地形对地震波传播的影响。本文基于谱元法与etop1′的地形模型,选取首都圈区域建立336×336×40个谱单元的计算模型,对该区域一个4.7级地震进行并行模拟,模拟地震波传播过程,对真实三维地形模型的模拟波形与台站记录进行对比,分析地形对速度和加速度波形记录的影响,模拟结果表明:① 考虑复杂三维地形模型模拟的地震波信号在0.02-0.5 Hz范围内接近真实地震波记录,较真实重现地震波传播过程;② 山顶、山脊、沟谷及发震断裂附近真实地形计算模型的三分量速度信号波幅比平坦地形大,相对于水平向,垂直方向速度信号的波幅变化更大,而在河谷区平坦地形计算模型的垂直分量速度信号波幅比真实地形略大;③ 由于地形对地震波的折射和反射影响,PGA分布模式较为复杂,并非总是峰顶、山脊得到放大或沟谷得到降低的模式。
| 高孟潭, 俞言祥, 张晓梅, 吴健, 胡平, 丁彦慧. 北京地区地震动的三维有限差分模拟[J]. 中国地震, 2002, 18(4): 356-364. | |
| 胡元鑫, 刘新荣, 罗建华, 等. 汶川震区地震动三维地形效应的谱元法模拟[J]. 兰州大学学报 (自然科学版), 2011, 47(4): 24-32. | |
| 李鼎容, 彭一民, 刘清泗, 谢振钊, 童有德. 北京平原区上新统-更新统的划分[J]. 地质科学, 1979, 4: 342-350. | |
| 刘昌铨, 杨健. 京津及其外围地区地壳速度结构的初步探测[J]. 地震学报, 1982, 4(3): 217-226. | |
| 宋松岩, 周雪松, 张先康, 宋建立, 龚怡, 王椿镛. 泰安-忻州剖面S波资料解释及其与邢台地震的相关性分析[J]. 地震学报, 1997, 19(1): 13-21. | |
| 孙若昧, 赵燕来, 吴丹. 京津唐地区地壳结构与强震的发生:Ⅱ. S波速度结构[J]. 地球物理学报, 1996, 39(3): 347-355. | |
| Komatitsch D, Tromp J. Introduction to the spectral-element method for 3-D seismic wave propagation[J]. Geophys J Int, 1999, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x | |
| Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-Ⅰ. Validation[J]. Geophys J Int, 2002a, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x | |
| Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-Ⅱ. 3-D models, oceans, rotation, and self-gravitation[J]. Geophys J Int, 2002b, 150(1): 303-318. DOI:10.1046/j.1365-246X.2002.01716.x | |
| Graves R W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bull Seism Soci Am, 1996, 86(4): 1091-1106. | |
| http://www.globalcmt.org/cgi-bin/globalcmt-cgi-bin/CMT4/form?itype=ymd&yr=2012&mo=1&day=1&oyr=1976&omo=1&oday=1&jyr=1976&jday=1&ojyr=1976&ojday=1&otype=nd&nday=365&lmw=0&umw=10&lms=0&ums=10&lmb=0&umb=10&llat=38&ulat=42&llon=116&ulon=120&lhd=0&uhd=1000<s=-9999&uts=9999&lpe1=0&upe1=90&lpe2=0&upe2=90&list=4 (last accessed 2014.10.12) | |
| Komatitsch D, Liu Q, Tromp J, Süss P, Stidham C, Shaw J H. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method[J]. Bull Seismol Soc Am, 2004, 94(1): 187-206. DOI:10.1785/0120030077 | |
| Lee S J, Komatitsch D, Huang B S, Tromp J. Effects of topography on seismic wave propagation:An example from northern Taiwan[J]. Bull Seismol Soc Am, 2009, 99(1): 314-325. DOI:10.1785/0120080020 | |
| Lee S J, Chen H W, Liu Q, Komatitsch D, Huang B S, Tromp J. Three-dimensional simulations of seismic wave propagation in the Taipei basin with realistic topography based upon the spectral element method[J]. Bull Seismol Soc Am, 2008, 98(1): 253-264. DOI:10.1785/0120070033 | |
| Magnoni F, Casarotti E, Michelini A, et al. Spectral-Element Simulations of Seismic Waves Generated by the 2009 L'Aquila Earthquake[J]. Bulletin of the Seismological Society of America, 2014, 104(1): 73-94. DOI:10.1785/0120130106 | |
| Nguyen K, Gatmiri B. Evaluation of seismic ground motion induced by topographic irregularity[J]. Soil Dynamics, Earthquake Engineering, 2007, 27(2): 183-188. DOI:10.1016/j.soildyn.2006.06.005 | |
| Olsen K B, Pechmann J C, Schuster G T. An analysis of simulated and observed blast records in the Salt Lake basin[J]. Bull Seismol Soc Am, 1996, 86: 1061-1076. | |
| Olsen K B, Archuleta R J, Matarese J R. Three-dimensional simulation of a magnitude 7.75 earthquake on the San Andreas fault[J]. Science, 1995, 270: 1628-1632. | |
| Patera A T. A spectral element method for fluid dynamics:laminar flow in a channel expansion[J]. J Comp Phys, 1984, 54: 468-488. DOI:10.1016/0021-9991(84)90128-1 | |
| Tarrass I, Giraud L, Thore P. New curvilinear scheme for elastic wave propagation in presence of curved topography[J]. Geophys Prospect, 2011, 59: 889-906. DOI:10.1111/gpr.2011.59.issue-5 | |
| Wald D J, Graves R W. The seismic response of the Los Angeles basin, California[J]. Bull Seismol Soc Am, 1998, 88: 337-356. |
 2017, Vol. 38
2017, Vol. 38