2. 黑龙江省普通高校科技创新团队"断层变形、封闭性及与流体运移", 大庆 163318
2. Science and Technology Innovation Team on Fault Deformation, Sealing and Fluid Migration, Daqing 163318, China
雷克子波的波形理论上是斯托克斯微分方程的解,在数学上,雷克子波是一个高斯函数二阶导数(Ricker, 1943, 1944),因此,在时域中是对称的.实际上,地震信号往往是不对称的,更接近于高斯函数的一阶导数或者1.5阶导数(Ricker, 1953;Hosken,1988).然而,高斯函数的各阶导数的振幅谱比较相似,且服从高斯分布,因此,雷克子波经常用于地震分析,例如,波场模拟,反射系数反演等(刘洁等, 2016).
频带的几何中心被称为中心频率.如果推导出雷克子波中心频率的解析表达式,就能够找到中心频率和平均频率之间的关系.后者是一个统计量,可以从地震数据的离散傅里叶谱得到.在已发表的文献中,通常使用功率谱(Cohen and Lee, 1989, 1990; Barnes, 1993; Loughlin and Tacer, 1997; Loughlin and Davidson, 2001; Carter and Kendal, 2006; Wang, 2014)或振幅谱(Quan and Harris, 1997; Hu et al., 2013)来实现平均频率的计算.我们推导了这两种统计量的解析表达式,证明了采用功率谱估算的平均频率,比采用振幅谱估算的平均频率更接近中心频率.在此基础上推导出n次频谱估算平均频率的方法,并得出当n≈2.15874时,n次谱估算平均频率可近似为中心频率.有的文献(Cohen and Lee, 1989, 1990; Gram-Hansen, 1991; Barnes, 1993)还表明,平均频率的标准差可以被视为半频带宽度.然而,在本文中,我们证明了标准差并不是雷克子波的半频带宽度.我们推导了频带宽度和标准差之间的关系,其中,前者是一个理论参数,后者则是基于雷克子波功率谱或振幅谱的一个统计性估算值.在地球物理分析中,频率量如中心频率和频带宽度可以用来描述地震分辨率(袁野等, 2006; 李红星等, 2013),这些量的变化可以用于测量地下介质的衰减系数(王小杰和印兴耀, 2011; 陈增保等, 2014).然而,野外地震信号不同于雷克子波,后者为高斯函数的二阶导数.如果野外地震信号接近高斯函数的分数阶导数,它们的谱也类似于雷克子波振幅谱.
在本文中,我们分析了雷克子波的特点,描述了频率谱的关键参数.首先定义雷克子波在时间域的子波宽度和在频率域的频带宽度.这两个量分别是根据时间域波峰和频率域波峰的一半所定义的.根据以上二者的定义则引入了一种逆指数方程,该方程的解是一个特殊函数—Lambert W函数(Lambert, 1758; Corless et al., 1996).通过对Lambert W函数的分析,利用它可以推算出雷克子波在频率域的频带宽度(Wang, 2015)和时间域的子波宽度.
1 雷克子波雷克子波在时域定义为

|
(1) |
式中,τ是时间(s),ωp为主频(rad/s).雷克子波在时域是对称的,且均值为0,即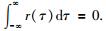
若将雷克子波做归一化处理,其最大振幅为1,雷克子波的宽度就可定义为子波振幅大于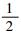


|
(2) |
方程(2) 也可用逆指数方程表示为

|
(3) |
其中,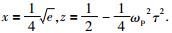
方程(3) 的解可以表示为

|
(4) |
式中,W(x)是Lambert W函数,详细表达请参阅相关文献(Wang, 2015),Lambert W函数曲线如图 1所示.

|
图 1 Lambert W函数 Figure 1 Lambert W function |
若令半时域宽度为τb,结合方程(4),求解方程(2) 可得到半时域宽度表达式为
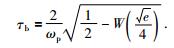
|
(5) |
当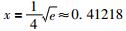
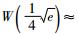

|
(6) |
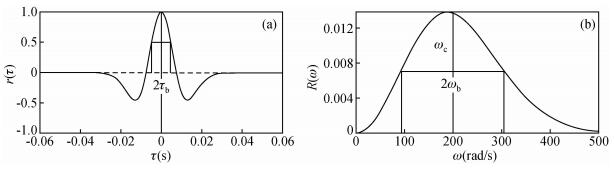
如果主频30 Hz,其对应的角频率60 πrad/s时,由雷克子波的定义,可得到如图 2a所示的雷克子波,其振幅谱R(ω)如图 2b所示,时域宽度约为2τb≈9.4 ms.
|
图 2 雷克子波及其频谱 (a)雷克子波; (b)雷克子波频谱. Figure 2 Ricker wavelet and frequency spectrum (a) Ricker wavelet; (b) Frequency spectrum of Ricker wavelet. |
雷克子波的傅里叶变换表达式为
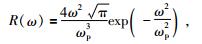
|
(7) |
式中,ω是角频率,该式为雷克子波的振幅谱.
令振幅谱R(ω)对频率的导数为零,即:
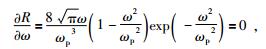
|
(8) |
则有ω=ωp,即主频ωp是对应最大振幅的峰值频率.
雷克子波为高斯函数二阶导数,虽然高斯函数的振幅谱仍然服从高斯分布,但是雷克子波的振幅谱则是乘以参数ω2后的高斯分布,因此频率域的雷克子波并非对称,峰值频率与中心频率(频带的几何中心)不同.雷克子波的频带宽度和中心频率可以表示成Lambert W函数的形式(Wang, 2015).
对于雷克子波的振幅谱,令峰值为
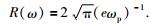
|
(9) |
进而可以推导出逆指数方程为

|
(10) |
该方程可以表示成Lambert W函数形式为

|
(11) |
Lambert W函数是一个多分支函数,当W(x)≤-1时取分支W-1(x),当W(x)≥-1时取分支W0(x),分界点为(-e-1, -1),如图 1所示.频带[ωe1, ωe2]中的两个参数的方程可以表示为
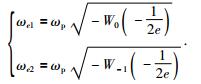
|
(12) |
中心频率的解析表达式为
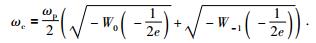
|
(13) |
半频带宽度为

|
(14) |
当x=-(2e)-1时,W0(x)和W-1(x)的近似值为

|
(15) |
因此,频率参数为
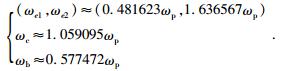
|
(16) |
对一个峰值频率为ωp≈188.5 rad/s的雷克子波来说,频带宽度为2ωb217.7 rad/s,如图 2b.
3 利用功率谱计算频率在实际应用中,我们能够获得地震数据的离散频谱,因此我们可以统计计算出平均频率和频率标准差,用功率谱计算平均频率和标准差的公式为
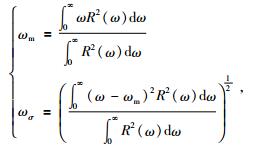
|
(17) |
式中R2(ω)是雷克子波的功率谱,为求解方程(17),我们需要以下三个定积分,推导过程本文不再赘述,公式为

|
(18) |
因此平均频率为
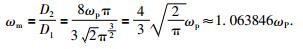
|
(19) |
标准差为

|
(20) |
对于峰值频率为60 πrad/s的雷克子波,平均频率为ωm=200.5 rad/s,中心频率为ωc=199.6 rad/s;双倍标准差为2ωσ=129.6 rad/s,频带宽度为2ωb=217.7 rad/s,使用两个统计参数ωm、ωσ,可以构造一个等效的高斯分布(如图 3b中虚线所示):
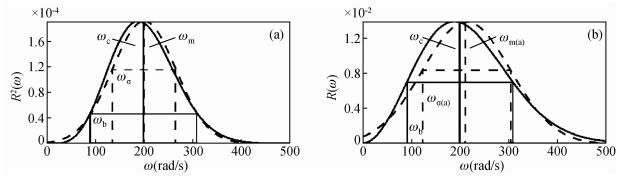
|
图 3 雷克子波功率谱分析及振幅谱分析 (a)用雷克子波功率谱进行的频率分析; (b)用雷克子波振幅谱进行的频率分析. Figure 3 The analysis of Ricker wavelet for the power spectrum and the amplitude spectrum (a)Frequency analysis using the power spectrum of the Ricker wavelet; (b) Frequency analysis using the amplitude spectrum of the Ricker wavelet. |
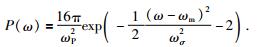
|
(21) |
如图 3a中实线所示,雷克子波的功率谱非常接近于高斯分布,只要计算出平均频率ωm和标准差ωσ,就可以得到峰值频率ωp,然后利用公式(16),得到中心频率ωc和半频带宽度ωb.由于中心频率、平均频率、半频带宽度和标准差都可以利用峰值频率ωp表示,可以推导出中心频率和半频带宽度的表达式为
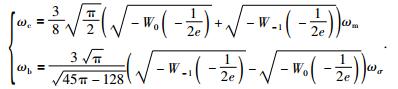
|
(22) |
可知ωc≈0.995534ωm,ωb1.679438ωσ.因为从功率谱得到的平均频率ωm非常接近中心频率ωc,所以实际上,在地震频率分析中我可以近似把平均频率当成中心频率.
4 利用振幅谱计算频率在一些已发表的文献中,根据振幅谱可以计算平均频率.对于雷克子波的振幅谱:|R(ω)|=R(ω),平均频率和标准差可以通过以下公式计算得到:
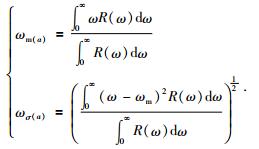
|
(23) |
公式(23) 中的角标“(a)”表明这些量是从振幅谱中计算得到的.振幅谱的平均频率和标准差的计算需要三个定积分公式为

|
(24) |
因此平均频率为
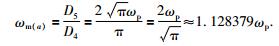
|
(25) |
标准差为
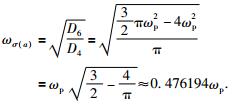
|
(26) |
对峰值频率为60 πrad/s的雷克子波,平均频率为ωm(a)=221.7 rad/s,双倍标准差是2ωσ(a)=179.5 rad/s.作为对比,根据参数ωm(a)、ωσ(a)可构造出等效的高斯函数(如图 3b中虚线所示):

|
(27) |
如果使用振幅谱来估算平均频率和标准差,可以得到以下关于中心频率和半频带宽度的关系式为

|
(28) |
可知ωc≈0.938598ωm(a),ωb1.212682ωσ(a).
如图 3所示,关于功率谱和振幅谱之间的比较,功率谱比振幅谱更集中.根据功率谱估算的平均频率ωm≈1.004486ωc比根据振幅谱估算的ωm(a)≈1.065454ωc更接近中心频率,并且标准差也更小,表达式为

|
另外根据图 3也可看出功率谱比振幅谱更接近于高斯分布.
5 利用n次方谱计算频率通过对运用功率谱和振幅谱估算频率的表达式分析,我们可以总结一个通用的n值来进行平均频率计算,用雷克子波的n次谱计算平均频率和标准差的公式为

|
(29) |
Rn(ω)是雷克子波的n次谱,公式(29) 中的角标“(n)”表明这些量是从n次谱中计算得到的.n次谱的平均频率和标准差的计算需要三个定积分公式为
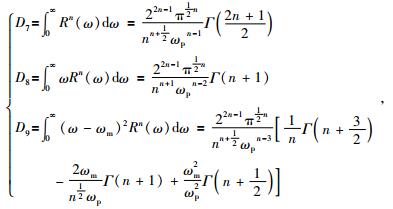
|
(30) |
式中Γ为伽马函数,其表达式为: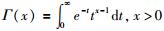
因此平均频率为
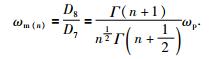
|
(31) |
标准差为

|
(32) |
利用以上两个统计参数ωm(n)、ωσ(n),可以构造一个等效的高斯分布为

|
(33) |
如果使用n次谱来评估平均频率和标准差,可以得到以下关于中心频率和半频带宽度的关系式为
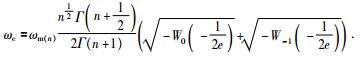
|
(34) |
我们令(34) 式中的系数为R,即:

|
(35) |
另外半频带宽度表达式为

|
(36) |
根据(35) 式可以得出,系数R随n的变化曲线,如图 4所示.当ωm(n)的系数R越接近1时,估算的平均频率越接近中心频率, 即当n≈2.15874时,ωc≈1.00000136ωm(n),并且得到标准差ωσ(n)≈0.33156ωp,比根据振幅谱、功率谱估算所得的平均频率更接近中心频率,并且标准差更小.

|
图 4 系数R与n的关系图 Figure 4 The relationship between the coefficient R and n |
在本文中,我们分析了雷克子波及其频率特性,结论可概括如下:
(1) 本文定义了雷克子波时间宽度和频带宽度,并且用Lambert W函数对它们进行了解析表达.
(2) 平均频率的标准差并不是其他文献中得出的半频带宽度.并根据雷克子波的功率谱和振幅谱建立了理论参数(中心频率和频带宽度)与统计量(平均频率和标准差)之间的数学关系.
(3) 本文推导了雷克子波的谱(功率谱、振幅谱)与平均频率、标准差之间的关系表达式,由于中心频率、平均频率、半频带宽度和标准差都可以利用峰值频率表示,进而得到中心频率与平均频率、半频带宽度与标准差之间的解析表达式.经推导计算得到,根据功率谱估算的平均频率和标准差分别为ωm≈1.004486ωc,ωσ≈0.344ωp;根据振幅谱估算的平均频率和标准差分别为ωm(a)≈1.065454ωc,ωσ(a)≈0.476ωp, 显然采用功率谱估算的平均频率,比采用振幅谱估算的平均频率更接近中心频率,标准差也更小,所以在实际地震频率分析中,我们可以把运用功率谱估算的平均频率当成中心频率.
(4) 在此基础上推导出n次谱估算平均频率的方法,得到关于n次频谱的中心频率与平均频率、半频带宽度与标准差之间的解析表达式.本文得出当n取不同值时,中心频率与平均频率的比例系数R的变化曲线,并得出当n≈2.15874时,R≈1.00000136, 此时n次谱估算的平均频率近似为中心频率.
致谢 感谢国家自然科学基金项目(41574117,41474118)、黑龙江省杰出青年科学基金项目(JC2016006)、大连理工大学海岸和近海工程国家重点实验室开放基金项目(LP1509)、黑龙江省自然科学基金项目(D2015011) 以及东北石油大学研究生创新科研项目(YJSCX2016-002NEPU)对本文研究的资助,感谢审稿专家对本文所提出的宝贵意见和本文编辑对本文所做出的细致修改!| [] | Barnes A E. 1993. Instantaneous spectral bandwidth and dominant frequency with applications to seismic reflection data[J]. Geophysics, 58(3): 419–428. DOI:10.1190/1.1443425 |
| [] | Carter A J, Kendall J M. 2006. Attenuation anisotropy and the relative frequency content of split shear waves[J]. Geophysical Journal International, 165(3): 865–874. DOI:10.1111/j.1365-246X.2006.02929.x |
| [] | Chen Z B, Chen X H, Li J Y, et al. 2014. A band-limited and robust inverse Q filtering algorithm[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 68–75. DOI:10.13810/j.cnki.issn.1000-7210.2014.01.007 |
| [] | Cohen L, Lee C. 1989. Standard deviation of instantaneous frequency[C].//Proceedings of International Conference on Acoustics, Speech, and Signal Processing. Glasgow:IEEE, 4:2238-2241, doi:10.1109/ICASSP.1989.266910. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=266910 |
| [] | Cohen L, Lee C. 1990. Instantaneous bandwidth for signals and spectrogram[C].//Proceedings of International Conference on Acoustics, Speech, and Signal Processing. Albuquerque, NM:IEEE, 2451-2454, doi:10.1109/ICASSP.1990.116086. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=116086 |
| [] | Corless R M, Gonnet G H, Hare D E G, et al. 1996. On the lambert W function[J]. Advances in Computational Mathematics, 5(1): 329–359. DOI:10.1007/BF02124750 |
| [] | Gram-Hansen K. 1991. A bandwidth concept for CPB time-frequency analysis[C].//Proceedings of International Conference on Acoustics, Speech, and Signal Processing. Toronto, Ont.:IEEE, 2033-2036, doi:10.1109/ICASSP.1991.150803. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=150803 |
| [] | Hosken J W J. 1988. Ricker wavelets in their various guises[J]. First Break, 6(1): 24–33. DOI:10.3997/1365-2397.1988002 |
| [] | Hu C H, Tu N, Lu W K. 2013. Seismic attenuation estimation using an improved frequency shift method[J]. IEEE Geoscience and Remote Sensing Letters, 10(5): 1026–1030. DOI:10.1109/LGRS.2012.2227933 |
| [] | Lambert J H. 1758. Observationes variae in mathesin puram[Z]. Acta Helvetica Physico-mathematico-anatomico-bota-nico-medica, 3:128-168. http://www.researchgate.net/publication/240484941_Observationes_vari_in_Mathesin_puram |
| [] | Li H X, Tao C H, Zhao F F, et al. 2013. The resolution study of seismic exploration in biphasic medium[J]. Chinese Journal of Geophysics (in Chinese), 56(3): 995–1002. DOI:10.6038/cjg20130327 |
| [] | Liu J, Zhang J Z, Sun Y B, et al. 2016. Comparison of methods for seismic wavelet estimation[J]. Progress in Geophysics (in Chinese), 31(2): 723–731. DOI:10.6038/pg20160230 |
| [] | Loughlin P J, Davidson K L. 2001. Modified Cohen-lee time-frequency distributions and instantaneous bandwidth of multicomponent signals[J]. IEEE Transactions on Signal Processing, 49(6): 1153–1165. DOI:10.1109/78.923298 |
| [] | Loughlin P J, Tacer B. 1997. Comments on the interpretation of instantaneous frequency[J]. IEEE Signal Processing Letters, 4(5): 123–125. DOI:10.1109/97.575553 |
| [] | Quan Y, Harris J M. 1997. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 62(3): 895–905. DOI:10.1190/1.1444197 |
| [] | Ricker N. 1943. Further developments in the wavelet theory of seismogram structure[J]. Bulletin of the Seismological Society of America, 33(3): 197–228. |
| [] | Ricker N. 1944. Wavelet functions and their polynomials[J]. Geophysics, 9(3): 314–323. DOI:10.1190/1.1445082 |
| [] | Ricker N. 1953. The form and laws of propagation of seismic wavelets[J]. Geophysics, 18(1): 10–40. DOI:10.1190/1.1437843 |
| [] | Wang X J, Yin X Y. 2011. Estimation of layer quality factors based on zero-phase wavelet[J]. Progress in Geophysics (in Chinese), 26(6): 2090–2098. DOI:10.3969/j.issn.1004-2903.2011.06.025 |
| [] | Wang Y H. 2014. Stable Q analysis on vertical seismic profiling data[J]. Geophysics, 79(4). DOI:10.1190/geo2013-0273.1 |
| [] | Wang Y H. 2015. The Ricker wavelet and the lambert W function[J]. Geophysical Journal International, 200(1): 111–115. DOI:10.1093/gji/ggu384 |
| [] | Xu S L. 2009. Common Algorithm Assembly (in Chinese)[M]. Beijing: Tsinghua University Press. |
| [] | Yuan Y, Luo Z W, Li Y. 2006. Influence of the variety of the apparent dominant frequency of Ricker wavelets on the detection effects of chaotic oscillator[J]. Progress in Geophysics (in Chinese), 21(1): 70–73. |
| [] | 陈增保, 陈小宏, 李景叶, 等. 2014. 一种带限稳定的反Q滤波算法[J]. 石油地球物理勘探, 49(1): 68–75. DOI:10.13810/j.cnki.issn.1000-7210.2014.01.007 |
| [] | 李红星, 陶春辉, 赵烽帆, 等. 2013. 双相介质地震勘探纵向分辨率研究[J]. 地球物理学报, 56(3): 995–1002. DOI:10.6038/cjg20130327 |
| [] | 刘洁, 张建中, 孙运宝, 等. 2016. 地震子波估计方法对比研究[J]. 地球物理学进展, 31(2): 723–731. DOI:10.6038/pg20160230 |
| [] | 王小杰, 印兴耀. 2011. 基于零相位子波地层Q值估计[J]. 地球物理学进展, 26(6): 2090–2098. DOI:10.3969/j.issn.1004-2903.2011.06.025 |
| [] | 徐士良. 2009. 常用算法程序集[M]. 北京: 清华大学出版社. |
| [] | 袁野, 罗正玮, 李月. 2006. Ricker子波视主频的变化对混沌振子检测效果的影响[J]. 地球物理学进展, 21(1): 70–73. |
 2017, Vol. 32
2017, Vol. 32


