2. 东北石油大学电气信息工程学院, 大庆 163318
2. School of Electrical Engineering and Information, North East Petroleum University, Heilongjiang Daqing 163318, China
由于受地质环境与采集条件的影响,地震数据易出现缺失道或空间采样不足等问题,而后续地震数据的处理与解释又对数据的完整性与规则性有很高的要求,因此地震缺失道数据的恢复重建是非常关键的问题.传统地震数据重建方法(Ronen, 1987; Spitz, 1991)受奈奎斯特(Nyquist)采样定理的限制,采样频率至少是信号最高频率的两倍,否则极易出现假频现象而影响重建质量.压缩感知(Compressed Sensing,CS)理论(Candes et al., 2006; Donoho, 2006)依靠信号本身的稀疏性和观测方式的非相关性,只要信号在某个变换域上是稀疏或可压缩的,就可以用一个与稀疏表示基不相关的测量矩阵对信号进行降维观测,并在接收端通过求解最优化问题,以较高的概率根据其低维观测值,高精度重建原始信号,为欠采样率下地震数据的重建问题提供了新思路.目前基于压缩感知的地震数据重建方法逐渐引起国内外学者的关注(Herrman and Hennenfent, 2008; 刘成明等, 2016),其重点研究的问题集中于:(1) 地震数据不相关的观测方法(王本锋等, 2015);(2) 地震数据最优的稀疏表示(Ma and Plonka, 2010);(3) 重建模型最优化的求解算法(白兰淑等, 2014),上述一系列问题中地震数据最优的稀疏表示方法是提高重建效果的关键.传统地震数据稀疏表示的方法有Fourier变换(陈双全和李向阳, 2015)、Radon变换(陈潜等,2015)、Wavelet变换(王晓凯等,2016)等,Fourier变换是一种全局变换,没有局部化分析功能,基于Fourier变换的重建方法容易产生吉布斯现象;Radon变换能够较好地捕捉地震数据中的直线特征,但地震波前在空间上通常呈曲线状;Wavelet是一种时频域的局域性变换,因而能有效表示各向同性的点奇异特征,虽然在地震数据处理方面表现出一定能力,但在边界和波前奇异线条附近存在不光滑和模糊现象.近年来发展的多尺度几何分析技术由于具有良好的多尺度性、多方向性和各向异性,更加适合稀疏表示地震波前特征,在地震数据处理中得到了广泛应用,如Ridgelets变换(包乾宗等, 2007)、Curvelet变换(张岩等, 2015;吴蔚等, 2016; Liu et al., 2016)等方向性变换也逐渐应用于地震数据重建等处理,并取得了较好的效果.虽然Ridgelets变换对直线奇异函数具有良好的逼近性能,但对于地震数据包含的曲线奇异函数,不具有最优的逼近能力.Curvelet变换(Candès and Donoho, 2004)由于具有良好的方向性、局部性与各向异性, 可以捕获到各个方向上地震数据的同相轴信息,进而很好地稀疏表示,在地震数据处理领域逐渐得到重视,但是Curvelet变换对于简单的纹理模型,如地震波前,不具有最优的稀疏表能力.
波原子变换(Wave Atoms Transform) (Demanet and Ying, 2007)是一种特殊的二维波包的变形,与Curvelet相比,其基的支撑区间是各向同性的,而其每个波包的振动周期和支撑尺寸满足抛物尺度关系,即波长约等于支撑尺寸的平方,在这个意义下可以简单地将波原子理解为方向小波和Gabor原子的插值.相对Wavelet、Gabor和Curvelet而言,波原子对于简单纹理模型具有最优的稀疏表示,对于给定的精度,只需要O(N)个波原子系数就可以表示,但需要O(N3/2)个Curvelet系数,O(N2)个Wavelet系数和Gabor系数才能达到同样的精度.陈书贞等(2010)将波原子变换引入图像的压缩感知重构处理中,由于波原子可以有效稀疏表示图像的纹理区域,因此得到了较好的重构效果.杨宁等(2011)利用波原子具有准确稀疏表示地震波前曲线的特点,通过系数相关性的方法对叠前地震数据进行去噪处理,具有较高的信噪比.
本文提出基于波原子域的地震数据压缩感知重建算法,在波原子域建立基于压缩感知框架的地震数据重建正则化模型,通过Landweber迭代算法反演求解L1范数最小优化问题,结合指数阈值收缩模型逐步促进编码系数的稀疏程度,保留地震数据主要特征,采用循环平移技术抑制重建数据中的噪声,实验结果表明本文算法重建数据反射同相轴清晰、连续性好,有利于后续地震资料的处理和解释.
1 波原子变换 1.1 波原子变换原理波原子(Wave atoms)是一种特殊二维波包的变形,实现了多尺度、方向性、和局域性较好的权衡.每个小波包的振动周期和支撑尺度满足抛物线函数,即波长约等于支撑尺寸的平方,相对于Wavelet,Gabor和Curvelet而言,波原子对于振荡函数(简单的纹理模型)具有最优的稀疏表示,因此具有较好的纹理保持性能.
1.1.1 波原子定义在二维空间考虑波原子形式的定义,记x=(x1, x2),Fourier变换为
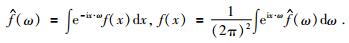
|
(1) |
设波原子为φμ,下标μ=(j, m, n)=(j, m1, m2, n1, n2),其中j、m1、m2、n1、n2均为整数,定位相空间中的点(xμ, ωμ),其中,
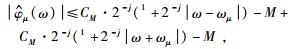
|
(2) |
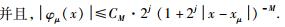
|
(3) |
以上两个条件是对波原子在时频局部化约束下的定性描述.
1.1.2 波原子构造在一维空间中,假设g为实值无穷可微的冲击函数,支撑区间为[-7π/6, 5π/6].当|ω|≤π/3时,满足:
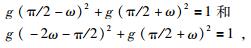
|
(4) |
利用g定义:
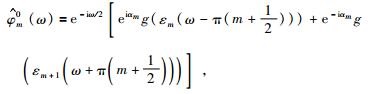
|
(5) |
其中,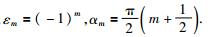
选择适当的m,使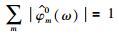

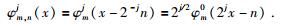
|
(6) |
虽然{φm, nj(x)}也称作波包(Villemoes,2002),但它与标准小波包有着本质的差异,其在空域与频域都具有一致有界局部化性质,这一点对于波原子的构造及其性质起着至关重要的作用.对于一维信号f(x),其波原子变换可视为
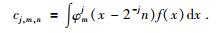
|
(7) |
进一步,由Plancherel公式,有:

|
(8) |
在二维空间中,波原子的构造可以通过一维波原子实现.设一维波原子为φmj(x-2-jn),μ=(j, m, n),m=(m1, m2),n=(n1, n2),令:
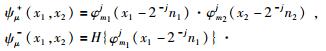
|
(9) |
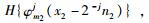
|
(10) |
其中H{·}表示Hilbert变换.则ψμ+(x1, x2)和ψμ-(x1, x2)都是规范正交基(事实上,它们是一对张量形式的波原子正交基),于是其组合

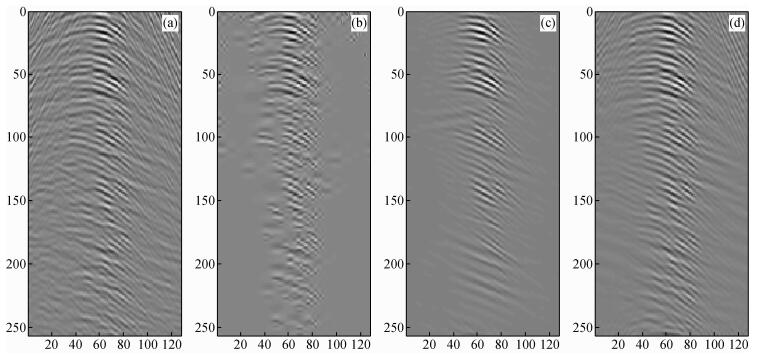
地震数据中的同相轴构成丰富的曲线状纹理,波原子变换对地震数据具有较好的稀疏逼近特性.如图 1a所示的地震数据包含256个采样点、128个记录道,分别采用小波变换、波原子变换、Curvelet变换3种不同的稀疏表示方法得到的系数数目如表 1所示,Curvelet得到的系数最多,小波得到的系数最少.分别取其中2000个最大的系数重构数据,效果分别如图 1b、c、d所示,可见波原子重构效果最好,Curvelet的曲线特征保持能力优于小波,而小波变换重构的整体SNR高于Curvelet. 图 2给出了三种不同稀疏表示方法重构的SNR随系数数目变化的曲线,可见在系数数目相同的条件下,波原子重构得到的SNR均高于小波与曲波变换.从而说明波原子变换得到的变换系数冗余程度相对低,并且能够更准确地稀疏表示地震数据.
|
图 1 不同稀疏表示方法重构效果对比 (a)原始数据;(b)小波重构;(c)波原子重构;(d)Curvelet重构. Figure 1 Comparison of reconstruction results with different sparse representation methods (a) Original data; (b) Wavelets reconstruction; (c) Wave atoms reconstruction; (d) Curvelet reconstruction. |
|
|
表 1 不同稀疏表示方法得到系数的数目 Table 1 The number of coefficients for different sparse representation methods |

|
图 2 不同稀疏表示方法随系数数目变化重构的SNR曲线 Figure 2 SNR curves of different sparse representation methods with the number of coefficients |
设完整的二维地震数据为f(Nt×Nr),Nr是检波器坐标样本数,Nt是时间轴坐标样本数,设V是向量化算子,f向量化后得x=V(f),x为(NtNr)向量.欠采样地震资料设为q(Nt×Mr),Mr < Nr,向量化后得y=V(q),y为(NtMr)维向量,则欠采样地震数据可以表示为

|
(11) |
R是一个二元采样矩阵,从x采样得到y,相当于从完整的地震资料f中Nr道抽取Mr道数据.因为Mr < Nr,显然式(11) 是欠定的方程组,无法根据y求解x,设地震资料x在Wave atoms变换域W下系数为α,有x=W-1α,W-1是W的反变换,则:
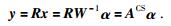
|
(12) |
在具备地震数据在Wave atoms域变换系数是稀疏的先验知识,和感知矩阵ACS满足有限等距性质(Restricted Isometric Property, RIP)(Candès, 2008)的前提下,为通过y恢复x提供了理论保证.求解欠定方程组(11) 的问题转化为L1范数优化问题,公式为
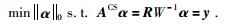
|
(13) |
求解式(13) 是极不稳定而且是NP难的非凸优化问题.在R和W不相关的条件下,可以转为求解一个等价的、更加简单的L1范数优化问题,公式为

|
(14) |
使问题转化为求解一个凸优化问题,进而可解.由于α是稀疏的,可以通过不断促进α的稀疏性通过式(15) 进行反演求解.公式为
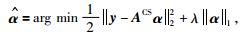
|
(15) |
其中λ是平衡因子,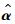
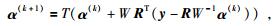
|
(16) |
其中T为阈值算子,公式为
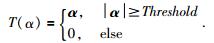
|
(17) |
冷却阈值法每次迭代缩减阈值Threshold,可以找到离超平面y=Rx距离最近的向量,对应式(15) 中
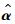
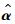
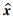
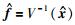
本文提出的地震数据重建过程中,利用波原子域冷却阈值迭代法反演求解L1最优化问题,由于波原子变换缺乏平移不变性,易在地震数据缺失道邻域产生伪吉布斯现象,导致重建数据失真,该失真与地震数据缺失道的位置密切相关.在图像处理领域Coifman和Donoho(1995)提出的循环平移技术(Cycle Spinning),通过对含噪声图像进行循环平移、阈值去噪、逆向循环平移,每次平移后的图像进行阈值去噪会使伪吉布斯现象出现在不同的地方,针对图像行和列方向上的每组平移量都会得到一个不同的去噪结果,对所有去噪结果进行线性平均,抑制噪声.循环平移技术对地震数据可分别在时间轴和检波器轴上进行平移,设Si, j表示平移量为i、j(i=0, 1, 2…K1,j=0, 1, 2…K2,K1和K2分别为时间轴和检波器轴最大平移量)的循环平移算子,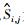

|
(18) |
其中,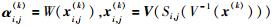
最大平移量K1和K2下(K1=0, 1, 2…Nt,K2=0, 1, 2…Nr),对应的重建地震数据向量可以表示为:
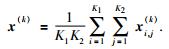
|
(19) |
地震数据重建过程中,阈值收缩迭代参数的选择方式对重建效率有重要影响.由于欠采样地震数据曲线状的波前信息被随机缺失的地震道所打断,在波原子域表现为噪声特征,且迭代初期该噪声的强度相对较大,阈值收缩的速度需要相对加快,加速噪声的去除;在迭代接近结束时,噪声相对较小,阈值收缩速度应该适当放缓,加强地震数据的细节信息的保留.线性变化的阈值收缩模型无法满足上述需求,Gao等(2010)在凸集投影(Projection Onto Convex Sets,POCS)框架下,利用指数型阈值集合模型在Fourier域进行地震数据重建,相对于线性模型阈值可以有效减少迭代次数,提高重建效率,因此本文提出波原子域的指数阈值收缩模型,指数阈值函数表示为
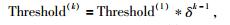
|
(20) |
其中k为迭代次数,Threshold(1)为初始阈值,δ为阈值收缩因子.
3 波原子域地震数据压缩感知重建算法基于波原子域稀疏表示的地震数据压缩感知重建算法的总体思想是:通过Landweber迭代算法反演求解提出的正则框架下L1范数最优化问题,每次迭代结合循环平移技术抑制重建数据中的噪声,采用指数阈值收缩模型逐步促进编码系数的稀疏程度,逼近原始地震数据.具体算法描述如下:
【算法1】:基于波原子域的地震数据压缩感知重建算法
算法步骤:
输入:给定迭代停止参数τ,最大迭代次数L,阈值收缩因子δ,地震数据观测采样矩阵R,地震欠采样观测数据q.
输出:重建地震数据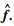
(1) 初始化:迭代计数器k=1,初始阈值Threshold(1),阈值收缩因子δ,最大循环平移量K1和K2,Wave Atoms变换算子为W,向量化算子V,y=V(q),重建初值为x(1)=RT(y).
(2) 重建处理过程:

|
实验的硬件平台采用双核CPU主频3.3 G的Intel I5微机,内存容量为4 G.系统软件为32位Windows7操作系统,仿真实验软件使用Matlab R2013b.实验用例分别采用合成地震数据、marmousi模型数据,以及实际地震数据.地震数据重建效果的衡量指标采用信噪比(SNR)与峰值信噪比(PSNR)分别为
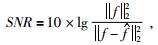
|
(21) |

|
(22) |
其中MSE为原始完整地震数据与重建后地震数据均方误差.
4.1 合成地震数据实验图 3a是截取原始合成单炮地震数据部分记录,包括128个记录道,128个采样点,图 3b为随机去除50%记录道后得到的欠采样数据,图 3c为本文算法迭代200次的效果,重建后PSNR约提高11.9 dB左右,SNR约提高6.6 dB左右,且地震数据的同向轴方向性与连续性保持较好,图 3d给出了原始地震数据与重建地震数据的差值图,可见本文算法重建得到的误差较小,图 4a是SNR随迭代次数的变化曲线,随着迭代次数的增加,重建效果不断增强,最后算法取得收敛,SNR基本稳定在最大值,从而说明本文算法具有较好的收敛性与稳定性.图 4b给出了阈值随迭代次数增加的变化曲线,迭代初期阈值缩减相对剧烈,以加速去除缺失地震道而产生的噪声,迭代后期阈值收缩相对缓慢,有利于地震数据细节的保留.
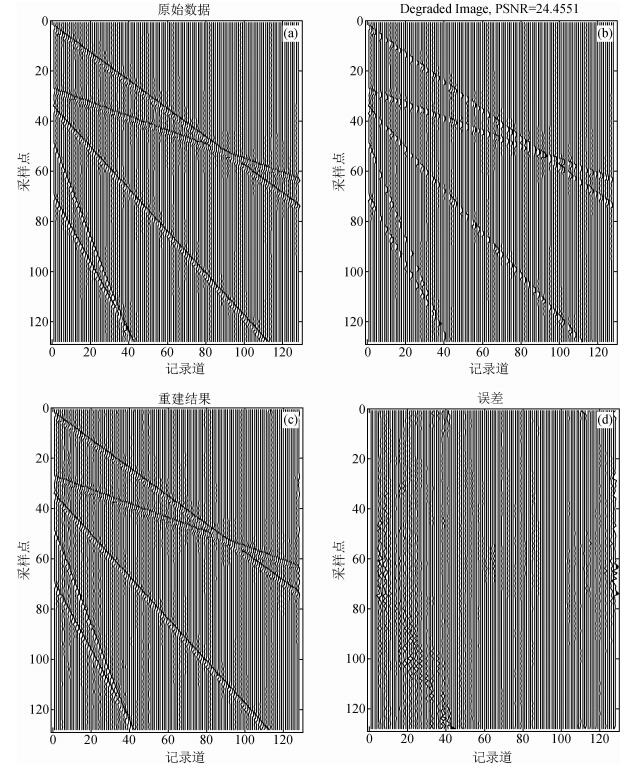
|
图 3 合成地震数据实验 (a)原始地震数据;(b)随机去除50%道欠采样地震数据;(c)本文算法重建数据;(d)本文算法重建数据与原始地震数据差值图. Figure 3 Experiment of synthetic seismic data (a) Original seismic data; (b) Under sampled seismic data with random removal of 50% traces; (c) Reconstruction data of the proposed algorithm; (d) The difference map between the reconstruction data of the proposed algorithm and the original seismic data. |
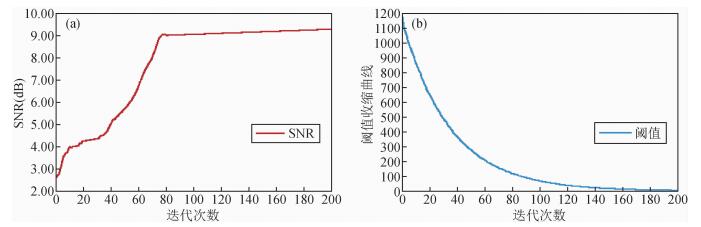
|
图 4 (a) SNR随迭代变化曲线;(b)阈值随迭代变化曲线 Figure 4 (a) PSNR curve with iteration-varying; (b) Threshold curve with iteration-varying |
在Marmousi模型数据中随机抽取单炮数据,截取原始地震数据200道,每道256个采样点,如图 5a所示,去除抽取40%记录道后得到的欠采样数据如图 5b所示,图 5c给出了本文算法重建效果.由于双树复小波(Dual-tree Complex Wavelet Transform, DTCWT)和Curvelet变换具有较好的方向性,二者是地震数据处理领域应用比较广泛的稀疏表示方法,接下来给出与DTCWT、Curvelet两种变换的重建效果对比,图 5d是DTCWT稀疏表示后阈值收缩迭代重建效果,可见重建后数据质量得到一定的改善,但在同相轴密集区域误差较大.图 5e是Curvelet稀疏表示后阈值收缩迭代重建效果,重建地震数据中同向轴比较连续,但在连续缺失多道处仍存在较大的误差.
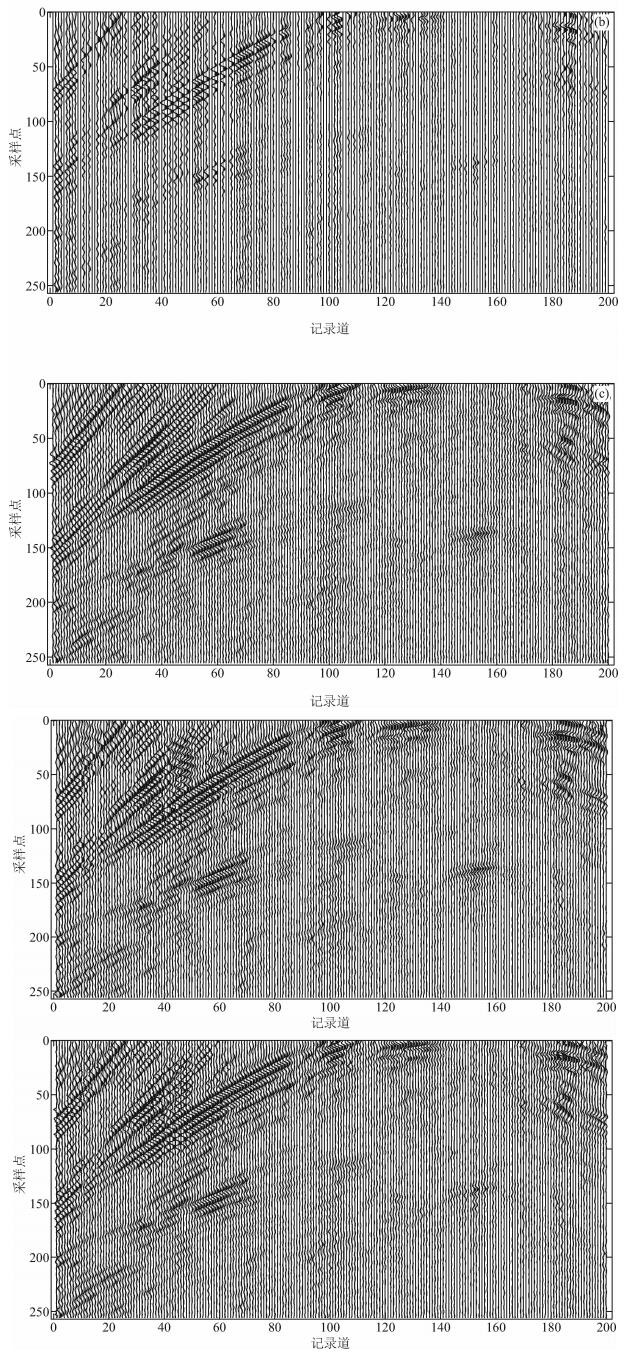
|
图 5 不同算法重建效果对比 (a)原始地震数据;(b)去除40%地震道效果;(c)本文算法重建效果;(d)DTCWT重建效果;(e)Curvelet重建效果. Figure 5 Reconstruction result comparison of different algorithms (a) Original seismic data; (b) Under sampled seismic data with random removal of 40% traces; (c) The reconstruction data of proposed algorithm; (d) The reconstruction data of DTCWT transform; (e) The reconstruction data of curvelet transform. |
表 2分别给出了DTCWT重建、Curvelet重建、未采用循环平移技术的波原子域线性阈值收缩与指数阈值收缩,及本文算法在不同的地震道采样率下的重建效果对比,可以得出,随着采样率的增加,各个算法的重建效果不断增强,本文算法在各个采样率下均能取得相对好的重建效果.
|
|
表 2 各算法在不同地震道采样率下的重建PSNR对比 Table 2 PSNR comparison of each algorithm under different sampling rates of seismic trace |
表 2所述各种重建算法在一次迭代过程中,DTWCT重建算法的运行时间为0.06 s,Curvelet重建算法的运行时间为0.13 s,未采用循环平移技术的波原子域线性阈值收缩与指数阈值收缩的运行时间为0.20 s,本文算法为0.81 s.不同重建算法计算量的主要区别在于进行变换与反变换运算的次数及复杂度.本文算法由于采用循环平移技术,在一次迭代中需要进行多次变换与反变换,而前4种算法在一次迭代过程仅需要一次变换与反变换,因此运行时间少于本文算法.由于DTWCT变换、Curvelet变换,波原子的计算复杂度依次增加,故运行的时间也依次增加.考虑地震道的缺失数据仅存在于检波器轴,而时间轴数据完整,本文仅在检波器轴进行循环平移,每次迭代采用4种方式平移,每种方式均需要进行一次变换与反变换,因此本文算法运行时间是未采用循环平移技术的4倍左右.
4.3 实际地震数据实验图 6a为某区海洋实际叠后地震数据,选取500道,每道400个采样点,采样间隔为1 ms,该数据中既包含强能量、连续性好的同相轴,又包含能量弱的、连续性差的信号,及部分噪声,重建处理难度较大.图 6b为随机去除50%的地震道后的数据,图 6c为本文算法重建结果,从图 6c中可见各缺失道均得到了很好的恢复,地震同相轴较为光滑、连续,其中强振幅同相轴恢复效果尤为明显.

|
图 6 (a) 实际叠后地震数据片段;(b)采样率为50%的欠采样数据;(c)本文算法重建效果 Figure 6 (a) The fragment of post stack seismic data; (b) The under sampled data of 50% sampling rate; (c) The reconstruction data of proposed algorithm |
为提高缺失地震数据的重建效果,本文在压缩感知框架下研究了基于波原子稀疏表示的地震数据重建.通过理论分析与模型实验可以得到以下结论:
(1) 利用波原子域有效稀疏表示地震数据的特点,建立的压缩感知重建求解模型是有效的.
(2) 结合循环平移技术,可以克服波原子缺乏平移不变性而引起重建失真的问题,抑制重建数据中的噪声.
(3) 地震数据重建迭代过程中,指数阈值收缩模型更适合促进编码系数的稀疏程度,去除波原子域由缺失道引起的噪声,反演逼近原始地震数据.由于本文算法在每次循环平移过程均需要进行波原子变换与反变换操作,从而增加了算法的运行时间,因此提高算法的运行效率是我们下一步研究的重点.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Bai L S, Liu Y K, Lu H Y, et al. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics (in Chinese), 57(9): 2937–2945. DOI:10.6038/cjg20140919 |
| [] | Bao Q Z, Gao J H, Chen W C. 2007. Ridgelet domain method of ground-roll suppression[J]. Chinese Journal of Geophysics (in Chinese), 50(4): 1210–1215. DOI:10.3321/j.issn:0001-5733.2007.04.030 |
| [] | Candès E J. 2008. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 346(9-10): 589–592. DOI:10.1016/j.crma.2008.03.014 |
| [] | Candès E J, Donoho D L. 2004. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities[J]. Communications on Pure and Applied Mathematics, 57(2): 219–266. DOI:10.1002/cpa.10116 |
| [] | Candes E J, Romberg J, Tao T. 2006. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 52(2): 489–509. DOI:10.1109/TIT.2005.862083 |
| [] | Chen Q, Fu C W, Liu J H, et al. 2015. Coherent integration based on random pulse repetition interval Radon-Fourier transform[J]. Journal of Electronics & Information Technology (in Chinese), 37(5): 1085–1090. DOI:10.11999/JEIT140818 |
| [] | Chen S Q, Li X Y. 2015. Seismic resolution enhancement based on the scale characteristics of Fourier transform[J]. Oil Geophysical Prospecting (in Chinese), 50(2): 213–218. |
| [] | Chen S Z, Hao P P, Lian Q S. 2010. Compressed sensing image reconstruction based on sparse image representation using dual-tree complex wavelet and wave atoms[J]. Signal Processing (in Chinese), 26(11): 1701–1706. |
| [] | Coifman R R, Donoho D L. 1995. Translation-invariant de-noising[J]. Neuroimage, 103(2): 125–150. |
| [] | Demanet L, Ying L X. 2007. Wave atoms and sparsity of oscillatory patterns[J]. Applied and Computational Harmonic Analysis, 23(3): 368–387. DOI:10.1016/j.acha.2007.03.003 |
| [] | Donoho D L. 2006. Compressed sensing[J]. IEEE Transactions on Information Theory, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [] | Gao J J, Chen X H, Li J Y, et al. 2010. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 7(3): 229–238. DOI:10.1007/s11770-010-0246-5 |
| [] | Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 173(1): 233–248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [] | Liu C M, Wang D L, Hu B, et al. 2016. Seismic data interpolation based on sparse constraint in Shearlet domain[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 46(6): 1855–1864. |
| [] | Liu W, Cao S Y, Chen Y K, et al. 2016. An effective approach to attenuate random noise based on compressive sensing and curvelet transform[J]. Journal of Geophysics and Engineering, 13(2): 135. DOI:10.1088/1742-2132/13/2/135 |
| [] | Ma J W, Plonka G. 2010. A review of curvelets and recent applications[J]. IEEE Signal Processing Magazine, 27(2): 118–133. DOI:10.1109/MSP.2009.935453 |
| [] | Ronen J. 1987. Wave-equation trace interpolation[J]. Geophysics, 52(7): 973–984. DOI:10.1190/1.1442366 |
| [] | Spitz S. 1991. Seismic trace interpolation in the F-X domain[J]. Geophysics, 56(6): 785–794. DOI:10.1190/1.1443096 |
| [] | Villemoes L F. 2002. Wavelet packets with uniform time-frequency localization[J]. Comptes Rendus Mathematique, 335(10): 793–796. DOI:10.1016/S1631-073X(02)02570-0 |
| [] | Wang B F, Chen X H, Li J Y, et al. 2015. Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain[J]. Oil Geophysical Prospecting (in Chinese), 50(1): 20–28. |
| [] | Wang X K, Gao J H, Chen W C, et al. 2016. Detecting method of seismic discontinuities based on high dimensional continuous wavelet transform[J]. Chinese Journal of Geophysics (in Chinese), 59(9): 3394–3407. |
| [] | Wu W, Qu Z D, He R Z, et al. 2016. Wave field reconstruction and denoise based on Curvelet transform in seismic reflection data[J]. Progress in Geophysics (in Chinese), 31(4): 1506–1512. DOI:10.6038/pg20160413 |
| [] | Yang N, He Z H, Huang D J. 2011. Signal and noise separation method for pre-stack seismic data in wave atomic domain based on coefficient correlation threshold[J]. Oil Geophysical Prospecting (in Chinese), 46(1): 53–57. |
| [] | Zhang Y, Ren W J, Tang G W. 2015. Algorithm of compressed sensing reconstruction of seismic data based on curvelet transform[J]. Journal of Jilin University (Information Science Edition) (in Chinese), 33(5): 570–577. |
| [] | 白兰淑, 刘伊克, 卢回忆, 等. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 57(9): 2937–2945. DOI:10.6038/cjg20140919 |
| [] | 包乾宗, 高静怀, 陈文超. 2007. 面波压制的Ridgelet域方法[J]. 地球物理学报, 50(4): 1210–1215. DOI:10.3321/j.issn:0001-5733.2007.04.030 |
| [] | 陈潜, 付朝伟, 刘俊豪, 等. 2015. 基于随机脉冲重复间隔Radon-Fourier变换的相参积累[J]. 电子与信息学报, 37(5): 1085–1090. DOI:10.11999/JEIT140818 |
| [] | 陈双全, 李向阳. 2015. 应用傅里叶尺度变换提高地震资料分辨率[J]. 石油地球物理勘探, 50(2): 213–218. |
| [] | 陈书贞, 郝鹏鹏, 练秋生. 2010. 基于双树复数小波和波原子稀疏图像表示的压缩传感图像重构[J]. 信号处理, 26(11): 1701–1706. DOI:10.3969/j.issn.1003-0530.2010.11.017 |
| [] | 刘成明, 王德利, 胡斌, 等. 2016. Shearlet域稀疏约束地震数据重建[J]. 吉林大学学报(地球科学版), 46(6): 1855–1864. |
| [] | 王本锋, 陈小宏, 李景叶, 等. 2015. POCS联合改进的Jitter采样理论曲波域地震数据重建[J]. 石油地球物理勘探, 50(1): 20–28. |
| [] | 王晓凯, 高静怀, 陈文超, 等. 2016. 基于高维连续小波变换的地震资料不连续性检测方法研究[J]. 地球物理学报, 59(9): 3394–3407. DOI:10.6038/cjg20160922 |
| [] | 吴蔚, 曲中党, 贺日政, 等. 2016. Curvelet变换在深地震反射数据波场重建中的应用[J]. 地球物理学进展, 31(4): 1506–1512. DOI:10.6038/pg20160413 |
| [] | 杨宁, 贺振华, 黄德济. 2011. 基于系数相关性阈值的波原子域叠前地震资料信噪分离方法[J]. 石油地球物理勘探, 46(1): 53–57. |
| [] | 张岩, 任伟建, 唐国维. 2015. 基于曲波变换的地震数据压缩感知重构算法[J]. 吉林大学学报(信息科学版), 33(5): 570–577. |
 2017, Vol. 32
2017, Vol. 32

