2. 许昌学院数学与统计学院, 许昌 461000
2. School of Mathematics and Statistics, Xuchang University, Henan Xuchang 461000, China
波动方程频率域正演模拟最早由Lysmer和Drake(1972)提出, 他们利用该方法研究了多种介质中波的传播特征;之后Marfurt和Shin等进一步发展了这种方法, Shin(1988)将频率域有限元模型应用于地震波形反演;这些算法都是基于有限元方法.之后Pratt(1990a, b)将频率域有限差分正演应用到井间层析成像和地震成像的反演中.频率域正演模拟的优势在于它采用有限差分算子对频率域弹性波方程进行离散, 不存在时间累积误差;由于每次使用独立的频率正演, 可以灵活选择频带, 方法更适用于并行计算.由于正演前需要建立选择适当的空间采样点数, 且正演过程中需要求解大型的稀疏矩阵方程, 这也给频率域正演模拟的快速发展带来了阻碍.
为克服这些局限性, Jo等(1996)提出了最优化9点差分格式, 极大的减小了数值频散效应;Štekl和Pratt(1998)在Jo的基础上, 将最优化9点差分格式引入到黏弹性介质的弹性波方程;Min等(2000)提出了一种25点差分格式, 通过计算最优化系数来减小数值频散, 且减小了空间采样点数;吴国忱教授(吴国忱和梁锴, 2005; 吴国忱等, 2007)分别将25点差分格式应用于VTI和TTI介质的正演模拟;Gu等(2013)提出了一种21点差分格式对二维弹性波进行了数值模拟, 该方法较25点差分格式能够保持精度相当且减少15%的计算内存和计算时间.此外, 还有一些学者在声波频率域数值模拟(马晓娜等, 2015)、标量波频率域正演(任浩然等, 2009;李美娟等, 2016)、各向异性介质频率域数值模拟(孙耀充等,2013;王涛等,2014)等方面进行了分析和对比研究.
作为一种改进, 我们在25点差分格式的基础上提出了15点差分格式的弹性波频率域正演方法, 重新计算了差分系数和频散条件, 并对比了15点差分格式得到的数值解与25点差分格式数值解及二者的的阻抗矩阵.最后给出利用15点差分格式计算的复杂模型.
1 频率域15点有限差分格式推导在二维各向同性介质中, 当体力为零时, 将时间域二维弹性波方程沿时间轴做傅里叶变换, 可得频率域弹性波方程为
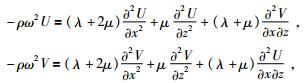
|
(1) |
其中, U(x, z, ω)和V(x, z, ω)分别表示水平位移和垂直位移, ω为角频率, ρ(x, z)为介质密度, λ(x, z)=ρ(vp2-2vs2)和μ(x, z)=ρvs2为拉梅系数.
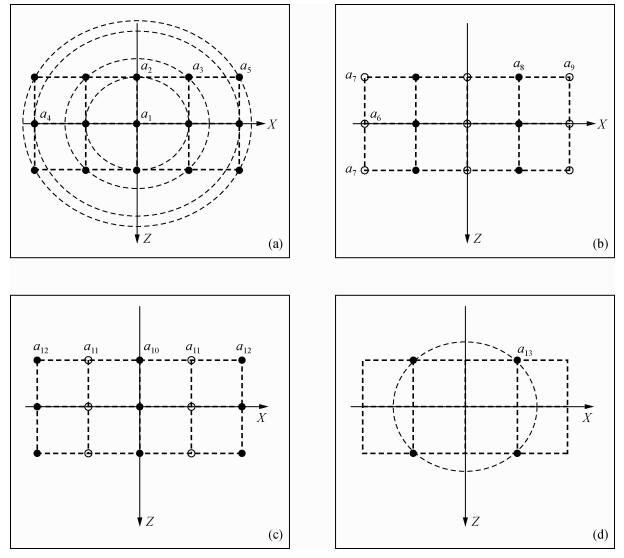
在公式(1) 中共有两个加速项和6个偏微分项, 图 1为利用15点差分格式对这些项进行离散所需的点数分布.
|
图 1 15点加权离散示意图
(a)是加速项系数分布;(b)、(c)、(d)分别对应偏微分项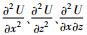 的系数分布.
Figure 1 The weighted discrete representation of 15-point scheme
(a) The coefficient distribution of acceleration term; (b)、(c)、(d) corresponding to the coefficient distribution of 的系数分布.
Figure 1 The weighted discrete representation of 15-point scheme
(a) The coefficient distribution of acceleration term; (b)、(c)、(d) corresponding to the coefficient distribution of 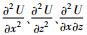 respectively. respectively.
|
对于加速项ρω2U, 将全部网格点的波场值进行加权平均, 假设与计算点距离相同的网格点的加权系数相同.加权系数分布如图 1a所示, 表达式为
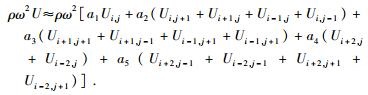
|
(2) |
对于偏微分项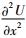
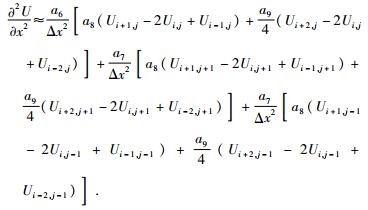
|
(3) |
对于偏微分项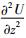
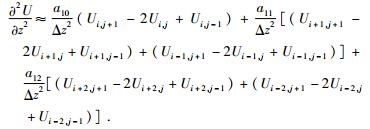
|
(4) |
对于偏微分项
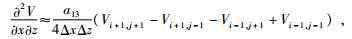
|
(5) |
同理, 可以构造其他几项的差分算子.
将这些差分算子带入公式(1) 中并进行适当整理后, 可以得到如下形式的一个矩阵方程为
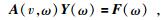
|
(6) |
这里, 假设计算区域网格数为Nz×Nx, 记N=Nz×Nx, 则A是一个2N×2N的阻抗矩阵, Y是待求解的一个2N×1的波场值(包含U, V), F大小为2N×1, 表示震源项.
2 加权系数及网格频散分析根据Min等(2000)的25点相速度频散公式, 可以得到15点相速度频散公式为

|
(7) |
其中, 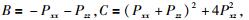
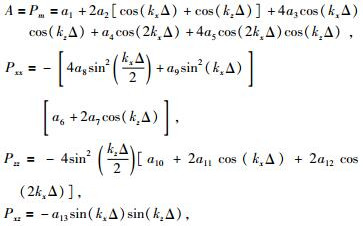
|
这里, Vp为纵波速度, Vs为横波速度, Vph为纵波相速度, Vsh为横波相速度, Gs是横波波长内的网格点数, 网格间距Δx=Δz=Δ, 波数kx和kz均为波传播方向与X轴夹角θ的函数, a1~a13为加权系数.
为计算加权系数a1~a13, 令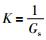

|
(8) |
综合考虑每一横波波长内网格数的倒数K、波传播角度θ、泊松比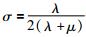
a1=0.6410, a2=0.1057, a3=0.0093, a4=0.0050, a5=0.0076, a6=1.0589, a7=0.0038, a8=-1.1013, a9=1.0101, a10=0.0033, a11=0.5164, a12=0.3259, a13=-0.0530.
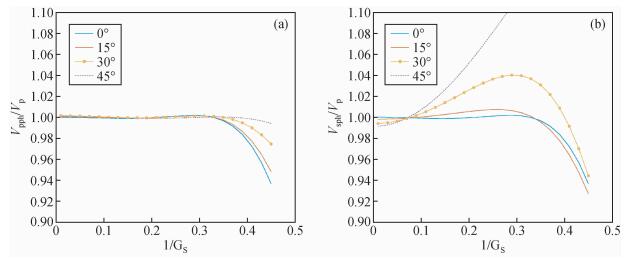
根据这一组系数及相速度频散公式(7), 可以得到在不同网格大小、不同角度、不同泊松比情况下的相速度频散曲线, 图 2、图 3分别是在泊松比为0.1的条件下, 15点和25点差分格式下的相速度频散曲线, 通过计算可以得到, 要使相速度误差控制在±1%内, 15点差分格式每一横波波长内需要10个网格以上, 25点差分格式中需要3.3个网格以上, 即横波速度2000 m/s, 频率25 Hz条件下, 15点格式网格间距最大为8 m, 25点格式网格间距最大可以为24.24 m, 15点格式网格间距要求略小一些.
|
图 2 15点差分格式相速度频散曲线(泊松比σ=0.1) Figure 2 The phase velocity dispersion curve of 15-point difference scheme (Poisson's ratio σ=0.1) |

|
图 3 25点差分格式相速度频散曲线(泊松比σ=0.1) Figure 3 The phase velocity dispersion curve of 25-point difference scheme (Poisson's ratio σ=0.1) |
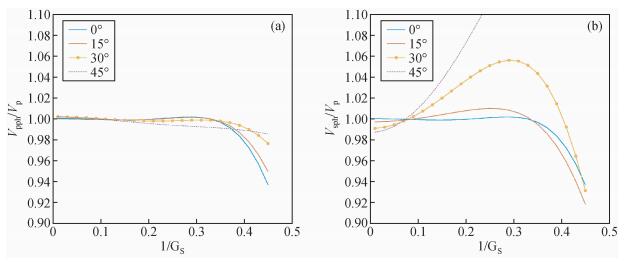
另外, 泊松比也是影响频散的一个因素, 图 4、图 5分别是在泊松比为0.25的条件下, 两种差分格式的频散曲线, 可以发现, 同样使相速度误差控制在±1%内, 15点差分格式每一横波波长内需要增加到25个网格以上, 25点差分格式中要求基本不变.这方面, 15点差分格式变化略大.
|
图 4 15点差分格式相速度频散曲线(泊松比σ=0.25) Figure 4 The phase velocity dispersion curve of 15-point difference scheme (Poisson's ratio σ=0.25) |

|
图 5 25点差分格式相速度频散曲线(泊松比σ=0.25) Figure 5 The phase velocity dispersion curve of 25-point difference scheme (Poisson's ratio σ=0.25) |
地层模型参数为:纵波速度为3000 m/s,横波速度2000 m/s,介质密度2500 kg/m3,差分近似计算网格采用矩形网格, X方向网格数NX=160, Z方向网格数NZ=160;空间步长Δx=Δz=4 m.采样时间间隔1 ms, 记录时间0.3 s, 震源采用为主频25 Hz的Richer子波(垂向), 震源坐标位置为(80, 80), 检波点坐标(120, 120)(以网格数为单位), 边界采用厚度为20个网格的PML边界.
观察将15点格式和25点格式在150 ms时刻波场快照, 可以发现二者几乎一致(见图 6和7).

|
图 6 15点格式175 ms时刻波场快照 Figure 6 The wave field snapshot of 15-point scheme at 175 ms |

|
图 7 25点格式175 ms时刻波场快照 Figure 7 The wave field snapshot of 25-point scheme at 175 ms |
为进一步进行对比分析, 将15点格式与25点格式及解析解(Pilant, 1979)在检波点处的vz、vx分量分别画出, 如图 8所示.15点格式与25点格式的vz、vx分量均能与解析解较好的对应, 在走时及初至方面一直, 仅在个别峰值附近稍有差异, 总体来讲二者模拟精度大致相同.

|
图 8 检波点处vz、vx分量数值解与解析解 Figure 8 Numerical solution and analytic solution of vz and、vx at geophone point |
更进一步, 以归一化vx分量为例给出误差分析, 见图 9.整体上看, 15点格式最大误差值为-0.035, 25点格式最大误差值为0.019, 二者最大误差绝对值均不超过0.04, 15点格式与解析解拟合程度稍弱于25点格式;25点格式整体平均误差为0.0032, 15点格式整体平均误差为0.0059, 二者均能够保持较高精度.

|
图 9 检波点处vx分量数值解与解析解误差 Figure 9 The error of vx between numerical solutions and analytic solution at geophone point |
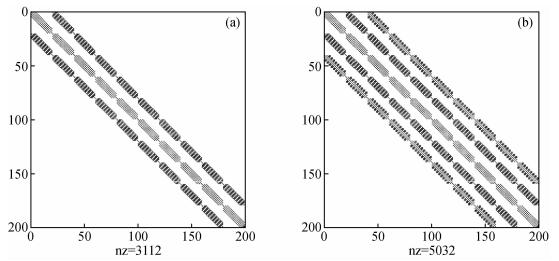
为了直观的比较二者的阻抗矩阵, 假设计算区域网格数为10×10, 则阻抗矩阵大小为200×200, 为15点格式(a)和25点格式(b)的阻抗矩阵中元素分布示意见图 10, 圆点表示阻抗矩阵中非零元素, nz表示阻抗矩阵中非零元素的个数, nz15=3112, nz25=5032.
|
图 10 当计算区域网格数为10×10时, 15点格式(a)和25点格式(b)的阻抗矩阵中元素分布示例 Figure 10 Examples of element distribution in the impedance matrices of the 15-point scheme (a) and the 25-point scheme (b) when the number of calculating grids are 10×10 |
在本文中计算区域网格数为160×160时, 四周均加上20个网格的边界后, 实际计算区域网格大小200×200, 阻抗矩阵大小为80000×80000, nz15=1505632, nz25=2606512, 15点格式阻抗矩阵非零元素比例为0.023%, 25点格式阻抗矩阵非零元素比例为0.04%, 采用稀疏格式存储后, 15点格式阻抗矩阵大小为3.86 M, 25点格式阻抗矩阵大小为7.19 M, 内存占用减少46.31%;对每个频率求解矩阵方程(6) 时, 取多次计算后耗时平均值, 得到15点格式平均耗时2.7931 s, 25点格式平均耗时5.7996s, 耗时减少51.84%.
为了更直观的说明问题, 我们将以上数据放入表格进行对比见表 1.
|
|
表 1 简单模型数值模拟15点格式和25点格式结果对比 Table 1 Comparison of 15-point scheme and 25-point scheme in simple model numerical simulation |
更进一步, 对于文中同一计算区域, 再分别采用8 m、5 m、3.2 m、2 m等网格间距(对应网格数分别为80×80、128×128、200×200、320×320, 每边加上20个网格的PML边界后, 实际计算网格数为120×120、168×168、240×240、360×360), 并将上次4m网格间距计算结果放入, 对比15点格式和25点格式的阻抗矩阵和单次求解方程平均耗时, 列表如表 2和表 3所示.
|
|
表 2 不同网格间距下15点格式和25点格式阻抗矩阵大小(M)对比 Table 2 Comparison of impedance matrix size of 15-point scheme and 25-point scheme with different mesh spacing |
|
|
表 3 不同网格间距下15点格式和25点格式单次求解方程平均耗时(s)对比 Table 3 Comparison of mean time consumption in solving the equation between 15-point scheme and 25-point scheme with different mesh spacing |
在其他网格间距条件下, 检波点处数值解与解析解与4 m网格间距无太大差异, 此处不再对比分析.由表 2、3可以看出, 随着网格数的增加, 阻抗矩阵和单次求解方程平均耗时比率大致保持不变, 但数值会随网格数的增加快速的增长.
3.2 复杂模型复杂模型截取自marmousi2模型, 详见图 11, 计算网格采用矩形网格, X方向网格数NX=300, Z方向网格数NZ=240;空间步长Δx=Δz=5 m.采样时间间隔1 ms, 记录时间1.2 s, 震源采用为主频25 Hz的Richer子波(垂向), 震源坐标位置为横向150网格、纵向10网格, 检波器置于模型第一层所有网格结点位置, 共300个检波器, 边界采用厚度为30个网格的PML边界.

|
图 11 复杂模型的纵波、横波速度 Figure 11 P-wave and S-wave velocity of the complex model |
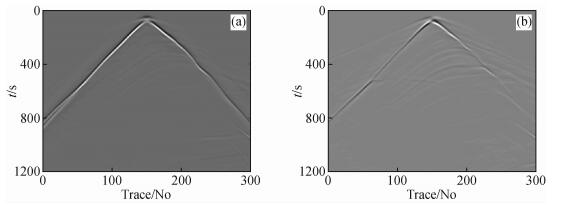
对于计算区域, 分别采用传统25点差分格式和15点差分格式分别进行正演, 单炮记录见图 12、图 13, 通过对比可以发现, 二者的波场记录形态、能量强弱基本一致, 均能够反映出模型的内部构造形态, 说明15点格式在复杂模型下的有效性.
|
图 12 传统25点格式单炮记录(a、b分别对应U、V分量) Figure 12 Single shot recording of traditional 25-point scheme (a、b correspond to U、V components respectively) |
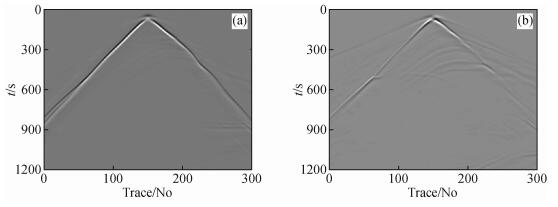
|
图 13 15点格式单炮记录(a、b分别对应U、V分量) Figure 13 Single shot recording of 15-point scheme (a、b correspond to U、V components respectively) |
加上边界后, 正演时实际计算网格数为300×360, 与表 1一致, 表 4给出了相应的指标值, 阻抗矩阵非零元素个数、阻抗矩阵大小和单次求解方程平均耗时的减少量与模型1结果基本一致, 说明, 15点格式和25点格式的这些参数值与实际计算网格数相关, 与模型构造复杂程度无关.另外, 在当前模型炮检排列及网格参数条件下, 数值频散基本消失, 说明该方法具有较好的适应性.
|
|
表 4 复杂模型15点格式和25点格式对比 Table 4 Comparison of 15-point scheme and 25-point scheme in complex model numerical simulation |
频率域15点格式弹性波正演模拟是通过改变空间导数项与质量加速度项来优化阻抗矩阵, 达到使用较少点数实现高精度波场模拟的效果.
4.2通过计算可以发现, 虽然15点格式在泊松比为0.1的条件下, 要使相速度误差控制在±1%内, 每一横波波长内需要10个网格以上, 较25点格式的3.3个网格要多一些, 但常规网格设置均能满足这一要求.
4.3从波场模拟结果来看, 二者与解析解的拟合程度大致相当, 均能保持较高精度.
4.4从内存占用上来分析, 不同网格数及不同模型条件下, 15点格式阻抗矩阵平均占用内存为25点格式的53.43%左右.
4.5从计算耗时角度分析, 不同网格数及不同模型条件下, 15点格式单次求解方程平均耗时为25点格式的57.13%.
4.6综上, 与25点格式相比, 二维弹性波频率域15点差分格式是一种网格设置要求略严格, 精度相当, 用时和内存占用较少的正演方法.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Gu B L, Liang G H, Li Z Y. 2013. A 21-point finite difference scheme for 2D frequency-domain elastic wave modelling[J]. Exploration Geophysics, 44(3): 156–166. DOI:10.1071/EG12064 |
| [] | Jo C H, Shin C, Suh J H. 1996. An optimal 9-point finite-difference frequency-space 2-D scalar wave extrapolator[J]. Geophysics, 61(2): 529–537. DOI:10.1190/1.1443979 |
| [] | Li M J, Wu G C, Chen H. 2016. Frequency domain scalar wave forward modeling method based on an average-derivative method[J]. Progress in Geophysics (in Chinese), 31(6): 2564–2573. DOI:10.6038/pg20160628 |
| [] | Lysmer J, Drake L A. 1972. A finite-element method for seismology[J]. Methods in Computational Physics:Advances in Research and Applications, 11: 181–216. DOI:10.1016/B978-0-12-460811-5.50009-X |
| [] | Ma X N, Li Z Y, Gu B L, et al. 2015. Comparisons and analysis of several optimization finite-differencing schemes in 2D acoustic frequency-domain numerical modeling[J]. Progress in Geophysics (in Chinese), 30(2): 878–888. DOI:10.6038/pg20150254 |
| [] | Min D J, Shin C, Kwon B, et al. 2000. Improved frequency-domain elastic wave modeling using weighted-averaging difference operators[J]. Geophysics, 65(3): 884–895. DOI:10.1190/1.1444785 |
| [] | Pilant W L. 1979. Elastic Waves in the Earth[M]. Amsterdam: Elsevier Press. |
| [] | Pratt R G. 1990a. Frequency-domain elastic wave modeling by finite differences:A tool for cross hole seismic imaging[J]. Geophysics, 55(5): 626–632. DOI:10.1190/1.1442874 |
| [] | Pratt R G. 1990b. Inverse theory applied to multi-source cross-hole tomography, Part 2:Elastic wave-equation method[J]. Geophysical Prospecting, 38(3): 311–329. DOI:10.1111/gpr.1990.38.issue-3 |
| [] | Ren H R, Wang H Z, Gong T. 2009. Seismic modeling of scalar seismic wave propagation with finite-difference scheme in frequency-space domain[J]. Geophysical Prospecting for Petroleum (in Chinese), 48(1): 20–26. |
| [] | Shin C S. 1988. Nonlinear elastic wave inversion by blocky parameterization[Ph. D. thesis]. Tulsa:University of Tulsa. http://www.mendeley.com/research/nonlinear-elastic-inversion-blocky-parameterization/ |
| [] | ŠteklI, PrattK G. 1998. Frequency-domain finite accurate differences visco-elastic modeling by using rotated operators[J]. Geophysics, 63(5): 1779–1794. |
| [] | Sun Y C, Zhang Y T, Bai C Y. 2013. Seismic wavefield simulation in 2D elastic and viscoelastic media:Comparison between four different kinds of finite-difference grids[J]. Progress in Geophysics (in Chinese), 28(4): 1817–1827. DOI:10.6038/pg20130423 |
| [] | Wang T, Zhang Y T, Bai C Y. 2014. Seismic wave field propagation on 2D anisotropic media through ray theory and wave-equation simulation and comparison[J]. Progress in Geophysics (in Chinese), 29(2): 580–587. DOI:10.6038/pg20140214 |
| [] | Wu G C, Liang K. 2005. Quasi P-wave forward modeling in frequency-space domain in VTI media[J]. Oil Geophysical Prospecting (in Chinese), 40(5): 535–545. |
| [] | Wu G C, Luo C M, Liang K. 2007. Frequency-space domain finite difference numerical simulation of elastic wave in TTI media[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 37(5): 1023–1033. |
| [] | 李美娟, 吴国忱, 陈浩. 2016. 基于平均导数的标量波频率域正演数值模拟方法[J]. 地球物理学进展, 31(6): 2564–2573. DOI:10.6038/pg20160628 |
| [] | 马晓娜, 李志远, 谷丙洛, 等. 2015. 2D声波频率域数值模拟中几种有限差分方法的对比分析[J]. 地球物理学进展, 30(2): 878–888. DOI:10.6038/pg20150254 |
| [] | 任浩然, 王华忠, 龚婷. 2009. 标量地震波频率-空间域有限差分法数值模拟[J]. 石油物探, 48(1): 20–26. |
| [] | 孙耀充, 张延腾, 白超英. 2013. 二维弹性及粘弹性TTI介质中地震波场数值模拟:四种不同网格高阶有限差分算法研究[J]. 地球物理学进展, 28(4): 1817–1827. DOI:10.6038/pg20130423 |
| [] | 王涛, 张延腾, 白超英. 2014. 2D各向异性TTI介质中地震波场的射线法和波动方程数值模拟对比[J]. 地球物理学进展, 29(2): 580–587. DOI:10.6038/pg20140214 |
| [] | 吴国忱, 梁锴. 2005. VTI介质频率-空间域准P波正演模拟[J]. 石油地球物理勘探, 40(5): 535–545. |
| [] | 吴国忱, 罗彩明, 梁锴. 2007. TTI介质弹性波频率-空间域有限差分数值模拟[J]. 吉林大学学报(地球科学版), 37(5): 1023–1033. |
 2017, Vol. 32
2017, Vol. 32


