孔隙介质声学是研究声波在多孔介质中的传播及其相互作用的一门学问,传播过程中会普遍观测到波的频散和衰减现象,这种现象在石油物探和测井领域尤为常见,可用于判断储层性质,进行流体识别,进而探明地下油气资源的位置和储量.然而由于实际地层岩石具有非匀质性等复杂的岩石特性,加之实际应用当中对地震资料或声波测井资料反演准确度的要求,建立一个接近实际的孔隙介质弹性理论,来描述弹性波在实际岩石中的传播一直是孔隙介质声学研究的热点和难点问题之一,具有重要的学术价值和很强的应用前景.
唐晓明 (2011, 2012) 考虑了地球表层岩石通常具有的孔隙和裂隙发育的特征,以及这种特征对弹性波传播产生的重要影响,发展了“孔隙、裂隙介质弹性波理论”,本文将其简称为孔裂隙理论.该理论能够合理地解释波在实际岩石的衰减和频散,模拟不同井眼条件下的含孔、裂隙地层井孔声场,从实验室数据反演岩石裂隙参数,发展了评价岩石裂隙发育情况的新技术,并在此基础上,将相应反演方法扩展到声波测井数据的分析处理中,为利用声波测井数据进行地层油气识别提供了一种新方法.
本文系统描述了近年来基于孔裂隙理论的方法、应用研究进展,重点介绍了在此理论基础上发展的声波测井油气识别技术及现场实例,最后对该理论及相应技术今后的改进和发展方向进行了展望和讨论.
1 孔隙介质声学理论研究进展过去的几十年中,人们提出了一些有意义的理论模型来研究孔隙介质中的声学问题,Biot (1956a, b, 1962) 建立了流体饱和孔隙介质中的声学理论,这成为了多相孔隙介质声学研究的经典理论 (王秀明,2009),接着,又出现了比较有代表性的Mavko-Jizba射流理论、BISQ理论、斑块饱和模型和双重孔隙介质理论 (White,1975;White et al., 1975;Mavko and Jizba, 1991;Dvorkin and Nur, 1993;Berryman,2006) 等等,这些理论对实际岩石中波的传播有一定指导意义,但同时也存在理论本身的缺陷和应用上的限制 (唐晓明,2011;王海洋等,2012;孙卫涛等,2015).
对于孔隙结构复杂、微裂隙发育的复杂介质,当岩石空间内充满液体时,由于裂隙与孔隙的压缩性不同,受压时会导致液体在裂隙与孔隙之间产生局部非均匀流动,这与经典Biot理论对基于均匀介质和理想流体的假设相违背.Biot理论只考虑了宏观平均渗流导致的液体与固体间的黏滞摩擦产生的能量耗散机制,其预测的快纵波速度、衰减远远小于实验测量值 (Biot, 1956a, b;Sams et al,1997).为适应新时期非常规油气勘探的需求,需要发展含裂隙的双相孔隙介质声学理论.Eshelby (1957)和Walsh (1965)等人研究了介质的弹性性质会受到裂隙多大的影响.之后,O’Connell和Budiansky (O’Connell and Budiansky, 1974,1977; Budiansky and O’Connell, 1976, 1980) 发表文章,认为裂隙不仅会对介质的弹性性质产生影响,由于尺度的非均匀性,还会造成“挤压喷流”(简称“挤喷流”) 现象,导致介质出现黏弹性质.Mavko和Jizba (1991)考虑了挤喷流效应,修正了Biot理论的低频近似——Gassmann方程,给出了岩石的高频流体饱和体积模量,但公式推导的严格性值得讨论 (宋永佳和胡恒山,2014).Dvorkin和Nur指出,在岩石弹性波速测量中所观测到的很可观的衰减和频散已经不能够用Biot理论给出很好的描述,这主要是因为,Biot理论假设孔隙是均匀分布的,而这一假设忽略了孔隙尺度上所产生的“局部流动”效应对岩石弹性性质的影响.Berryman等人 (2006)发展了双重孔隙介质理论和方法.在这种双孔介质中,局部流动是由不同孔隙结构的两类孔隙之间的流体压力发生变化造成的.从岩石非均匀性的尺度出发,White提出了一种符合沉积岩中普遍存在的流体流动机制的斑块饱和模型,Ba等学者 (2011)在此基础上引入了双孔隙双流体,并给出了非饱和岩石的双孔介质波传播方程 (巴晶等,2012).
1.1 孔裂隙理论模型综合经典的Biot孔隙介质弹性波理论 (Biot, 1956a, b) 和O’connell和Budiansky (1974)的裂隙弹性力学,及Thomsen (1985)的低频的孔、裂隙介质相恰理论,唐晓明 (2011, 2012) 提出了“含孔隙、裂隙介质弹性波动理论”,模型如图 1所示.相对于经典的Biot理论,新的理论增加了裂隙密度和裂隙纵横比这两个描述裂隙介质的重要参数.孔裂隙理论中的饱和岩石模量,公式为
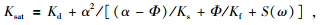
|
(1) |
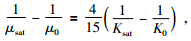
|
(2) |

|
图 1 含孔隙、裂隙岩石的挤喷流分析模型 (唐晓明, 2011; Tang et al., 2012) Figure 1 The squirt flow analysis model for porous media containing cracks (Tang et al., 2011; Tang et al., 2012) |
其中,μ0和Kd是没有挤喷流时的含裂隙岩石弹性模量,可通过Biot自洽理论计算,Ks为岩石基质体积模量.式 (1) 中的S(ω) 定义为随频率变化的挤喷流函数,公式为
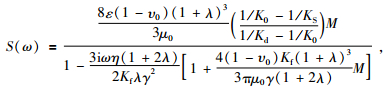
|
(3) |
其中,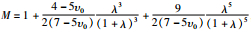
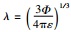
通过对低孔隙致密地层纵、横波速度随着裂隙密度和裂隙纵横比的变化趋势,可以看出孔裂隙理论中引入的两个重要的裂隙参数对识别油气的影响,见图 2,计算时选取的频率为10 kHz (在声波测井频段内).由图 2a可见,裂隙密度的发育会使纵、横波速度逐渐降低,饱含气与饱含油的纵波速度差异明显.从图 2b可以看到,由于纵横比控制着弛豫频率的大小,只有在弛豫频率附近饱含气时的速度才会发生明显变化,而在其他频段,影响较弱.

|
图 2 含孔隙、裂隙岩石的挤喷流分析模型 (改自陈雪莲等, 2014) Figure 2 The squirt flow analysis model for porous media containing cracks (revised from Chen et al., 2014) |
针对唐晓明的孔裂隙模型,宋永佳 (2012)提出一些有待改进的地方,例如:(1) 采用隐式修正封闭体积模量的时候导致了快纵波的低频速度与Biot理论不一致,而Biot的低频极限可以理解为裂隙中的应力得到充分松弛时的特殊情况,未见学术界指出Biot理论的低频情况有何不合理之处;(2) 剪切模量的修正公式在低频极限下不成立;(3) 对排水状态 (而非干燥状态下) 是否会有挤喷机制,未做进一步研究.宋永佳 (2012)考虑了全频域中挤喷流对排水体积模量的影响,但所提理论忽略了液体的可压缩性对裂隙变形的影响.针对此,宋永佳和胡恒山 (2013)推导获得了裂隙液体压强欠松弛时的排水体积模量,并用此模量替换原Gassmann公式中的排水体积模量,计算了全频域中岩石的液体饱和有效体积模量,指出与挤喷流相关的裂隙附加柔度会引起排水体积模量随频率变化,使得孔隙介质呈现黏弹性.低频极限下,他们的慢纵波解答趋向Biot解,快纵波趋向Gassmann公式;在高频时,退化为Mavko-Jizba公式.然而宋永佳和胡恒山 (宋永佳, 2012; 宋永佳和胡恒山,2013) 只认识到了修正K (孔隙介质的排水体积模量),忽略了对Ks (固体基质的体积模量) 和Kφ (孔道体积模量) 的修正,因此讨论了(2014)这种忽略对流体饱和体积模量产生的误差的大小,他们基于双重孔隙介质理论,推导出含孔隙、裂隙的流体饱和岩石的高频体积模量表达式,并与前人已有的结果 (Mavko and Jizba, 1991; Gurevich et al., 2009) 进行比较,考虑裂隙含量对Mavko-Jizba公式适用性的影响.吴国忱等 (2014)将孔裂隙理论扩展到周期性层状地层,讨论了模型的频散和衰减特征,吴建鲁等 (2015)综合考虑了孔隙中硬币型和尖灭型两种裂隙形状 (如图 1所示),建立了含孔裂隙介质声学模型,得到了流体饱和岩石的弹性波频散和衰减特性.
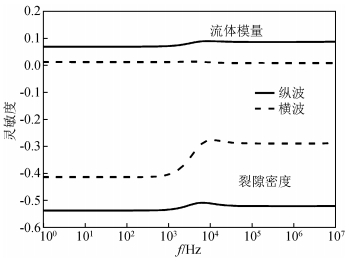
1.2 含孔、裂隙地层声场研究陈雪莲和唐晓明 (2012)应用孔裂隙理论计算了含孔、裂隙地层情况下充流体井眼中的多极子声场,主要是分析了两个裂隙参数——裂隙密度和裂隙纵横比对多极子模式波频散和衰减的影响,为利用声波测井资料得到地层孔、裂隙参数提供了指导.陈雪莲等 (2013, 2014) 应用孔裂隙理论侧重分析了低孔含气地层不同频率下弹性波速度对裂隙密度的响应特征,提出实验室数据反演裂隙参数的思路,并进一步验证了由井孔模式波衰减识别地层含气的可行性,发现多极子波速度和波形对含气饱和度有明显的响应特征,分析了有无泥浆侵入的开孔和闭孔条件下各模式波的激发谱特征,为含气地层的声波测井响应特征提供了参考,从图 3纵波和横波速度对流体模量和裂隙密度的灵敏度模拟效果图可见,在测井频段,纵波速度对流体模量的灵敏度很高,同时孔裂隙理论中引入的参数裂隙密度也会明显影响纵横波速度的大小,这为根据地层速度反演流体模量并进一步确定流体性质提供了依据.许松等 (2014)将孔裂隙理论引入随钻充液井眼地层,主要考查的是地层裂隙密度与含气饱和度对随钻地层条件下井孔多极子模式波速度、衰减等特征的影响,现场实例和交会图能够有效说明孔裂隙理论对随钻声波测井数据的适用性.
|
图 3 纵、横波速度对流体模量和裂隙密度的灵敏度 Figure 3 Sensitivity coefficients of Vp, Vs with respect to fluid modulus and crack density |
伴随着孔裂隙理论的提出,发展了一系列针对实验室、现场测井数据的处理方法,来对岩石的裂隙发育程度及孔隙流体性质进行评价,有效描述了岩心裂隙发育情况,通过反演理论和交会图版技术能够提高识别流体性质的可靠性.
2.1 岩心速度数据重构由于孔裂隙理论能够很好的预测超声实验中岩石纵、横波速度的变化,唐晓明等 (2013)和钱玉萍等 (2014)利用该理论进行了实验研究,给出了不同压力下岩心纵横波速度数据反演岩石裂隙参数的方法.反演的目标函数是通过孔、裂隙理论公式对实验室测量数据做最小二乘拟合得到的,公式为
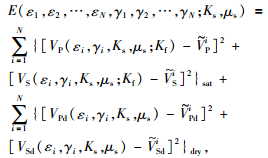
|
(4) |
其中,
根据该方法,本节对一组渤海某区块实测岩心的实验室测量数据进行分析、处理,能够预测出岩石饱和状态下的纵横波速度.
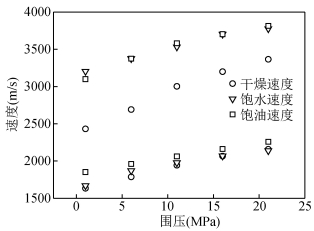
图 4是渤海某区块0~40 MPa围压变化范围内测量的岩心A的纵、横波速度,可见随着围压的增大,速度逐渐增大,且速度的变化趋势在高围压范围逐渐趋于平缓,这里饱油状态下的速度是最后测量的,可能几次测量对岩石有压实效应,饱含油的纵、横波速度除了1 MPa,其他围压下的速度都略大于饱水的纵横波速度,明显不符合一般规律 (这里可认为1 MPa的围压情况下饱含油的岩石速度是准确的).此时为了得到准确的饱含油的纵横波速度,可应用孔裂隙实验数据反演理论对结果进行校正,具体思路是:
|
图 4 不同饱和状态岩心A纵、横波速度随围压变化 Figure 4 Vp, Vs of core A versus confining pressure in different saturated states |
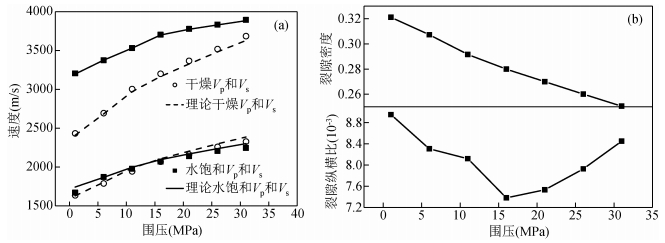
(1) 应用图 5a所示的准确的干燥和饱含水状态下的纵、横波速度数据反演得到岩石的裂隙参数,如图 5b所示,上下分别是裂隙密度和裂隙纵横比.
|
图 5 岩心A实验数据的裂隙参数反演与理论模拟结果 Figure 5 Inversion-fitting between theoretical (curves) and the laboratory (markers) velocities of core A |
(2) 将反演结果 (裂隙密度、裂隙纵横比、岩石骨架体积模量Ks=72.03 GPa和剪切模量μs=39.86 GPa) 代入到孔裂隙理论中,得到图 5a所示的理论纵、横波速度,可见理论结果与实际数据几乎完全重合,意味着反演的参数值使得理论与实验结果符合得非常好.
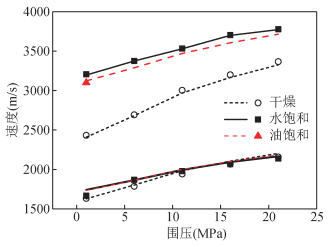
(3) 将该地区油的参数:密度ρoil=840 g/cm3,体积模量Koil=1.2 GPa,黏度ηoil=10 cP,代入孔裂隙理论,得到图 6中的油饱和状态下岩石的速度 (红色虚线),测量与计算的5个压力下的纵横波速度数据如表 3所示,可见反演得到的饱含油的纵波速度相比实验结果普遍降低,而且通过图 6可见均低于饱含水是的岩石纵波速度.在围压为1 MPa时,计算的饱含油的纵波速度与实验数据几乎一致,也进一步证明了反演结果的准确性.
|
图 6 岩心A饱含油纵、横波速度预测结果 Figure 6 The prediction result of Vp, Vs for core A in oil-saturated state |
随着石油、天然气资源勘探开发的深入,对测井油气识别符合率的要求愈来愈高,发展出一系列较为成熟的测井流体识别技术,如电阻率特征判别法、三孔隙度重叠法、阵列声波能量法、纵横波时差法、声阻抗与声波时差重叠法、交会图法以及神经网络识别技术等 (赵佐安等,2002),其中阵列声波测井技术的引入可以提高储层 (特别是致密砂岩储层、碳酸盐岩储层) 评价精度 (章成广等,2004;唐军和章成广,2012;张永军等,2012).然而单一的常规测井解释方法在应用中会受到自身适用性的限制,需要对上述方法进行合理的组合,同时测井资料中缺少对储层的岩石物理表征,近年来发展了一些基于岩石物理的流体识别技术,在致密气藏识别中取得了比较好的应用效果 (洪忠等,2015;许孝凯等,2016).
最近提出的含孔隙、裂隙介质的弹性波动理论,通过对测井频率下纵、横波速度对裂隙密度及流体模量的灵敏度分析 (钱玉萍等,2014),在此声学岩石物理模型基础上发展的声波测井油气识别技术为地层油气识别提供了一个新的解决方案.
孔裂隙理论与实际地层声波测井数据拟合所得的均方误差可作为反演的目标函数,公式为
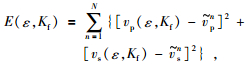
|
(5) |
式中vp、vs代表理论计算得到的纵、横波速度,
下面给出该方法的现场应用实例.研究区块地质情况复杂,物性较差,具有复杂的岩性特征,束缚水饱和度较大,存在低阻油气层,这些都给常规测井解释带来了困难.针对孔隙结构复杂、微裂隙发育的复杂介质,孔裂隙理论具有很好的适应性.图 7显示的是B11井应用孔裂隙理论的处理结果,crackdensity、sq和kf分别代表反演得到的裂隙密度、含烃饱和度和流体模量,最右侧代表解释结论,其余为常规的伽马、井径、电阻率、中子-密度曲线.经实际观测,岩心多含溶蚀孔,偶极横波远探测显示井外溶蚀孔洞发育,因此裂隙密度较大,近50 m的深度剖面上发育油层.序号为95和101的油层电阻率和中子-密度交会指示并不十分明显,流体模量对应有比较清晰的指示.几处非储层位置流体模量同样降低可能是因为该深度段碳酸盐岩发育.值得注意的是含烃饱和度sq是对含油气多少的一个定量的表示,更主要的是结合流体模量kf来识别流体性质.
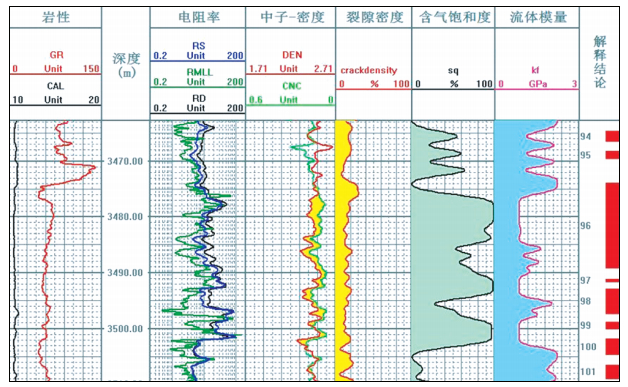
|
图 7 B11井有效储层预测成果图 Figure 7 B11 well effective reservoir prediction result |
图 8是研究区块B11井应用孔裂隙理论反演的处理结果,可以看到在井径变化不大的情况下,流体模量突变位置与解释层段完全一致,流体模量减小的多少与含烃饱和度的大小能够定性的表征流体性质,模量减小量最大的层段对应气层 (黄色),模量减小量最小的层段对应水层 (蓝色),处于二者中间的代表油层 (红色).1820 m处即使中子、密度交会面积较大,但从流体模量变化来看,结合上面的气层和油层,仍可将其定性为水层.
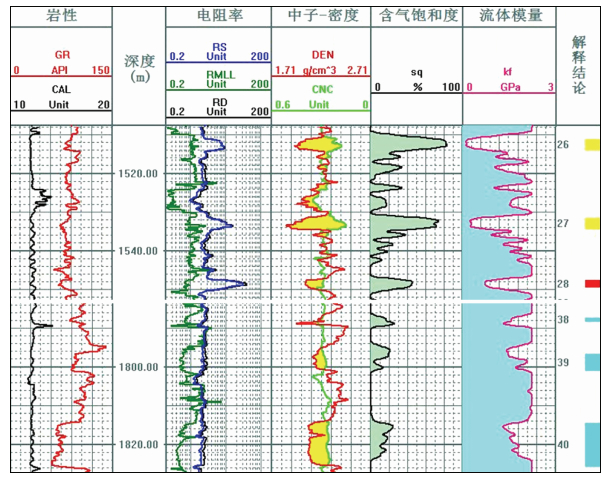
|
图 8 B12井有效储层预测成果图 Figure 8 B12 well effective reservoir prediction result |
研究孔隙流体性质及其含量的岩石物理学工具是vp/vs比与纵波时差的交会图 (唐晓明和郑传汉,2004),应用基于孔裂隙理论的交会图版方法对B区块声波测井数据进行处理分析,可以有效划分储层.
图 9是同一区块两口井的纵横波速度比-纵波时差交会图,两个理论图版的参数相同,孔隙度设为8%,裂隙密度变化范围为0.1~0.35,岩石骨架参数为Ks=30 GPa,μs=10 GPa.由于考虑了裂隙密度的影响,随着含气饱和度增大,岩石纵横波速比会随着含气饱和度增大而明显下降,这就使得油、气、水层 (红点、黄点和蓝点) 的实际数据在图版上有效地分开,从图 9a、b可以看到虽然油和水的纵横波速度比相差不大,但它们的纵波时差有比较明显的区分.两口井的数据点都能够准确投在使用统一参数的图版范围内,说明了图版在同一区块的适用性.
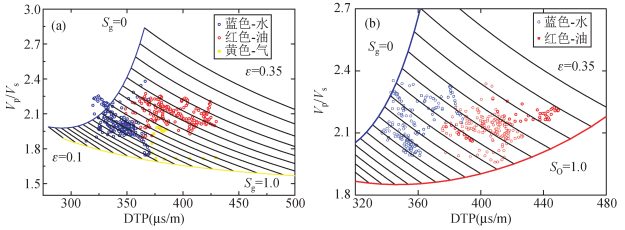
|
图 9 B4井不同裂隙密度下的交会图 Figure 9 Crossplot with different crack densities of B4 well |
本文贯穿了孔裂隙理论从提出到应用的过程,涉及到对理论模型介绍、含裂隙地层的声场研究进展、实验室数据裂隙参数反演、地层油气识别等几个方面.对实际岩石声波测井数据的模拟表明,实际的岩石往往是孔隙、裂隙并存的,因此需要考虑孔隙和裂隙的共同影响后,才能真实地描述岩石介质的弹性波传播特征.人们对基础理论的充分研究展现了孔隙介质声学模型发展的活力,孔裂隙理论在预测岩石饱和速度和地层流体识别方面的有效性也体现了理论的应用价值.而正是由于裂隙介质的裂隙密度和纵横比这两个重要参数对弹性波速的重大影响,我们可以从弹性波速的测量来反演和估计这些参数的值,进而评价和解释地层岩石的裂隙发育状况和识别岩石中所含油气,这将为致密裂隙型油气储层的测井解释和识别提供了一种方法和途径.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Ba J, Carcione J M, Cao H, et al. 2012. Velocity dispersion and attenuation of P waves in partially-saturated rocks:Wave propagation equations in double-porosity medium[J]. Chinese J. Geophys. (in Chinese), 55(1): 219–231. DOI:10.6038/j.issn.0001-5733.2012.01.021 |
| [] | Ba J, Carcione J M, Nie J X. 2011. Biot-Rayleigh theory of wave propagation in double-porosity media[J]. J. Geophys. Res., 116(B6): B06202. |
| [] | Berryman J G. 2006. Effective medium theories for multicomponent poroelastic composites[J]. J. Eng. Mech., 132(5): 519–531. DOI:10.1061/(ASCE)0733-9399(2006)132:5(519) |
| [] | Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅰ. Low-frequency range[J]. J. Acoust. Soc. Am., 28(2): 168–178. DOI:10.1121/1.1908239 |
| [] | Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid[J]. Ⅱ. Higher frequency range[J]. J. Acoust. Soc. Am., 28(2): 170–191. |
| [] | Biot M A. 1962. Generalized theory of acoustic propagation in porous dissipative media[J]. J. Acoust. Soc. Am., 34(9A): 1254–1264. DOI:10.1121/1.1918315 |
| [] | Brie A, Pampuri F, Marsala A F, et al. 1995. Shear sonic interpretation in gas-bearing sands[C].//SPE Annual Technical Conference and Exhibition. Dallas, Texas:Society of Petroleum Engineers, 701-710. |
| [] | Budiansky B, O'Connell R J. 1976. Elastic moduli of a cracked solid[J]. Int. J. Solids Struct., 12(2): 81–97. DOI:10.1016/0020-7683(76)90044-5 |
| [] | Budiansky B, O'Connell R J. 1980. Bulk dissipation in heterogeneous media[J]. Solid Earth Geophys. Geotech., 42: 1–10. |
| [] | Chen X L, Qian Y P, Tang X M. 2013. Infuence of crack on acoustic propagation characteristics in low porosity and low permeability gas reservoir[J]. Journal of China University of Petroleum (in Chinese), 37(4): 88–93. |
| [] | Chen X L, Tang X M. 2012. Numerical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium[J]. Chinese J. Geophys. (in Chinese), 55(6): 2129–2140. DOI:10.6038/j.issn.0001-5733.2012.06.035 |
| [] | Chen X L, Tang X M, Qian Y P. 2014. Propagation characteristics of multipole acoustic logging in cracked porous tight formations[J]. Chinese J. Geophys. (in Chinese), 57(9): 2961–2970. DOI:10.6038/cjg20140921 |
| [] | Dvorkin J, Nur A. 1993. Dynamic poroelasticity:A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 58(4): 524–533. DOI:10.1190/1.1443435 |
| [] | Eshelby J D. 1957. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London. Series A:Mathematical and Physical Sciences, 241(1226): 376–396. DOI:10.1098/rspa.1957.0133 |
| [] | Gurevich B, Makarynska D, Pervukhina M. 2009. Ultrasonic moduli for fluid-saturated rocks:Mavko-Jizba relations rederived and generalized[J]. Geophysics, 74(4): N25–N30. DOI:10.1190/1.3123802 |
| [] | Hong Z, Zhang M G, Zhu X M. 2015. Prediction on lithology and fluid probabilities of tight clastic gas reservoir based on rock physics[J]. Geophysical Prospecting for Petroleum (in Chinese), 54(6): 735–744. |
| [] | Mavko G, Jizba D. 1991. Estimating grain-scale fluid effects on velocity dispersion in rocks[J]. Geophysics, 56(12): 1940–1949. DOI:10.1190/1.1443005 |
| [] | O'Connell R J, Budiansky B. 1974. Seismic velocities in dry and saturated cracked solids[J]. J. Geophys. Res., 79: 5412–5426. DOI:10.1029/JB079i035p05412 |
| [] | O'Connell R J, Budiansky B. 1977. Viscoelastic properties of fluid-saturated cracked solids[J]. J. Geophys. Res., 82: 5719–5735. DOI:10.1029/JB082i036p05719 |
| [] | Qian Y P, Tang X M, Chen X L. 2014. Estimating the rock crack parameters from the velocity data under pressure loading in the laboratory[J]. Well Logging Technology (in Chinese), 38(5): 517–521. |
| [] | Song Y J. 2012. A theoretical study on the attenuation of elastic waves in porous media containing cracks (in Chinese)[MSc thesis]. Harbin:Harbin Institute of Technology. |
| [] | Song Y J, Hu H S. 2013. Effects of squirt-flow in cracks on drained bulk modulus of porous media[J]. Chinese Journal of Theoretical and Applied Mechanics (in Chinese), 45(3): 395–405. |
| [] | Song Y J, Hu H S. 2014a. Variation of effective elastic moduli of a solid with transverse isotropy due to aligned inhomogeneities[J]. Acta Physica Sinica (in Chinese), 63(1): 016202. DOI:10.7498/aps.63.016202 |
| [] | Song Y J, Hu H S. 2014b. High-frequency bulk moduli of fluid-saturated cracked porous rocks[J]. Science China Physics, Mechanics & Astronomy (in Chinese), 44(6): 610–620. DOI:10.1360/SSPMA2013-00092 |
| [] | Sun W T, Liu J W, Ba J, et al. 2015. Theoretical models of elastic wave dispersion-attenuation in porous medium[J]. Progress in Geophysics (in Chinese), 30(2): 586–600. DOI:10.6038/pg20150215 |
| [] | Tang J, Zhang C G. 2012. Application of array sonic logging technology in the identification of carbonate reservoir types[J]. Journal of Oil and Gas Technology (in Chinese), 34(3): 101–105, 109. |
| [] | Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks-an extension of Biot's poroelastic wave theory[J]. Sci. China Earth Sci., 54: 1441. DOI:10.1007/s11430-011-4245-7 |
| [] | Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations[J]. Geophysics, 77(6): D245–D252. DOI:10.1190/geo2012-0091.1 |
| [] | Tang X M, Qian Y P, Chen X L. 2013. Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples[J]. Chinese J. Geophys. (in Chinese), 56(12): 4226–4233. DOI:10.6038/cjg20131225 |
| [] | Thomsen L. 1985. Biot-consistent elastic moduli of porous rocks:Low-frequency limit[J]. Geophysics, 50(12): 2797–2807. DOI:10.1190/1.1441900 |
| [] | Walsh J B. 1965. The effect of cracks on the compressibility of rock[J]. J. Geophys. Res., 70(2): 381–389. DOI:10.1029/JZ070i002p00381 |
| [] | Wang H Y, Sun Z D, Chapman M. 2012. Velocity dispersion and attenuation of seismic wave propagation in rocks[J]. Acta Petrolei Sinica (in Chinese), 33(2): 332–342. |
| [] | Wang X M. 2009. Research progress in acoustics for multiphase porous reservoirs[J]. Applied Acoustics (in Chinese), 28(1): 1–9. |
| [] | White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophysics, 40(2): 224–232. DOI:10.1190/1.1440520 |
| [] | White J E, Mikhaylova N G, Lyakhovitsky F M. 1975. Low-frequency seismic waves in fluid-saturated layered rocks[J]. Izvestija Academy of Sciences. USSR, Physics of the Solid Earth, 11(10): 654–659. |
| [] | Wu G C, Wu J L, Zong Z Y. 2014. The attenuation of P wave in a periodic layered porous media containing cracks[J]. Chinese J. Geophys. (in Chinese), 57(8): 2666–2677. DOI:10.6038/cjg20140825 |
| [] | Wu J L, Wu G C, Zong Z Y. 2015. Attenuation of P waves in a porous medium containing various cracks[J]. Chinese J. Geophys. (in Chinese), 58(4): 1378–1389. DOI:10.6038/cjg20150424 |
| [] | Xu S, Su Y D, Chen X L, et al. 2014. Numerical study on the characteristics of multipole acoustic logging while drilling in cracked porous medium[J]. Chinese J. Geophys. (in Chinese), 57(6): 1999–2012. DOI:10.6038/cjg20140630 |
| [] | Xu X K, Liu M J, Zhu L F, et al. 2016. Tight gas reservoir recognition method based on the rock physics model[J]. Applied Acoustics (in Chinese), 35(2): 116–121. |
| [] | Zhang C G, Jiang W Z, Xiao C W, et al. 2004. On methods of gas-formation indication by using acoustic full waveform log data[J]. Well Logging Technology (in Chinese), 28(5): 397–401. |
| [] | Zhang Y J, Gu D N, Ma S B, et al. 2012. The application of array acoustic wave data to tight sandstone gas reservoir in Tuha oilfield[J]. Well Logging Technology (in Chinese), 36(2): 175–178. |
| [] | Zhao Z A, He X Q, Tang X P. 2002. Logging technology of identifying low-resistivity hydrocarbon reservoirs[J]. Natural Gas Industry (in Chinese), 22(4): 34–37. |
| [] | 巴晶, CarcioneJ M, 曹宏, 等. 2012. 非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程[J]. 地球物理学报, 55(1): 219–231. DOI:10.6038/j.issn.0001-5733.2012.01.021 |
| [] | 陈雪莲, 唐晓明. 2012. 孔、裂隙并存地层中的声波测井理论及多极子声场特征[J]. 地球物理学报, 55(6): 2129–2140. DOI:10.6038/j.issn.0001-5733.2012.06.035 |
| [] | 陈雪莲, 钱玉萍, 唐晓明. 2013. 裂隙发育对低孔低渗含气地层声传播特征的影响[J]. 中国石油大学学报 (自然科学版), 37(4): 88–93. |
| [] | 陈雪莲, 唐晓明, 钱玉萍. 2014. 含孔隙、裂隙致密介质中多极子声波的传播特征[J]. 地球物理学报, 57(9): 2961–2970. DOI:10.6038/cjg20140921 |
| [] | 洪忠, 张猛刚, 朱筱敏. 2015. 基于岩石物理的致密碎屑岩气藏岩性及流体概率预测[J]. 石油物探, 54(6): 735–744. |
| [] | 钱玉萍, 唐晓明, 陈雪莲. 2014. 利用实验室加压条件下声速测量数据估计岩石裂隙参数[J]. 测井技术, 38(5): 517–521. |
| [] | 宋永佳. 2012. 含裂隙的孔隙介质中弹性波衰减机制理论研究[硕士论文]. 哈尔滨: 哈尔滨工业大学. |
| [] | 宋永佳, 胡恒山. 2013. 裂隙挤喷流对孔隙介质排水体积模量的影响[J]. 力学学报, 45(3): 395–405. DOI:10.6052/0459-1879-12-230 |
| [] | 宋永佳, 胡恒山. 2014a. 含定向非均匀体固体材料的横观各向同性有效弹性模量[J]. 物理学报, 63(1): 016202. DOI:10.7498/aps.63.016202 |
| [] | 宋永佳, 胡恒山. 2014b. 含孔隙、裂隙岩石的高频体积模量[J]. 中国科学:物理学力学天文学, 44(6): 610–620. DOI:10.1360/SSPMA2013-00092 |
| [] | 孙卫涛, 刘嘉玮, 巴晶, 等. 2015. 孔隙介质弹性波频散-衰减理论模型[J]. 地球物理学进展, 30(2): 586–600. DOI:10.6038/pg20150215 |
| [] | 唐军, 章成广. 2012. 阵列声波测井技术在识别碳酸盐岩储层类型中的应用研究[J]. 石油天然气学报, 34(3): 101–105, 109. |
| [] | 唐晓明. 2011. 含孔隙、裂隙介质弹性波动的统一理论-Biot理论的推广[J]. 中国科学:地球科学, 41(6): 784–795. |
| [] | 唐晓明, 钱玉萍, 陈雪莲. 2013. 孔隙、裂隙介质弹性波理论的实验研究[J]. 地球物理学报, 56(12): 4226–4233. DOI:10.6038/cjg20131225 |
| [] | 王海洋, 孙赞东, ChapmanM. 2012. 岩石中波传播速度频散与衰减[J]. 石油学报, 33(2): 332–342. DOI:10.7623/syxb201202024 |
| [] | 王秀明. 2009. 多相孔隙储层声学研究进展[J]. 应用声学, 28(1): 1–9. DOI:10.11684/j.issn.1000-310X.2009.01.001 |
| [] | 吴国忱, 吴建鲁, 宗兆云. 2014. 周期性层状含孔隙、裂隙介质模型纵波衰减特征[J]. 地球物理学报, 57(8): 2666–2677. DOI:10.6038/cjg20140825 |
| [] | 吴建鲁, 吴国忱, 宗兆云. 2015. 含混合裂隙、孔隙介质的纵波衰减规律研究[J]. 地球物理学报, 58(4): 1378–1389. DOI:10.6038/cjg20150424 |
| [] | 许松, 苏远大, 陈雪莲, 等. 2014. 含孔隙、裂隙地层随钻多极子声波测井理论[J]. 地球物理学报, 57(6): 1999–2012. DOI:10.6038/cjg20140630 |
| [] | 许孝凯, 刘美杰, 朱留方, 等. 2016. 基于岩石物理的致密气层识别方法研究[J]. 应用声学, 35(2): 116–121. |
| [] | 章成广, 江万哲, 肖承文, 等. 2004. 声波全波资料识别气层方法研究[J]. 测井技术, 28(5): 397–401. |
| [] | 张永军, 顾定娜, 马肃滨, 等. 2012. 阵列声波测井资料在吐哈油田致密砂岩气层识别中的应用[J]. 测井技术, 36(2): 175–178. |
| [] | 赵佐安, 何绪全, 唐雪萍. 2002. 低电阻率油气层测井识别技术[J]. 天然气工业, 22(4): 34–37. |
 2017, Vol. 32
2017, Vol. 32

