地球物理学进展  2017, Vol. 32 Issue (2): 516-521   PDF    
引用本文
王少博, 李桐林, 苏晓波. 2017. 大地电磁三维矢量有限元正演误差分析及其优化. 地球物理学进展, 2017, 32(2): 516-521, doi: 10.6038/pg20170209  
WANG Shao-bo, LI Tong-lin, SU Xiao-bo. 2017. Error analysis of three-dimensional magnetotelluric forward modelling by using edge-based finite element method and its improving method. Progress in Geophysics (in Chinese), 32(2): 516-521, doi: 10.6038/pg20170209   
大地电磁三维矢量有限元正演误差分析及其优化
王少博1, 李桐林1, 苏晓波2     
1. 吉林大学地球探测科学与技术学院, 长春 130026
2. 核工业二四三大队, 赤峰 024000
收稿日期：2016-07-17; 修回日期：2017-01-17.
作者简介：王少博, 男, 1991年生, 硕士, 主要从事电磁法勘探理论模拟与应用研究.(E-mail:nashwangshaobo@vip.qq.com)
通讯作者：李桐林, 男, 1962年生, 教授, 博导, 从事电磁法勘探理论问题及其应用和固体矿产地球物理综合地质解释等研究.(E-mail:litl@jlu.edu.cn)
摘要：利用基于六面体的矢量有限元法进行大地电磁正演模拟时，在电性变化剧烈的区域有可能因为网格剖分的不够细致，导致六面体单元中的场值无法通过十二条棱边的插值准确表达，从而形成误差.另外，由于有限元剖分网格不可能无限延伸，而大地电磁场的边界条件在无穷远处才能得到满足；所以不恰当的网格剖分策略可能造成数值模拟计算结果误差过大.本文研究了不同频率下误差产生的规律及原因，并提出了减小误差的方法.最后根据误差分析对正演过程进行了优化，即保证了计算精度又大大提高了正演速度.
关键词：大地电磁    三维正演模拟    矢量有限元    误差分析    正演优化    
Error analysis of three-dimensional magnetotelluric forward modelling by using edge-based finite element method and its improving method
WANG Shao-bo1 , LI Tong-lin1 , SU Xiao-bo2     
1. College of Geoexploration Science and Technology, Jilin University, Changchun 130026, China
2. Geologic Party No.243, CNNC, Inner Mongolia, Chifeng 024000, China
Abstract: When using hexahedral edge-based finite element method to conduct a three-dimensional magnetotelluric forward experiment, it is possible that in regions of severe electrical changes, unreasonable partition of mesh may lead to the result that the values of hexahedral elements cannot be expressed correctly by interpolation functions of their twelve edges, thus causing errors. Moreover, the width-limited mesh does not satisfy magnetotelluric boundary conditions that are correct at infinity. Therefore, inappropriate mesh generation strategy may cause serious errors in numerical simulation results. In this paper, reasons and rules of errors under different frequencies are analyzed, and the improving method is advanced. Finally, basing on error analysis, we optimized the process of forward, which not only ensured the computational precision but improved efficiency.
Key words: magnetotellurics     three-dimensional forward modelling     edge-based finite element method     error analysis     improving forward method    
0 引言

大地电磁法 (Magnetotellutic Method) 是一种利用天然电磁场研究地球内部电性结构的地球物理勘探方法.由于其不用人工发射电磁波，成本低廉，工作方便, 因而被广泛的用于地质普查及矿场勘探和地壳、上地幔结构研究等领域.

国内外学者对大地电磁法有限元正演模拟做了大量工作.早在20世纪70年代Coggon便提出了将有限元法应用于大地电磁数值模拟中的方案，并详细阐述了如何利用有限单元模拟大地电磁场.随后，Rijo、Wannamaker、Myung等人对电磁场的有限元正演模拟进行了发展和完善.国内，1981年，陈乐寿详细介绍了有限元在大地电磁场正演中的应用，并使用矩形-三角形网格对正演进行了优化.传统的节点有限元法不满足电性分界面上法向电场不连续和无源区单元内电流密度无散，其违反麦克斯韦方程组，因此会出现伪解.Jin (2002)和柳建新 (2012)提出了引入散度矫正来压制伪解的方法，取得了一定效果，但不能将伪解完全消除.矢量有限元法把自由度赋予单元的棱边而不是节点，所以自动满足了麦克斯韦方程组，可以从根本上去除伪解，在近些年中得到了广泛的应用.2008年王烨进行了基于矢量有限元的高频大地电磁三维正演；同年，刘长生等应用非结构四面体H型自适应网格对MT进行了正演研究.2013年汤井田等分析了二维MT有限元模拟中截断边界的影响，并总结出适合二维大地电磁正演模拟的网格边界.2014年，顾观文对三维地形影响下的矢量有限元正演模拟进行了较全面的研究.

本文以大地电磁矢量有限元三维正演程序为基础，通过其数值模拟结果与一维均匀半空间模型的解析解对比，发现了正演模拟结果误差的规律，并找出了误差产生的原因与减小误差的方法.最后，提出了根据不同频率划分不同网格的正演优化方法，在保证精度的情况下大大提高了正演速度，并对经典的层状介质模型进行正演计算，将其结果与解析解对比，验证了正演的正确性.随后又对三维地质体模型进行计算，获得了良好的效果.

1 MT三维矢量有限元正演理论及误差分析 1.1 正演理论

首先，以e-iωt为时谐因子，麦克斯韦方程组中法拉第电磁感应定律和安培定律可写为

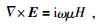
(1)
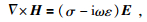
(2)

其中ω是角频率，磁导率μ=4π×10-7H/m，介电常数ε=8.85×10-12F/m，σ是介质电导率，i为虚数单位.对 (1) 式等号两边求旋度，并将 (2) 式代入 (1) 式有：

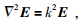
(3)

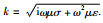
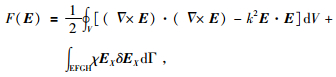
其中波数.由广义变分原理可得上式泛函为

(4)

六面体单元中：

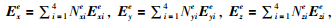
(5)

其中Exie、Eyie、Ezie表示第e条棱边的场值，Nxie、Nyie、Nzie表示相应的插值基函数 (形函数)，把 (5) 代入 (4) 中便可得到每一个子单元中电场值的表达式，用矩阵表示为

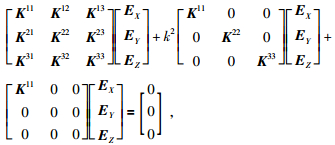
(6)

其中各个子式均为4×4的复系数矩阵，在边界条件的约束下再将其进行不完全乔列斯基分解并与双复共轭梯度法相结合求解矩阵方程，六面体各个棱边上的电场值.视电阻率的表达式为

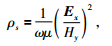
(7)

其中：
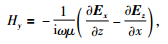
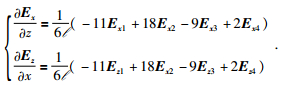
(8)
1.2 误差分析 1.2.1 误差产生原因

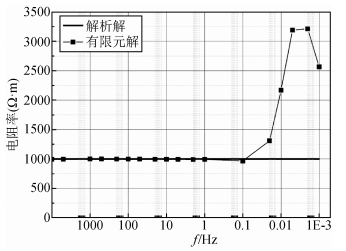
现建立电阻率为1000 Ω·m的均匀半空间模型，我们将整个区域以x方向45块×y方向45块×z方向42块 (空气层10块) 剖分；x，y方向剖分均为63250 m，z方向空气36900 m，地下131950 m.正演模拟表明，在此模型下，有限元解与解析解在高频部分基本一致，而在0.1 Hz以下时出现较明显的误差，在0.01 Hz时误差达到200%以上，如图 1.

图 1 1000 Ω·m均匀半空间有限元解与解析解对比 Figure 1 Comparison of finite element solution with analytical solution in 1000 Ω·m half homogeneous space

在电磁场理论中，电磁波随着传播距离的增大逐渐衰减至零，我们把某一频率的电磁波能量衰减至它初始时的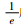所经历的距离称为趋肤深度，趋肤深度；其中ρ为介质的电阻率，单位为Ω·m、f为电磁波频率，单位为Hz.由上式可见，介质电阻率越大，频率越低，趋肤深度越大，电磁波衰减越慢.而有限元模拟中的网格边界是截断边界，所以作者分析此误差出现是因为在低频、高阻的情况下由于剖分深度不够，电磁波在网格边界未衰减至所给定的边界条件，造成计算结果高于解析解.

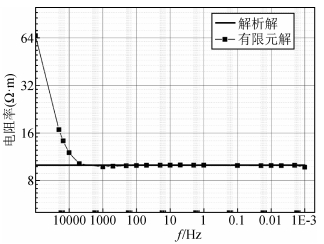
模型网格剖分方式不变，把地下均匀半空间电阻率变为10 Ω·m时：有限元解在低频部分与解析解基本一致，在1000 Hz及以上的高频段出现明显的误差，如图 2.

图 2 10 Ω·m均匀半空间有限元解与解析解对比 Figure 2 Comparison of finite element solution with analytical solution in half homogeneous space

用有限元法进行数值模拟时，只要在一个六面体单元内各个棱边的场值与其形函数的组合可以准确的表达六面体单元的场值时，我们得到的解是精确的；如果其不能，我们所得到的解是近似的.显然，在一般情况下，形函数与棱边场值的组合不可能完全准确的表达场值；所以误差的出现难以避免.大地电磁的高频段分辨率较高，视电阻率对近地表区域的电性结构敏感，当频率超过一定数值，而近地表电阻率又较低时，近地表电磁场变化很快.所以，作者认为近地表网格剖分不够细致造成了此误差.

1.2.2 误差消除

上文已经分析了误差产生的原因，所以针对高频段与低频段出现的误差分别采用两种不同的网格修改策略.

对于高阻低频域，以趋肤深度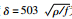为标准，经过多次针对不同网格，不同模型的试验后作者发现：当网格深度大于3倍趋肤深度时，误差大多小于1%；随着网格深度/趋肤深度的减小，误差不断变大，在1.5倍趋肤深度左右误差增长最快；当网格深度小于趋肤深度时，误差基本大于100%.

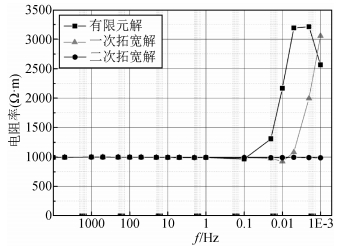
低频段的误差，我们采取拓宽网格的下边界的方式进行改正，保持上一小节对正演模拟的其他模型参数不变，我们先将地下网格向下扩宽至311950 m，其剖分深度为0.02 Hz对应的趋肤深度的2.77倍；然后继续将地下网格拓宽至1511950 m，其剖分深度为最低频0.001 Hz对应趋肤深度的3.0倍.结果如图 3所示，随着剖分深度增大，误差得到了更好的修正.

图 3 向下拓宽网格与原来剖分结果比较 Figure 3 Comparison the result of the broader mesh with the old one

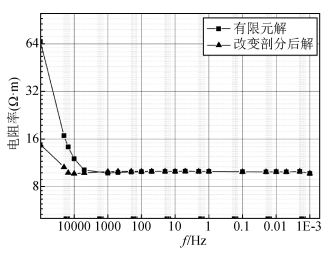
对于低阻 (10 Ω·m) 高频时出现的因为地表网格剖分不够细致造成的误差，我们尝试用更细致的网格 (本文将近地表1~4层单元的z方向缩小2.5倍，5~8层单元的z方向缩小2倍；x、y方向不变) 代替原有网格以提高正演精度；结果如图 4所示，收到了较好效果.

图 4 细致剖分地表网格与原来剖分结果比较 Figure 4 Comparison the result of the surface-detailed mesh with the old one

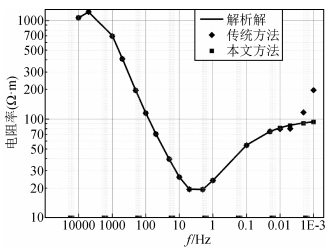
图 5 本文方法与传统有限元法结果对比图 Figure 5 Comparison the result of this paper with the traditional FEM

这里要特别说明，在二维有限元正演模拟的三角形网格中一般认为三角形过钝或过锐会对计算结果造成不良影响 (徐世浙，1994).而在结构化六面体中，经过验证，当我们仅把六面体某一方向的边缩小，造成六面体各方向棱边长度相差很大时对结果并没有不良影响；从单元剖分的角度来看, 此举相当于用更多的棱边场值来表达六面体单元的场值.

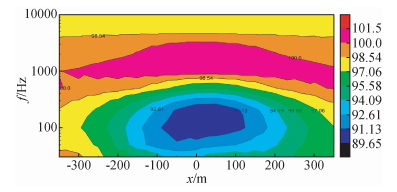
2 MT三维矢量有限元正演过程优化 2.1 正演过程优化策略

前文已完成针对网格剖分所造成误差的分析，由其结论可知：对于均匀半空间模型而言，当网格深度是趋肤深度的3倍以上时，数值模拟解与解析解相差小于1%，不会因为底层网格不满足底边界条件造成误差；所以我们把网格深度定为趋肤深度的3倍及以上.趋肤深度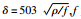为频率；ρ为地下介质电阻率，不同情况下ρ的取值遵循以下规则：(1) 在均匀半空间模型中ρ等于地下模型的电阻率；(2) 在层状介质模型中，为电阻率最高层的电阻率；(3) 在低阻异常体区域附近，ρ为高阻围岩的电阻率；(4) 在高阻异常体区域附近，ρ为异常体电阻率.进行计算时，我们从最低频开始，逐个向最高频计算；当从地表到网格某层的深度大于所求频率下趋肤深度的3倍时，便删去该层以下的所有网格，以此减小计算量，达到加快计算速度的目的.计算过程从低频到高频，趋肤深度只会越来越小，而网格深度时刻保持在趋肤深度的3倍以上，所以不必担心因为删去网格影响计算精度.

2.2 正演优化方法算例及结果分析

首先我们对一维层状介质模型进行计算，对比本文算法与传统有限元法的计算速度，并与解析解对比，验证算法精度.模型一层电阻率为1000 Ω·m，层厚300 m；第二层电阻率为10 Ω·m，层厚600 m；基底100 Ω·m.取从0.001 Hz到10000 Hz的18个频点，计算结果如下图 6，二者计算耗时与误差对比如表 1所示.

图 6 3维低阻异常剖面图 Figure 6 Profile of three-dimensional low-resistant anomalous body

表 1 传统有限元法和本文方法误差及耗时对比 Table 1 Comparison the error and time-consuming of this paper with the traditional FEM

由上图及上表可见，本文算法比传统矢量有限元法拥有更快的计算速度及更高的低频计算精度.

下面我们建立一个三维模型：100 Ω·m的均匀半空间中，在-75 m至125 m处存在一个电阻率为10 Ω·m，埋深200 m，长200 m，宽200 m，高200 m的低阻异常体.测线位于y=0，以异常体的中心为中点沿x方向每隔50 m取一测点，共取15测点，结果如图 7所示.视电阻率剖面图在低阻体位置出现了明显的低阻异常闭合区，且视电阻率分布基本沿x=0对称.

3 结论 3.1

本文详细的分析了传统的大地电磁三维矢量有限元中误差的成因，并提出了减小误差的方法；并通过采用随着频率的变化变换网格的方式对正演进行了优化.

3.2

大地电磁三维矢量有限元正演模拟中：当频率高于一定数值，近地表区域低阻时，会因为近地表网格剖分不够细致而造成误差；当频率小于一定数值，地下空间阻值较高时，可能会因为电磁波在底界面不满足边界条件造成误差.当网格深度大于3倍趋肤深度时，误差大多小于1%；随着网格深度与趋肤深度之比变小，误差不断变大，在1.5倍趋肤深度左右误差增长最快；当网格深度小于趋肤深度时，误差基本大于100%.

3.3

随着频率不断增大，只要保证网格剖分大于趋肤深度的3倍，删掉深层网格不会对计算结果造成影响，此举能减小计算量，加快正演速度.

致谢 感谢审稿专家提出的修改意见和编辑部的大力支持！
参考文献
[] Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 54(6): 1649–1659. DOI:10.3969/j.issn.0001-5733.2011.06.025
[] Chen X B, Zhao G Z. 2004. An essential structure finite element (ESFE) algorithm and its application to MT 1D forward modeling of continuous medium[J]. Chinese Journal of Geophysics, 47(3): 535–541. DOI:10.3321/j.issn:0001-5733.2004.03.026
[] Fang S, Luo Y Z. 1991. Magnetotelluric response on vertically inhomo geneous earth having conductivity varying linearly with depth by layers[J]. Acta Geophysica Sinica, 34(2): 216–227.
[] Fu C M, Di Q Y, Wang M Y. 2010. Calculate electromagnetic fields in stratified medium with layer-matrix method[J]. Chinese Journal of Geophysics, 53(1): 177–188. DOI:10.3969/j.issn.0001-5733.2010.01.020
[] Gu G W, Wu W L, Li T L. 2014. Modeling for the effect of magnetotelluric 3D topography based on the vector finite-element method[J]. Journal of Jilin University (Earth Science Edition), 44(5): 1678–1686.
[] Jin J M. 2002. The Finite Element Method in Electromagnetics[M]. 2nd ed. New York: Wiley-Interscience Publication.
[] Liang S X, Zhang S Y, Wushouaili, et al. 2012. Magnetotelluric forward modeling in complex three-dimensional media[J]. Progress in Geophysics, 27(5): 1981–1988. DOI:10.6038/j.issn.1004-2903.2012.05.019
[] Liu C S, Ren Z Y, Tang J T, et al. 2008. Three-dimensional magnetotellurics modeling using edgebased finite-element unstructured meshes[J]. Applied Geophysics, 5(3): 170–180. DOI:10.1007/s11770-008-0024-4
[] Liu C S, Tang J T, Ren Z Y, et al. 2010. Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J]. Journal of Central South University (Science and Technology), 41(5): 1855–1859.
[] Lü Y Z, Ruan B Y. 2006. 3-D resistivity FEM numerical modeling based on tetrahedral element division under complicated terrain[J]. Progress in Geophysics, 21(4): 1302–1308. DOI:10.3969/j.issn.1004-2903.2006.04.040
[] Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference equations-theory and comparisons to integral equation Solutions[J]. Geophysics, 58(2): 215–226. DOI:10.1190/1.1443407
[] Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-(finite-element method[J]. Geophysics, 69(1): 108–119. DOI:10.1190/1.1649380
[] Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography[J]. Geophysical Prospecting, 55(2): 277–287. DOI:10.1111/gpr.2007.55.issue-2
[] Qiang J K, Luo Y Z. 2007. The resistivity FEM numerical modeling on 3-D undulating topography[J]. Chinese Journal of Geophysics, 50(5): 1606–1613. DOI:10.3321/j.issn:0001-5733.2007.05.038
[] Reddy I K, Phillips R J, Rankin D. 1977. Three-dimensional modelling in magnetotelluric and magnetic variational sounding[J]. Geophysical Journal, 51(2): 313–325.
[] Shi X M, Utada H, Wang J, et al. 2004. Three dimensional magnetotelluric forward modeling using vector Finite element method combined with divergence corrections (VFE++)[C].//17th IAGA WG 1.2 Workshop on Electromagnetic Induction in the Earth Hyderabad. India, 465-473.
[] Su X B, Li T L, Zhu C, et al. 2015. Study of three-dimensional MT forward modeling using vector finite element method[J]. Progress in Geophysics, 30(4): 1772–1778. DOI:10.6038/pg20150433
[] Tan H D, Tong T, Lin C H. 2006. The parallel 3D magnetotelluric forward modeling algorithm[J]. Applied Geophysics, 3(4): 197–202. DOI:10.1007/s11770-006-4001-5
[] Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 46(5): 705–711. DOI:10.3321/j.issn:0001-5733.2003.05.019
[] Tang J T, Wang F Y, Ren Z Y. 2010. 2^5-D DC resistivity modeling by adaptive finite-element method with unstructured triangulation[J]. Chinese Journal of Geophysics, 53(3): 708–716. DOI:10.3969/j.issn.0001-5733.2010.03.026
[] Tang J T, Xue S. 2013. Influence of truncated boundary in FEM numerical simulation of MT[J]. Journal of Jilin University (Earth Science Edition), 43(1): 267–274.
[] Wang Y. 2008. A Study of 3D high frequency magnetotellurics modeling by edge-based finite element method (in Chinese)[Ph. D. thesis]. Changsha:Central South University.
[] Wu X P, Wang T T. 2003. A 3-D finite element resistivity forward modeling using conjugate gradient algorithm[J]. Chinese Journal of Geophysics, 46(3): 428–432. DOI:10.3321/j.issn:0001-5733.2003.03.023
[] Xu S Z. 1994. The Finite Element Method in Geophysics[M]. Beijing: Science Press.
[] Xu S Z, Liu B. 1995. A numerical method for calculating MT field on a layered model with Continuous change of conductivity in each layer[J]. Acta Geophysica Sinica, 38(2): 262–268.
[] Yoshimura R, Oshiman N. 2002. Edge-based finite element approach to the simulation of geoelectromagnetic induction in a 3-D sphere[J]. Geophysics Research Letters, 29(3): 9–1.
[] Zhang J, Mackie R L, Madden T R. 1995. 3-D resistivity forward modeling and inversion using conjugate gradients[J]. Geophysics, 60(5): 1313–1325. DOI:10.1190/1.1443868
[] Zhang J F, Tang J T, Wang Y, et al. 2009a. Effects of boundary conditions on calculation result in finite element simulation[J]. Progress in Geophysics, 24(5): 1905–1911. DOI:10.3969/j.issn.1004-2903.2009.05.049
[] Zhang J F, Tang J T, Yu Y, et al. 2009b. Three dimensional controlled source electromagnetic numerical simulation based on electric field vector wave equation using finite element method[J]. Chinese Journal of Geophysics, 52(12): 3132–3141. DOI:10.3969/j.issn.0001-5733.2009.12.023
[] Zheng S T, Zeng Z F, Zhang D G, et al. 2007. Calculation about high-frequency electromagnetic response and cases analyzing[J]. Progress in Geophysics, 22(6): 1772–1776. DOI:10.3969/j.issn.1004-2903.2007.06.014
[] 陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报, 54(6): 1649–1659. DOI:10.3969/j.issn.0001-5733.2011.06.025
[] 陈小斌, 赵国泽. 2004. 基本结构有限元算法及大地电磁测深一维连续介质正演[J]. 地球物理学报, 47(3): 535–541. DOI:10.3321/j.issn:0001-5733.2004.03.026
[] 方胜, 罗延钟. 1991. 电导率随深度分层线性变化的大地电磁响应[J]. 地球物理学报, 34(2): 216–227.
[] 付长民, 底青云, 王妙月. 2010. 计算层状介质中电磁场的层矩阵法[J]. 地球物理学报, 53(1): 177–188. DOI:10.3969/j.issn.0001-5733.2010.01.020
[] 顾观文, 吴文鹂, 李桐林. 2014. 大地电磁场三维地形影响的矢量有限元数值模拟[J]. 吉林大学学报 (地球科学版), 44(5): 1678–1686.
[] 梁生贤, 张胜业, 吾守艾力, 等. 2012. 复杂三维介质的大地电磁正演模拟[J]. 地球物理学进展, 27(5): 1981–1988. DOI:10.6038/j.issn.1004-2903.2012.05.019
[] 刘长生, 汤井田, 任政勇, 等. 2010. 基于非结构化网格的三维大地电磁自适应矢量有限元法模拟[J]. 中南大学学报 (自然科学版), 41(5): 1855–1859.
[] 吕玉曾, 阮百尧. 2006. 复杂地形条件下四面体剖分电阻率三维有限元数值模拟[J]. 地球物理学进展, 21(4): 1302–1308. DOI:10.3969/j.issn.1004-2903.2006.04.040
[] 强建科, 罗延钟. 2007. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 50(5): 1606–1613. DOI:10.3321/j.issn:0001-5733.2007.05.038
[] 苏晓波, 李桐林, 朱成, 等. 2015. 大地电磁三维矢量有限元正演研究[J]. 地球物理学进展, 30(4): 1772–1778. DOI:10.6038/pg20150433
[] 谭捍东, 余钦范, BookerJ, 等. 2003. 大地电磁法三维三维交错采样有限差分数值模拟[J]. 地球物理报, 46(5): 705–711. DOI:10.3321/j.issn:0001-5733.2003.05.019
[] 汤井田, 王飞燕, 任政勇. 2010. 基于非结构化网格的2^5-D直流电阻率法自适应有限元数值模拟[J]. 地球物理学报, 53(3): 708–716. DOI:10.3969/j.issn.0001-5733.2010.03.026
[] 汤井田, 薛帅. 2013. MT有限元模拟中截断边界的影响[J]. 吉林大学学报 (地球科学版), 43(1): 267–274.
[] 王烨. 2008. 基于矢量有限元的高频大地电磁法三维数值模拟[博士论文]. 长沙: 中南大学.
[] 吴小平, 汪彤彤. 2003. 利用共轭梯度算法的电阻率三维有限元正演[J]. 地球物理学报, 46(3): 428–432. DOI:10.3321/j.issn:0001-5733.2003.03.023
[] 徐世浙. 1994. 地球物理中的有限单元法[M]. 北京: 科学出版社.
[] 徐世浙, 刘斌. 1995. 电导率分层连续变化的水平层的大地电磁正演[J]. 地球物理学报, 38(2): 262–268.
[] 张继峰, 汤井田, 王烨, 等. 2009a. 有限元模拟中边界条件对计算结果的影响[J]. 地球物理学展, 24(5): 1905–1911. DOI:10.3969/j.issn.1004-2903.2009.05.049
[] 张继锋, 汤井田, 喻言, 等. 2009b. 基于电场矢量波动方程的三维可控源电磁法有限单元法数值模拟[J]. 地球物理学报, 52(12): 3132–3141. DOI:10.3969/j.issn.0001-5733.2009.12.023
[] 郑圣谈, 曾昭发, 张代国, 等. 2007. 层状介质高频电磁场计算方法及计算结果分析[J]. 地球物理学进展, 22(6): 1772–1776. DOI:10.3969/j.issn.1004-2903.2007.06.014