2. 安庆师范大学资源环境学院, 安庆 246133
3. 江苏省地理信息资源开发与利用协同创新中心, 南京 210023
4. 同济大学经济与管理学院, 上海 201804
5. 齐齐哈尔大学理学院地理系, 齐齐哈尔 161006
2. School of Resources and Environment, Anqing Normal University, Anqing 246133, China
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
4. School of Economics and Management, Tongji University, Shanghai 201804, China
5. College of Science, Qiqihar University, Qiqihar 161006, China
众多研究表明,太阳活动具有周期性变化的规律 (Hood and Jirikowic, 1991; Charvátová, 2000),其中以太阳黑子准11年周期 (李可军等, 2010; 杨东红和杨学祥, 2013) 和太阳磁场极性准22年周期 (曲维政等, 2007) 的变化最为显著.赵明宇等 (2014)、杨若文等 (2009)对太阳黑子与太阳活动之间的关系进行了深入的研究,Haigh (1996)、Friis.Christensen和Lassen (1991)、赵新华和冯学尚 (2014)、刘立波等 (2011)、赵平等 (2011)在太阳活动对全球气候及地表环境的影响取得了可喜的成果.由于太阳活动的周期性变化进而导致了地球表层环境和气候同样也具有相似的周期性变化 (曲维政等, 2004).近年来关于太阳活动的周期性变化的形成机制 (Suess, 1980; Sonett and Finney, 1990) 众说纷纭,其中以太阳绕太阳系质心运动的周期性变化对太阳活动的影响逐渐成为目前关注的焦点 (Jose, 1965; Damon and Linick, 1986; Damon et al, 1989; Tlatov, 2007; 孙威等, 2017).由于太阳绕太阳系质心运动与行星系质心绕太阳系质心运动具有相似的周期性规律,而行星系质心绕太阳系质心运动与行星系质心的日心经度和行星会合指数具有必然的联系.因此构建行星系日心经度运动学方程和深入探讨行星会合指数,对进一步研究太阳活动、地球环境以及全球气候变化的周期性都具有十分重要的意义.目前,刘复刚已经完成了行星会合指数运动学方程的构建 (刘复刚和王建, 2013),对于探讨行星会合以及绕日运动奠定了基础.但是行星系质心绕日运动的日心经度运动学方程还尚未建立.行星系质心绕日运动的日心经度运动学方程的建立,对正确认识太阳绕太阳系质心运动轨迹以及太阳活动的周期性变化起着十分重要的作用,是研究行星系质心、太阳系质心和太阳质心三者相互运动规律必不可少的一部分.因此,构建一个准确计算行星系质心绕日运动的日心经度运动学方程已迫在眉睫.
在前期的研究成果中发现,较多学者利用行星会合采用近似方法研究太阳活动 (杨志根和赵铭, 1988; 杨志根, 1991; 陈协珍, 1996),这样虽然对解决少量行星会合的问题具有一定的成效,但对于多个行星会合却十分困难.同时也很难准确反映行星会合和背离的程度、行星会合的形态特征和变化过程,刘复刚通过构建行星会合指数的方法解决了这一难题 (刘复刚等, 2013).虽然行星会合指数在研究行星会合和分散程度方面具有一定优势,但是在研究行星系质心以及太阳质心绕太阳系质心运动轨迹方面,仅仅利用行星会合指数还远远不够.因为研究行星系质心和太阳质心绕太阳系质心运动轨迹时不仅需要考虑行星会合指数,同时还要充分考虑行星系质心与太阳质心或太阳系质心的准确方位,即行星日心经度或太阳系质心经度.作者通过构建行星系日心经度的运动学方程,利用行星系日心经度研究行星系质心的准确方位,即行星日心经度或太阳系质心经度.通过对行星系日心经度运动学方程的研究,利用行星系质心日心经度研究行星系质心的准确方位和日心经度的周期性变化规律.同时结合行星会合指数共同确定行星系质心或太阳质心的运动轨迹和运动轨迹连续变化的形态特征.此研究方法的最大优势在于行星系日心经度和会合指数都能够随行星运动时间建立一一对应的关系,无论是行星系质心还是太阳质心都可以运用这种对应关系推之过去或者预测未来的运动轨迹和变化特征.此动力学模型的构建为研究太阳准11年的黑子周期、准22年的磁场极性周期,以及地球全球气候变化的世纪、双世纪等周期提供了新的研究方法和途径.本文构建的动力学模型目的并非单一地构建模型,而是通过构建动力学模型为研究行星运动与太阳活动、全球气候变化之间的关系奠定理论基础,具有十分重要的科学价值和意义.
1 行星系日心经度运动学方程的建立 1.1 太阳系行星系统质心的确定太阳系各行星轨道平面与不变平面之间的夹角都非常小,太阳系中以水星的轨道倾角最大也仅有6°17′,而木星、土星以及海王星的倾角都小于6°,因此将太阳系各行星的轨道平面视为一个不动平面进行研究 (戴文赛, 1979).以太阳坐标为原点,以不动平面作为太阳系行星系统的平均轨道平面 (垂直于太阳系各天体的角动量的矢量和的平面).
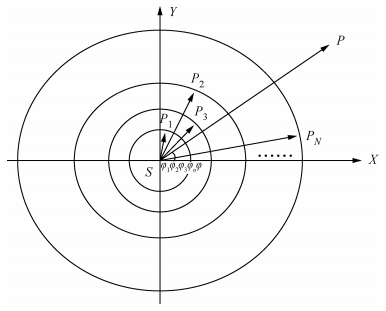
如图 1所示,把太阳系各行星视为质点进行研究,各行星质量权重位矢末端分别位于P1,P2,P3,……Pn,质量分别为m1, m2, m3, ……mn, 相对于太阳质心的位矢半径分别为r1,r2,r3,……rn,φ1、φ2、φ3……φn为太阳系各行星的日心经度,φ为行星系质心的日心经度,则行星系质心P相对于太阳质心S的位矢rs的关系为 (周衍柏, 1986):
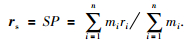
|
(1) |
式 (1) 即为太阳质心到行星系质心的位矢方程,rs是行星系质心相对于太阳质心的位矢,通过对各行星的质量与其位矢的乘积求和,再除以行星系的总质量获得.位矢的始端即为太阳质心,末端即为行星系质心.为了便于计算行星系日心经度和会合指数,利用式 (1) 将太阳系各行星的平均轨道半径ri转换为质量权重半径ri,如表 1所示.通过行星系质心方程计算,行星系质心距太阳质心的位矢主要由各行星距太阳质心的位矢与质量共同决定 (即权重半径).由表 1获知,木星、土星、天王星、海王星的权重半径相对其他行星较大,对行星系质心的确定具有主要作用.而其他行星的权重半径较小,对行星系质心的影响也较小.
|
图 1 行星会合示意图 Figure 1 The sketch map of planetary rendezvous |
|
|
表 1 太阳系行星轨道有关天文参数 Table 1 The astronomical data about the planetary orbits |
通过行星系质心方程不难发现,行星系质心是各行星以质量为权重距太阳质心的权重半径的矢量和.根据这一原理,刘复刚把太阳系各行星绕日运动轨道的权重半径矢量和的模定义为行星系质心的会合指数,由此给出的太阳系行星会合指数 (K) 的运动学方程为 (刘复刚和王建, 2013):
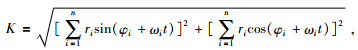
|
(2) |
式中,K、ri、φi、ωi和t分别为行星会合指数、行星的轨道权重半径、行星初始日心经度、平均角速度和时间.若太阳系各行星高度会合时 (即各行星日心经度近似相等时),行星会合指数K将达到极大值.若太阳系各行星高度背离时 (即木星的日心经度与其他行星的日心经度相差约180°时),行星会合指数K将达到极小值.因此,利用行星会合指数可以表征行星系质心距太阳质心距离的大小,甚至在一定程度上可以表征太阳质心距太阳系质心距离的大小.同时,也可以表征太阳系行星会合与背离的程度.
根据美国航天航空局NASA (National Aeronautics and Space Administration) 提供的2000年1月1日太阳系各行星日心经度 (φi)(表 2) 和表 1中八大行星的质量权重半径以及各行星运动轨道角速度值.利用行星会合指数运动学方程即可获得太阳系行星系统会合指数图,图 2即为行星系统会合指数图.
|
|
表 2 2000年1月1日12时八大行星的日心经度 (φi)(J2000历年,世界时) Table 2 The heliocentric longitude of the eight planet at 12 o'clock on January 1st, 2000 |

|
图 2 行星系统质心P绕日S的会合指数图 (步长为1年) Figure 2 The juncture index of planetary system mass center (P) orbiting the fixed point of the sun (S)(the time unit was 1-year) |
理论上,当太阳系各行星在太阳同一侧会合 (即具有相同日心经度) 时,其行星会合指数达到最大值Kmax=7.520204.然而,各行星往往很难同时具有相同日心经度,因此行星会合指数的极大值常常略小于此最大值.图 2为行星系统质心P绕日S的会合指数图,其中图 2a是行星会合指数从2000AD向过去推演100年 (至1900AD),行星会合指数在从1900AD至2000AD的100年期间大约经历了5个极大值或极小值周期,此5个波动周期的平均周期约为19.8585年.图 2b是行星会合指数从2000AD向前推演1000年 (至1000AD),行星会合指数从1000AD至2000AD的1000年的时间段中行星会合指数极大值中的相对最大值具有约180年的双世纪周期.这些显著的行星会合周期对于研究太阳活动具有重要的科学意义.图 2表明太阳系行星会合指数具有比较明显的周期性,行星会合指数用于表征行星系质心距太阳质心的距离大小或者表征太阳系各行星的会合或背离程度方面具有一定的优势.但行星会合指数却不能用于表示行星系质心绕太阳质心的运动轨迹或者太阳质心绕太阳系质心的运动轨迹,因为研究太阳质心绕太阳系质心的运动轨迹除需考虑行星会合指数外,行星系质心日心经度 (或太阳质心太阳系质心经度) 是不可或缺的重要参数.因此构建行星系质心日心经度的运动学方程势在必行.
1.3 行星系日心经度运动学方程的构建如图 1所示,行星系质心的日心经度为行星系质心和太阳质心之间的连线与基准轴 (横轴) 的夹角.若行星系质心的日心经度为φ,则:
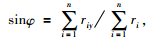
|
(3) |
由此,可以获得太阳系行星系统质心日心经度的动力学运动方程为
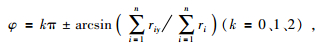
|
(4) |
其中,φ、k、riy和ri分别表示行星系质心的日心经度 (0≤φ < 2π)、常数、各行星质量权重位矢在坐标轴上的分位矢、各行星质量权重位矢.把表 1与表 2中相关的天文参数分别带入行星系日心经度 (φ) 的运动学方程,即可得到太阳系行星系质心在任意时刻的日心经度,进而获得行星系日心经度变化图,如图 3所示.
|
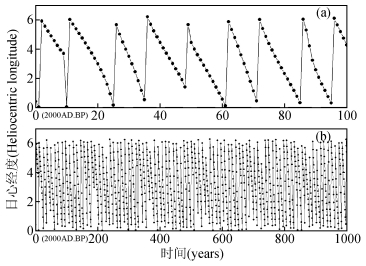
图 3 行星系统质心日心经度图 (步长为1年) Figure 3 The heliocentric longitude of planetary system mass center (P) orbiting the fixed point of the sun (S) (the time unit was 1-year) |
图 3为行星系质心的日心经度随时间变化图,横坐标表示以2000AD作为坐标原点向过去进行推演,纵坐标为行星系质心的日心经度,以弧度制表示.图 3a表示行星系质心的日心经度从2000AD向过去推演100年的变化情况,图 3b表示行星系质心的日心经度从2000AD向过去推演1000年的变化情况.图 3a和图 3b中行星系质心日心经度 (即行星系质心位于太阳质心的方位) 的变化在0到2π范围内呈周期性变化.图 3a中行星系质心日心经度在1900AD至2000AD期间进行约8.5次的周期性变化 (即行星系质心绕太阳质心运动约8.5圈).因此行星系日心经度具有明显的准11.5年的周期,此周期正好与太阳活动中的太阳黑子周期相似.同时,图 3b中行星系日心经度在1000AD至2000AD期间,行星系日心经度极小值中的最小值也具有明显5.5次的周期性变化,其周期准180年左右.此周期与行星会合指数所表现出的180年周期一致,同时与全球气候变化的双世纪周期近似一致.行星系日心经度变化图直接反映了行星系质心位于太阳质心的方位变化特征,其日心经度的周期性变化在一定程度上可以表征行星系质心绕太阳运动的周期性变化,也可表征太阳绕太阳系质心运动的周期性变化特征.如果进一步研究行星系质心绕太阳质心或太阳质心绕太阳系质心运动轨迹的变化特征,需结合行星系日心经度运动学方程和行星会合指数运动学方程进行数值模拟.
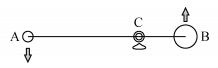
2 行星系质心与太阳质心运动轨迹的数值模拟研究行星系质心和太阳质心的运动轨迹时,因为太阳质量占整个太阳系总质量的99.865%,于是可把太阳在太阳系中作为中心天体进行研究.由于行星系质心与太阳质心在相互运动过程中同时围绕着它们的共同的质心 (即太阳系质心) 运动,于是行星系质心和太阳质心以太阳系质心为中心的运动可以看作二体运动,太阳系质心总是处于太阳质心和行星系质心的连线上,如图 4所示.图 4中A代表行星系质心,B代表太阳质心,C代表太阳系质心.行星系质心 (A)、太阳系质心 (C) 和太阳质心 (B) 在一条直线上,并且行星系质心 (A) 和太阳质心 (B) 分别位于太阳系质心 (C) 的两侧,行星系质心 (A) 和太阳质心 (B) 的太阳系质心经度刚好相差180°.若对行星系质心绕太阳质心运动的轨迹进行数值模拟,需同时考虑各行星日心经度和行星会合指数.同样,若对太阳质心绕太阳系质心的运动轨迹进行数值模拟,也需同时考虑太阳质心的太阳系质心经度和太阳质心距太阳系质心的距离大小.
|
图 4 行星系质心和太阳质心绕太阳系质心的运转图 Figure 4 Both of the centroid of planetary system and the sun moving around the mass center of the solar system |
行星系质心绕太阳质心的运动轨迹可由行星系质心日心经度运动学方程和行星会合指数运动学方程联立共同获得,即:
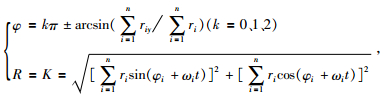
|
(5) |
式 (5) 方程组中,行星系日心经度即为行星系质心和太阳质心的连线与基准轴之间的夹角,行星会合指数即为行星系质心到太阳质心的距离大小.把表 1和表 2中相关的天文数据分别带入上面的方程组中即可获得行星系质心绕太阳质心的运动轨迹,如图 5所示.
|
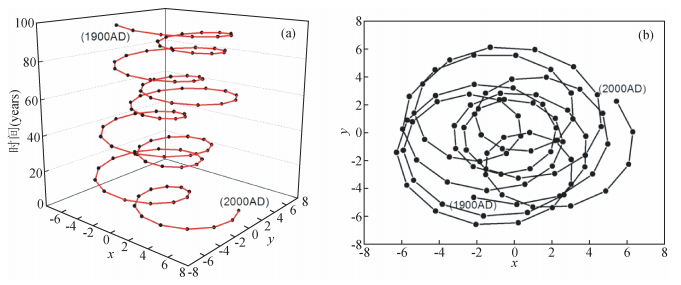
图 5 行星系质心绕日运动轨迹图 Figure 5 Trajectory of the centroid of planetary system relative to the sun |
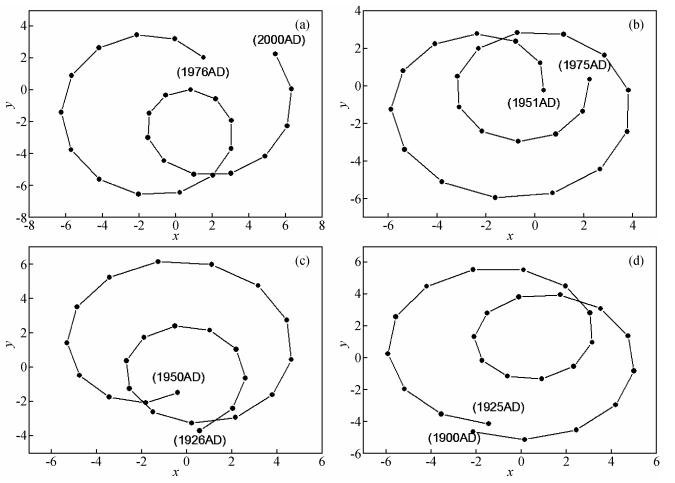
图 5a和图 5b为2000AD推演至1900AD期间的行星系质心绕太阳质心的运动轨迹图,两图中XY平面上的坐标轴原点 (0,0) 为太阳质心坐标.图 5a中垂直坐标为时间轴,垂直坐标的零点时间为2000AD,时间点100为1900AD.图 5b为图 5a中行星系质心绕太阳质心运动轨迹在XY平面上的投影图.图 5a和图 5b中,行星系质心运动轨迹曲线上的点距坐标原点 (即太阳质心) 的距离即为行星会合指数,行星系质心位于坐标原点的具体方位即为行星系质心的日心经度.图 5中不难发现,行星系日心经度和行星会合指数随时间变化都呈周期性变化.在1900AD至2000AD期间,行星系日心经度共经历了约8.5个周期,平均每个周期约11.5年,此周期与太阳黑子的周期极为相似.为了方便进一步研究行星系质心绕太阳质心运动轨迹特征,把图 5b分解为以25年为间隔的分运动轨迹图,如图 6所示.图 6a为1976AD至2000AD的行星系质心绕日运动轨迹图,图 6b为1951AD至1975AD的行星系质心绕日运动轨迹图,图 6c为1926AD至1950AD的行星系质心绕日运动轨迹图,图 6d为1900AD至1925AD的行星系质心绕日运动轨迹图.图 6中显示,在行星系质心运动的25年期间行星系质心绕太阳质心运动轨迹约两个周期,且总有一个相对较小周期和另外一个相对较大的周期组成.去除行星系质心运动的重叠部分,其中较小周期约10年,大周期约13年,此行星系质心绕太阳质心运动轨迹具有平均约11.5年的周期,这与行星系质心日心经度的周期性一致.
|
图 6 行星系质心绕日运动轨迹图 Figure 6 Trajectory of the centroid of planetary system relative to the sun |
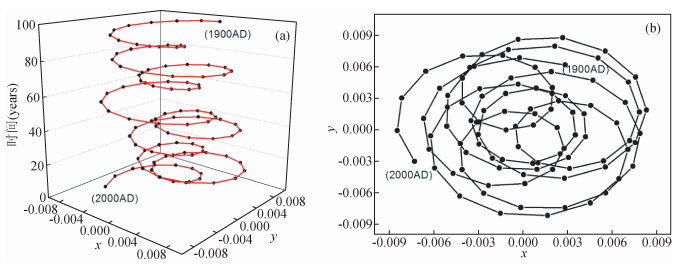
图 7为太阳质心绕太阳系质心运动轨迹的数值模拟图,图 7a和图 7b为2000AD推演至1900AD期间的太阳质心绕太阳系质心的运动轨迹图,两图中XY平面上的原点坐标轴 (0,0) 为太阳系质心坐标,黑色圆点代表太阳质心.图 7a中垂直坐标为推演时间轴,垂直坐标的零点时间为2000AD,时间点100为1900AD,图中红色曲线为太阳质心绕太阳系质心的运动轨迹.图 7b为图 7a中太阳质心绕太阳系质心运动轨迹在XY平面上的投影图.图 7a显示太阳质心绕太阳系质心做周期性运动,其周期性与行星质心绕太阳质心运动轨迹的周期性相似,在2000AD至1900AD的100年期间太阳质心绕太阳系质心运动约8.5个周期,其周期也为11.5年.此结论验证了太阳质心和行星系质心共同绕太阳系质心做二体运动这一结论.为了更加明显地显示太阳质心绕太阳系质心运动的周期性,把图 7a中太阳质心绕太阳系质心的运动轨迹投影到XY平面上进而获得图 7b.图 7b显示太阳质心在绕太阳系质心做周期性旋转运动,其太阳质心绕太阳系质心运动轨迹具有11.5年的周期,也表明了太阳质心的太阳系质心经度的周期性与此周期一致.同时,太阳质心距太阳系质心的距离也具有一定的周期性,此周期性可通过行星会合指数进行深入研究.
|
图 7 太阳质心绕太阳系质心运动轨迹图 Figure 7 Trajectory of the Sun center relative to the mass center of the solar system |
图 8为太阳系质心绕太阳质心运动轨迹的数值模拟图,图 8a和图 8b为2000AD向过去推演至1900AD的太阳系质心绕太阳质心运动的轨迹图,两图中XY平面中的原点坐标为太阳质心坐标.图 8a中红色曲线为太阳系质心的运动轨迹,黑色圆点为太阳系质心,纵坐标为从2000AD开始向过去的推演时间.与图 7相似,图 8a显示太阳系质心绕太阳质心做周期性运动,其周期性与行星质心绕太阳质心的周期性相同,大约在100年的时间里太阳系质心相对于太阳质心运动约8.5个周期,其周期约11.5年.通过对太阳质心与太阳系质心之间相互运动的数值模拟发现,无论是太阳质心绕太阳系质心的运动轨迹还是太阳系质心相对于太阳质心的运动轨迹都与Charvátová I (2000)和Jose P D (1965)

|
图 8 太阳系质心相对于太阳质心运动轨迹图 Figure 8 Trajectory of the mass center of the solar system relative to the Sun |
的研究成果保持了一致性.此结论也进一步验证了太阳质心和行星系质心共同绕太阳系质心做二体运动.图 8b通过图 8a中太阳系质心运动轨迹在XY平面上的投影获得,图 8b中XY平面的原点坐标为太阳质心,红色的圆曲线为太阳本体.图 8b显示太阳系质心相对于太阳质心呈周期性运动,其太阳系质心的日心经度也具有明显的11.5年的周期.同时,太阳系质心与太阳本体位置之间的关系不断地发生着旋入和旋出的过程,即在整个太阳与太阳系质心相对运动过程中,太阳系质心一部分时间处于太阳本体内,其余时间处于太阳本体之外.为了更加精确地了解太阳系质心与太阳本体位置之间的关系,利用计算统计法给出了1001AD至2000AD的1000年期间太阳系质心在太阳本体内外的统计表,如表 3所示.表 3显示,1001AD至1100AD的100年期间,太阳系质心位于太阳本体内35年;1101AD至1200AD的
|
|
表 3 太阳系质心与太阳本体位置关系的统计表 Table 3 Statistics relating to the position relationship of the solar system barycenter and the sun ontology. |
100年期间,太阳系质心位于太阳本体内29年;1201AD至1300AD的100年期间,太阳系质心位于太阳本体内35年;1301AD至1400AD的100年期间,太阳系质心位于太阳本体内34年;1401AD至1500AD的100年期间,太阳系质心位于太阳本体内30年;1501AD至1600AD的100年期间,太阳系质心位于太阳本体内33年;1601AD至1700AD的100年期间,太阳系质心位于太阳本体内34年;1701AD至1800AD的100年期间,太阳系质心位于太阳本体内42年;1801AD至1900AD的100年期间,太阳系质心位于太阳本体内33年;1901AD至2000AD的100年期间,太阳系质心位于太阳本体内40年;合计1001AD至2000AD的1000年期间,太阳系质心位于太阳本体内345年、太阳本体外655年.经过统计太阳本体与太阳系质心在相互运动过程的位置关系,太阳系质心位于太阳本体内的时间约占34.5%,即太阳系质心在与太阳本体相互运动过程中,在太阳本体内的时间约占总时间的三分之一.此结论的获得,对学者认为的“太阳系质心绕太阳运转有近半程时间位于太阳本体内”这一认识,其精度提高了约16%.
3 不同模型数值模拟结果对比与分析本文构建了行星系日心经度运动学模型,能够准确地确定任意时刻行星系质心位于太阳质心的具体方位.而行星会合指数方程能够准确地确定行星系质心距太阳质心的距离大小.因此,把行星系日心经度运动学方程与行星会合指数运动学方程结合起来进行数值模拟,能够准确模拟行星系质心绕太阳质心的运动轨迹.由于行星系质心与太阳质心做二体运动,依据行星系质心、太阳质心和太阳系质心三者之间的关系,利用行星系日心经度运动学方程和行星会合指数运动学方程还可以进行模拟行星系质心与太阳系质心和太阳质心与太阳系质心之间的相对运动规律.
行星系日心经度运动学方程与行星会合指数运动学方程都是首先保证太阳系各行星的运动特征基础上,对各行星的运动特征进行合理、科学地简化进而构建的动力学模型,此模型有别于以往考虑“N体问题”基础上的动力学方程.所构建的运动学模型较“N体问题”动力学方程结构简洁、便于理解,进行数值模拟时不需要“N体问题”动力学方程过于繁杂的编程语言,同时保证了数值模拟结果的高度准确性.通过对此模型进行数值模拟发现其结果与“N体问题”动力学方程所获得的结果保持了高度一致,说明了所构建的动力学模型是科学、合理、准确的.图 9即为其他学者的研究成果与本文所构建模型数值模拟的对比图.
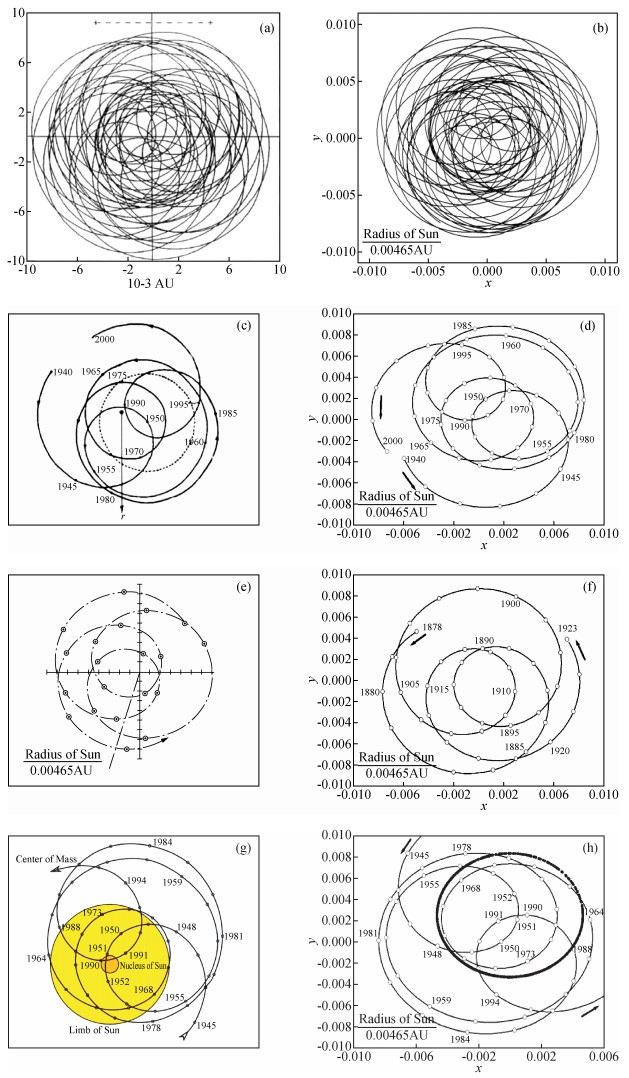
图 9a和图 9b为1600AD至2060AD期间太阳质心绕太阳系质心运动轨迹图,图 9a引自文献 (Charvátová, 2000),图 9b为构建模型的数值模拟图.从图 9a与图 9b不难发现,两者太阳质心相对于太阳系质心具有相同的运动轨迹和运动特征,保持了太阳质心与太阳系质心相对运动的一致性,从而说明所构建的动力学模型是科学、正确的; 图 9c和图 9d为1940AD至2000AD期间太阳中心相对于太阳系质心的运动轨迹图,图 9c引自文献 (任振球, 1990),图 9d为构建模型的数值模拟图,经过对图 9c和图 9d进行分析发现,两者太阳质心的运动轨迹和特性高度一致.同时,图 9c和图 9d中太阳质心距太阳系质心的距离呈周期性变化规律,其周期约20年,此周期特征与图 2的周期特征一致,即与行星会合指数的周期性相同.图 9c和图 9d中太阳质心的日心经度同样呈周期性变化规律,其周期约11.5年,此周期特征与图 3的周期特征一致,即与行星系日心经度的周期性相同,这一结果说明了行星系质心与太阳质心做二体运动;图 9e和图 9f为1878AD至1923AD期间太阳质心绕太阳系质心的运动轨迹图,图 9e引自文献 (Jose, 1965),图 9f为构建模型的数值模拟图.图 9e和图 9f与图 9c和图 9d具有相同的研究结论;图 9g和图 9h为1945AD至1995AD期间太阳系质心相对于太阳质心的运动轨迹图,图 9g引自 (Wikimedia Commons),图 9h为构建模型的数值模拟图;从图 9g和图 9h中发现,太阳系质心周期性旋进、旋出太阳本体,此特征与图 2、图 8保持一致.太阳质心与太阳系质心相对位置呈周期性变化,变化周期与图 3保持一致.并且太阳系质心位于太阳本体内的时间少于位于太阳本体外的时间,位于太阳本体内的时间约占总运动时间的1/3,此特征与表 3所获得的结论保持一致.通过对不同文献研究的结论分析证明所构建的动力学模型是科学、正确的.同时,本文构建的动力学模型目的并非为了单一地构建行星系日心经度动力学模型,以及通过星系质心日心经度与行星会合指数研究太阳质心与太阳系质心的周期性运动特征.而是在通过构建动力学模型获得太阳质心与太阳系质心相互运动的周期性规律基础上,为研究太阳活动的周期性特征以及更深一层研究地球全球气候变化的周期性规律奠定基础.即为研究行星系统运动规律与太阳活动、全球气候变化之间的相互关系提供新的途径和方法,因此,此动力学模型的构建不仅对研究太阳活动和全球气候变化的周期性特征提供了便利,而且具有十分重要的科学价值和意义.
|
图 9 不同模型的数值模拟结果对比图 Figure 9 Numerical simulation of different models. |
构建了行星系质心日心经度的运动学方程,利用行星系质心日心经度运动学方程可以获取任意时刻行星系质心位于太阳质心的准确方位.通过对行星系质心日心经度的研究发现,行星系质心日心经度具有准11.5年的运动周期,此周期与太阳黑子活动具有相似性.行星系质心日心经度运动学方程不仅为进一步研究行星系质心的变化特征、周期性奠定理论基础,而且为进一步研究太阳活动的周期性开辟了新的研究途径.
4.2通过对行星系质心日心经度和行星会合指数的比较分析,行星系质心日心经度较行星会合指数在表征行星质心以及太阳系质心绕太阳质心运动的周期性研究更加准确、更具优势.而行星会合指数适合于表征行星系质心距和太阳系质心距太阳质心的距离大小,以及行星系统的会合和分离程度.
4.3通过对行星系质心和太阳质心运动轨迹的数值模拟研究发现,无论是行星系质心绕太阳质心的运动轨迹,还是太阳质心与太阳系质心的相互运动轨迹,其运动轨迹都具有准11.5年的周期性.此周期与太阳活动中的太阳黑子的周期性具有一定的相似性,为进一步研究深入研究行星系统运动与太阳活动的关系提供理论指导.
4.4通过对1001AD至2000AD的1000年期间太阳系质心与太阳本体之间位置关系的统计,准确地统计出太阳系质心位于太阳本体内的时间为345年,位于太阳本体外的时间为655年.在整个太阳系质心与太阳相对运动过程中太阳系质心位于太阳本体内的时间占34.5%(即三分之一),此结论的获得,对学者认为的“太阳系质心绕太阳运转有近半程时间位于太阳本体内”这一认识,其精度提高了约16%.
4.5利用所构建的动力学模型数值模拟了太阳质心与太阳系质心的相对运动特征,并把数值模拟结果与不同文献的研究结论对比,发现数值模拟的结果与其他文献的研究成果保持一致,说明了此模型的构建是科学、正确的.同时,本论文的目的并非为了单一地构建动力学学模型,而是通过构建动力学模型为研究行星运动、太阳活动和全球气候变化奠定理论基础,因此具有十分重要的科学意义和价值.
致谢 感谢审稿专家提出的宝贵意见和编辑部的大力支持!| [] | Charvátová I. 2000. Can origin of the 2400-year cycle of solar activity be caused by solar inertial motion?[J]. Annales Geophysicae, 18(4): 399–405. DOI:10.1007/s00585-000-0399-x |
| [] | Chen X Z. 1996. Solar activity modulation by planetary perturbations[J]. Acta Astrophysica Sinica, 16(2): 207–212. |
| [] | Dai W S. 1979. The Development of Solar System (Rudin)[M]. Shanghai: Shanghai Scientific & Technical Publishers: 22-23. |
| [] | Damon P E, Cheng S L, Linick T W. 1989. Fine and hyperfine structure in the spectrum of secular variations of atmospheric 14C[J]. Radiocarbon, 31(3): 704–718. DOI:10.1017/S0033822200012303 |
| [] | Damon P E, Linick T W. 1986. Geomagnetic-heliomagnetic modulation of atmospheric radiocarbon production[J]. Radiocarbon, 28(2A): 266–278. DOI:10.1017/S0033822200007360 |
| [] | Friis-Christensen E, Lassen K. 1991. Length of the solar cycle:An indicator of solar activity closely associated with climate[J]. Science, 254(5032): 698–700. DOI:10.1126/science.254.5032.698 |
| [] | Haigh J D. 1996. The impact of solar variability on climate[J]. Science, 272(5264): 981–984. DOI:10.1126/science.272.5264.981 |
| [] | Hood L L, Jirikowic J L. 1991. A probable approx. 2400 year solar quasi-cycle in atmospheric delta 14C[J]. Holocene, 12: 98–105. |
| [] | Jose P D. 1965. Sun's motion and sunspots[J]. The Astronomical Journal, 70(3): 193–200. |
| [] | Li K J, Feng W, Liang H F. 2010. The abnormal 24th solar cycle-The first complete solar cycle of the new millennium[J]. Scientia Sinica Physics, Mechanics & Astronomy, 40(10): 1293–1301. |
| [] | Liu F G, Wang J. 2013. Changes of the planet juncture index and solar revolution cycle around the mass center of the solar system[J]. Chinese Journal of Geophysics, 56(5): 1457–1466. DOI:10.6038/cjg20130504 |
| [] | Liu F G, Wang J, Bai S B, et al. 2013a. The planetary motion and the change of 22-year cycle of the Sun spin velocity[J]. Progress in Geophysics, 28(4): 1678–1683. DOI:10.6038/pg20130406 |
| [] | Liu F G, Wang J, Shang Z Y, et al. 2013b. Study on long-term cyclical rhythm of solar activity[J]. Progress in Geophysics, 28(2): 570–578. DOI:10.6038/pg20130205 |
| [] | Liu L B, Wan W X, Chen Y D, et al. 2011. Solar activity effects of the ionosphere:A brief review[J]. Chinese Science Bulletin, 56(12): 1202–1211. DOI:10.1007/s11434-010-4226-9 |
| [] | Qu W Z, Deng S G, Huang F, et al. 2004. Influence of magnetic index abnormal change in the solar magnetic field on climate at the middle latitudes of North Hemisphere[J]. Chinese Journal of Geophysics, 47(3): 398–404. DOI:10.3321/j.issn:0001-5733.2004.03.005 |
| [] | Qu W Z, Huang F, Zhao J P, et al. 2007. The significance of solar magnetic field direction variation on anomalous variability of the atmosphere temperature on the earth[J]. Chinese Journal of Geophysics, 50(5): 1304–1310. DOI:10.3321/j.issn:0001-5733.2007.05.005 |
| [] | Sonett C P, Finney S A, Berger A. 1990. The spectrum of radiocarbon[J]. Philos. Trans. Roy. Soc. A Math. Phys. Eng. Sci., 330(1615): 413–426. DOI:10.1098/rsta.1990.0022 |
| [] | Suess H E. 1980. The radiocarbon record in tree rings of the last 8000 years[J]. Radiocarbon, 22(2): 200–209. DOI:10.1017/S0033822200009462 |
| [] | Sun W, Wang J, Chen J R, et al. 2017. Variations of the planet juncture index and heliocentric longitude with spectral analysis for approximately 2000 years[J]. Chinese Science Bulletin, 62(5): 407–419. DOI:10.1360/N972016-00447 |
| [] | Tlatov A G. 2007. 22-year variations of the solar rotation and solar activity cycles[J]. Astronomy Letters, 33(11): 771–779. DOI:10.1134/S1063773707110084 |
| [] | Ren Z Q. 1990. Global Change[M]. Beijing: Science Press: 23. |
| [] | Yang D H, Yang X X. 2013. Study and model on variation of Earth's Rotation speed[J]. Progress in Geophysics, 28(1): 58–70. DOI:10.6038/pg20130107 |
| [] | Yang R W, Cao J, Huang W, et al. 2009. Cross wavelet analysis of the relationship between total solar irradiance and sunspot number[J]. Chinese Science Bulletin, 54(7): 871–875. |
| [] | Yang Z G. 1991. The possible influence of the orbital motion of the major planets on sunspot activities[J]. Acta Astrophysica Sinica, 11(4): 370–377. |
| [] | Yang Z G, Zhao M. 1988. An investigation for the cause of formation of the major period of the relative sunspot numbers with bipolarity[J]. Acta Astronomica Sinica, 29(3): 297–304. |
| [] | Zhao M Y, Chen J Q, Liu Y, et al. 2014. Statistical analysis of sunspot groups and flares for solar maximum and minimum[J]. Scientia Sinica Physics, Mechanics & Astronomy, 44(1): 109–120. |
| [] | Zhao P, Zhou X J, Liu G. 2011. Decadal-centennial-scale change in Asian-Pacific summer thermal contrast and solar activity[J]. Chinese Science Bulletin, 56(28-29): 3012–3018. DOI:10.1007/s11434-011-4591-z |
| [] | Zhao X H, Feng X S. 2014. Periodicities of solar activity and the surface temperature variation of the Earth and their correlations[J]. Chinese Science Bulletin, 59(14): 1284–1292. DOI:10.1360/972013-1089 |
| [] | Zhou Y B. 1986. The Course of Theoretical Mechanics[M]. 2nd ed. Beijing: Higher Education Press: 112-114. |
| [] | 陈协珍. 1996. 行星摄动力对太阳活动的调制[J]. 天体物理学报, 16(2): 207–212. |
| [] | 戴文赛. 1979. 太阳系演化学 (上册)[M]. 上海: 上海科技出版社: 22-23. |
| [] | 李可军, 冯雯, 梁红飞. 2010. 异常的第24太阳活动周——新千年的第一个完整的太阳活动周[J]. 中国科学:物理学力学天文学, 40(10): 1293–1301. |
| [] | 刘复刚, 王建. 2013. 行星会合指数变化与太阳绕太阳系质心运转的周期[J]. 地球物理学报, 56(5): 1457–1466. DOI:10.6038/cjg20130504 |
| [] | 刘复刚, 王建, 白世彪, 等. 2013a. 行星运动与太阳自转角速度22年周期变化[J]. 地球物理学进展, 28(4): 1678–1683. DOI:10.6038/pg20130406 |
| [] | 刘复刚, 王建, 商志远, 等. 2013b. 太阳轨道运动长周期性韵律的成因[J]. 地球物理学进展, 28(2): 570–578. DOI:10.6038/pg20130205 |
| [] | 刘立波, 万卫星, 陈一定, 等. 2011. 电离层与太阳活动性关系[J]. 科学通报, 56(7): 477–487. |
| [] | 曲维政, 邓声贵, 黄菲, 等. 2004. 太阳磁场磁性指数异常变化对南北半球中纬度气候的影响[J]. 地球物理学报, 47(3): 398–404. DOI:10.3321/j.issn:0001-5733.2004.03.005 |
| [] | 曲维政, 黄菲, 赵进平, 等. 2007. 太阳磁场方向变化对于地球大气温度异常变化的意义[J]. 地球物理学报, 50(5): 1304–1310. DOI:10.3321/j.issn:0001-5733.2007.05.005 |
| [] | 任振球. 1990. 全球变化:地球四大圈异常变化及其天文成因[M]. 北京: 科学出版社: 23. |
| [] | 孙威, 王建, 陈金如, 等. 2017. 近两千年以来行星会合指数与行星系日心经度变化及频谱分析[J]. 科学通报, 62(5): 407–419. |
| [] | 杨东红, 杨学祥. 2013. 地球自转速度变化规律的研究和计算模型[J]. 地球物理学进展, 28(1): 58–70. DOI:10.6038/pg20130107 |
| [] | 杨若文, 曹杰, 黄玮, 等. 2009. 太阳常数与太阳黑子数关系的交叉小波分析[J]. 科学通报, 54(7): 871–875. |
| [] | 杨志根. 1991. 大行星运动对太阳黑子活动的可能影响[J]. 天体物理学报, 11(4): 370–377. |
| [] | 杨志根, 赵铭. 1988. 太阳极性黑子相对数主周期的成因探讨[J]. 天文学报, 29(3): 297–304. |
| [] | 赵明宇, 陈军权, 刘煜, 等. 2014. 太阳活动峰年和谷年期间黑子群与耀斑的统计分析[J]. 中国科学:物理学力学天文学, 44(1): 109–120. |
| [] | 赵平, 周秀骥, 刘舸. 2011. 夏季亚洲-太平洋热力差异年代-百年尺度变化与太阳活动[J]. 科学通报, 56(25): 2068–2074. |
| [] | 赵新华, 冯学尚. 2014. 太阳活动与地球表面温度变化的周期性和相关性[J]. 科学通报, 59(14): 1284–1292. |
| [] | 周衍柏. 1986. 理论力学教程[M]. 2版. 北京: 高等教育出版社: 112-114. |
 2017, Vol. 32
2017, Vol. 32


