2. 中国地震局地球物理研究所, 北京 100081
2. Institute of Geophysics, China Administration of Earthquake, Beijing 100081, China
地震波衰减伴随着地震波传播的整个过程,反映着传播介质的非弹性性质 (Akinci et al., 1995).一般认为,地震波衰减机制主要分为2种:固有衰减和散射衰减 (Akinci et al., 1995; Hoshiba et al., 2001).固有衰减是地震波在传播过程中,介质微粒运动克服微粒之间的摩擦力,将地震波能量转化成热能,从而导致地震波能量的衰减;散射衰减是指由于介质的不均匀性,地震波遇到散射体而发生散射,能量重新分配而导致台站接收到的能量减少 (Akinci et al., 1995; Hoshiba et al., 2001).
地震波的衰减程度可以采用介质的品质因子Q值来衡量.与地震波传播速度相比,地震波振幅衰减对地下介质的性质更加敏感.如地壳上地幔地震波速度的横向变化通常只有百分之几,而地壳上地幔Q值的横向变化的量级却在数十倍以上.因此借助于地壳Q值的研究,可以更有效地认识地壳的精细结构特征.
现有相关研究中,地球物理学家先后利用地震体波、面波、尾波、Lg波、Sn波、Pg波等震相来研究地震波的衰减特性 (Herrmann, 1980; Lees and Lindley, 1994; Mitchell, 1995; Myers et al., 1998; Gök et al., 2003; Schurr et al., 2003; Stachnik et al., 2004; Bao et al., 2011b; Liang et al., 2014; Bao et al., 2016).与其他震相相比,Lg波的优点在于:其一,它是大陆近震记录中振幅最大、承载能量最大、群速度相对稳定,且最易于识别的震相;其二,它是地壳内传播的导波,被广泛应用于地壳Q值横向变化研究 (Campillo et al., 1985).此外,在新生代火山及构造活动地区,Lg波衰减强烈.因此,Lg波Q值有助于研究地壳内部的岩石物性和温度,以及地震波的强地面运动特征 (张怀等, 2009) 等,是研究地壳介质不均匀性的有效方法之一 (周连庆等, 2008b).本文系统地总结了Lg波的传播特性和Lg波Q值的研究方法、以及中国大陆及周边地区Lg波Q值成像的研究现状.
现有相关研究中,地球物理学家先后利用地震体波、面波、尾波、Lg波、Sn波、Pg波等震相来研究地震波的衰减特性 (Herrmann, 1980; Lees and Lindley, 1994; Mitchell, 1995; Myers et al., 1998; Gök et al., 2003; Schurr et al., 2003; Stachnik et al., 2004; Bao et al., 2011b; Liang et al., 2014; Bao et al., 2016).与其他震相相比,Lg波的优点在于:其一,它是大陆近震记录中振幅最大、承载能量最大、群速度相对稳定,且最易于识别的震相;其二,它是地壳内传播的导波,被广泛应用于地壳Q值横向变化研究 (Campillo et al., 1985).此外,在新生代火山及构造活动地区,Lg波衰减强烈.因此,Lg波Q值有助于研究地壳内部的岩石物性和温度,以及地震波的强地面运动特征 (张怀等, 2009) 等,是研究地壳介质不均匀性的有效方法之一 (周连庆等, 2008b).本文系统地总结了Lg波的传播特性和Lg波Q值的研究方法、以及中国大陆及周边地区Lg波Q值成像的研究现状.
1 Lg波Q值的地球物理含义介质品质因子Q值被定义为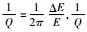
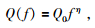
|
(1) |
其中Q0为Q在1 Hz时的值,η表征了Q值对频率的依赖程度.一般来说,介质的固有衰减对频率的依赖性比较弱,η较小;而散射衰减对频率依赖性比较强,η较大.
低Q值代表强衰减,而高Q值则意味着弱衰减.Q值对介质的物质组成及均匀程度、温度、孔隙流体以及主要的深大断裂带和板块构造边界等比较敏感 (Xie, 2002; 刘建华等, 2004a).Q值被应用到地震学的各个方面.在勘探中,利用地层对地震波的衰减来确定岩性的空间变化、含流体类型以及含油气性,进而进行油气藏的预测 (周连庆等, 2008b).在工程地震中,Q值是进行强地面运动模拟以及地震危险性评估的重要介质参数,可为防震减灾工作提供较为可靠的量化参数.有研究显示,一些较大地震发生前后,Q值具有较为显著的异常变化,因此,Q值也是地震预测研究的重要参数之一 (高龙生, 1985).Q值与构造活动有着明显的相关性 (Rodgers et al., 1997; Xie, 2002; Bao et al., 2011a),尤其对温度变化特别敏感,是探测壳幔介质部分熔融与否的重要工具 (Rapine and Ni, 2003).
Press和Ewing (1952)首次提出Lg波的概念.Lg波是一个复杂的含高频P和S波能量的短周期地壳导波,群速度比较稳定,一般为3.0~3.5 km/s,频率主要集中于0.5~5 Hz.相对于海洋地壳,Lg波在大陆地壳中比较发育,在稳定的地壳,如东欧克拉通以及西伯利亚克拉通,甚至可以传播3000~4000 km以上.然而若传播路径上存在100 km以上的海洋地壳,我们将无法在地震波形中观测到明显的Lg波 (Press and Ewing, 1952; Bostock and Kennett, 1990).传播150 km以后,震源辐射花样似乎对Lg波的振幅影响不大 (垂直走滑地震震源除外),但是震源深度对其有一定的影响 (Shi et al., 2000).当震源处于同一速度层时,震源深度的影响可以忽略;但若是处于不同的速度层,震源深度对Lg波传播会有较大的影响 (Shi et al., 2000).普遍认为Lg波的几何扩散衰减在时间域类似于体波,在频率域则类似于面波 (Yang, 2002).地震观测表明当地震波穿过海洋以及薄的大陆地壳、地壳厚度突变地区、巨厚的沉积盆地以及部分熔融的地壳时,Lg波会迅速衰减 (Nuttli, 1980; Kennett, 1986; Mitchell and Hwang, 1987; Bostock and Kennett, 1990; Mitchell et al., 1997; Rodgers et al., 1997; Xie et al., 2004).相对于天然地震来说,爆炸源以及核试验的Lg波几乎不发育.因此,鉴于Lg波的一系列特性,Lg波被广泛地应用于地震学的许多研究领域,如确定区域地震的震级、进行核监测、估算核爆破的当量以及研究地壳衰减的横向变化等 (葛焕称等, 1985; Nuttli, 1986; 葛焕称, 1988; Xie and Mitchell, 1990b; 黄才中等, 1990; 靳平等, 2004; 周连庆等, 2008a).
当前,对于Lg波的形成以及传播机制尚存一些疑问.如,根据Lg波群速度频散曲线与面波高阶振型群速度的相似性,Lg波被认为是大陆地壳内高阶振型的Love和Rayleigh波的叠加 (Knopoff et al., 1973; Der et al., 1984; Kennett and Mykkeltveit, 1984),大陆地壳内高阶振型的叠加理论能够很好地解释薄的海洋地壳Lg波衰减消失的原因,但是无法解释Lg波的群速度为什么稳定在3.5 km/s左右 (Bouchon, 1982).另外,Lg波还被认为是S波在Moho面的超临界反射形成的各种反射波叠加而成的导波 (Herrin and Richmond, 1960; Bouchon, 1982),但是超临界反射叠加理论无法解释为什么在纯海洋地壳的传播路径中很难观测到Lg波.
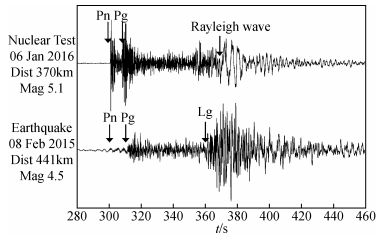
|
图 1 MDJ台站记录到的两个不同震源的地震事件波形图,分别是2016年01月06日的朝鲜核测试和2015年02月08日发生的一次体波震级为4.5的天然地震 Figure 1 Seismograms recorded at station MDJ, comparison between the North Korea nuclear test on 6th Jan., 2016 (upper panel) and an earthquake on 8th Feb., 2015 (bottom panel). The nuclear test cause a sudden onset of P-waves and weak shear waves, whereas the earthquake leads to a presence of P-waves and strong shear waves at relatively lower speed |
Lg波Q值成像结果主要反映了地壳介质的衰减程度,体现了地震波传播的衰减特征,是描述区域地壳结构及活动性的重要参数之一.已有的研究表明,Lg波Q值与构造活动性以及地震活动性有关联 (Bao et al., 2011a).低Q值往往与地壳活动性、火山和高热流值 (Xie, 2002; Zor et al., 2007)、松散的沉积层 (Mitchell and Hwang, 1987) 以及速度等具有一定的相关性 (Gallegos et al., 2014; Ranasinghe et al., 2015).低Q值、强衰减地区通常位于构造活跃地区,高Q值一般位于地壳稳定地区,代表弱衰减.地震对建筑物的破坏一般是由Lg波造成的 (Cornell et al., 1979),因此,Lg波衰减特征同工程设计紧密相关,近场强地面运动的Lg波衰减研究对于抗震设计具有重大的应用价值 (Chen and Nuttli, 1984).随着观测资料的积累,Lg波已经广泛地用于地震波衰减的研究 (Xie and Nuttli, 1988; Mitchell et al., 1997; Rodgers et al., 1997; Phillips et al., 2000; Sandvol et al., 2001; Xie et al., 2006; Zor et al., 2007; 周连庆等, 2008a; Zhao et al., 2010; Bao et al., 2011a; Zhao et al., 2013a; Zhao et al., 2013b; Gallegos et al., 2014; McNamara et al., 2014; Zhao and Xie, 2016).
2 Lg波Q值研究的方法及进展近五十年来,科学家们对天然地震Lg波的衰减特性进行了一系列卓有成效的研究.Press (1964)利用台阵记录到的核爆炸波形记录,采用时间域高阶面波振幅随震中距衰减的理论关系,首次测定了Lg波的Q值.Nuttli (1973)直接测出美国东部地区1 s周期的Lg波在时间域的滞弹性衰减系数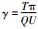
利用天然地震计算Lg波Q值的方法按台站事件数量主要分为三类:单台法、双台法和反双台法或反事件法.我们将简要介绍各种方法的基本原理.一般地,大家都选择信噪比高的垂直分量计算Lg波的Q值.估算近震波形Q值频率域的振幅公式都是基于Sato (1967)提出的体波频率域振幅公式而修改的, 公式为
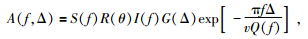
|
(2) |
其中A表示频率域的谱密度,S为震源函数,R为震源辐射效应,I为仪器响应,E为场地响应,Δ为震中距,单位为千米,f为给定的频率,v为Lg波群速度 (3.5 km/s),G为几何扩散参数,定义为 (Street et al., 1975):
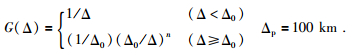
|
(3) |
对于Lg波,G可以简化为
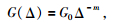
|
(4) |
G0是一个常数,m为几何扩散指数 (Yang, 2002).Shin和Herrmann (1987)首先将频率域与时间域的几何扩散指数分开考虑.被普遍认可的是频率域m为0.5,时间域为0.83或者时间域几何扩散参数为G=Δ-1/3(sinD)-1/2,其中Δ和D为震中距,单位分别为千米和度.下述几种方法除单台叠加频谱比法SSR以外,其余的几种方法都是运用上述的几何扩散参数.
2.1 单台法 (Single Station Method) (SSM) 2.1.1 单台叠加谱比法 (Stacked Spectral Ratio method)(SSR)Xie和Nuttli (1988)基于Lg尾波的随机散射模型以及单次各向同性散射模型,即单台记录的Lg尾波Q0值是一个椭球内介质衰减的平均值,并提出了单台叠加频谱比法 (SSR).该方法由于使用的是一个台站记录到的波形,有效地避免了震源效应和仪器响应的影响,误差小且具有较好的稳定性 (Xie and Nuttli, 1988).SSR计算的是震中和台站的椭球区域内的平均Q值.其是将垂直方向的Lg尾波分成个等长的时间窗,并对每个时间窗的波形进行傅里叶变换,得到第k个频率在第m个时间窗口的平均振幅值〈Ak, m〉,第k个频率值叠加频谱比法的定义为
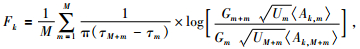
|
(5) |
其中
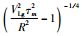
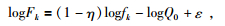
|
(6) |
其中ε为误差,fk表示第k个频率值.
Xie和Nuttli (1988)首次运用公式 (6),获得了非洲大陆的Lg尾波Q的观测值.Mitchell等 (1997)利用SSR方法研究欧亚地区的地壳衰减情况,研究表明Q值与构造活动性、高热流及空隙流体有关.该方法也被广泛应用于研究中东 (Cong and Mitchell, 1998)、美国大陆 (Baqer and Mitchell, 1998) 以及澳大利亚 (Mitchel et al., 1998) 的地壳衰减情况以及Q值的横向不均匀性.同时SSR方法在中国也得到了广泛的应用如成都地区 (曾健等, 1997)、云南及周边地区 (胡家富等, 2003)、华北地区 (刘建华等, 1999; 刘建华等, 2004b, c)、四川及邻区 (毛燕等, 2005)、新疆及周边地区 (徐彦等, 2005)、以及中国大陆和邻区 (丛连理等, 2002; 苏伟等, 2006) 的Q值估计等.
2.1.2 尾波归一化方法 (Coda Normalization Method)(CNM)尾波归一化方法是基于区域横波尾波的方法来获得Lg波的Q-1值,其假设区域横波尾波在时空域是均匀分布的,能够有效地去除震源谱和场地效应 (Aki, 1980).其同时也假设尾波振幅C(f) 近似于给定传播时间tC的震源谱
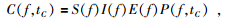
|
(7) |
其中传播时间tC是大于Lg波到时的2倍,P(f, tC) 与震源和震中距无关,表示着频谱振幅随时间的传播而衰减.尾波归一化方法就是利用公式 (2) 除以公式 (7) 来去除震源函数、仪器响应以及场地效应的影响,同时通过使用方位分布范围较大的台站来消除震源辐射效应的影响R (θ).因此可以获得归一化后的公式为
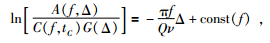
|
(8) |
其中几何扩散参数为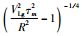
Frankel等 (1990)利用尾波归一化方法使用不同的n值获得了纽约、南加州和南非的地壳Lg波Q值.Chung和Lee (2003)利用南北分量的地震记录,应用该方法获得了韩国地区的地壳Lg波Q-1值,这些结果基本上均与地震活动性相关.
McNamara等 (1996)和Benz等 (1997)等将波形的振幅跟几何扩散参数结合在一起视为是随时间变化的函数,如公式 (9) 的左边.这样公式 (9) 在给定的频率f下,就是一个关于震中距Δ的线性函数,其斜率为Q-1,其原理与尾波归一化方法基本上相似.该方法被应用到研究青藏高原 (McNamara et al., 1996)、美国大陆 (Benz et al., 1997) 以及阿拉斯加州中南部地区 (McNamara, 2000) 的地壳Lg波Q值.周连庆等 (2008a)利用该方法采用奇异值分解方法,获得了川滇地区的Lg波Q值成像结果,结果表明:构造活动强烈、强震活动区、介质破裂区以及低速区等呈现低Q值、强衰减特征.公式为
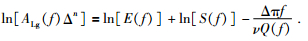
|
(9) |
尾波震源归一化方法是利用尾波提取震源函数的方法 (Walter et al., 2007).公式 (2) 中的震源函数可表示为 (Aki and Richards, 1980)
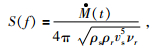
|
(10) |
其中Ṁ(t) 是震源矩率函数对时间的一阶导数,ρ和ν分别表示震源s和台站r附近介质的密度和速度.对于S波,震源辐射参数R(θ) 取0.6,对于P波R(θ) 取0.44(Walter et al., 2007).几何扩散参数为G(Δ)=G0Δ-m,G0是一个常数,m为0.5.假设E(f) 为单位变量1,即所有的场地效应都归于震相的衰减,根据公式 (8) 和公式 (9) 可以得到 (Walter et al., 2007):
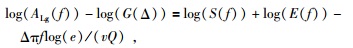
|
(11) |
其中ALg(f) 为去除仪器响应I(f) 后的Lg波频率域振幅.从尾波中提取震源矩率函数 (Mayeda et al., 2003),通过给定密度ρ、速度ν以及震源辐射参数R(θ),我们可以获得对数域Q值随频率的变化.
Walter等 (2007)采用该方法对韩国地区的Pn、Pg、Sn以及Lg波的衰减情况进行了研究.Pasyanos等 (2009a)获得了中东、欧洲西南亚以及东非地区等大范围的P波和S波的地壳上地幔衰减情况,且还对中东地区的Lg波Q值进行了研究 (Pasyanos等, 2009b).Taylor等 (2003)采用不同的成像方法对东亚地区的Lg波Q值进行了研究,结果都显示青藏高原地区呈现明显的低Q值.
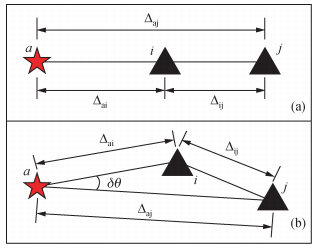
2.2 双台法 (Two Station Method) (TSM)Tsai和Aki (1969)首次提出了双台法,并用于计算面波的Q值.Xie和Mitchell (1990a)将其进一步修改并运到Lg波Q值的计算.双台法,顾名思义就是两个台站接收的Lg波进行频率域的振幅比,从而消除射线路径的影响,提高Q值测定的横向分辨率.台站分布的理想情况是如图 2a所示,2个台站与事件位于一个大圆弧路径上.为提高射线的数量以及分辨率,通常采用满足图 2b所示的地震射线.Der等 (1984)发现台站接收到的包含Lg波的前向散射波有一定的方向性,这些波偏离大圆弧路径的最大范围为±15°.为了减少误差且保持Lg波的完全发育,δθ要少于等于15°,Δij大于等于150 km (Xie et al., 2004).
|
图 2 双台法的几何路径示意图 (a) 为理想情况下的双台法几何路径;(b) 为实际情况中运用的几何路径示意图.红色五角星代表着地震事件a.黑色三角形i, j是地震台站. Figure 2 A map shown the geometry of the TSM (a) An ideal recording geometry for the application of TSM for Q measurement; (b) A more practical geometry in TSM. The red star a represent earthquake and the black triangles i and j are seismic stations. |
台站i接收到地震事件a在频率域的振幅为
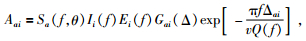
|
(12) |
其中Sa(f, θ) 为包含震源辐射效应的震源函数,I为仪器响应,E为场地响应,Δ为震中距,v为Lg波群速度 (3.5 km/s),G为几何扩散参数G(Δ)=G0Δ-m,m为0.5.结合公式 (12),可以得到近距离的台站i与远距离的台站j接收 (即Δaj>Δai) 的Lg波振幅谱比值为

|
(13) |
其中Aai和Aaj分别表示台站i和台站j记录到的事件a的频率域的振幅.因此,忽略场地效应的影响,台站i与台站j之间的Q值为 (Xie and Mitchell, 1990a)
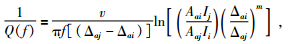
|
(14) |
同时Q(f)=Q0fη,则
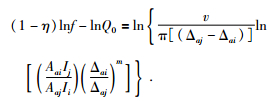
|
(15) |
随着数据的积累以及台站数量的增加,双台法被广泛地运用到青藏高原地区 (Xie, 2002; Xie et al., 2004)、东欧地区 (Xie et al., 2006)、土耳其高原 (Zor et al., 2007)、中东地区 (Kaviani et al., 2015) 等.在国内,Zhao等 (2010)运用双台法得到了东北地区的Lg波Q值成像.
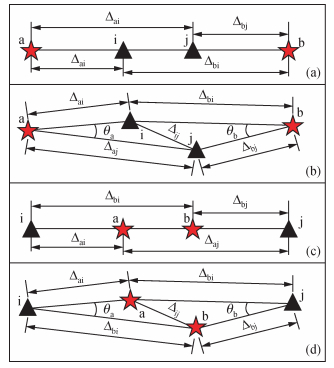
2.3 反 (逆) 双台法/反双事件法 (Reverse Two-station Method/Reverse Two-event Method) (RTM)Chun等 (1987)等首先采用逆双台法 (RTM) 即双台双震源的方法,测定了加拿大东部地区的Lg波滞弹性衰减系数值.若2个台站和两个地震事件位于同一大圆弧附近,如图 3所示,通过两个台站记录到的两次地震事件的Lg波的振幅谱之比获得Q值,可以有效地减少震源辐射效应、震源机制、以及两个台站的场地效应和仪器响应的影响.图 3所示包含2种情况:一种是反双台法,如图 3a所示,另一种是反双事件法 (图 3c),其中图 3a和图 3c是理想的几何路径,事件和台站都在大圆弧上,图 3b和图 3d是实际情况中的几何路径.为减少误差,θa和θb被限制在15°以内,事件a和b的间距以及台站i和j的间距需不少于150 km.结合公式 (13),2个台站记录到的2个事件的振幅谱比可以得到 (Bao et al., 2011a):
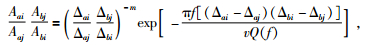
|
(16) |
其中Δaj>Δai, Δbi>Δbj.因此结合公式 (1) 和 (16),得到:
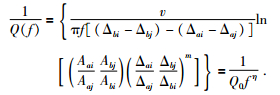
|
(17) |
进而,可以获得对数域Q值随频率的变化,公式为
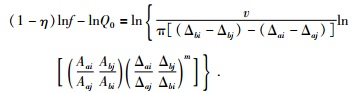
|
(18) |
反双台法或反双事件法由于对事件与台站位置的要求很高,符合要求的射线路径没有双台法多,射线的覆盖率不高,事件的利用率完全取决于台阵的布局.Chung等 (2007)采用反双台法对朝鲜半岛的地壳衰减情况进行了研究.Gallegos等 (2014)和Kaviani等 (2015)利用双台法和反双台法,分别获得美国东部地区和土耳其—伊朗高原地区的Lg波Q值成像.整体上,双台法和反双台法获得的Q值结果具有一定的一致性.但是由于反双台法的射线较少,部分地区的分辨率不是很高.Fan和Lay (2003b)利用反双台法或反双事件法,揭示青藏高原中北以及中南部地区呈现低Q值. Bao等 (2011a)的研究表明青藏高原北部大部分地区的Q值较小,可能反映藏北地区地壳部分熔融的广泛分布,高Q值则位于构造稳定地区,如柴达木盆地等.Zhao等 (2013b)获得了华北及周边地区的地壳衰减Lg波Q值成像.Ranasinghe等 (2015)利用NECESSArray的数据,采用反双台法或反双事件法获得了东北地区的Lg波衰减成像,结果显示低Q0值地区主要位于松辽盆地、三江盆地以及五大连池等第四纪火山地区,强衰减主要与松散的盆地沉积层和全新世的火山活动等有关.
2.3.1 震源对/事件对方法 (Source Pair/Receiver Pair Method)(SPRP)Shih等 (1994)将反双台法或反双事件法扩展到时间域,同时扩大了反双台法的适应范围,称为震源对/事件对方法 (Source Pair/Receiver Pair Method)(SPRP).时间域的几何扩散参数为 (Nuttli, 1973):G=Δ-1/3(sinD)1/2或G=G0Δ-m,m=0.83, Δ与D都为震中距,Δ的单位为千米,D是用弧度表示的震中距,单位为度.则公式 (14) 可以变化为
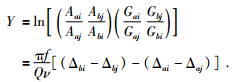
|
(19) |
同时ΔA2>(SP2+ΔB2),ΔA为Δaj和Δbi两者中的最大值,ΔB为Δai和Δbj两者中的最小值,SP为反双台法中两台站的间距 (图 2b中Δij) 或反双事件法中两事件的间距 (图 2d中Δab),要求大于50 km (Chung et al., 2005).对给定的频率内,在群速度为2.9~3.6 km/s的时间窗口内,获得时间域的振幅最大值,这样可以获得给定的频率范围内Y随震中距的变化,其斜率为Q-1.该方法大大地扩大了反双台法的适应范围,在符合条件的震中距内,路径中间的台站间距或事件间距可以到达70°(Ford et al., 2008).Chung等 (2005)利用该方法对韩国地区的Lg波Q-1进行了研究.
3 几种方法的比较单台法中,SSR方法是通过自身振幅的比值来获得Q值,有效地避免了震源和仪器响应的影响.SSR方法基于尾波单次各向同性散射模型,受观测资料以及单台法方法本身的限制,获得的Q值是一个椭球内的平均值,其中台站和震源是这个椭球的两个焦点,椭球大小与尾波持续时间有关.因此,所得到的Q值横向分辨率比较低,体现Q值的横向不均匀性特征的能力不足.CNM方法基于空间某一点散射的尾波呈均匀分布的假设,可应用于所有接收到Lg波的射线路径,能消除震源和场地效应的影响.CSM方法利用其他方法获得的震源函数,能应用于所有射线路径,但其受场地效应以及几何扩散参数的影响较大.
TSM方法利用台站到事件的夹角小于15°的限制,有效地消除了震源函数的影响,但也限制了能用于估算Q值的射线路径数量.同时TSM所计算的Q值包含了场地效应的影响.RTM能有效地去除震源以及场地效应的影响进而获得准确的Q值,但是由于其要求θa和θb(图 2) 少于15°,所以其适应范围受台站以及事件的位置分布影响.
SPRP方法基于各向同性震源的假设,能去除震源及场地效应的影响.相对于RTM来说,其放宽了对射线路径的限制,但是要求反双台法的双台间距或者反双事件法的双事件间距大于50 km.
|
图 3 反双台法和反双事件法的几何路径示意图 红色五角星代表着地震事件a和b.黑色三角形i, j是地震台站.(a) 和 (c) 分别为理想情况下的反双台法和反双事件法的几何路径.(b) 和 (d) 为实际情况中运用的几何路径示意图.θa和θb表示两个事件到一个台站或者两个台站到一个事件的夹角. Figure 3 A map shown the geometry of the RTM The red stars "a" and "b" represent earthquakes and the black triangles i and j are seismic stations. (a) and (c) are ideal recording geometries for the application of reverse two-station method or reverse two-event method, respectively. (b) and (d) are more practical geometries in reverse two-station method and reverse two-event method, respectively. θa and θb are the subtended angles between earthquakes "a" and "b" for stations i and j, respectively. |
Ford等 (2008)对单台法中的CNM和CSM方法、双台法、反双台法以及SPRP方法进行了系统的比较.CNM方法可能由于使用固定的尾波窗口的原因,对震中距比较敏感.由于对几何扩散参数比较敏感,CSM方法比较适合于计算所有路径下的衰减情况.用TSM方法获得的Q值随频带宽度的变化而变化,可能是受场地效应的影响.在RTM方法中,各种参数的设置对其结果的影响都不是很大.然而SPRP由于在时间域内计算,η受各种参数设置的影响很大.整体上,就目前来说,用RTM方法获得的Q值结果相对比较稳定,误差较少 (Ford et al., 2008).
4 Lg波Q值成像在中国大陆地区的研究现状我国在Lg波Q值成像研究中取得了长足的进步,获得了众多区域性、乃至整个中国大陆及其邻区的Lg波Q值分布,如云南地区 (胡家富等, 2003)、成都地区 (曾健等, 1997)、华北地区 (刘建华等, 2004b, c; Zhao et al., 2013b)、四川及邻区 (毛燕等, 2005)、新疆及周边地区 (徐彦等, 2005)、川滇地区 (周连庆等, 2008b)、东北地区 (Zhao et al., 2010; 孙莲等, 2012; Ranasinghe et al., 2015)、中国及邻区 (葛焕称等, 1989; Phillips et al., 2000; 丛连理等, 2002; Taylor et al., 2003; Phillips et al., 2005; Xie et al., 2006; 苏伟等, 2006) 等.结果显示:中国大陆及邻区Q0值的主要变化范围约为80到800,最低的Q值在川滇青藏高原地区,最高值则位于西伯利亚南端以及蒙古南部地区.Q值的横向分布与Pn以及Sn波的速度成像结果拥有很好的相关性 (Phillips et al., 2005; Pei et al., 2006),高速对应着高Q值,反之亦然.整体上与最新的构造活动或者地幔热活动距今的时间相关 (Mitchell et al., 1997).低Q值、强衰减地区主要分布在构造活跃的块体,如青藏高原、川滇地区、华北平原以及渤海湾等地区;而高Q值弱衰减则主要分布在稳定的盆地地区,如塔里木盆地、四川盆地、鄂尔多斯盆地以及华南等地区 (葛焕称等, 1985; 丛连理等, 2002; Phillips et al., 2005; 苏伟等, 2006; 汪素云等, 2007; 汪素云等, 2008; Zhao et al., 2013a; Zhu, 2014).
青藏高原地区的Lg波Q0值在100左右,整体上呈现低Q值强衰减的特征,与该区的下地壳部分熔融、活跃的构造活动以及特殊的地质背景有关 (McNamara et al., 1996; Phillips et al., 2000; Fan and Lay, 2002; Xie, 2002; Fan and Lay, 2003a; Fan and Lay, 2003b; Taylor et al., 2003; Xie et al., 2004; Xie et al., 2006; 周连庆等, 2008a; Bao et al., 2011a; Singh et al., 2012; Singh et al., 2015; Singh et al., 2016).Zhao等 (2013a)根据青藏高原地区低的Lg波Q值分布,结合其他地质地球物理资料,推测了青藏高原地区可能存在的地壳通道流的分布区域.
华北地区的Lg波Q值略高于青藏高原,Q0的平均值约为350(Zhao et al., 2013b),总体上还是属于低Q值强衰减区,可能与该地区地壳减薄、地壳内部介质破碎、拉张环境造成的热物质上涌等有关 (刘建华等, 2004b; 苏伟等, 2006; Zhao et al., 2013b).
龙门山断裂带、昆仑山、祁连山、天山等造山带地区 (Bao et al., 2011a; Zhao et al., 2013a) 受印度洋板块与欧亚板块碰撞的影响,新生代以来构造活动强烈、深大断裂发育,地壳介质破碎、强地震活动频繁,从而导致这些地区Q值较低,地震波衰减强烈.
蒙古高原中南部、阿拉善、鄂尔多斯盆地、四川盆地等地区地壳比较稳定,表现为高Q值、弱衰减 (苏伟等, 2006; Bao et al., 2011a; Zhao et al., 2013a; Zhu, 2014).然而,松辽盆地、海拉尔盆地等盆地地区,由于存在较厚且松散的沉积层,导致强烈的散射衰减,因此,这些地区Lg波Q值较低,呈现强衰减的特征 (Zhao et al., 2010; 孙莲等, 2012; Ranasinghe et al., 2015).
第四纪火山发育地区,如五大连池、长白山火山、腾冲火山等地区存在岩浆上涌,具有典型的第四纪构造活动区的高热流值特性,表现为低Q值和强地震波衰减特征 (胡家富等, 2003; Ranasinghe et al., 2015).
5 结论Lg波是在地壳中传播的导波,反映了地壳结构特点.Lg波能够区分不同的震源从而可以利用它来进行核监测.研究Lg波Q值分布特征是研究地壳结构和组分横向变化,以及其热状态的有效方法之一.地震波衰减研究有利于研究地震波传播介质的非弹性性质.整体上,地震波衰减分为固有衰减以及散射衰减.计算天然地震波Lg波Q值的方法按台站及事件数量主要分为:单台法,双台法以及反双台法/反双事件法,其中单台法又分为三种.单台叠加频谱比法能有效地避免震源和仪器响应的影响,但是其所获得的Q值横向分辨率较低;尾波归一化方法能有效去除震源和场地效应,但其结果对震中距较敏感;而尾波震源归一化方法对几何扩散参数敏感;双台法能有效地消除射线路径与震源函数的影响,提高了分辨率,但其计算的Q值包含场地效应且受台站于事件的夹角少于15°的限制;反双台法能有效去除震源、场地效应以及仪器响应的影响,获得的Q值较稳定,但其对台站与事件的位置要求较高,限制了计算Q值的射线数量;震源对/事件对方法能去除震源和场地效应的影响,然而由于在时间域计算Q值对各种参数的设置较敏感.中国大陆及邻区Q0值的主要变化范围约为80到800,最低的Q值在川滇青藏高原地区,最高值则位于西伯利亚南端以及蒙古南部地区.整体上与最新的构造活动、地震活动性或者地幔热活动距今的时间相关.
| [] | Aki K. 1969. Analysis of the seismic coda of local earthquakes as scattered waves[J]. Journal of Geophysical Research, 74(2): 615–631. DOI:10.1029/JB074i002p00615 |
| [] | Aki K. 1980. Scattering and attenuation of shear waves in the lithosphere[J]. Journal of Geophysical Research:Solid Earth, 85(B11): 6496–6504. DOI:10.1029/JB085iB11p06496 |
| [] | Aki K, Richards P G. 1980. Quantitative Seismology[M]. New York: W.H. Freeman & Co Ltd. |
| [] | Akinci A, Del Pezzo E, Ibáñez J M. 1995. Separation of scattering and intrinsic attenuation in southern Spain and western Anatolia (Turkey)[J]. Geophysical Journal International, 121(2): 337–353. DOI:10.1111/gji.1995.121.issue-2 |
| [] | Bao X Y, Sandvol E, Ni J, et al. 2011a. High resolution regional seismic attenuation tomography in eastern Tibetan Plateau and adjacent regions[J]. Geophysical Research Letters, 38(16): L16304. |
| [] | Bao X, Sandvol E, Zor E, et al. 2011b. Pg attenuation tomography within the northern Middle East[J]. Bulletin of the Seismological Society of America, 101(4): 1496–1506. DOI:10.1785/0120100316 |
| [] | Bao X Y, Dalton C A, Jin G, et al. 2016. Imaging Rayleigh wave attenuation with USArray[J]. Geophysical Journal International, 206(1): 241–259. DOI:10.1093/gji/ggw151 |
| [] | Baqer S, Mitchell B J. 1998. Regional variation of Lg Coda Q in the continental United States and its relation to crustal structure and evolution[J]. Pure and Applied Geophysics, 153(2-4): 613–638. |
| [] | Benz H M, Frankel A, Boore D M. 1997. Regional Lg attenuation for the continental United States[J]. Bulletin of the Seismological Society of America, 87(3): 606–619. |
| [] | Bollinger G A. 1979. Attenuation of the Lg phase and the determination of mb in the southeastern United States[J]. Bulletin of the Seismological Society of America, 69(1): 45–63. |
| [] | Bostock M G, Kennett B L N. 1990. The effect of 3-D structure on Lg propagation patterns[J]. Geophysical Journal International, 101(2): 355–365. DOI:10.1111/gji.1990.101.issue-2 |
| [] | Bouchon M. 1982. The complete synthesis of seismic crustal phases at regional distances[J]. Journal of Geophysical Research:Solid Earth, 87(B3): 1735–1741. DOI:10.1029/JB087iB03p01735 |
| [] | Campillo M, Plantet J L, Bouchon M. 1985. Frequency-dependent attenuation in the crust beneath central France from Lg waves:Data analysis and numerical modeling[J]. Bulletin of the Seismological Society of America, 75(5): 1395–1411. |
| [] | Chen P S, Nuttli O W. 1984. Estimates of magnitudes and short-period wave attenuation of Chinese earthquakes from Modified Mercalli intensity data[J]. Bulletin of the Seismological Society of America, 74(3): 957–968. |
| [] | Chun K Y, West G F, Kokoski R J, et al. 1987. A novel technique for measuring Lg attenuation-results from eastern Canada between 1 to 10 Hz[J]. Bulletin of the Seismological Society of America, 77(2): 398–419. |
| [] | Chung T W, Lee K. 2003. A study of high-frequency Q (super-1) Lg in the crust of South Korea[J]. Bulletin of the Seismological Society of America, 93(3): 1401–1406. DOI:10.1785/0120020199 |
| [] | Chung T W, Park Y K, Kang I B, et al. 2005. Crustal in South Korea using the source pair/receiver pair method[J]. Bulletin of the Seismological Society of America, 95(2): 512–520. DOI:10.1785/0120030223 |
| [] | Chung T W, Noh M H, Kim J K, et al. 2007. A study of the regional variation of low-frequency around the Korean Peninsula[J]. Bulletin of the Seismological Society of America, 97(6): 2190–2197. DOI:10.1785/0120070066 |
| [] | Cong L, Mitchell B J. 1998. Lg coda Q and its relation to the geology and tectonics of the middle east[J]. Pure and Applied Geophysics, 153(2-4): 563–585. |
| [] | Cong L L, Hu J F, Fu Z W, et al. 2002. Lg coda Q value and its relation with the tectonics in Chinese mainland and adjacent regions[J]. Science in China (Ser. D), 32(8): 617–624. |
| [] | Cornell C A, Banon H, Shakal A F. 1979. Seismic motion and response prediction alternatives[J]. Earthquake Engineering & Structural Dynamics, 7(4): 295–315. |
| [] | Der Z A, Marshall M E, O'Donnell A, et al. 1984. Spatial coherence structure and attenuation of the Lg phase, site effects, and the interpretation of the Lg coda[J]. Bulletin of the Seismological Society of America, 74(4): 1125–1147. |
| [] | Dwyer J J, Herrmann R B, Nuttli O W. 1983. Spatial attenuation of the Lg wave in the central United States[J]. Bulletin of the Seismological Society of America, 73(3): 781–796. |
| [] | Fan G W, Lay T. 2002. Characteristics of Lg attenuation in the Tibetan Plateau[J]. Journal of Geophysical Research:Solid Earth, 107(B10): 2256. |
| [] | Fan G W, Lay T. 2003a. Strong Lg wave attenuation in the Northern and Eastern Tibetan Plateau measured by a two-station/two-event stacking method[J]. Geophysical Research Letters, 30(10): 1530. |
| [] | Fan G W, Lay T. 2003b. Strong Lg attenuation in the Tibetan plateau[J]. Bulletin of the Seismological Society of America, 93(5): 2264–2272. DOI:10.1785/0120030052 |
| [] | Ford S R, Dreger D S, Mayeda K, et al. 2008. Regional attenuation in Northern California:A comparison of five 1D Q methods[J]. Bulletin of the Seismological Society of America, 98(4): 2033–2046. DOI:10.1785/0120070218 |
| [] | Frankel A, McGarr A, Bicknell J, et al. 1990. Attenuation of high-frequency shear waves in the crust:Measurements from New York State, South Africa, and southern California[J]. Journal of Geophysical Research:Solid Earth, 95(B11): 17441–17457. DOI:10.1029/JB095iB11p17441 |
| [] | Gallegos A, Ranasinghe N, Ni J, et al. 2014. Lg attenuation in the central and eastern United States as revealed by the EarthScope transportable array[J]. Earth and Planetary Science Letters, 402: 187–196. DOI:10.1016/j.epsl.2014.01.049 |
| [] | Gök R, Sandvol E, Türkelli N, et al. 2003. Sn attenuation in the Anatolian and Iranian plateau and surrounding regions[J]. Geophysical Research Letters, 30(24): 8042. |
| [] | Gao L S. 1985. Developments and problems of research on Q value[J]. Seismological and Geomagnetic Observation and Research, 6: 3–6. |
| [] | Ge H C. 1988. Historical advances in research on the Lg wave[J]. Recent Development in World Seismology (in chinese), 10: 1–7. |
| [] | Ge H C, Ni Y W, Huang C Z, et al. 1989. Velocity, attenuation and magnitude of Lg waves in the continent of China[J]. Science Bulletin (in chinese), 34(24): 1889–1892. |
| [] | Ge H C, Ye P Y, Huang C Z, et al. 1985. Lg wave attenuation and near shock magnitude in the Eastern Region of China[J]. North China Earthquake Sciences (in chinese), 3(4): 1–14. |
| [] | Hasegawa H. 1985. Attenuation of Lg waves in the Canadian Shield[J]. Bulletin of the Seismological Society of America, 75(6): 1569–1582. |
| [] | Herrin E, Richmond J. 1960. On the propagation of the Lg phase[J]. Bulletin of the Seismological Society of America, 50(2): 197–210. |
| [] | Herrmann R B. 1980. Q estimates using the coda of local earthquake[J]. Bulletin of the Seismological Society of America, 70(2): 447–468. |
| [] | Hoshiba M, Rietbrock A, Scherbaum F, et al. 2001. Scattering attenuation and intrinsic absorption using uniform and depth dependent model-application to full seismogram envelope recorded in Northern Chile[J]. Journal of Seismology, 5(2): 157–179. DOI:10.1023/A:1011478202750 |
| [] | Hu J F, Cong L L, Su Y J, et al. 2003. Distribution characteristics of Q value of the Lg coda in Yunnan and its adjacent regions[J]. Chinese Journal of Geophysics, 46(6): 809–813. DOI:10.3321/j.issn:0001-5733.2003.06.013 |
| [] | Huang C Z, Gao Z M, Shi L Q, et al. 1990. Lg wave attenuation and magnitude in northeast China region[J]. Northeastern Seismological Research (in chinese), 6(2): 41–50. |
| [] | Jin P, Xiao W G, Duan K M. 2004. Estimating seismic moments and Q_Lg using Lg spectra[J]. Acta Seismological Sinica (in chinese), 17(S1): 21–30. |
| [] | Kaviani A, Sandvol E, Bao X Y, et al. 2015. The structure of the crust in the Turkish-Iranian Plateau and Zagros using Lg Q and velocity[J]. Geophysical Journal International, 200(2): 1252–1266. DOI:10.1093/gji/ggu468 |
| [] | Kennett B L N. 1986. Lg waves and structural boundaries[J]. Bulletin of the Seismological Society of America, 76(4): 1133–1141. |
| [] | Kennett B L N, Mykkeltveit S. 1984. Guided wave propagation in laterally varying media-Ⅱ[J]. Lg-waves in north-western Europe[J]. Geophysical Journal International, 79(1): 257–267. |
| [] | Knopoff L, Schwab F, Kauselt E. 1973. Interpretation of Lg[J]. Geophysical Journal International, 33(4): 389–404. DOI:10.1111/j.1365-246X.1973.tb02375.x |
| [] | Lees J M, Lindley G T. 1994. Three-dimensional attenuation tomography at Loma Prieta:Inversion of t* for Q[J]. Journal of Geophysical Research:Solid Earth, 99(B4): 6843–6863. DOI:10.1029/93JB03460 |
| [] | Liang X F, Sandvol E, Kay S, et al. 2014. Delamination of southern Puna lithosphere revealed by body wave attenuation tomography[J]. Journal of Geophysical Research:Solid Earth, 119(1): 549–566. DOI:10.1002/2013JB010309 |
| [] | Liu J H, Liu F T, Wang F X, et al. 1999. A measuring study for single-trace Lg coda[J]. Chinese Journal of Geophysics, 42(3): 371–382. DOI:10.3321/j.issn:0001-5733.1999.03.010 |
| [] | Liu J H, Liu F T, Yan X W, et al. 2004b. A study of Lg coda attenuation beneath North China:Seismic imaging of Lg coda Q0[J]. Chinese Journal of Geophysics, 47(6): 1044–1052. DOI:10.3321/j.issn:0001-5733.2004.06.017 |
| [] | Liu J H, Liu F T, Yan X W, et al. 2004c. A study of Lg coda attenuation in North China——the measurement of Lg coda Q[J]. Chinese Journal of Geophysics, 47(5): 822–831. DOI:10.3321/j.issn:0001-5733.2004.05.013 |
| [] | Liu J H, Xu Y, Hao T Y. 2004a. Study on physical mechanism of the seismic wave attenuation[J]. Progress in Geophysics, 19(1): 1–7. DOI:10.3969/j.issn.1004-2903.2004.01.001 |
| [] | Mayeda K, Hofstetter A, O'Boyle J L, et al. 2003. Stable and transportable regional magnitudes based on coda-derived moment-rate spectra[J]. Bulletin of the Seismological Society of America, 93(1): 224–239. DOI:10.1785/0120020020 |
| [] | Mao Y, Xu Y, Wang B, et al. 2005. Distribution Characteristics of the value Q of Lg coda in Sichuan and its adjacent regions[J]. Journal of Seismological Research (in chinese), 28(1): 38–42. |
| [] | McNamara D E. 2000. Frequency dependent Lg attenuation in south-central Alaska[J]. Geophysical Research Letters, 27(23): 3949–3952. DOI:10.1029/2000GL011732 |
| [] | McNamara D E, Gee L, Benz H M, et al. 2014. Frequency-dependent seismic attenuation in the eastern United States as observed from the 2011 Central Virginia earthquake and aftershock sequence[J]. Bulletin of the Seismological Society of America, 104(1): 55–72. DOI:10.1785/0120130045 |
| [] | McNamara D E, Owens T J, Walter W R. 1996. Propagation characteristics of Lg across the Tibetan Plateau[J]. Bulletin of the Seismological Society of America, 86(2): 457–469. |
| [] | Mitchell B J. 1980. Frequency dependence of shear wave internal friction in the continental crust of eastern North America[J]. Journal of Geophysical Research:Solid Earth, 85(B10): 5212–5218. DOI:10.1029/JB085iB10p05212 |
| [] | Mitchell B J. 1995. Anelastic structure and evolution of the continental crust and upper mantle from seismic surface wave attenuation[J]. Reviews of Geophysics, 33(4): 441–462. DOI:10.1029/95RG02074 |
| [] | Mitchell B J, Baqer S, Akinci A, et al. 1998. LgCoda Q in Australia and its relation to crustal structure and evolution[J]. Pure and Applied Geophysics, 153(2-4): 639–653. DOI:10.1007/s000240050211 |
| [] | Mitchell B J, Hwang H J. 1987. Effect of low Q sediments and crustal Q on Lg attenuation in the United States[J]. Bulletin of the Seismological Society of America, 77(4): 1197–1210. |
| [] | Mitchell B J, Pan Y, Xie J K, et al. 1997. Lg coda Q variation across Eurasia and its relation to crustal evolution[J]. Journal of Geophysical Research:Solid Earth, 102(B10): 22767–22779. DOI:10.1029/97JB01894 |
| [] | Myers S C, Beck S, Zandt G., et al. 1998. Lithospheric-scale structure across the Bolivian Andes from tomographic images of velocity and attenuation for P and S waves[J]. Journal of Geophysical Research:Solid Earth, 103(B9): 21233–21252. DOI:10.1029/98JB00956 |
| [] | Nuttli O W. 1973. Seismic wave attenuation and magnitude relations for eastern North America[J]. Journal of Geophysical Research, 78(5): 876–885. DOI:10.1029/JB078i005p00876 |
| [] | Nuttli O W. 1980. The excitation and attenuation of seismic crustal phases in Iran[J]. Bulletin of the Seismological Society of America, 70(2): 469–485. |
| [] | Nuttli O W. 1981. On the attenuation of Lg waves in western and central Asia and their use as a discriminant between earthquakes and explosions[J]. Bulletin of the Seismological Society of America, 71(1): 249–261. |
| [] | Nuttli O W. 1986. Yield estimates of nevada test site explosions obtained from seismic Lg waves[J]. Journal of Geophysical Research:Solid Earth, 91(B2): 2137–2151. DOI:10.1029/JB091iB02p02137 |
| [] | Pasyanos M E, Matzel E M, Walter W R, et al. 2009b. Broad-band Lg attenuation modelling in the Middle East[J]. Geophysical Journal International, 177(3): 1166–1176. DOI:10.1111/gji.2009.177.issue-3 |
| [] | Pasyanos M E, Walter W R, Matzel E M. 2009a. A simultaneous multiphase approach to determine P-wave and S-wave attenuation of the crust and upper mantle[J]. Bulletin of the Seismological Society of America, 99(6): 3314–3325. DOI:10.1785/0120090061 |
| [] | Pei S P, Zhao J M, Rowe C A, et al. 2006. ML amplitude tomography in North China[J]. Bulletin of the Seismological Society of America, 96(4A): 1560–1566. DOI:10.1785/0120060021 |
| [] | Phillips W S, Hartse H E, Taylor S R, et al. 2000. 1 Hz Lg Q tomography in central Asia[J]. Geophysical Research Letters, 27(20): 3425–3428. DOI:10.1029/2000GL011482 |
| [] | Phillips W S, Hartse H E, Rutledge J T. 2005. Amplitude ratio tomography for regional phase Q[J]. Geophysical Research Letters, 32(21): L21301. DOI:10.1029/2005GL023870 |
| [] | Press F. 1964. Seismic wave attenuation in the crust[J]. Journal of Geophysical Research, 69(20): 4417–4418. DOI:10.1029/JZ069i020p04417 |
| [] | Press F, Ewing M. 1952. Two slow surface waves across North America[J]. Bulletin of the Seismological Society of America, 42(3): 219–228. |
| [] | Ranasinghe N R, Gallegos A C, Trujillo A R, et al. 2015. Lg attenuation in northeast China using NECESSArray data[J]. Geophysical Journal International, 200(1): 67–76. |
| [] | Rapine R R, Ni J F. 2003. Propagation characteristics of Sn and Lg in northeastern China and Mongolia[J]. Bulletin of the Seismological Society of America, 93(2): 939–945. DOI:10.1785/0120010157 |
| [] | Rodgers A J, Ni J F, Hearn T M. 1997. Propagation characteristics of short-period Sn and Lg in the Middle East[J]. Bulletin of the Seismological Society of America, 87(2): 396–413. |
| [] | Sandvol E, Al-Damegh K, Calvert A, et al. 2001. Tomographic imaging of Lg and Sn propagation in the Middle East[J]. Pure and Applied Geophysics, 158(7): 1121–1163. DOI:10.1007/PL00001218 |
| [] | Sato R. 1967. Attenuation of seismic waves[J]. Journal of Physics of the Earth, 15(2): 32–61. DOI:10.4294/jpe1952.15.32 |
| [] | Schurr B, Asch G, Rietbrock A, et al. 2003. Complex patterns of fluid and melt transport in the central Andean subduction zone revealed by attenuation tomography[J]. Earth and Planetary Science Letters, 215(1-2): 105–119. DOI:10.1016/S0012-821X(03)00441-2 |
| [] | Shi J H, Richards P G, Kim W Y. 2000. Determination of seismic energy from Lg waves[J]. Bulletin of the Seismological Society of America, 90(2): 483–493. DOI:10.1785/0119980011 |
| [] | Shih X R, Chun K Y, Zhu T. 1994. Attenuation of 1-6 s Lg waves in Eurasia[J]. Journal of Geophysical Research:Solid Earth, 99(B12): 23859–23874. DOI:10.1029/94JB02163 |
| [] | Shin T C, Herrmann R B. 1987. Lg attenuation and source studies using 1982 Miramichi data[J]. Bulletin of the Seismological Society of America, 77(2): 384–397. |
| [] | Singh C, Shekar M, Singh A, et al. 2012. Seismic attenuation characteristics along the Hi-CLIMB profile in tibet from Lg Q inversion[J]. Bulletin of the Seismological Society of America, 102(2): 783–789. DOI:10.1785/0120110145 |
| [] | Singh C, Mondal P, Singh S, et al. 2015. Lg attenuation tomographic models of Himalaya and southern Tibet[J]. Tectonophysics, 664: 176–181. DOI:10.1016/j.tecto.2015.09.009 |
| [] | Singh S, Herrmann R B. 1983. Regionalization of crustal coda Q in the continental United States[J]. Journal of Geophysical Research:Solid Earth, 88(B1): 527–538. DOI:10.1029/JB088iB01p00527 |
| [] | Singh S, Singh C, Biswas R, et al. 2016. Attenuation characteristics in eastern Himalaya and southern Tibetan Plateau:An understanding of the physical state of the medium[J]. Physics of the Earth and Planetary Interiors, 257: 48–56. DOI:10.1016/j.pepi.2016.05.005 |
| [] | Stachnik J C, Abers G A, Christensen D H. 2004. Seismic attenuation and mantle wedge temperatures in the Alaska subduction zone[J]. Journal of Geophysical Research:Solid Earth, 109(B10): B10304. |
| [] | Street R L, Herrmann R B, Nuttli O W. 1975. Spectral characteristics of the Lg wave generated by central United States earthquakes[J]. Geophysical Journal International, 41(1): 51–63. DOI:10.1111/j.1365-246X.1975.tb05484.x |
| [] | Su W, Wu J P, Ming Y H, et al. 2006. Lg coda Q0 value and its relation with the tectonics in Chinese mainland and adjacent regions[J]. Earthquake Science (in chinese), 19(2): 136–144. |
| [] | Sun L, Li Y H, Wu Q J, et al. 2012. Q0 tomography of S wave attenuation in Northeast China and adjacent regions[J]. Chinese Journal of Geophysics, 55(4): 1179–1185. DOI:10.6038/j.issn.0001-5733.2012.04.014 |
| [] | Taylor S R, Yang X N, Phillips W S. 2003. Bayesian Lg attenuation tomography applied to eastern Asia[J]. Bulletin of the Seismological Society of America, 93(2): 795–803. DOI:10.1785/0120020010 |
| [] | Tsai Y B, Aki K. 1969. Simultaneous determination of the seismic moment and attenuation of seismic surface waves[J]. Bulletin of the Seismological Society of America, 59(1): 275–287. |
| [] | Walter W R, Mayeda K, Malagnini L, et al. 2007. Regional body-wave attenuation using a coda source normalization method:Application to MEDNET records of earthquakes in Italy[J]. Geophysical Research Letters, 34(10): L10308. DOI:10.1029/2007GL029990 |
| [] | Wang S Y, Pei S P, hearn T M, et al. 2008. Crustal S-wave Q estimated from ML amplitude Ⅱ:Q lateral variation in China[J]. Chinese Journal of Geophysics, 51(1): 133–139. DOI:10.3321/j.issn:0001-5733.2008.01.017 |
| [] | Wang S Y, Pei S P, Xu Z H, et al. 2007. Crustal S-wave Q estimated from ML amplitude Ⅰ:Attenuation in different tectonic regions of China[J]. Chinese Journal of Geophysics, 50(6): 1740–1747. DOI:10.3321/j.issn:0001-5733.2007.06.014 |
| [] | Xie J, Gok R, Ni J, et al. 2004. Lateral variations of crustal seismic attenuation along the INDEPTH profiles in Tibet from Lg Q inversion[J]. Journal of Geophysical Research:Solid Earth, 109(B10): B10308. |
| [] | Xie J, Mitchell B J. 1990a. Attenuation of multiphase surface waves in the Basin and Range province, part Ⅰ:Lg and Lg coda[J]. Geophysical Journal International, 102(1): 121–137. DOI:10.1111/gji.1990.102.issue-1 |
| [] | Xie J, Mitchell B J. 1990b. A back-projection method for imaging large-scale lateral variations of Lg coda Q with application to continental Africa[J]. Geophysical Journal International, 100(2): 161–181. DOI:10.1111/j.1365-246X.1990.tb02477.x |
| [] | Xie J, Nuttli O W. 1988. Interpretation of high-frequency coda at large distances:Stochastic modelling and method of inversion[J]. Geophysical Journal International, 95(3): 579–595. DOI:10.1111/j.1365-246X.1988.tb06705.x |
| [] | Xie J, Wu Z, Liu R, et al. 2006. Tomographic regionalization of crustal Lg Q in eastern Eurasia[J]. Geophysical Research Letters, 33(3): L03315. |
| [] | Xie J K. 2002. Lg Q in the eastern Tibetan Plateau[J]. Bulletin of the Seismological Society of America, 92(2): 871–876. DOI:10.1785/0120010154 |
| [] | Xu Y, Mao Y, Hu J F, et al. 2005. Distribution of Lg coda Q in Xinjiang and its adjacent regions[J]. Earthquake Science (in chinese), 18(2): 162–170. |
| [] | Yang X N. 2002. A numerical investigation of Lg geometrical spreading[J]. Bulletin of the Seismological Society of America, 92(8): 3067–3079. DOI:10.1785/0120020046 |
| [] | Zeng J, Chen C T, Han W B, et al. 1997. Attenuation of coda waves and Qc values beneath the Chengdu telemetered seismic network[J]. Earthquake Science (in chinese), 10(3): 246–253. |
| [] | Zhang H, Zhou Y Z, Wu Z L, et al. 2009. Finite element analysis of seismic wave propagation characteristics in Fuzhou basin[J]. Chinese Journal of Geophysics, 52(5): 1270–1279. DOI:10.3969/j.issn.0001-5733.2009.05.016 |
| [] | Zhao L F, Xie X B. 2016. Strong Lg-wave attenuation in the Middle East continental collision orogenic belt[J]. Tectonophysics, 674: 135–146. DOI:10.1016/j.tecto.2016.02.025 |
| [] | Zhao L F, Xie X B, He J K, et al. 2013a. Crustal flow pattern beneath the Tibetan Plateau constrained by regional Lg-wave Q tomography[J]. Earth and Planetary Science Letters, 383: 113–122. DOI:10.1016/j.epsl.2013.09.038 |
| [] | Zhao L F, Xie X B, Wang W M, et al. 2010. Seismic Lg-wave Q tomography in and around Northeast China[J]. Journal of Geophysical Research:Solid Earth, 115(B8): B08307. |
| [] | Zhao L F, Xie X B, Wang W M, et al. 2013b. Crustal Lg attenuation within the North China Craton and its surrounding regions[J]. Geophysical Journal International, 195(1): 513–531. DOI:10.1093/gji/ggt235 |
| [] | Zhou L Q, Zhao C P, Xiu J G, et al. 2008a. Tomography of QLg in Sichuan-Yunnan zone[J]. Chinese Journal of Geophysics, 51(6): 1745–1752. DOI:10.3321/j.issn:0001-5733.2008.06.015 |
| [] | Zhou L Q, Zhao C P, Xiu J G, et al. 2008b. Methods and developments of research on crustal Q value by using earthquakes[J]. Recent Development in World Seismology (in chinese), 2: 1–11. |
| [] | Zhu X Y. 2014. An Inversion of Lg-wave attenuation and site response from seismic spectral ratios in the Eastern China region[J]. Bulletin of the Seismological Society of America, 104(3): 1389–1399. DOI:10.1785/0120120359 |
| [] | Zor E, Sandvol E, Xie J K, et al. 2007. Crustal attenuation within the Turkish Plateau and surrounding regions[J]. Bulletin of the Seismological Society of America, 97(1B): 151–161. DOI:10.1785/0120050227 |
| [] | 丛连理, 胡家富, 傅竹武, 等. 2002. 中国大陆及邻近地区Lg尾波的Q值分布[J]. 中国科学 (D辑), 32(8): 617–624. |
| [] | 高龙生. 1985. Q值研究的进展和问题[J]. 地震地磁观测与研究(6): 3–6. |
| [] | 葛焕称, 叶培元, 黄才中, 等. 1985. 中国东部地区Lg波的衰减和近震震级[J]. 华北地震科学, 3(4): 1–14. |
| [] | 葛焕称. 1988. Lg波研究的历史进展[J]. 国际地震动态(10): 1–7. |
| [] | 葛焕称, 倪岳伟, 黄才中, 等. 1989. 中国大陆地区Lg波速度、衰减和震级[J]. 科学通报, 34(24): 1889–1892. |
| [] | 胡家富, 丛连理, 苏有锦, 等. 2003. 云南及周边地区Lg尾波Q值的分布特征[J]. 地球物理学报, 46(6): 809–813. DOI:10.3321/j.issn:0001-5733.2003.06.013 |
| [] | 黄才中, 高则明, 拾礼勤, 等. 1990. 东北地区Lg波的衰减系数和震级[J]. 东北地震研究, 6(2): 41–50. |
| [] | 靳平, 肖卫国, 段克敏. 2004. 由Lg波振幅谱估算地震矩及Lg波Q值[J]. 地震学报, 17(S1): 21–30. |
| [] | 刘建华, 刘福田, 王凤霞, 等. 1999. 单台Lg尾波的测量研究[J]. 地球物理学报, 42(3): 371–382. DOI:10.3321/j.issn:0001-5733.1999.03.010 |
| [] | 刘建华, 刘福田, 阎晓蔚, 等. 2004b. 华北地区Lg尾波衰减研究——Lg尾波Q0地震成像[J]. 地球物理学报, 47(6): 1044–1052. DOI:10.3321/j.issn:0001-5733.2004.06.017 |
| [] | 刘建华, 刘福田, 阎晓蔚, 等. 2004c. 华北地区Lg尾波衰减研究——Lg尾波Q的测量[J]. 地球物理学报, 47(5): 822–831. DOI:10.3321/j.issn:0001-5733.2004.05.013 |
| [] | 刘建华, 胥颐, 郝天珧. 2004a. 地震波衰减的物理机制研究[J]. 地球物理学进展, 19(1): 1–7. DOI:10.3969/j.issn.1004-2903.2004.01.001 |
| [] | 毛燕, 徐彦, 王彬, 等. 2005. 四川及邻区Lg尾波的Q值分布特征[J]. 地震研究, 28(1): 38–42. |
| [] | 苏伟, 吴建平, 明跃红, 等. 2006. Lg尾波Q0值与中国大陆及邻区的地质构造关系[J]. 地震学报, 28(2): 132–140. |
| [] | 孙莲, 李永华, 吴庆举, 等. 2012. 中国东北及周边地区地壳横波衰减的成像研究[J]. 地球物理学报, 55(4): 1179–1185. DOI:10.6038/j.issn.0001-5733.2012.04.014 |
| [] | 汪素云, 裴顺平, HearnT M, 等. 2008. 利用ML振幅研究地壳横波Q值Ⅱ:Q横向变化特征[J]. 地球物理学报, 51(1): 133–139. DOI:10.3321/j.issn:0001-5733.2008.01.017 |
| [] | 汪素云, 裴顺平, 许忠淮, 等. 2007. 利用ML振幅研究地壳横波Q值Ⅰ:不同构造区的衰减特征[J]. 地球物理学报, 50(6): 1740–1747. DOI:10.3321/j.issn:0001-5733.2007.06.014 |
| [] | 徐彦, 毛燕, 胡家富, 等. 2005. 新疆及周边地区Lg尾波的Q值分布[J]. 地震学报, 27(2): 155–162. |
| [] | 曾健, 陈天长, 韩渭宾, 等. 1997. 成都遥测台网区域尾波衰减特性及Qc值研究[J]. 地震学报, 19(3): 246–253. |
| [] | 张怀, 周元泽, 吴忠良, 等. 2009. 福州盆地强地面运动特征的有限元数值模拟[J]. 地球物理学报, 52(5): 1270–1279. DOI:10.3969/j.issn.0001-5733.2009.05.016 |
| [] | 周连庆, 赵翠萍, 修济刚, 等. 2008a. 川滇地区Lg波Q值层析成像[J]. 地球物理学报, 51(6): 1745–1752. DOI:10.3321/j.issn:0001-5733.2008.06.015 |
| [] | 周连庆, 赵翠萍, 修济刚, 等. 2008b. 利用天然地震研究地壳Q值的方法和进展[J]. 国际地震动态(2): 1–11. |
 2017, Vol. 32
2017, Vol. 32


