2. 中南大学地球科学与信息物理工程学院, 长沙 410083
2. School of geosciences and info-physics of central south university, Changsha 410083, China
地球介质基本为黏弹性各向异性介质,研究黏弹性各向异性介质中地震波的传播特征对提高地震勘探精度及准确性有着重要意义.相速度与群速度是认识黏弹性各向异性地震波传播规律的主要参数,对地震数据解释具有重要意义.Samec和Blangy (Samec and Blangy, 1992; Blangy, 1994) 对各向异性介质中的黏弹性、衰减、吸收、AVO等现象进行了研究.Carcione (Carcione, 1995, 2001; Carcione and Cavallini, 1997) 研究了黏弹各向异性介质的本构方程 (即应力-应变关系),发展并完善了黏弹各向异性介质基本理论.Červený和Pšenčík (2005)研究了黏弹性单斜各向异性介质中SH波相速度、偏振方向等随非均匀角的变化规律,杜启振 (杜启振等, 2002, 2006; 杜启振和杨慧珠2003, 2004) 通过数值计算研究黏弹各向异性介质中的速度频散和衰减特征;方勇 (2005)研究了EDA裂隙中液体性质对地震响应的影响,以便于进行流体识别.
本文主要研究了黏弹性HTI和EDA介质中地震波的波动参数,包括相速度、慢度、偏振向量和群速度计算公式及其特征.
1 黏弹性EDA介质中的Christoffel方程黏弹性介质的弹性系数矩阵为

|
(1) |
其中,cij=cijR+cijI.仍然可采用极端各向异性介质中的特殊分量法求解方式.
将 (1) 式代入voigt形式得极端各向异性方程并整理得 (何现启,2010):
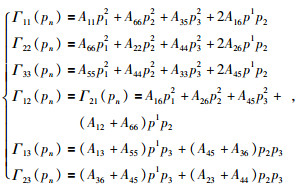
|
(2) |
代入Γik(pn)Uk=Ui, i=1, 2, 3, (U为极化向量的笛卡尔分量) 式可得:

|
(3) |
要上式有非零解必有:

|
(4) |
利用上式可以求解黏弹性EDA介质中均匀SH, SV, P平面波及非均匀SH, SV, P平面波的复慢度向量p,实相速度C,传播向量P等参数.下面分两种情况进行讨论计算.
2 黏弹性EDA介质中均匀平面波的传播特征 2.1 由HTI弹性参数所表示的EDA介质的均匀平面波的精确传播特征本节所考虑的EDA介质是由HTI介质绕z轴旋转所得到的,其弹性系数均匀用HTI的弹性系数间接表示.
(1) 黏弹性EDA介质中均匀平面波精确相速度
对于均平面波慢度向量p表达式p=σn+iDm, m·n=0中的D=0,因而有p=σn,令偏振向量U=(Ux, Uy, Uz),传播方向N为
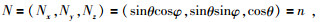
|
θ和φ分别为传播方向的极化角和方位角,由 (2) 式和 (3) 式得:
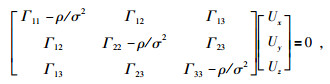
|
(5) |
其中:
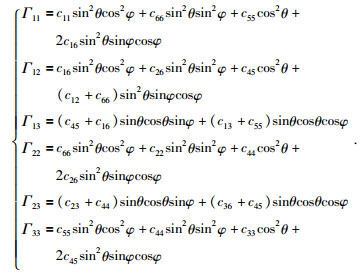
|
(6) |
在此考虑的是由HTI介质旋转得到的EDA的介质,因此下文除特别说明外,所采用的EDA弹性系数均用HTI介质的弹性系数表示.要使 (5) 式有非零解, 必须有det[Γ]=0即:
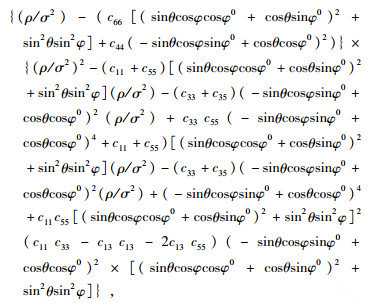
|
(7) |
求解方程可得:
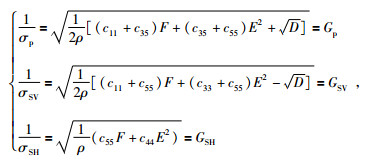
|
(8) |
其中:
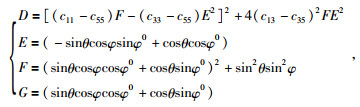
|
(9) |
由实传播向量P,衰减向量A,单位向量N和M,相速度c,衰减传播比δ和衰减角γ的关系式,可得黏弹性EDA介质中qP波、qSV波和SH波的相速度公式为 (何现启,2010):
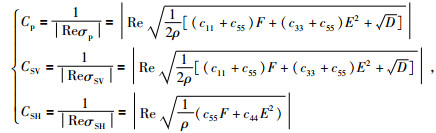
|
(10) |
φ=0时,即xoz面内二维相速度为
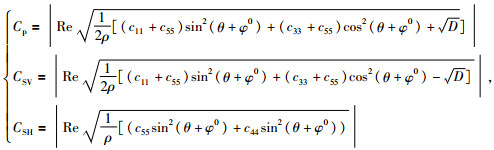
|
(11) |
其中:
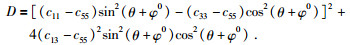
|
当黏弹性EDA介质对称轴倾角φ0=0时,黏弹性EDA介质就退化为黏弹性HTI介质,则黏弹性HTI介质的地震波相速度为
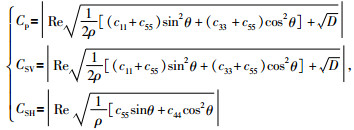
|
(12) |
其中:D=[(c11-c55) sin2θ-(c33-c55) cos2]2+4(c13+c55)2sin2θcos2θ.
(2) 黏弹性EDA介质中均匀平面波的精确群速度
将 (8) 代入一般各向异性介质群速度的矢量公式可得:
qP波的群速度为

|
(13) |
qSV波群速度为
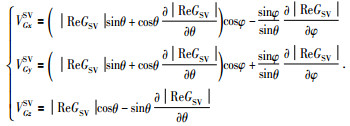
|
(14) |
SH波群速度为
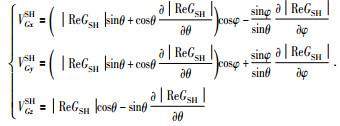
|
(15) |
(3) 黏弹性EDA介质中均匀平面波的精确偏振方向
将特征值代入黏弹性EDA介质Christoffel方程并求解方程可得:
SH波偏振向量为
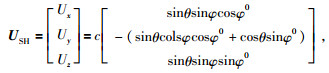
|
(16) |
因为PSH·n=0,说明黏弹性EDA介质中SH波偏振方向PSH与传播方向n垂直,为纯SH波.
qP波偏振向量为
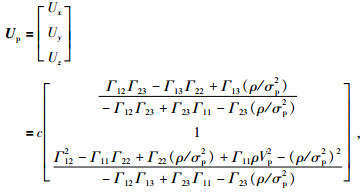
|
(17) |
因为Pp×n=0,说明黏弹性EDA介质中P波偏振方向Pp与传播方向n不平行,而是存在一定角度,因此黏弹性EDA介质中P波称为准P波或qP波.
qSV波偏振向量为
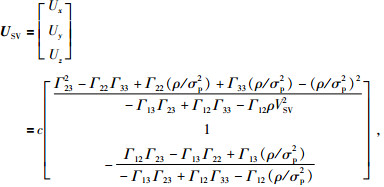
|
(18) |
因为PSV×n≠0,说明黏弹性EDA介质中波偏振方向PSV与传播方向n不垂直,而是存在一定角度,因此黏弹性EDA介质中SV波称为准SV波或qSV波.
(4) 黏弹性EDA介质中均匀平面波的精确慢度向量
由慢度向量p表达式p=σn+iDm, m·n=0式得:
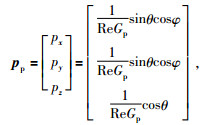
|
(19) |
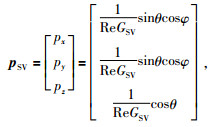
|
(20) |
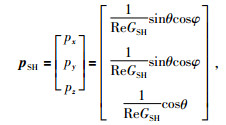
|
(21) |
以上所采用的黏弹性EDA弹性系数均用黏弹性HTI介质的弹性系数表示,所考虑的黏弹性EDA介质是由黏弹性HTI介质经坐标旋转得到的.为了对比下面计算由黏弹性EDA介质弹性系数表示的地震波波动参数.
2.2 EDA介质中均匀平面波的传播特征在xoy平面内p3=0,(6) 式变为
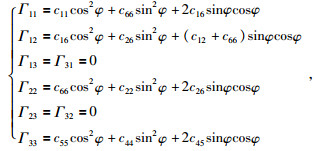
|
(22) |
由 (4) 式得:
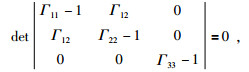
|
(23) |
即:

|
(24) |
(1) SH波的传播特征
由 (23)(24),对SH波有:
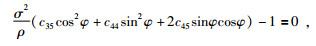
|
(25) |
求解得:
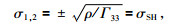
|
(26) |
由实传播向量P,衰减向量A,单位向量N和M,相速度c,衰减传播比δ和衰减角γ的关系式得:
①相速度
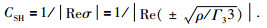
|
(27) |
②慢度
由 (26) 和慢度的表达式,可得SH波的慢度为
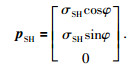
|
(28) |
③偏振向量
由 (26) 和 (5) 可得:

|
(29) |
④群速度
将 (26) 式代入一般各向异性介质群速度的矢量公式可得:
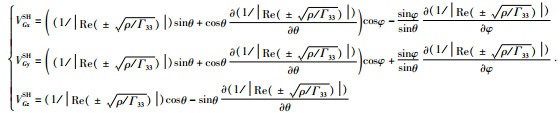
|
(30) |
(2) P、SV波的传播特征
对P、SV波,由 (24) 式得:
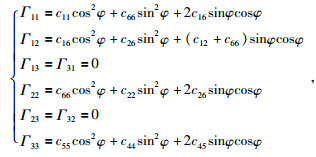
|
(31) |
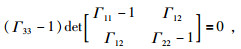
|
(32) |
整理得:
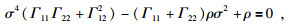
|
(33) |
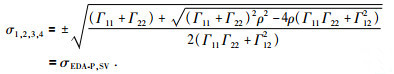
|
(34) |
由实传播向量P,衰减向量A,单位向量N和M,相速度c,衰减传播比δ和衰减角γ的关系式得:
①相速度
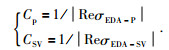
|
(35) |
②慢度
由 (34) 和慢度的一般式可得P、SV波的慢度为

|
(36) |
③偏振向量
由 (35) 和 (34) 可得:
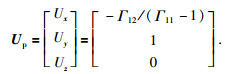
|
(37) |
④群速度
将 (35) 式代入一般各向异性介质的群速度表达式可得:
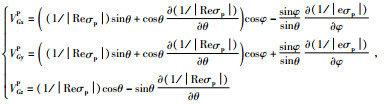
|
(38) |

|
(39) |
3黏弹性EDA介质中非均匀平面波的传播特征
将慢度向量的一般表达式代入 (2) 式得:
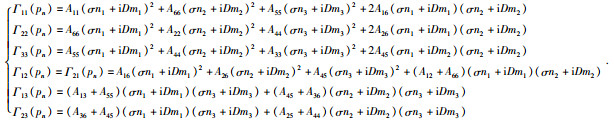
|
(40) |
在xoy平面内有:
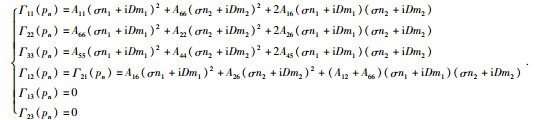
|
(41) |
代入 (3) 式可得:
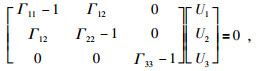
|
(42) |
要上式有非零解必有:
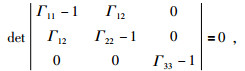
|
(43) |
即:
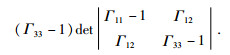
|
(44) |
令传播方向N为N=(Nx, Ny, Nz)=(cosφ, sinφ, 0)=n,φ为传播方向的方位角,由慢度向量的一般表达式得:

|
(45) |
代入 (41) 式得:
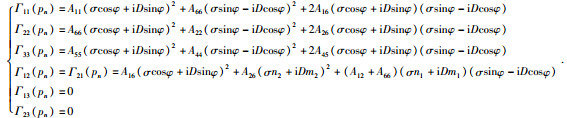
|
(46) |
(1) SH波的传播特征
由 (44)(46),对SH波有:
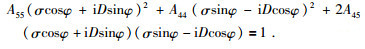
|
(47) |
整理得:
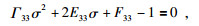
|
(48) |
其中
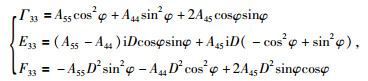
|
(49) |
求解得:

|
(50) |
由实传播向量P,衰减向量A,单位向量N和M,相速度c,衰减传播比δ和衰减角γ的关系式得:
①相速度
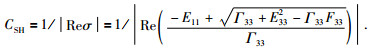
|
(51) |
②慢度
由 (50) 和慢度向量表达式可得:
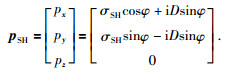
|
(52) |
③偏振向量
由 (42)(51) 式得:
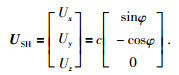
|
(53) |
④群速度
由一般各向异性介质群速度的矢量公式、(51) 式得:
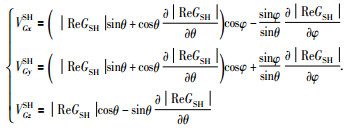
|
(54) |
(2) P、SV波的传播特征
对P、SV波有:

|
(55) |
其中
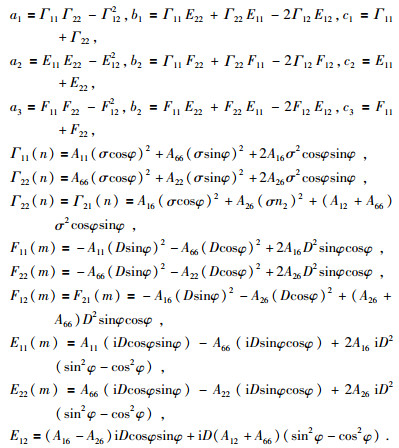
|
当弹性参数和D已知时,可以通过数值计算求出σ值,代入实传播向量P,衰减向量A,单位向量N和M,相速度c,衰减传播比δ和衰减角γ的关系式、一般各向异性介质群速度的矢量公式和黏弹性HTI介质中非均匀平面波的传播特征的求解公式即可得到P、SV波的特征参数 (何现启,2010).
3.2 三维非均匀平面波的传播特征由 (42) 式可得:
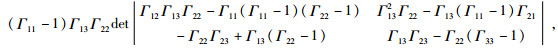
|
(56) |
其中
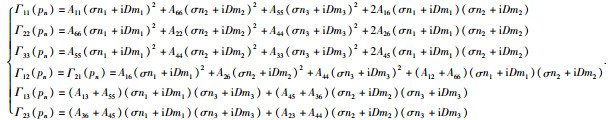
|
(57) |
令n=(nx, ny, nz)=(sinθcosφ, sinθsinφ, cosθ),则:
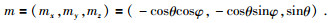
|
(58) |
将上式代入 (57) 即可求解σ,然后代入相关公式即可得到P、SV、SH波的特征参数.
4 模型计算EDA介质模型弹性系数矩阵如下:

|
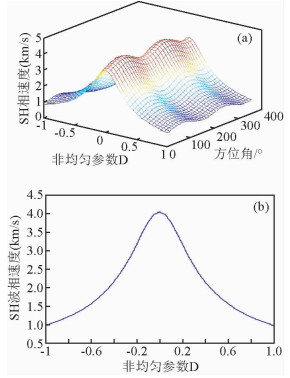
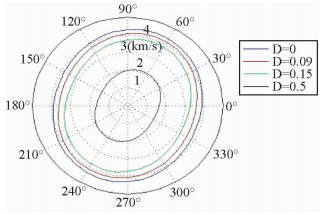
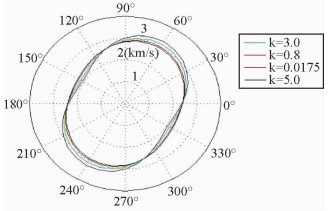
由 (51) 式可计算出非均匀SH波的相速度,计算结果见图 1,其中图 1b为极角为20°时,SH波相速度随D的变化关系.与HTI介质一样,在D=0时,SH波相速度取最大值,随着D的增大或减小相速度都减小,以D=0处为对称轴呈对称关系.图 2为D取0、0.09、0.15、2.0时,相速度与D的关系,随着D的增加相速度不断减小,但其对称性不变,方位各向异性不变,只是大小产生变化.与弹性介质一样,其相速度随方位角的变化关系也与介质对称轴相关,相速度椭圆仍然指示介质对称轴方向和地层中裂隙的走向.令,其他不变.k取不同值时由 (51) 计算SH波的相速度.图 2~3为D=0.3, k分别取0.0175、0.8、3.0、5.0时由 (51) 计算的SH波相速度,由此可见k也对相速度的各向异性产生影响,随着k的增加对称轴方向相速度不断增加, 但椭圆的长短轴方向不变.
|
图 1 SH波相速度与入射角和非均匀系数D的关系 (a) 相速度与入射角和非均匀系数D关系; (b) 相速度与非均匀系数D的关系. Figure 1 Phasevelocity of SH wavevaryingwithincidence or inhomogeneityparameter |
|
图 2 SH波相速度与D的关系 Figure 2 The relation between phase velocity and inhomogeneityparameter |
|
图 3 SH波相速度与k的关系 Figure 3 The relation between phase velocityandparameterk |
本文基于特殊分量法,通过求解christoffel方程,推导出黏弹性EDA介质中均匀、非均匀波的精确相速度、慢度和群速度公式,并通过模型计算研究了SH波的相速度特征及其随相角和不均匀参数D的变化规律.结果表明D影响了地震波的相速度大小,但对其方位特性无影响,在EDA介质中相速度随方位角变化的规律仍然可指示介质的对称轴方向和裂隙的走向.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Blangy J P. 1994. AVO in transversely Isotropic media-An overview[J]. Geophysics, 59(5): 775–781. DOI:10.1190/1.1443635 |
| [] | Carcione J M. 1995. Constitutive model and wave equations for linear, viscoelastic, anisotropic media[J]. Geophysics, 60(2): 537–548. DOI:10.1190/1.1443791 |
| [] | Carcione J M. 2001. Wave Fields in Real Media:Wave Propagation in Anisotropic, Anelastic and Porous Media[M]. Amsterdam: Pergamon. |
| [] | Carcione J M, Cavallini F. 1997. Forbidden directions for TM waves in anisotropic conducting media[J]. IEEE Transactions on Antennas and Propagation, 45(1): 133–139. DOI:10.1109/8.554250 |
| [] | Červený V, Pšenč ík I. 2005. Plane waves in viscoelastic anisotropic media-Ⅰ[J]. Theory[J]. Geophysical Journal International, 161(1): 197–212. DOI:10.1111/gji.2005.161.issue-1 |
| [] | Du Q Z, Dong Y, Yang H Z. 2002. Estimation of normal moveout velocity of S-wave in horizontal transverse isotropic (HTI) media[J]. Journal of the University of Petroleum, China (in Chinese), 26(2): 26–30. |
| [] | Du Q Z, Wang Y G, Fu S H. 2006. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media[J]. Progress in Geophysics (in Chinese), 21(2): 502–504. DOI:10.3969/j.issn.1004-2903.2006.02.025 |
| [] | Du Q Z, Yang H Z. 2003. Detection method for fractures in azimuthally anisotropic media[J]. Journal of the University of Petroleum, China (in Chinese), 27(4): 32–36. |
| [] | Du Q Z, Yang H Z. 2004. Viscoelastic wave equations of seismic multi-wave in fractured media[J]. Acta Physica Sinica (in Chinese), 53(8): 2801–2806. |
| [] | Fang Y. 2005. Research of seismic response in fluid-filled EDA media (in Chinese)[MSc. Thesis]. Chengdu:Chengdu University of Technology. |
| [] | He X Q. 2010. The study of seismic wave propagation in EDA medium and parameters inversion (in Chinese)[Ph. D. thesis]. Changsha:Central South University. |
| [] | Samec P, Blangy J P. 1992. Viscoelastic attenuation, anisotropy, and AVO[J]. Geophysics, 57(3): 441–450. DOI:10.1190/1.1443258 |
| [] | Shen Z H, Wang X J. 2013. The approximation of P waves reflection and transmission coefficient in viscoelastic medium and comparative analysis[J]. Progress in Geophysics (in Chinese), 28(1): 257–264. DOI:10.6038/pg20130127 |
| [] | Tang Y M, Zhao B, Zhang Z J. 2007. The analysis of the wave field characteristics in viscoelastic VTI medium[J]. Progress in Geophysics (in Chinese), 22(4): 1305–1311. DOI:10.3969/j.issn.1004-2903.2007.04.041 |
| [] | Wang J, Li Z C. 2014. Vector wave imaging and wave separation in the TI media[J]. Progress in Geophysics (in Chinese), 29(6): 2754–2760. DOI:10.6038/pg20140642 |
| [] | Zhang Z, Xu Jiao, Xu YJ, et al. 2014. The study on rotational motion of seismic wave in TI media[J]. Progress in Geophysics (in Chinese), 29(6): 2609–2613. DOI:10.6038/pg20140621 |
| [] | 杜启振, 董渊, 杨慧珠. 2002. HTI介质横波正常时差速度反演[J]. 石油大学学报 (自然科学版), 26(2): 26–30. |
| [] | 杜启振, 王延光, 付水华. 2006. 方位各向异性粘弹性介质波场数值模拟[J]. 地球物理学进展, 21(2): 502–504. DOI:10.3969/j.issn.1004-2903.2006.02.025 |
| [] | 杜启振, 杨慧珠. 2003. 方位各向异性介质的裂缝预测方法研究[J]. 石油大学学报 (自然科学版), 27(4): 32–36. |
| [] | 杜启振, 杨慧珠. 2004. 裂缝性地层黏弹性地震多波波动方程[J]. 物理学报, 53(8): 2801–2806. |
| [] | 方勇. 2005.流体EDA质的地震响应特征研究[硕士论文].成都:成都理工大学. |
| [] | 何现启. 2010. EDA介质中地震波的传播特征及参数反演研究[博士论文].长沙:中南大学. |
| [] | 沈章洪, 王小杰. 2013. 粘弹性介质P波反射透射系数近似及对比分析[J]. 地球物理学进展, 28(1): 257–264. DOI:10.6038/pg20130127 |
| [] | 谭未一, 赵兵, 张中杰. 2007. 粘弹性VTI介质地震波模拟特征分析[J]. 地球物理学进展, 22(4): 1305–1311. DOI:10.3969/j.issn.1004-2903.2007.04.041 |
| [] | 王娟, 李振春. 2014. TTI介质矢量波成像及波型分解[J]. 地球物理学进展, 29(6): 2754–2760. DOI:10.6038/pg20140642 |
| [] | 张智, 徐佼, 徐艳杰, 等. 2014. TI介质中地震波旋转运动特性研究[J]. 地球物理学进展, 29(6): 2609–2613. DOI:10.6038/pg20140621 |
 2017, Vol. 32
2017, Vol. 32

