2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
地震波能量衰减现象是其传播的一个重要特征,分为介质的吸收衰减和散射衰减.研究表明,在地壳结构中,非均匀体引起的散射衰减占主导地位(Hatzidimitriou,1994;Pezzo et al.,1995).传统的模型难以解释介质中分布的大量小尺度非均匀性信息,而以统计学为基础的随机介质理论可以描述地壳中分布的各种不同尺度的非均匀体.因此,研究随机介质中波场传播的散射衰减规律,对于推断非均匀体的分布状态和性质有重要意义.
国内外很多学者已经对此进行了研究,在散射理论研究方面,Aki(1969)基于标量波单次散射理论模拟了地震尾波,得出结论,岩石圈随机非均匀性是地球维持长时间振动的主要原因;Aki(1973)和Berteussen等(1975)利用标量波散射理论来解释大孔径台阵远震P波记录的振幅和相位波动现象;Wu(1982)发展了标量波前向多重散射近似方法,用于解释S波频率特征和尾波衰减现象.散射理论大多建立在假设和近似的基础上,事实上,可能有些近似条件或者假设是不成立的,因此,模拟随机介质中波场传播的数值实验显得越来越重要.Frankel和Clayton(1986)利用有限差分方法研究了不同类型随机介质中的散射衰减规律;Hong(2004)基于小波方法研究了随机介质中P波,S波散射衰减比率与归一化频率的关系;Liu等(2010)研究了随机孔隙介质中的散射衰减机制.
本文主要目的是利用数值模拟实验来研究随机介质中的散射衰减规律,并与散射理论结果进行对比,来确定二维随机介质中最小散射角的范围.由于间断有限元方法有较强的压制数值频散能力,更加适应变化复杂的随机非均匀介质(Hu et al.,1999;贺茜君等,2014),因此本文使用龙格库塔间断有限元方法(Cockburn et al.,1989)求解二维弹性波动方程,模拟球面波在不同弹性随机介质中的传播,然后利用振幅衰减法估计随机介质的逆品质因子,最后分析讨论了二维随机介质中的波场特征,散射衰减规律,以及最小散射角的取值范围.
1 基本理论与方法 1.1 随机介质理论随机介质的速度可以描述为背景速度v0(平均速度)和速度波动δv(x)的叠加(奚先和姚姚,2004),公式为
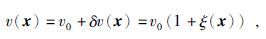
|
(1) |
这里x代表空间位置矢量,ξ(x)是速度场的波动部分,平均速度是速度场的平均值,速度场波动部分的平均值为零.公式为
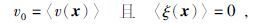
|
(2) |
〈…〉 符号代表统计平均值.
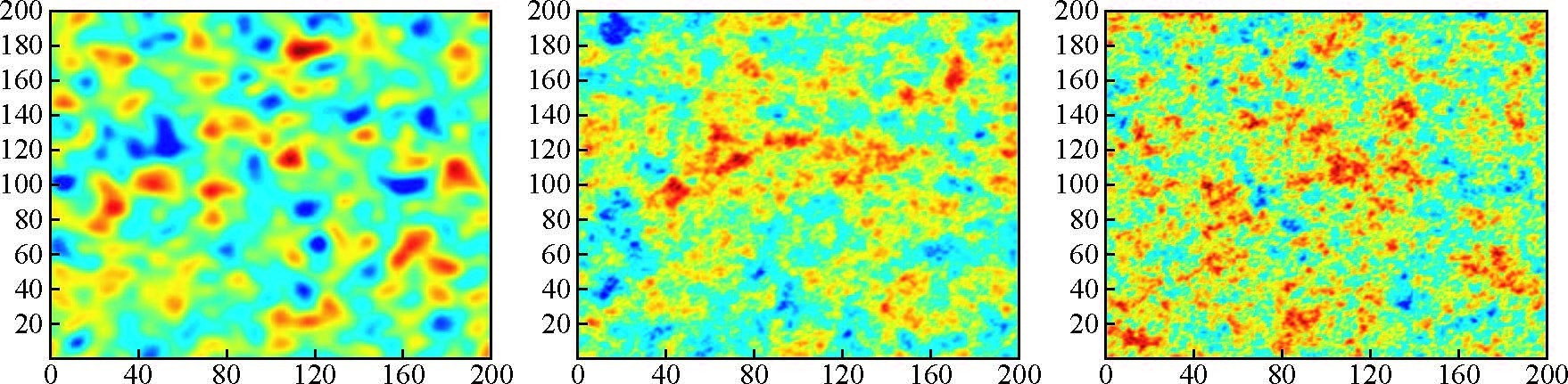
随机介质的性质由自相关函数和相应的功率谱密度函数来描述(Ikelle et al.,2012),通常有高斯型,冯卡门型,指数型自相关函数.自相关函数和对应的功率谱密度函数详见表 1.三种类型的随机介质详见图 1.在高斯型和指数型随机介质中,介质中非均匀体的尺度与相关长度a有关,相关长度越长,非均匀体的尺度越大.
|
|
表 1 自相关函数与功率谱密度(Frankel and Clayton,1986) Table 1 Autocorrelation function and power spectrum density(Frankel and Clayton,1986) |
|
图 1 随机介质模型 从左到右分别对应高斯型,指数型,冯卡门型随机介质. Figure 1 Different random media models Left to right corresponds to Gaussian,exponential and Von Karman random media respectively. |
二维各向同性弹性介质中的速度—应力弹性波方程表示为
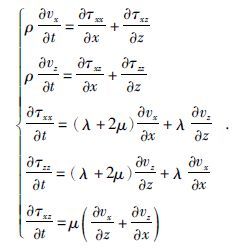
|
(3) |
考虑基本方程
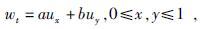
|
(4) |
简单起见,假设对研究区域作矩形网格划分,每个单元可以表示为
Ii,j={(x,y):xi-1/2≤x≤xi+1/2,yj-1/2≤y≤yj+1/2},
定义一个由分片多项式组成的空间,公式为
Vhk={v:v|Ii,j∈Pk(Ii,j);1≤i≤Nx,1≤i≤Ny},
这里Pk(Ii,j)代表定义在Ii,j 上的k 次多项式,注意到,在Vhk中的函数在单元边界上可以不连续.
间断有限元方法可以表述为:寻找wh,uh∈Vhk,使得对于任意的试验函数vh∈Vhk,在所有的Ii,j,1≤i≤Nx,1≤j≤Ny上,满足公式为
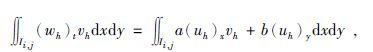
|
(5) |
积分并整理可得
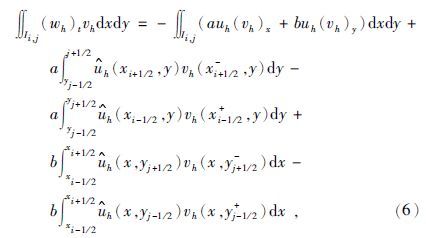
|
(6) |
因为uh 在单元边界上不连续,边界值需要单独定义,DG方法中用所谓的数值流通量来定义单元边界上的值(贺茜君等,2014),即公式中的
设Pk(Ii,j)的一组基为φi,jl(x,y),l=1,2…K=(k+1)(k+2)/2,可以把数值解在这组基上展开为
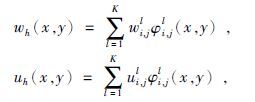
|
把数值解展开式,以及φi,jl(x,y),l=1,2…K=(k+1)(k+2)/2作为试验函数代入方程,整理得到
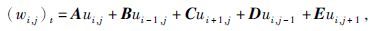
|
(7) |
式中wi,j,ui,j 代表数值解在Ii,j 上的展开系数,A,B,C,D,E 为K×K 的矩阵,可以看到,在每个单元内,只要处理一个K 维线性方程组,避免了大规模线性方程组的求解.
把方程(12)写成一般的常微分方程形式:ut=L(u,t),L 为空间离散算子,对于时间的离散,本文采用3阶Runge-Kutta离散化方法,公式为
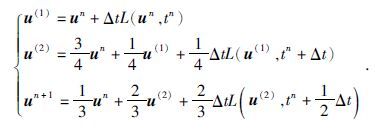
|
(8) |
同一传播路径上r1和r2 位置上的两个地震波记录,经过几何扩散校正后,满足如下衰减规律为(Liu et al.,2010):
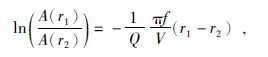
|
(9) |
其中A(r1),A(r2)为r1和r2 处接收到的最大幅值,f一般取震源子波中心频率,V为波传播的速度,1/Q 为衡量地震波在传播过程中衰减程度的逆品质因子.因此,首先对地震记录作几何扩散校正,然后统计不同传播距离对应的振幅对数,作线性拟合,根据曲线斜率可以估计出介质的逆品质因子1/Q(Frankel and Clayton,1986).
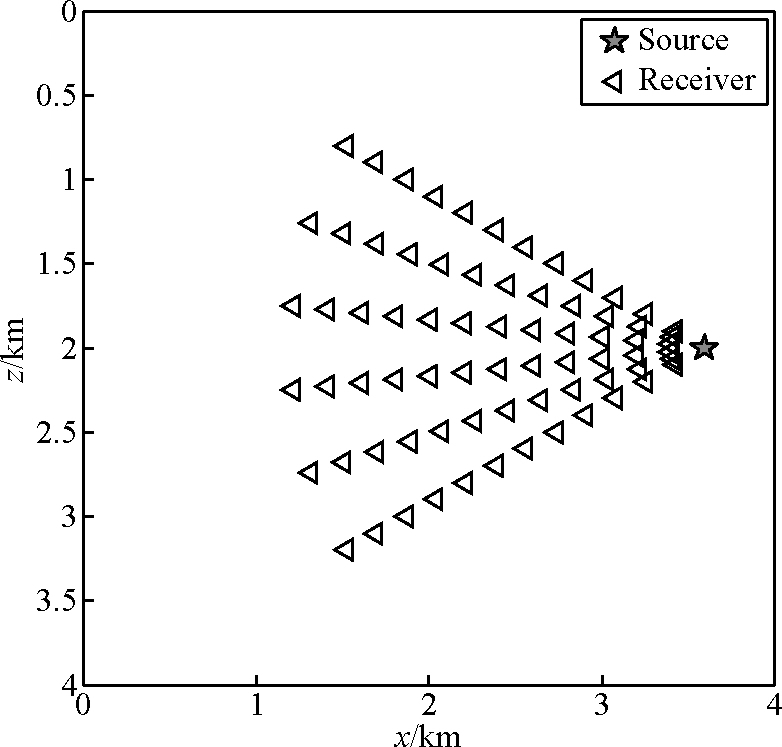
2 数值模拟实验方案本文的随机介质模型范围是4 km×4 km 的正方形区域,平均密度为2.6 kg/m3,平均P波波速6.53 km/s,平均S波波速为3.85 km/s.在靠近区域右边界的(3.5 km,2 km)位置加载爆炸震源,本文震源加载方式为,以震源为中心加载高斯区域分布的主应力,主应力大小为震源子波乘以对应高斯系数,这种震源加载方式可以在粗网格或是低阶间断有限元方法中产生比较纯净的纵波源(董良国等,2014),本文使用的震源子波为雷克子波.本文使用完全匹配层吸收边界条件(PML)(Collino and Tsogka,2012)来处理边界反射.为了对随机介质中的衰减特性作定量分析,本文在介质中设置了72个虚拟检波器,来记录空间质点振动情况.检波器分布于6条不同方向的传播路径上(自上而下,路径编号分别为1~6),相邻路径之间的夹角相等(间隔为12°),每条传播路径上等距离(间距为200 m)布置了12个检波器.详见图 2,五角星代表震源所在位置,三角形代表虚拟检波器.
|
图 2 震源检波器分布 Figure 2 Distribution of source and detectors |
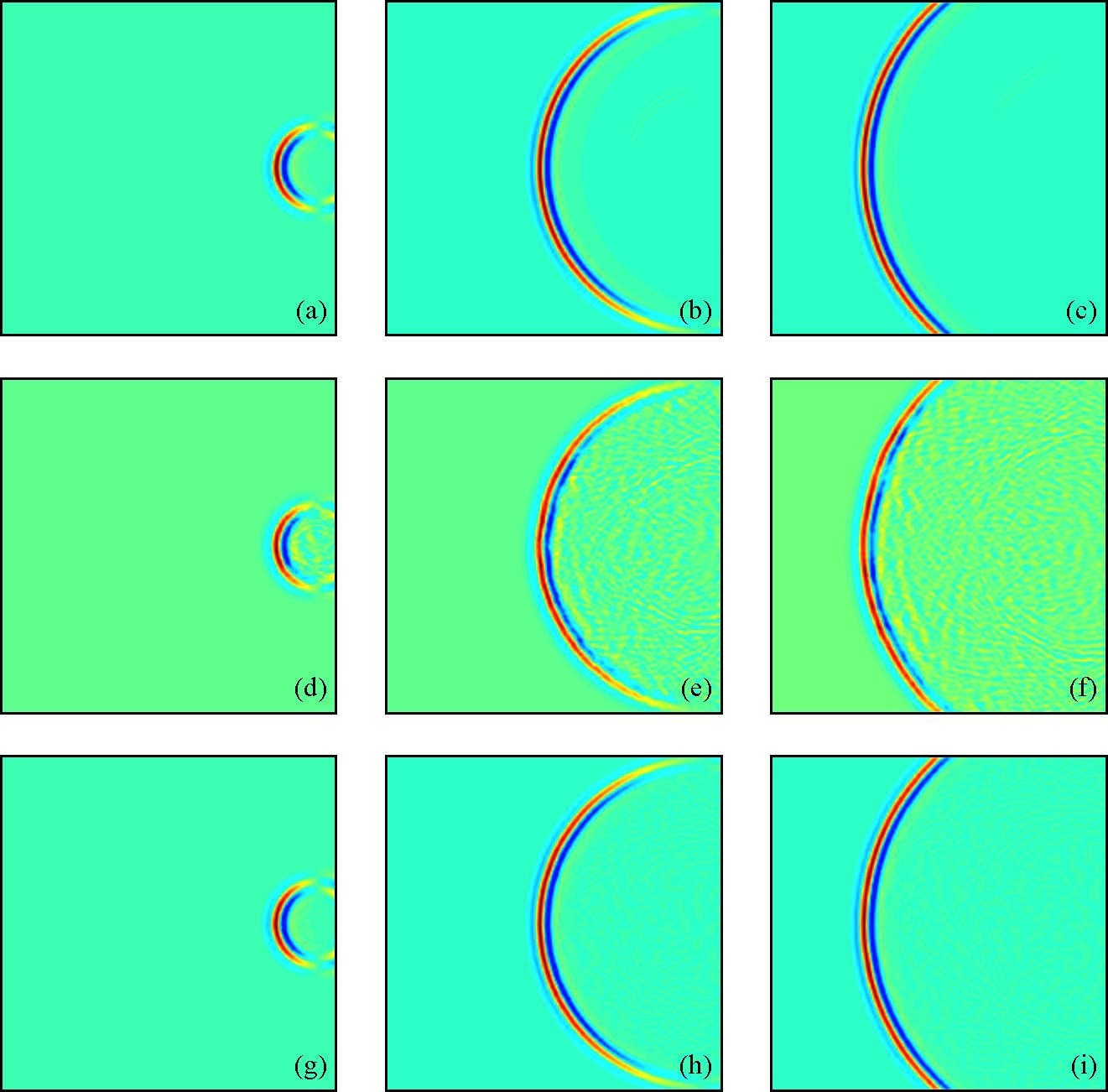
图 3是地震波传播过程的波场快照,a,b,c分别是均匀介质中0.1 s,0.3 s,0.4 s时的X方向位移的波场快照,d,e,f分别是相关长度为10 m,标准差为0.1的随机介质中X方向位移的波场快照,g,h,i分别是相关长度位30 m,标准差0.01的随机介质中X方向位移的波场快照.
|
图 3 不同介质中的波场快照 Figure 3 Snapshots in different random medias |
从这些快照中,可以总结出随机介质中波场传播的一些规律:
1)本文数值实验中加载的震源是爆炸震源,因此在均匀介质中传播时只产生P波.当圆形波前传播到随机介质中,由于非均匀体的散射,波前开始扭曲,圆形波前变成不规则的圆,波峰,波谷等相位面也变得不连续,这说明P波的到时和振幅都有一定的波动.
2)在初至P波之后,可以观察到大量的尾波,这是因为随机介质的非均匀性使地震波传播时发生散射,P波能量转换为散射波能量,P波能量显著减小.在传播了较长时间后,研究区域中质点不会立刻停止振动,这是随机介质中,非均匀性引起了散射,空间中分布大量散射波的结果.
3)介质扰动标准差很小时,例如σ=0.01时,波场快照和均匀介质中几乎一致,圆形波前清晰规则,区域中初至波之后只有能量非常微弱的散射波,此时介质的非均匀性可以忽略不计,可以近似作为均匀介质处理(姚姚和奚先,2002).
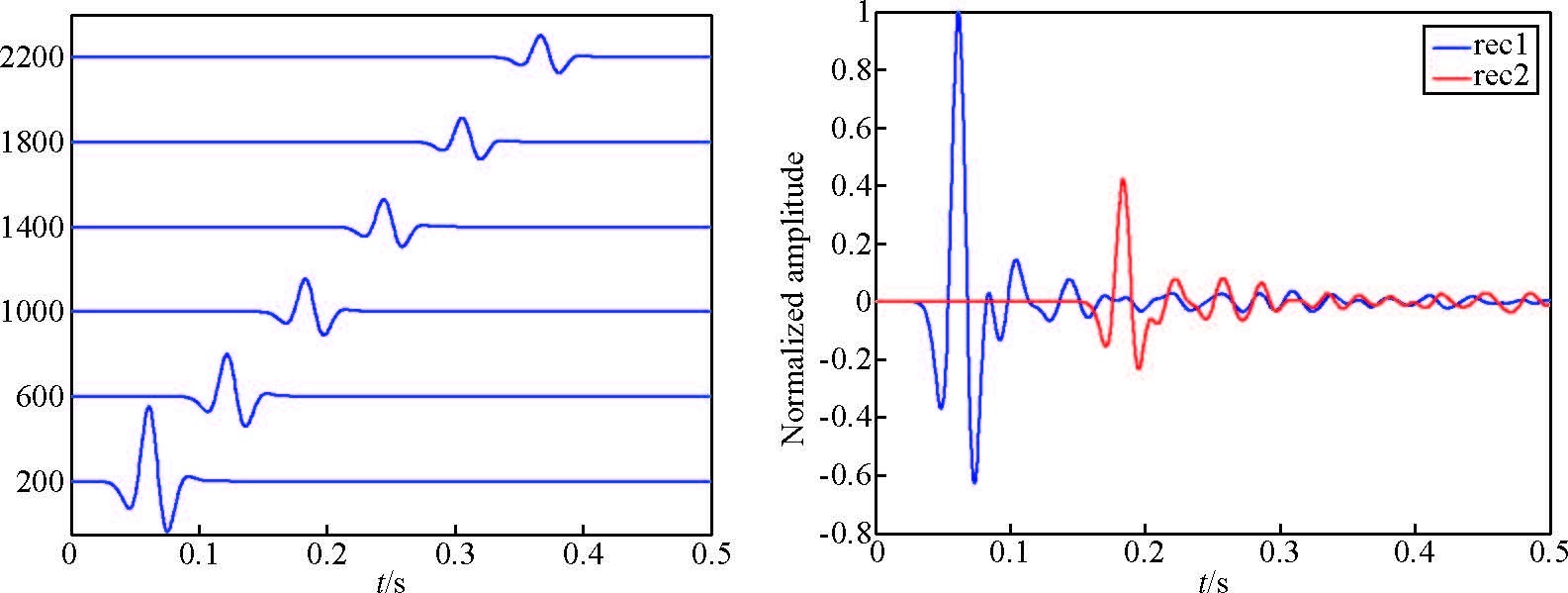
图 4左边所示为均匀介质中得到的合成地震记录,图中是同一传播路径上6个等间隔的虚拟检波器接收到的P波记录,可以看到,在二维介质中,点源产生的地震波会发生柱面扩散,随着传播距离增加,地震波振幅不断衰减,与传播距离的均方根成反比.几何扩散引起的地震波衰减只与传播距离有关,与频率及介质参数无关.均匀介质波形记录中,只出现了初至P波,没有其他震相,说明本文使用的PML吸收边界条件较好的处理了人为反射.
|
图 4 2号播路径上的波形记录 Figure 4 Waveform recordings on path2 |
图 4右边所示为随机介质中得到的合成地震记录(图示波形经过了几何扩散改正,并且进行了归一化处理).从图中可以得到一些定性的结论,在初至波之后有大量的地震尾波,相比于均匀介质中的情形,随机介质中的P波在几何扩散校正后,振幅随着传播距离的增加依然有很明显的衰减.本文数值实验中不考虑介质的本征衰减(地震波能量转化为热能),因此测量得到的地震波衰减完全由非均匀体散射引起.
3.2 散射衰减分析本文利用间断有限元方法得到了随机介质中的地震波合成记录,以此来定量研究随机介质中地震波传播的衰减规律.
图 6所示的统计结果对应的随机介质,其相关长度为30 m,扰动标准差为0.1.图中每种符号对应一条传播路径,每条路径上有12个接收点.分析可知,沿着不同路径传播的地震波的衰减情况不同,主要是因为随机介质中不同路径上的非均匀体分布不同,因此地震波的散射情况在不同路径上有较大差别,这是随机介质的固有特征.即使满足相同类型,相同参数的自相关函数的随机介质,在每一次数值实验中也会得到不同的结果,因此本文对每种介质均进行了5次随机数值实验.结果表明,6条传播路径的振幅距离关系有明显的区别,并非严格遵循随传播距离的增大而减小,例如三角形代表的传播路径,在传播至1公里时,振幅没有衰减,传播至1.7公里时,振幅有所增加,本文认为这是由于散射波之间相长干涉造成了局部振幅增强(Frankel and Clayton,1986;Hong and Kennett,2003).5次随机试验中不同传播路径得到的逆品质因子详见表 2.虽然每条路径上波场传播表现出不同的特点,但是从整体来看,振幅随着传播距离的增加呈现减小的趋势.图 7所示为不同传播路径的平均振幅与传播距离的关系,空心圆代表六条传播路径的平均振幅,红色直线代表对统计结果的线性拟合,直线的斜率反映了随机介质的逆品质因子.从统计意义上来看,平均振幅的对数关于传播距离呈现出线性递减的趋势.

|
图 5 振幅对数随传播距离的变化 Figure 5 Log-amplitude with different propagation distance |
|
图 6 逆品质因子随相关长度的变化 Figure 6 Inverse quality factors with different correlation length |
|
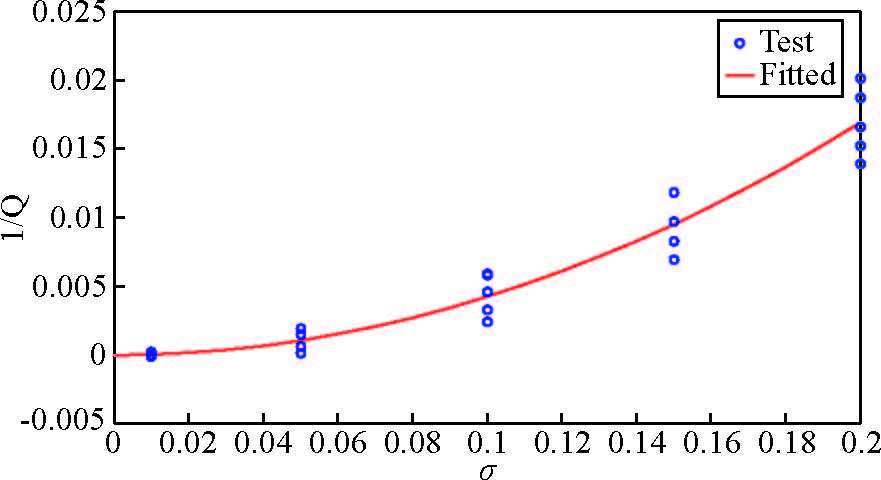
图 7 逆品质因子随扰动标准差的变化 Figure 7 Inverse quality factors with different standard deviation |
|
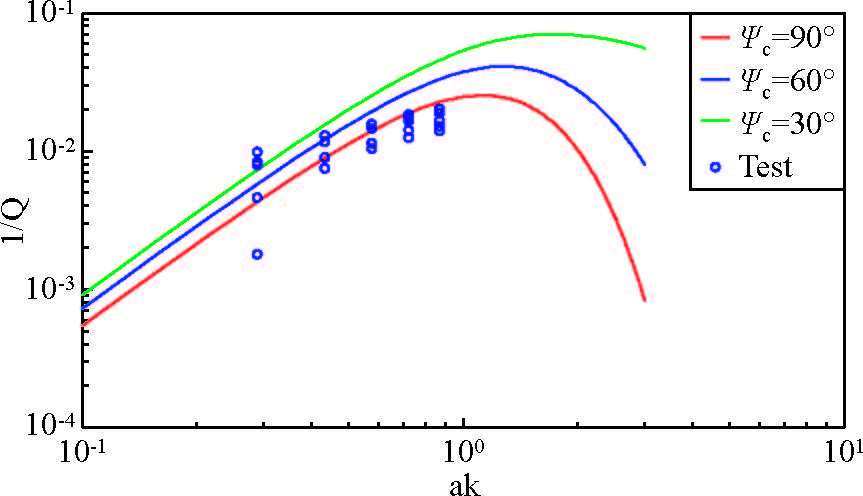
图 8 逆品质因子随地震波频率的变化 Figure 8 Inverse quality factors with different frequency |
|
|
表 2 不同传播路径的逆品质因子 Table 2 Inverse quality factors with different propagation path |
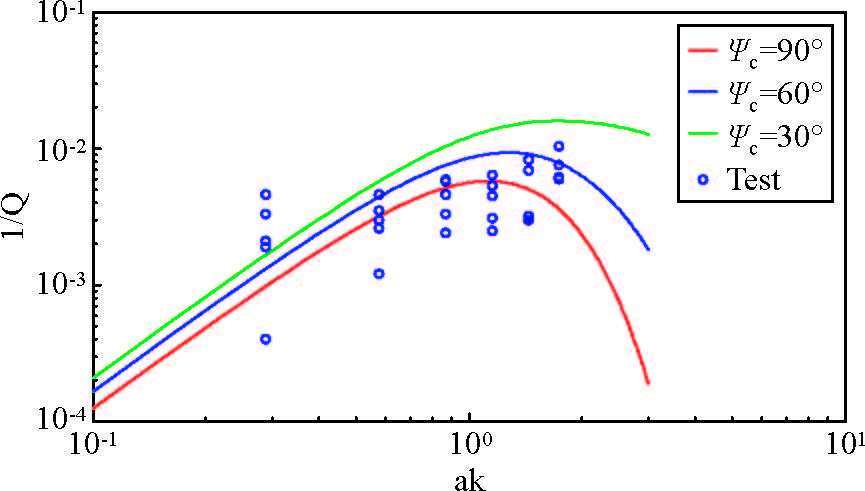
散射理论表明,地震波散射衰减与介质中散射体尺寸有关,本文生成了六组不同参数的随机介质,其扰动标准差σ 均为0.1,相关长度分别为a=10,20,30,40,50,60 m,对于每组随机介质分别进行5次随机数值模拟,利用振幅衰减法估计出相应的逆品质因子,为了和散射理论比较,利用公式
|
|
表 3 不同相关长度对应的逆品质因子 Table 3 Inverse quality factors with different correlation length |
当扰动标准偏差σ≤0.01 时,波场快照与均匀介质中几乎一致,此时的逆品质因子趋近于0,散射衰减可以忽略不计,可以近似作为均匀介质处理.为了定量分析散射衰减与介质扰动标准差的关系,本文生成了5组不同参数的随机介质,其相关长度a均为30 m,扰动标准差分别为σ=0.01,0.05,0.1,0.15,0.2,对于每组随机介质分别进行5次随机数值模拟,利用振幅衰减法估计出相应的逆品质因子,见表 4和图 11,图 11中圆圈代表每次数值实验得到的结果,红线是对25次数值实验统计结果的二次曲线拟合,分析可知,逆品质因子随标准偏差的增大而增大,从曲线拟合结果本文得出结论,逆品质因子1/Q 正比于标准偏差的平方σ2,这一点与散射理论也是一致的.
|
|
表 4 不同扰动标准差对应的逆品质因子 Table 4 Inverse quality factors with different standard deviation |
散射理论表明,不同频率的地震波在随机介质中的传播情况不同,其散射衰减程度也不一样.为了分析随机介质对不同频率地震波的响应,本文生成了五组a=30,σ=0.2 的随机介质模型,每组模型分别加载不同主频的爆炸震源f=10,15,20,25,30 Hz,进行波场数值模拟,利用振幅衰减法估计出相应的逆品质因子,然后利用公式
|
|
表 5 不同频率对应的逆品质因子 Table 5 Inverse quality factors with different frequency |
最小散射角是依赖于随机介质本身的一个固有属性,在不同扰动水平下,本文的数值结果与散射理论给出的最小散射角在60°~90°曲线符合的比较好,因此本文得出结论高斯型随机介质中,最小散射角范围是60°~90°.Frankel和Clayton(1986)基于有限差分法得到,在二维弹性随机介质中(指数型,自相似型),Ψmin 在30°~45°.Jannaud等(1991)在速度扰动较小时,给出高斯型随机介质中最小散射角约为90°.Roth和Korn(1993)认为在二维各向异性声学介质中,Ψmin 在20°~40°内.Kawahara(2002)在考虑传播时改正的情况下给出了二维声学介质中,最小散射角约为65°.Hong(Hong and Kennett,2003; Hong,2004)基于小波方法,给出了二维弹性随机介质(高斯型,指数型,冯卡门型)中,最小散射角范围在60°~90°.Hong和Kennett(2003)指出,在变化剧烈的随机介质(扰动标准差较大)中,有限差分法的平滑假设可能是其散射衰减系数估计值较高(最小散射角估计值较小)的原因.综上,与前人的结果比较,本文与Kawahara(2002)给出的理论结果,Jannaud等(1991)和Hong(Hong and Kennett,2003; Hong,2004)给出的数值模拟结果相似.
4 结 论4.1 本文基于随机过程理论生成了可以描述复杂随机结构的随机介质模型,采用间断有限元方法模拟了球面波在弹性随机介质中的传播过程.首先生成不同参数的随机介质模型,然后模拟不同频率的地震波在介质中的传播,用振幅衰减法处理波形记录,估计出随机介质的逆品质因子,最后把数值结果与散射理论作比较,来分析随机介质中的散射衰减特征
4.2 对于高斯型随机介质,本文得到的数值结果与散射理论吻合较好,本文总结出以下结论:
(1) 地震波在随机介质中传播时,相位和振幅均有一定的波动,非均匀体引起的散射,造成地震波能量重新分配,使初至P波能量随着传播距离的增加显著减小,散射波是质点维持长时间振动的原因.
(2) 当散射体尺寸与波长相当或小于波长时,随着散射体尺寸的增加,地震波振幅的散射衰减增强,介质的逆品质因子增大,地震波频率越高,在随机介质中的散射衰减越强.
(3) 扰动标准差越大,地震波的散射衰减越强,介质的逆品质因子与扰动标准差的平方成正比.
(4) 二维高斯型随机介质中,考虑P波散射衰减时,最小散射角应不小于60°,本文的实验结果显示60°≤Ψc≤90°,与Jannaud等(1991),Kawahara(2002),Hong(Hong and Kennett,2003; Hong,2004)的研究成果一致.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Aki K.1969. Analysis of the seismic coda of local earthquakes as scattered waves[J]. Journal of Geophysical Research, 74 (2) : 615–631. DOI:10.1029/JB074i002p00615 |
| [2] | Aki K.1973. Scattering of P waves under the Montana Lasa[J]. Journal of Geophysical Research, 78 (8) : 1334–1346. DOI:10.1029/JB078i008p01334 |
| [3] | Berteussen K A, Christoffersson A, Husebye E S, et a.1975. Wave scattering theory in analysis of P-wave anomalies at NORSAR and LASA[J]. Geophysical Journal of the Royal Astronomical Society, 42 (2) : 403–417. |
| [4] | Cockburn B, Lin S Y, Shu C W.1989. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: One-dimensional systems[J]. Journal of Computational Physics, 84 (1) : 90–113. DOI:10.1016/0021-9991(89)90183-6 |
| [5] | Collino F, Tsogka C.2012. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 66 (1) : 294–307. |
| [6] | Etienne V, Chaljub E, Virieux J, et a.2010. An hp-adaptive discontinuous Galerkin finite-element method for 3-D elastic wave modelling[J]. Geophysical Journal International, 183 (2) : 941–962. DOI:10.1111/j.1365-246X.2010.04764.x |
| [7] | Frankel A, Clayton R W.1986. Finite difference simulations of seismic scattering: Implications for the propagation of short-period seismic waves in the crust and models of crustal heterogeneity[J]. Journal of Geophysical Research, 91 (B6) : 6465–6489. DOI:10.1029/JB091iB06p06465 |
| [8] | Guo N C, Wang S X, Dong C H, et a.2012. Description of small scale inhomogeneities in seismic prospecting and long-wavelength theory[J]. Chinese Journal of Geophysics (in Chinese), 55 (7) : 2385–2401. DOI:10.6038/j.issn.0001-5733.2012.07.023 |
| [9] | Hatzidimitriou P M.1994. Scattering and anelastic attenuation of seismic energy in northern Greece[J]. Pure and Applied Geophysics, 143 (4) : 587–601. DOI:10.1007/BF00879499 |
| [10] | He X J, Yang D H, Wu H.2014. Numerical dispersion and wave-field simulation of the Runge-Kutta discontinuous Galerkin method[J]. Chinese Journal of Geophysics (in Chinese), 57 (3) : 906–917. DOI:10.6038/cjg20140320 |
| [11] | Hong T K.2004. Scattering attenuation ratios of P and S waves in elastic media[J]. Geophysical Journal International, 158 (1) : 211–224. DOI:10.1111/gji.2004.158.issue-1 |
| [12] | Hong T K, Kennett B L N.2003. Scattering attenuation of 2D elastic waves: Theory and numerical modeling using a wavelet-based method[J]. Bulletin of the Seismological Society of America, 93 (2) : 922–938. DOI:10.1785/0120020059 |
| [13] | Hu F Q, Hussaini M Y, Rasetarinera P.1999. An analysis of the discontinuous Galerkin method for wave propagation problems[J]. Journal of Computational Physics, 151 (2) : 921–946. DOI:10.1006/jcph.1999.6227 |
| [14] | Ikelle L T, Yung S K, Daube F.2012. 2-D random media with ellipsoidal autocorrelation functions[J]. Geophysics, 58 (9) : 1359. |
| [15] | Jannaud L R, Adler P M, Jacquin C G.1991. Frequency dependence of the Q factor in random media[J]. Journal of Geophysical Research, 96 (B11) : 18233–18243. DOI:10.1029/91JB01426 |
| [16] | Kawahara J.2002. Cutoff scattering angles for random acoustic media[J]. Journal of Geophysical Research, 107 (B1) : ESE 4-1–ESE 4-5. DOI:10.1029/2001JB000429 |
| [17] | Lian X M, Zhang R X.2013. Numerical simulation of seismic wave equation by local discontinuous Galerkin method[J]. Chinese Journal of Geophysics (in Chinese), 56 (10) : 3507–3513. DOI:10.6038/cjg20131025 |
| [18] | Liu J, Ba J, Ma J W, et a.2010. An analysis of seismic attenuation in random porous media[J]. Science China Physics, Mechanics and Astronomy, 53 (4) : 628–637. DOI:10.1007/s11433-010-0109-y |
| [19] | Liu J, Wei X C, Ji Y X, et a.2011. An analysis of seismic scattering attenuation in a random elastic medium[J]. Applied Geophysics, 8 (4) : 344–354. DOI:10.1007/s11770-011-0296-y |
| [20] | Pezzo E D, Ibanez J, Morales J, et a.1995. Measurements of intrinsic and scattering seismic attenuation in the crust[J]. Bulletin of the Seismological Society of America, 85 (5) : 1373–1380. |
| [21] | Roth M, Korn M.1993. Single scattering theory versus numerical modelling in 2-D random media[J]. Geophysical Journal International, 112 (1) : 124–140. DOI:10.1111/gji.1993.112.issue-1 |
| [22] | Wu R S.1982. Attenuation of short period seismic waves due to scattering[J]. Geophysical Research Letters, 9 (1) : 9–12. DOI:10.1029/GL009i001p00009 |
| [23] | Xi X, Yao Y.2004a. The analysis of the wave field characteristics in 2-D viscoelastic random medium[J]. Progress in Geophysics (in Chinese), 19 (3) : 608–615. DOI:10.3969/j.issn.1004-2903.2004.03.019 |
| [24] | Xi X, Yao Y.2004b. The wave field characteristics of 2-D transversely isotropic elastic random medium[J]. Progress in Geophysics (in Chinese), 19 (4) : 924–932. DOI:10.3969/j.issn.1004-2903.2004.04.037 |
| [25] | Xi X, Yao Y.2005. The characteristic frequency of the elastic random medium models[J]. Progress in Geophysics (in Chinese), 20 (3) : 681–687. DOI:10.3969/j.issn.1004-2903.2005.03.017 |
| [26] | Xue Z, Dong L G, Li X B, et a.2014. Discontinuous Galerkin finite-element method for elastic wave modeling including surface topography[J]. Chinese Journal of Geophysics-Chinese Edition (in Chinese), 57 (4) : 1209–1223. DOI:10.6038/cjg20140418 |
| [27] | Yao Y, Xi X.2002. Modeling in random medium and its seismic wavefield analysis[J]. Geophysical Prospecting for Petroleum (in Chinese), 41 (1) : 31–36. |
| [28] | 郭乃川, 王尚旭, 董春晖, 等.2012. 地震勘探中小尺度非均匀性的描述及长波长理论[J]. 地球物理学报, 55 (7) : 2385–2401. DOI:10.6038/j.issn.0001-5733.2012.07.023 |
| [29] | 贺茜君, 杨顶辉, 吴昊.2014. 间断有限元方法的数值频散分析及其波场模拟[J]. 地球物理学报, 57 (3) : 906–917. DOI:10.6038/cjg20140320 |
| [30] | 廉西猛, 张睿璇.2013. 地震波动方程的局部间断有限元方法数值模拟[J]. 地球物理学报, 56 (10) : 3507–3513. DOI:10.6038/cjg20131025 |
| [31] | 奚先, 姚姚.2004a. 二维粘弹性随机介质中的波场特征分析[J]. 地球物理学进展, 19 (3) : 608–615. DOI:10.3969/j.issn.1004-2903.2004.03.019 |
| [32] | 奚先, 姚姚.2004b. 二维横各向同性弹性随机介质中的波场特征[J]. 地球物理学进展, 19 (4) : 924–932. DOI:10.3969/j.issn.1004-2903.2004.04.037 |
| [33] | 奚先, 姚姚.2005. 弹性随机介质模型的特征频率[J]. 地球物理学进展, 20 (3) : 681–687. DOI:10.3969/j.issn.1004-2903.2005.03.017 |
| [34] | 薛昭, 董良国, 李晓波, 等.2014. 起伏地表弹性波传播的间断Galerkin有限元数值模拟方法[J]. 地球物理学报, 57 (4) : 1209–1223. DOI:10.6038/cjg20140418 |
| [35] | 姚姚, 奚先.2002. 随机介质模型正演模拟及其地震波场分析[J]. 石油物探, 41 (1) : 31–36. |
 2016, Vol. 31
2016, Vol. 31

