2. 中国地质科学院地质研究所, 北京 100037
3. 中国地质科学院, 北京 100037
2. Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China
3. Chinese Academy of Geological Sciences, Beijing 100037, China
深地震反射测线长度大,剖面横跨山川、湖泊等复杂地表条件,常有坏道及空白道;又因记录时间长,地震波穿过构造多且复杂即记录到的反射信号能量弱、信噪比低,有时还存在不明震源的干扰(朱小三等,2013). 这些现象在石油地震数据采集中也不可避免(Alsdorf et al.,1998;Langin et al.,2003;Karplus et al.,2011;Kumar et al.,2011). 如果坏道或死道发生在关键构造目标区内,不利于揭示复杂构造带下的结构特征. 因此有效地对地震炮集数据中死道、空道及干扰严重道进行波场重建有利于地震数据后期处理与解释.
地震数据插值是地震数据前期处理中不可避免的问题. 地震数据插值的方法大致可分为基于滤波的重建方法、基于波场延拓算子的重建方法、基于变换域的重建方法以及相干倾角插值等方法(霍志周等,2013). 本文采用的方法属于基于变换域的重建方法中的一种,其优势是根据已知波场特征对稀疏数据的重建,且对波场是否规则采样无要求,其理论基础是压缩感知理论(Candès,2006;Donoho,2006;Candès and Tao,2006),即要求信号具有稀疏性,通过与稀疏变换不相关的观测数据来恢复稀疏数据,进而重建信号. 自从该理论产生以来,受到各领域的广泛关注(焦李成等,2011). Curvelet变换是一种新的稀疏变换,具有多尺度、多方向的特点,适用于压缩感知(Herrmann and Hennenfent,2008;孔丽云等,2012;张华和陈小宏,2013).
Curvelet变换是由Candès和Donoho为解决边缘表示问题于2000年提出(Candès and Donoho,2000). 在2004年Candès等又提出了第二代Curvelet变换(Candès and Donoho,2004). 2006年,Candès等提出了两种基于第二代Curvelet变换理论能够实际运用的快速离散实现方法(Candès et al.,2006):非均匀空间抽样的二维FFT算法(Unequally-Spaced Fast Fourier Transform,USFFT)和Wrap算法(Wrapping-Based Transform). Ying等(2005)提出了三维的Curvelet变换. 目前,Curvelet变换已经广泛应用于图像和地震数据处理(薛念等,2011),流体力学,偏微分方程求解和压缩感知(Ma and Plonka,2009). Curvelet变换在地震数据处理中主要用于噪声压制(包乾宗等,2010;王德利等,2010;刘磊等,2011;袁艳华等,2013;薛诗桂,2015)和波场重建(Herrmann and Hennenfent,2008;刘国昌等,2011;Yang et al.,2012;孔丽云等,2012).
利用Curvelet变换对地震数据进行波场重建基本方法是迭代收缩阈值法(iterative shrinkage-thresholding :IST)(Daubechies et al.,2004),凸集投影法(projection onto convex sets :POCS)(Bregman,1965)是在IST方法基础上发展而来的. Yang等(2012)通过理论数据实验对比认为POCS方法优于IST法. 因此本文利用POCS法进行波场重建.
本文通过实际数据检验,效果明显,适用于波场重建,并对随机噪声和规则噪声有很好的压制.
1 波场重建方法 1.1 压缩感知简介如果信号x∈RN×1在某个变换域Ψ是稀疏的即

|
(1) |
其中Ψ∈RN×N代表某个稀疏变换,θ∈RN×1代表展开系数,θ是K-稀疏的,即其中有K(K
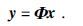
|
(2) |
实际上要通过y恢复x,是一个欠定问题,有无穷多组解. 然而将(1)式带入(2)式并且记A=ΦΨ,得到

|
(3) |
尽管此时求解θ仍然是一个欠定问题,由于θ是K-稀疏的,既有K个非零值,这样求解θ的问题转化为
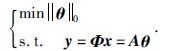
|
(4) |
求解公式(4)Chen等(1998)提出转化为求解L1范数问题,即

|
(5) |
公式(1)~(5)中x表示期望得到的完整的地震数据,Φ表示对数据x的采集方法,y表示对x采集后得到缺失数据,Ψ表示与Φ不相关的稀疏变换,本文采用的是Curvelet变换,θ表示对数据x进行稀疏变换后的得到的稀疏系数.
1.2 Curvelet变换原理第二代Curvelet变换公式为
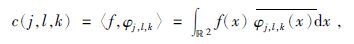
|
(6) |
式(6)中,j表示尺度,l表示角度,k表示位置,函数 f∈L2(
|
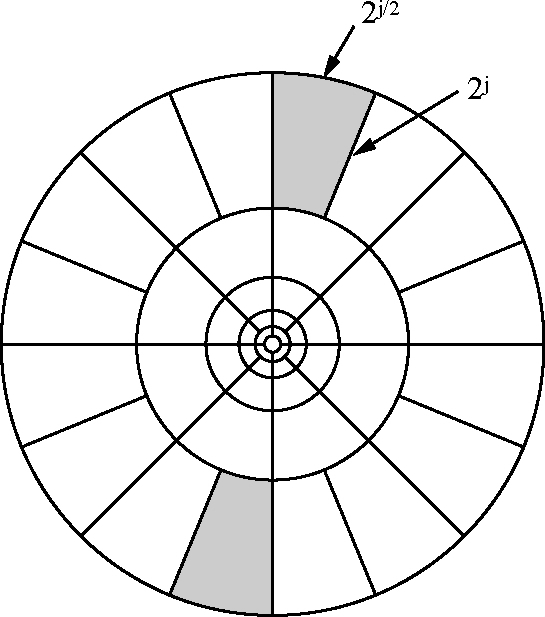
图 1 Curvelet窗函数频域覆盖图 Figure 1 Curvelet tiling of frequency domain |
在图 1中从内向外的每一个同心圆代表一个尺度,尺度控制Curvelet窗函数的大小,角度控制Curvelet窗函数的旋转,位置控制Curvelet窗函数的平移,Curvelet窗函数覆盖整个频率域. 粗糙尺度(图 1的中心圆)的Curvelets函数是无方向的. 完整的curvelet变换是由无方向性的粗糙尺度和有方向的精细尺度共同构成.
1.3 软阈值滤波方法
基于Curvelet变换的软阈值法不仅对缺失的地震数据进行插值(Donoho,1995),而且同时去除随机噪声并提高信噪比. 软阈值是指在稀疏变换后对绝对值大于阈值λ的系数在其绝对值上减去λ,对于绝对值小于λ的系数置零. 利用POCS算法对地震数据进行插值,选取阈值参数λ很重要,阈值λ收敛快则可以提高运算效率,本文选取阈值参数采用按e-
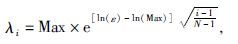
|
(7) |
公式(7)中Max是Curvelet变换系数的最大值,ε是接近零的小值且与噪声的能量有关,N是迭代次数. 缺失地震数据波场重建问题描述如下,假设Y是采集到的部分缺失的数据,D是期望得到的地震数据,则有Y=D×M.M是一个对角矩阵,正常道对应的对角元素是1,缺失道对应的对角元素是0. 软阈值滤波方法步骤如下:
(1) 选择阈值参数λ1λ2…λN其中N为迭代次数. 初始化i=1,Y0=Y.
(2) 对Yi-1进行Curvelet变换,得到变换后的系数Xi-1=CYi-1,并对Xi-1进行软阈值处理,阈值参数为λi即Xi=TλiCXi-1.
(3) 将软阈值处理后的Xi进行反变换得到重构的数据,即Yi=C-1Xi,并将重构的缺失数据填充进Y中得到新的Yi即Yi=(I-M)Yi+MY. 将Yi代回到(2),进行迭代,迭代N次,将最后得到的系数XN进行反变换,得到插值后的数据YN=C-1XN.
2 实例检验波场重建方法在理论模型上有很好的效果(刘国昌等,2011;Yang et al.,2012;张华和陈小宏,2013;薛诗桂,2015),本文采用实际数据进行检验. 本文数据采用盆山结合带深部结构与油气远景研究项目(He et al.,2008;Gao et al.,2013;侯贺晟等,2012). 地表条件复杂,经过平原带、盆山结合带、基岩裸露的高山区等,野外观测多变,原始单炮资料属典型山地的低信噪比资料. 图 2为所选取的原始单炮记录,清楚地显示了在单炮记录存在着较强的噪声干扰,且初至也不连续,更难识别出深层反射波组.

|
图 2 原始单炮记录 Figure 2 Raw shot gather |
通过频谱分析,低频能量集中在9~15 Hz,高频能量集中在25~40 Hz. 为了得到深部结构信息,选取角频率9~15 Hz进行零相位Butterworth带通滤波,结果如图 3所示. 图 3去除了随机干扰,提高了信噪比,地表初至明显恢复(图 3a). 但图 3b区7~10 s时间段存在规则噪声,及图 3c区全道记录中存在无法压制强规则噪声. 因此本文试图利用基于压缩感知原理的POCS算法重建波场(图 3c),并去除规则噪声(图 3b).

|
图 3 零相位Butterworth带通滤波(角频率9~15 Hz)后的单炮记录(原始单炮记录见图 2) 红框a 区用于实际数据检验,检验结果见图 4;红框b 区存在规则噪声;红框c 区存在强规则噪声. Figure 3 Filtered shot gather of zero phase band-pass Butterworth filter with angular frequency 9~15 Hz,which raw data shows in Fig. 2. Data in Red box a has been used to examine the validation of the method,shown in Fig. 4; Red box b shows weak regular noise; Red box c shows strong regular noise. |
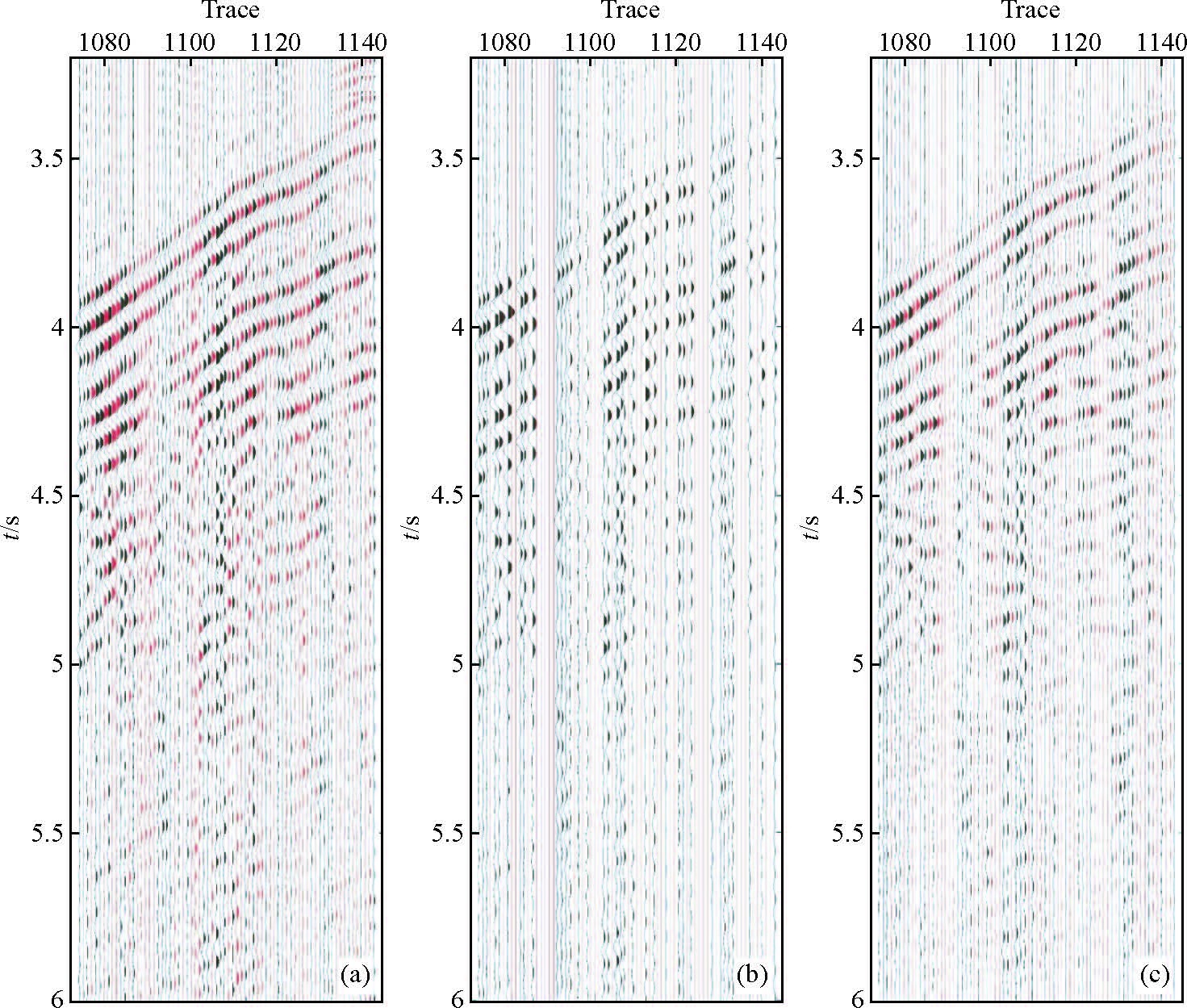
为验证Curvelet波场重建及阈值滤波在实际数据上的有效性,我们选择初至连续且信噪比高的图 3a区的波场,做深入分析. 首先在图 3a区的波场中随机抽稀50%(图 4a中的红色道),然后在Curvelet域中重建缺失道(图 3b)的波场,结果见图 4c.
|
图 4 用实际数据检验Curvelet波场重建效果对比图 (a)真实波场数据(位置见图 3a;红色道为随机抽取50%道,用于重建对比试验);(b)随机抽取50%道数据 (红色道为置零后的待重建道);(c)波场重建数据(红色道为Curvelet域中重建的波场). Figure 4 The result of real data exam (a)Real data(Fig. 3a).The red traces are going to interpolate;(b)50% random sampling data; (c)Wave-filed interpolate result(Interpolate traces are in red). |
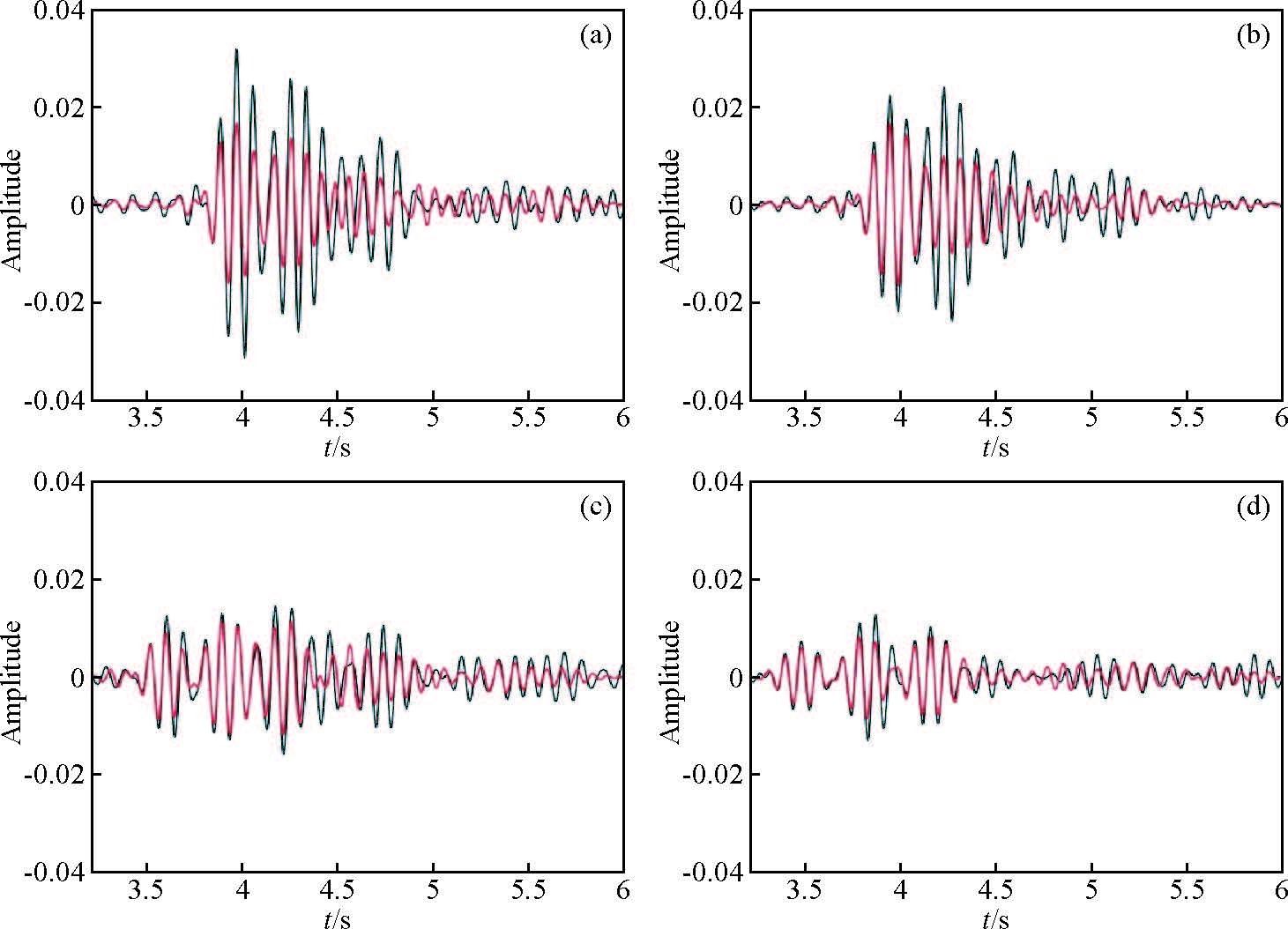
基于各向同性均匀介质模型验证结果(薛念,2010;孔丽云等,2012;白兰淑等,2014)显示波场缺失数据越少波场重建效果越好,这与用实际数据检验结果类似(图 4). 图 4b与图 4c二者差异特征显示空道带越宽插值效果越差. 显然,空道带波场重建依据空道带外部的已知波场特征信息,因此空道带边缘波场重建效果好于内部. 为此,我们特别选取四道插值数据与真实波场数据比较(图 5),显示重建数据相位恢复较好,但能量整体恢复差,特别是在深层反射信号的能量较弱尤为明显. 利用重建数据道与真实数据逐道互相关分析显示,图 4中被抽稀的36道中,互相关系数大于75%的有13道,且靠近真实波场数据;而位于空道带中心的7道因其远离已知波场,对应的波形相似度较差,互相关系数小于50%. 其余的插值道数据与真实波场相似度介于50%~75%之间. 而被重建波场的能量是真实波场能量的40%,这直接表明Curvelet域重建波场是基于各向同性的均匀介质模型(Yang et al.,2012;孔丽云等,2012;张华和陈小宏,2013),也因西南天山下的深部物质属性相当复杂,所以在实际数据重建过程中无法恢复出全部能量. 在理论模型检验结果(孔丽云等,2012;白兰淑等,2014)尚未发现这种显著差异. 另外,图 4a与图 4c波场有明显差异,波场重建压制了随机噪声,且使同相轴平滑、连续. 总体上,在Curvelet域中能够很好地恢复并重建波场.
|
图 5 重建的波形(红色)与真实波形(黑色)对比 (a)为第1078道;(b)为第1081道;(c)为第1122道;(d)为第1139道. Figure 5 Comparison between reconstruction of the waveform in red and the real waveform in black presents real wavefield is complicated Subfigure(a),(b),(c),and(d)illustrate trace number 1078,1081,1122,and 1139,respectively. |
前述的真实波场重建对比效果表明,通过压缩感知原理能够很好地识辨并重建波场. 图 3清楚地显示了利用常规的带通滤波器无法剔除规则噪声,如图 3b及图 3c. 这可能因为该规则噪声的频率与有效波场频率相同,难以分辨. 而图 3c的规则噪声覆盖整个记录长度,必须对其置零(图 6c)后再在Curvelet域中波场重建. 此外,把与图 3c区的规则噪声规律相似的部分道也被置零(图 6). 最后,利用基于Curvelet变换的POCS算法(Daubechies et al.,2004;Candès et al.,2006; Yang et al.,2012)施行波场重建和软阈值滤波,再逆变换,波场重建及定向滤波结果如图 7所示.

|
图 6 重采样后信号(红色道为置零道) 红框b 区7~10 s存在弱规则干扰,不宜置零;红框c 区存在强规则干扰被置零. Figure 6 Resampled data. Red traces have set to zero Red box b shows weak regular noise between 7~10 s that could not be cleared at all; Red box c illustrates strong regular noise that could be reset to be zero. |

|
图 7 Curvelet变换插值结果(红色道为插值道) 红框b 为波场重建后未能压制的噪声;红框c 为连续多条空白道波场重建结果. Figure 7 The result of Curvelet interpolation. Interpolated traces are in red Red box b shows regular noise still exist after wave-field reconstruction; Red box c shows interpolation within large gap. |
与图 3c区相比,图 7c初至明显. 对插值道进行频谱分析,插值后的数据存在高频成分,重新进行9~15 Hz零相位Butterworth带通滤波. 而图 7b区中位于7~10 s的规则噪声与有效波场在传播方向上具有明显差异,利用如图 1所示的Curvelet变换多尺度、多方向特点,通过方向控制(王德利等,2010)很容易地定向去除图 7b区的规则噪声,即其位于Curvelet域的最外层系数矩阵中,只须在该系数矩阵中对应系数置零即可实现. 图 8显示了定向剔除的规则噪声,表明图 7b中的规则噪声(见图 8b)及与其类似的规则噪声都被分离出来,如图 8第1100道附近的规则噪声,和接近爆炸震源位置的数十道记录到的在地下介质中传播的爆炸震源声场噪声.
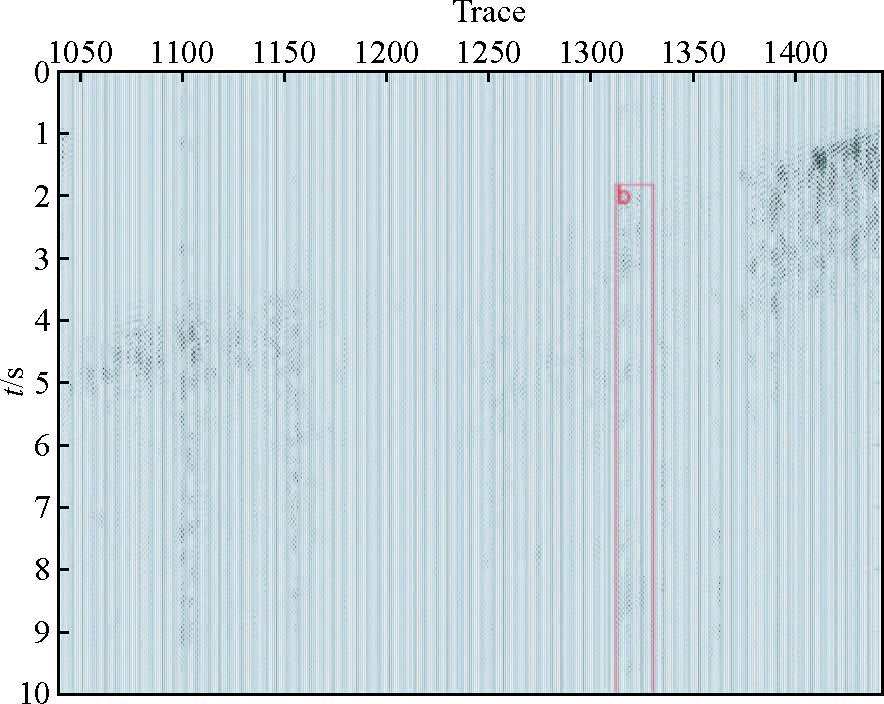
|
图 8 Curvelet域下软阈值滤波剔除的规则噪声 红框b 表示图 7b中存在的规则噪声. Figure 8 Regular noise isolated by soft-thresholding in Curvelet domain Red box b shows the regular noise in Fig. 7b. |
图 9是经过带通滤波及Curvelet变换滤波后的处理结果显示整体上同相轴更加平滑. 图 9c是重建波场,图 10为图 9d放大,红色道表示重建道,黑色道表示原始道. 地表初至波能量强,在重建道恢复两条清晰的同相轴. 与实际数据检验结果(图 4、图 5)类似,在重建区边缘的空道重建效果好,重建区的道集相位特点也很好恢复. 如图 10中t1、t2、t3、t4所示. 图 10中第1374道为真实记录,在第1374~1377道及第1375、1376道重建道波场与邻近波场的同相轴相似,如图中t1、t2、t3、t4所示.

|
图 9 Curvelet变换滤波结果(红色道为重建道) 红框b显示了弱规则噪声被明显压制;红框c 为波场重建区;红框d 突出显示初至插值效果区域(放大图见图 10). Figure 9 The result of Curvelet filter. Interpolated traces are in red Weak regular noise has been suppressed shows in Red box b; Red box c shows gap of interpolation; Red box d illustrates interpolation for first-break round gap,which zoomed in Fig. 10. |

|
图 10 空白带初至波阻插值效果(位置见图 9d,红色道为插值道,黑色道为原始道) t1、t2、t3、t4四条虚线突出指示插值道中同相轴变化. Figure 10 Illustration for first-break interpolation in blank gap in Fig. 9d. Interpolation traces are in red,original traces are in black; dotted line t1,t2,t3 and t4 represent wiggle interpolated in Curvelet domain. |
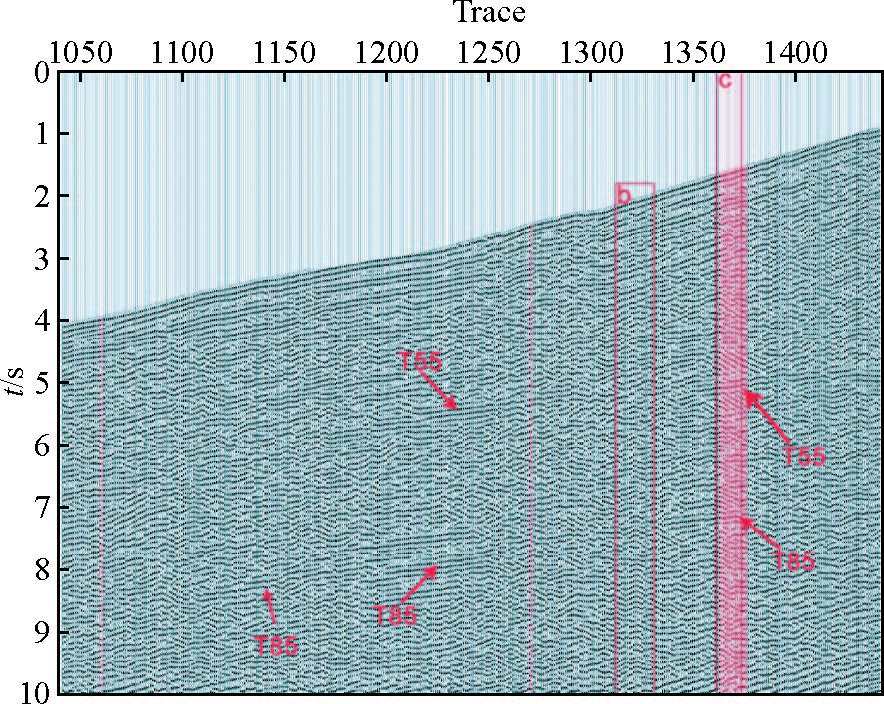
对Curvelet域重建及滤波的数据集,切除初至前的背景场,并瞬时自动增益(256 ms)炮集结果见图 11. 与图 7b相比,图 11b规则噪声被明显压制. 图 11c同相轴(如地表、T55、T85)较为明显,且T55、T85两个反射界面更加连续.
|
图 11 显示图 9切除初至后256 ms瞬时 自动增益数据(红色道为插值道)红框b 显示了弱规则噪声被压制区;红框c 为波场重建区;T55代表时间5.5 s处的同相轴;T85代表时间8.5 s处的同相轴. Figure 11 256 ms instantaneous automatic gain data after cut off the first break in Fig. 9.Interpolated traces are in red Weak regular noise has been suppressed shows in Red box b; Red box c shows gap of interpolation; T55 represent the event round time 5.5 s; T85 represent the event round time 8.5 s |
显然通过本文尝试性处理方法,效果明显,这为深地震反射数据去噪插值提供了很好的实例.
4 结 论利用Curvelet变换多方向,多尺度的特点,容易地重建地震数据波场,并去除规则噪声,效果明显. 为后续地震数据处理奠定基础. 但因地下介质复杂,对于连续缺失道集较多的炮集波场重建时,深部波场的相位能很好地恢复,但其能量较弱. 此外,Curvelet逆变换后容易产生假的高频效应,因此需要再次带通滤波.
致谢 感谢中国石化集团华东石油局第六物探大队采集了野外资料,感谢侯贺晟副研究员提供了本文处理所需的原始数据,感谢北京沃派森科技发展有限公司在数据处理中提供的宝贵经验,感谢中国地质科学院地质研究所岩石圈中心的所有成员对作者写作过程中的指导与帮助. 文中的数据处理采用的Candès等编写的Curvelab工具包,成图是通过Matlab软件完成.| [1] | Alsdorf D, Brown L, Nelson K D, et al.1998. Crustal deformation of the Lhasa terrane, Tibet plateau from Project INDEPTH deep seismic reflection profiles[J]. Tectonics, 17 (4) : 501–519. DOI:10.1029/98TC01315 |
| [2] | Bai L S, Liu Y K, Lu H Y, et al.2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics (in Chinese), 57 (9) : 2937–2945. DOI:10.6038/cjg20140919 |
| [3] | Bao Q Z, Chen W C, Gao J H.2010. Stratal configuration extraction method based on instantaneous phase and curvelet transform[J]. Progress in Geophysics (in Chinese), 25 (4) : 1413–1423. DOI:10.3969/j.issn.1004-2903.2010.04.033 |
| [4] | Bregman L M.1965. The method of successive projection for finding a common point of convex sets (Theorems for determining common point of convex sets by method of successive projection)[J]. Soviet Mathematics, 6 (3) : 688–692. |
| [5] | Candès E, Demanet L, Donoho D, et al.2006. Fast discrete curvelet transforms[J]. Multiscale Modeling & Simulation, 5 (3) : 861–899. |
| [6] | Candès E J, Donoho D L. 2000. Curvelets: A surprisingly effective nonadaptive representation for objects with edges[R]. Stanford Univ Ca Dept of Statistics. |
| [7] | Candès E J, Donoho D L.2004. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities[J]. Communications on Pure and Applied Mathematics, 57 (2) : 219–266. DOI:10.1002/cpa.v57:2 |
| [8] | Candès E J. 2006. Compressive sampling[C].//Proceedings of the International Congress of Mathematicians. Madrid, Spain, 1433-1452. |
| [9] | Candès E J, Tao T.2006. Near-optimal signal recovery from random projections: Universal encoding strategies[J]. IEEE Transactions on Information Theory, 52 (12) : 5406–5425. DOI:10.1109/TIT.2006.885507 |
| [10] | Chen S S, Donoho D L, Saunders M A.1998. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 20 (1) : 33–61. DOI:10.1137/S1064827596304010 |
| [11] | Daubechies I, Defrise M, De Mol C.2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 57 (11) : 1413–1457. DOI:10.1002/(ISSN)1097-0312 |
| [12] | Donoho D L.1995. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 41 (3) : 613–627. DOI:10.1109/18.382009 |
| [13] | Donoho D L.2006. Compressed sensing[J]. IEEE Transactions on Information Theory, 52 (4) : 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [14] | Gao R, Hou H S, Cai X Y, et al.2013. Fine crustal structure beneath the junction of the southwest Tian Shan and Tarim Basin, NW China[J]. Lithosphere, 5 (4) : 382–392. DOI:10.1130/L248.1 |
| [15] | He R Z, Gao R, Sai X. 2008. Evidence from seismic reflection profiling for crustal deformation across the juncture zone between the Tarim Basin and the southwestern Tian Shan Mountains[C].//Bogomolov L M, Zakupin A S, Mubassarova V A, et al, eds. Geodynamics of Intracontinental Orogens and Geoenvironmental Problems: Moscow-Bishkek. Scientific Station of the Russian Academy of Science, No. 4, 170-173. |
| [16] | Herrmann F J, Hennenfent G.2008. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 173 (1) : 233–248. DOI:10.1111/gji.2008.173.issue-1 |
| [17] | Hou H S, Gao R, He R Z, et al.2012. Shallow-deep tectonic relationship for the junction belt of western part of South Tianshan and Tarim basin-Revealed from preliminary processed deep seismic reflection profile[J]. Chinese Journal of Geophysics (in Chinese), 55 (12) : 4116–4125. DOI:10.6038/j.issn.0001-5733.2012.12.024 |
| [18] | Huo Z Z, Xiong D, Zhang J F.2013. The overview of seismic data reconstruction methods[J]. Progress in Geophysics (in Chinese), 28 (4) : 1749–1756. DOI:10.6038/pg20130415 |
| [19] | Jiao L C, Yang S Y, Liu F, et al.2011. Development and Prospect of Compressive Sensing[J]. Acta Electronica Sinica (in Chinese), 39 (7) : 1651–1662. |
| [20] | Karplus M S, Zhao W, Klemperer S L, et al.2011. Injection of Tibetan crust beneath the south Qaidam Basin: Evidence from INDEPTH IV wide-angle seismic data[J]. Journal of Geophysical Research: Solid Earth, 116 (B7) : B07301. DOI:10.1029/2010JB007911 |
| [21] | Kong L Y, Yu S W, Cheng L, et al.2012. Application of compressive sensing to seismic data reconstruction[J]. Acta Seismologica Sinica (in Chinese), 34 (5) : 659–666. |
| [22] | Kumar V, Oueity J, Clowes R M, et al.2011. Enhancing crustal reflection data through curvelet denoising[J]. Tectonophysics, 508 (1-4) : 106–116. DOI:10.1016/j.tecto.2010.07.017 |
| [23] | Langin W R, Brown L D, Sandvol E A.2003. Seismicity of central Tibet from project INDEPTH III seismic recordings[J]. Bulletin of the Seismological Society of America, 93 (5) : 2146–2159. DOI:10.1785/0120030004 |
| [24] | Liu G C, Chen X H, Guo Z F, et al.2011. Missing seismic data rebuilding by interpolation based on Curvelet transform[J]. Oil Geophysical Prospecting (in Chinese), 46 (2) : 237–246. |
| [25] | Liu L, Liu Z, Zhang J H.2011. Denoising and detecting seismic weak signal based on curvelet thresholding method[J]. Progress in Geophysics (in Chinese), 26 (4) : 1415–1422. DOI:10.3969/j.issn.1004-2903.2011.04.037 |
| [26] | Ma J W, Plonka G.2009. A review of curvelets and recent applications[J]. IEEE Signal Processing Magazine . |
| [27] | Wang D L, Tong Z F, Tang C, et al.2010. An iterative curvelet thresholding algorithm for seismic random noise attenuation[J]. Applied Geophysics, 7 (4) : 315–324. DOI:10.1007/s11770-010-0259-8 |
| [28] | Xue N. 2010. Seismic data interpolation and denoising based on curvelet transformation (in Chinese) [Ph. M. thesis]. Chengdu: Southwest Jiaotong University. |
| [29] | Xue N, Zhou L X, Yin Z K.2011. Curvelet thresholding for seismic data denoising and interpolating[J]. Journal of Transportation Engineering and Information (in Chinese), 9 (2) : 86–91. |
| [30] | Xue S G.2015. The curvelet transform for seismic random de-noising using cycle spinning method[J]. Progress in Geophysics, 30 (1) : 372–377. DOI:10.6038/pg20150154 |
| [31] | Yang P L, Gao J H, Chen W C.2012. Curvelet-based POCS interpolation of nonuniformly sampled seismic records[J]. Journal of Applied Geophysics, 79 : 90–99. DOI:10.1016/j.jappgeo.2011.12.004 |
| [32] | Ying L L, Demanet L, Candès E. 2005. 3D Discrete Curvelet transform[C].//Proceedings of SPIE-The International Society for Optical Engineering. San Diego, California, USA: SPIE, 5914: 351-361. |
| [33] | Yuan Y H, Wang Y B, Liu Y K, et al.2013. Non-dyadic Curvelet transform and its application in seismic noise elimination[J]. Chinese Journal of Geophysics (in Chinese), 56 (3) : 1023–1032. DOI:10.6038/cjg20130330 |
| [34] | Zhang H, Chen X H.2013. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics (in Chinese), 56 (5) : 1637–1649. DOI:10.6038/cjg20130521 |
| [35] | Zhu X S, Gao R, Li Q S, et al.2013. Review of the noises attenuation of deep reflection seismic data[J]. Progress in Geophysics (in Chinese), 28 (6) : 2878–2900. DOI:10.6038/pg20130609 |
| [36] | 白兰淑, 刘伊克, 卢回忆, 等.2014. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 57 (9) : 2937–2945. DOI:10.6038/cjg20140919 |
| [37] | 包乾宗, 陈文超, 高静怀.2010. 基于瞬时相位和Curvelet变换的地层结构提取方法[J]. 地球物理学进展, 25 (4) : 1413–1423. DOI:10.3969/j.issn.1004-2903.2010.04.033 |
| [38] | 侯贺晟, 高锐, 贺日政, 等.2012. 西南天山—塔里木盆地结合带浅深构造关系——深地震反射剖面的初步揭露[J]. 地球物理学报, 55 (12) : 4116–4125. DOI:10.6038/j.issn.0001-5733.2012.12.024 |
| [39] | 霍志周, 熊登, 张剑锋.2013. 地震数据重建方法综述[J]. 地球物理学进展, 28 (4) : 1749–1756. DOI:10.6038/pg20130415 |
| [40] | 焦李成, 杨淑媛, 刘芳, 等.2011. 压缩感知回顾与展望[J]. 电子学报, 39 (7) : 1651–1662. |
| [41] | 孔丽云, 于四伟, 程琳, 等.2012. 压缩感知技术在地震数据重建中的应用[J]. 地震学报, 34 (5) : 659–666. |
| [42] | 刘国昌, 陈小宏, 郭志峰, 等.2011. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 46 (2) : 237–246. |
| [43] | 刘磊, 刘振, 张军华.2011. 曲波阈值法地震弱信号识别及去噪方法研究[J]. 地球物理学进展, 26 (4) : 1415–1422. DOI:10.3969/j.issn.1004-2903.2011.04.037 |
| [44] | 王德利, 仝中飞, 唐晨, 等.2010. Curvelet阈值迭代法地震随机噪声压制[J]. 应用地球物理(英文版), 7 (4) : 315–324. |
| [45] | 薛念. 2010. 基于Curvelet变换的地震数据插值和去噪[硕士论文]. 成都: 西南交通大学. http://cdmd.cnki.com.cn/article/cdmd-10613-2010122253.htm |
| [46] | 薛念, 周黎霞, 尹忠科.2011. 基于Curvelet变换阈值法的地震数据插值和去噪[J]. 交通运输工程与信息学报, 9 (2) : 86–91. |
| [47] | 薛诗桂.2015. 基于曲波变换的循环平移地震随机噪声衰减[J]. 地球物理学进展, 30 (1) : 372–377. DOI:10.6038/pg20150154 |
| [48] | 袁艳华, 王一博, 刘伊克, 等.2013. 非二次幂Curvelet变换及其在地震噪声压制中的应用[J]. 地球物理学报, 56 (3) : 1023–1032. DOI:10.6038/cjg20130330 |
| [49] | 张华, 陈小宏.2013. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 56 (5) : 1637–1649. DOI:10.6038/cjg20130521 |
| [50] | 朱小三, 高锐, 李秋生, 等.2013. 深反射地震数据的噪音衰减方法综述[J]. 地球物理学进展, 28 (6) : 2878–2900. DOI:10.6038/pg20130609 |
 2016, Vol. 31
2016, Vol. 31


