地球物理学进展  2016, Vol. 31 Issue (3): 992-998   PDF    
引用本文
杨锦玲, 关玉梅, 钟继茂, 洪旭瑜. 2016. 厦门重力固体潮海潮负荷改正研究[J]. 地球物理学进展, 31(3): 992-998, doi: 10.6038/pg20160309  
YANG Jin-ling, GUAN Yu-mei, ZHONG Ji-mao, HONG Xu-yu. 2016. Study on ocean tidal loading correction of tidal gravity at Xiamen Station. Progress in Geophysics, 31(3): 992-998, doi: 10.6038/pg20160309   
厦门重力固体潮海潮负荷改正研究
杨锦玲, 关玉梅, 钟继茂, 洪旭瑜    
福建省地震局, 福州 350003
收稿日期: 2015-10-10 修回日期: 2016-02-22.
基金项目: 福建省地震局科研基金专项(SF201513)和福建省地震局青年科技基金(Y201305)联合资助.
作者简介: 杨锦玲,女,1986年生,福建南安人,工学硕士,工程师,主要从事重力与形变固体潮观测研究.(E-mail:yangjinling86@foxmail.com)
摘要: 厦门台重力固体潮观测长期受海潮负荷影响.应用重力固体潮观测资料进行地震预报和地球物理研究时,需要对其海潮负荷的影响和改正进行研究.本文应用TSOFT软件对厦门台弹簧重力仪五年的连续观测数据进行预处理,并采用Venedikov调和分析方法获得重力固体潮潮汐参数.基于DTU10、EOT11a、HAMTIDE11a、GOT4.7、FES2004、NAO99b、TPXO7.2和TPXO7.2atlas八个较新的全球海潮模型,结合osu.chinasea.2010和NAO.99Jb两个区域海潮模型,研究了厦门台的重力海潮负荷特征并对其进行海潮负荷改正.数值结果表明,经过区域海潮模型修正后的厦门台海潮负荷为7.3 μgal.八个全球海潮模型对主要潮波的负荷改正有效性的差异不大.应用NAO.99Jb区域海潮模型修正的M2波剩余残差值比osu.chinasea.2010小.观测残差负荷改正有效性大致在40%~70%.统计对比O1、K1、M2波的残差平方和结果表明,对厦门台进行海潮负荷改正时,应用经NAO.99Jb区域海潮模型改正的NAO.99b全球海潮模型残差结果最小,经NAO.99Jb区域海潮模型改正的DTU10全球海潮模型次之.这可能与NAO.99Jb模型考虑日本沿岸验潮站资料有关.考虑高精度近海海潮模型的构建和验潮站资料的弥补以及数据预处理方法的改进,可以进一步提高厦门台的海潮负荷的改正效果.
关键词: 重力固体潮     海潮负荷     海潮模型     潮汐分析    
Study on ocean tidal loading correction of tidal gravity at Xiamen Station
YANG Jin-ling, GUAN Yu-mei, ZHONG Ji-mao, HONG Xu-yu    
Earthquake Administration of Fujian Province, Fuzhou 350003, China
Abstract: Tidal gravity observation at Xiamen Station is critically affected by ocean tide loading (OTL). To obtain high-precision tidal gravity parameters and apply them to earthquake prediction and geophysical research, calculation and correction of the OTL effect is required. In this study, tidal gravity data through 5 years were preprocessed based on the Tsoft software, which is recommended by the International Center of Earth Tides, and then precise tidal gravity parameters were obtained using Venedikov method for tidal analysis. In order to evaluate the efficiency of different ocean loading corrections, gravity data were analyzed for various tidal waves(O1,P1,Q1,K1,M2,N2,S2,K2) based on eight up-to-date global OTL models (DTU10, EOT11a,FES2004, HAMTIDE11a, NAO99b, TPXO7.2, and TPXO7.2atlas), supplemented with two regional oceanic models (osu.chinasea.2010 and NAO.99Jb), in combination with an ocean loading calculation program(SPOTL).The numerical results show that, the average OTL effect at Xiamen Station was 13.9 μgal when calculated with the global oceanic tidal models. After supplementation with the two regional ocean models, the average OTL effect decreased to 7.3 μgal. The values of the ocean tide corrections had relatively small discrepancies between the eight global models.The final residual of M2 harmonics supplemented with NAO.99Jb was smaller than that with osu.chinasea.2010. The loading effect efficiency varied from 40% to 70% for the three major waves (O1, M2, K1), indicating that the remaining load effects might have been from the atmosphere, tidal force caused by regional tectonics, and observation errors. From comparisons of the combined misfit for the three major waves, the most optimum ocean tide model was found to be NAO.99b supplemented with NAO.99Jb, followed by the DTU10 model supplemented with NAO.99Jb.This shows that the Nao.99Jb regional OTL model, which takes into account tide gauge measurements, is more suitable for Xiamen Station than osu.chinasea.2010. To improve ocean loading correction at stations near coastal lines, accuracy of regional OTL models, tide gauge measurements, high-precision gravity measurements, and data preprocessing method should be taken into consideration.
Key words: gravity     ocean tide loading     regional OTL models     tidal analysis    
0 引 言

海洋潮汐是重力固体潮观测的重要干扰源.研究表明，在沿海地区重力固体潮中的海潮负荷一般可达微伽量级.在精密固体潮汐研究中，海潮负荷的影响不容忽视.但由于海潮和固体潮都受日月引力的共同作用，用滤波方法难以将固体潮中的海潮负荷影响剔除.1972年Farrell提出用海潮潮高和负荷格林函数的褶积积分求得海潮负荷效应.此后很多学者在此基础上开展了广泛的海潮负荷研究.而随着验潮站数据的积累和现代卫星测高技术的发展，高精度的海潮模型不断推出.目前应用较为广泛的有CSR4.0、NAO.99b、FES2004、GOT04、TPXO7.2、DTU10、EOT11a、HAMTIDE11a等模型(Kim et al.，2011；Kim et al.，2013).当前国内外很多学者围绕海潮模型的构建和优化、海潮负荷对重力、地倾斜固体潮的影响和改正以及针对某地区的最优海潮模型的选择等方面做了很多深入系统的研究工作(Neumeyer et al.，2005；Bos and Baker，2005；孙和平等，2005；周江存和孙和平，2005；孙和平等，2006；周江存和孙和平，2007；周江存，2008；Florsch et al.，2009；Kim et al.，2011；Arnoso et al.，2011； Kim and Shibuya，2013；Zhou et al.，2013；Ducarme et al.，2014；徐建桥等，2014).

虽然目前全球海潮模型的分辨率和精度不断提高，但由于近海几何形状复杂，海潮梯度变化大，全球海潮模型在中国近海区域的精度仍较低.利用高精度的验潮站资料对评估全球海潮模型的精度评估，结果表明全球海潮模型与中国验潮站偏差在16 cm左右，在中国海域全球海潮模型实用性较差(李大炜等，2012).研究也表明东南部地区的重力场负荷研究需要顾及近海效应(周江存，2008).因此，在沿海地区计算海潮负荷时，需要应用分辨率较高、潮汐资料较准确的近海模型资料对全球海潮模型做局部的修正和补充.

目前中国近海的区域海潮模型主要有osu.chinasea.2010、NAO.99Jb和国家海洋局第一海洋研究所的中国近海区域海潮模型.三个区域海潮模型的分辨率和包含潮波和覆盖范围见表 1.osu.chinasea.2010是俄勒冈州立大学基于流体动力学方程同化TOPEX/POSEIDON卫星测高资料构建的中国近海区域海潮模型.该模型测深数据来自GEBCO数据库，应用中国55个沿海验潮站资料以及Richard Ray采用的6SW验潮站资料对比验证其精度.结果表明M2波潮位误差小于5cm，K1波潮位误差小于2cm，精度较高.NAO.99Jb是日本国家天文台应用五年的TOPEX/POSEIDON卫星测高资料，结合日本沿岸验潮站资料构建的日本附近海域的区域海潮模型.国家海洋局第一海洋研究所的中国近海区域海潮模型，是中国近海及邻近大洋最新的网格化的近海数字海潮模型.考虑到中国近海区域海潮模型只包含四个潮波，且从整体而言模型的分辨率和构建方法不统一(张杰，2014)，本文只选用osu.chinasea.2010和NAO.99Jb两个区域海潮模型展开研究.本文应用的全球和区域海潮模型的基本信息见表 1，区域海潮模型具体覆盖范围见图 1.

表 1 中国近海区域海潮模型基础信息 Table 1 Basic information of three regional OTL models

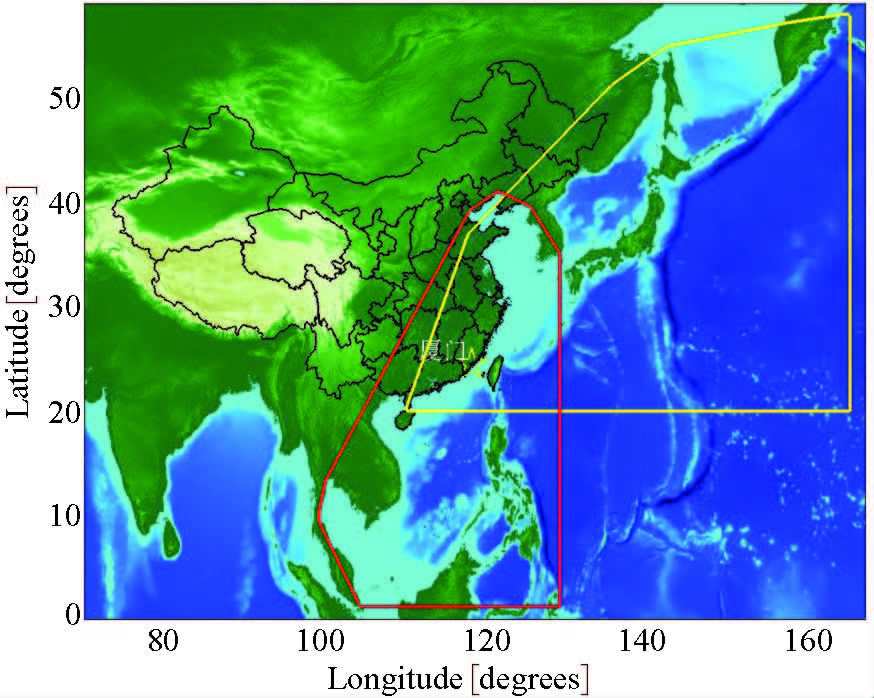
图 1 厦门台和osu.chinasea.2010和NAO.99Jb近海海潮模型的区域范围
(红色：osu.chinasea.2010；黄色：NAO.99Jb) Fig. 1 Xiamen Station and area limits of osu.chinasea. 2 010 and NAO.99Jb regional OTL models
(red: osu.chinasea.2010;yellow: NAO.99Jb)

福建地区地处中国东海沿海，厦门台距离海岸线距离不到1km，是全国距海岸线最近的台站之一，固体潮资料受海潮影响显著.为真实客观分析固体潮受海潮负荷的影响程度，本文应用经osu.chinasea.2010和NAO.99Jb高精度区域海潮模型修正前后的DTU10、EOT11a、HAMTIDE11a、GOT4.7、FES2004、NAO99b、TPXO7.2和TPXO7.2atlas八个全球海潮模型，计算了厦门台M2，S2，N2，K2，K1，O1，P1，Q1八个主要潮波的重力固体潮海潮负荷效应.该研究可提高实际观测工作中精密固体潮的精度，在此基础上展开进一步的地球物理分析研究，也可为东南沿海地区最佳海潮模型的选择提供依据.

1 计算方法 1.1 海潮负荷和近海效应计算

根据Farrell理论，海潮对地面点重力固体潮的影响可以由重力的负荷格林函数与负荷质量作褶积积分求得，其公式(周江存，2008)为

式中，

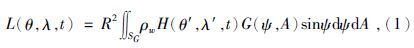
R是地球半径，ρw是海水密度，θ、λ是计算点的坐标，θ′、λ′是负荷点的坐标，ψ、A是计算点到负荷点的角距离和方位角，H(θ′，λ′，t)是(θ′，λ′)处的瞬时潮高，SG是整个海面.Gg(ψ)是重力负荷的格林函数.G(θ，λ，t)是重力负荷.

当考虑近海效应时，需要将全球海潮模型中的相应区域用精度较高的近海潮汐模型代替.式(1)应改为

式(4)中，HL(θ′，λ′，t)表示近海区域SL的瞬时潮高.则近海潮汐效应即为(4)式和(1)式之差，公式为

1.2 重力固体潮的海潮负荷改正

如图 2所示，设向量O为固体潮观测值，T为固体潮理论值，Ta为T的相位滞后，L’为观测残差负荷矢量，L为海潮负荷效应，R为剩余残差矢量.则有

图 2 重力固体潮海潮负荷改正矢量图 Fig. 2 Vector diagram for the comparison between the observedtidal gravity and the corrected residual gravity
2 计算结果和讨论

2.1 厦门台重力固体潮潮汐分析

厦门台地处长乐诏安断裂带南段，台站从2001年开始展开重力固体潮观测.仪器为国产DZW弹簧重力仪，采样率为分钟采样.在资料处理中，首先应用国际地潮中心ICET推荐的固体潮预处理软件Tsoft(Van Camp and Vauterin，2005)对厦门台2006年1月1日至2010年12月31日五年的原始数据进行预处理，对缺记部分和地震造成的突跳、台阶等进行处理(徐伟民等，2012；韦进等，2012).之后应用Venedikov调和分析方法对预处理后的重力固体潮整时值资料进行分析，得到了M2，S2，N2，K2，K1，O1，P1，Q1多个主要潮波的观测振幅因子、相位滞后和相应的误差结果.从表 2可见，厦门地区的观测振幅较大的有重力潮汐半日波M2波振幅72.1454 μgal，O1波振幅29.7982 μgal，K1波振幅39.8419 μgal，S2波振幅34.5023 μgal.除S2和K2波外，其他六个潮波均表现为相位滞后.八个主波的振幅因子标准差测定精度均在2％之内，达到较高精度.

表 2 厦门台实测重力潮汐参数 Table 2 Observed tidal gravity parameters at Xiamen station
2.2 海潮负荷效应数值计算和讨论

根据上文提及的计算方法和模型，本文利用DTU10、EOT11a、HAMTIDE11a、GOT4.7、FES2004、NAO99b、TPXO7.2和TPXO7.2atlas八个全球海潮模型，基于SPOTL(Agnew，1997)程序计算了厦门台未经近海模型修正以及分别应用osu.chinasea.2010和NAO.99Jb两个近海模型修正后的M2，S2，N2，K2，K1，O1，P1，Q1 多个主要潮波的重力海潮负荷，结果见图 3.表 3列出受海潮影响较为显著的周日波O1波、K1波和半日波M2波的海潮负荷振幅和相位值.

表 3 应用八个海潮模型计算厦门台主要潮波(O1，K1，M2)的重力海潮负荷(单位：振幅μgal，相位 °) Table 3 Ocean tidal loading effect estimated by eight different models for four waves(O1，K1，M2，S2)at Xiamen Station. Data represent the amplitudes(in μgal)and the local phase(lag positive，in degree)

据表 3和图 3a可见，未经近海模型修正前，八个潮波振幅大小顺序依次为M2>K1>O1>S2>N2>P1>Q1>K2.从振幅上反映出厦门台受半日频段M2波和周日频段K1波和O1波的影响较大.M2，K1，O1潮波的振幅值占潮波振幅的70%以上.应用八个海潮模型计算的O1，K1，M2主要潮波的平均值都大于2 μgal.对于半日频段的M2波，TPXO7.2atlas模型给出的振幅值最大，达到5.679 μgal，大约为观测振幅的7.9%；FES2004模型给出的振幅值最小为4.815 μgal，为观测振幅的6.6%.对于周日频段的K1波，NAO99b模型给出的振幅值最大，达到2.583 μgal，大约为观测振幅的6.4%，由FES2004模型得到2.291最小振幅值也占观测振幅的5.7%.据图 3A，多个海潮模型计算的八个分潮波的海潮负荷值分布在13.5 μgal至14.2 μgal，均值为13.9 μgal.可见目前的全球海潮模型差异不大.另一方面也说明，厦门台海潮负荷对重力的影响不容忽视，需要进行海潮改正.

图 3 厦门台重力海潮负荷振幅(单位：μgal)
(a)未修正;(b)CHINASEA.2010修正;(c)NAO.99Jb修正. Fig. 3 OTL at Xiamen supplemented without and with regional models
(a)Represents OTL amplitude;(b)Represents OTL supplemented withCHINASEA.2010 and(c)Represents OTL supplemented with NAO.99Jb.

图 3b和图 3c分别给出了在应用osu.chinasea.2010和NAO.99Jb两个近海海潮模型对八个全球海潮模型修正后的八个潮波的海潮负荷影响.和修正前相比，M2波振幅有较大程度的减小，振幅平均值分别下降为2.246 μgal和1.855 μgal，标准差从0.304减小为0.01和0.016，修正效果较好.周日波K1波和O1波在经过近海模型修正后，振幅和相位的标准差也都有所减小.这表明两个近海海潮模型都能对全球海潮模型进行较好地修正和改进.从八个潮波的海潮负荷看，经NAO.99Jb修正后计算的八个潮波的海潮负荷较小，平均为7.01 μgal；经osu.chinasea.2010修正后的八个海潮潮波海潮负荷平均值为7.58 μgal；二者综合平均可得厦门台的海潮负荷为7.3 μgal.但相比NAO.99Jb，经osu.chinasea.2010修正的O1，K1，M2主要潮波的振幅和相位标准差都更小.综合看来，两个近海海潮模型对全球海潮模型的修正和补充能更真实客观反映厦门台的重力海潮负荷情况.

根据上述海潮负荷分析结果可见，厦门台受海潮负荷影响大，需要进行海潮改正，且应重点考虑近海效应的影响.经过两种近海海潮模型修正的八个海潮模型计算的海潮负荷效应基本表现出较好的一致性.应用osu.chinasea.2010和NAO.99Jb对全球海潮模型进行修正后，厦门台的海潮负荷效应平均值从13.9 μgal减少为7.3 μgal.

2.3 海潮负荷改正

用不同的全球海潮模型和近海海潮模型进行海潮负荷改正的结果表明，重力固体潮中的剩余残差相对于观测残差有明显的减小.表 4列出重力观测残差和剩余残差结果.以半日波M2波为例，观测残差为2.44 μgal，在应用FES2004全球海潮模型并分别加入osu.chinasea.2010和NAO.99Jb改正后，剩余残差分别减小为1.340 μgal和0.697 μgal，可见海潮负荷改正能有效降低残差矢量.计算了O1、K1和M2主波剩余残差的平方和，最小的是7.23 μgal(经NAO.99Jb 修正的NAO.99b)，7.39 μgal(经NAO.99Jb 修正的DTU10)次之，最大的是9.0 μgal(经osu.chinasea.2010修正的TPXO72atlas).从表 4可见，八个全球海潮模型对主要潮波的负荷改正有效性的差异不大，而近海海潮模型对负荷改正的影响较大.

表 4 海潮负荷改正前后的厦门重力观测残差和剩余残差(单位：振幅μgal，相位 °) Table 4 Observation residuals and final residuals of tidal gravity before and after ocean loading correction Data represent the amplitudes(in μgal)and the local phase(lag positive，in degree)

“负荷改正有效性”概念是用观测残差矢量振幅减去最终残差的振幅再除以观测残差振幅(孙和平等，2006).为综合评价负荷改正效果，统计了主要潮波的负荷改正有效性.图 4给出了两种近海海潮模型的O1、K1和M2波负荷改正有效性.应用八个海潮模型和osu.chinasea.2010作海潮改正，O1波负荷改正有效性从48%到50%，M2波负荷改正有效性从42%到46%，K1波负荷改正有效性从39%到42%.应用八个海潮模型和NAO.99Jb作海潮改正，M2波负荷改正有效性从68%到71%.对于这几个主要潮波，观测残差负荷改正有效性大致分布在40%~70%.可见，目前的全球海潮模型和近海海潮模型只能解释厦门台重力潮汐观测残差的40%~70%，剩下的部分可能来自大气负荷效应、台站区域构造导致的对日月引潮力响应的小差异以及观测仪器的标定误差(徐建桥等，2014).而对于M2波，应用NAO.99Jb的负荷改正有效性大致是应用osu.chinasea.2010负荷改正有效性的两倍.这可能与NAO.99Jb模型考虑日本沿岸验潮站资料有关.

图 4 区域海潮模型修正前后的八个海潮模型计算的K1、O1和M2波的海潮负荷改正有效性
(括号中(N)指代NAO.99Jb，括号中(C)指代CHINASEA.2010) Fig. 4 Loading effect efficiency for main constituents (K1、O1 and M2)estimated by eight different models supplemented with NAO.99Jb and CHINASEA.2010 regional models
(N represents NAO.99Jb and C represents CHINASEA.2010)

最优的NAO.99b和NAO.99Jb的海潮模型组合剩余残差值仍较大，这一方面是由于厦门地区海湾地形复杂，导致近海模型误差较大，另一方面，厦门台的DZW重力仪运行时间长，长期零漂，且在预处理工作中没有考虑大气负荷的影响.因此在厦门台重力固体潮工作中，下一步将从近海海潮模型的分辨率提高、验潮站资料的参与以及数据预处理方法改进等方面展开研究.

3 结 论

基于八个较新的全球海潮模型和两个区域海潮模型，定量分析厦门台受海潮负荷的影响，对厦门台五年的重力固体潮进行海潮负荷改正，对比了区域海潮模型在厦门的适用性.本文结论总结如下：

(1) 应用Tsoft软件处理了厦门台2006-2010五年的长期连续重力观测资料，并采用Venedikov调和分析方法获得M2，S2，N2，K2，K1，O1，P1，Q1主要潮波高精度的潮汐参数.

(2) 基于DTU10、EOT11a、HAMTIDE11a、GOT4.7、FES2004、NAO99b、TPXO7.2和TPXO7.2atlas八个较新的全球海潮模型，计算出重力海潮负荷振幅达到14 μgal；经osu.chinasea.2010和NAO.99Jb两个近海海潮模型修正后，厦门重力固体潮的海潮负荷值为7.3 μgal.从修正前后八个主要潮波的海潮负荷振幅数值上看，M2波最大，O1和K2次之.对比八个全球海潮模型，主要潮波的海潮负荷振幅差异小，相位差稍大.相比NAO.99Jb，经osu.chinasea.2010修正的O1，K1，M2主要潮波的振幅和相位标准差都更小.

(3) 展开了重力潮汐参数的负荷改正.结果说明，海潮负荷改正能有效降低残差矢量，提高固体潮的观测精度.应用八个海潮模型和osu.chinasea.2010及NAO.99Jb作海潮改正，观测残差负荷改正有效性大致分布在40%~70%.应用NAO.99Jb对M2波的负荷改正更有效.这可能与NAO.99Jb模型考虑日本沿岸验潮站资料有关.统计对比O1、K1、M2波的残差平方和结果表明，对厦门台进行海潮负荷改正时，应用经NAO.99Jb区域海潮模型改正的NAO.99b全球海潮模型残差结果最小，经NAO.99Jb区域海潮模型改正的DTU10全球海潮模型次之.考虑高精度近海海潮模型的构建和验潮站资料的弥补以及数据预处理方法的改进，可以进一步提高厦门台的海潮负荷的计算精度.

致 谢 感谢审稿专家的宝贵意见和编辑部老师的帮助.

参考文献
[1] Agnew D C. 1997. NLOADF: A program for computing ocean-tide loading[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 102(B3): 5109-5110.
[2] Arnoso J, Benavent M, Bos M S, et al. 2011. Verifying the body tide at the Canary Islands using tidal gravimetry observations[J]. Journal of Geodynamics, 51(5): 358-365.
[3] Bos M S, Baker T F. 2005. An estimate of the errors in gravity ocean tide loading computations[J]. Journal of Geodesy, 79(1-3): 50-63.
[4] Ducarme B, Pálinkáš V, Meurers B, et al. 2014. On the comparison of tidal gravity parameters with tidal models in central Europe[J]. Journal of Geodynamics, 80: 12-19.
[5] Florsch N, Llubes M, Wöppelmann G, et al. 2009. Oceanic loading monitored by ground-based tiltmeters at Cherbourg (France)[J]. Journal of Geodynamics, 48(3-5): 211-218.
[6] Kim T H, Shibuya K. 2013. Verification of the ellipsoidal earth model with an inelastic and convective mantle using tidal gravity variations revisited[J]. Geophysical Journal International, 194(1): 230-248.
[7] Kim T H, Shibuya K, Doi K, et al. 2011. Validation of global ocean tide models using the superconducting gravimeter data at Syowa Station, Antarctica, and in situ tide gauge and bottom-pressure observations[J]. Polar Science, 5(1): 21-39.
[8] Li D W, Li J C, Jin T Y, et al. 2012. Accuracy estimation of recent global ocean tide models using tide gauge data[J]. Journal of Geodesy and Geodynamics (in Chinese), 32(4): 106-110.
[9] Neumeyer J, Del Pino J, Dierks O, et al. 2005. Improvement of ocean loading correction on gravity data with additional tide gauge measurements[J]. Journal of Geodynamics, 40(1): 104-111.
[10] Sun H P, Ducarme B, XU H Z, et al. 2005a. Adaptability of the ocean and Earth tidal models based on global observations of the superconducting gravimeters[J]. Science in China Series D: Earth Sciences, 48(11): 1859-1869.
[11] Sun H P, Hsu H, Chen W, et al. 2006. Study of Earth's gravity tide and oceanic loading characteristics in Hongkong area[J]. Chinese Journal of Geophysics, 49(3): 657-670, doi: 10.1002/cjg2.880.
[12] Sun H P, Hsu H Z, Chen W, et al. 2006. Study of Earth's gravity tide and oceanic loading characteristics in Hong Kong area[J]. Chinese Journal of Geophysics (in Chinese), 49(3): 724-734, doi: 10.3321/j.issn:0001-5733.2006.03.016.
[13] Sun H P, Hsu H Z, Zhou J C, et al. 2005. Latest observational results from the superconducting gravimeter at station Wuhan and investigation of ocean tide models[J]. Chinese Journal of Geophysics, 48(2): 331-341.
[14] Sun H P, Xu H Z, Zhou J C, et al. 2005b. Latest observation results from superconducting gravimeter at station Wuhan and investigation of the ocean tide models[J]. Chinese Journal of Geophysics (in Chinese), 48(2): 299-307, doi: 10.3321/j.issn:0001-5733.2005.02.010.
[15] Van Camp M, Vauterin P. 2005. Tsoft: Graphical and interactive software for the analysis of time series and Earth tides[J]. Computers & Geosciences, 31(5): 631-640.
[16] Wei J, Li H, Liu Z W, et al. 2012. Observation of superconducting gravimeter at Jiufeng seismic station[J]. Chinese Journal of Geophysics (in Chinese), 55(6): 1894-1902, doi: 10.6038/j.issn.0001-5733.2012.06.010.
[17] Xu J Q, Zhou J C, Chen X D, et al. 2014. Long-term observations of gravity tides from a superconducting gravimeter at Wuhan[J]. Chinese Journal of Geophysics (in Chinese), 57(10): 3091-3102, doi: 10.6038/cjg20141001.
[18] Xu W M, Chen S, Gao M T, et al. 2012. The preliminary analysis to the temporal variation characteristics of non-tidal changes of gravity in mainland China[J]. Progress in Geophysics (in Chinese), 27(3): 861-871, doi: 10.6038/j.issn.1004-2903.2012.03.005.
[19] Zhang J. 2014. Research on ocean tide loading problem in GPS precision surveying (in Chinese)[Ph. D. thesis]. Wuhan: Wuhan University, 40-51.
[20] Zhou J C. 2008. Loading problem in earth's tides and satellite gravity field recovery and its applications (in Chinese)[Ph. D. thesis]. Wuhan : Institute of Geodesy and Geophysics, Chinese Academy of Science, 39-43.
[21] Zhou J C, Hwang C, Sun H P, et al. 2013. Precise determination of ocean tide loading gravity effect for absolute gravity stations in coastal area of China: Effects of land-sea boundary and station coordinate[J]. Journal of Geodynamics, 68: 29-36.
[22] Zhou J C, Sun H P. 2005. Influence of the modified global ocean tide model with local tides of East and South China Season load gravity in China and its neighbor area[J]. Acta Seismologica Sinica (in Chinese), 27(3): 332-338.
[23] Zhou J C, Sun H P. 2007. Effect of ocean tide on recovery of satellite gravity field[J]. Chinese Journal of Geophysics (in Chinese), 50(1): 115-121, doi: 10.3321/j.issn:0001-5733.2007.01.016.
[24] 李大炜, 李建成, 金涛勇,等. 2012. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学, 32(4): 106-110.
[25] 孙和平, Ducarme B, 许厚泽,等. 2005a. 基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J]. 中国科学 D辑: 地球科学, 35(7): 649-657.
[26] 孙和平, 许厚泽, 周江存,等. 2005b. 武汉超导重力仪观测最新结果和海潮模型研究[J]. 地球物理学报, 48(2): 299-307, doi: 10.3321/j.issn:0001-5733.2005.02.010.
[27] 孙和平, 许厚泽, 陈武,等. 2006. 香港地区重力固体潮和海潮负荷特征研究[J]. 地球物理学报, 49(3): 724-734, doi: 10.3321/j.issn:0001-5733.2006.03.016.
[28] 韦进, 李辉, 刘子维,等. 2012. 武汉九峰地震台超导重力仪观测分析研究[J]. 地球物理学报, 55(6): 1894-1902, doi: 10.6038/j.issn.0001-5733.2012.06.010.
[29] 徐建桥, 周江存, 陈晓东,等. 2014. 武汉台重力潮汐长期观测结果[J]. 地球物理学报, 57(10): 3091-3102, doi: 10.6038/cjg20141001.
[30] 徐伟民, 陈石, 高孟潭,等. 2012. 中国大陆重力场非潮汐时空变化特征的初步分析[J]. 地球物理学进展, 27(3): 861-871, doi: 10.6038/j.issn.1004-2903.2012.03.005.
[31] 张杰. 2014. GPS精密测量中的海潮负荷问题研究[博士论文]. 武汉: 武汉大学, 40-51.
[32] 周江存. 2008. 固体潮和卫星重力场恢复中的负荷问题及其应用研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所, 39-43.
[33] 周江存, 孙和平. 2005. 用东海和南海潮汐资料修正全球海潮模型对中国及邻区重力场负荷计算的影响[J]. 地震学报, 27(3): 332-338.
[34] 周江存, 孙和平. 2007. 海潮对卫星重力场恢复的影响[J]. 地球物理学报, 50(1): 115-121, doi: 10.3321/j.issn:0001-5733.2007.01.016.