2. 中国石油大学(北京)博士后流动站, 北京 102249
2. China University of Petroleum (Beijing) Post-doctoral Research Station, Beijing 102249, China
地震方法在油气勘探中占有非常重要的地位,而地下介质的地震波场响应是地震方法的基础.实际应用中的许多情况下,地下介质可以近似为弹性介质,数值方法是弹性介质中波场模拟的有效方法.Kelly 等人(1976)最先使用有限差分法在标准网格上进行弹性波模拟,Virieux(1984)随后提出了交错网格有限差分法,还有许多其它种类的有限差分法也得到了发展(Tessmer,1995;Fornberg,1998;董良国等,2000;殷文等,2006;刘洪林等,2010).除了有限差分法,有限元法,比如有限体积法(Dormy and Tarantola, 1995)、混合有限元(Cohen and Fauqueux, 2000)、谱元法(Patera,1984)等也可以用来模拟弹性介质中的波传播.
实际应用中必须根据介质参数的特点选择合适的数值模拟方法,使地震波模拟精度和计算效率满足要求.有很多工作对现有各种方法的波场模拟精度进行了研究(Kummer et al., 1987;Muir et al., 1992;Zahradník et al., 1993;Moczo et al., 2002;曹军等,2004;皮红梅等,2009); Podgornova和Lisitsa(2010)给出了使用交错网格有限差分法的计算参数优化方法,提高地震波模拟的精度;Moczo等人(2011)通过数值模拟结果与解析解的对比,研究了有限差分法、有限元法以及谱元法在具有不同泊松比的均匀介质中波场模拟的精度;何彦峰等人(2013)对比研究了边界元法与有限差分法在复杂介质中的地震波传播.
当前油气勘探对象日益复杂,许多油田地下介质复杂,大多高度非均匀,介质参数相对变化剧烈,在界面两侧具有强反差.当介质参数变化剧烈,比如裂缝,孔隙等,传统的交错网格有限差分法可能产生不稳定的现象.Saenger等人(2000)提出了旋转交错网格有限差分法,这种方法不需要对界面附近的弹性模量进行平均处理,避免了稳定性问题的出现,能够模拟复杂介质中的地震波传播.另一方面,Käser和Dumbser(2006)提出了任意高阶间断有限元法,将间断有限元法和任意高阶时间积分法相结合,可以模拟参数变化剧烈的复杂介质中的地震波传播,并且能够得到任意高阶时间精度和空间精度的数值解.
本文对旋转交错网格有限差分法与任意高阶间断有限元法在非均匀弹性介质中的地震波模拟精度与计算效率进行了研究,为参数变化剧烈的复杂介质中波场数值模拟方法的选择提供依据.本文首先介绍了旋转交错网格有限差分法与任意高阶间断有限元法的基本原理;然后模拟了水平层状介质中的地震波传播,改变界面两侧介质参数的相对变化量,同时也改变有限差分法的矩形网格大小以及有限元法使用的多项式基函数的阶数,分析了不同方法计算结果的振幅精度及相位精度;接着模拟了具有倾斜界面介质中的波传播,改变界面的倾角,分析了界面倾角及网格剖分大小对波场模拟精度的影响;最后对全文进行了讨论和总结. 1 方法原理 1.1 旋转交错网格有限差分法
本文使用旋转交错网格有限差分法求解2维(x,z)平面中的位移—应力弹性波动方程组(x为水平方向,z为垂直方向),该方程组可以表示如下(Saenger et al., 2000):


使用旋转交错网格有限差分法求解上述方程组时,弹性介质参数在网格中的位置分布如图 1所示.网格剖分时,网格垂直和水平方向的空间距离都为h,2维(x,z)平面被离散为若干个网格点(xI=Ih,zL=Lh),I和L为整数;时间步长Δt由有限差分格式的稳定性条件控制.在时间和空间进行离散化后,有限差分法在每个网格点上计算的x和z方向上的质点位移数值解分别为ux(xI,zL,tm)=ux(Ih,Lh,mΔt),uz(xI,zL,tm)=uz(Ih,Lh,mΔt),m为整数,将ux(xI,zL,tm)和uz(xI,zL,tm)分别记为Umx(I,L)和Umz(I,L).同样,σxx(x, t),σzz(x, t)和σxz(x, t)离散化后分别记为Smxx(I,L)、Smzz(I,L)和Smxz(I,L).
 | 图 1 物理量在旋转交错网格上的分布.应力分量定义在实心方框所在整数网格点,位移分量定义在实心圆所在非整数网格点上Fig. 1 The distribution of modeling parameters within the Rotated staggered grid(RSG). The stresses are placed at the filled rectangles,the displacements are placed at the filled circles |
本文使用(2)式中的2阶中心差分算子计算(1)式中的2阶时间求导项,用(3)式中的4阶差分算子计算(1)式中的空间求导项.
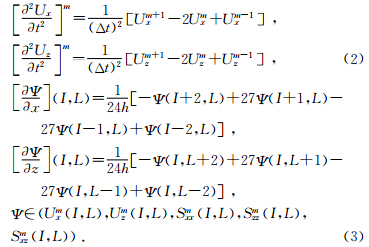
除了使用有限差分法求解弹性波动方程来实现地震波场模拟外,另一种常用方法便是有限元法.2006年,Käser和Dumbser提出了弹性介质中的任意高阶间断有限元地震波数值模拟方法,该方法将间断有限元法和任意高阶时间积分法相结合,能够得到空间和时间上任意高阶精度的解.任意高阶间断有限元法将计算区域Ω∈R2剖分成不规则的三角形单元T(m),(m)是三角形单元的编号.方程组的数值解u(m)h在三角形单元内表示为以时间为变量的函数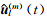 和以空间坐标为变量的多项式基函数Φl(x)的线形组合:
和以空间坐标为变量的多项式基函数Φl(x)的线形组合:
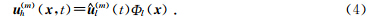
对于2维η—ξ平面,2阶正交多项式基函数为:
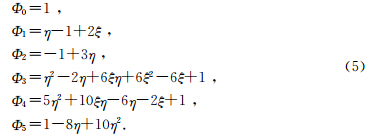
多项式基函数Φl(x)的阶数决定了任意高阶间断有限元法的计算精度,阶数越高,有限元法的精度也越高. 2 数值实例与分析
本节将模拟两种介质模型中的波传播,对旋转交错网格有限差分法和任意高阶间断有限元法的波场模拟精度及计算效率进行研究.第一个模型为水平层状介质模型,第二个模型为具有倾斜界面的两层介质模型. 2.1 水平层状介质模型
如图 2所示,水平层状介质模型有两层介质,模型大小为[0,1000 m]×[0,500 m].第一层介质厚度为400 m,波速度为VP1=3000 m·s-1,波速度为VS1=1700 m·s-1,密度为ρ1=2000 kg·m-3.第二层介质波速度为VP2=1500 m·s-1,波速度为VS2=850 m·s-1,密度为ρ2=1000 kg·m-3.两种介质参数(波速、密度)的相对变化量为Δ=(VP1-VP2)/VP1=(VS1-VS2)/VS1=(ρ1-ρ2)/ρ1=50%,界面两侧参数变化剧烈,可以认为是强反差.震源是一个胀缩源,只产生P波,其位置为 x s=(200 m,200 m).震源子波为Ricker子波:
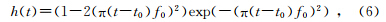
 | 图 2 水平界面介质模型示意图Fig. 2 Diagram of the two-layer model |
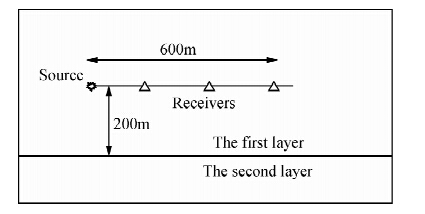
旋转交错网格有限差分使用2种不同的网格间距h(水平与垂直网格间距相同)进行计算,分别是h=2 m,=1 m,对应的总的网格点数分别为501×251,1001×501.对于主频率为30 Hz的S波,h=2 m时单位波长内包含14个网格点,h=1 m时单位波长内包含28个网格点.根据稳定性条件,时间步长分别为Δt=0.0002 s,Δt=0.0001 s.图 3a为h=2 m时有限差分法模拟的地震记录(位移垂直方向分量uz)及其对应的解析解(Berg et al., 1994).
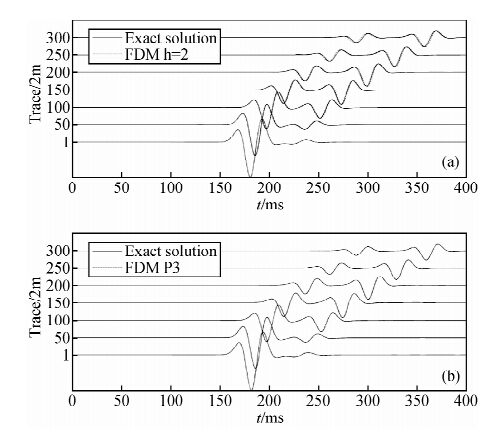 | 图 3 有限差分法(a)和有限元法(b)数值模拟地震记录(位移垂直分量)与解析解对比图Fig. 3 The seismograms of vertical displacement component.(a)the results of the FDM. (b)the results of the P3 FE scheme |
任意高阶间断有限元法进行波场模拟时,基函数为3阶多项式(P3).模型区域使用非规则三角形单元进行剖分,在两个介质间界面上剖分有100个三角形单元的边,第一层介质的左边界和右边界上分别有20个三角形单元的边,第二层介质的左边界和右边界上分别有10个三角形单元的边,模型的底边界上有100个三角形单元的边,顶边界上有50个三角形单元的边(图 4).网格剖分生成了7564个三角形单元,对于主频为30 Hz的S波,单位波长内至少含有3个三角形单元.根据稳定性条件,有限元法时间步长取为0.0001 s.任意高阶间断有限元法求解的是一阶速度—应力波动方程组,数值计算的结果为质点速度的垂直和水平分量,为了与有限差分法进行比较,本文将有限元法数值解在时间域进行积分,得到质点位移.由于有限元法的时间步长为0.0001 s,时间积分引入的误差可以忽略不计.
 | 图 4 有限元法三角形单元剖分结果Fig. 4 The meshes generated for layered model |
本文还使用基函数为2阶多项式(P2)的任意高阶间断有限元法进行了波场模拟.此外,我们还改变了界面两侧介质参数(速度、密度)之间的相对变化量Δ,第一层介质的参数保持不变,第二层介质的参数取值如表 1所示,然后分别使用两种不同网格间距的旋转交错网格有限差分法(FDM h=2 m和FDM h=1 m),以及使用两种不同多项式基函数的任意高阶间断有限元法(FEM P2和FEM P3)模拟了Δ不同取值时的地震波场.本文使用一种基于时频表示的误差计算方法(Kristeková et al., 2006),以解析解作为参考值,计算出数值模拟地震记录每一道的振幅误差和相位误差(图 5).
|
|
表 1 水平界面模型中第二层介质的参数Table 1 The material property of the second layer with different ratio to the first layer |
 |
图 5 介质参数不同取值时有限差分法和有限元法计算的每一道地震记录与解析解之间的误差 (a)Δ=30%时的振幅误差;(b)Δ=30%时的相位误差;(c)Δ=40%时的振幅误差;(d)Δ=40%时的相位误差;(e)Δ=50%时的振幅误差;(f)Δ=50%时的相位误差.Fig. 5 The single-valued envelop misfit and phase misfit of each trace for FD schemes and FE schemes (a)The envelope misfit when Δ=30%,(b)The phase misfit when Δ=30%,(c)The envelope misfit when Δ=40%, (d)The phase misfit when Δ=40%,(e)The envelope misfit when Δ=50%,(f)The phase misfit when Δ=50%. |
图 5给出了Δ不同取值时4种数值计算结果与解析解的振幅误差和相位误差.图 5a、c、e为振幅误差,网格间距h对旋转交错网格有限差分法计算结果的振幅误差影响较大,增加单位波长内的网格点数,可以显著减小振幅误差.对于任意高阶间断有限元法,多项式基函数从2阶变为3阶,其计算结果的振幅误差变化很小.此外,Δ的变化对于上述4种计算结果的振幅误差影响都很小.由于有限元法使用多项式基函数来近似三角形单元内的波场值,当检波器位置靠近三角形单元边时,数值解的误差可能会增大(Käser et al., 2008),因此有限元法的误差曲线不如有限差分法的误差曲线平滑.
图 5b、d、f为相位误差,对于旋转交错网格有限差分法,增加单位波长内的网格点数对其相位精度的改善有限;偏移距增加时,使用3阶多项式基函数的任意高阶间断有限元法计算结果的相位误差没有随之增加,优于另外3种结果.当Δ变化时,旋转交错网格有限差分法计算结果的相位误差变化不大,而使用2阶多项式基函数的任意高阶间断有限元法计算结果的相位精度则有明显变化,强反差情况下(Δ=40%及Δ=50%),需要使用3阶多项式基函数才能得到较高的相位精度.
表 2为不同方法计算一个时间步长所需的计算时间.本文所用方法都使用C语言进行编程,运行在同一台电脑上(CPU为2.7 GHz,内存为4 GB).相比有限差分法,任意高阶间断有限元法的计算量更大,所需的计算时间更长.
|
|
表 2 不同方法计算一个时间步长所需的计算时间Table 2 The CPU time of the four numerical schemes to calculate one time step. |
本节将模拟具有倾斜界面的两层介质中的地震波,研究界面倾角对旋转交错网格有限差分法和任意高阶间断有限元法计算精度的影响.含倾斜界面的两层介质模型如图 6所示,模型大小为[0,1000 m]×[0,1500 m].第一层介质中波速度为3000 m·s-1,波速度为1700 m·s-1,密度为2000 kg·m-3.第二层介质中波速度为1500 m·s-1,波速度为850 m·s-1,密度为1000 kg·m-3.界面的倾角为40°.震源是一个胀缩源,位置为xs=(200 m,200 m),与倾斜界面垂直方向的距离为1000 m.震源子波为Ricker子波,时间延迟为0.05 s,主频为30 Hz.数值模拟总时长为1 s.检波器放置在震源右边,与震源同深,水平距离为8 m.
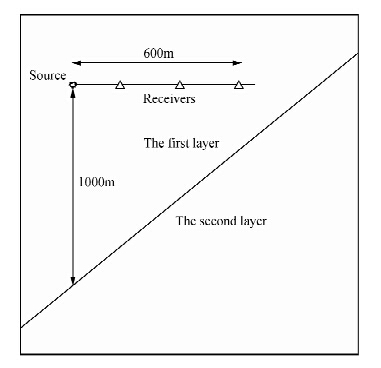 | 图 6 倾斜界面模型示意图Fig. 6 Diagram of the model with dipping interface |
对于倾斜界面目前没有时间—空间域的波场解析解,本文首先使用不同网格间距的旋转交错网格有限差分法进行波场模拟,3种不同的网格间距分别是h=4 m,h=2 m,h=1 m,对应的网格点数分别为251×376,501×751,1001×1501.时间步长分别为=0.0002 s,=0.0001 s,=0.00005 s,对于主频为30 Hz的S波,h=4 m时单位波长内包含7个网格点.利用这三个数值模拟结果,使用Richardson外推法构造出精度更高的数值解,并以此作为参考值,计算旋转交错网格有限差分法和任意高阶间断有限元法模拟结果的振幅误差和相位误差.
对于倾斜界面模型,任意高阶间断有限元法选取基函数为2阶多项式,计算区域使用两种不同大小的三角形单元进行剖分.第一种三角形单元剖分中,倾斜界面上剖分有130个三角形单元的边,第一层介质的左边界上有70个三角形单元的边,右边界有27个三角形单元的边,第二层介质的左边界上有14个三角形单元的边,右边界有98个三角形单元的边,模型的底边界有100个三角形单元的边,顶边界有50个三角形单元的边.网格剖分总共产生了24396个三角形单元,频率为30 Hz的S波在单位波长内至少含有3个三角形单元,该剖分记为H=10 m(倾斜界面上的三角形单元边长的近似值),相应的时间步长为0.0001 s.第二种三角形单元剖分记为H=5 m,将第一种三角形网格加密一倍,倾斜界面上有260个三角形单元的边,频率为30 Hz的S波在单位波长内含有6个三角形单元.
本节计算了4种波场模拟结果与参考值的振幅误差和相位误差,4种方法分别是=4 m,=2 m的有限差分法,H=10 m,H=5 m的有限元法.本节还将模型中界面的倾角变为20°,保持震源和倾斜界面的垂直距离不变,同样计算了上述4种数值模拟结果的振幅误差和相位误差.
图 7给出了不同倾角时4种数值计算结果与参考值的 振幅误差和相位误差.单位波长内含有7个网格点(h=4 m)的旋转交错网格有限差分法模拟结果的振幅误差和相位误差远远大于其它3种计算结果,且受倾角变化影响大;单位波长内含有14个网格点的旋转交错网格有限差分法模拟结果的振幅误差和相位误差则不受界面倾角变化的影响.此外,对于倾斜界面,增加三角形单元网格剖分密度不能提高任意高阶间断有限元法的振幅精度和相位精度.
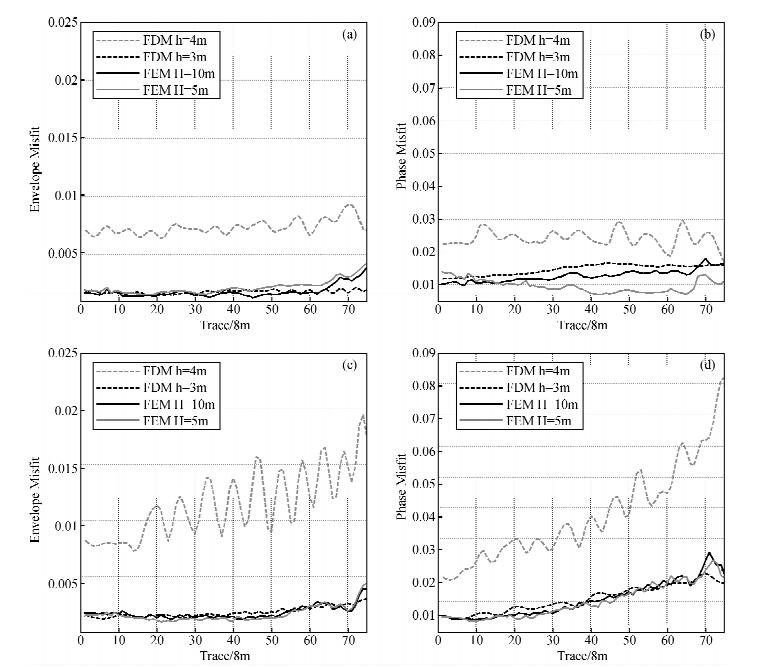 |
图 7 4种数值模拟地震记录与参考值之间的振幅误差和相位误差 (a)倾角为20°时的振幅误差;(b)倾角为20°时的相位误差;(c)倾角为40°时的振幅误差;(d)倾角为40°时的相位误差.Fig. 7 The single-valued envelop misfit and phase misfit of each trace for the 4 numerical results (a)The envelope misfit when dip angle is 20°;(b)The phase misfit when dip angle is 20°; (c)The envelope misfit when dip angle is 40°;(d)The phase misfit when dip angle is 40°. |
对于倾斜界面,旋转交错网格有限差分法必须使用较密的网格来达到高的振幅精度和相位精度;此时,当倾角在一定范围内变化时计算结果的误差不会改变.需要注意此处计算误差时使用的参考值并不是真值,计算结果的误差相接近,并不表示这几种结果都以同样的精度接近真值. 3 结 论
本文使用旋转交错网格有限差分法和任意高阶间断有限元法模拟了水平及具有倾斜界面的两层介质中的地震波场,初步研究了界面两侧介质参数相对变化量及界面倾角对这两种方法波场模拟的振幅精度和相位精度的影响,对比了两种方法使用不同参数时的计算效率,可以为实际应用中选取合适的数值模拟方法及参数提供一定的依据.
对于水平界面,界面两侧介质参数相对变化量的改变对旋转交错网格有限差分法的振幅精度和相位精度没有影响;介质参数的变化对任意高阶间断有限元法的振幅精度也没有影响,但使用2阶多项式基函数的任意高阶间断有限元法的相位精度则有较大变化,在介质参数存在强反差情况下,任意高阶间断有限元法需要使用高阶多项式基函数.对于倾斜界面,旋转交错网格有限差分法需要使用较密的网格来达到高的振幅精度和相位精度,界面倾角的变化对旋转交错网格有限差分法和任意高阶间断有限元法的精度影响都很小.
致 谢 感谢国家科技重大专项(2011ZX05023-005)的资助.| [1] | Berg P, If F, Nielsen P, et al. 1994. Analytical reference solutions: Advanced seismic Modeling[A]. Helbig K, ed. Modeling the Earth for Oil Exploration[M]. Pergamon Press, 421-427. |
| [2] | Cohen G, Fauqueux S. 2000. Mixed finite elements with mass-lumping for the transient wave equation[J]. Journal of Computational Acoustics, 8(1): 171-188. |
| [3] | Cao J, Gai Z X, Zhang J, et al. 2004. A comparative study on seismic wave methods for multi-layered media with irregular interfaces Part 1: irregular topography problem[J]. Chinese J. Geophys. (in Chinese), 47(3): 495-503. |
| [4] | Dormy E, Tarantola A. 1995. Numerical simulation of elastic wave propagation using a finite volume method[J]. Journal of Geophysical Research, 100(B2): 2123-2133. |
| [5] | Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation [J]. Chinese J. Geophys.(in Chinese), 43(3): 411-419. |
| [6] | Fornberg B. 1998.A practical guide to pseudospectral methods[M]: Cambridge: Cambridge University Press. |
| [7] | He Y F, Sun W J, Fu L Y. 2013. Comparison of boundary element method and finite-difference method for simulating seismic wave propagation in complex media[J]. Progress in Geophys. (in Chinese), 28(2): 664-678, doi: 10.6038/pg20130215. |
| [8] | Köser M, Dumbser M. 2006. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes-I. The two-dimensional isotropic case with external source terms[J]. Geophysical Journal International, 166(2): 855-877. |
| [9] | Köser M, Hermann M,de la Puente J. 2008. Quantitative accuracy analysis of the discontinuous Galerkin method for seismic wave propagation[J]. Geophys. J.Int., 173(3): 990-999 |
| [10] | Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms; a finite-difference approach[J]. Geophysics, 41(1): 2-27. |
| [11] | Kristeková M, Kristek J, Moczo P, et al. 2006. Misfit criteria for quantitative comparison of seismograms[J]. Bulletin of the Seismological Society of America, 96(5): 1836-1850. |
| [12] | Kummer B, Behle A, Dorau F. 1987. Hybrid modeling of elastic-wave propagation in two-dimensional laterally inhomogenous media[J]. Geophysics, 52(6): 765-771. |
| [13] | Liu H L, Chen K Y, Yang W. et al. 2010. Numerical modelling of P- and S-wave field separation with high-order staggered-grid finite-difference scheme[J]. Progress in Geophys. (in Chinese), 25(3): 877-884, doi: 10.3969/j.issn.1004-2903.2010.03.021. |
| [14] | Muir F, Dellinger J, Etgen J, et al. 1992. Modeling elastic fields across irregular boundaries[J]. Geophysics, 57(9): 1189. |
| [15] | Moczo P, Kristek J, Vavry čuk V, et al. 2002. 3D heterogeneous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities[J]. Bulletin of the Seismological Society of America, 92(8): 3042-3066. |
| [16] | Moczo P, Kristek J, Galis M, et al. 2011. 3-D finite-difference, finite-element, discontinuous-Galerkin and spectral-element schemes analysed for their accuracy with respect to P-wave to S-wave speed ratio[J]. Geophysical Journal International, 187(3): 1645-1667. |
| [17] | Patera A T. 1984. A spectral element method for fluid dynamics: laminar flow in a channel expansion[J]. Journal of Computational Physics, 54 (3): 468-488. |
| [18] | Pi H M, Jiang X Y, Liu C, et al. 2009. Three methods of wave equation forward modeling and comparision[J]. Progress in Geophys. (in Chinese), 24(2): 391-397, doi: 10.3969/j.issn.1004-2903.2009.02.004. |
| [19] | Podgornova O, Lisitsa V. 2010. Accuracy analysis of finite-difference staggered-grid numerical schemes for elastic-elastic and fluid-elastic interfaces[C].//80th Annual Meeting, Society of Exploration Geophysicists. Expanded Abstracts, 3087-3091 |
| [20] | Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 31(1): 77-92. |
| [21] | Tessmer E. 1995. 3-D seismic modelling of general material anisotropy in the presence of the free surface by a Chebyshev spectral method[J]. Geophysical Journal International, 121(2): 557-575. |
| [22] | Virieux J. 1984. SH-wave propagation in heterogeneous media; velocity-stress finite-difference method[J]. Geophysics, 49(11): 1933-1942. |
| [23] | Yin W, Yin X Y, Wu G C, et al. 2006. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation[J]. Chinese J. Geophys. (in Chinese), 49(2): 561-568, doi: 10.3321/j.issn:0001-5733.2006.02.032. |
| [24] | Zahradník J, Moczo P, Hron F. 1993. Testing four elastic finite-difference schemes for behavior at discontinuities[J]. Bulletin of the Seismological Society of America, 83(1): 107-129. |
| [25] | 曹军, 盖增喜, 张坚,等. 2004. 用于不规则界面多层介质的地震波方法比较研究: 不规则地形问题[J]. 地球物理学报, 47(3): 495-503. |
| [26] | 董良国, 马在田, 曹景忠,等. 2000. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 43(3): 411-419. |
| [27] | 何彦峰, 孙伟家, 符力耘. 2013. 复杂介质地震波传播模拟中边界元法与有限差分法的比较研究[J]. 地球物理学进展, 28(2): 664-678, doi: 10.6038/pg20130215. |
| [28] | 刘洪林, 陈可洋, 杨微,等. 2010. 高阶交错网格有限差分法纵横波波场分离数值模拟[J]. 地球物理学进展, 25(3): 877-884, doi: 10.3969/j.issn.1004-2903.2010.03.021. |
| [29] | 皮红梅, 蒋先艺, 刘财,等. 2009. 波动方程数值模拟的三种方法及对比[J]. 地球物理学进展, 24(2): 391-397, doi: 10.3969/j.issn.1004-2903.2009.02.004. |
| [30] | 殷文, 印兴耀, 吴国忱,等. 2006. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 49(2): 561-568, doi: 10.3321/j.issn:0001-5733.2006.02.032. |
 2015, Vol. 30
2015, Vol. 30

