2. 中国石油集团科学技术研究院, 北京 100083
2. Geophysical Department, Research Institute of Petroleum Exploration and Development, PetroChina 100083, China
复杂介质中地震波传播导致的衰减和耗散问题,一直以来吸引着科学和工程领域工作者的广泛关注.在以弹性波传播为主要手段的勘探方法中,波的频散和衰减现象十分普遍.其中,衰减指波的振幅在传播过程中呈现出的减弱效应,频散则指波速随频率发生改变的现象,两者常用于地震数据分析中储层性质的判断.
在过去几十年里,地震勘探方面涌现了大量关于岩石物理性质的研究(Aki,1980; Berryman, 1980a,b,c; Plona,1980a; Bourbié et al., 1987; Mavko and Jizba, 1991; Dvorkin and Nur, 1993; Mavko and Jizba, 1994; Mavko and Nolen-Hoeksema, 1994; Geerits and Kelder, 1997; Carcione,2001; Carcione and Seriani, 2001; Smith et al., 2003; Carcione et al., 2004; Pride et al., 2004; Santos et al., 2004; 王明秀,2009),特别是孔隙介质流体流动引起波的非弹性衰减和频散过程,发展出了许多理论模型(Gassmann,1951; Biot, 1956b,a; Biot and Willis, 1957; Biot, 1962a,b; White,1975; White et al., 1975; Dutta and Ode, 1979; Bourbié et al., 1987; Mavko and Jizba, 1991; Dvorkin and Nur, 1993; Berryman and Wang, 2001; Johnson,2001; Pride et al., 2004; Ba et al., 2011; 巴晶等,2013)和实验方法(Domenico,1976; Gregory,1976; Murphy,1984; Winkler,1985; Jones,1986; Tarif and Bourbie, 1987; Wang and Nur, 1988; Cadoret et al., 1998; Batzle et al., 2006).地震波传播一直是研究饱和流体孔隙岩石性质的关键,研究者可以通过地震波的传播时间、反射振幅和相变量等,得到地下储层岩石及孔隙流体的性质.
流体饱和孔隙介质中弹性波传播的较早研究出现在20世纪40年代(Frenkel,1944; Beranek,1947; Kosten,1950),其后Gassmann(Gassmann,1951)提出了流体替换理论,引入了孔隙度的概念. Gassmann方程的出现为含流体孔隙介质的波速及弹性模量(固体和流体)反演提供了理论基础.Wyllie等于1956年提出了“时间平均关系”(Wyllie et al., 1956),假设多相孔隙介质可以用一系列不同尺寸的固体与流体交错层等效代替,根据声波的传播时间来计算波速.Wyllie公式具有相对简单、应用方便的优点,但是仍然无法深入揭示岩石物理属性和孔隙流体等因素对储层声学性质的影响.1972年,Goodman和Cowin发展了干骨架(即只包含空气的孔隙岩)中波传播的连续介质理论(Goodman and Cowin, 1972).人们普遍认为波的衰减和耗散是由孔隙空间中流体流动引起的,故研究重心应放在包含流体的孔隙介质上.当压缩波传播时,固、流相之间产生压力梯度,从而引起流体和固体间的相对运动,这种相对运动产生内部摩擦,直至达到压力平衡状态.根据流动产生的压力梯度特征长度尺寸,可以将其分为三类:宏观流动,微观流动和介观流动.
宏观流动又称为全局流动,在孔隙介质单元体远小于弹性波波长的前提下,近似认为流体“均匀”分布在岩石内部,即孔隙介质为宏观均匀的,在固体骨架和孔隙流体的任意接触面上,由波传播导致的流体流动损耗都是一致的.Biot(Biot, 1956a,b,1962a,b)在这方面做了开拓性的工作,建立了完全饱和孔隙介质中波传播的动力学方程,并且与Willis推导出了方程中的弹性参数(Biot and Willis, 1957).在Biot理论中,固体颗粒和孔隙流体间的流体动力学相互作用一般可以分为惯性作用和粘性作用,这两种相互作用引起全局流动,这种流动导致的速度衰减和频散称为全局流体流动效应.均匀介质中典型的Biot全局流动是由波场波峰和波谷之间的压力梯度产生的,它导致了固体骨架和孔隙流体之间的相互运动,从而产生能量损耗过程.Biot理论预测了两类纵波和一类横波,Plona于1980年在实验室观测到了孔隙介质中传播的慢纵波(Plona,1980a),根据Santos(Santos et al., 1990a,b)的理论,完成了部分饱和孔隙介质中两类慢波的模拟过程.这些工作对进一步研究Biot孔隙介质理论及其应用产生了极大的推动作用.近50年来,Biot理论不断得到发展,在各类流体饱和孔隙介质中得到应用,例如非固结的沉积岩(Tarif and Bourbie, 1987; Yamamoto et al., 1994)、高渗透率的沉积岩(Géli et al., 1987)等.但是,人们发现只有在探测频率超过100 kHz时,一般岩石中全局流动引起的衰减才比较明显(Carcione et al., 2010).
为此,研究者们提出基于局部流动的模型来突破Biot理论的局限性.Mavko和Nur(Mavko and Nur, 1975; Mavko et al., 1979; Mavko and Nur, 1979),Budiansky和O’Connell(Budiansky and Oconnell, 1976),O’Connell和Budianasky(O'connell and Budiansky, 1977)提出微观尺度的流体流动机制,以期解释裂缝中产生的比孔隙流体大得多的流体压力,此类微观流动被称为“喷射流”(Mavko and Nur, 1975).喷射流机制的一大特点在于它受到单个孔隙结构(如孔洞的纵横比等)的影响,故它并不适用于实际复杂孔隙介质的数据分析,无法替代宏观流动方法.某种程度上,我们可以将喷射流看为与Biot理论对等的另一种声学能量损耗机制.Bourbie 等(Bourbié et al., 1987)通过比较孔隙介质中不同损耗机制与实验观测数据验证了这一点,同时提出不论是喷射流模型还是宏观模型,都无法单独完全解释复杂孔隙介质中的损耗机制,而应该将二者结合起来.基于这个理念,产生了结合Biot理论和喷射流机制的动力学理论,即BISQ理论(Dvorkin and Nur, 1993).但BISQ理论中的计算构造需要微观参数(喷射流特征长度等),大大降低了这种理论的实用性(Gurevich and Lopatnikov, 1995).
当压缩波通过多相孔隙介质时,在介观尺度上(即孔隙介质中的非均匀性特征尺度要大于孔隙尺寸,但是远小于波长尺寸)会产生局部流体流动,从而引起弹性波能量衰减和速度频散.介观机制导致的流体流动现象大量出现在沉积岩中,能够解释许多重要现象,从而引起了研究者的关注(Pride et al., 2004).White及其合作者(White,1975; White et al., 1975)建立了第一个介观尺度非均匀孔隙岩石的流体流动模型,该模型是一种内部包含气泡的部分水饱和孔隙模型,也被称为斑块饱和模型.压缩波通过部分饱和孔隙介质时,引起内部气泡和外层水相之间的压力差,从而产生流体流动,导致波的衰减和频散.White模型建立了介观非均匀孔隙岩石中P波和固体孔隙介质间的物理平衡过程(Rubino et al., 2009),成为介观流体流动中最典型的模型之一.
此后学者们运用各种方法来研究和模拟此类模型.Dutta和Ode(Dutta and Ode, 1979a; Dutta and Ode, 1979b)从Biot的场方程出发重新推导了White模型,他们的工作验证了White模型对于介观流体流动的有效性,同时做出了进一步修正,使之可以较好应用于模拟内气-外液饱和流体孔隙介质中的衰减和频散现象.1994年Gist用与饱和度相关的体积模量替代White模型中的干骨架体积模量,将流体饱和度与原始White模型结合起来.孙卫涛等改进了White模型(Sun et al., 2014),将其应用到内部包含非气体(内油外水)饱和的情况,并得到了与实验数据吻合很好的速度预测.Johnson(Johnson,2001)建立了任意几何形状斑块的分析模型,通过不同极限情况下体积模量的分支函数,模拟与介观尺度相关的中间频段体积模量.Pride和Berryman(Pride and Berryman, 2003a,b)发展了两种不同孔隙岩石复合体的斑块饱和模型,巴晶等(Ba et al., 2011)进一步将此机制发展到包含不同流相和固相物质的部分饱和孔隙介质模型.
在本文下面的章节中,首先介绍孔隙介质波动理论中的宏观和微观模型:Gassmann模型,宏观的Biot模型,微观的喷射流模型以及BISQ模型.然后基于斑块饱和模型,阐述了介观尺度衰减和频散模型:White模型,Dutta模型,Johnson模型,Biot-Rayleigh(BR)模型理论框架.之后,通过模型分析和数值算例探讨了这几类模型的适用性.最后,通过几类主要模型流动机制的探讨,指出模型假设条件与实际问题之间存在的差异,并讨论了需要解决的问题和未来研究方向. 1 孔隙介质波动理论的“宏观模型” 1.1 流体替换方法-Gassmann方程
随着地震波数据在油藏监测技术中的应用,如何根据此类数据准确分析地下流体的分布及流动,已经成为一个引起广泛关注的问题.在测井和地震资料的岩石物理分析中,一个重要的问题就是,如何根据一种流体饱和的岩石地震波速度,预测出另一种流体饱和的岩石地震波速,这等同为建立地震波速在岩石干骨架和流体饱和岩石之间的关系,也被称为流体替换问题.流体替换方法的目的在于模拟地震特征数据(地震波速度)和给定储层条件(如压力、温度、孔隙度、矿物类型等)的储层特性(如孔隙度、体积模量等)之间的关系.对一种饱和流体替换另一种饱和流体的建模,首先需要建立初始饱和流体模型,然后再考虑替换为新的流体模型.
流体替换公式为流体变换的建模和定量分析提供了理论模型.各向同性介质模型的地震波速可以通过岩石体积模量和剪切模量计算.描述弹性介质力学特征的主要参数包括:平面波模量M,体积模量K,杨氏模量E,泊松比σ,拉梅系数λ和μ.在各向同性介质中,可以根据这六个弹性参数中任意两个求出其他四个的值(Gassmann,1951).因此,流体替换对波速的影响可以用体积模量之间的关系表示,其中用得最广泛的是Gassmann方程(Wyllie,1956; Stoll et al., 1973; Berryman and Milton, 1991; Batzle and Wang, 1992; Berryman,1999; Berryman and Wang, 2001; Mavko et al., 2003; Smith et al., 2003).
1 951年,Gassmann通过分析饱和流体孔隙介质在外力作用下的应变过程,推导出流体替换效应模型的方程(Gassmann,1951).Gassmann方程通过矿物颗粒体积模量、干骨架体积模量、孔隙流体体积模量以及孔隙度来估计流体饱和单元体的体积模量Ksat(Smith et al., 2003):

 为通过体积比例定义的孔隙度,Vf和V是孔隙流体和混合介质的体积.
为通过体积比例定义的孔隙度,Vf和V是孔隙流体和混合介质的体积.
当骨架中有多种矿物颗粒时,通过Voigt-Reuss-Hill平均法(VRH)(Mavko et al., 2003),可以求解与KE及Ksat相关的固体颗粒体积模量Ks.VRH平均法由Reuss平均(几何平均)和Voigt平均(算术平均)组合而成,算法与矿物组分的体积模量Ksi、体积比Fi(i=1,…,n)相关,其中n为混合固体颗粒的种类数(Mavko et al., 2003):
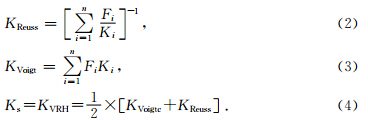
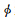 求取(Gassmann, 1951):
求取(Gassmann, 1951):
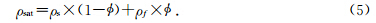
对于包含多相流体的储层岩石,需要单独计算每种流体的体积模量和密度,然后求取混合流体的值.流体替换理论中,假设所有孔隙空间是连通的,而且孔隙流体压力一直处于平衡状态,流体在孔隙空间中处于均匀分布状态,故可以通过Reuss平均方法将混合流体的体积模量表示为(Smith et al., 2003):


其后,Brown和Korringa(Brown and Korringa, 1975)更进一步将Gassmann方程扩展到各向异性岩石,即孔隙流体的体积模量和密度可以用每种流体(如盐水、油、空气)的均值表示.根据上面的公式,可以由固体颗粒体积模量和密度、流体体积模量和密度、干骨架的体积模量以及孔隙度求取纵横波速度.同时,可以根据弹性波传播速度大小(波速大小Vp,Vs和密度ρ)估算出给定储层的体积模量Ksat和剪切模量μ(Gassmann,1951):
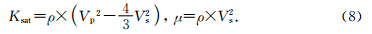
由上述模型分析可知,根据已知饱和流体岩石的地震波和岩石物理数据,能够预测给定储层包含某种流体时的纵横波速度.首先,从初始的波速数据出发,确定流体饱和孔隙岩的体积模量和剪切模量;然后,考虑岩石排出流体情况,计算孔隙骨架的体积模量、剪切模量以及密度;在确定孔隙骨架物理性质后,考虑岩石充满另一种孔隙流体,计算新的有效体积模量和密度;最后,求出特定饱和流体岩石的纵横波速度.这就是流体替换模型的计算过程.
根据公式(1)的替换过程,也可以用代数方法消去公式中的干岩石体积模量,用初始流体的体积模量Kf1、替换后的流体体积模量Kf2和初始饱和岩石体积模量Ksat1来直接表示替换后的岩石体积模量Ksat2(Mavko et al., 2003):

Gassmann方程有两个重要假设条件:(1)矿物模量相同;(2)孔隙空间具有统计各向同性.这就要求波长要远大于岩石的颗粒和孔隙尺寸,在多数岩石样本和实验频率条件下,Gassmann的模型假设是合理的.但Gassmann方程中不考虑孔隙的几何特征,这一点为微观尺度上研究孔隙介质带来困难.
根据流体是否与外界存在相互作用,Gassmann理论将流体饱和孔隙体系分为封闭和开放两种.在处理实际流体饱和孔隙介质时,将体系的边界看为封闭的,即没有流体流入或流出.此时,孔隙介质表面由波传播引起的应力变化不会影响到选取的孔隙介质单元体,这也间接要求选定的样本单元要远离岩石表面.这是Gassmann方程中计算孔隙流体对混合体系影响的重要假设.如果将系统看为开放的,即流体在受到应力作用时,可以自由流入流出,则不会出现应变效应,将无法体现流体体积模量的影响,此时孔隙流体变化的影响只与流体密度相关.
在验证流体替换理论的预测结果时,发现干燥岩石样本(如真空炉处理过的样品)干骨架体积模量实际测量值比Gassmann方程的预测值高(Mavko et al., 2003),需要在其中加入几个百分点的流体,这表明流体替换理论中的干岩石模量实际是指稍潮湿的岩石模量.流体替换理论假设孔隙流体与岩石骨架之间无任何物理化学作用,该假设条件也会带来预测误差.实际上,孔隙流体与岩石固体骨架之间不可避免的相互作用将会改变骨架表面应力.例如,松散的岩石颗粒中混入重油,骨架的体积模量和剪切模量会增加;而层状砂岩充满水时,则会因为粘土膨胀而弱化.这些都说明Gassmann方程中的干骨架等同于包含一定量流体的岩石骨架.同时,干骨架也不同于气体饱和的岩石.干骨架模量反映的是孔隙内压力不变的情况下,外部压力增加所导致的体积形变量,相当于孔隙流体体积模量为零的情况,近似于标准温度和压强下空气填充样品的情况.但在一般的油藏条件下(高孔隙压力),岩石孔隙内部气体会具有不可忽略的体积模量,此时不可把岩石骨架作为干骨架处理.
Gassmann方程处理的是各向同性单矿物介质的体积和剪切模量问题,其中假设剪切模量不依赖于孔隙流体.Gassmann理论中的孔隙介质是一类特殊的弹性材料,在应力变化足够小时,可近似看为完全弹性介质,即当低频弹性波的能量损耗以及介质状态改变量都不明显时,可将其看为理想的完全弹性介质,并建立对应本构关系式.同时,Gassmann方程中假设孔隙流体压力在单元体内不随空间变化.该假设不仅需要所有孔隙空间都是内部连通的(如果有孤立的孔隙,则将其看为固体的一部分,这点在Biot理论中也是一样的),而且只有在频率足够低情况下,孔隙压力在空间中达到平衡时才成立(即孔隙流体有充足的时间流动,并且没有波动诱发产生的孔隙压力梯度).这一低频限制说明 了为什么Gassmann公式最适用于低频地震资料(<100 Hz)的解释,当频率增加到声波测井(≈104 Hz)和实验室超声波测量(≈106 Hz)频率时,流体替换理论效果略差.
如何确定Gassmann方程的低频范围是一个关键问题.理想无裂缝饱和流体孔隙岩中存在三种特征频率:散射频率、粘弹性频率、Biot特征频率.这三种频率与波的衰减和频散紧密相关.为了保证Gassmann模型的适用性,选取的频率一般要小于上面三种频率的最小值.三者中最小的往往是Biot频率,一般情况下,当实验频率小于Biot频率时,就可以保证流体压力在波峰和波谷之间有足够的时间达到平衡.
如果孔隙介质中包含了裂缝,裂缝和邻近孔洞间的流体则需要时间去达到压力平衡状态.根据裂缝中流体的流动范围,孔隙流体运动可以分为全局流动(Biot流动)、喷射流(矿物颗粒大小的尺寸)和介观流动(裂缝或非均匀掺杂体尺寸要远大于孔隙尺寸,但小于波长).此时,裂缝的存在将引出与这个流动相关的额外特征频率.介观尺度特征频率的特点在于,其流体耗散长度与裂缝的特征长度相当(依赖于特殊的几何形状,可以为裂缝空间、裂缝直径或其他特征长度),即裂缝的几何特征会影响耗散效应.理论和实验研究表明(Pride et al., 2004;Batzle et al., 2006),特征频率依赖于固体渗透率、流体粘性和裂纹的特征尺寸.
总的来说,Gassmann方程具备预测低频情况下流体饱和孔隙介质中的弹性波波速的能力,被广泛用于估计油气藏中的地震波波速(Carmichael,1989; Wang,2001).然而,一般来讲,地震波传播的真实情况往往与Gassmann理论中的准静态假设不符,从而引起Gassmann方程预测结果出现偏差,需要考虑发展更为完善的宏观尺度孔隙介质波动理论. 2 孔隙介质弹性力学方法Biot 理论
Gassmann方程给出了低频极限下流体饱和孔隙介质中弹性波速度的估计方法.但在一般岩石中,地震波传播往往会违背其平衡态假设,造成Gassmann预测结果出现偏差.另外,波的衰减和相速度频散无法直接通过Gassmann方程模拟,需要引入宏观弹性力学理论.
基于弹性动力学机制,Biot方程(Biot, 1956a,b; Bourbié et al., 1987; Allard,1993; Carcione et al., 2007)给出了模拟饱和流体孔隙介质中弹性波传播的一般理论框架.Biot模型中对骨架和孔隙流体做了单相和双相耦合两种情况的研究,流体借助粘滞力和惯性力作用随着固体一起运动,由于孔隙流体相对于骨架运动引起模能量损耗,波衰减和相速度频散与介质内部的全局宏观流体流动相关,称之为“Biot耗散”.Biot能量衰减一般出现在孔隙流体压力远大于压缩波引起的空间压力梯度情况下,因此,该理论模型中假设弹性波波长要远大于样品单元的特征尺寸和孔隙尺寸.根据Biot特征频率fc的定义,这个假设对于大部分岩石都是适用的.同时,Biot理论假设孔隙岩石骨架是均匀和各向同性的,其各向同性体现在所有流体通道横截面上的流体、固体比例一致,即孔隙度不变;均匀性体现在骨架体积模量、旋转模量、密度和渗透率不变,且由同一类型的颗粒组成.同时,孔隙岩石中是单一流体,且不与固体骨架发生反应.此外,Biot理论还假设流固间的相对移动由Darcy定律控制,忽略流体流动过程中产生的热效应.
Biot模型通过孔隙介质体积微元的平均位移选定广义坐标,同时引入只依赖于固、流相对位移的耗散函数,根据Lagrangian方法推导出运动方程.利用带耗散项的运动方程,Biot模型给出沉积岩中声波速度和衰减因子关于频率、沉积颗粒弹性性质、孔隙流体、孔隙度、平均颗粒尺寸、渗透率和有效应力的依赖关系.
当频率足够低,即低于Biot特征角频率 1 956年发表的高频Biot理论通过引入复修正算子F,将原始Biot方程推广到全频段范围,这是对低频理论的一个推广(Biot,1956b).但通过比较分析发现(Ba,2013),对于一般实际岩石工程中的地震波或声波频段来说,Biot理论中关于泊肃叶(Poiseuille)流动失效的超高频段模型并不适用,在后续研究中,通常只采用Biot低频理论的工作.
对于饱和流体孔隙介质,Biot理论给出了六个常系数线性偏微分方程.根据假设条件中单元体的均匀和各向同性性质,可以先只考虑坐标轴x上方程的解(Biot, 1956a,b; Dvorkin and Nur, 1993; Toms et al., 2006; Xu,2009).均匀介质中的平面波传播,振幅可以表示为A(x,t)=A0ei(kx-ωt),其中ω为角频率,k为波数.通过将波数定义为复数k≡kr+iki,引入衰减表达,逆品质因子表示为(Johnson,2001)Q-1=αVp/ω=ki/kr.波数k为线性代数方程组的特征值,特征方程为k2的二次函数,故存在两对复根.相应的,在孔隙介质中存在两类压缩波,其速度大小为Vp±=ω/kr±,衰减因子(逆品质因子)为Q±-1=ki±/kr±,其中用“+”和“-”分别表示快P波(第一类压缩波)、慢P波(第二类压缩波).相应的旋转波方程有一个根,对应了唯一的旋转波(Biot, 1956a,b; Berryman and Holland ,1980; Dvorkin and Nur, 1993; Toms et al., 2006; Xu,2009).
Biot理论中预测的快纵波和慢纵波,只在固体和流体质点为同相(即孔隙骨架和孔隙流体同时压缩的情况)或异相移动(即一相为压缩另一相为膨胀的情况)时出现.其中快波是弹性固体中一般压缩波的直接模拟,其衰减和相速度频散都很小.慢波在低频区间的衰减十分明显,类似于扩散和热传导效应,但在高频传播则近似无损耗,这种从粘弹性区域到惯性区域的过渡一般通过Johnson等人(Johnson et al., 1987)提出的动力学渗透率来模拟.
Berryman(Berryman,1998)研究了快P波和旋转波在低频范围的波速和衰减情况.Plona(Plona,1980b)等人在水饱和的烧结玻璃构成的孔隙介质中观测到了慢P波,从实验上定性的证实了Biot理论中第二类压缩波的存在性.Berryman(Berryman,1980a)将Plona(Plona,1980b)观测到的结果与Biot理论中的预测结果进行了比较,证明了Biot理论的正确性.Kelder和Smeulders(Kelder and Smeulders, 1997)则第一个在超声波频率的水饱和砂岩中观测到慢P波的存在.
与Gassmann方程一样,Biot理论仍然无法完全解释干燥孔隙岩石充满流体时骨架模量的变化现象.Biot理论中的孔隙骨架在充满流体时会弱化(可能由于粘土矿物的存在),从而导致其弹性模量小于干燥的孔隙岩.例如,当砂岩具有少量的湿度时,Pandit和King(Pandit and King, 1979),Goertz和Knight(Goertz and Knight, 1998)都观测到P波和S波波速的急剧下降.Goertz和Knight(Goertz and Knight, 1998)将速度的急剧下降归于干燥岩表面自由能的下降和相关表面粘附力的下降,该解释违背了Biot理论中流体和固体相互不反应的假设.故Mavko和Mukerji(Mavko and Mukerji, 1998)认为,Biot理论中预测流体饱和孔隙介质的波速时,要用包含一定湿度的岩石样品波速替代干燥孔隙岩的波速.
Biot(Biot, 1941,1956a,b,1962b)提出的准静态动力学弹性理论为大量实际工作提供了理论基础,如增压腔的应力扩散(Rice,Cleary,1976)、饱和沉积岩的声传播性质(Stoll et al., 1973)、各向异性孔隙介质的研究(Brown and Korringa, 1975; Wu and Chiang, 1990; Thompson and Willis, 1991; Parra,1997; Carcione,2001; Sharma,2004; 聂建新等,2010).Burridge和Keller(Burridge and Keller, 1981)基于固体的线性弹性方程和流体的线性化Navier-Stokes方程,将Biot理论扩展到饱含压缩性粘性流体的孔隙弹性介质中,其中当流体的粘性很小时,推广的方程会退化成Biot理论中的模式.刘洋和魏修成(刘洋和魏修成,2003)基于Biot双相各向异性介质理论和动态问题的哈密顿原理,推导出任意双相各向异性介质中弹性波传播的有限元方程,且对其弹性波传播特征进行模拟和分析,魏修成等(魏修成等,2008)基于Biot理论进一步考虑各向异性的孔隙介质.
Biot理论作为一种描述弹性波衰减和损耗的机制被广泛应用,该理论在预测慢P波的存在性方面十分有效(Plona,1980b; Nagy et al., 1990; Kelder and Smeulders, 1997),也可用于复杂介质中的地震波数值模拟(孟庆生等,2003; 裴正林和牟永光,2004; 李信富等,2007; 刘洋和魏修成,2008; 李国平等,2011).但同时也发现无法完全解释地震波衰减和频散观测数据,特别是在低频范围内的数据(Johnston et al., 1979; Gist,1994; Winkler,1985; Jones,1986; Buckingham,2000).对于多数地表岩石,当岩石的渗透率较小时(如固结良好的砂岩),速度频散和能量衰减主要由微观的流动产生.而Biot理论基础是孔隙流体和固相骨架的全局相对运动,得到的速度预测结果产生误差,此时需要引进基于微观模型的孔隙介质波动理论.
3 孔隙介质波动理论的“微观模型” 3.1 微观尺度下的喷射流模型 基于宏观流动的Biot模型中,孔隙流体在波的传播方向上流动,研究对象是孔隙介质中固体、流体微元的平均运动,忽略了微观流动场和孔隙尺寸的影响.Mavko等人(Mavko and Nur, 1975)研究了十字状的单个岩石裂缝中的流体运动,提出了微观喷射流模型.该模型假设在波导致的孔隙压力下,岩石水平裂缝中的流体会喷射到垂直的裂缝中.此时,流体流动的时间和特征长度都将远小于Biot理论中的全局流动,这虽然是一个十分快速的过程,但也会导致孔隙介质中出现额外的能量耗散(Mavko and Nur, 1975).
1 979年,Mavko和Nur(Mavko and Nur, 1979)等人通过分析在垂直入射的纵波挤压下,扁平裂缝模型中流体和孔隙壁面上力的相互作用,研究了弹性波传播的衰减和频散的微观过程,得到的衰减预测值远高于Biot理论中流体完全饱和情况.Mavko等人(Mavko et al., 1979)建立了包含气体和液体两相的孔隙介质衰减机制,在波传播导致的孔隙体积压缩下,包含在液体中的气体会发生一定程度的自由流动.而早在1974年,Domenico(Domenico,1974),Kuster和Toksoz(Kuster and Toksoz, 1974a,b),Elliott和Wiley(Elliott and Wiley, 1975)就发现了岩石骨架中充满液体和部分气体时,得到的压缩波速度相差很大.这些表明了波衰减不仅与孔隙流体的粘性等有关,也与气体、流体的实际体积比(即孔隙介质的饱和度)相关.Mavko等人(Mavko et al., 1979)通过实验数据比较了几种混合介质中波衰减随液体饱和度的变化情况,他们的工作表明,当孔隙岩石包含非常扁长的孔隙(微观裂缝)时,即使含量很小的水也会大大增加压缩波的能量损耗,这也解释了流体非饱和岩石中波的强衰减现象.
Mavko等人(Mavko et al., 1979)提出的喷射流模型考虑了单个微观裂缝(孔隙纵横比αc小于0.1)的流体流动和能量损耗.同时,根据Walsh(Walsh,1965)关于硬币状和二维狭缝状微观裂缝中应力、应变的比较,可以将模型中的扁长孔隙放到二维空间处理(如图 1所示).
上图中地震波垂直挤压孔壁,内部流体在壁面压力的作用下沿着x轴喷出,Mavko等人(Mavko et al., 1979)发现,流体产生的压力梯度而非压力本身是决定能量损耗的重要因素.如图 1,如果假设扁平裂缝的壁面近似平行,即其高度随坐标x的变化不明显,则孔隙界面发生小振荡时(即裂缝受压产生的应变很小),流体流动的控制方程为(Mavko et al., 1979)
对于同样构造的流体饱和孔隙介质,Walsh(Walsh,1969)认为相应流体流动的表达式为
Winkler(Winkler, 1985,1986)通过实验发现,超声波频率下的地震波速度要远高于根据Gassmann或Biot理论得到的预测值,他认为其中存在与频率、流体粘性成正比,与有效应力成反比的“non-Biot”耗散.根据上面研究的喷射流模型(O'connell and Budiansk, 1974,1977; Mavko et al., 1979)与相关的实验(Murphy et al.,1984; Wang and Nur, 1988)可知,“non-Biot”耗散与矿物颗粒尺度上的微观流动场有关.针对此类问题,Mavko和Jizba(Mavko and Jizba, 1991)仿照Gassmann方程,通过结合Biot理论建立了关于喷射流的孔隙介质模型.
当孔隙介质中存在波传播时,由于孔隙尺寸、饱和度、孔隙朝向等变化引起的非均匀性会产生孔隙压力梯度,从而出现Murphy(Murphy,1979)提到的单个孔隙中的局部流体流动.这样的局部流动在大量孔隙上的平均值为零,因此被传统的Biot理论(Biot, 1956b,a)所忽略.但局部非均衡应力往往也会影响岩石的体积和剪切模量.特别在高频情况下,由于流体的粘性效应,孔隙中会产生非松弛应力,需要利用流体硬化后的湿骨架模量(也称为非松弛骨架模量),得到新的介质压缩性质.同时,Mavko等人(Mavko and Jizba, 1991)推导出了非松弛与松弛情况下体积模量与剪切模量之间的关系式.
将Biot模型宏观流体流动的影响包括进来,就可以计算高频饱和岩石中的波速.对于多数地表岩石,喷射流频散要相当于或大于Biot频散,因此需要使用非松弛模量替代原始Biot理论中的干骨架模量.Mavko和Jizba(Mavko and Jizba, 1991,1994),Wulff和Burkhardt(Wulff and Burkhardt, 1997)通过实验验证了微观喷射流模型的测量结果.
微观喷射流模型预测了超高频流体饱和岩石模量,在低频极限情况下,狭缝中的应力为松弛的,此时模量可以根据流体替换理论进行估计.但Mavko和Jizba(Mavko and Jizba, 1991)并没有考虑中间频段裂缝应力为低松弛的情况.
根据等效介质的思想,Dvorkin,Mavko和Nur(Dvorkin et al., 1995)引入了计算全频段的模量、波速度和衰减的模型,建立了低频本构方程(Gassmann方程)和高频估计(如Kuster和Toksoz(Kuster and Toksoz, 1974a);O’connel和Budiansky(O'Connel and Budiansky, 1977);Mavko和Jizba(Mavko and Jizba, 1991)之间的联系.他们处理的是自然储层中常见的流体近似全饱和的孔隙介质(即孔隙中压缩性大的气体含量非常少),其中假设喷射流过程中单一孔隙流体仍从扁平的软孔隙中喷入周围的大孔洞.同时,根据经验观测可知,高压力下速度衰减很小,这与Biot理论的预测相符(Mavko and Jizba, 1991),故应将低压力下出现的速度衰减归于高压情况下封闭的软孔隙.据此,将孔隙介质中的孔隙空间分为软孔隙so和固化孔隙st(Mavko and Jizba, 1991; Dvorkin et al., 1995).
为了求取压缩波、剪切波速度和衰减随频率的变化函数,需要流体饱和孔隙介质的有效体积模量Kr、剪切模量μm与频率ω之间的关系式,Dvorkin 等(Dvorkin et al., 1995; Dvorkin,2008),杨顶辉和陈小宏(杨顶辉和陈小宏,2001),Mavko和Jizba(Mavko and Jizba, 1991)给出了相关计算公式.Song等(Song et al., 2013)通过将整个孔隙空间分为固化孔隙和微观裂缝来解释低松弛情况下全频段的衰减、频散现象,建立了低松弛应力下,全频段的“湿骨架体积模量”表达式(Song et al., 2013):
喷射流机制描述的物理过程,在空间、频率上与传统Biot理论处于不同的尺度,处理的是微观裂缝中高频波与流体流动效应的关系,在一定程度上解释了观测结果中强衰减现象.但Bourbie等(Bourbié et al., 1987)通过对不同损耗机制和实验数据的比较发现,喷射流机制只能部分解释观测到的速度衰减和频散现象.一般情况下,无法把复杂的孔隙介质看为一个纯粹的局部或全局流动模型,因此Biot理论和喷射流理论均无法独立解释整个流动的损耗机制.以此为契机,发展出了宏观Biot理论与微观喷射流理论相结合的BISQ理论(Mavko and Nur, 1975; Mavko and Jizba, 1991; Dvorkin and Nur, 1993; Dvorkin et al., 1995; King,2009).
3.2 BISQ模型 含流体孔隙介质力学研究中,宏观尺度的Biot理论和微观尺度的喷射流模型是固、流相互作用的两种重要力学机制,但是往往分别使用这两种理论处理问题,例如Biot理论用于处理宏观岩石骨架,喷射流动模型用于处理孔隙构造问题.在实际应用中,由于两者相互耦合且同时影响波速度衰减和频散,分开处理的方法有很大局限性.Dvorkin和Nur(Dvorkin and Nur, 1993)将喷射流机制融入Biot理论,提出了统一的Biot-Squirt(BISQ)模型.BISQ模型将Biot理论和喷射流机制结合起来,在弹性波速度频散/衰减与固体弹性常数、孔隙度、渗透率、饱和度、流体粘滞度、压缩波频率以及新引入的微观参数—特征喷射流动等之间建立了关系式.
基于Biot理论和喷射流理论的BISQ模型假设岩石骨架为均匀各向同性,同时也引入Biot理论中的质量耦合密度ρa来描述固、流体之间相互作用产生的耦合效应.如图 2所示,为了将两种流体流动机制结合起来,选取平行于波传播方向的圆柱体作为样品单元,孔隙流体在波传播方向的自由流动体现了Biot全局流动效应;孔隙流体在垂直于波传播的方向上自由流动并产生喷射流.此外,假设在圆柱边界处的流体压力不随时间变化,孔隙流体在波的激发作用下能够从细小裂缝中喷出并进入临近较大孔隙中.
BISQ模型首先处理固、流体在波传播方向上运动出现的单轴形变过程,通过引入Biot(Biot, 1941,1956b,a),Rice和Cleary(Rice and Cleary, 1976)动力学弹性关系式,得到双相固、流介质中的运动方程为(Biot, 1956b,a; Dvorkin and Nur, 1993):
上式描绘了图 2中孔隙流体在波传播方向(即沿圆柱体轴向)上流动的动力学关系式,在BISQ模型中,垂直于波传播方向上(圆柱体横截面的径向)会同时发生横向的喷射流动,此时需要在流体形变表达中加入横向(径向)流体流动项(Biot, 1956b,a; Dvorkin and Nur, 1993):
Dvorkin等在1993年引入系数Fsq(Dvorkin and Nur, 1993):
当频率ω→∞时,λ→∞,Fsq→F,此时BISQ理论会退化为Biot理论,这表明了BISQ模型和Biot模型的高频极限一致.而当ω→0,Fsq→0时,Biot理论与Gassmann方程一致,故大部分学者认为Gassmann理论即岩石地震波速度的零频极限的最佳估计值.由于BISQ的零频极限速度要低于Biot理论的值,因此Dvorkin等人(Dvorkin and Nur, 1993; Dvorkin et al.,1994)认为BISQ模型适用于处理流体部分饱和的孔隙介质.但流体替换理论中仅考虑了宏观Biot理论的零频极限,而忽略了局部流动的影响,因此流体替换理论并不完全等同于实际岩石的零频极限.实际上,由于松弛效应的影响,低频段岩石的纵波速度往往低于Gassmann方程的估测值.
Dvorkin等人基于实验观测(Dvorkin et al.,1994),通过引入饱和度S考虑非饱和岩石中的BISQ理论,从而得到部分饱和情况下基于BISQ模型的压缩波相速度和衰减.建立了特征喷射流动长度R与S之间的关系(Dvorkin et al.,1994):
BISQ模型建立了多孔弹性介质动力学变化与其固体弹性参数、孔隙度、渗透率、特征喷射流动长度等参数之间的联系,而不去考虑单个孔隙的几何结构,使其既能像Biot理论一样在宏观上描述孔隙结构弹性性质,又能像喷射流动那样解释预测弹性波速度的强衰减和频散现象.
目前讨论的传统Biot-Gassmann等理论考虑的双相介质中往往都仅包含一种流体,或借助Gassmann方程中的等效介质理论来处理混合流体的问题.但对于一般的含气、水两相流体的孔隙岩石,由于流体之间不相溶,一类流体会以斑块状嵌入另一类流体,即斑块饱和(patchy-saturation),下面将详细介绍此类模型.
4 孔隙介质波动理论的“介观模型”
4.1 等效球体斑块饱和方法 前面章节中讨论了宏观流动理论(Biot理论)和微观喷射流理论,由于介观尺度流动机制可以定性说明许多重要现象,因而引起众多学者的注意(White,1975; White et al., 1975; Dutta and Ode, 1979; Dutta and Seriff, 1979; Murphy,1984; Gist,1994; Cadoret et al., 1998; Carcione,2001; Johnson,2001; Pride et al., 2004; Toms et al., 2006; Carcione et al., 2007; 王秀明,2009; 赵海波等,2010; Ba et al., 2011; 邓继新等,2012; Sun et al., 2014; 吴国忱等,2014).
Biot理论(Biot, 1956b,a,1962a,b)对于波速衰减和频散的理论预测值与实验数据之间存在差异(Johnston et al., 1979; Winkler,1985; Gist,1994; Toms et al., 2006),对这些差异的深入思考引发了介观尺度部分饱和流体孔隙介质的研究.弹性波在包含一种流体的均匀孔隙介质中传播时,波引起的流体内部压力差很小,局部流动不明显,可以忽略不计.但处理实际饱和流体孔隙岩石时(如碳酸盐岩),其中往往包含气、水混合流体,且互不相溶.此时,由于介质可压性不同,压缩波下气泡受到的孔隙压力要大于水相部分,从而出现由流体流动引发的明显能量损耗过程,这一能量损耗机制在地震波频段十分明显.
在Biot理论框架内,White(White,1975)首次引入介观尺度的耗散机制.假设孔隙岩石骨架均一,通过内部嵌入球状气泡、外部为水的单位体周期分布模型来模拟孔隙介质中流体非均匀性(如图 3),后来的研究者也多用这种方法处理介观尺度的流体非均匀性.White给出部分饱和孔隙介质中波衰减/频散关于频率、渗透率、孔隙度和流体性质等参数的函数,这也被称为首个“斑块饱和”模型.
包含介观尺度流体非均匀性的孔隙介质模型如图 3所示,整个模型由同时含气和水的部分饱和单元立方体(边长b′)构成,每个单元体中的球状气泡(半径a)都位于立方体中心,同时为了简化计算,将最初立方体-球体模型等体积转化为同心球体模型(外球半径b)(如图 3).在不考虑单元体之间相互作用情况下,White模型研究了包含单个气泡单元的体积模量平均值.但是,从图 3也可以看出,由于模型几何特征的限制,中心球状气泡半径最大只能达到b′,这就决定了原始White球状斑块模型中含气饱和度只能达到π/6的临界值.后来学者在研究White模型时考虑过含气饱和度超过此临界值的情况(巴晶,2013),但严格来说此模型已不再适用,此时White模型会高估局部流体流动对地震波传播的影响.
White模型假设斑块尺寸要远小于波长,此时可以将作用于介质上的应力近似看为均匀的.如图 3所示,当压缩波通过介质时,特征单元外表面受到一致应力,从而引发流体流动.在考虑流体内部流动的情况下,混合介质体积模量可以通过压力P*和体积改变量D*之间的关系得到(White,1975):
White等人(White,1975; White et al., 1975)首次从理论上对部分饱和流体引起的强衰减和频散现象进行研究,同一时期,Domennico(Domenico,1976)和Gregory(Gregory,1976)等人也通过实验证明当孔隙介质中为部分饱和流体时,其波速会不同于完全饱和的孔隙介质.其后,Murphy(Murphy, 1982,1984),Cadoret等(Cadoret et al., 1998)通过实验验证了White理论对于部分饱和流体孔隙介质的速度衰减和频散预测结果.Gist(Gist,1994)利用排水实验来得到一定的饱和度,再利用White模型处理超声波速;同时,将White模型中的干骨架体积模量表示为饱和度的函数,在此基础上得到考虑了局部流动的波速,该波速要高于White的理论预测(Gist,1994; Helle et al., 2003).
Dutta等学者(Dutta and Ode, 1979)根据Biot理论中的弹性耦合方程求解White模型时发现,推导阻抗Z使用的等效体积模量KE为流体、固体矿物颗粒和干骨架弹性系数的函数.在考虑岩石的体积膨胀和流体变化时,White只考虑了沿波传播方向的值,忽略了同心球体径向的体积变化,故采用了平面波模量M来计算KE.但在实际模型中,作用于同心球体外边界的径向应力会产生径向形变,导致径向流体和固体材料的位移,固体应变将不止发生在单一的平面波传播方向,因此Dutta等认为应该用体积模量K来替代平面波模量M.经过Dutta修正后的White模型(记为White-Dutta模型)广泛应用于部分饱和孔隙介质数值模拟.
在White模型及White-Dutta模型的数值计算中,同心球体内部仍然仅考虑为气体的情况,内部气体与外壳中的另一种流体互不相溶.White模型认为内部气体与外部流体相比影响很小,因此,在导出的泊松比公式中舍去了与内部气体相关的参数Q1,R1,Z1.在一般实际情况下,必须考虑内部流体的影响.我们从流体动力学本身出发,推导了包含内部流体影响的流、固复合介质泊松比、密度和体积模量公式(Sun et al., 2014),得到推广后的White-G模型.该公式能够适用于内部非气体饱和的情况,也能够退化为传统的White模型.
Johnson(Johnson,2001)根据准静态的Biot理论,针对包含两种不同流体的孔隙介质,提出了动态体积模量模型.Johnson模型与White模型不同,没有建立固定的几何模型来分析内部受外力影响情况,而是根据低频时体积模量Biot-Gassmann-Woods(BGW)极限值与高频时体积模量Biot-Gassmann-Hill(BGH)极限值来构建函数,用于描述中间频率段的体积模量:
Johnson模型中得到的体积模量与Biot理论的模型参数以及饱和度有关,但与斑块的几何特征无关,当饱和度确定时,斑块模型本身的形状特征对频散和衰减无影响.因此,我们无法根据Johnson预测的结果来对斑块形状做出分析,如判断其是否为球体等.同时,Johnson模型在理论推导中并没有忽略内部气体参数,该模型可直接用于预测内部非气体的岩石样本.Johnson通过引入新的几何参数(斑块面积-体积比),将White模型推广到处理任意尺寸的斑块.类似的,其后Pride和Berryman(Pride and Berryman, 2003a)提出处理双重孔隙、双重渗透率介质的部分饱和孔隙介质模型,将White模型进行了进一步推广.Pride等(Pride et al., 2004)对双重孔隙模型进行进一步修正,得到高低频极限值与Johnson预测值相一致的结果.随后巴晶等学者(Ba et al., 2011)进一步提出了双孔隙双流体的斑块饱和模型.
4.2 局部流动的双重孔隙方法 Johnson模型适用于处理不相溶流体非均匀分布导致的频散问题,并舍去了对于斑块几何尺寸的限制条件.但是,孔隙介质介观尺度的非均匀性不仅体现在流体上,孔隙结构的非均匀性也会导致波的频散和衰减.以往理论模型一般将岩石看为包含裂缝的均匀孔隙介质,对于同时包含多种岩性物质的实际介质来说,这往往并不是一个合适的假设条件.许多学者开始致力于研究多重孔隙介质模型(Berryman and Wang, 2000; Pride and Berryman, 2003a,b; Pride et al., 2004; Toms et al., 2006; Carcione et al., 2010; Müller et al., 2010; Ba et al., 2011; 巴晶等,2012).
地层岩石中几乎包含各种尺寸和形状的孔隙结构,由两种孔隙尺寸组成的复合孔隙介质是一种重要的简化模型.针对这种情况,出现了双重孔隙、双重渗透率模型(Pride et al., 2004).该模型假设双相介质整体仍为各向同性的,孔隙介质由相同的流体-固体非均匀性单元体组成.Berryman和Milton(Berryman and Milton, 1991)基于静力学理论将传统流体替换方法中的单孔介质推广到双重孔隙介质.双重孔隙模型的核心在于模拟不同孔隙弹性介质之间由于流体受力不同而导致的流动效应,假设两相之间的流体流动正比于波导致的应力差,且其比例系数依赖于频率(Pride and Berryman, 2003a,b): 根据Biot的弹性理论(Biot,1962a),宏观各向同性双重孔隙渗透率介质的控制方程表示为(Pride et al., 2004):
此后,巴晶等(Ba et al.,2011)提出了Biot-Rayleigh双孔隙度模型,该模型适用于两种不相溶流体饱和的单一孔隙固体介质或者单流体饱和的双重孔隙介质.在模型中分别给出双孔介质的势能、动能和耗散函数,然后利用拉格朗日方程导出波动方程(Ba et al.,2011):
方程组中包含10个固体位移ui、流体位移U(m)i和局部流动变量ζ,(i=1,2,3,m=1,2),还包含6个刚度系数(A,N,Qm,Rm),5个密度系数(ρ00,ρ0m,ρmm),3个几何系数( 通过对波动方程平面波分析,可以导出频率ω和波数k之间的函数关系式,进而得到相速度大小Vp,衰减系数α和品质因子Q的表达式(Ba et al.,2011):
Biot-Rayleigh模型可用于计算流体或岩性非均匀孔隙介质的衰减和频散问题,其中孔隙系统的动能是通过Rayleigh(Rayleigh,1917)提出的液体内部球形空腔塌缩模型得到的.但是,该模型仅仅计算了空腔外部的液体动能,如果空腔内部是一种不可忽略的液体(如油或者水),则通过Rayleigh模型计算的系统动能将产生较大偏差,由此带来的速度误差将十分显著.此外,Biot-Rayleigh模型忽略了斑块外边界的影响,当斑块内部流体饱和度较高,即内、外球体半径之比较大时,外部边界将不满足封闭条件假设,此时外边界会出现能量损耗,Biot-Rayleigh模型将会高估P波速度.
为了进一步了解P波衰减和频散模型之间的差异,我们给出了一个算例对比.该算例以 2001年Johnson(Johnson,2001)给出的斑块模型计算参数为基础,使用改进的White模型(White-G)、Jonhson模型和Biot-Rayleigh(BR)模型对P波衰减和频散进行了计算,斑块为内部气体-外部油饱和,孔隙度为10%,气体的饱和度为0.1,斑块半径为0.01 m.图 4给出White,Johnson和BR模型的速度预测结果.
这里White-G、Johnson、BR分别代表改进的White模型(White,1975; Sun et al., 2014),Johnson模型(Johnson,2001),Biot-Rayleigh模型(Ba et al., 2011),BGW和BGH分别代表低频和高频速度极限.
从图中可以发现,改进White模型和Johnson模型的预测结果基本一致.BR模型衰减曲线出现了两个峰值,其中较高峰值表示局部流动引起的衰减,较低峰值是Biot全局流动引起的衰减,体现出了宏观Biot耗散效应(波长尺寸的流体应力平衡效应),而White和Johnson模型衰减曲线中观察不到Biot衰减峰值.同时,与White和Johnson模型的频散曲线相比较,BR模型预测速度较高,这也与前面对模型的理论分析结果一致.
5 目前的问题及未来研究方向 本文详细介绍了孔隙介质波动理论中的宏观Gassmann模型、Biot模型和微观喷射流模型,然后基于斑块饱和模型,介绍了介观尺度上几类非均匀模型:White模型、Dutta模型、Johnson模型,以及固相非均匀的双重孔隙模型.相关研究对现有理论模型作了深入探讨,通过数值计算和实验数据对比,结果显示(Sun et al., 2014): (2)未修正的White模型(White,1975)在高频下与上述其他模型接近,在低频下速度过高,差别很大.
(3)在多数情况下,Biot-Rayleigh模型的速度预测较Dutta、Johnson模型速度高一些.在频散分析中,Biot-Rayleigh发生速度转变的频率范围稍低于其他两个模型;在相同频率下,Biot-Rayleigh速度稍大.在速度-饱和度分析中,在中高含水饱和度时,Biot-Rayleigh模型速度预测比其他两个模型稍高一些.
(4)在接近真实斑块尺寸时,Biot-Rayleigh模型的预测速度更接近实验数据.
在中低频(地震频段)情况下,Biot-Rayleigh模型预测速度略高于Dutta和Johnson模型,该现象与斑块边界的能量损耗被忽略有关,且与斑块尺寸密切相关.在高频下,Dutta、Johnson,Biot-Rayleigh模型的频散曲线基本是一致的,但是Biot-Rayleigh模型在高频极限下衰减曲线的渐近线较陡,斜率达到-1/ω.该现象与Biot-Rayleigh模型同时考虑了Biot衰减和局部流动衰减机理有关.对于介观尺度的频散效应,Johnson模型效果更稳定;对于P波衰减效应,Biot-Rayleigh模型能够反映Biot衰减峰值,对P波衰减的预测更细致.
在对比基础上,我们给出了理论模型的适用范围和特点,这里的“不适用”表示可能会产生较大误差: (1)White,Dutta(修正的White模型)模型 ① 不适用于骨架包含固体掺杂物的岩石波速预测; ② 主要适用于非固结砂岩的低频波速预测.
(2)Johnson模型 ① 不适用于微观喷射流机理占主导地位的岩石; ② 不适用中高频的高渗透率岩石波速预测(或误差较大); ③ 不适用于低渗透率小孔隙尺寸(毛细管效应明显)的岩石波速预测; ④ 不适用于骨架包含固体掺杂物的岩石波速预测.
(3)Biot-Rayleigh模型 ① 不适用于斑块内部流体动能不可忽略的岩石波速预测; ② 不适用于斑块边界动能损耗明显的岩石波速预测; 关于各种模型的适应性,表 1给出了速度预测模型的出对比情况.
目前,含流体孔隙介质中波的频散和衰减模型还面临着一些问题和困难,如流体或固体单一非均匀、流体饱和斑块规则分布等问题.在未来研究工作中,可以尝试做出突破的几个方向包括:
1 )将非均匀性双重孔隙问题中的球体用椭球体模型替代,通过变换椭球体的三条轴线长度来引入适用于多种孔隙形状的模型.
2)研究非均匀随机分布的斑块模型,引入固体掺杂物和流体斑块尺寸的随机分布函数,考虑更为符合真实情况的孔隙介质非均匀性分布特征.
3)考虑低孔渗岩石孔隙结构特征,建立更为真实的复杂介质流体流动模型,并在此基础上研究弹性波的频散和衰减.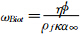 时(Müller et al., 2010),岩石孔隙通道中的流体流动可近似看为泊肃叶(Poiseuille)流动,这意味着流动为层状状态(流动的雷诺数要小于临界雷诺数),这里η为流体粘性,
时(Müller et al., 2010),岩石孔隙通道中的流体流动可近似看为泊肃叶(Poiseuille)流动,这意味着流动为层状状态(流动的雷诺数要小于临界雷诺数),这里η为流体粘性, 为孔隙度,ρf为流体密度,κ为渗透率,α∞为弯曲度.一般用Biot特征频率fc=ωBiot/2π来划分低频范围(f<
为孔隙度,ρf为流体密度,κ为渗透率,α∞为弯曲度.一般用Biot特征频率fc=ωBiot/2π来划分低频范围(f<
图 1 孔隙界面振荡下的孔隙流体Fig. 1 Pore fluid of vibrating interface 


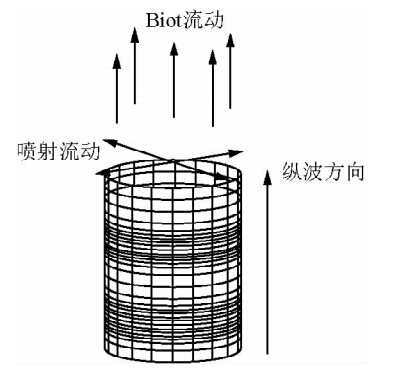
图 2 BISQ模型示意图:地震波激励下的Biot流和喷射流 Fig. 2 Diagram of BISQ model: Biot flow and squirt flow under seismic stimulation 
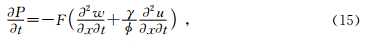
 为流体中的声波速度,
为流体中的声波速度,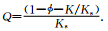 .
.
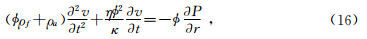
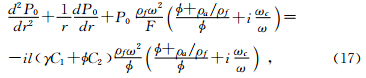
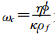 为Biot理论中的特征频率,根据边界处(即r=R,R为圆柱体半径)压力为常数的假设,进一步得到方程的解(Dvorkin and Nur, 1993):
为Biot理论中的特征频率,根据边界处(即r=R,R为圆柱体半径)压力为常数的假设,进一步得到方程的解(Dvorkin and Nur, 1993):

 为r的函数,J0为零阶贝塞尔函数,通过对上式求积分,得到单位体积的平均流体压力Pavr为(Dvorkin and Nur, 1993):
为r的函数,J0为零阶贝塞尔函数,通过对上式求积分,得到单位体积的平均流体压力Pavr为(Dvorkin and Nur, 1993):

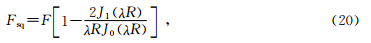

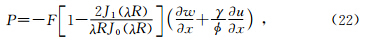
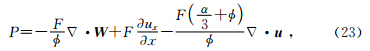
 为流体相对于固体的位移矢量,非黑斜体的u,w表示固体和流体在x方向的位移分量,α为Biot理论中的构造因子.由此可以将纵波速度和衰减系数表示为可测量岩石物理参数的式子,提出了改进的BISQ模型(RBISQ).
为流体相对于固体的位移矢量,非黑斜体的u,w表示固体和流体在x方向的位移分量,α为Biot理论中的构造因子.由此可以将纵波速度和衰减系数表示为可测量岩石物理参数的式子,提出了改进的BISQ模型(RBISQ).
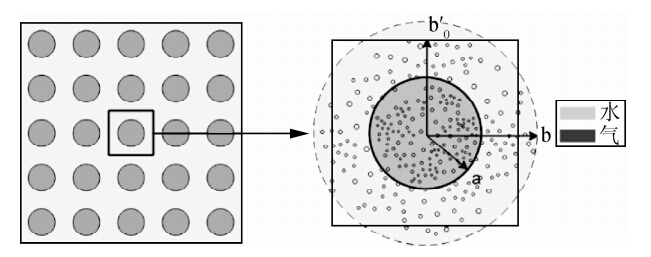
图 3 White斑块饱和模型特征单元示意图Fig. 3 Element of White patchy saturation model 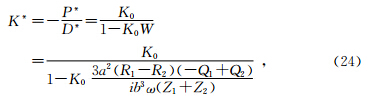

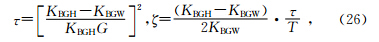

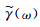 可由低高频极限情况确定.然后,仿照Pride 等(Pride et al., 1993)的方法,引入连接高、低频率极限的分支函数方法,确定依赖于中间频段的流体移动系数(Pride and Berryman, 2003a,b):
可由低高频极限情况确定.然后,仿照Pride 等(Pride et al., 1993)的方法,引入连接高、低频率极限的分支函数方法,确定依赖于中间频段的流体移动系数(Pride and Berryman, 2003a,b):
基于孔隙介质Biot理论,Pride和Berryman(Pride and Berryman, 2003a,b)研究了由不同孔隙介质组成的复合体中的弹性效应,从而得到单重流体、双重孔隙渗透率介质中的衰减和频散.通过将孔隙介质弹性理论中的Biot方程的系数变为空间函数,可以得到高频极限下与Mavko-Jizba一样的预测结果(Pride and Berryman, 2003a).Pride 等(Pride et al., 2004)利用同一模型进一步模拟了孔隙介质内单相介观流体流动、单相微观流体流动和不相溶的多相流体,得到了与Johnson等(Johnson,2001)相类似的结果,同时表明喷射流机制并不适用于解释地震波频段观测到的耗散现象.
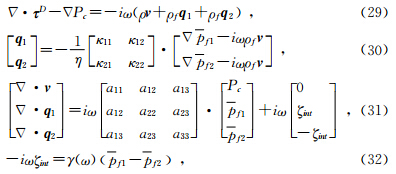
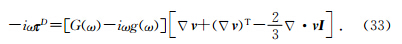
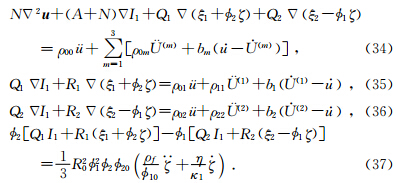
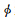 m,R0),渗透率κ和流体粘性系数η,这些系数都能够通过可测量的参数
m,R0),渗透率κ和流体粘性系数η,这些系数都能够通过可测量的参数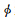 0,Ks,N,Kf1,Kf2,Kb,ρs,ρf1,ρf2表示(Ba et al.,2011).方程中I1表示固体骨架第一应变不变量,ξm=ε11(m)+ε22(m)+ε33(m)(m=1,2)表示流体应变不变量,其中流体应变分量定义为
0,Ks,N,Kf1,Kf2,Kb,ρs,ρf1,ρf2表示(Ba et al.,2011).方程中I1表示固体骨架第一应变不变量,ξm=ε11(m)+ε22(m)+ε33(m)(m=1,2)表示流体应变不变量,其中流体应变分量定义为 表示m相的孔隙度,
表示m相的孔隙度,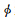 m满足
m满足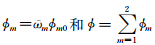 其中
其中 表示第m相所占体积比.
表示第m相所占体积比.
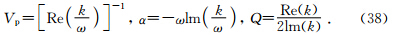

图 4 单孔隙双流体介质P波速度衰减(a)及频散(b)曲线.Q为品质因子,Vp为纵波速度Fig. 4 P wave velocity attenuation and dispersion in single-porosity double-fluid medium. Q is Quality factor and Vp is P wave velocity
(1)从低频(地震频段)到高频(超声波频段)范围内,Dutta(修正的White模型)(Dutta and Seriff, 1979),Johnson(Johnson,2001),Biot-Rayleigh(Ba et al., 2011)模型能够给出基本一致的P波频散、衰减和速度-饱和度变化曲线.
![]()
表 1 各种P波速度预测模型适用性说明Table 1
| [1] | Aki K. 1980. Scattering and attenuation of shear waves in the lithosphere[J]. J. Geophys. Res., 85(B11): 6496-6504. |
| [2] | Allard J F, Atalla N. 1993. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials[M]. University of Michigan: Elsevier Applied Science. |
| [3] | Ba J, Carcione J M, Nie J X. 2011. Biot-Rayleigh theory of wave propagation in double-porosity media[J]. J. Geophys. Res., 116(B6): B06202, doi: 10.1029/2010JB008185. |
| [4] | Ba J, Carcione J M, Cao H, et al. 2012. Velocity dispersion and attenuation of P waves in partially-saturated rocks: Wave propagation equations in double-porosity medium[J]. Chinese J. Geophys. (in Chinese), 55(1): 219-231, doi: 10.6038/j.issn.0001-5733.2012.01.021. |
| [5] | Ba J. 2013. Progress and Review of Rock Physics (in Chinese)[M]. Beijing: Tsinghua University Press. |
| [6] | Ba J, Yan X F, Chen Z Y, et al. 2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs[J]. Chinese J. Geophys. (in Chinese), 56(5): 1696-1706, doi: 10.6038/cjg20130527. |
| [7] | Batzle M, Wang Z J. 1992. Seismic properties of pore fluids[J]. Geophysics, 57(11): 1396-1408. |
| [8] | Batzle M L, Han D H, Hofmann R. 2006. Fluid mobility and frequency-dependent seismic velocity-direct measurements[J]. Geophysics, 71(1): N1-N9. |
| [9] | Beranek L L. 1947. Acoustical properties of homogeneous, isotropic rigid tiles and flexible blankets[J]. J. Acoust. Soc. Am., 19(4): 556-568. |
| [10] | Berryman J G, Holland C J. 1980. Stability of the separable solution for fast diffusion[J]. Arch. Rational Mech. Anal., 74(4): 379-388. |
| [11] | Berryman J G. 1980a. Confirmation of biot's theory[J]. Appl. Phys. Lett., 37(4): 382-384. |
| [12] | Berryman J G. 1980b. Long-wavelength propagation in composite elastic media I. spherical inclusions[J]. J. Acoust. Soc. Am., 68(6): 1809-1819. |
| [13] | Berryman J G. 1980c. Long-wavelength propagation in composite elastic media II. ellipsoidal inclusions[J]. J. Acoust. Soc. Am., 68(6): 1820-1831. |
| [14] | Berryman J G, Milton G W. 1991. Exact results for generalized Gassmann's equations in composite porous media with two constituents[J]. Geophysics, 56(12): 1950-1960. |
| [15] | Berryman J G. 1998. Seismic wave attenuation in fluid-saturated porous media[J]. Pure and Applied Geophysics, 128(1-2): 424-432. |
| [16] | Berryman J G. 1999. Origin of Gassmann's equations[J]. Geophysics, 64(5): 1627-1629. |
| [17] | Berryman J G, Wang H F. 2000. Elastic wave propagation and attenuation in a double-porosity dual-permeability medium[J]. Int. J. Rock. Mech. Min., 37(1-2): 63-78. |
| [18] | Berryman J G, Wang H F. 2001. Dispersion in poroelastic systems[J]. Phys. Rev. E., 64: 011303. |
| [19] | Biot M A. 1941. General theory of three-dimensional consolidation[J]. ,J. Appl. Phys. 12(2): 155-164. |
| [20] | Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. J. Acoust. Soc. Am., 28(2): 168-178. |
| [21] | Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range[J]. J. Acoust. Soc. Am., 28(2): 179-191. |
| [22] | Biot M A, Willis D G. 1957. The elastic coefficients of the theory of consolidation[J]. Journal of Applied Mechanics, 24(4): 594-601. |
| [23] | Biot M A. 1962a. Generalized theory of acoustic propagation in porous dissipative media[J]. J. Acoust. Soc. Am., 34(9A): 1254-1264. |
| [24] | Biot M A. 1962b. Mechanics of Deformation and Acoustic Propagation in Porous Media[J]. J. Appl. Phys., 33(4): 1482-1498. |
| [25] | Bourbié T, Coussy O, Zinszner B. 1987. Acoustics of Porous Media[M]. Paris: Editions Technip. |
| [26] | Brown R J S, Korringa J. 1975. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid[J]. Geophysics, 40(4): 608-616. |
| [27] | Buckingham M J. 2000. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments[J]. J. Acoust. Soc. Am., 108(6): 2796-2815. |
| [28] | Budiansky B, Oconnell R J. 1976. Elastic moduli of a cracked solid[J]. Int. J. Solids Struct., 12(2): 81-97. |
| [29] | Burridge R, Keller J B. 1981. Poroelasticity equations derived from microstructure[J]. J. Acoust. Soc. Am., 70(4): 1140-1146. |
| [30] | Cadoret T, Mavko G, Zinszner B. 1998. Fluid distribution effect on sonic attenuation in partially saturated limestones[J]. Geophysics, 63(1): 154-160. |
| [31] | Carcione J M. 2001. Energy balance and fundamental relations in dynamic anisotropic poro-viscoelasticity[J]. Proceedings: Mathematical, Physical and Engineering Sciences, 457(2006): 331-348. |
| [32] | Carcione J M, Seriani G. 2001. Wave simulation in frozen porous media[J]. J. Comput. Phys., 170(2): 676-695. |
| [33] | Carcione J M, Cavallini F, Santos J E, et al. 2004. Wave propagation in partially saturated porous media: simulation of a second slow wave[J]. Wave Motion, 39(3): 227-240. |
| [34] | Carcione J M, Campanella O H, Santos J E. 2007. A poroelastic model for wave propagation in partially frozen orange juice[J]. J. Food Eng., 80(1): 11-17. |
| [35] | Carcione J M, Morency C, Santos J E. 2010. Computational poroelasticity-A review[J]. Geophysics, 75(5): 75A229-75A243. |
| [36] | Carmichael R S. 1989. Practical Handbook of Physical Properties of Rocks and Minerals[M]. Boca Raton, Fla.: CRC Press. |
| [37] | Deng J X, Wang S X, Du W. 2012. A study of the influence of mesoscopic pore fluid flow on the propagation properties of compressional wave-a case of periodic layered porous media[J]. Chinese J. Geophys. (in Chinese), 55(8): 2716-2727, doi: 10.6038/j.issn.0001-5733.2012.08.024. |
| [38] | Diallo M S, Appel E. 2000. Acoustic wave propagation in saturated porous media: reformulation of the Biot/Squirt flow theory[J]. J. Appl. Geophys., 44(4): 313-325. |
| [39] | Domenico S N. 1974. Effect of water saturation on seismic reflectivity of sand reservoirs encased in shale[J]. Geophysics, 39(6): 759-769. |
| [40] | Domenico S N. 1976. Effect of brine-gas mixture on velocity in an unconsolidated sand reservoir[J]. Geophysics, 41(5): 882-894. |
| [41] | Dutta N C, Ode H. 1979a. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model); Part II, results[J]. Geophysics, 44(11): 1789-1805. |
| [42] | Dutta N C, Ode H. 1979b. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model); Part I, Biot theory[J]. Geophysics, 44(11): 1777-1788. |
| [43] | Dutta N C, Seriff A J. 1979. On White's model of attenuation in rocks with partial gas saturation[J]. Geophysics, 44(11): 1806-1812. |
| [44] | Dvorkin J, Nur A. 1993. Dynamic poroelasticity; a unified model with the squirt and the Biot mechanisms[J]. Geophysics, 58(4): 524-533. |
| [45] | Dvorkin J, Nolen-Hoeksema R, Nur A. 1994. The squirt-flow mechanism; macroscopic description[J]. Geophysics, 59(3): 428-438. |
| [46] | Dvorkin J, Mavko G, Nur A. 1995. Squirt flow in fully saturated rocks[J]. Geophysics, 60(1): 97-107. |
| [47] | Dvorkin J P. 2008. Yet another Vs equation[J]. Geophysics, 73(1): E35-E39. |
| [48] | Elliott S E, Wiley B F. 1975. Compressional velocities of partially saturated, unconsolidated sands[J]. Geophysics, 40(6): 949-954. |
| [49] | Frenkel J. 1944. Problems of modern physics[J]. Nature, 154(3910): 450-454. |
| [50] | Gassmann F. 1951. Uber die elastizitat poroser medien[J]. Vier Der Natur Gesellschaft, 96: 1-23. |
| [51] | Geerits T W, Kelder O. 1997. Acoustic wave propagation through porous media: Theory and experiments[J]. J. Acoust. Soc. Am., 102(5): 2495-2510. |
| [52] | Géli L, Bard P Y, Schmitts D P. 1987. Seismic wave propagation in a very permeable water-saturated surface layer[J]. J. Geophys. Res., 92(B8): 7931-7944. |
| [53] | Gist G A. 1994. Interpreting laboratory velocity measurements in partially gas-saturated rocks[J]. Geophysics, 59(7): 1100-1109. |
| [54] | Goertz D, Knight R. 1998. Elastic wave velocities during evaporative drying[J]. Geophysics, 63(1): 171-183. |
| [55] | Goodman M A, Cowin S C. 1972. A continuum theory for granular materials[J]. Arch. Rational Mech. Anal., 44(4): 249-266. |
| [56] | Gregory A R. 1976. Fluid saturation effects on dynamic elastic properties of sedimentary rocks[J]. Geophysics, 41(5): 895-921. |
| [57] | Gurevich B, Lopatnikov S L. 1995. Velocity and attenuation of elastic waves in finely layered porous rocks[J]. Geophys. J. Int., 121(3): 933-947. |
| [58] | Helle H B, Pham N H, Carcione J E M. 2003. Velocity and attenuation in partially saturated rocks: poroelastic numerical experiments[J]. Geophys. Prospect., 51(6): 551-566. |
| [59] | Johnson D L, Koplik J, Dashen R. 1987. Theory of dynamic permeability and tortuosity in fluid-saturated porous media[J]. J. Fluid Mech., 176: 379-402. |
| [60] | Johnson D L. 2001. Theory of frequency dependent acoustics in patchy-saturated porous media[J]. J. Acoust. Soc. Am., 110(2): 682-694. |
| [61] | Johnston D H, Toksoz M N,Timur A. 1979. Attenuation of seismic waves in dry and saturated rocks; II, Mechanisms[J]. Geophysics, 44(4): 691-711. |
| [62] | Jones T D. 1986. Pore fluids and frequency-dependent wave propagation in rocks[J]. Geophysics, 51(10): 1939-1953. |
| [63] | Kelder O, Smeulders D M J. 1997. Observation of the Biot slow wave in water-saturated Nivelsteiner sandstone[J]. Geophysics, 62(6): 1794-1796. |
| [64] | King M S. 2009. Recent developments in seismic rock physics[J]. Int. J. Rock Mech. Min., 46(8): 1341-1348. |
| [65] | Kosten C W. 1950. Sound absorption by porous materials II[J]. Appl. Sci. Res. B, 1(1): 241-250. |
| [66] | Kuster G T, Toksoz M N. 1974a. Velocity and attenuation of seismic waves in two-phase media; Part I, Theoretical formulations[J]. Geophysics, 39(5): 587-606. |
| [67] | Kuster G T, Toksoz M N. 1974b. Velocity and attenuation of seismic waves in two-phase media; Part II, Experimental results[J]. Geophysics, 39(5): 607-618. |
| [68] | Li X F, Li X F, Zhang M G. 2007. Review of seismic wave numerical modeling methods[J]. Journal of Disaster Prevention and Mitigation Engineering (in Chinese), 27(2): 241-248. |
| [69] | Li G P, Yao F C, Shi Y M, et al. 2011. Several key issues of finite-difference seismic wave numerical simulation[J]. Progress in Geophysics (in Chinese), 26(2): 469-476, doi: 10.3969/j.issn.1004-2903.2011.02.011. |
| [70] | Liu Y, Wei X C. 2003. Finite element equations and numerical simulation of elastic wave propagation in two-phase anisotropic media[J]. Acta Seismologica Sinica (in Chinese), 25(2): 154-162. |
| [71] | Liu Y, Wei X C. 2008. Numerical Simulation of Seismic Wave Propagation in Complex Structures[J]. Xinjiang Petroleum Geology (in Chinese), 29(1): 12-14. |
| [72] | Mavko G, Nur A. 1975. Melt squirt in the asthenosphere[J]. J. Geophys. Res., 80(11): 1444-1448. |
| [73] | Mavko G, Kjartansson E, Winkler K. 1979. Seismic wave attenuation in rocks[J]. Rev. Geophys., 17(6): 1155-1164. |
| [74] | Mavko G, Jizba D. 1991. Estimating grain-scale fluid effects on velocity dispersion in rocks[J]. Geophysics, 56(12): 1940-1949. |
| [75] | Mavko G, Nolen-Hoeksema R C. 1994. Estimating seismic velocities at ultrasonic frequencies in partially saturated rocks[J]. Geophysics, 59(2): 252-258. |
| [76] | Mavko G, Jizba D. 1994. The relation between seismic P- and S-wave velocity dispersion in saturated rocks[J]. Geophysics, 59(1): 87-92. |
| [77] | Mavko G, Mukerji T. 1998. Bounds on low-frequency seismic velocities in partially saturated rocks[J]. Geophysics, 63(3): 918-924. |
| [78] | Mavko G, Mukerji T, Dvorkin J. 2003. The Rock Physics Handbook[M]. Cambridge: Cambridge University Press. |
| [79] | Mavko G M, Nur A. 1979. Wave attenuation in partially saturated rocks[J]. Geophysics, 44(2): 161-178. |
| [80] | Meng Q S, He Q D, Zhu J W, et al. 2003. Seismic modeling in isotropic porous media based on BISQ model[J]. Journal of Jilin University(Earth Science Edition)(in Chinese),33(2):217-221. |
| [81] | Müller T M, Gurevich B, Lebedev M. 2010. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review[J]. Geophysics, 75(5): 75A147-75A164. |
| [82] | Murphy H D. 1979. Convective instabilities in vertical fractures and faults[J]. J. Geophys. Res., 84(B11): 6121-6130. |
| [83] | Murphy W F. 1982. Effects of partial water saturation on attenuation in Massilon sandstone and Vycor porous glass[J]. J. Acoust. Soc. Am., 71(6): 1458-1468. |
| [84] | Murphy W F. 1984. Acoustic measures of partial gas saturation in tight sandstones[J]. J. Geophys. Res., 89(B13): 11549-11559. |
| [85] | Murphy W F, Winkler K W, Kleinberg R L. 1984. Contact microphysics and viscous relaxation in sandstones [J]. AIP Conf. Proc., 107(1): 176-190. |
| [86] | Nagy P B, Adler L, Bonner B P. 1990. Slow wave propagation in air-filled porous materials and natural rocks[J]. Appl. Phys. Lett., 56(25): 2504-2506. |
| [87] | Nie J X, Yang D H, Ba J. 2010. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay[J]. Chinese J. Geophys. (in Chinese), 53(5 2): 38-392, doi: 10.3969/j.issn.0001-5733.2010.02.016. |
| [88] | O'connell R J, Budiansky B. 1974. Seismic velocities in dry and saturated cracked solids[J]. J. Geophys. Res., 79(35): 5412-5426. |
| [89] | O'connell R J, Budiansky B. 1977. Viscoelastic properties of fluid-saturated cracked solids[J]. J. Geophys. Res., 82(36): 5719-5735. |
| [90] | Pandit B I, King M S. 1979. The Variation of elastic wave velocities and quality factor Q of a sandstone with moisture content[J]. Can. J. Earth. Sci., 16(12): 2187-2195. |
| [91] | Parra J O. 1997. The transversely isotropic poroelastic wave equation including the Biot and the squirt mechanisms; theory and application[J]. Geophysics, 62(1): 309-318. |
| [92] | Pei Z L, Mu Y G. 2004. Numerical simulation of seismic wave propagation[J]. Progress in Geophysics (in Chinese), 19(4): 933-941. |
| [93] | Plona T J. 1980a. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies[J]. Appl. Phys. Lett., 36(4): 259-261. |
| [94] | Plona T J. 1980b. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies[J]. Appl. Phys. Lett., 36(4): 259-261. |
| [95] | Pride S R, Morgan F D, Gangi A F. 1993. Drag forces of porous-medium acoustics[J]. Phys. Rev. B, 47: 4964-4978. |
| [96] | Pride S R, Berryman J G. 2003a. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation[J]. Phys. Rev. E, 68(3 Pt 2): 036603. |
| [97] | Pride S R, Berryman J G. 2003b. Linear dynamics of double-porosity dual-permeability materials. II. Fluid transport equations[J]. Phys. Rev. E, 68(3 Pt 2): 036604. |
| [98] | Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow[J]. J. Geophys. Res., 109(B1): B01201, doi: 10.1029/2003JB002639. |
| [99] | Rayleigh L. 1917. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine Series 6, 34(200): 94-98. |
| [100] | Rice J R, Cleary M P. 1976. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents[J]. Rev. Geophys., 14(2): 227-241. |
| [101] | Rubino J G, Ravazzoli C L, Santos J E. 2009. Equivalent viscoelastic solids for heterogeneous fluid-saturated porous rocks[J]. Geophysics, 74(1): N1-N13. |
| [102] | Santos J E, Corberó J M, Douglas J Jr. 1990a. Static and dynamic behavior of a porous solid saturated by a two-phase fluid[J]. J. Acoust. Soc. Am., 87(4): 1428-1438. |
| [103] | Santos J E, Douglas J, Corberó J, et al. 1990b. A model for wave propagation in a porous medium saturated by a two-phase fluid[J]. J. Acoust. Soc. Am., 87(4): 1439-1448. |
| [104] | Santos J E, Ravazzoli C L, Gauzellino P M, et al. 2004. Simulation of waves in poro-viscoelastic rocks saturated by immiscible fluids: numerical evidence of a second slow wave[J]. J. Comp. Acous., 12(1): 1-21. |
| [105] | Sharma M D. 2004. Wave propagation in a general anisotropic poroelastic medium with anisotropic permeability: phase velocity and attenuation[J]. Int. J. Solids Struct., 41(16-17): 4587-4597. |
| [106] | Smith T M, Sondergeld C H, Rai C S. 2003. Gassmann fluid substitutions: A tutorial[J]. Geophysics, 68(2): 430-440. |
| [107] | Song Y J, Hu H, Li C. 2013. Unrelaxed drained bulk modulus for fluid-saturated rocks on full frequency range[J]. The Journal of the Acoustical Society of America, 133(5): 3456. |
| [108] | Stoll R D, Bryan G M, Cheh H Y. 1973. Solidified Gas in Sediments[J]. Geophysics, 38: 1223-1223. |
| [109] | Sun W T, Ba J, Müller T M, et al. 2014. Comparison of P-wave attenuation models of wave-induced flow[J]. Geophys. Prospect., doi: 10.1111/1365-2478.12196. |
| [110] | Tarif P, Bourbie T. 1987. Experimental Comparison between Spectral Ratio and Rise Time Techniques for Attenuation Measurement[J]. Geophys. Prospect., 35(6): 668-680. |
| [111] | Thompson M, Willis J R. 1991. A reformation of the equations of anisotropic poroelasticity[J]. J. Appl. Mech., 58(3): 612-616. |
| [112] | Toms J, Müller T M, Ciz R, et al. 2006. Comparative review of theoretical models for elastic wave attenuation and dispersion in partially saturated rocks[J]. Soil Dyn. Earthq. Eng., 26(6-7): 548-565. |
| [113] | Walsh J B. 1965. The effect of cracks on the compressibility of rock[J]. J. Geophys. Res., 70(2): 381-389. |
| [114] | Walsh J B. 1969. New analysis of attenuation in partially melted rock[J]. J. Geophys. Res., 74(17): 4333-4337. |
| [115] | Wang X M. 2009. Research progress in acoustics for multiphase porous reservoirs[J]. Applied Acoustics (in Chinese), 28(1): 1-9. |
| [116] | Wang Z J. 2001. Fundamentals of seismic rock physics[J]. Geophysics, 66(2): 398-412. |
| [117] | Wang Z J, Nur A M. 1988. Velocity dispersion and the “local flow” mechanism in rocks[J]. SEG Technical Program Expanded Abstracts, (4): 548-550. |
| [118] | Wei X C, Lu M H, Ba J, et al. 2008. Dispersion and attenuation of elastic waves in a viscous fluid-saturated anisotropic porous solid[J]. Chinese Journal of Geophysics (in Chinese), 51(1): 213-220. |
| [119] | White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophysics, 40(2): 224-232. |
| [120] | White J E, Mihailova N, Lyakhovitsky F M. 1975. Low-frequency seismic waves in fluid-saturated layered rocks[J]. J. Acoust. Soc. Am., 57: 654-659. |
| [121] | Winkler K W. 1985. Dispersion analysis of velocity and attenuation in berea sandstone[J]. J. Geophys. Res., 90(B8): 6793-6800. |
| [122] | Winkler K W. 1986. Estimates of Velocity Dispersion between Seismic and Ultrasonic Frequencies[J]. Geophysics, 51(1): 183-189. |
| [123] | Wu G C, Wu J L, Zong Z Y. 2014. The attenuation of P wave in a periodic layered porous media containing cracks[J]. Chinese J. Geophys. (in Chinese), 57(8): 2666-2677, doi: 10.6038/cjg20140825. |
| [124] | Wu C Y, Chiang J Y. 1990. Linearly anisotropic scattering in a rectangular medium exposed to collimated radiation[J]. Int. J. Heat Mass Tran., 33(5): 1032-1034. |
| [125] | Wulff A M, Burkhardt H. 1997. Mechanisms affecting ultrasonic wave propagation in fluid-containing sandstones under high hydrostatic pressure[J]. J. Geophys. Res., 102(B2): 3043-3050. |
| [126] | Wyllie H A. 1956. A mcleod gauge for measuring a wide range of pressures[J]. J. Sci. Instrum., 33(8): 317-317. |
| [127] | Wyllie M R J, Gregory A R, Gardner L W. 1956. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 21(1): 41-70. |
| [128] | Xu L. 2009. Seismic wave propagation and modelling in poro-elastic media with mesoscopic inhomogeneities[D]. Australia: The University of Adelaide. |
| [129] | Yamamoto T, Nye T, Kuru M. 1994. Porosity, permeability, shear strength: crosswell tomography below an iron foundry[J]. Geophysics, 59(10): 1530-1541. |
| [130] | Yang D H, Cheng X H. 2001. BISQ model for fluid-filled, porous medium[J]. Oil Geophysical Prospecting (in Chinese), 36(2): 146-159. |
| [131] | Zhao H B, Wang X M, Chen S M, et al. 2010. Acoustic response characteristics of unsaturated porous media[J]. SCIENTIA SINICA Phys, Mech & Astron (in Chinese), 40(7): 819-827. |
| [132] | 巴晶, Carcione J M, 曹宏,等. 2012. 非饱和岩石中的纵波频散与衰减: 双重孔隙介质波传播方[J]. 地球物理学报, 55(1): 219-231, doi: 10.6038/j.issn.0001-5733.2012.01.021. |
| [133] | 巴晶. 2013. 岩石物理学进展与评述[M]. 北京: 清华大学出版社. |
| [134] | 巴晶, 晏信飞, 陈志勇,等. 2013. 非均质天然气藏的岩石物理模型及含气饱和度反演[J]. 地球物理学报, 56(5): 1696-1706, doi: 10.6038/cjg20130527. |
| [135] | 邓继新, 王尚旭, 杜伟. 2012. 介观尺度孔隙流体流动作用对纵波传播特征的影响研究—以周期性层状孔隙介质为例[J]. 地球物理学报, 55(8): 2716-2727, doi: 10.6038/j.issn.0001-5733.2012.08.024. |
| [136] | 李信富, 李小凡, 张美根. 2007. 地震波数值模拟方法研究综述[J]. 防灾减灾工程学报, 27(2): 241-248. |
| [137] | 李国平, 姚逢昌, 石玉梅,等. 2011. 有限差分法地震波数值模拟的几个关键问题[J]. 地球物理学进展, 26(2): 469-476, doi: 10.3969/j.issn.1004-2903.2011.02.011. |
| [138] | 刘洋, 魏修成. 2003. 双相各向异性介质中弹性波传播有限元方程及数值模拟[J]. 地震学报, 25(2): 154-162. |
| [139] | 刘洋, 魏修成. 2008. 复杂构造中地震波传播数值模拟[J]. 新疆石油地质, 29(1): 12-14. |
| [140] | 孟庆生, 何樵登, 朱建伟,等. 2003. 基于BISQ模型双相各向同性介质中地震波数值模拟[J]. 吉林大学学报(地球科学版), 33(2): 217-221. |
| [141] | 聂建新, 杨顶辉, 巴晶. 2010. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究[J]. 地球物理学报, 53(2): 385-392, doi: 10.3969/j.issn.0001-5733.2010.02.016. |
| [142] | 裴正林, 牟永光. 2004. 地震波传播数值模拟[J]. 地球物理学进展, 19(4): 933-941. |
| [143] | 王秀明. 2009. 多相孔隙储层声学研究进展[J]. 应用声学, 28(1): 1-9. |
| [144] | 魏修成, 卢明辉, 巴晶,等. 2008. 含黏滞流体各向异性孔隙介质中弹性波的频散和衰减[J]. 地球物理学报, 51(1): 213-220. |
| [145] | 吴国忱, 吴建鲁, 宗兆云. 2014. 周期性层状含孔隙、裂隙介质模型纵波衰减特征[J]. 地球物理学报, 57(8): 2666-2677, doi: 10.6038/cjg20140825. |
| [146] | 杨顶辉, 陈小宏. 2001. 含流体多孔介质的BISQ模型[J]. 石油地球物理勘探, 36(2): 146-159. |
| [147] | 赵海波, 王秀明, 陈树民,等. 2010. 未饱和孔隙介质的声场响应[J]. 中国科学: 物理学 力学 天文学, 40(7): 819-827. |
 2015, Vol. 30
2015, Vol. 30

