地球物理学进展  2015, Vol. 30 Issue (2): 559-564   PDF    
引用本文
孟繁磊, 李月, 杨宝俊. 2015. 分形守恒定律在地震数据去噪与增强上的应用[J]. 地球物理学进展, 30(2): 559-564, doi: 10.6038/pg20150211  
MENG Fan-lei, LI Yue, YANG Bao-jun. 2015. Application of fractal conservation law in the simultaneous denoising and enhancement of seismic data. Progress in Geophysics, 30(2): 559-564, doi: 10.6038/pg20150211   
分形守恒定律在地震数据去噪与增强上的应用
孟繁磊1, 李月1 , 杨宝俊2    
1. 吉林大学通信工程学院, 长春 130012;
2. 吉林大学地球探测科学与技术学院, 长春 130026
收稿日期: 2014-07-18 修回日期: 2014-12-18 .
基金项目：国家自然科学基金重点项目(41130421)资助.
作者简介：孟繁磊,男,1985年生,吉林长春人,博士研究生,从事地震信号处理方面的研究.(E-mail:419257823@qq.com)
通讯作者：李月,女,1958年生,教授,博士生导师,从事现代信号处理与微弱信号检测方面的研究.(E-mail:liyue@jlu.edu.cn)
摘要：分形守恒定律是一种基于偏微分方程的滤波方法.方程最显著的特征是将互为矛盾的两项——分形反扩散项与经典的扩散项结合在一起.反扩散项起信号增强的作用, 而去噪的作用在扩散项中体现.通过分形指数, 扩散与反扩散的系数可实现滤波器的调节.本文应用这个新颖的滤波模型来实现地震资料中随机噪声的消减, 同时又能增强有效的地震信号.方程的求解基于傅里叶变换.对合成地震记录的测试表明, 本算法在不同强度的噪声环境中(信噪比为-5 dB至10 dB)都能很好地恢复同相轴, 提高信噪比.通过对实际共炮点资料的处理结果表明, 基于分形守恒定律的新滤波方法能有效的压制随机噪声并改善同相轴的连续性.
关键词： 分形守恒定律     偏微分方程滤波     去噪     增强     傅里叶变换    
Application of fractal conservation law in the simultaneous denoising and enhancement of seismic data
MENG Fan-lei1, LI Yue1 , YANG Bao-jun2    
1. College of Communication Engineering, Jilin University, Changchun 130012, China;
2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China
Abstract: The fractal conservation law is based on the partial differential equation filtering. The main advantage of the equation is the combined use of fractal anti-diffusion and classical diffusion, which are two antagonistic terms. The nonlocal anti-diffusion is used to enhance the contrast, whereas the diffusion is used to reduce the noise. The tuning of the filter can be achieved by controlling the fractal exponent, the amount of anti-diffusion and diffusion. This paper applied this new filtering method for the simultaneous noise reduction and enhancement of seismic signals. Numerical simulations based on the FFT are given. The properties of this novel method are tested on synthetic seismic data. The experimental results show that our method can recover the seismic events and improve the SNR in the different noise levels (the SNR is from -5 dB to 10 dB). In real common shot point (CSP) seismic records, the experimental results illustrate the superior performance of our method in the improvement the continuity and clarity of reflection events by removing random noise.
Key words: fractal conservation law     partial differential equation filtering     denoising     enhancement     fourier transform    
0 引 言

包含在地震记录中的同相轴信息对于认知实际的地下地质结构起到了重要的作用，可以帮助人们透视地球内部、探查油气与矿产.地震数据的质量直接影响到后续的处理与解释过程.而随着地震勘探环境和条件的复杂化，勘探难度会随之增大，相应地，人们采集到的地震勘探资料中所包含的噪声也会增多，使得反射同相轴的清晰度下降从而严重影响了地质信息.因此，有效地压制噪声是一个至关重要的问题.本文将抑制强随机噪声，提高信噪比进而恢复同相轴作为首要目标.

近年来，人们发展了多种提高信噪比的技术并成功地应用于地震勘探随机噪声压制.比如共反射面元叠加(杨锴等，2005；李振春等，2006)，信号子空间方法变换(陆文凯等，2005)，小波变换(Cao and Chen， 2005；高静怀等，2006)，多项式拟合技术(钟伟等，2006；Liu et al., 2011)，Hilbert-Huang(汤井田等，2008)，独立分量分析(刘喜武等，2003；Tian et al., 2012)，支持向量机(邓小英和李月，2007)，经验模态分解(李月等，2013)，时频峰值滤波(李月等，2009；林红波等，2011)等方法.这些方法均是压制噪声的有效途径，但是在强随机噪声(低于 0 dB)的背景下，反射同相轴已经难以辨认，此时应用上述方法就不够理想，滤波后，有效信号的幅度有不同程度的衰减，这影响了后续的地震信号处理.

分形守恒定律是一种能够同时对信号去噪与增强的滤波算法，Azerad等(2012)首次提出该算法并成功将其应用在心电图信号中.使用基于富比尼定理的积分公式对反扩散项做适当的变形，然后对方程进行傅里叶变换，可求解出在频率域中的滤波函数表达式.经过研究表明该滤波器可以削弱低频信号，放大中频信号，保护低频信号.这个良好特性可以在去噪的同时有效地保护甚至放大信号的某些特征，比如信号的相对最大值与最小值，而常规的去噪方法并不具备这样的特性. 1 算法的来源与理论基础

基于分形守恒定律的滤波算法源于Fowler等(2001，2002)所研究的方程模型为

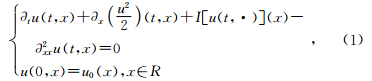
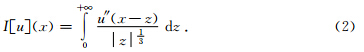
模型基于柯西问题的偏微分方程，最早用于描述沙丘经流体流动后，其地貌动力学特性.其中u=u(t，x)表示沙丘的高度，I 是一个非局部算子，定义为

对于方程(1)的更多理论背景，可参阅Fowler的文献.

2012年，Azerad将方程(1)修改成方程(3)

并将其应用在信号处理中.方程(3)含有一对矛盾项：一个经典的拉普拉斯扩散项－ ∂xx2和一个非局部低阶次分数阶反扩散项Iλ，方程按道来处理地震记录.

方程(3)是以数学的形式给出的，但将其应用到地震信号处理的时候，t和x不再表示数学中的时间和空间，它们的物理意义会有相应的变化.这里t只表示一个参数，而x则表示一道地震数据的采样点.其中u=u(t，x)是滤波后的信号，u0是方程的初始条件，表示所获得的初始含噪地震记录，T代表任意正的时间量，a和b是正的常数，Iλ是分数阶算子，当λ∈(1，2)时，Iλ定义为

其中αλ是一个适当的常量. 因为ε只是一个被积符号，所以(3)式中用“·”来代替.将Iλ的积分限由R替换为(0，∞)并做适当变换可以得到

这是Riemann Liouville所定义的分数阶导数，其中Γ是Gamma函数.

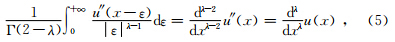
经过以上分析可以看出，经过修改的方程(3)的建立及其求解方法是算法的核心. 2 基于傅立叶变换的数值求解

本节详细介绍基于傅里叶变换的数值求解方法，并讨论了方程参数(a，b，λ)的选择.

2.1 数值计算方案

首先记F[u(t，x)]=U(t，ω)，F[u(0，x)]=U0(ω)，F表示傅里叶变换算子.将t作为参数，对方程(3)两端做关于x的傅里叶变换得

用积分公式对Iλ做变形，可得

公式(7)的数学证明见附录1.

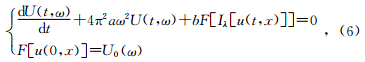
其中Cλ是常数，最终可与b合并.这样Iλ的傅里叶变换可重写为

其中

这里aI和bI为正的常数，φ(ω)的推导过程见附录2.

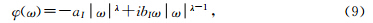
式子(9)的推导思路源于Alibaud等(2010)等人的研究成果.根据式子(6)，(8)，(9)，可以得到一个关于U(t，ω)的常微分方程，它的解为

其中

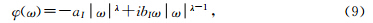
方程(11)为变换域中的滤波函数表达式.其中常数aI合并在b中，为了计算方便，t可设为1.根据式子(10)，可以推断出方程(3)的任何解都满足

其中*表示卷积，k(t，x)=F－1 Ka，bλ(t，ω)，它是Iλ－∂xx2的核函数，符号4π2ω2对应－∂2xx，符号－|ω|λ与分数阶算子Iλ相对应. 正的参数a和b分别控制着局部扩散和非局部反扩散的强度.图 1给出了变换域滤波函数Ka，bλ，在图中可以看出该滤波函数可以保护低频信号，放大中频信号，削弱高频信号.非局部反扩散项对信号起增强的作用，而扩散项起去噪的作用.
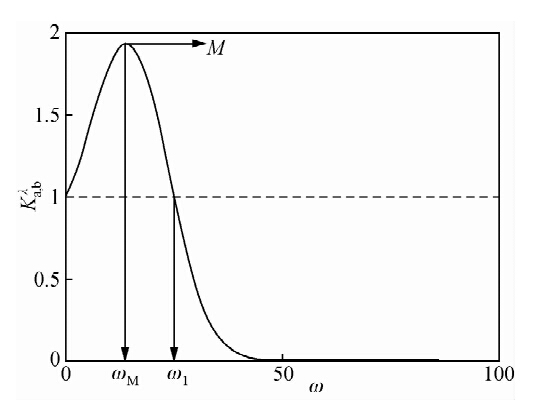图 1 变换域滤波函数
Ka，bλ，4π2a=0.01，b=0.05 and λ=1.5Fig. 1 The filter Ka，bλ in the transform domain with
4π2a=0.01，b=0.05 and λ=1.5

根据公式(12)，可以推出

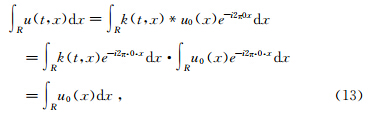
上式相当于k(t，x)*u0(x)的傅里叶变换(并令ω=0)，而两个函数卷积的傅里叶变换等于两个函数各自傅里叶变换的乘积.式子(13)体现了“守恒”的特性. 2.2 参数的选择

根据图 1的示意，需要知道三个重要的数值. 第一个是门限频率ω1= b/(4π2a)1/(2－λ)，ω1是当Ka，bλ(ω1)=1所对 应的频率值，并且当ω>ω1时满足Ka，bλ(ω)<1.因此ω1控制着保护/放大频率段的范围.另外两个重要的数值分别是M和ωM，对Ka，bλ求导可得到ωM= λb/(8π2a)1/(2－λ)，而M是Ka，bλ的最大值，并且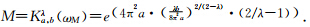

只有在0<λ<2时M为大于1的值，并且注意到比值ω1/ωM=(2/λ)1/(2－λ)，这是一个仅仅关于λ的函数，当λ从0到2变化时，这个比值的范围是从+∞到 e，因此可以给λ一个固定值.另外根据实际情况，也可以将ω1和M设置为一个定值.因此通过ω1和λ可以确定比值b/a，再将这个比值代入M可以反求出a.最终根据比值b/a可确定参数b.拉普拉斯项前面的系数a控制着去噪的强度.系数b控制反扩散项并与拉普拉斯项的作用相反.根据上述分析，增强与去噪不再是一对矛盾. 3 仿真结果与分析

首先给出一个简单的例子来更好的理解算法对信号的去噪与增强的能力.如图 2a，理想信号包含一个主频为30 Hz的雷克子波.信号有512个采样点，采样频率是1000 Hz.在理想信号中添加信噪比为10 dB的高斯白噪声组成了噪声信号.图 2b是去噪后的结果.图 2c强调了算法对信号同时去噪与增强的能力.

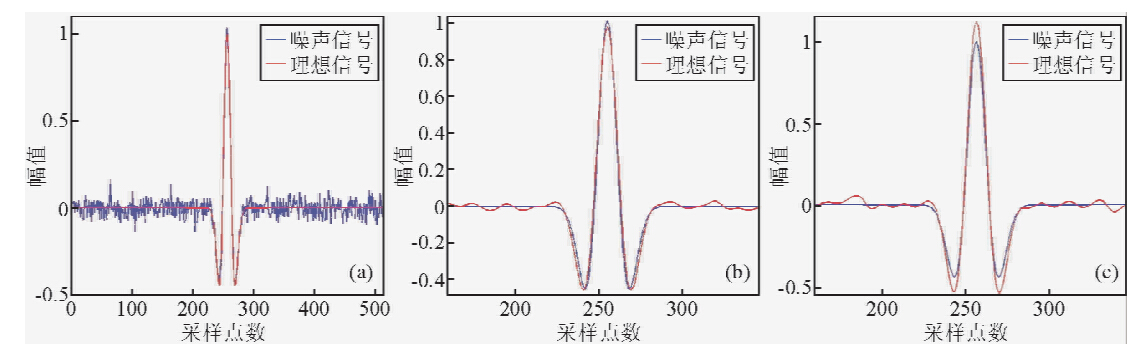图 2 单道地震模型实验
(a)噪声信号与原始信号;(b)理想信号与滤波信号，4π2a=0.0140，b=0.0188 and λ=1.9 (c)理想信号与滤波信号，4π2a=0.0135，b=0.0188 and λ=1.9Fig. 2 Example of a single trace seismic model
(a)Noisy signal and ideal signal;(b)Ideal signal and filtered signal with 4π2a=0.0140，b=0.0188 and λ=1.9(c)Ideal signal and filtered signal with 4π2a=0.0135，b=0.0188 and λ=1.9.

从图 2b可以看出，算法可以很好的保护滤波后信号的局部极值，几乎没有衰减.在图 2c中，由于反扩散项的作用，滤波信号在降噪的同时，其波峰与波谷都放大了.

接着对理想信号添加不同信噪比的高斯白噪声(分别为5 dB，0 dB和-5 dB)，并选用与图 2b相同的参数进行滤波.图 3a，b和c分别表示理想信号在不同噪声强度下的滤波结果.从滤波结果中可以看出，本文算法有很强的抗噪性，并且在去噪的同时，对信号的幅度又有很好的保护.

为了有一个量化的结果，针对图 2b所选择的参数，计算了在不同噪声环境下滤波前后的信噪比，如表 1所示.信噪比的公式为

其中u0表示纯净理想信号，u表示滤波信号，N 是数据点数.
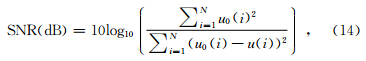
表 1 滤波前后信噪比Table 1 Snrs of the filtering results

从表 1可以看出，滤波后信号的信噪比与滤波前相比有大幅度的提高.

第二个实验对象是合成地震记录.记录由100道雷克子波组成，采样频率为1000 Hz.记录中包含了两个双曲同相轴，主频分别为30 Hz和25 Hz，速度分别为1200 m/s和1500 m/s.在合成记录中添加了信噪比为-5 dB的高斯白噪声组成了噪声记录.图 3a和图 3b分别给出了原始记录和噪声记录.

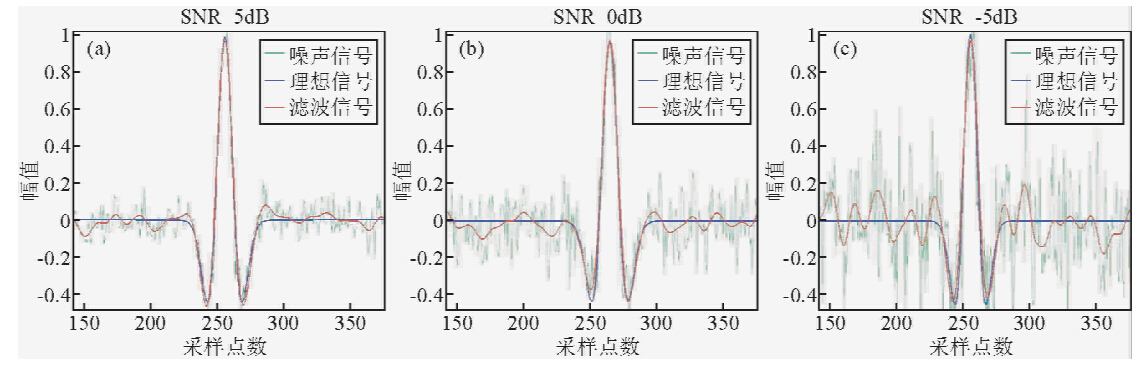图 3 理想信号在不同信噪比下的滤波结果
(a)信噪比为5 dB;(b)信噪比为0 dB；(c)信噪比为-5 dBFig. 3 The filtering results of the ideal signal under different signal-to-noise ratio
(a)SNR=5 dB;(b)SNR=0 dB;(c)SNR=-5 dB.

滤波结果如图 4a所示，图 4b表示原始记录与滤波记录的差记录.从图中可以看出，本文算法在低信噪比下仍然有较好的去噪效果，并且同相轴的幅值几乎没有衰减.

图 4 合成地震记录实验
(a)原始记录；(b)噪声记录(信噪比为-5 dB)；(c)滤波记录4π2a=0.0031，b=0.0043 and λ=1.9；(d)原始记录与滤波记录的差记录Fig. 4 Example of a synthetic seismic model
(a)Clean record.(b)Noisy record with the SNR of -5 dB.(c)Record filtered by the FCL method with 4π2a=0.0031，b=0.0043 and λ=1.9.(b)Difference between the clean and filtered records.

最后，将两处实际共炮点记录作为实验对象，如图 5所示.两幅记录均包含168道信号，每道有6145个采样点，采样频率为1000 Hz.图 5a和图 5c给出了两个地区的原始记录；图 5b和图 5d分别对应各自的滤波记录.从原始记录中可以看到，强随机噪声布满了整片区域，有效的反射轴很难辨认，大部分都被掩盖了.

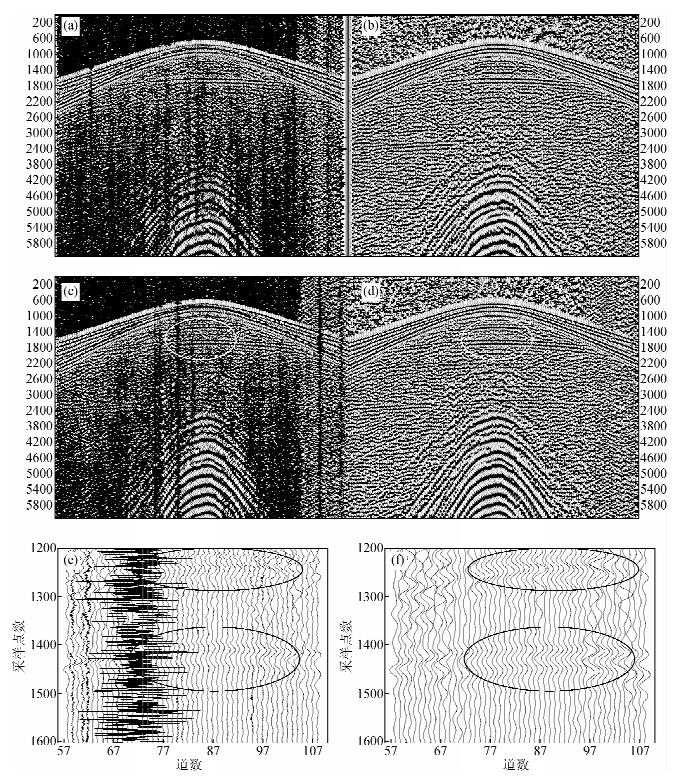图 5 实际共炮点地震记录实验
(a)原始记录1；(b)滤波记录1，4π2a=0.0016，b=0.0025 and λ=1.9；(c)原始记录2；(d)滤波记录2，4π2a=0.0033，b=0.0051 and λ=1.9；(e)原始记录2的局部放大；(f)滤波记录2的局部放大Fig. 5 Example of a real common shot point(CSP)seismic records
(a)Real seismic record.(b)Filtered record with 4π2a=0.0016，b=0.0025 and λ=1.9；(c)Real seismic record. (d)Filtered record with 4π2a=0.0033，b=0.0051 and λ=1.9.(e)Partial enlarged drawings of(e). (f)Partial enlarged drawings of(d).

本文算法对于共炮点记录是按道处理的.从图 5b和图 5d中可以看出，两幅记录的处理效果比较理想，大部分随机噪声都被去除了，反射同相轴清晰可见.为了有更好的细节对比，将图 5c和图 5d中椭圆框的部分局部放大，分别为图 5e和图 5f，从图中可以看出，算法可以有效地压制强噪声，同时又很好地改善了同相轴的连续性. 4 结 论

分形守恒定律是一个能同时对信号去噪与增强的滤波方法.这个新算法可以放大低、中频信号，减弱高频信号.本文详细介绍了算法的理论，并将其应用于地震信号处理.数值计算方案基于傅里叶变换，此方案在MATLAB中的运行速度很快，非常适合实际的应用.通过对合成地震记录与实际共炮点记录的测试可以发现，基于分形守恒定律的滤波方法可以有效地去除强随机噪声，进而显著改善反射同相轴的连续性与清晰度.

致 谢 作者感谢国家自然科学基金(41130421)的资助. 附录1. 对公式(7)的证明

注意到公式(7)中的Cλ是常数，最终可与b合并，所以在证明的过程省略了Cλ.

证明：因为

令y=tz，上式可得到：

将(15)，(16)的结果代入(7)，然后使用富比尼定理，可以得到：

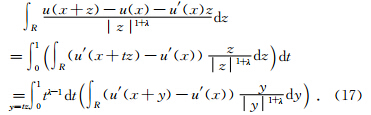
这里使用与式子(15)和(16)同样的积分方法，可以推出：

将式子(18)代入(17)的最后一个等号，可得

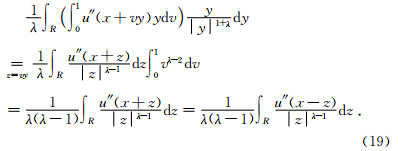
证毕. 附录2 公式(9)中φ(ω)的推导过程

根据傅里叶变换的时移、微分性质，可以从式子(8)得到：

再根据欧拉公式将上式中的 e 指数展开，可得到：

令z′=ωz，则上式存在正数aI，bI，使得：

参考文献
[1] Alibaud N, Azerad P, Isebe D. 2010. A non-monotone nonlocal conservation law for dune morphodynamics[J]. Differ. Integral. Equat., 23(1-2): 155-188.
[2] Azerad P, Bouharguane A, Crouzet J F. 2012. Simultaneous denoising and enhancement of signals by a fractal conservation law[J]. Commun. Nonlinear Sci. Numer. Si., 17: 867-811.
[3] Cao S Y, Chen X P. 2005. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2(2): 70-74.
[4] Deng X Y, Li Y. 2007. Study of parameters setting for least square support vector machine based on Ricker wavelet kernel in the denoising applications of seismic prospecting signals[J]. Progress in Geophysics (in Chinese), 22(3): 953-959.
[5] Fowler A C. 2001. Dunes and drumlins[A].//Provenzale A, Balmforth N J eds. Geomorphological Fluid Mechanics[M]. Berlin: Springer-Verlag, 430-454.
[6] Fowler A C. 2002. Evolution equations for dunes and drumlins[J]. Rev. R. Acad. de Cienc. Exactas Fis. Nat. Ser. A. Mat., 96(3): 377-387.
[7] Gao J H, Mao J, Man W S, et al. 2006. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese J. Geophys. (in Chinese), 49(4): 1155-1163.
[8] Li Y, Lin H P, Yang B J, et al. 2009. The influence of limited linearization of time window on TFPT under the strong noise background[J]. Chinese J. Geophys. (in Chinese), 52(7): 1899-1906.
[9] Li Y, Peng J L, Ma H T, et al. 2013. Study of the influence of transition IMF on EMD do-noising and the improved algorithm[J].Chinese J. Geophys. (in Chinese), 56(2): 626-634, doi: 10.6038/cjg20130226.
[10] Li Z C, Sun X D, Liu H. 2006. Common reflection surface stack for rugged surface topography[J]. Chinese J. Geophys. (in Chinese), 49(6): 1794-1801.
[11] Lin H B, Li Y, Xu X C. 2011. Segmenting time-frequency peak filtering method to attenuation of seismic random noise[J]. Chinese Journal of Geophysics (in Chinese), 54(5): 1358-1366, doi:10.3969/j.issn.00015733.2011.05.025.
[12] Liu G C, Chen X H, Li J Y, et al. 2011. Seismic noise attenuation using nonstationary polynomial fitting[J]. Applied Geophysics, 8(1): 18-26.
[13] Liu X W, Liu H, Li Y M. 2003. Independent component analysis and its testing application on seismic signal processing[J]. Chinese J. Geophys. (in Chinese), 18(1): 90-96.
[14] Lu W K, Ding W L, Zhang S W, et al. 2005. A high-resolution processing technique for 3-D seismic data based on signal sub-space decomposition[J]. Chinese J. Geophys. (in Chinese), 48(4): 896-901.
[15] Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J. Geophys. (in Chinese), 51(2): 603-610.
[16] Tian Y N, Li Y, Wang B, et al. 2012. A novel convolutive ICA for seismic data denoising[C].//Qian Z H, Cao L, Su W L, et al, eds. Recent Advances in Computer Science and Information Engineering: Lecture Notes in Electrical Engineering. Berlin: Springer, 95-101.
[17] Yang K, Xu S Y, Wang H Z, et al. 2005. A method of dip decomposition common reflection surface stack[J]. Chinese J. Geophys.(in Chinese), 48(5): 1148-1155.
[18] Zhong W, Yang B J, Zhang Z. 2006. Research on application of polynomial fitting technique in highly noisy seismic data[J]. Progress in Geophys. (in Chinese), 21(1): 184-189.
[19] 邓小英, 李月. 2007. Ricker子波核最小二乘支持向量机在地震勘探信号去噪应用中的参数设置研究[J]. 地球物理学进展, 22(3): 953-959.
[20] 高静怀, 毛剑, 满蔚仕,等. 2006. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 49(4): 1155-1163.
[21] 李月, 林红波, 杨宝俊,等. 2009. 强随机噪声条件下时窗类型局部线性化对TFPF技术的影响[J]. 地球物理学报, 52(7): 1899-1906.
[22] 李月, 彭蛟龙, 马海涛,等. 2013. 过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J]. 地球物理学报, 56(2): 626-634, doi: 10.6038/cjg20130226.
[23] 李振春, 孙小东, 刘洪. 2006. 复杂地表条件下共反射面元(CRS)叠加方法研究[J]. 地球物理学报, 49(6): 1794-1801.
[24] 林红波, 李月, 徐学纯. 2011. 压制地震勘探随机噪声的分段时频峰值滤波方法[J]. 地球物理学报, 54(5): 1358-1366, doi:10.3969/j.issn.00015733.2011.05.025.
[25] 刘喜武, 刘洪, 李幼铭. 2003. 独立分量分析及其在地震信息处理中应用初探[J]. 地球物理学进展, 18(1): 90-96.
[26] 陆文凯, 丁文龙, 张善文,等. 2005. 基于信号子空间分解的三维地震资料高分辨率处理方法[J]. 地球物理学报, 48(4): 896-901.
[27] 汤井田, 化希瑞, 曹哲民,等. 2008. Hilbert-Huang 变换与大地电磁噪声压制[J]. 地球物理学报, 51(2): 603-610.
[28] 杨锴, 许士勇, 王华忠,等. 2005. 倾角分解共反射面元叠加方法[J]. 地球物理学报, 48(5): 1148-1155.
[29] 钟伟, 杨宝俊, 张智. 2006. 多项式拟合技术在强噪声地震资料中的应用研究[J]. 地球物理学进展, 21(1): 184-189.