2. 防灾科技学院, 三河 065201
2. Institute of Disaster Prevention, Sanhe 065201, China
谱元法(Spectral Element Method,SEM)属于广义有限元法,是建立在波动方程的变分或弱形式理论基础上,求解偏微分方程的一种有效的数值计算方法(严珍珍等,2009).该法最早由Patera在求解Navier-Stokes方程数值解时提出(Patera,1984).它将有限元法和伪谱法相结合,不仅具有有限元法处理复杂结构的几何灵活性,还具有伪谱法高精度和快速收敛的特性.谱元法的基本思想是首先将计算区域划分成有限个单元,然后在每个单元上采用伪谱法,通过在每个单元中配置不均匀的分布节点,把单元的近似解表示成截断的正交多项式展开式,最后采用Galerkin方法求解得到全局的近似解,从而完成对区域内波传播过程的数值模拟(王秀明等,2007;彭海阔,2007;严珍珍等,2009;刘启方等,2013).
采用不同的正交多项式,就可以得到不同形式的谱元法,常见的有Chebyshev谱元法和Legendre谱元法.Priolo和Seriani(1991)首先在声波的传播过程中采用了Chebyshev谱元法,随后该法才被应用于地震波传播问题的数值模拟(Tessmer and Kosloff, 1994;Laurenzano et al., 2008).Maday和Patera(1989)最早将Lagrange插值基函数引入到谱元法中,并与GLL(Gauss-Lobatto-Legendre)积分相结合,将积分节点取为插值点,从而形成了Legendre谱元法.Komatitsch和Vilotte(1998)通过模拟地震波在复杂地质体中的传播过程,证明了Legendre谱元法在地震动模拟中的有效性.此后,科研工作者在此基础上开展了大量的研究工作,使谱元法不仅能用于非均匀、各向异性以及复杂地质构造区域二维或三维地震动场的模拟,还能用于全球地震波的传播模拟,并认为在达到同等精度的前提下,该法能够通过采用较稀疏单元划分,很好的解决有限元方法因单元内高阶插值带来的Runge现象,且易于实现并行计算(Komatitsch and Tromp, 1999; Priolo,2001; Komatitsch and Tromp, 2002; Komatitsch et al., 2004; Lee et al., 2008; Tromp et al., 2008;Stupazzini et al., 2009; 严珍珍等,2009; Smerzini and Villani, 2012).
与传统方法相比,谱元法是一种新的数值计算方法.虽然其在理论上还有待进一步完善,但由于结合了有限元法处理复杂结构的几何灵活性和伪谱法高精度、快速收敛的特性,目前已成为进行大尺度、复杂地质结构模型地震动数值模拟分析的重要工具.然而,根据目前掌握的资料,在中国采用谱元法进行地震动模拟分析的研究并不多,对其理论进行详细分析和总结的更少.与Chebyshev谱元法相比,Legendre谱元法由于将GLL积分节点取为插值点,生成的质量矩阵为对角矩阵,数值计算为简单的显示时间积分过程,具有计算实现过程简单、计算效率高等特点.因此,本文将以Legendre谱元法为例,首先从多个方面对其理论进行阐述,然后对其在国内外的应用现状进行分析和总结,最后采用该法简单分析了埋藏基岩地形对地表地震动的影响作用.本文对推动谱元法在地震动模拟中的应用具有重要的理论价值.
1 谱元法理论 1.1 弹性波动方程及其弱形式假定有一非均匀各向异性的介质空间,如图 1所示.图中模型的区域为



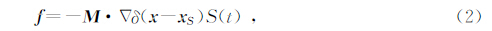
在弹性各向异性介质中,应力张量 σ 可按Hooke定律表示如下:


 | 图 1 介质空间 Fig. 1 The media space |
在谱元法中,为了对波动方程进行数值求解,需采用加权余量原理在方程(1)的两端同时点乘一个任意的测试函数 w,然后在整个计算域 Ω 内进行积分,即:

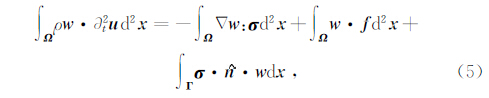
理论上,对任何的测试函数 w,波动方程的强形式和弱形式都是一样的.弱形式最明显的特征是它自然满足σ·n= 0 的边界条件.故采用弱形式不仅能很好的模拟波动在线弹性介质中的传播,而且对非弹性介质、表面地形和面波传播的模拟也更为精确(Komatitsch and Viotte, 1998; Komatitsch and Tromp, 1999).但是,弱形式的计算量较大,对计算机的内存空间有一定要求.
1.2 空间离散为了求解方程(5)的弱形式解,与有限元法类似,首先将整个计算区域 Ω 分解成Ne个不重叠的单元,如图 2所示.若将第 e个单元记为Ω e,则有:
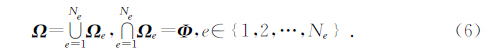
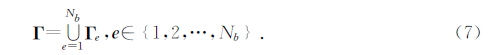
 | 图 2 介质空间的单元划分 Fig. 2 The element division for media space |
谱元法中,常将计算单元划分为结构网格,如二维模拟中的四边形单元和三维模拟中的六面体单元.这样不仅具有通过张量积构造基函数的方便性,还能保证模拟结果具有谱方法的高阶精度性,且易于实现并行运算(Komatitsch and Tromp, 1999; Komatitsch et al.,2001).但是,对于不能全划分为结构网格的复杂模型,也可以划分为非结构网格,如二维模拟中的三角形单元和三维模拟中的四面体单元.不同的是,此时需要经过一些特殊的处理,如通过集合投影方式构建Fekete内插节点进行精确近似时,就需要特殊的投影算子等( Taylor & Wingate,2000; Taylor et al.,2000).为了探讨采用非结构网格划分单元时的模拟精度,Komatitsch等(2001)分别采用结构网格、非结构网格和混合网格对均匀介质中弹性波的传播特性进行了数值模拟研究.研究结果表明,在相同单元尺寸下,非结构网格上的谱元法精度比结构网格上的低.
为了保证叙述的简洁性,文中以下部分的论述以二维谱元法为例,三维谱元法的情况依此类推.
在将二维模型域剖分成Ne个四边形单元后,为了便于计算,常引入一个正方形标准参考单元区域 Λ =[-1,1]×[-1,1],其上任意一点 ψ = ξ,η 都满足-1≤ξ,η≤1的条件.其中,ψ 中的元素也常用ξi(i=1,2)来表示,并计
ξ1=ξ,ξ2=η .
现假定对任意单元 Ω e,在单元局部坐标和标准参考单元间存在一个可逆的映射函数Fe: Λ Ω e,通过它可进行实际物理区域与参考单元之间的转换,从而使计算统一在参考单元中进行.因此,对于单元 Ω e上的任意一点 x = x,y,在参考单元中都有一点 ψ = ξ,η 与其相对应,即有

 | 图 3 不同节点数的四边形单元 Fig. 3 Quadrangles of different control nodes |
在谱元法中,形函数Na(ξ,η)常由1阶或2阶的Lagrange插值基函数构成.式(9)为n阶Lagrange插值基函数的表达式,即:
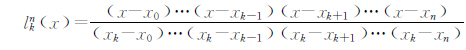


根据式(9)和(10),很容易得出1阶Lagrange插值基函数的两个插值点:x0=-1,x1=1,其对应的多项式分别为:l10 x = 1-x /2,l11 x = 1+x /2;同理,2阶Lagrange插值基函数的三个插值点:x0=-1,x1=0,x2=1,其对应的多项式分别为:l20 x =x x-1 /2,l21 x =1-x2,l22 x =x x+1 /2.这样一来,将这些不同的插值基函数进行不同的组合就能得到一系列不同形式的形函数Na(ξ,η).
在二维谱元法中,形函数的个数与插值基函数的阶数是相关的,并满足如下关系式为

根据式(11)可知,图 3中4节点四边形单元的形函数可由1阶Lagrange插值基函数的多项式组合而成,即N1(ξ,η)=l10(ξ)l10(η),N2(ξ,η)=l11(ξ)l10(η),N3(ξ,η)=l10(ξ)l11(η),N4(ξ,η)=l11(ξ)l11(η).同理,9节点四边形单元的形函数则可由2阶Lagrange插值基函数的多项式组合而成.
由于进行了映射变换,任意一个物理单元与标准参考单元间的面积关系可表示为

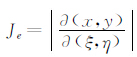

在完成区域剖分后,为了求解方程(5)的解,还需确定计算单元的具体函数表达式.在传统的有限单元法中,表征单元特性的函数表达式一般都选用低阶的Lagrange插值多项式做基函数,而在谱元法中则常选用高阶的Lagrange插值多项式做基函数,这是谱元法与有限单元法的主要区别.一般认为选用4-8阶Lagrange多项式作为基函数能很好地保证计算的精度和稳定性(Seriani and Priolo, 1994; Komatitsch and Vilotte, 1998).此外,在谱元法中,Lagrange多项式的插值节点常取为GLL积分节点.GLL积分节点定义为方程

 | 图 4 5个4阶Lagrange多项式的GLL配置点分布图 Fig. 4 5 Lagrange Polynomials of degrees N=4 at the GLL points |
GLL积分节点确定后,按照1.2节中的方法构造Lagrange插值多项式,得到每个单元的形函数,然后再按照一定的映射规则就可以得到每个单元 Ω e上函数的多项式逼近函数.如对二维空间内的任意函数f(u或w 的分量)可近似的表示为



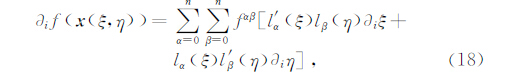
f(x(ξ,η))在单元 Ω e上的数值积分,则可通过GLL积分进行计算,即:

1.4 全局聚合计算
根据以上对离散单元 Ω e内插函数地分析,易得:
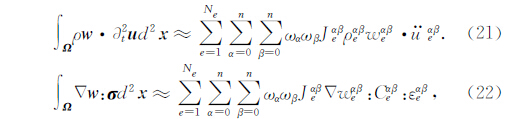
对于震源项,根据式(2)并结合Dirac Delta分布的性质,可得到


最后,整理以上公式,并按照一定的顺序进行叠加,就可得到单元 Ω 在时间域上的二阶线性常微分方程组,即:

1.5 时间离散
为了求解(25)式所示的线性方程组,谱元法中采用的方法有经典Newmark方法、4阶6步龙格库塔法(RK4-6)和4阶4步龙格库塔法(RK4).其中经典Newmark方法为最常采用的方法,该法是1959年由N.M.Newark发展的一类时间步进法,它基于两个公式(Newmark,1959):
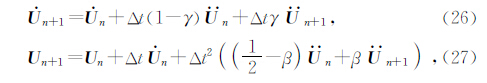
在谱元法中,常取γ=,β=0来进行计算,此时式(26)、(27)变为
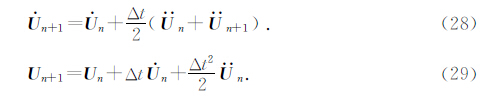
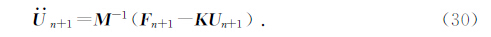
1.6 算法的精度与稳定性
研究结果表明,采用谱元法进行数值计算时,为了使地震波场能得到合理准确的模拟,保证计算结果的精度,要求在每个波长内至少包含5个GLL积分点(Faccioli et al., 1997; Komatitsch and Vilotte, 1998).这实质上就是要求模型的单元尺寸、Lagrange多项式的阶数和传播介质的最短波长之间需满足一定的关系(Cupillard et al., 2012),即:

此外,与其它数值计算方法一样,谱元法中也需要保证计算的稳定性.若采用Newmark积分方法,由于该法为条件稳定,为了保证整个计算过程的稳定,则要求时间步长Δt的取值必须满足CFL(Courant-Friedrichs-Lewy)条件(Chaljub et al., 2007; Cupillard et al., 2012),即:

|
|
表 1 弹性模拟中CFL条件数的上限值(Vp/Vs= 2) Table 1 CFL upper bound for an elastic simulation with Vp/Vs= 2 |
Seriani 等(1992)最先将谱元法引入弹性波动方程的数值求解中,此后科研工作者在此基础上开展了大量的研究工作,使其不仅适用于非均匀、各向异性以及复杂地质构造区域的二维或三维地震动场模拟,还能用于全球地震波的传播模拟.例如,Komatitsch和Vilotte(1998)用谱元法对弹性波在复杂地质体中的传播进行了模拟,证明该法是一种进行二维或三维地震动模拟的有效方法,特别是能较准确的模拟瑞利波的传播、地震波的表面衍射以及不规则表面瑞利波与体波的转换等;Komatitsch和Tromp(1999)分别采用谱元法和离散波数法/ 反射率法模拟了三维层状模型的地震动响应,
结果表明无论是采用单点力震源,还是采用地震矩张量震源,谱元法对体波和面波的传播过程都能较好的模拟,且还能考虑粘弹性衰减、地形等因素对地震动的影响;Priolo(1999,2001)从网格划分、震源定义、模拟精度以及计算效率等方面详细讨论了谱元法在工程地震中的应用,并根据对意大利西西里岛东岸卡塔里亚市地震动反应的模拟结果,开展了地震危险性评价工作.Komatitsch 等(2004)用谱元法模拟了洛杉矶盆地在Hollywood(2001,MW 4.2)地震和Yorba Linda(2002,MW 4.2)地震作用下的三维地震动反应,结果表明该法能较好地模拟盆地模型中周期大于2 s、区域模型中周期大于6 s的地震动.Laurenzano等(2008)采用二维谱元法研究了Marche地区Treia和Cagli市在同一参考地震作用下的地震动反应,结果表明震源机制、地质构造以及场地条件是影响该区地震动反应大小的主要因素,并认为大面积深厚冲积物沉积层是导致Cagli市出现部分烈度异常现象的主要原因.Smerzini和Villani(2012)对2009年L’Aquila地震(MW 6.3)的地震动反应进行了三维谱元法模拟,通过对模拟结果与实际震害分布情况的对比分析,认为该法能很好地模拟震中区频率不超过2.5 Hz的地震动,所合成的地震动波形与L’Aquila镇周围地区实际的强震动记录波形吻合良好.
此外,Lee 等(2008,2009)基于谱元法分别研究了台北盆地内和阳明山地区的地震动反应,结果表明盆地深度和浅层剪切波速是控制盆地内地震动放大的主要因素,山顶或山脊处的PGA值相对水平地表的变化一般在50%左右,而与山谷之间的差值最大可达2倍以上.严珍珍等(2009)根据弹性波理论,在考虑地表地形、地球介质衰减及地球椭率等特性的基础上,采用AK135理论地球模型,利用谱元法分别模拟了由人工点源和复合源激发的汶川大地震地震波全球传播过程,结果不仅显示了地震波在地球表面的传播形态,还证明了汶川大地震破裂过程为一个由多阶段破裂组成的复合破裂过程.周红(2010)采用谱元法模拟了点源激发下SH波的地表地震动反应,研究了地形几何形态、地震震源特性对地表地震动的影响,结果表明地震动的放大作用不仅受震源位置的控制,还受局部的地表张角控制,张角越小放大作用越强.胡元鑫等(2011)在同时考虑三维真实地形和介质衰减特性的条件下,结合ASTER DEM模型,采用谱元法对汶川地震的地形效应进行了模拟,结果较好地表现出了地震波波前形态在龙门山陡峻复杂地形影响下发生变形或扭曲,以及水平分量变化幅度大于竖向分量的特征,并且与平坦地形相比,震中附近大部分区域地形的PGA相对放大系数约为10%,部分区域地形对PGA分布及放大效应的影响强于震中距.刘启方等(2013)在考虑地形影响的基础上,采用谱元法模拟了施甸盆地在中等设定地震作用下的地震动反应,结果表明小型盆地内的地震动在这种地震作用下具有很大的空间差异,较深的小型凹陷和覆盖层厚度剧烈变化处是地震动强度增大的多发区,并认为盆地内地震动持续时间较基岩地震动明显增加,也是造成盆地震害严重的重要原因之一.
通过以上对谱元法在国内外应用现状的总结,可以看出谱元法的确是一种进行地震动数值模拟的有效方法.它不仅能模拟出各种地震波的传播过程,还能较好地反映出地形条件、场地土特性、土层结构以及断裂构造等多个因素对地震动的影响.
3 算 例
通过以上对谱元法理论和应用现状的介绍,接下来将采用该法对埋藏基岩凸起地形下地表地震动的变化情况进行简单分析.众所周知,研究埋藏基岩地形对地震动的影响,首先应研究同一震源发出的地震波在基岩面上不同部位的变化趋势,然后再研究地震波经过基岩面到达覆盖层表面后的变化趋势.因此,下面的分析中,将建立两个模型,一个为只有基岩层的基岩模型,另一个为在基岩模型上增加一覆盖层的组合模型.为了较好地体现出基岩地形对地震动的影响作用,所建模型的介质都为均匀且各向同性的.
3.1 模型建立
图 5为建立的基岩凸起地形模型,其中凸起基岩面的形状由标准椭圆方程x2/a2+z2/b2=1决定.若取椭圆地形宽度的一半为w=400 m,最大凸起高度为d=200 m,则基岩凸起地形的陡度为d/w=0.5.规定模型的左下角顶点为坐标原点,模型的横向(或水平向)为X方向,纵向(或垂直向)为Z方向,其中X方向取向右为正,Z方向取向上为正.
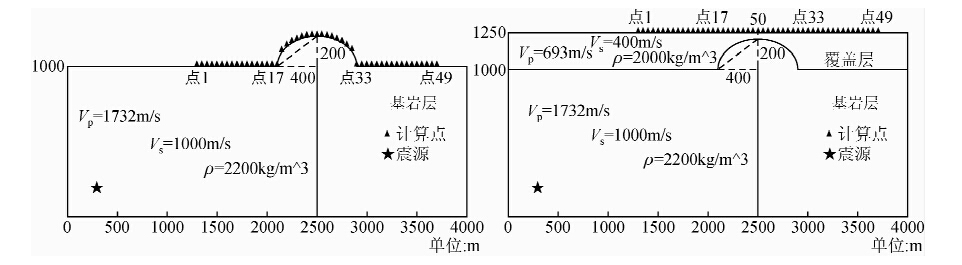 | 图 5 基岩凸起地形模型(左:基岩模型;右:组合模型) Fig. 5 The model of convex bedrock terrain(Left: Bedrock model; Right: Combined model) |
在图 5中,基岩模型为局部凸起的不规则模型,其横向尺寸为4000 m,纵向尺寸最小为1000 m,最大为1200 m;组合模型为规则的四边形模型,其横向尺寸为4000 m,纵向尺寸为1250 m.两个模型的表面都设置有49个横向间隔为50 m的计算点,每个计算点的具体位置如图中黑色小三角形所示,其中点17与点33之间的点位于基岩凸起界面或与凸起区相对应的地表面上.模型中各层介质的物理力学性质参数值和尺寸大小如图所示.
采用二维谱元法进行模拟,每个模型中的震源均设定为位于模型(300 m,300 m)处(图中五角星标记处)的双力偶点源.震源子波选用Ricker子波,取其峰值频率为fp=6 Hz,截止频率为fc=15 Hz.输入地震波的类型为P-SV波,模拟过程中同时记录X、Z方向上的加速度值.
为了满足计算的精度和稳定性要求,模型中划分单元的尺寸和时间步长都按1.6节中的要求选取,每个方向上划分单元的多少由该方向的最短尺寸确定.对于基岩模型,横向划分单元210个,纵向划分单元40个,总单元8400个;对于组合模型,横向划分单元210个,基岩层纵向划分单元40个,覆盖层纵向划分单元13个,总单元11130个.每个单元均为具有9个节点的四边形单元,并选用4阶Lagrange插值多项式为其函数表达式的基函数.两个模型设定一样的边界条件,即上边界为自由边界,左、右和下边界均为完美匹配层吸收边界,其中完美匹配层的厚度为8个单元层厚.每个模型的计算时间步长均为0.0003 s,计算总时长为15 s.
3.2 时程分析图 6为基岩凸起地形模型在P-SV波作用下的加速度时程图.为了更好地体现出各计算点波形的变化特征,图中的波动传播时长均取为8 s,且各计算点的时程曲线按震源距的大小从下到上依次排列.
 | 图 6 加速度时程图 Fig. 6 The time history of acceleration |
从图中可以看出,虽然每个图的加速度时程在整体上都具有随震源距的增大而逐渐减小的变化趋势,但在它们之间还是表现出了一些明显的差别.例如,基岩模型中,水平分量的加速度值在点17与点25之间明显偏小,而这种现象在垂直分量上却表现的不够明显,垂直分量上的加速度值除在点17附近有一定突变外,其余各点的变化都较为平缓.与基岩模型相比,组合模型中各点的加速度时程则表现出了不一样的变化特点,其内各点的波形不仅持续时间较长,还包含有较为丰富的面波成份.此外,从图中还可以看出,组合模型中水平、垂直两个方向上的加速度时程值,在与基岩凸起地形(点17与点33之间)相对应的区域都明显偏小,且偏小的范围较基岩凸起区大.
通过以上对基岩凸起地形模型中各计算点加速度时程图的定性分析,可以得出:
(1)基岩凸起地形的存在,对基岩面和地表面上的地震动强度都具有一定的影响,但影响程度各不相同.
(2)基岩凸起地形的存在,常会导致基岩面和地表面上部分计算点的地震动强度降低.其中,基岩面上地震动强度降低的点一般位于凸起基岩地形的上坡段,并且水平分量的变化幅度大于垂直分量;地表面上地震动强度降低的点则主要位于与基岩凸起地形相对应的区域,并且降低的范围较凸起区域大.
(3)覆盖层的存在,不仅延长了其上各计算点波形的持续时间,还使得它们的波形变得复杂,包含了较为丰富的面波成份.
3.3 PGA值分析
为了更好的反映出模型中各计算点地震动强度的差异,图 7给出了基岩凸起地形模型中各计算点PGA值的变化关系.可以看出,两个模型的PGA值在整体上都较好地表现出了随震源距增大而逐渐减少的变化趋势.
在基岩模型中,两个方向上的PGA值在基岩面起伏处(点17、点33附近区域)的变化幅度都较大,而在其它地方则变化不大.对于水平分量,PGA值曲线在接近基岩凸起处(点14、15、16)开始发生变化,到点17处出现陡降现象,尔后(点18、19、20)经过小幅振动后又逐渐增加,直到在点33附近区域又出现较大幅度的振动,最后才逐渐趋于平稳.而对于垂直分量,虽然其PGA值曲线在基岩面凸起处也有一定的变化,但变化的幅度不大.总之,从图中可明显看出垂直分量受基岩面起伏的影响比水平分量要小.在组合模型中,由于覆盖层的存在,其上各点PGA值的变化情况与基岩模型相比具有一定的差别.两个方向PGA值曲线的变化趋势基本相同,其中PGA值的突变区都在点17和点38附近,突变区之间则都为变化平缓且分布范围较广的PGA值减弱区.水平方向上PGA值减弱区的范围为点16与点38之间的区域,垂直方向上则为点17与点38之间的区域,两者之间相差不大,并且都大于基岩地形凸起区.
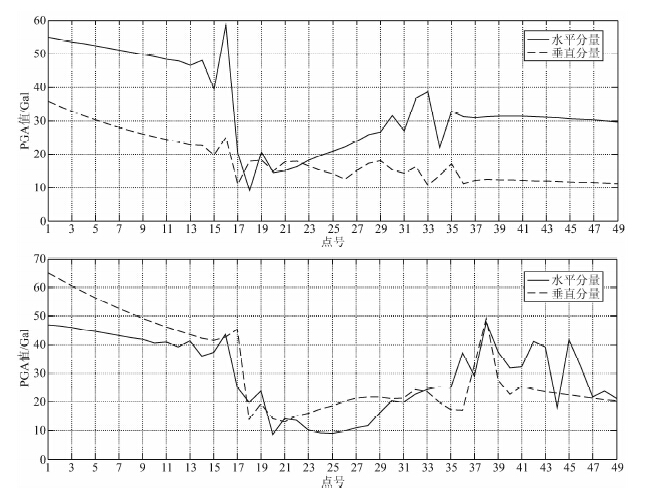 | 图 7 PGA值变化图(上:基岩模型;下:组合模型) Fig. 7 The change trend of PGA(Up: Bedrock model; Down: Combined model) |
此外,根据组合模型与基岩模型之间各点PGA比值的变化关系也可以反映出基岩地形对地震动的影响.图 8为基岩凸起地形模型中各计算点PGA比值的变化关系曲线.从图中可以看出,PGA比值即放大系数,在水平和垂直两个方向上都具有相同的变化趋势,其中垂直方向的放大系数值整体上偏大.与图 7中出现PGA值减弱区一样,图 8中也出现了放大系数减弱区,并且两者的范围基本相等.这说明,在与基岩凸起地形相对应的区域内,地表面地震动不仅强度较小,其相对基岩面地震动的放大倍数也较小.
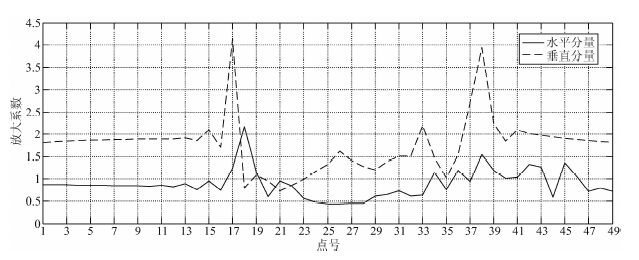 | 图 8 PGA比值图 Fig. 8 The ratio of PGA |
同理,通过以上对基岩凸起地形模型中各计算点PGA值变化关系的分析,可以发现同一震源发出的地震波,由于基岩地形的不同,其上接受波的形态和能量大小也不一样.主要表现为:
(1)基岩面上地震动强度的分布受基岩地形和地震波入射方向的控制.一般来说,地震波入射方向越接近基岩面的切线方向,其上接收的能量越小;越接近基岩面的法线方向,其上接收的能量越多.
(2)基岩地形的起伏对基岩面地震动水平分量的影响大于垂直分量.水平分量与垂直分量相比,不仅地震动强度大,在基岩面起伏处的变化幅度也大.
(3)基岩凸起地形的存在,使与凸起地形相对应区域的地表面地震动强度和放大系数都相对较小,形成地震动强度相对减弱区.与基岩凸起区相比,地震动强度相对减弱区的范围较大.
综上所述,可以看出对基岩凸起地形模型的谱元法研究,无论是时程分析还是PGA分析,都较好地体现出了基岩凸起地形对地表地震动的影响作用,即基岩凸起地形的存在,减少了地面地震动的强度,形成了地震动强度减弱区.这与Dezfulian和Seed(Dezfulian and Seed, 1970; 1971)采用有限元法得出的结论是一致的.究其原因,主要是由于凸起地形的存在,改变了地震波的射线路径,使其在基岩与覆盖层的交界面上出现多次折射、反射和透射现象,造成地震波能量在地表的发散,从而导致与凸起地形相对应区域处的地震动强度减小,形成地震动强度减弱区.
4 讨论与结论通过本文的分析,可以看出谱元法是一种进行地震动数值模拟的有效方法.它不仅能模拟出各种地震波的传播过程,还能较好地反映出地形条件、场地土特性、土层结构以及断裂构造等多个因素对地震动的影响.然而,与国外相比,国内采用谱元法进行地震动反应分析的明显偏少,其发展是明显滞后的,并且对谱元法理论进行详细总结的也很少,这很不利于该法在地震动模拟中的推广应用.因此,本文首先从弹性波动方程及其弱形式、空间离散、单元内插函数及积分、全局聚合计算、时间离散以及算法的精度和稳定性等多个方面,对谱元法的理论进行了详细的分析和总结,然后对其在地震动模拟中的应用现状进行了归纳,最后通过一个简单算例的分析,在证明采用谱元法进行地震动反应分析有效性的同时,也较好地体现出了基岩凸起地形对地表地震动的影响作用.本文不仅对推广谱元法在国内的应用具有重要的理论意义,还对开展全面的地震动模拟工作具有重要的参考价值.
当前,在地震工程领域内,科研工作者已不再满足对一些局部、简单模型的数值模拟分析,而逐渐趋向于一些大尺度、复杂的区域性甚至全球性模型的数值模拟分析.因为,这不仅能加深对研究问题的认识,探究问题的本质规律,还能发现一些新的科学问题,从而得出更加完善、合理、科学的解释.例如,若要对沉积盆地、烈度异常区等一些尺度较大、地质构造和局部场地条件比较复杂地区的地震动反应进行全面的研究,都需要建立大尺度、复杂的数值模型,这不仅能保证模拟结果的相对真实性,还能减少由模型简化、尺寸缩小等带来的变异性和不确定性.然而,建立大尺度、复杂的模型就会出现计算量增大、精度和稳定性不易保证等问题,即使在计算机技术空前发展的今天,这也对所采用的数值计算方法提出了较高的要求.谱元法的提出正好解决了这些问题,它不仅具有高精度和快速收敛的特性,还易于实现并行运算,用其进行数值模拟计算能大大减少内存需求和计算时间.
总的来说,只要合理考虑介质的各向异性、地质构造背景、场地条件、地形地貌以及地震动衰减特征等多种影响因素,建立正确的计算模型,在对盆地效应、地形效应、烈度异常、地震危险性评价以及区域或全球地震波传播进行研究的过程中,采用谱元法进行数值模拟分析是可行的.
| [1] | Aki K, Richards P G. 1986. Quantitative Seismology-the Theory and Method (the first volume) (in Chinese) [M]. Beijing: Seismological Press: 41-130. |
| [2] | Chaljub E, Komatitisch D, Vilotte J P, et al. 2007. Spectral-element analysis in seismology [J]. Advances in Geophysics, 48(7): 365-419. |
| [3] | Cupillard P, Delavaud E, Burgos G, et al. 2012. RegSEM: a versatile code based on the spectral element method to compute seismic wave propagation at the regional scale [J]. Geophys. J. Int., 188(3): 1203-1220. |
| [4] | De Martin F. 2011. Verification of a spectral-element method code for the Southern California earthquake center LOH. 3 viscoelastic case [J]. Bull. Seismol. Soc. Am., 101(6): 2855-2865. |
| [5] | De Basabe J D, Sen M. 2010. Stability of the high-order finite elements for acoustic or elastic wave propagation with high-order time stepping [J]. Geophys. J. Int., 181(1): 577-590. |
| [6] | Dezfulian H, Seed H B. 1970. Seismic response of soil deposits underlain by sloping rock boundaries [J]. Journal of the Soil Mechanics and Foundations Division, 96(6): 1893-1916. |
| [7] | Dezfulian H, Seed H B. 1971. Response of nonuniform soil deposits to travelling seismic waves[J]. Journal of the Soil Mechanics and Foundation Division, 97(SM1): 27-46. |
| [8] | Faccioli E, Maggio F, Paolucci1 P, et al. 1997. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method [J]. Journal of Seismology, 1(3): 237-251. |
| [9] | Hu Y X, Liu X R, Luo J H, et al. 2011. Simulation of the three-dimensional topographic effects on seismic ground motion in Wenchuan earthquake region based upon the spectral-element method [J]. Journal of Lanzhou University (Natural Sciences)(in Chinese), 47(4): 24-32. |
| [10] | Komatitsch D, Barnes C, Tromp J. 2000. Simulation of anisotropic wave propagation based upon a spectral element method [J]. Geophysics, 65(4): 1251-1260. |
| [11] | Komatitsch D, Liu Q Y, Tromp J, et al. 2004. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method [J]. Bull. Seismol. Soc. Am., 94(1): 187-206. |
| [12] | Komatitsch D, Martin R, Tromp J, et al. 2001. Wave propagation in 2-D elastic media using a spectral element method with triangles and quadrangles [J]. Journal of Computational Acoustics, 9(2): 703-718 |
| [13] | Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation [J]. Geophys. J. Int., 139(3): 806-822. |
| [14] | Komatitsch D, Tromp J. 2002. Spectral-element simulations of global seismic wave propagation Ⅱ. Three-dimensional models, oceans, rotation and self-gravitation [J]. Geophys. J. Int., 150(1): 303-318. |
| [15] | Komatitsch D, Vilotte J P. 1998. The spectral-element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures [J]. Bull. Seismol. Soc. Am., 88(2): 368-392. |
| [16] | Laurenzano G, Priolo E, Tondi E. 2008. 2D numerical simulations of earthquake ground motion: examples from the Marche region, Italy [J]. Journal of Seismology, 12(3): 395-412. |
| [17] | Lee S J, Chen H W, Liu Q Y, et al. 2008. Three dimensional simulations of seismic-wave propagation in the Taipei basin with realistic topography based upon the spectral-element method [J]. Bull. Seismol. Soc. Am., 98(1): 253-264. |
| [18] | Lee S J, Chan Y C, Komatitsch D, et al. 2009. Effects of realistic surface topography on seismic ground motion in the Yangminshan region of Taiwan based upon the spectral-element method and LiDAR DTM [J]. Bull. Seismol. Soc. Am., 99(2A): 681-693. |
| [19] | Liu Q F, Yu Y Y, Zhang X B. 2013. Three-dimensional ground motion simulation for Shidian Basin [J]. Journal of Earthquake Engineering and Engineering Vibration (in Chinese), 33(4): 54-60. |
| [20] | Maday Y, Patera A T. 1989. Spectral element methods for the incompressible Navier-Stokes equations [Z]. New York: American Society of Mechanical Engineers, 71-413. |
| [21] | Newmark N M. 1959. A method for computation of structural dynamics [C]// Engineering Mechanics Division: Proceedings of the American Society of Civil Engineers, 85(EM3): 67-94 |
| [22] | Patera A T. 1984. A spectral element method for fluid dynamics: laminar flow in a channel expansion [J]. Journal of Computational Physics, 54(3): 468-488. |
| [23] | Peng H K. 2007 Research on spectral element method-based characteristics of guided wave propagation and damage identification in structures[Ph. D. thesis]. Shanghai: Shanghai Jiaotong University, 1-140. |
| [24] | Peter D, Komatitsch D, Luo Y, et al. 2011. Forward and adjoint simulations of seismic wave propagation on fully unstructured hexahedral meshes [J]. Geophys. J. Int., 186(2): 721-739. |
| [25] | Priolo E. 1999. 2-D spectral element simulations of destructive ground shaking in Catania (Italy) [J]. Journal of Seismology, 3(3): 289-309. |
| [26] | Priolo E. 2001. Seismic ground motion simulation through the 2-D spectral element method [J]. Journal of Computational Acoustics, 9(4): 1561-1581. |
| [27] | Priolo E, Seriani G. 1991. A numerical investigation of Chebyshev spectral element method for acoustic wave propagation[C]// Dublin: Proceedings of the 13th IMACS Conference on Comparative Applied Mathematics. Dublin: Ireland, 551-556. |
| [28] | Seriani G, Priolo E. 1994. Spectral element method for acoustic wave simulation in heterogeneous media [J]. Finite Elements in Analysis and Design, 16(3-4): 337-348 |
| [29] | Seriani G, Priolo E, Carcione J M, et al. 1992. High-order spectral element method for elastic wave modeling [C]// 62nd Annual International Meeting, SEG, Expanded Abstracts: 1285-1288. |
| [30] | Smerzini C, Villani M. 2012. Broadband numerical simulations in complex near-field geological configurations: the case of the 2009 Mw 6. 3 L'Aquila earthquake [J]. Bull. Seismol. Soc. Am., 102(6): 2436-2451. |
| [31] | Stupazzini M, Paolucci R, Igel H. 2009. Near-fault earthquake ground-motion simulation in the Grenoble valley by a high-performance spectral element code [J]. Bull. Seism. Soc. Am., 99(1): 286-301. |
| [32] | Taylor M A, Wingate B A. 2000. A generalized diagonal mass matrix spectral element method for non-quadrilateral element [J]. Applied Numerical Mathematics, 33(1-4): 259-265. |
| [33] | Taylor M A, Wingate B A, Vincent R E. 2000. An algorithm for computing fekete points in the triangle [J]. SIAM Journal on Numerical Analysis, 38(5): 1707-1720. |
| [34] | Tessmer E, Kosloff D. 1994. 3-D elastic modeling with surface topography by a Chebyshev spectral method [J]. Geophysics, 59(3): 464-473. |
| [35] | Tromp J, Komatitsch D, Liu Q Y. 2008. Spectral-element and adjoint methods in seismology [J]. Commun. Comput. Phys., 3(1): 1-32. |
| [36] | Wang W S, Li X F, Lu M W, et al. 2012. Structure-preserving modeling for seismic wavefields based upon a multisymplectic spectral element method [J]. Chinese J. Geophys. (in Chinese), 55(10): 3427-3439. |
| [37] | Wang X M, Seriani G, Lin W J. 2007. Some theoretical problems of calculating elastic wave field by using the spectral element method [J]. Science China Physics, Mechanics & Astronomy (in Chinese), 37(1): 41-59. |
| [38] | Xing Y F, Guo J. 2012. A self-adaptive Newmark method with parameters dependent upon structural dynamic characteristics [J]. Chinese Journal of Theoretical and Applied Mechanics (in Chinese), 44(5): 904-911. |
| [39] | Yan Z Z, Zhang H, Yang C C, et al. 2009. The numerical simulation of seismic wave propagation by the spectral element method in Wenchuan great earthquake [J]. Science China Earth Sciences (in Chinese), 39(4): 393-402. |
| [40] | Zhou H, Gao M T, Yu Y X. 2010. A study of topographical effect on SH waves [J]. Progress in Geophys. (in Chinese), 25(3): 775-782. |
| [41] | 安艺敬一, 理查兹P G. 1986. 定量地震学——理论和方法(第一卷)[M]. 北京: 地震出版社: 41-130. |
| [42] | 胡元鑫, 刘新荣, 罗建华, 等. 2011. 汶川震区地震动三维地形效应的谱元法模拟[J]. 兰州大学学报(自然科学版), 47(4): 24-32. |
| [43] | 刘启方, 于彦彦, 章旭斌. 2013. 施甸盆地三维地震动研究[J]. 地震工程与工程振动, 33(4): 54-60. |
| [44] | 彭海阔. 2007. 基于谱元法的导波传播机理及结构损伤识别研究[博士论文]. 上海: 上海交通大学: 1-140. |
| [45] | 汪文帅, 李小凡, 鲁明文, 等. 2012. 基于多辛结构谱元法的保结构地震波场模拟[J]. 地球物理学报, 55(10): 3427-3439. |
| [46] | 王秀明, Seriani G, 林伟军. 2007. 利用谱元法计算弹性波场的若干理论问题[J]. 中国科学(G辑): 物理学 力学 天文学, 37(1): 41-59. |
| [47] | 邢誉峰, 郭静. 2012. 与结构动特性协同的自适应Newmark方法[J]. 力学学报, 44(5): 904-911. |
| [48] | 严珍珍, 张怀, 杨长春,等. 2009. 汶川大地震地震波传播的谱元法数值模拟研究[J]. 中国科学(D辑): 地球科学, 39(4): 393-402. |
| [49] | 周红, 高孟潭, 俞言祥. 2010. SH波地形效应特征的研究[J]. 地球物理学进展, 25(3): 775-782. |
 2014, Vol. 29
2014, Vol. 29

