地球物理学进展  2014, Vol. 29 Issue (2): 718-724   PDF    
引用本文
冯德山, 杨炳坤, 戴前伟, 王鹏飞. 2014. 超高密度电法全四极装置正反演[J]. 地球物理学进展, 29(2): 718-724, doi: 10.6038/pg20140233  
FENG De-shan, YANG Bing-kun, DAI Qian-wei, WANG Peng-fei. 2014. The simulation and inversion for the full-four-pole array of Ultra-High density resistivity method. Progress in Geophysics, 29(2): 718-724, doi: 10.6038/pg20140233   
超高密度电法全四极装置正反演
冯德山1,2, 杨炳坤1,2, 戴前伟1,2 , 王鹏飞1,2    
1. 中南大学 地球科学与信息物理学院, 长沙 410083;
2. 有色金属成矿预测教育部重点实验室, 长沙 410083
收稿日期: 2013-11-15 修回日期: 2014-2-22 .
基金项目：国家自然科学基金项目（41074085）、教育部新世纪优秀人才支持计划（NCET-12-0551）、教育部博士点基金（No. 20120162110015）和中南大学升华育英人才支持计划项目共同资助.
作者简介：冯德山，男，1978年生，湖南祁阳人，博士，副教授，从事地球物理数据处理与正反演研究.（E-mail：fengdeshan@126.com）
通讯作者：戴前伟，男，1968年生，湖南涟源人，博士，教授，从事电磁法方法及理论、工程地球物理勘探等方向的研究.（E-mail：qwdai@csu.edu.cn）
摘要：超高密度电法是一种新型、高效且实用的电法勘探方法，数据信息量是常规方法的数十倍以上. 本文从超高密度电法的基本理论与数据采集方式入手，阐述了超高密度电法的全四极装置观测方式，推导了基于双线性插值、三角形剖分的超高密度电法正问题有限单元法求解方法；提出了超高密度电法的偏导数矩阵混合求解及最小二乘广义线性反演算法.以一个典型地电模型为例，分别采用超高密度全四极装置与五种常规排列装置进行正演模拟并反演成像，反演结果表明，超高密度全四极装置相对于单一装置采集方式具有探测数据量大、抗干扰能力强、数据反演异常结果能够更好的刻画实际地质情况的特点.最后，采用超高密度电法对倾斜板状体地电模型进行正反演，说明了该方法能较好的反映出地下电性的分布，有效提高物探解释的可靠性及勘探的准确性.
关键词： 超高密度电法     全四极装置观测方式     有限单元法     正演模拟     反演成像    
The simulation and inversion for the full-four-pole array of Ultra-High density resistivity method
FENG De-shan1,2, YANG Bing-kun1,2, DAI Qian-wei1,2 , WANG Peng-fei1,2    
1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083, China
Abstract: The Ultra-High density resistivity method(UHDRM) is a new, efficient and practical electrical prospecting method. The amount of its data information is ten times more than conventional method. This paper firstly focuses on the full four-pole device observing way of the Ultra-High density resistivity method starting from its basic theories and data collection methods. Secondly, it applies the finite element method to solve the forward simulation of Ultra-High density resistivity method based on the bilinear interpolation and triangulation; and it also puts forward the hybrid algorithm of partial derivative matrix and the inversion algorithm of the least square generalized linear for the super density electrical method; Taking the typical geoelectric model as an example, it uses the full four-pole device of Ultra-High density and five conventional arrangement of devices respectively to do the forward simulaition and inversion imaging. The inversion result showes, the Ultra-High density resistivity method has the advantages such as large amount of detecting datas, strong anti-disturbing ability and abnormal results of data inversion could characterize the actual geological conditions better. Lastly, this paper does the modeling and inversion to the tilt plate-shaped body model through the Ultra-High density resistivity method, which shows this method can reflect the underground electrical distribution better, and improve the reliability and the accuracy of the geophysical interpretation and exploration.
Key words: Ultra-High density resistivity method     full-four-pole array     finite element method     forward simulation     inversion imaging    
0 引 言

电法勘探已有近百年的发展历史，其理论、技术、仪器、正反演方法都日趋成熟(Loke & Dahlin，2002；李金铭，2005；Shashi，2012).但常规电法常采用某一装置，采集数据量少，工作效率低；而高密度电法按装置固有的布极方式进行测量(Zhou & Dahlin，2003；黄俊革等，2006)，按设定装置进行电阻率断面图反演(Zhang & Liu，2011).它未能充分利用电极阵，造成采集数据信息非常有限，反演的精度也较低，很难满足复杂地质问题的实际勘探要求.针对此类缺陷，阿德雷德大学Australia ZZ Resistivity Imaging研发中心设计出Flash RES多通道超高密度直流电法勘探系统(Greenhalgh，Zhou and Green. 2006;Zhe，Greenhalgh and Marescot， 2007).该系统不受电极装置和数据采集方式的限制，采用多通道技术，所有电极可同时进行数据采集，充分利用已布置好的电极，只需一次布极可完成全部电极上的测量(王鹏飞，2012)，且采集时间与普通高密度电阻率法一样.并且因为采集的信息量大，所以反演后的结果更准确、精度更高.

因为超高密度电法具有上述诸多优点，它作为新方法被工程地质界快速接受并被广泛应用.如：矿山边坡的采空区的勘查(王德中等，2010)；岩溶、破碎带追索(黄杰等，2009；胡树林等，2011)；深部矿体的走向确定(毛洪江，2011)；富水异常区圈定(宋洪伟，2011)；煤矿砂体探测(孙林，2012).为了更好地了解超高密度电法的特点，对超高密度电法的勘探技术及资料处理方法提出有效的指导，本文针对超高密度电法的全四极装置开展了正反演，并将该方法探测的反演效果与其他装置的反演效果进行了对比，验证了该方法的准确性和有效性，可为超高密度电法的进一步研究、应用与推广奠定基础.

1 超高密度电法基本原理

超高密度电法与传统电法勘探的原理是相同的，也是以岩、矿石的电性差异为物性基础的探测方法.通过用供电电极AB向地下输入电流强度为I的供电电流，再测量电极MN上电流I在介质(地下土壤、岩石等)中产生的电位差ΔU.超高密度激电法不受任何采集装置和单一的采集参数的限制，可在同等的测量时间和测量电极中采集数十倍于常规高密度电阻率法所采集的数据量，它突破了原有的单一装置排列模式的限制，不再区分观测装置方式，而是采用除供电电极AB外对所有MN进行数据采集，可能出现如偶极排列、温纳排列和施伦贝谢尔排列等，故我们暂称为“全四极装置观测方式”.在全四极装置中现假设以64根电极为例，将每个排列的64根电极分为奇数组32个(1，3，5，…，61，63)和偶数组32个(2，4，6，…，62，64)的2组电缆，然后在这两组电极中任选取一个作为供电电极A和B，具体的采集方式采用供电电极奇偶配对，供电电极AB变化规律分别为1-2，1-4，…，1-64；3-2，3-4，…，63-64；…；63-2，…，63-64.在一次通电过程中同时测量其它电极所能组成的MN的电位差，这就可以得到最多61个电位(MN1，MN2，MN3，…，MN60，MN61)数据信息.而奇数组32个电极和偶数组32个电极互相配对作为供电电极，即有32×32=1024(次)供断电过程，若在保证所有电极接触良好的条件下，每次供电可最多同时采集61个电位差数据，故总的数据量大约最多为32×32×61=62464(个)，采集数据量超过常规方法40倍以上.超高密度激电法全四极装置工作如图 1所示.

图 1 超高密度电法全四极装置工作示意图
Fig. 1 Working figure of UHDRM full four-pole device
2 超高密度电法有限单元法正演

由已知电阻率的空间分布求解地电场分布情况的过程称之为超高密度电法正演，本文采用有限单元法(Finite Element Method，FEM)进行超高密度电法进行正演.假设地下介质的导电性沿走向无变化，对点电源产生的稳定电流场的电位函数作余弦傅氏变换变成二维偏微分方程，并通过沿走向y方向傅氏变换转换到波数域中进行(戴前伟等，2012；Zhou & Greenhalgh，1999).则点电流源场各节点电位的计算所满足的变分问题为

其中Ω为模拟区域，Γ∞为边界条件，σ为电导率，I为供电电极的电流强度，rA是电源点(xA，zA)至积分点的距离，k是傅氏变换波数，n 边界处法线向量，K0(λrk)，K1(λrk)分别为零阶和一阶修正贝塞尔函数.

为了更精确地拟合地形和复杂地电体，并注意到岩矿石的物性参数变化特性，有限元网格剖分方式采用三角单元，单元内转换电 位U和电导率σ设计为双线性变化，将积分区域剖分成节点总数为 N 的三角单元，对区域Ω和边界Γ∞的积分可分为对各三角单元Δ和ΓΔ的积分之和.则在单个三角单元内有

式(2)中，下标1、2和3为三角单元的三角节点号，σ=(σ1，σ2，σ3)T是节点上的电导率； U =(U1，U2，U3)T是三角单元节点上的波数域电位； N =(N1，N2，N3)T，Nl=(alx+blz+cl)/2Δ是x和z的线性函数，Δ=(a1b2－a2b1)是三角单元的面积.其中：

(x1，z1)，(x2，z2)和(x3，z3)是三角单元三角节点x和z坐标，则三角单元中的面积为

又因为

将(5)式代入(4)式，求得三角单元上积分为 

上式中：

特别注意的是，δiA当i与电流源节点A重合时则等于1，不重合则等于0.边界单元的线积分ΓΔ，假设三角单元Δ的12边落在ΓΔ上，由于无穷远边界离电源比较远，可将kσK1(krA)cos(rA，n)/K0(krA)看作常数C，提至积分号外，则积分可为

式中：

是边界单元Δ的12边边长，而θ11=3σ1+σ2，θ12=σ1+σ2，θ21=σ1+σ2，θ22=σ1+3σ2，其余θij=0.对所有三角单元求和，可得到泛函F(U)的数值表达式为

式中 K是由全部三角单元和边界单元的 K Δ1+ K Δ2+ K Δ3 相加而组成的N×N阶对称带宽矩阵，U 是由所有N个三角网格节点上的转换电位所组成的列矢量，S则是由S Δ相加而成的与源有关的列矢量.(8)式泛函F(U)对U 求变分，并令其为0，则可得到求波数域中各节点上电位的线性方程组

有限单元法求解该超高密度电法正演问题时，在(9)式带宽矩阵K 中，会存放较多零元素，占据了大量内存，因此选用恰当的求解线性方程组方法是十分重要的.本文采用Cholesky分解法(吴小平等，1998)进行求解. 3 超高密度电法二维反演

超高密度激电法的反演是根据地面上观测到的信号推测地下异常体的物理参数.其过程是首先建立一个初始的电阻率预测模型，并针对该模型进行正演计算，得到与之对应的预测数据，计算预测数据与实测数据之间的均方根误差，如果误差满足要求，则建立的模型就近似符合地下介质真实的电阻率分布，否则修正模型参数，再次进行正演，并通过不断的修正模型参数使误差函数取得极小值，这样修正后的模型参数就是地下地质体的真实参数(Mukanova & Orunkhanov，2010).

3.1 最小二乘广义线性正则化反演

在电法反演过程中，已知电阻率值变化较大，故采用对数值表示视电阻率和模型电阻率参数(Rodi & Mackie. 2001；阮百尧，2011).超高密度电阻率的线性反演方程为

其中Δ d 为数据残差矢量，其值等于实测视电阻率与模拟的视电阻率之间的对数值差值(Δdi=lnρai－lnρci，i=1，2，…，n)；Δ m 为模型参数的改正向量(Δmj=lnΔρj，j=1，2，…m)； A 为偏导数矩阵(aij=lnρci/lnρj)，ρj为第j个网格节点的电阻率.在反演过程中，方程(10)是欠定的.因此在模型空间引入某种稳定化泛函，即对模型参数施加某种先验约束，能提高反演的稳定性和得到较精确的解估计.可以单独施加光滑模型或背景模型约束，或将两者同时施加.其稳定化泛函可表示为：

局部光滑约束：

其中 m为模型参数向量；C为光滑度矩阵，可用一阶或者二阶平滑度方式进行计算.如果(13)式中C 为单位矩阵，则表示为仅施加了背景模型约束.这样同时引入光滑模型和背景模型约束的目标函数Φ为

(14)式右端第一项为数据拟合差的最小二乘项，后一项为同时引入光滑模型和基本模型约束项.其中 m b为背景模型；λ为正则化因子或拉格朗日乘子.然后将(14)式两端对Δ m T进行求导并令其为零，可得到最小二乘线性反演方程

上式也可等效为下面的线性方程组

从方程组(16)中求得的模型修改量Δ m代入下式

如此便可得到新的预测模型参数矢量m (k).重复上述操作直到实测数据和模拟数据之间的平均均方误差满足要求为止.其中，平均均方误差RMS定义为

4 模型反演对比与分析

为了说明超高密度电法的特点，应用超高密度全四极装置同传统高密度电法中的偶极排列、α排列、β排列、γ排列和施伦贝谢尔排列进行反演精度对比，所有排列都采用有限单元法进行正演计算，然后再反演成像.由于超高密度激电法自身数据采集的特点，兼含几种不同装置类型，深度不能统一划定，故不绘制正演的视电阻率断面图和视极化率断面，而是直接提供反演后的结果图.由于在实际的超高密度激电法勘探中，如果电极数越多，数据量就会成倍增加，为了减少计算量和节约反演时间，本文选用48根电极进行模拟，其数据量大约为25000个.

4.1 全四极装置与传统单一装置反演对比与特征分析

低阻的混合结构模型如图 2所示，背景电阻率ρ0=100 Ωm；左边矩状异常体电阻率为ρ1=50 Ωm，最上部浅层及右边矩状异常体电阻率为ρ2=5 Ωm.图 3为超高密度电法全四极装置数据采集方式电阻率反演图，图 4为全四极装置加入5%随机干扰的电阻率反演图，图 5~8分别为偶极排列、α排列、β排列、γ排列和施伦贝谢尔排列电阻率反演图，其反演图蓝色方框对应模型投影区域.

图 2 地电模型示意图 Fig. 2 Sketch map of geoelectric model

图 3 超高密度电法全四极装置电阻率反演图
Fig. 3 Resistivity inversion section of UHDRM full four-pole device

图 4 超高密度电法全四极装置加入5%随机干扰电阻率反演图
Fig. 4 Resistivity inversion section of UHDRM full four-pole device adding 5% r and om interference

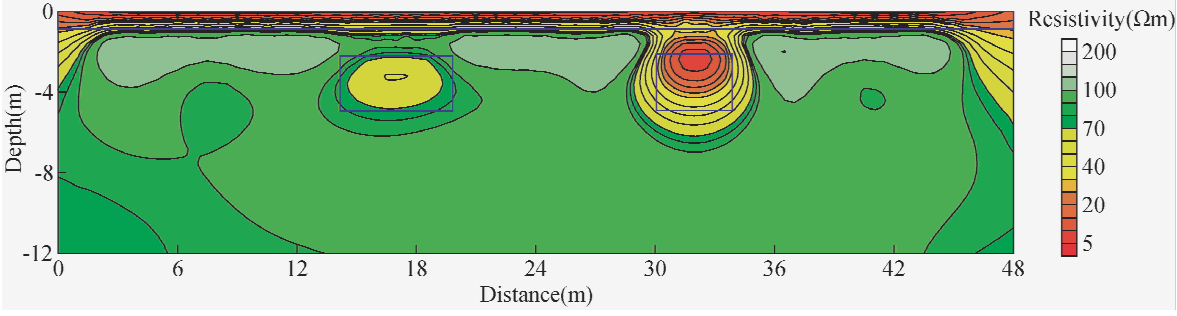图 5 偶极排列电阻率反演图
Fig. 5 Dipole array resistivity inversion section

图 6 α排列装置电阻率反演图
Fig. 6 α array device resistivity inversion section

图 7 β排列装置电阻率反演图
Fig. 7 β array device resistivity inversion section

图 8 γ排列装置电阻率反演图
Fig. 8 γ array device resistivity inversion section

分析图 3可知，浅层的低阻薄层及右边中心位置33 m处的低阻矩状异常体在反演图中为0~10 Ωm红色区间反映，左边中心位置18 m处的次低阻矩状异常体在反演图中为35~55 Ωm黄色区间反映，该反演结果在表达异常体大小、空间位置、电阻率大小等参数上与模型非常一致，说明了超高密度电法数据反演精度非常高；图 4为加入5%随机干扰进行反演，对比图 3可知，超高密度激电法数据采集方式反演能较好地压制干扰信号、抗噪能力强，具有较好的稳定性.再分析图 5~图 9可知，采用偶极排列、α排列、β排列、γ排列和施伦贝谢尔排列五种采集装置的电阻率反演图中，效果参次不齐，对于上层低阻覆盖异常均能对应，但对于右侧低阻异常虽能反映出，可形态及位置不能对应，产生较大误差，而左侧次低阻模型只有偶极排列和β排列能模糊反映，其余根本无异常显示.采用超高密度激电法的电阻率反演结果图却很好的反映模型的形态和位置，对于左侧较低阻异常也能较好对应，达到了很好的探测效果，有效地反映出了地下的电性分布状况，达到准确探测的目的.

图 9 施伦贝谢尔排列电阻率反演图
Fig. 9 Schlumberger array device resistivity inversion section

4.2 倾斜板状体全四极反演与特征分析

模型为低阻、高极化的倾斜板状体，如图 10，每行排列有48根电极，数据层数为12层，模型背景电阻率ρ0=100 Ωm，极化率η0=1.0%；模型边长为2×4，中心位置为(24，-4)，模型电阻率ρ1=5 Ωm，极化率η1=5.0%.图 11为倾斜板状体模型超高密度电法全四极装置电阻率反演图，其中反演图蓝色方框对应模型投影区域.分析全四极装置的电阻率反演图可知，该倾斜板状异常体能得到清晰的反映，异常体的具体位置、大小和深度大致形态能与模型异常体对应，且电阻率值与模型示意图中设置的数值也较为对应，全四极装置能较好的反映出地下电性的分布状况.

图 10 倾斜板状体模型示意图
Fig. 10 The Sketch map of tilt plate body model

图 11 倾斜板状体模型全四极装置电阻率反演图
Fig. 11 The resistivity inversion figure of the full four-pole device for the tilt plate body model
5 结 论 5.1    超高密度电法采用多电极、多通道技术，野外采集一次性布极，数据采集自动化，采集速度快，工作效率非常高，弥补了常规电法及高密度电法数据采集的不全面性.在同样电极数的情况下，它可采集到几十倍于常规电法数据采集方式采集到的数据，大大提高了反演结果的准确性和可靠性.同时，也避免了常规数据采集方法中数据采集的片面性，而导致在同一地点因采用不同数据采集方式所产生的反演结果不同的缺点，提高了探测精度.

5.2    超高密度电法装置与采用不同装置对模型反演进行对比，证明了超高密度激电法比单一排列装置反演精度高，反演效果好，在探测效果上要胜于单一排列装置.通过对倾斜板状体地电模型采用超高密度电法反演可知，超高密度激电法全四极装置有较高的准确性和较好的适用性.

参考文献
[1] Dai Q W, Xiao B, Feng D S, et al. 2012. 3-D inversion of high density resistivity method based on 2-D exploration data and its application[J].   Journal of Central South University (Science and Technology), 43(1): 293-300.
[2] Huang J, Zhong T, Ma W D. 2009. Ultra-High Density Resistivity method applied to exploration of fracture zone[J].   Computing Technology for Geophysical and Geochemical Exploration, 31(6): 586-589.
[3] Huang J G, Wang J L, Ruan B Y. 2006. A study on FEM modeling of anomalies of 3-D high-density E-SCAN resistivity survey. Chinese J.Geophys, 49 (4): 1206-1214.
[4] Hu S L, Chen X, Shuai E H. 2011. The application of the Ultra-High Density Resistivity method to the investigation of Karst caves and fracture zones[J].   Geophsical & Geochemical Exploration, 35(6): 821-824.
[5] Mao H J. Determination of the space trend for depth Ore body by the Ultra-High Density Resistivity[J]. Computing Technology for Geophysical and Geochemical Exploration, 2011, 3(3): 304-308.
[6] Li J M.2005. Electric Field and Electrical Prospecting[M].   Beijing: The Geology Press.
[7] Ruan B Y. 2011. A generation method of the partial derivatives of the apparentresistivity with respect to the model resistivity parameter[J].   Geologyand Prospecting, 37 (6): 29-41.
[8] Song H W, Zhang Y L, Xia F, et al. 2011. Analysis of the water investigation by Super Density Electrical method and IP in Hebei[J].   South-to-North Water Diversion and Water Science & Technology, 9(4): 60-62.
[9] Sun Y. 2012. Application of High Density Electrical method in detecting sandbody in Coal mine[J]. Coal mining Technology, 17(3): 25-27.
[10] Wang D Z, Zhou B, Zhao K, et al. 2010. Application of the Ultra-high Density Resistivity method in engineering Geology investigation[J].   Jiangxi Nonferrous Metals, 24(1):10-12.
[11] Wang P F. Research for data acquisition and forward and inverse interpretation of Ultra-High density resistivity and induced polarization method[D][Ms.D. thesis]. Changsha:School of Geosciences and Info-Physics,Central South University,2012.
[12] Wu X P, Xu G M, Li S C. 1998. The calculation of three-dimensional Geoelectric fiedl of point source by incomplete cholesky conjugate gradient method. Chinese J.Geophys, 41(6): 1206-1214.
[13] Greenhalgh S A, B Zhou, A G Green. 2006. Solutions, algorithms and inter-relations for local minimisation search geophysical inversion[J].   Journal of Geophysics and engineering, 3, 101-113.
[14] Loke M H, Dahlin T. 2002. A comparison of the Gauss-Newton and quasi-Newton methods in resistivity imaging inversion[J].   Journal of Applied Geophysics, 49: 149-162.
[15] Mukanova B, Orunkhanov M. 2010. Inverse resistivity problem: Geoelectric uncertainty principle and numerical reconstruction method[J].   Mathematics and Computers in Simulation, 80: 2091–2108.
[16] Rodi W, Mackie R L. 2001. Non-linear conjugate gradients algorithm for 2-D magnetotelluric inversion[J].   Geophysics, 66: 174-187.
[17] Shashi P S. 2012. VFSARES-a very fast simulated annealing FORTRAN program for interpretation of 1-D DC resistivity sounding data from various electrode arrays[J].   Computers & Geosciences, 42: 177-188.
[18] Zhang L Y, Liu H F. 2011. The application of ABP method in high-density resistivity method inversion[J].   Chinese Journal of Geophysics, 54(1): 64-71.
[19] Zhe Jing ping, Greenhalgh S, Marescot L. 2007. Multi-channel, full waveform and flexible electtode combination resistivity imagingsystem[J].Geophysics, 72(2): 57-64.
[20] Zhou B, Dahlin T. 2003. Properties and effects of measurement errors on 2D resistivity imaging surveying[J].   Near Surface Geophysics, 1: 105-117.
[21] Zhou Bing, S.A. 1999. Greenhalgh. Explicit expressions and numerical calculations for the Fre'chet and seeond derivatives in 2.5D Helmholtz equation inversion[J].GeoPhysical Prospecting, 47, 443-468.
[22] 戴前伟,肖波,冯德山,等,2012. 基于二维高密度电阻率勘探数据的三维反演及应用[J]. 中南大学学报(自然科学版), 43(1):293-300.
[23] 黄杰,钟韬,马文德. 2009. 超高密度电法在追索破碎带中的应用[J].   物探化探计算技术, 31(6):586-589.
[24] 黄俊革,王家林,阮百尧. 2006. 三维高密度电阻率E-SCAN 法有限元模拟异常特征研究[J].   地球物理学报,49 (4):1206-1214.
[25] 胡树林,陈烜,帅恩华. 2011. 超高密度电阻率法在岩溶及破碎带探测中的应用[J].   物探与化探,35(6):821-824.
[26] 毛洪江. 2011. 井-井超高密度电阻率法确定黑牛洞深部矿体的走向研究——以四川九龙县黑牛洞铜矿为例[J].   物探与化探,33(3):304-308.
[27] 李金铭.2005. 地电场与电法勘探[M].北京:地质出版社.
[28] 阮百尧. 2011. 视电阻率对模型电阻率的偏导数矩阵计算方法[J].   地质与勘探,37 (6):29-41.
[29] 宋洪伟,张翼龙,夏凡,等. 2011. 超高密度电法和激电法在河北某地找水实例分析[J].   南水北调与水利科技, 9(4):60-62.
[30] 孙林. 2012. 超高密度电法在煤矿砂体探测中的应用[J].   煤矿开采, 17(3):25-27.
[31] 王德中,周斌,赵奎,等. 2010. 超高密度电法在工程地质勘查中的应用[J]. 江西有色金属, 24(1):10-12.  
[32] 王鹏飞. 2012. 超高密度激电数据采集与正反演解释方法研究[D][硕士论文].   长沙:中南大学
[33] 地球科学与信息物理学院.
[34] 吴小平,徐果明,李时灿. 1998. 利用不完全Cholesky共扼梯度法求解点源三维地电场[J]. 地球物理学报,41(6):848-854.