2. 中国石油长庆油田分公司, 西安 710018
2. PetroChina Changqing Oilfield Company, Xi'an 710018, China
0 引 言
鄂尔多斯盆地LD地区是举世闻名的黄土塬区,区内地表沟壑纵横,地表起伏变化剧烈,地表相对高差在300 m左右,黄土巨厚,黄土覆盖厚度在200~400 m之间,且干燥、疏松,地震激发、接收条件差,地震资料信噪比低、分辨率低,次生干扰强、规律性差.如图 1.地下储层为河道沉积,物性变化大,山1、盒8发育三角洲平原和前缘相带石英砂岩储集体,砂体多期叠合,复合连片.山1、盒8发育石英砂岩储层,孔隙类型以岩屑溶孔、晶间孔为主,次为粒间孔,具有较好的储集性能.广泛分布的储集砂体与下覆的煤系烃源岩有效配置,天然气近距离运移成藏,形成了大面积分布的深层致密砂岩气藏(朱筱敏等,2002;Wang et al., 2004; 窦伟坦等,2011; 王红伟等,2013).
 | 图 1 鄂尔多斯盆地黄土塬地貌图 Fig. 1 The geomorphologic map of loess Plateau,Erdos Basin |
由于黄土塬地表起伏大、低降速带横向变化剧烈,导致静校正问题严重,深层地震反射能量弱,发育多次折射、散射噪声,线性和非线性等各种干扰严重,信噪比非常低.这对地震资料处理上带来了相当大的困难.
同时盒8、山1段储层厚度小(砂岩5~20 m),纵横向非均质性强,储层预测难度大,叠后反演不能满足深层致密气的预测需求,需要大力推广叠前技术,但由于工区勘探程度低,探井尤其横波测井非常少,一直制约叠前技术的应用,本文创新性地采用果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)反演构建虚拟井,并最终得到纵横波速度及密度,然后利用虚拟井约束进行叠前同时反演,以期解决黄土塬少井区叠前反演问题,这方面Stoffa和Sen(1991)采用模拟退火、遗传算法以及梯度优化算法对叠前波形反演进行了深入的研究,取得了较好的效果,Mallick等(1999;2000)利用遗传算法在构建虚拟井方法做过一些有益的尝试,岳碧波等(2009)探讨了粒子群优化(PSO)算法在叠前地震角道集子波反演中的应用.而叠前反演领域中应用FOA算法,尚未在文献中看到,如何将FOA算法有效应用于勘探地球物理值得进一步深入研究.本文试图将FOA应用到地震叠前反演中,以挖掘这种算法在地球物理领域中的发展潜力,为解决地球物理反演问题提供新的途径. 1 黄土塬地震处理关键技术
面对多种难题,攻克制约黄土塬地震处理的瓶颈,形成三项处理关键技术:
(1)在叠前应用GMseis近地表层析反演、地表一致性剩余静校正和线性拟合静校正技术有效地解决了黄土塬区复杂地表资料基础静校正问题.
(2)在叠前炮集上应用T-X域滤除法去除线性干扰,在动校炮集上应用复数预测法去除随机噪声和τ-p域RAMUR去除多次波来提高黄土塬区资料信噪比.
(3)在叠前应用地表一致性预测反褶积,叠后应用频率域约束谱外推和蓝色滤波来提高地震资料的分辨率.
最终处理的剖面连续性好,层序齐全,波组特征清晰,分 辨率高,分偏移距叠加资料信噪比、分辨率高,近远道振幅能量、相位一致性好;处理的道集保幅及相位一致性较好,信噪比较高,为后续的叠前储层预测奠定了坚实的基础.如图 2所示.
 | 图 2 LD地区H11××测线分偏移距叠加剖面和CRS处理道集 Fig. 2 The different offset-stack section and gather by CRS of line H11××,LD area |
Pan(2011;2012)提出一种算法—果蝇优化算法,果蝇优化算法是一种基于果蝇觅食行为而推演出的寻求全局优化的新的仿生类进化算法,可以为许多复杂的优化问题提供新 的解决途径(李泓泽等,2012),其主要流程如图 3.原文中作者将其应用在多个方向的研究中,使用比较灵活,效果不错.
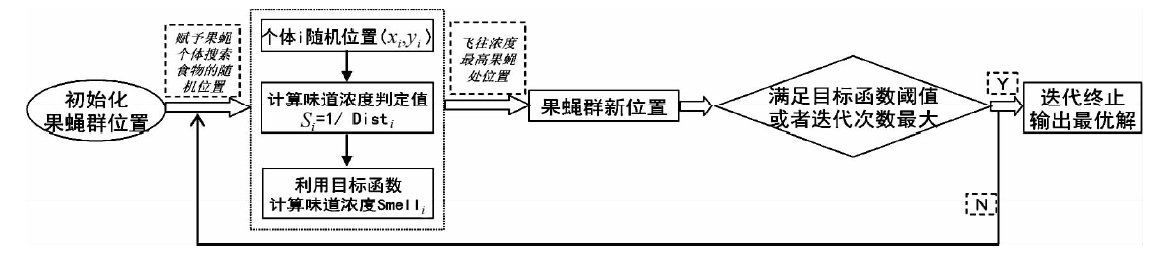 | 图 3 果蝇优化算法流程图 Fig. 3 The flow diagram of Fruit Fly Optimization Algorithm |
在优化算法的研究领域中,通常采用一定的测试函数来测试与比较各个算法的性能,本文选取Schaffer函数F6(如图 4)进行性能测试与比较,公式为
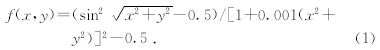
本函数只有一个全局最小值f(0,0)=-1,且被一圈局部极小值包围,故一般算法求其极小值有较大难度.
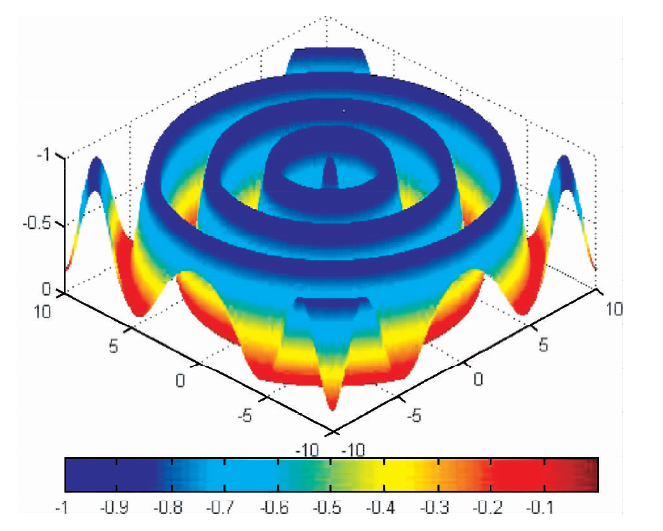 | 图 4 Schaffer函数F6 Fig. 4 Schaffer function F6 |
本文分别利用四种优化算法(遗传算法(GA)、模拟退火算法(SA)、粒子群算法(PSO)和果蝇优化算法(FOA))同时求解本函数,四种算法求解结果如表 1所示,图 5为FOA求解Schaffer函数F6优化过程图及果蝇飞行轨迹图,比较可以看出:FOA算法只需要迭代62次就能迅速收敛到全局最优点-1,而且果蝇搜索路径平稳,行进速度快,表明FOA算法稳定.结果表明FOA算法无论收敛速度和计算精度都比较高,不逊于其它优化算法.
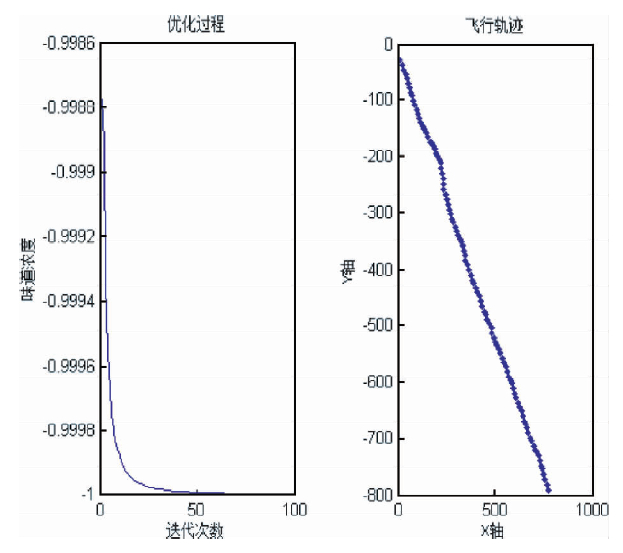 | 图 5 优化过程图及果蝇飞行轨迹图 Fig. 5 Optimization process and Fruit fly flying route |
|
|
表 1 四种算法求解Schaffer函数F6结果对比 Table 1 Comparison of the results of sloving Schaffer function F6 by four algorithm |
本文采用果蝇优化算法的虚拟井纵横波速度及密度反演步骤如下:
(1)由模型AVO正演数据或者实际地震数据抽取≥3个角道集数据Seis(θ),作为观测值.
通过文献调研,AVO正演过程采用精度较高的Fatti近似公式(王保丽等,2008;张进,2011)为
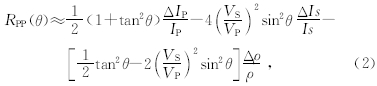
式中RPP(θ)为反射系数,θ、VP、VS、ρ为界面两侧介质弹性参数的平均值,IP、Is为纵横波阻抗.
(2)提取各角道集数据Seis(θ)分角度子波W(θ).
(3)利用FOA算法生成各角道集的反射序列候选初始解.
首先在区间[0,100]生成每个果蝇的初始位置向量(X0,Y0),并赋予迭代的果蝇搜寻食物的随机飞行方向与距离(R and omX,R and omY),其区间设为[-1,1],此时得到果蝇位置为(X0+R and omX,Y0+R and omY),然后求得味道浓度判定值Si为
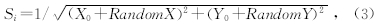
此即为反射系数序列候选初始解.
(4)计算反演目标函数J m,通过计算合成记录Syn(θ)与Seis(θ)比较.
将味道浓度判定值Si代入到味道浓度判定函数(这里就是反演的目标函数J m),并计算味道函数取其最小值,亦即保留味道浓度最小的果蝇浓度值和位置.公式为
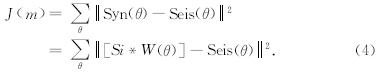
(5)利用FOA算法循环迭代,判断味道浓度是否优于前一迭代味道浓度,对最优解不断进行优化,直到满足终止条件(如J m 小于某截断误差,或达到最大迭代次数),则果蝇个体最优与与果蝇群体最优一致,所有果蝇收敛于一个位置,通过此时果蝇的位置向量即可求得反射系数序列.即利用FOA算法求各角道集的反射系数序列,使得反演出的反射系数序列与角度子波的褶积结果与对应实际地震数据角道集之间误差函数J m 最小.
并利用基于Fatti公式的EI方程来最终计算各个角度EI曲线为
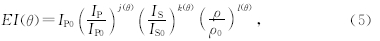
式中,IP0=VP0ρ0, IS0=VS0ρ0为归一化因子,对应地层的纵波阻抗和横波阻抗,可以根据测井曲线计算.j(θ)=1+tan2θ,k(θ)=-8Ksin2θ, l(θ)=4Ksin2θ-tan2θ.
在角度相同的情况下,同一岩石物性参数在各采样点处所对应j(θ)、k(θ)、l(θ)相同.
(6)虚拟井纵横波速度及密度参数提取.
将式(5)两边分别取对数,并采用井旁道测井曲线,对某个角度的各采样点可得到系数j(θ)、k(θ)、l(θ),对于多个不同的角度范围,可得到
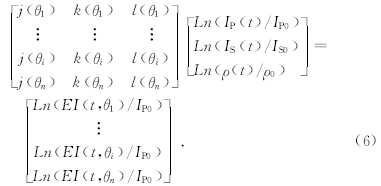
通过利用反演获得的n(n≥3)个角度的EI数据体,解方程组(6)即可得到各道任意点处的岩性参数IP、IS、ρ.亦即提取得到了虚拟井的纵横波速度及密度参数. 2.3 一维模型试验
选取一段实际测井曲线共175个样点进行一维模型试验,如图 6所示为原始测井纵波速度、横波速度与密度曲线.
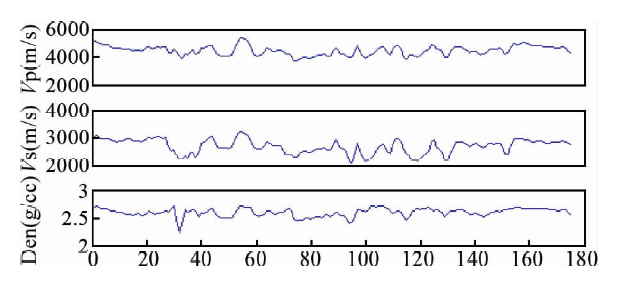 | 图 6 原始测井曲线 Fig. 6 Original well curves |
假设地层为层状介质,据前述3.2节中Fatti公式,每隔5°、10°、15°、20°、25°和30°各反射系数,计算得到的反射系数序列如图 7a,然后反射系数序列同各分角度子波褶积即得到相应的角道集如图 7b.
利用FOA反演各角道集反射系数时,其中关键参数设置为:果蝇群规模为50,果蝇初始搜索位置为100乘以1~2之间的随机数,迭代的果蝇搜寻食物的随机飞行方向与距离区间为[-1,1],果蝇种群迭代步进值设置为15,误差函数小于0.000001(或者迭代次数最大10000).
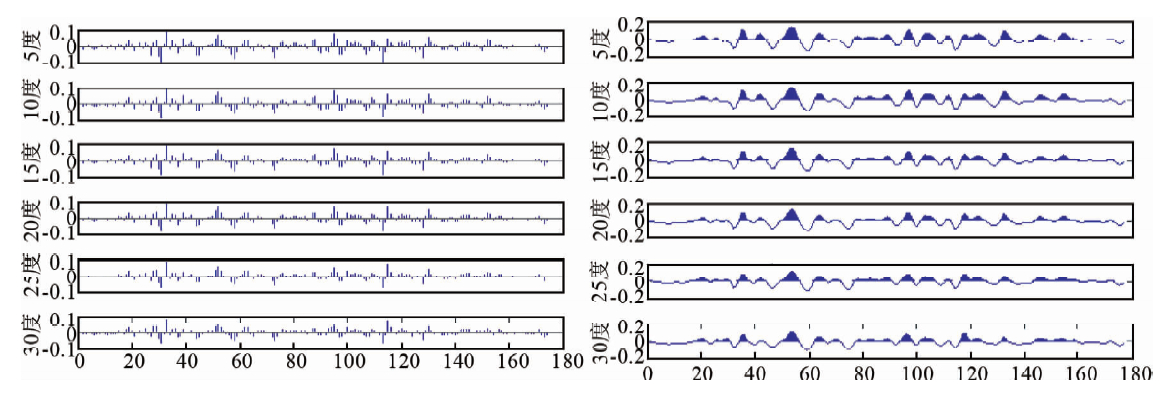 | 图 7 反演出的反射系数序列(a)及相应角道集(b) (a)5°、10°、15°、20°、25°、30°反射系数序列;(b)5°、10°、15°、20°、25°、30°角道集. Fig. 7 The inverted reflection coefficient sequences and corresponding angle gathers |
以10°角道集为例,反演出的反射系数(红色实心点)与真实的反射系数(蓝色线段)吻合较好,如图 8所示.同理依次反演出5°、15°、25°反射系数,并得到5°、15°、25°EI曲线,如图 9.最终按照前文所述可提取纵横波速度及密度曲线,并与原始测井曲线(蓝色)对比,如图 10,红色为反演得到的纵横波速度及密度曲线,从反演结果来看,仅仅密度曲线误差稍大,纵横波速度吻合较好.证明本文所述方法是一种行之有效的提取纵横波速度及密度参数的反演方法,而且不依赖初始模型,直接从多个角道集出发求解弹性参数,易达到全局最优解.
 | 图 8 10°角道集反演出的反射系数(红色实心点) 与真实反射系数(蓝色线段)对比 Fig. 8 Comparison of the inverted reflection coefficient of 10° angle gather(red filled dot) and real reflection coefficient(blue lines) |
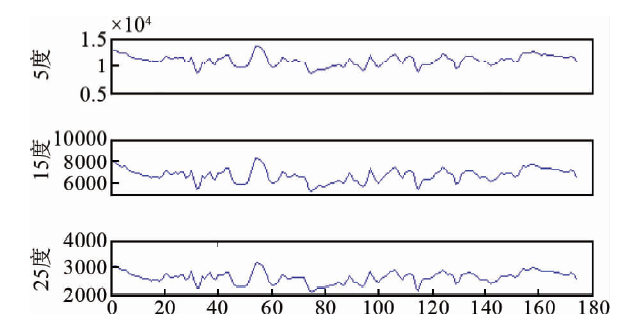 | 图 9 5°、15°、25°EI曲线 Fig. 9 The EI curves of 5°、15°、25° |
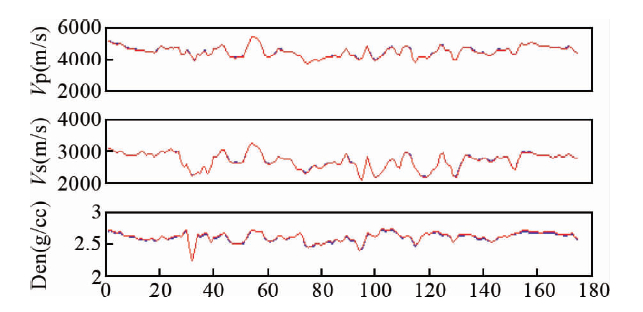 | 图 10 反演得到(红)与原始(蓝)纵横波速度及密度对比 Fig. 10 Comparison of the inverted(red) and original(blue)Vp、Vs、Den |
鄂尔多斯盆地LD地区的主要含气目标层为上古生界二叠系底部盒8、山1砂岩段,砂体埋藏深约4300~5000 m,厚度薄约5~10 m,储层致密,与围岩的波阻抗差异小,且横向变化较快,其有效储层预测难度非常大,这个特点决定了LD地区的储层预测必须使用叠前反演方法开展有效储层预测,才能满足气田勘探目标的优选.
但同时LD地区勘探程度比较低,井比较少,横波测井更少,那么这种情况下如何解决叠前反演问题?本文创新性地采用果蝇优化算法反演构建虚拟井,并最终得到纵横波速度及密度,然后利用虚拟井约束进行叠前同时反演.
以T井钻前预测为例,部署T井之前只有一口井A距离H10FZ××Z1测线最近,但是也距离测线12公里之远,如图 11,那么之前叠前同时反演通常的做法是把井A按照砂体走向移至测线上,构造一口伪井A’,然后利用伪井A’约束进行叠前同时反演,此种办法缺陷很多:(1)距离测线太远,合成记录与地震匹配较差;(2)测线较长,仅仅利用一口井所建立的低频模型与实际沉积规律有差距.
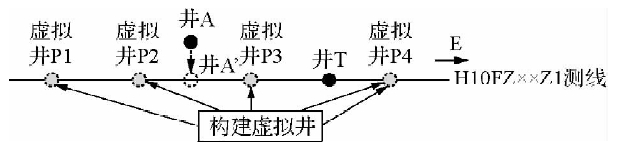 | 图 11 H10FZ××Z1测线构建虚拟井位置示意图 Fig. 11 The sketch map of constructing virtual wells in line H10FZ××Z1 |
那么本文中对于黄土塬少井区进行叠前同时反演的解决办法是:
在整条测线H10FZ××Z1上,首先选取四个控制点,并在所选控制点的角道集数据上进行精细的叠前地震波形反演,来构建控制处的虚拟井曲线,然后以虚拟井作为控制信息进行反演.主要利用四口虚拟井产生初始低频模型,然后用此低频模型作为背景趋势实施叠前同时反演.其中确定虚拟井位置原则是:(1)地震资料品质好;(2)速度可靠.
层位标定是联系地震和测井的桥梁,在叠前反演中占有非常重要的地位,只有在精确的层位标定的前提下,才能获得高精度反演结果.如图 12,是四口虚拟井的层位标定结果,其相关度分别为75.5%、86.1%、65.3%和79.3%,可见合成地震记录与井旁地震地震道吻合较好,可以满足后续的叠前同时反演要求.
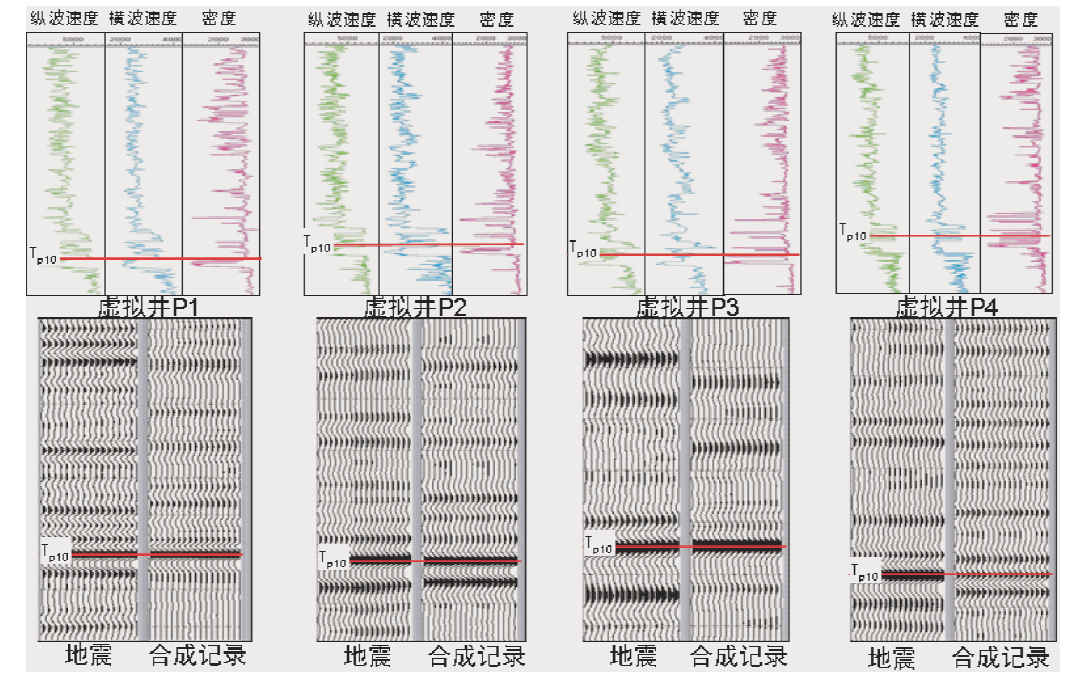 | 图 12 虚拟井合成记录 Fig. 12 The synthetic seismograms of virtual wells |
根据测线的层位和沉积模式的约束,通过线性内插方法分别构造出纵波阻抗、横波阻抗和密度模型,通过多口虚拟井控建立的精细低频模型,横向变化自然,符合地质规律,可以定性地反应砂体的空间分布规律(严建文等,2007).
图 13是H10FZ××Z1测线利用一口伪井A’约束进行叠前同时反演得到的拟横波阻抗和泊松比剖面.图 14是H10FZ××Z1测线利用四口虚拟井约束进行叠前同时反演得到的拟横波阻抗、泊松比及纵波阻抗和泊松比交会剖面.两者均为钻前检测剖面,两者在整体趋势上相似,但伪井A’约束反演的结果显示砂岩不连续,横波阻抗为小值(绿色),含气性检测结果也较差,泊松比剖面为大值(偏绿色);而利用四口虚拟井约束反演的结果显示横波阻抗为中高值(红黄色),表明砂体较为连续,同时较低的泊松比(红色)表明山1段有效储层厚度大,含气性好,纵波阻抗与泊松比交会剖面黑色的异常区也同样指示山1段含气性好.
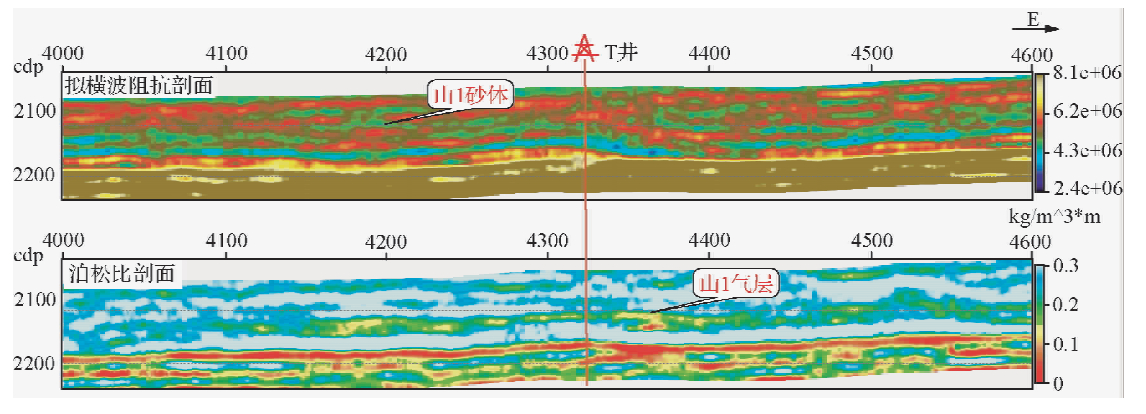 | 图 13 H10FZ××Z1测线利用伪井A’约束进行叠前同时反演结果 Fig. 13 The pre-stack inversion result with well A’constrain of line H10FZ××Z1 |
 | 图 14 H10FZ××Z1测线利用四口虚拟井约束叠前同时反演结果 Fig. 14 The pre-stack inversion result with four virtual wells constrain of line H10FZ××Z1 |
而T井实钻上古生界山西组山1石英砂岩厚7.5 m,气层厚7.5 m,试气获无阻流量7.1万方/日工业气流,进一步落实并扩大了LD地区上古生界有利含气目标区.该井的成功实施,预示上古生界气藏的巨大勘探潜力,展示了LD地区良好的勘探前景.
可以看出,利用四口虚拟井约束的叠前同时反演结果更符合实际情况,更为重要的是利用本方法的叠前反演剖面,分辨率明显较高,信噪比较高,横向变化比较自然,反演结果稳定程度高.表明采用果蝇优化算法的虚拟井纵横波速度及密度反演方法可行性和适用性较高,具有良好的发展潜力和应用前景. 3 结 论
鄂尔多斯盆地LD地区巨厚的黄土,给地震资料处理带来巨大难度,同时本地区的低勘探程度和较差资料也一度制约叠前储层预测的发展,本文首次将FOA引入EI反演中,通过了一维模型试算,反演结果稳定,表明了方法的有效性;利用FOA全局寻优优势构建虚拟井,并将其引入到叠前同时反演中,在LD地区少井区取得较好反演效果.下一步进行算法优化,减少运算时间是一个研究重点,同时将FOA与其它线性甚至非线性反演算法进行结合,进行混合优化反演,也是下一步需要开展的研究内容.
致 谢 本文得到中国海洋大学海洋地球科学学院张进博士的指导与帮助,在此表示感谢!
| [1] | Dou W T, Du Y B, Yu B, et al. 2011. The acquisition technology of 3D off-line seismic exploration in the JiYuan area,Erdos Basin[J]. OGP(in Chines), 46(6):844-850. |
| [2] | Li H Z, Guo S, Li C J. 2012. A hybrid forecasting model based on Fruit Fly Optimization Algorithm and Least Squares Support Vector Machine-the case of logistics demand forecasting of China[J]. Journal of Quantitative Economics, 29(3):103-106. |
| [3] | Mallick S. 1999. Some practical aspects of prestack waveform inversion using a genetic algorthm: An example from the east Texas Woodbine gas sand[J].Geophysics, 64:326-336. |
| [4] | Mallick S. 2000. Hybrid seismic inversion: Areconnaissance tool for deepwater exploration. The Leading Edge, 19(11): 1230-1237. |
| [5] | Pan W C. 2011. Using Fruit Fly Optimization Algorithm optimized general regression Neural Network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology(Social Sciences Edition) , 29(4):1-5. |
| [6] | Pan W C. 2011. A new evolutionary computation approach:Fruit Fly Optimization Algorithm[C]. 2011 Conference of Digital Technology and innovation Management Taipei. |
| [7] | Pan W C.2012. A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems, 26(1):69-74. |
| [8] | Sen M K, Stoffa P L. 1991. Nonlinear one dimensional seismic waveform inversion using simulated annealing[J].Geophysics, 56(10):1624-1638. |
| [9] | Stoffa P L and Sen M K. 1991. Nonlinear multi-parameter optimization using genetic algorithms: inversion of plane wave seismograms[J].Geophysics, 56(11):1794-1810. |
| [10] | Wang B L,Yin X Y,Zhang F C,et al. 2008. Elastic impedance equation based on Fatti approximation and inversion[J].Progress in Geophys. (in Chines) 23(1):192-197. |
| [11] | Wang D X, Gao J H, Li Y M,et al. 2004. Mesozoic Reservoir Prediction in the Longdong Loess Plateau[J]. Applied Geophysics, 1(1): 24-29. |
| [12] | Wang H W, Chen D S, Liu B X, et al. 2013. Seismic prediction of sand body in upper Paleozoic and new exploration breakthrough in the southwest Ordos basin. Progress in Geophys.(in Chinese), 28(4):2132-2140. |
| [13] | Yan J W, Yang S G. 2007. Using prestack seismic waveform inversion to construct visual curves in wells[J]. OGP (in Chines), 42(6):678-681. |
| [14] | Yue B B, Peng Z M, Hong Y G, et al. 2009. Wavelet inversion of pre-stack seismic angle-gather based on particle swarm optimization algorithm[J]. Chinese J. Geophys.(in Chinese), 52(12):3116-3123. |
| [15] | Zhang J. 2011. Study on nonlinearinversion methods for elastic impedance of seismic prestack data[D] [Ph. D. thesis]. Qingdao: Ocean University of China. |
| [16] | Zhu X M, Kang A, Wang G W, et al. 2002. The Upper Paleozoic sequence stratigraphic and sedimentary system characteristics of the southwest Ordos basin[J]. Petroleum Geology and Experiment (in Chines), 24(4):327-333. |
| [17] | 窦伟坦,杜玉斌,于波,等.2011. 鄂尔多斯盆地姬塬地区非纵三维地震勘探采集技术[J].石油地球物理勘探, 46(6):844-850. |
| [18] | 李泓泽,郭森,李春杰.2012. 果蝇优化最小二乘支持向量机混合预测模型-以我国物流需求量预测为例[J].经济数学,29(3):103-106. |
| [19] | 潘文超. 2011. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报社会科学版, 29(4):1-5. |
| [20] | 王保丽,印兴耀,张凡昌,等. 2008. 基于Fatti近似的弹性阻抗方程及反演[J].地球物理学进展. 23(1):192-197. |
| [21] | 王红伟,陈调胜,刘宝宪,等. 2013.鄂尔多斯盆地西南部地区上古生界砂体地震预测及勘探新突破[J].地球物理学进展,28(4):2132-2140. |
| [22] | 严建文, 杨绍国. 2007. 基于遗传算法的叠前地震波形反演构建虚拟井曲线[J]. 石油地球物理勘探, 42(6):678-681. |
| [23] | 岳碧波,彭真明,洪余刚,等. 2009. 基于粒子群优化算法的叠前角道集子波反演[J].地球物理学报, 52(12):3116-3123. |
| [24] | 张进. 2011. 地震叠前数据的弹性阻抗非线性反演方法研究[D][博士论文]. 青岛: 中国海洋大学. |
| [25] | 朱筱敏,康安,王贵文,等. 2002. 鄂尔多斯盆地西南部上古生界层序地层和沉积体系特征[J].石油实验地质,24(4):327-333. |
 2014, Vol. 29
2014, Vol. 29

