2014, Vol. 29
有限元法(Finite Element Method，FEM)作为数值计算领域最重要的里程碑之一，适用于求解区域形状不规则或区域物性复杂分布的问题，有着坚实的理论基础和数学证明，在科学与工程界得到了广泛的应用.伴随着结构力学的发展，各种有限元分析软件相继出现，并很快广泛的应用于热传导、电磁场、流体力学等领域，较流行的商用软件有ANSYS、ADINA、ABAQUS、MSC.
有限元法的核心在于将连续的求解域离散为一组单元的组合体，用在每个单元内假定的近似函数来分片表示求解域内的未知场量函数，近似函数通常由未知场函数及其导数在单元各节点的插值函数来表示，是一种基于网格的数值方法.其最大缺陷在于求解高维问题时网格生成复杂.此外，某些复杂问题用有限元法求解较困难，这些问题主要包括：超大变形问题、动态裂纹扩展问题、金属材料成型问题、高速冲击及大爆炸问题.用有限元法求解这些问题时，由于巨大的网格畸变或单元分裂，计算中必须不断重新划分网格，极大的增加了计算时间，并且有时重新划分网格并不能完全解决问题(顾元通等,2005).要想从根本上解决有限元法的缺陷就必须避免事先定义的网格，无网格的思想由此诞生.
无网格法通常利用加权残量法构造求解问题的弱式(积分)形式或配点(微分)形式，并通过局部支持域内的节点构造形函数及建立离散系统方程，是一种基于节点的数值方法.该方法避免了网格的划分，具有构造高阶形函数方便，自适应分析容易等特点.无网格法种类繁多，目前已提出的无网格法近四十种.有些方法已较为成熟，开始进入实用阶段，如光滑粒子流体动力学法(smoothed particle hydrodynamics method，SPHM)、再生核粒子法(reproducing kernel particle method，RKPM)、无单元Galerkin法(element-free Galerkin method，EFGM).有些仍处于研究阶段，如径向基点插值法(radial point interpolation method，RPIM)、单位分解法(the partition of unity method，PUM)、无网格局部Petrov-Galerkin法(meshfree local Petrov-Galerkin method，MLPGM)、边界点插值法(Boundary Point Interpolation Method,BPIM)、有限点法(the finite point method,FPM).
各种无网格法的差异主要体现在场量函数的近似方式及加权残量法的选择上.无网格法可分为基于弱式(积分)的无网格法和基于配点(微分)的无网格法两大类.根据选用加权残量法(配点法、子域法、最小二乘法、Galerkin法)的不同可将无网格法进一步划分为基于全域弱式的无网格法(如EFGM、RPIM、RKPM、PUM)、基于局部弱式的无网格法(如 MLPGM)、基于配点的无网格法(如SPHM、FPM)以及基于边界积分方程的无网格法(如BPIM).
无网格法的历史可追溯到(SPHM Lucy,1977)，此方法最初应用于天体物理学领域，近年来，SPHM也被应用于高速碰撞及不可压缩流体问题的模拟.无网格法的早期发展较为缓慢，直到(Nayroles et al.，1992)将移动最小二乘近似应用于Galerkin法形成了扩散单元法(diffuse element method，DEM)，Belytschko等(1994)在DEM法的基础上提出了无单元Galerkin法(EFGM)后，才掀起了无网格法的研究热潮.经过十几年的快速发展，无网格法不但被成功的应用于有限元法所触及的领域，而且解决了许多有限元法难以处理的问题，如大变形问题、动态裂纹扩展问题、金属成型问题、高速冲击问题.无网格法现已成为计算力学领域最热门的研究方向之一，期间出现了几本介绍无网格方法的中文专著(张雄等,2004; 刘更等,2005; Liu et al.,2005; 刘欣,2011)及各种无网格法的综述(李九红等,2006; Nguyen et al.,2008; 张雄等,2009; Liu et al.,2010).然而无网格法作为一种新兴的数值方法，其严格的数学论证、计算效率、实用性还不能和成熟的有限元法相媲美.
无网格法在地球物理学领域的应用极少，至今笔者检索到的相关文献不到十篇，为此有必要将无网格法引入地球物理学领域，观察其应用效果.本文介绍了几种典型无网格法的近似原理及其研究进展，以大地电磁二维问题为例详细论述了无网格Galerkin弱式法的求解过程，评述了各种无网格法的优缺点，并讨论了无单元Galerkin法在地球物理学领域的应用效果.
无网格法中未知场量函数可由位于其支持域内有限个节点的场量来表示
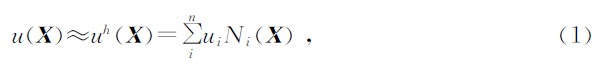
求解域Ω中任意一点 X 处的场变量u( X )，公式为
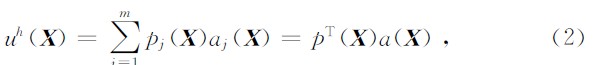
基函数的形式并不只局限于多项式，也可采用其它不同特性的函数.署恒木等(2008)用楔形基函数代替多项式基，用它构造的形函数具有插值特性，楔形基函数参数的选取是保证其近似精度的关键,但最优参数只能通过数值试验确定.赵云亮(2008)采用带权的正交函数作为基函数，避免了病态方程组的求逆运算，从而提高了计算效率，但解的精度没有提高.吴琛等(2006)用B样条小波基函数代替多项式基函数，利用小波基多尺度的特性提高了无单元法处理时频局域化问题的能力.
(2)式为超定方程组(m>n)，系数向量 a(X )可通过加权残量法求得
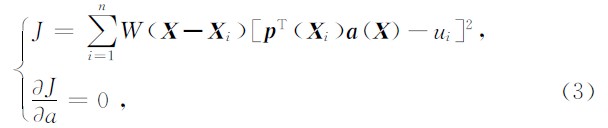
常用无网格权函数有三次样条函数、四次样条函数及指数函数(Liu et al.,2005).此外，权函数也可选用B样条小波函数，其优点是形函数计算过程中受权函数域尺寸的影响较其它常用权函数小，间接提高了计算精度与效率(邹鹏等,2011).
MLS近似最大的优点在于能够通过权函数的适当选取来得到具有高阶连续性的形函数，这是有限元法无法比拟的.有限元法通过增加节点个数来达到此目的的，因而极大增加了计算耗时.MLS近似的缺点在于形函数是通过拟合方法构造的，它不满足Kronecker delta函数的性质，因此不利于第一类边界条件加载.为了克服这一缺陷，Kaljevic等(1997)采用含奇异性的权函数提出了具有插值特性的MLS近似方法.
点插值法近似表达式为
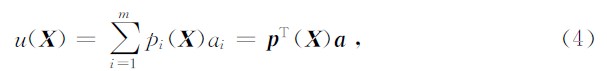
PIM形式简单，场量函数求导方便，且构造出来的形函数满足Kronecker delta函数性质，第一类边界条件加载容易.PIM对于规则分布的场节点具有较高的精度，但由于PIM形函数构造过程中涉及矩阵的逆运算，当多项式基函数选择不当时，形函数矩阵的条件数可能很大甚至奇异.为克服PIM这一缺陷，Liu G R等(2010)先后提出了随机移点法、局部坐标变换法和矩阵三角化法，这些方法基本可解决PIM插值的奇异性，但技术上仍存在一些问题.另一种处理方法是采用PIM与径向基函数(radial basis function，RBF)相结合的径向基点插值法(RPIM)(Wang et al.,2002)，RPIM综合了径向基函数近似与点插值近似的优点，是一种高精度的无网格全局弱式法.张琰等(2008)与Kumar R P等将RPIM用于流固耦合问题的计算.陈瑜等以RPIM求解中厚板弯曲问题和温度场问题为例研究了RPIM中影响计算精度的因素.Gu Y T等对径向基函数(RBF)做了改进，提出了改进的径向基点插值法(e-RPIM)(Gu et al.,2011), 并将其成功应用于裂纹尖端场的模拟中.
G.R.Liu等还将梯度光滑技术(Chen et al.,2010)引入点插值法及有限元法中，提出了光滑点插值法(smoothed point interpolation method，S-PIM)(Tang et al,2011, 2012)、光滑径向点插值法(smoothed radial point interpolation method，S-RPIM)(Cui et al.,2010)及光滑有限单元法(S-FEM)(Liu et al.,2010)，并将这些改进的方法用于计算力学问题的模拟，数值计算结果表明梯度光滑技术能提高PIM及FEM的计算精度、收敛率及稳定性.(徐旭等,2011)将FEM及基于节点的光滑点插值方法(NS-PIM)相结合，通过引入可调参数，假设应变场为协调应变和光滑应变的线性组合，提出一种应变重构点插值无网格方法(SC-PIM)，数值模拟结果表明当可调参数选用适当时，SC-PIM可以产生上界解、下界解甚至超收敛解.
求解域Ω内场函数u( X )的核积分近似表达式为
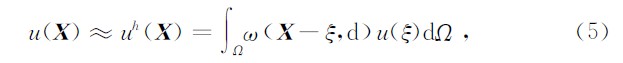
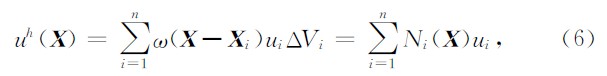
光滑粒子流体动力学法(smoothed particle hydrodynamics method，SPHM)(Liu et al.,2010)通过对质点周围一定范围内分布的粒子的物理量进行插值来估算质点的物理量，本质上是对周围粒子的物理量进行加权求和，使之满足连续性条件.SPHM公式简单、计算效率高，在天体物理学及流体力学领域得到广泛应用.陈思(2007)在常规SPHM中引入背景函数概念并应用于弹性力学问题，提高了SPHM的计算精度，但该方法在流体力学计算中精度无明显提高.SPHM计算精度较低，核函数在求解域边界附近发生截断，对于节点均匀分布的情况，核近似不满足零阶一致性要求，对于节点非均匀分布的情况，核近似不满足零阶和一阶一致性要求，收敛性无法保证(Belytschko et al.,1996).因此应用SPHM时应尽量使节点均匀分布，且边界附近需做特殊处理(Randles et al.,1996).此外，SPHM形函数属于拟合型，因此也不具备Kronecker delta函数性质.
Liu W K等用SPHM求解有限区域问题时发现数值解在边界附近精度急剧下降，原因可能在于离散形式的SPHM不满足一致性条件，他们在核近似理论的基础上引入校正函数(correction function)，使其满足了一致性要求，形成了再生核粒子法(reproducing kernel particle method，RKPM)(Liu et al.,1995).在RKPM中，场函数u( X )近似值可表示为
径向基函数近似(RBF)具有形式简单、计算效率高等优点，是一种很有发展前景的无网格近似方法.MQ(multi-quadrics)函数、薄板样条(thin plate spline,TPS)函数、高斯(Gaussian)函数及对数(Logarithmic)函数为几种典型的RBF函数(Liu et al.,2005).Frank(1982)比较了29种离散数据插值的精度，通常情况下MQ函数与薄板样条函数(TPS)精度最高.用RBF插值时，近似函数的导数在区域边界处的误差很大，Hermite插值法(Zhang et al.,2000)可以很好的解决这一问题.
上述几种典型径向基函数都是定义在整个求解域上的，因此方程的系数矩阵是满秩矩阵，条件数高，不便于大型问题的求解.Wendland(1998)提出了紧支径向基函数(compactly supported radial basis function,CSRBF)插值，用它构造的方程系数矩阵具有稀疏、带状的特点.此外，Kriging 插值法也是一种较常用的插值近似方法，Dai等(2003)证明了它是RBF插值的另一种表达形式.RBF形状参数最优值目前只能通过数值试验的方法确定，不同领域形状参数的最优值可能不同.
除以上几种典型无网格近似法外，无网格法还包括基于自然邻接点插值近似的自然元法(natural element method,NEM)(Sukumar et al.,2001)、基于单位分解近似的单位分解有限元法(the partition of unity method，PUM)(Melenk et al.,1996)、扩展有限元法(extended finite element method,XFEM)(Moes et al.,1999)以及hp云法(hp-clouds method)(Armando et al.,1996).自然元法根据Voronoi多边形分割面积的比例来定义形函数，因能较好的处理网格畸变被用于几何大变形、动力弹塑性分析、固体力学、岩土工程等问题的数值计算.
PUFEM与XFEM具有常规有限元法的优点, 它的网格与结构内部的几何或物理界面无关, 克服了在诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分带来的困难, 模拟裂纹生长时也无需对网格进行重新剖分而被大量用于断裂力学问题的计算.Simpson等(2011)还利用单位分解的思想改进了双重边界元法(Dual Boundary Element Method,DBEM),并将其应用于断裂力学的高精度计算，结果表明此方法较常规DBEM精度约高出一个数量级.
Hp云法利用Sheperd函数作为单位分解函数，然后在单位分解的框架内建立场量函数的近似表达，这种方法适合进行hp型自适应分析，Oden等(1996)对其进行了严格的数学分析.
加权残量法是求解常微分方程(ODEs)或偏微分方程(PDEs)近似解的通用方法，有限元法(FEM)、边界元法(BEM)、无网格法(meshfree method)均可看作加权残量法的特例.常用的加权残量法有配点法、子域法、最小二乘法、力矩法、伽辽金法以及边界积分方程法(Liu et al.,2005).加权残量法作为无网格法的另一大核心，是无网格法的具体实现方式，不同的无网格近似方式与加权残量法结合就形成了不同的无网格法.
许多工程物理问题均可表示为如下一组带边界条件的微分方程形式
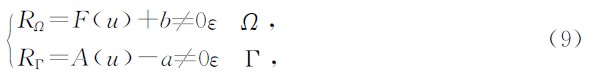
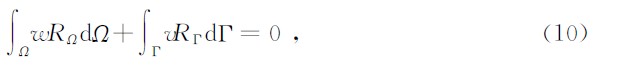
现以大地电磁二维问题为例阐述其加权残量表达式的形成过程,其满足的控制方程为Maxwell方程组，表达式为
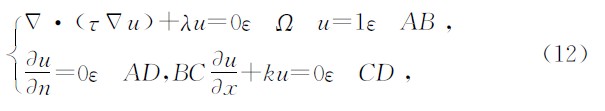
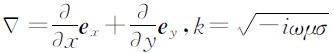,对于电场极化模式(TE模式)：
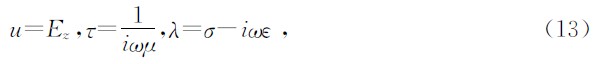
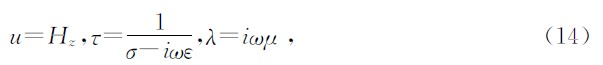
当近似解满足边界条件时要求在求解域Ω上残量加权积分为零，即
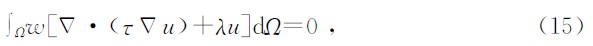
全域Galerkin 弱式法中取w=∇u ,权函数w与势函数u位于同一函数空间，现以无单元Galerkin法(EFGM)求解大地电磁二维问题为例介绍无网格全域弱式法的基本原理，与有限元法类似，EFGM有如下的Galerkin 弱式形式
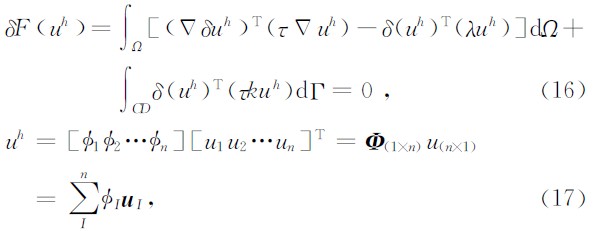
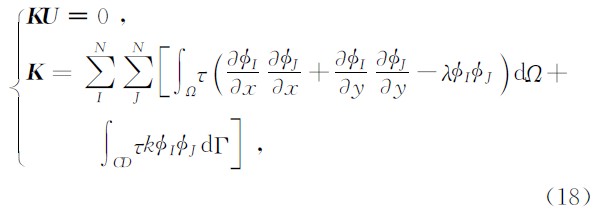
值得说明的是EFGM中各矩阵的组装均基于高斯积分点 X Qi，不同高斯点对应的支持域可能不同，因而对应的形函数也可能不同，每次积分都会重新构造形函数，这点与有限元法有区别，在有限元法中同一单元内的所有高斯点均采用相同的节点进行插值运算.
背景网格积分是全域Galerkin弱式无网格法中最耗时的环节，为了确保积分求解的精度，背景网格中的高斯点数目不能太少，一般取支持域内场节点的数量的3~9倍(Liu et al.,2005)，这极大的降低的无网格法的求解效率.因此Beissel等(1996)提出用节点积分法来近似求解 K 中的积分，与高斯积分相比，节点积分极大地提高了全域Galerkin法的计算效率，但也显著降低了计算精度，且节点积分存在稳定性问题.Chen等(2010)提出用光滑应变稳定方法来消除节点积分的不稳定性，Le等(2010)利用这种方法进行了自适应EFGM的研究，黄乐建等(2007)将光滑应变稳定技术与RPIM相结合，改进的RPIM可以在满足全域相容性的同时精确地加载第一类边界条件.此外，(Carpinteri et al.,2002)还提出了基于单位分解的积分方法.
高精度、高效率且稳定的积分方法一直是全域Galerkin弱式法努力的目标，近年来又出现了几种新型积分方法，刘岩等(2007)采用蒙特卡罗方法(Monte Carlo)进行积分运算,摆脱了EFGM对背景积分网格的依赖并成功将其应用于自由面的渗流问题，但Monte Carlo法收敛速度慢，计算效率相对较低.Khosravifard等(2010)提出了一种笛卡尔变换方法(Cartesian transformation method,CTM)来计算区域积分，相比使用背景网格的高斯积分法，该方法具有更高的计算效率和精度，使全域无网格法成为一种真正意义上的无网格法.
用数值积分方法将总体刚度矩阵 K 离散化后，下一步就是各类边界条件的加载.罚函数法、拉格朗日乘子法、修正变分原理、奇异权函数法、边界配点法及边界变换法均是典型的边界条件加载方法，其中最实用的方法是罚函数法.另外，将EFGM与其它方法相耦合也可以解决边界条件加载的问题，如EFGM与RPIM的耦合.
EFGM是一种成熟的具有高精度及高收敛率的典型无网格全域Galerkin弱式法，该方法不但成功地应用于有限元法所触及的领域，而且解决了某些有限元法难以处理的问题.除EFGM外，PIM、RPIM及PKPM也是典型的基于全域Galerkin弱式的无网格法，有关这三种方法的研究前文已有介绍，在此不再累述.
全域Galerkin弱式法要求将求解域划分为形状规则的背景单元，不是真正意义上的无网格法，为避免使用背景网格，Atluri等(2002)应用局部Galerkin弱式原理提出了无网格局部Petrov-Galerkin法(MLPGM).
对于局部Galerkin弱式法，加权残量要求在局部积分域Ωq上消除，即
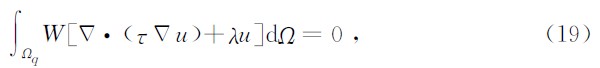
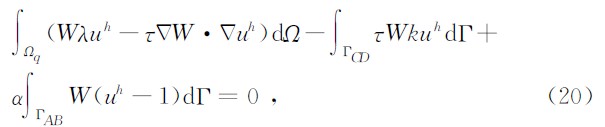
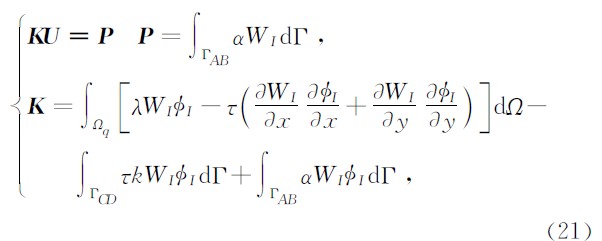
MLPGM形成的总体矩阵 K 一般为稀疏、带状但却是非对称的，非对称性主要是由于试函数uh和权函数W取自不同的函数空间及边界积分的不对称所致(Benz,1988). K 的不对称性增加了方程组求解的难度及计算量.MLPGM另一个缺点在于当求解域边界较复杂时，局部积分域可能与其相交构成形状复杂的积分域，造成数值积分的不便.MLPGM的应用远没有EFGM那么广，但也成功用于弹性材料、断裂力学、电磁场问题及瞬态温度场等问题的求解.此外，龙述尧等(2009)还研究了基于无网格局部Galerkin弱式的h型自适应分析算法.
MLPGM采用MLS近似构造形函数，因此第一类边界条件加载困难.赵美玲(2005)提出了MLPGM与FEM相耦合的MLPG-FE法，实现了场变量及其导数在两种方法使用区域交界处的连续过渡及第一类边界条件的精确加载，并通过电磁场问题的计算验证了方法的有效性.蔡永昌等(2003)利用自然邻接点插值近似思想提出了基于Voronoi结构的无网格局部Petrov-Galerkin法，计算结果表明该方法精度与四边形单元有限元法相当，但计算耗时却不到有限元法的一半.郑保敬(2010)采用滑动Kriging插值法构造近似函数，使用Heaviside分段函数作为权函数，建立了改进的无网格局部Petrov-Galerkin法，并将其成功应用于位势问题、瞬态热传导问题、弹性力学和弹性动力学问题.
类似于全域Galerkin弱式法，PIM及RPIM也可被用于局部Galerkin弱式形函数的构造，
两者结合形成的方法称为局部点插值法(local point interpolation method，LPIM)(Liu et al.,2001)及局部径向点插值法(local radial point interpolation method，LRPIM)(Liu et al.,2001).由于LPIM与LRPIM形函数具有插值特性，第一类边界条件的处理较MLPGM便利.另外，局部Galerkin弱式法不需要满足全域相容性要求(Liu et al.,2005),因此LRPIM更能突显出RPIM的优点，是一种很有前景的无网格局部弱式法.
基于边界积分方程的无网格法是边界积分方程与无网格思想相结合而发展起来的数值计算方法.边界型无网格法具有降维、计算精度高，形函数构造不依赖单元等优点，这类无网格法在近十年来发展迅速，并形成了一系列有效的方法，其中较典型的边界型无网格法有局部边界积分方程法(local boundary integral equation method,LBIEM)(Zhu et al.,1998)、边界点法(boundary node method,BNM)(Mukherjee et al.,1997)、杂交边界点法(hybrid boundary node method,HBNM)(Zhang et al.,2002)、边界云团法(boundary cloud method,BCM)(Aluru et al.,2002)、边界点插值法(boundary point interpolation method,BPIM)(Liu et al.,2004)和边界径向点插值法(boundary radial point interpolation method,BRPIM)(Liu et al.,2002)等.LBIEM做为MLPGM的特例需要在区域内配置节点，不适合无限域问题的求解.BNM、HBNM、BCM和LBIEM利用MLS近似构造形函数,第一类边界条件处理困难.Mukherjee等(1997)采用添加一组额外方程的方法来满足边界条件，但这一处理增加了总体方程的数目，降低了计算效率.BPIM与BRPIM构造的形函数具有插值特性，但形成的总体矩阵是非对称的,同样影响了计算效率.秦义校(2007)将具有插值特性的重构核粒子法(RKPM)形函数与边界积分方程法相结合，提出了重构核粒子边界无单元法及其与有限元的耦合方法，该方法具有较高的计算精度及效率但存在奇异积分的问题.另外，以上基于边界积分方程的无网格方法都缺乏包括收敛性分析和误差估计在内的理论基础，李小林(2009)将将边界积分方程的弱式形式与移动最小二乘近似相结合提出了Galerkin边界点法(Galerkin boundary node method,GBNM)，并分析了该方法的收敛性及误差.
配点法取∇函数(Dirac Delta function)为权函数，是一种直接离散微分方程的数值方法，与通过积分平均方式消除残量的弱式方法不同，它的实质是使残量函数在求解域Ω上的一组特定点上得到满足.无网格配点法离散控制方程的过程直接，计算效率高，是真正的无网格法.然而，配点法得到的总体矩阵 K 往往是病态的，导致了解的不稳定，当研究的问题涉及导数边界条件时数值解的精度与稳定性更是显著下降(Liu et al.,2005).无网格配点法求解大地电磁二维问题的表达式只需将(12)式中的场量u及u的导数用任意一种无网格近似法直接表示即可.当总体矩阵为非奇异且使用合理的配点方案时， K 具有稀疏、带状及非对称的性质(Liu et al.,2005).配点法第一类边界条件可利用类似于局部Galerkin弱式法中的直接插值法精确加载，导数边界条件加载则较困难，必须采用特殊的处理方法，无网格配点法的研究也主要集中在提高方法的稳定性及导数边界条件的处理上.张雄等(2003)提出的加权最小二乘无网格法(weighted least-squares collocation method,WLSCM)就是一种稳定的配点法，其效率远高于Galerkin型无网格法，WLSCM已被成功应用于热传导问题.孟庆东(2008)利用径向基函数插值，得到了基于局部插值的加权最小二乘无网格法, 当区域节点数较多时该方法效率较WLSCM高，但由于采用了径向基函数插值，最佳形状参数只能通过数值试验获得.肖大舟等(2006)将基于Voronoi图的双重点移动最小二乘近似与加权最小二乘法(WLSCM)相结合，导出了双重点最小二乘配点无网格法(meshless double grid least-square collocation method,MDGLSCM)，数值计算表明MDGLSCM较WLSCM计算效率、精度及收敛率均有所提高.
最小二乘法的欧拉方程不是原来的微分方程，而是其高阶导数，若采用不恰当的边界条件将可能得到错误的解答(Zienkiewicz et al.,2000).Pan等(2005)将Galerkin法与最小二乘法相耦合，建立了Galerkin-最小二乘无网格法(meshless Galerkin least-square method, MGLSM)，该方法的核心是将求解域划分为内部区域与边界区域，在内部区域采用最小二乘法，在边界区域采用Galerkin法.Galerkin区域通常只需包含一层背景网格即可，因此MGLSM计算量接近配点法却远小于Galerkin法，且导数边界条件也被自然地融入Galerkin弱式中.
基于径向基函数(RBF)近似的无网格法(radial point collocation method，RPCM)是另一种较常用的配点方法，该方法被成功应用于流体力学、材料力学、计算电磁学及声学等问题的求解.鉴于常规径向基函数法较难处理解具有多尺度性质的问题，张云新(2006)还提出了多尺度无网格径向基函数插值法，并将其成功应用于不可压缩流体的计算.此外，有限点法(FPM)(Onate et al.,1996)也是配点法的一种，该方法采用MLS近似生成形函数，用配点方法离散代数方程，在流体力学领域应用较成功(孟庆东,2008).
无网格耦合方法包括无网格法之间的耦合及无网格法与其它数值方法的耦合.各种无网格法存在不同的优缺点，某些无网格法之间可能是优势互补的，因此很自然地想到将两者结合.无网格法相比传统数值方法最大的缺陷在于计算效率低，若能将无网格法与其它成熟数值方法(如FEM与BEM)相结合，发挥它们各自的优势，很多问题便能得到最佳的解决.
无网格局部Galerkin弱式法与无网格配点法相耦合的无网格弱强式法(meshless weak-strong method,MWSM)(Liu et al.,2003)及前文所述的Galerkin-最小二乘无网格法(MGLSM)(Pan et al.,2005)就是两种典型的无网格耦合方法.它们综合了配点法高效、实现过程简单及弱式法精度高、稳定性好等优点，是较为理想的无网格方法.
无网格法与成熟网格数值方法的耦合可极大的提高计算效率，为其进入实用创造条件.无单元Galerkin法与有限元法的耦合(EFGM-FEM)(荚颖等,2010)是最常见的一种无网格法与网格方法相耦合的形式，它的核心是在网格区域与无网格区域之间建立一个过渡的耦合区，耦合区内使用修正的形函数(刘更等,2005)，从而实现了无网格区与网格区的连续过渡.径向基点插值法与有限元法的耦合(RPIM-FEM)(张琰等,2008)原理与EFGM-FEM类似，但是由于其采用的是RPIM形函数，因此第一类边界条件的加载相对容易.此外，无网格耦合方法还包括局部边界积分方程法与有限元法的耦合(LBIEM-FEM)(张春霞,2007)、局部点插值法与边界元法的耦合(LPIM-BEM)(Njiwa,2011)、无单元Galerkin法与分形有限元法(fractal finite element method,FFEM)的耦合(EFGM-FFEM)(Rao,2011)及径向基配点法与边界元法的耦合(RPCM-BEM)(Nicolas et al.,2012).
计算效率低是无网格法的普遍缺点，尽管已经提出了一些改善无网格法计算效率的措施(Barbieri et al.,2012)，但其耗时仍无法与经典的网格方法(如FEM)相提并论.近年来出现的并行计算方法有望突破无网格法计算效率的瓶颈，曾清红(2006)研究了无单元Galerkin法、基于单位分解积分的Galerkin无网格法以及无网格局部Petorv-Galerkin法等三类无网格数值模拟的并行实现，结果表明三类无网格数值模拟均具有很高的并行效率，其中MLPGM可并行性最高.相信随着电子计算机的发展，并行计算必将在提高无网格法效率方面发挥更大的作用.
经历十多年的快速发展无网格法现已成为计算力学领域最有效的数值分析手段之一，至今出现的无网格法已有三十余种，发表的相关论文达数千篇之多，然而笔者检索到的有关无网格法在地球物理学中的应用文献却不到十篇，且文献中采用的方法全为无单元Galerkin法.有关EFGM在地震领域的应用研究主要可参考(贾晓峰, 2005; 贾晓峰等,2005,2006a,2006b,2010)及(王月英等,2007)所做的工作，他们的研究表明：EFGM在地震波正演模拟中效果良好；基函数类型对无网格计算精度及效率有直接影响，高阶次的基函数在提高模拟精度的同时也极大地增加了计算成本，综合考虑一般选取线性基函数或者二次基函数即可；节点必须在满足空间采样要求的条件下,才可以自由分布,否则会引起频散现象；采用衰减边界条件,可以有效处理EFGM第一类边界条件的加载难题.
EFGM在电法领域的应用较少，王洪华等(2013)研究了探地雷达二维无单元法正演模拟，文中详细推导了探地雷达波动方程的无单元法离散公式，并就正演模拟中的基本边界和吸收边界的加载问题进行了讨论，最后通过一系列地电模型的数值计算，验证了无网格算法的有效性.此外，苏洲等(2012)还将EFGM成功应用于大地电磁二维正演模拟，文中采用四次样条函数为权函数，以拉格朗日乘子法加载边界条件，并给出了支持域尺寸的推荐值.有关无网格法在重磁领域的研究至今还未见报导.
由此可见，无网格法在地球物理学中的研究才处在起步阶段，作为一种发展历史较短的新型数值方法，无网格法却已在计算力学中显露锋芒，并逐渐向诸如生命科学、纳米技术等新兴领域渗透，其独特的优点必将为地球物理场的正演模拟提供新的思路.
本文详细介绍了移动最小二乘近似(MLS)、点插值近似(PIM)、核积分近似(SPH)、径向基函数近似(RBF)等典型的无网格近似方式，评述了每种近似方式的优缺点并结合无网格法的最新研究进展列举了相应的改进方法.阐述了基于全域Galerkin弱式、基于局部Galerkin弱式、基于边界积分方程、基于配点等典型的无网格加权残量离散方法，推导了大地电磁二维问题的无网格Galerkin弱式离散公式，并以其为例介绍了无网格法的具体求解过程及其与有限元法的差异.综述了无网格法最新进展，介绍了无网格耦合方法，最后讨论了无单元Galerkin法(EFGM)在地球物理学中的应用效果.
无网格法是为了克服网格方法的缺陷而诞生的新型数值方法，其精度高、无网格、自适应分析容易等优点使其在工程界有着强大的生命力.无网格法现已成功解决了许多常规数值方法难以处理的问题，虽然有关无网格法在地球物理学领域中的研究很少，但报导的文献均表明无网格法同样适合地球物理场的正演模拟，相信不久的将来无网格法的价值会
被更多的凸现出来.最后值得说明的是，无网格法由于发展历史较短，理论还不很完善，其应用过程中难免会出现这样那样的问题，但这也恰恰为无网格法的发展指明了方向.
| [1] | Armando D C, Oden J T. 1996. H-p clouds-an h-p meshless method[J]. Numerical Methods for Partial Differential Equations, 12(6): 673-705. |
| [2] | Atluri S N, Shen S P. 2002. The Meshless Local Petrov-Galerkin (MLPG) Method[M]. USA: Tech Science Press. |
| [3] | Barbieri E, Meo M. 2012. A fast object-oriented Matlab implementation of the Reproducing Kernel Particle Method[J]. Computational Mechanics, 49(5): 581-602. |
| [4] | Beissel S, Belytschko T. 1996. Nodal integration of the element-free Galerkin method[J]. Computer Methods in Applied Mechanics and Engineering, 139(1-4): 49-74. |
| [5] | Belytschko T, Lu Y Y, Gu L. 1994. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 37(2): 229-256. |
| [6] | Belytschko T, Krongauz Y, Organ D, et al. 1996. Meshless methods: An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 139(1-4): 3-47. |
| [7] | Benz W. 1988. Applications of smooth particle hydrodynamics (SPH) to astrophysical problems[J]. Computer Physics Communications, 48(1): 97-105. |
| [8] | Carpinteri A, Ferro G, Ventura G. 2002. The partition of unity quadrature in meshless methods[J]. International Journal for Numerical Methods in Engineering, 54(7): 987-1006. |
| [9] | Chen J S, Han W M, Yang Y, et al. 2003. A reproducing kernel method with nodal interpolation property[J]. International Journal for Numerical Methods in Engineering, 56(7): 935-960. |
| [10] | Chen L, Nguyen-Xuan H, Nguyen-Thoi T, et al. 2010. Assessment of smoothed point interpolation methods for elastic mechanics[J]. International Journal for Numerical Methods in Biomedical Engineering, 26(12): 1635-1655. |
| [11] | Chen S. 2007. Theory study on high precision meshfree method in computational mechanics [Ph. D. thesis] (in Chinese). Shanghai: Shanghai Jiaotong University of Naval Architecture, Ocean and Civil Engineering. |
| [12] | Cui X Y, Liu G R, Li G Y. 2010. A cell-based smoothed radial point interpolation method (CS-RPIM) for static and free vibration of solids[J]. Engineering Analysis with Boundary Elements, 34(2): 144-157. |
| [13] | Dai K Y, Liu G R, Lim K M, et al. 2003. Comparison between the radial point interpolation and the Kriging interpolation used in meshfree methods[J]. Computational Mechanics, 32(1-2): 60-70. |
| [14] | Feng D S, Wang H H, Dai Q W. 2013. Forward simulation of Ground Penetrating Radar based on the element-free Galerkin method[J]. Chinese Journal of Geophysics (in Chinese), 56(1): 298-308. |
| [15] | Frank R. 1982. Scattered data interpolation: tests of some method[J]. Mathematics of Computation, 38(157): 181-200. |
| [16] | Gai Y C, Zhu H H, Wang J H. 2003. The meshless local-Petrov Galerkin method based on the Voronoi cells[J]. Acta Mechanica Sinica (in Chinese), 35(2): 187-193. |
| [17] | Gu Y T, Liu G R. 2002. A boundary radial point interpolation method (BRPIM) for 2-D structural analyses[J]. Structural Engineering Mechanics, 15(5): 535-550. |
| [18] | Gu Y T, Liu G R. 2004. A boundary point interpolation method for stress analysis of solids[J]. Computational Mechanics, 28(1): 47-54. |
| [19] | Gu Y T, Ding H. 2005. Recent developments of meshless method[J]. Advances in Mechanics (in Chinese), 35(3): 323-337. |
| [20] | Gu Y T, Wanga W, Zhang L C, et al. 2011. An enriched radial point interpolation method (e-RPIM) for analysis of crack tip fields[J]. Engineering Fracture Mechanics, 78(1): 175-190. |
| [21] | Huang L J. 2007. Study of the meshfree method based on stabilized conforming nodal integration and RPIM shape function [Ph. M. thesis] (in Chinese). Ji’nan: Shandong University of Mechanical Engineering. |
| [22] | Jia X F. 2005. Element-free Galerkin method for seismic numerical modeling and imaging in complex media[D] (in Chinese). Beijing: Peking University of Earth and Space Sciences. |
| [23] | Jia X F, Hu T Y. 2005. Solving seismic wave equation by moving least squares (MLS) method[J]. Progress in Geophysics (in Chinese), 20(4): 920-924. |
| [24] | Jia X F, Hu T Y, Wang R Q. 2006a. Wave equation modeling and imaging by using element-free method[J]. Progress in Geophysics (in Chinese), 21(1): 11-17. |
| [25] | Jia X F, Hu T Y, Wang R Q. 2006b. A mesh-free algorithm of seismic wave simulation in complex medium[J]. Oil Geophysical Prospecting (in Chinese), 41(1): 43-48. |
| [26] | Jie Y, Tang X W, Luan M T. 2010. Finite-element free Galerkin coupling method for sand liquefaction-induced deformation[J]. Rock and Soil Mechanics (in Chinese), 31(8): 2643-2647, 2654. |
| [27] | Jie Y X, Liu Y. 2007. Element-free Galerkin method based on Monte Carlo integration and its application in seepage analysis[J]. Chinese Journal of Geotechnical Engineering (in Chinese), 29(12): 1794-1799. |
| [28] | Kaljevic ＇ I, Saigal S. 1997. An improved element free Galerkin formulation[J]. International Journal for Numerical Methods in Engineering, 40(16): 2953-2974. |
| [29] | Khosravifard A, Hematiyan M R. 2010. A new method for meshless integration in 2D and 3D Galerkin meshfree methods[J]. Engineering Analysis with Boundary Elements, 34(1): 30-40. |
| [30] | Le C V, Askes H, Gibert M. 2010. Adaptive element-free Galerkin method applied to the limit analysis of plates[J]. Computer Methods in Applied Mechanics and Engineering, 199(37-40): 2487-2496. |
| [31] | Li D M, Peng M J, Cheng Y M. 2011. The complex variable element-free Galerkin (CVEFG) method for elastic large deformation problems[J]. Scientia Sinica Physica, Mechanica & Astronomica (in Chinese), 41(8): 1003-1014. |
| [32] | Li G, Aluru N R. 2002. Boundary cloud method: a combined scattered point/boundary integral approach for boundary-only analysis[J]. Computer Methods in Applied Mechanics and Engineering, 191(21-22): 2337-2370. |
| [33] | Li J H. 2004. Researches on meshless method with complex variables and its applications [Ph. D. thesis] (in Chinese). Xi’an: Xi'an University of Technology of Civil Engineering and Architecture. |
| [34] | Li J H, Cheng Y M. 2006. Advances and expectations of meshless methods[J]. Chinese Quarterly of Mechanics (in Chinese), 27(1): 143-152. |
| [35] | Li X L. 2009. A meshless Galerkin method based on boundary integral equations [Ph. D. thesis] (in Chinese). Chongqing: Chongqing University College of Mathematics and Physics. |
| [36] | Liu G, Liu T X, Xie Q. 2005. Meshfree methods and their applications[M] (in Chinese). Xi’an: Northwestern Polytechnical University Press. |
| [37] | Liu G R, Gu Y T. 2001. A local point interpolation method for stress analysis of two-dimensional solids[J]. Structural Engineering and Mechanics, 11(2): 22l-236. |
| [38] | Liu G R, Gu Y T. 2001. A local radial point interpolation method (LRPIM) for free vibration analyses of 2-D solids[J]. Journal of Sound and Vibration, 246(1): 29-46. |
| [39] | Liu G R, Gu Y T. 2003. A meshfree method: meshfree weak-strong (MWS) form method, for 2-D solids[J]. Computational Mechanics, 33(1): 2-14. |
| [40] | Liu G R, Gu Y T. 2005. An Introduction to Meshfree Methods and Their Programming[M]. Berlin: Springer. |
| [41] | Liu G R, Nguyen-Xuan H, Nguyen-Thoi T. 2010. A theoretical study on the smoothed FEM (S-FEM) models: Properties, accuracy and convergence rates[J]. International Journal for Numerical Methods in Engineering, 84(10): 1222-1256. |
| [42] | Liu H S, Yang Y Y, Li J. 2007. Automatic nonuniform arrangement of nodes and generation of background cell in meshless method[J]. Rock and Soil Mechanics (in Chinese), 28(1): 201-205. |
| [43] | Liu H S, Xing Z W, Sun Z Z, et al. 2011. Adaptive multiple scale meshless simulation on springback analysis in sheet met al. forming[J]. Engineering Analysis with Boundary Elements, 35(3): 436-451. |
| [44] | Liu M B, Liu G R. 2010. Smoothed Particle Hydrodynamics (SPH): an overview and recent developments[J]. Archives of Computational Methods in Engineering, 17(1): 25-76. |
| [45] | Liu W K, Jun S, Zhang Y F. 1995a. Reproducing Kernel particle methods[J]. International Journal for Numerical Methods in Fluids, 20(8-9): 1081-1106. |
| [46] | Liu W K, Chen Y J. 1995b. Wavelet and multiple scale reproducing kernel methods[J]. International Journal for Numerical Methods in Fluids, 21(10): 901-931. |
| [47] | Liu W K, Li S F, Belytschko T. 1997. Moving least-square reproducing kernel method (I) methodology and convergence[J]. Computer Methods in Applied Mechanics and Engineering, 143(1-2): 113-154. |
| [48] | Liu X. 2011. Meshless method[M] (in Chinese). Beijing: Science Press. |
| [49] | Long S Y, Wu Z P. 2009. h-adaptive analysis based on the meshless local Petrov-Galerkin method[J]. Journal of Hunan University (Natural Sciences) (in Chinese), 36(1): 68-71. |
| [50] | Lucy L B. 1977. A numerical approach to the testing of the fission hypothesis[J]. Astronomical Journal, 82: 1013-1024. |
| [51] | Melenk J M, Babuska I. 1996. The partition of unity finite element method: basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 139(1-4): 289-314. |
| [52] | Meng Q D. 2008. The weighted least squares collocation meshless method of RBF local interpolation and preliminary study of finite point difference method [Ph. M. thesis] (in Chinese). Suzhou: Soochow University of Mathematical Sciences. |
| [53] | Meng Z. 2007. Optimized radius of influence domain for MLS weight function and its applications [Ph. M. thesis] (in Chinese). Xi’an: Northwestern Polytechnical University of Natural and Applied Sciences. |
| [54] | Moes N, Dolbow J, Belytschko T. 1999. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 46(1): 131-150. |
| [55] | Monaghan J J. 1988. An introduction to SPH[J]. Computer Physics Communications, 48(1): 89-96. |
| [56] | Mukherjee Y X, Mukherjee S. 1997. The boundary node method for potential problems[J]. International Journal for Numerical Methods in Engineering, 40(5): 797-815. |
| [57] | Nayroles B, Touzot G, Villon P. 1992. Generalizing the finite element method: diffuse approximation and diffuse elements[J]. Computational Mechanics, 10(5): 307-318. |
| [58] | Nguyen V P, Rabczuk T, Bordas S, et al. 2008. Meshless methods: A review and computer implementation aspects[J]. Mathematics and Computers in Simulation, 79(3): 763-813. |
| [59] | Nicolas T, Richard K N, Taghite M B. 2012. A simple solution procedure to 3D-piezoelectric problems: Isotropic BEM coupled with a point collocation method[J]. Engineering Analysis with Boundary Elements, 36(11): 1513-1521. |
| [60] | Njiwa R K. 2011. Isotropic-BEM coupled with a local point interpolation method for the solution of 3D-anisotropic elasticity problems[J]. Engineering Analysis with Boundary Elements, 35(4): 611-615. |
| [61] | Onate E, Idelsohn S, Zienkiewicz O C, et al. 1996. A finite point method in computational mechanics: Applications to convective transport and fluid flow[J]. International Journal for Numerical Methods in Engineering, 39(22): 3839-3866. |
| [62] | Pan X F, Zhang X, Lu M W. 2005. Meshless Galerkin least-squares method[J]. Computational Mechanics, 35(3): 182-189. |
| [63] | Qin Y X. 2007. Researches on the reproducing kernel particle boundary element-free methods [Ph. D. thesis] (in Chinese). Shanghai: Shanghai University College of Sciences. |
| [64] | Randles P W, Libersky L D. 1996. Smoothed particle hydrodynamics: some recent improvements and applications[J]. Computer Methods in Applied Mechanics and Engineering, 139(1-4): 375-408. |
| [65] | Rao B N. 2011. Coupled meshfree and fractal finite element method for unbounded problems[J]. Computers and Geotechnics, 38(5): 697-708. |
| [66] | Shu H M, Huang Z Q, Li C W. 2008. A novel meshless method based on ridge basis function[J]. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 32(3): 108-113. |
| [67] | Simpson R, Trevelyan J. 2011. A partition of unity enriched dual boundary element method for accurate computations in fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 200(1-4): 1-10. |
| [68] | Su Z, Hu W B, Zhu Y. 2012. Meshfree method used in two-dimensional magnetotelluric forwarding[J]. Journal of Oil and Gas Technology (in Chinese), 34(5): 87-90. |
| [69] | Sukumar N, Moran B, Semenov A Y, et al. 2001. Natural neighbor Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 50(1): 1-27. |
| [70] | Tang Q, Zhong Z H, Zhang G Y, et al. 2011. An efficient adaptive analysis procedure for node-based smoothed point interpolation method (NS-PIM)[J]. Applied Mathematics and Computation, 217(21): 8387-8402. |
| [71] | Tang Q, Zhang G Y, Liu G R, et al. 2012. An efficient adaptive analysis procedure using the edge-based smoothed point interpolation method (ES-PIM) for 2D and 3D problems[J]. Engineering Analysis with Boundary Elements, 36(9): 1424-1443. |
| [72] | Wang J G, Liu G R. 2002. A point interpolation meshless method based on radial basis functions[J]. International Journal for Numerical Methods in Engineering, 54(11): 1623-1648. |
| [73] | Wang Y Y. 2007. Study of element-free Galerkin method in the seismic forward modeling[J]. Progress in Geophysics (in Chinese), 22(5): 1539-1544. |
| [74] | Wen J B, Zhou J X, Zhang H Y, et al. 2003. A realistic technique based on Delaunay Traingnlation for post-processing of Meshless numerical results[J]. Chinese Journal of Applied Mechanics (in Chinese), 20(4): 105-107. |
| [75] | Wendland H. 1998. Error estimates for interpolation by compactly supported radial basis functions of minimal degree[J]. Journal of Approximation Theory, 93(2): 258-272. |
| [76] | Wu C, Zhou R Z. 2006. Element-free Galerkin method with wavelet basis and its comparison with finite element method[J]. Engineering Mechanics (in Chinese), 23(4): 28-32. |
| [77] | Xiao D Z, Zhang X, Lu M W. 2006. Meshless double grid least-square collocation method[J]. Chinese Journal of Computational Mechanics (in Chinese), 23(6): 711-717. |
| [78] | Xu X, Zhou M M, Yu D Y, et al. 2011. A strain-constructed point interpolation method (SC-PIM)[J]. Journal of Jilin University (Science Edition) (in Chinese), 49(6): 969-972. |
| [79] | Yan S W. 2010. Element-free method applied in siesmic modeling and imaging in high-resolution[D] (in Chinese). Heifei: University of Science and Technology of China of Earth and Space Sciences. |
| [80] | Zeng Q H. 2006. Parallel algorithms and parallel implementation of meshless numerical simulation [Ph. D. thesis] (in Chinese). Hefei: University of Science and Technology of China of Engineering Science. |
| [81] | Zhang C X. 2007. Research on the coupling of Finite Element method and Local Boundary Integral Equation for plane problem in linear elasticity [Ph. M. thesis] (in Chinese). Chongqing: Chongqing University College of Civil Engineering. |
| [82] | Zhang J M, Yao Z H, Li H. 2002. A hybrid boundary node method[J]. International Journal for Numerical Methods in Engineering, 53(4): 751-763. |
| [83] | Zhang X, Song K Z, Lu M W, et al. 2000. Meshless methods based on collocation with radial basis functions[J]. Computational Mechanics, 26(4): 333-343. |
| [84] | Zhang X, Hu W, Pan X F, et al. 2003. Meshless weighted least-square method [J]. Acta Mechanica Sinica (in Chinese), 35(4): 425-431. |
| [85] | Zhang X, Liu Y. 2004. Meshless method[M] (in Chinese). Beijing: Tsinghua University Press. |
| [86] | Zhang X, Liu Y, Ma S. 2009. Meshfree methods and their applications[J]. Advances in Mechanics (in Chinese), 39(1): 1-36. |
| [87] | Zhang Y, Wang J G, Zhang B Y. 2008. Coupled FEM and meshless radial point interpolation method[J]. Journal of Tsinghua University (Science and Technology) (in Chinese), 48(6): 951-954. |
| [88] | Zhang Y X. 2006. Meshless radial basis function method and its application in the calculation of incompressible fluid [Ph. D. thesis]. Shanghai: Fudan University of Mathematical Sciences. |
| [89] | Zhao M L. 2005. Research and application of meshless method in the calculation electromagnetic field [Ph. M. thesis] (in Chinese). Xi’an: Northwestern Polytechnical University of Natural and Applied Sciences. |
| [90] | Zhao Y L. 2008. Improvement and Application of the Basis of Element-free method [Ph. D. thesis] (in Chinese). Changchun: Jilin University of Mechanical Science and Engineering. |
| [91] | Zheng B J. 2010. Study of meshless local Petrov-Galerkin method based on moving Kriging interpolation [Ph. M. thesis] (in Chinese). Taiyuan: Taiyuan University of Science and Technology of Applied Science. |
| [92] | Zhu T, Zhang J D, Atluri S N. 1998. A local boundary integral equation (LBIE) method in computational mechanics, and a meshless discretization approach[J]. Computational Mechanics, 21(3): 223-235. |
| [93] | Zienkiewicz O C, Taylor R L. 2000. The Finite Element Method (5th Edition)[M]. Oxford: Butterworth-Heinemann. |
| [94] | Zou P. 2011. Study of meshless method based on B-spline wavelet function [Ph. D. thesis] (in Chinese). Changchun: Jilin University of Mechanical Science and Engineering. |
| [95] | 陈思. 2007. 计算力学中高精度无网格法基础理论研究 [博士论文]. 上海: 上海交通大学船舶海洋与建筑工程学院. |
| [96] | 冯德山, 王洪华, 戴前伟. 2013. 基于无单元Galerkin法探地雷达正演模拟[J]. 地球物理学报, 56(1): 298-308. |
| [97] | 蔡永昌, 朱合华, 王建华. 2003. 基于Voronoi结构的无网格局部Petrov-Galerkin方法[J]. 力学学报, 35(2): 187-193. |
| [98] | 顾元通, 丁桦. 2005. 无网格法及其最新进展[J]. 力学进展, 35(3): 323-337. |
| [99] | 黄乐建. 2007. 基于稳定相容节点积分和RPIM形函数的无网格法研究 [硕士论文]. 济南: 山东大学机械工程学院. |
| [100] | 贾晓峰. 2005. 复杂介质中地震波模拟与成像的无单元数值算法 [博士论文]. 北京: 北京大学地球与空间科学学院. |
| [101] | 贾晓峰, 胡天跃. 2005. 滑动最小二乘法求解地震波波动方程[J]. 地球物理学进展, 20(4): 920-924. |
| [102] | 贾晓峰, 胡天跃, 王润秋. 2006a. 无单元法用于地震波波动方程模拟与成像[J]. 地球物理学进展, 21(1): 11-17. |
| [103] | 贾晓峰, 胡天跃, 王润秋. 2006b. 复杂介质中地震波模拟的无单元法[J]. 石油地球物理勘探, 41(1): 43-48. |
| [104] | 荚颖, 唐小微, 栾茂田. 2010. 砂土液化变形的有限元-无网格耦合方法[J]. 岩土力学, 31(8): 2643-2647, 2654. |
| [105] | 介玉新, 刘岩. 2007. 基于蒙特卡罗积分的无网格伽辽金法及其在渗流分析中的应用[J]. 岩土工程学报, 29(12): 1794-1799. |
| [106] | 李冬明, 彭妙娟, 程玉民. 2011. 弹性大变形问题的复变量无单元Galerkin方法[J]. 中国科学: 物理学 力学 天文学, 41(8): 1003-1014. |
| [107] | 李九红. 2004. 复变量无网格方法及其应用研究 [博士论文]. 西安: 西安理工大学土木建筑工程学院. |
| [108] | 李九红, 程玉民. 2006. 无网格方法的研究进展与展望[J]. 力学季刊, 27(1): 143-152. |
| [109] | 李小林. 2009. 基于边界积分方程的Galerkin无网格方法 [博士论文]. 重庆: 重庆大学数理学院. |
| [110] | 刘更, 刘天祥, 谢琴. 2005. 无网格法及其应用[M]. 西安: 西北工业大学出版社. |
| [111] | 刘红生, 杨玉英, 李晶. 2007. 无网格法中节点非均匀自动布置及背景网格生成[J]. 岩土力学, 28(1): 201-205. |
| [112] | 刘欣. 2011. 无网格方法[M]. 北京: 科学出版社. |
| [113] | 龙述尧, 邬昭平. 2009. 基于无网格局部Petrov-Galerkin方法的h型自适应分析[J]. 湖南大学学报(自然科学版), 36(1): 68-71. |
| [114] | 孟庆东. 2008. 局部径向插值型最小二乘配点无网格法和有限点差分法初探 [硕士论文]. 苏州: 苏州大学数学科学学院. |
| [115] | 孟卓. 2007. MLS法中权函数影响半径的优化及其应用 [硕士论文]. 西安: 西北工业大学理学院. |
| [116] | 秦义校. 2007. 重构核粒子边界无单元法研究 [博士论文]. 上海: 上海大学理学院. |
| [117] | 署恒木, 黄朝琴, 李翠伟. 2008. 基于楔形基函数的一种新型无网格法[J]. 中国石油大学学报(自然科学版), 32(3): 108-113. |
| [118] | 苏洲, 胡文宝, 朱毅. 2012. 二维大地电磁正演中无网格算法研究[J]. 石油天然气学报, 34(5): 87-90. |
| [119] | 王月英. 2007. 地震波正演模拟中无单元Galerkin法初探[J]. 地球物理学进展, 22(5): 1539-1544. |
| [120] | 文建波, 周进雄, 张红艳,等. 2003. 基于Delaunay三角化的无网格法计算结果后处理[J]. 应用力学学报, 20(4): 105-107. |
| [121] | 吴琛, 周瑞忠. 2006. 小波基无单元法及其与有限元法的比较[J]. 工程力学, 23(4): 28-32. |
| [122] | 肖大舟, 张雄, 陆明万. 2006. 双重点最小二乘配点无网格法[J]. 计算力学学报, 23(6): 711-717. |
| [123] | 徐旭, 周敏敏, 于东元,等. 2011. 一种应变重构点插值无网格方法(SC-PIM)[J]. 吉林大学学报(理学版), 49(6): 969-972. |
| [124] | 阎树文. 2010. 无单元法用于高分辨率地震模拟与成像 [硕士论文]. 合肥: 中国科学技术大学地球和空间科学学院. |
| [125] | 曾清红. 2006. 无网格数值模拟的并行算法及并行实现研究 [博士论文]. 合肥: 中国科学技术大学工程科学学院. |
| [126] | 张春霞. 2007. 线弹性平面问题有限元法与无网格局部边界元法的耦合研究 [硕士论文]. 重庆: 重庆大学土木工程学院. |
| [127] | 张雄, 胡炜, 潘小飞,等. 2003. 加权最小二乘无网格法[J]. 力学学报, 35(4): 425-431. |
| [128] | 张雄, 刘岩. 2004. 无网格法[M]. 北京: 清华大学出版社. |
| [129] | 张雄, 刘岩, 马上. 2009. 无网格法的理论及应用[J]. 力学进展, 39(1): 1-36. |
| [130] | 张琰, 王建国, 张丙印. 2008. 径向基点插值无网格法与有限元耦合法[J]. 清华大学学报(自然科学版), 48(6): 951-954. |
| [131] | 张云新. 2006. 无网格径向基函数方法与不可压缩流体计算 [博士论文]. 上海: 复旦大学数学科学学院. |
| [132] | 赵美玲. 2005. 无网格方法在电磁场计算中的研究与应用 [硕士论文]. 西安: 西北工业大学理学院. |
| [133] | 赵云亮. 2008. 无网格法基函数的改进与应用 [博士论文]. 长春: 吉林大学机械科学与工程学院. |
| [134] | 郑保敬. 2010. 基于滑动Kriging插值的无网格局部Petrov-Galerkin法研究 [硕士论文]. 太原: 太原科技大学应用科学学院. |
| [135] | 邹鹏. 2011. 基于B样条小波基的无网格法研究 [博士论文]. 长春: 吉林大学械科学与工程学院. |