2. 中国地质大学地球物理与信息技术学院, 北京 100083
2. Key Laboratory of Geo-detection (China University of Geosciences, Beijing), Ministry of Education, Beijing 100083, China
今年的诺贝尔化学奖授予Martin Karplus, Michael Levitt和Arieh Warshel三人在“发展复杂化学系统的多尺度模型(for the development of multiscale models for complex chemical systems)”方面的贡献(Levitt, 2001).该模型在生物学和材料科学方面都已经获得了广泛的应用.
在地球物理学领域,诸多基本难题研究地磁场发电机理论、地幔对流、大气和海洋环流、震源物理,都涉及多尺度计算.当前,地震勘探领域的海量计算,更需要解决多尺度计算问题.今年SEG展览上,色塞尔公司已经发展出50万道地震仪,可控震源和不间断采样技术已经使得每日采集TB级数据的高密度、宽方位角勘探成为可能,MEMS技术有可能使得多波多分量采集更为经济,这样要求处理的数据量非常大,为了解决复杂问题如高陡构造、盐下成像,也会不断需要逆时偏移和全波形反演等精度大但计算量大的方法.在非常规油气勘探和开发中,为了处理提高精度,网格还需要加细.在裂缝的尖端和孔隙介质的孔喉附近(Hudson,1980,1981;杨天鸿等,2004),地震波的不同模式、不同方向之间具有较强烈的耦合,在数值模拟中需要较精细的计算;而由于裂缝和孔隙在1个或两个方向上延伸的规模较大较长,对宏观波传播的计算又需要涉及较大的规模,模型网格数目较大,需要超出单个计算单元(中央计算单元和图形计算单元)的内存范围,多个计算单元的并行计算,又涉及到多划分涉及的附近需要较精细的计算.这都为海量计算提出更高要求,多尺度计算是其中的关键问题.
多尺度计算的思想,是用精确的方法计算近区作用,积分近似的方法计算远区作用,如这次化学诺奖用量子力学计算酶的活性,用经典力学计算长距离多分子相互作用(Levitt, 2001),又如BO近似(Born-Oppenheimer approximation)(Born and Oppenheimer,1927)、快速多极子(Rokhlin, 1990; Greengard and Rokhlin, 1987;Barnes and Hut, 1986; Coifman et al.,1993;Chew et al.,1997;Ying et al., 2004).其中所包含的数学思想,实际上在各个领域的多尺度计算中具有共性,包括分子动力学、原子间多体作用、长链分子分子动力学、颗粒流体体系的模拟(多相复杂系统国家重点实验室、多尺度离散模拟项目组,2009).目前,在地球物理学中,利用局部平均得到本构方程,称为岩石物理理论,其实也是一种跨尺度计算(Backus, 1962).
目前已有的多尺度计算方法,如粒子模型、快速多极子是在不同领域内发展出来的,主要适合均匀背景中的场的模拟,不一定适合地下声波和弹性波的模拟.对一般非均匀介质,虽然提出了HSS(分级半可分)(Xia et al,2009,2010; Xia and Gu, 2010),但由于是根据矩阵理论发展的,其物理意义还不易显示出来.针对原有快速多极子算法只适合于均匀介质或者层面起伏分层均匀的问题,需要发展波动方程的非均匀介质频率波数的求解方法,其中基于李代数和拟微分算子象征的方法,发展较为迅速.本文针对一般非均匀介质声波和弹性波的模拟问题,综合评述发展多尺度计算算法的研究基础和进展,以便促进该领域的发展.
随着塞舌尔公司发展出50万道地震,可控震源和不间断采样技术已经使得每日采集TB级数据的高密度、宽方位角勘探成为可能,MEMS技术有可能使得多波多分量采集更为经济,这样要求处理的数据量非常大,为了解决复杂问题如高陡构造、盐下成像,也会不断需要逆时偏移和全波形反演等精度大但计算量大的方法.在非常规油气勘探和开发中,为了处理提高精度,网格还需要加细.
一个重要的例子是美国勘探地球物理协会即将推出的模型,SEAM (SEG Advanced Model)(Brice,2009; Fehler, 2012).
该模型的规格: 35km EW x 40km NS x 15km Depth,
速度模型采样间隔是10 m,数据量共有 84.1 GB (21,000,000,000网格点).总炮数是62000;数据量是220TB.采样长度是16 s,单炮计算网格是3000×3000×1500=13,500,000,000.
单炮偏移计算量= 网格点数×延拓步数×单个网格单个时间步计算量×2=13.5G×16000×68×2=29376T,
总计算量:29376T×62000=1821312P(单程波计算量=NW×NX×NY×NZ×log2(NX)×log2(Ny)*4=500×3000×3000×1500×log2(3000)×log2(3000)×4=3570T).
目前最强大的并行计算机器是图形处理器.以T10GPU为例,它拥有14亿个晶体管,共有240个核心,一块这样的GPU卡的单精度浮点运算性能可达到每秒1万亿次,作为对比现在一颗四核CPU只有每秒700亿次浮点计算.“天河一号”以峰值速度大约4700万亿次,持续速度大约2566万亿次每秒.这样,SEAM模型的总计算量相当于单个主频为3.2 G的单核CPU计算3300年,相当于单个T1060计算57年,相当于“天河一号”持续运行8.2天.但是,因为对于大模型,单个GPU不能装下,需要将大模型分成多块,在单炮范围内多显卡多CPU运行,同一模型不同区域放置在不同显卡不同CPU上,其间之通讯也需要占据大量时间.
多尺度计算方法是在地球物理领域、数学领域、复杂系统的多尺度模拟,生命和材料科学的研究中发展起来的,其基本思想是不同尺度采用不同的算法.
在地球物理领域的混合算法含有多尺度计算的思想,温联星利用数值和解析方法结合研究D”(下地幔)不均匀性引起的散射(Wen and Helmberger, 1998).有限差分方法仅应用于不均匀区,入射波利用广义射线理论,利用Kirchhoff方法将散射波传回地面.
在数学领域的多尺度计算方法的代表是快速多极算法.快速多极算法(Fast Multipole Methods,简称FMM) (Greengard and Rokhlin, 1987)用于快速计算多体问题,被誉为20世纪 10个最显著的计算数学进展,该算法使矩阵向量乘积O(N*N) 变成O(NlogN).该算法原始形式是多体问题,所用核函数是引力势,不具有空间振荡特性.
该算法的框架是这样的,将粒子分为不同的区域,区域内的粒子相互作用称为近区作用, 区域和区域的相互作用称为远区作用. 近区作用直接使用核函数(格林函数)进行计算,远区作用利用波数域展开进行计算,即把近区粒子利用拉当变换变换到斜率域(慢度域,波数除以频率),利用波数域可分展开计算相互作用,然后变回到空间域.可分展开就是将空间变量与角度(斜率)变量写成乘积和,并适当截断,这样计算量较小.
为了具体化,用该方法求解(但不限于)以下方程




这种算法需要较大内存和计算量,计算成本较高.如果GPU可以成功使用,则成本会降低.目前适合GPU的是快速多极算法.在该算法中
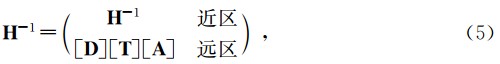
 | 图 1 SEAM模型 (http://www.seg.org/resources/research/seam) Fig. 1 SEG Advanced Model (http://www.seg.org/resources/research/seam) |
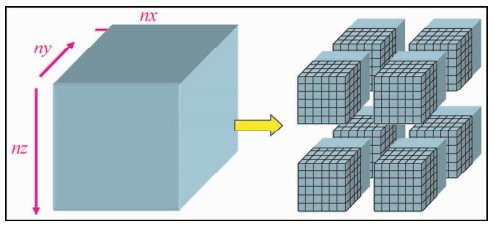 | 图 2 对于大模型,单个GPU的存储不能装下,需要将大模型分成多块 (Liu et al., 2012) Fig. 2 for larger models, storage for a single GPU does not fit, require large divide the model into severial blocks (Liu et al.,2012) |
Chew C W将其应用于电磁场中波动方程(Chew et al.,1997),所用核函数是频率域格林函数,具有空间振荡特性,并进一步改进为多层快速多极算法(Multi Level Fast Multipole Methods),应用于电大物体(物体尺寸比波长大很多倍)的电磁散射截面的计算.
复杂系统的多尺度模拟,生命和材料科学的研究中,多尺度计算方法的代表是多尺度离散模拟系统(Li et al., 2005;Ge et al., 2007).多尺度离散模拟系统包括分子动力学模拟、原子间多体作用、长链分子分子动力学模拟、颗粒流体体系宏观粒子模拟.文献(多相复杂系统国家重点实验室、多尺度离散模拟项目组,2009)引言介绍了多尺度方法的应用现状:
“多尺度方法总体上在20世纪90年代后才引起广泛关注,目前它的应用也还是相当有限.单尺度方法现在依然流行,但它们不仅会掩盖所考虑尺度之下结构的效应,也会抹平大尺度上的结构,从而造成显著的误差”“我们可以用离散化方法对不同尺度上的复杂系统模拟提出一种比较通用的算法框架,即多尺度离散模拟.在此框架下,大量单元间发生近程作用,同时与若干上层单元相互作用,而上层单元之间又发生近程作用,并与更上层单元相互作用,以此类推组成多尺度结构系统.举例来说,社会系统有最基本的组成单元—人.人大多与他/她周围的人关系较密切,远程的则联系较少.但社会不仅是单个人之间的作用,每个人还会参加不同的团体和组织,如家庭、工作单位、社区、俱乐部等,它们对组成或者参与它们的个体的行为有约束作用,同时作为整体也会发生相互作用,并且能组成更高层次的团体,在物质世界中,从基本粒子到整个宇宙也有相似的特征”.
在计算化学领域有一个玻恩奥本海默近似(BO近似)处理原子分子轨道的,将原子的波函数看做核的波函数与电子波函数的乘积,由于核的质量远大于电子质量,近似的认为核不动,波函数不变,因此可以将原子的波函数看做电子的波函数来近似,这是处理原子分子物理的基本方法——玻恩奥本海默近似.该方法可以认为是远区近区分离处理的一个方法.
在地震成像领域,全波形反演开始进入实用化研究(刘国峰等,2012).原有基于频率域LU分解的全波形反演用于三维时,由于占用存储太多,很难用GPU实现,用CPU实现成本较高(刘璐等,2013).目前三维全波形反演的实用研究,主要都是基于时间域有限差分,计算量大约是逆时偏移的100倍.为了改进频率域正演,基于方向波分解的波数域积分解及其快速计算十分重要.单程波方法是方向波分解方法的基础,其改进仍很重要.与LU分解和共轭梯度方法相比,快速多极算法计算频率域波动方程(亥姆赫兹方程)具有较大优势,因为LU分解需要大内存,后者共轭梯度方法需要较多次数的迭代.
多尺度离散模拟的思想“大量单元间发生近程作用,同时与若干上层单元相互作用,而上层单元之间又发生近程作用,并与更上层单元相互作用,以此类推组成多尺度结构系统”,可否用来加速地震波场的时间域有限差分,是个尚未得到研究的问题.在地球物理中,大量实际问题需要精细划分网格,当模型特别大时,需要利用多个计算节点分块并行计算.当对大模型开展有限差分计算时,单个节点便于计算近程作用,而节点之间需要用简单的数据计算远程作用,因为节点之间的通讯量的大小是提高并行计算效率的关键,如何减少通讯量是提高加速比的重要研究方向.
快速多极算法虽然非常成功,但其核函数(格林函数)是从均匀背景导出的,因而对变系数微分方程还难以使用.目前可以将地下介质分成边界起伏厚薄横向变化层内均匀的地层,从而利用快速多极算法进行处理.为了进一步研究非均匀背景下的快速算法,需要求出快速多极算法所需的远区相互作用表达式,这实际上需要研究亥姆赫兹方程积分解-格林函数的可分表达式.近年来基于李代数方法与拟微分算子方法的结合,变系数亥姆赫兹方程积分解的研究取得了很大进展.
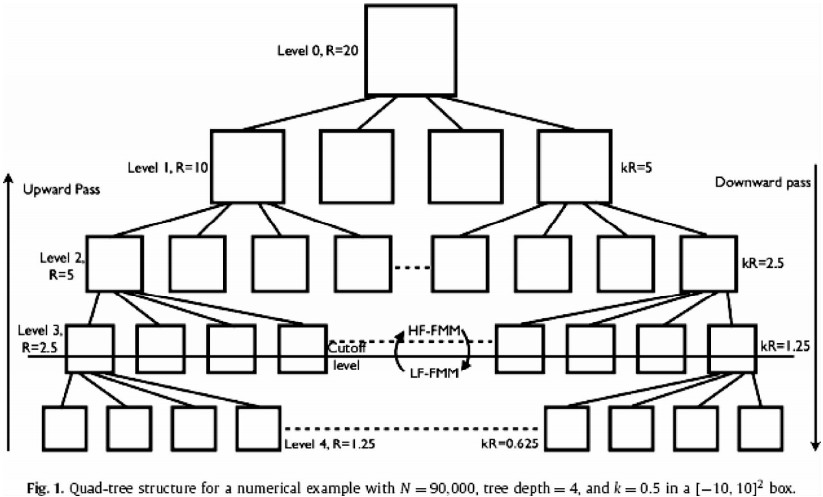 | 图 3 多层快速多极算法 Fig. 3 Multi Level Fast Multipole Methods(Cho M H and Cai W,2010) |
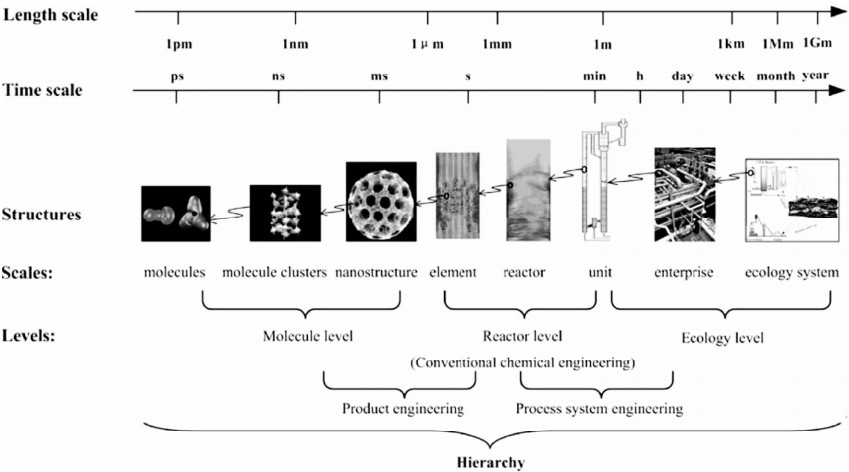 | 图 4 化学工程中的级联多层多尺度时空结构(Li et al.,2005) Fig. 4 Hierarchical multi-levels and multi-scales of spatio-temporal structures in chemical engineering |
由于微分几何和有限维李群理论(SU(3)、SU(2)、O(1))在规范场论得到成功应用,数学工作者也在探讨微分几何和李群在求解微分方程方面应用.规范场论试图通过构造拉格朗日作用量,以解释亚原子领域的强相互作用、弱相互作用和电磁相互作用的统一,例如为什么光子的作用距离长,而派(Pi)介子、陶(Tao)介子等传递中子和质子相互作用的粒子作用距离短.这说明微分几何和李群理论在构造微分方程方程方面有重要作用.人们进一步思考,微分几何和李群理论在求解微分方程方面如孤立子、控制论中的有没有重要应用,这方面的重要进展见专著(Rokhlin, 1990).这些研究取得了丰富的结果,包括一些大模型的局部解性质进行研究,包括向量场的局部分析,外微分组成的流形和几何(即多项式系数的计算),Riccati方程的稳相解,等谱流变换,几何控制论,Voterra级数, Voterra路径积分,矩阵数值分析中LR和QR算法与李群理论的关系,这些研究对不同学科的研究者相互交流,起到了重要的推动作用.
国内这方面研究的一个重要带头人是冯康院士.冯康研究了物理系统离散化算法中微分几何和李群理论的应用(Feng,1985).冯端对此回忆道(冯端,2004) “文革后期一直到80年代中他经常和我谈论这方面的问题:诸如Thom的突变论,P rigogine的耗散结构,孤立子,Radon变换等.这种搜索过程,有点像老鹰在天空中盘旋,搜索目标,也可以比拟为“独上高楼,望尽天涯路”.70年代Arnold的“经典力学的数学问题”问世,阐述了哈密顿方程的辛几何结构,给他很大的启发,使他找到了突破口.他在计算数学中长期实践,使他深深领悟到同一物理定律的不同的数学表述,尽管在物理上是等价的;但在计算上是不等价的(他的学生称之为冯氏大定理),这样经典力学的牛顿方程、拉格朗日方程和哈密顿方程,在计算上表现出不同的格局,由于哈密尔顿方程具有辛几何结构,他敏锐地察觉到如果在算法中能够保持辛几何的对称性,将可避免人为耗散性这类算法的缺陷,成为具有高保真性的算法.这样他就开拓了处理哈密尔顿系统计算问题的康庄大道,他戏称为哈密尔顿大道(The Hamiltonian way),” 冯康团队对更广泛的物理系统进行研究,发现为了保持某些物理系统的李群结构,需要李群算法.李群算法的基础可以追踪到1905年(Baker,1905;Hausdorff,1906;Magnus, 1954).
为了具体说明李代数方法,考虑单程波方程和多次波的研究中遇到的以下齐次微分方程 (Claerbout,1985a,b;刘洪,2008,2009)

李代数方法提出先求u(z),称为李代数积分或李代数解,即

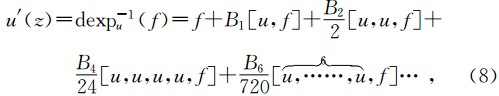

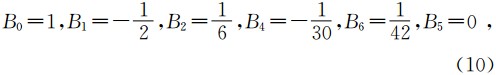
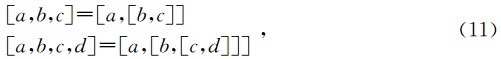
类似的工作,在国内控制论领域程代展等针对“非线性系统的几何理论”的发展方向指出 “几何方法的最大优点是, 它将对微分流形的子流形的研究转换为对切空间的子分布的研究, 如将’ 能达子流形’与’能控性李代数’对应起来等. 用纤维丛的语言’来说, 一般地说, 状态流形与其切空间形成一个局部平凡丛, 因为切丛同胚于R 空间, 研究切丛比研究状态空间本身方便的多, 因此, 几何方法对非线性系统的结构分析、分解及与结构有关的控制设计带来极大的方便. 线性化、解祸、零动力系统与反馈镇定等, 都是几何方法的直接应用.” (程代展等,1997)
李代数方法与拟微分算子方法结合可以求变系数亥姆赫兹方程积分解.
拟微分算子是微分算子的推广,它允许对含微分算子的多项式进行开方、求逆甚至求指数运算.在地震成像领域,单平方根算子和单程波算子就是拟微分算子的具体事例.
拟微分算子理论引入了象征的概念,把算子转化为函数,大致可以通俗称为“算子变函数”.象征指的是算子对平面波函数的作用为象征.两个拟微分算子的乘法的象征可以用两个象征的乘法加上导数修正来表示,如果后一个算子是常系数微分算子的函数的,则导数修正为零,算子乘法的象征退化为象征的乘法,此时算子对应于褶积,象征对应于褶积核函数的Fourier变换.
假定
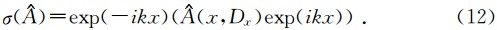
拟微分算子运算的基础是以下公式
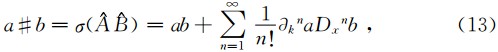

由于一般情况下算子乘法的象征并不等于象征的乘法,算子的除法、指数函数的象征并不等于,象征的除法、象征的指数函数,而是在其基础上做一些修正.文献(刘洪等,2007)对此进行了讨论,给出了变系数微分算子及其开方、倒数、幂、指数函数及其复合函数的象征的求法.
可以这样说,象征方法将拟微分算子变为波数和空间两个变量的函数,李代数方法将算子的指数映射变换成函数的指数函数,但要将象征解变回为空间域的解,还必须对波数变量进行积分,这涉及该积分是否可以足够快速的问题.对单程波算子,利用李代数方法和象征方法得到波数域解再进行波数积分,传统的算法计算量为O(N*N).而Fourier变换方法计算量为O(N*LogN),因而传统的算法不具有计算优势.快速多极算法等多尺度算法,计算量为O(N*LogN),为快速计算波数积分提出了算法框架,值得深入研究.
李代数方法与拟微分算子方法的结合可以将微分算子的指数映射的象征写成相位多项式的指数函数,也就是将微分几何计算变成代数几何计算.指数函数中的相位多项式获得后,可以通过鞍点法求走时.优点就是在相位多项式系数求出后,走时计算很容易并行运算,多项式系数存储很少.该方法现在时间偏移中(算子没有透镜项,Claerbout,1985b)得到应用,发展出“非对称走时叠前时间偏移”技术(刘洪,2007,2009).进一步研究还可用于深度偏移.
对层状介质,李代数方法可以简化其解的表达式.O’Doherty和Anstey曾经提出了一个描述地层滤波的公式(O’Doherty and Anstey, 1971),被后人称为O’Doherty和Anstey公式.地层滤波指的是当一个脉冲通过一个薄互层地层组成地层组,波的频谱会发生变化.O’Doherty和Anstey公式说,透射波的频谱的对数与透过地层反射系数频谱的对数差一个负号(O’Doherty and Anstey, 1971; Haney et al., 2005).
根据辐射传递理论(Haney et al., 2005),Riccatii方程(Shapiro and Zien, 1993),给出了一些近似的证明,但因为使用了平均场近似、因果关系等过多的假设,使得结果局限性很大.利用李代数方法可以给出一个级数表达式,使得该级数的第一项正好为O’Doherty和Anstey公式(刘洪等, 2008;史小东等,2013).根据李代数方法还可以给出透射算子的很多性质.例如透射算子的对数不是因果的,透射算子不是解析函数,等等.
对水平薄互层的测井曲线,其中一个问题是如何计算测井曲线的低频响应,即接近稳态的近似的问题-准静态问题.通过解析方法精确积分(Kennett, 1983),计算低频响应计算量较大.如果用等效介质理论(Backus,1962)对测井曲线进行粗化,在粗网格上积分,所得低频响应还不准.Backus(1962)提出的等效介质理论能对零频成立,但是不能应用于频率不等于零的情况.SK Chang基于Kennett 的精确公式(Chang,2009),对频率进行台劳展开,给出了准静态近似的公式,可以用来快速进行测井曲线粗化.Stovas利用李代数方法(BCH公式)也推导了薄互层低频响应(准静态近似)的公式(Stovas et al.,2013),其物理意义更为明确.
本文评述了多尺度计算的思想,这种思想在近区进行精细计算,对远区的影响用近区的积分近似表示.这种方法在计算化学、多体问题、分子动力学、颗粒流体动力学中取得了较大成功.在全波形反演中,在频率域需要快速算法,多尺度计算的算法有很大意义.为了多尺度计算,需要波动方程解波数域的表达式,李代数积分和拟微分算子的方法可以用来求出这种表达式,目前这些方面已经有了部分进展.总的框架是,从微分方程到代数函数(指数、多项式、有理分式、开方),对系数代数函数系数进行特殊的积分(李代数积分,进行微分和矩阵运算的积分)形成新的代数函数(指数、多项式).对于计算较大的模型的地震波频率域响应,利用近区和远区不同的算法,有可能快速完成数值积分.在空间差分方法中,多尺度计算思想对模型分块计算中减少并行计算的通讯量也有指导意义.
| [1] | Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering[J]. J. Geophys. Res. , 67(11): 4427-4440. |
| [2] | Baker H E. 1905. Altemants and continuous groups[C]. Proc. London Math. Soc., Second Series 3, 24-47. |
| [3] | Barnes J, Hut P. 1986. A hierarchical O(N log N) force-calculation algorithm[J]. Nature, 324(6096): 446-449. |
| [4] | Born M, Oppenheimer R. 1927. Zur Quantentheorie der Molekeln[J]. Annalen der Physik, 389(20): 457-484. doi:10.1002/andp. 19273892002. |
| [5] | Brice T. 2009. Seismic acquisition design for the SEG Advanced Modeling (SEAM) project[J]. The Leading Edge, 28(5): 530-537. doi: 10.1190/1. 3124927. |
| [6] | Chang S K. 2009. A high-order quasi-static theory for P-SV waves in finely layered media[C]. 79th Ann. SEG Meeting. SM3. 1: 903-906, doi: 10.1190/1.1822650. |
| [7] | Cheng D Z, Hong Y G, Chen H F, et al. 1997. Hierarehy structure and mechanization of nonlinear control systems-An exploration on new developing direction [J]. Control Theory and Application (in Chinese), 14(5): 617-622. |
| [8] | Chew W C, Jin J M, Lu C C, et al. 1997. Fast solution methods in electromagnetics[J]. IEEE Trans. Antennas Propagat. , 45(3): 533-543. |
| [9] | Cho M H, Cai W. 2010. A Wideband Fast Multipole Method for the two-dimensional complex Helmholtz equation [J]. Computer Physics Communications, 181(12): 2086-2090. |
| [10] | Claerbout J F. 1985a. Fundamentals of geophysical data processing[M]. England: Blackwell Scientific Publications, 1-266. |
| [11] | Claerbout J F. 1985b. Imaging the Earth’s interior[M]. Oxford: Blackwell Scientific Publications. |
| [12] | Coifman R, Rokhlin V, Wandzura S. 1993. The fast multipole method for the wave equation: A pedestrian prescription[J]. IEEE Antennas Propagat. Mag. , 35(3): 7-12. |
| [13] | Cordes H O. 1995. The Technique of Pseudodifferential Operators[M]. Cambridge: Cambridge University Press, 1-382. |
| [14] | Engquist B, Ying L X. 2008. Fast directional multilevel algorithms for oscillatory kernels[J]. SIAM J. Sci. Comput., 29(4): 1710-1737. |
| [15] | Engquist B, Ying L X. 2009. A fast directional algorithm for high frequency acoustic scattering in two dimensions[J]. Commun. Math. Sci. , 7(2): 327-345. |
| [16] | Fehler M. 2012. Seam update: elastic simulations [J]. The Leading Edge, 31(1): 24-25, doi: 10.1190/1. 3679323. |
| [17] | Feng K, Qin M Z. 2003. Symplectic Geometric Algorithm for Hamiltonian Systems (in Chinese)[M]. Hangzhou: Zhejiang Science & Technology Press. |
| [18] | Feng K. 1985. On difference schemes and symplectic geometry[C]//Differential Geometry and Differential Equations. Beijing: Science Press. |
| [19] | Feng D. 2004. Scientific Life of Fengkang-My memory (in Chinese)[Z]. http://blog.sina.com.cn/s/blog_542dafc80100bmcb. html. |
| [20] | Ge W, Chen F G, Gao J, et al. 2007. Analytical multi-scale method for multi-phase complex systems in process engineering-Bridging reductionism and holism [J]. Chemical Engineering Science, 62(13): 3346-3377. |
| [21] | Greengard L, Rokhlin V. 1987. A fast algorithm for particle simulations[J]. J. Comput. Phys. , 73(2): 325-348. |
| [22] | Haney M M, van Wijk K, Snieder R. 2005. Radiative transfer in layered media and its connection to the O’Doherty-Anstey formula[J]. Geophysics, 70(1): T1-T11. |
| [23] | Hausdorff E. 1906. Die symbolische exponential formel in der gruppen theorie[J]. Berichte der Siichsischen Akademie der Wissenschaflen, 58: 19-48. |
| [24] | Hermann R. 1985. Cartanian Geometry, Nonlinear Waves, and Control Theory, Part A B[M]. MA: Math Science Press. |
| [25] | Hudson J A. 1981. Wave speeds and attenuation of elastic waves in material containing cracks[J]. Geophys. J. Int. , 64(1): 133-150. |
| [26] | Hudson J A. 1980. Overall properties of a cracked solid[J]. Math. Proc. Camb. Phil. Soc. , 88(2): 371-384. |
| [27] | Iserles A, Munthe-Kaas Z, N?rsett S P, et al. 2000. Lie-group Methods [J]. Acta Numerica, 9: 215-263. |
| [28] | Kennett B L N. 1983. Seismic Wave Propagation in Stratified Media[M]. Cambridge: Cambridge University Press. |
| [29] | Levitt M. 2001. The birth of computational structural biology[J]. Nature Structural Biology, 8(5): 392-393, doi: 10. 1038/87545. |
| [30] | Li J H, Ge W, Zhang J, et al. 2005. Multi-scale compromise and multi-level correlation in complex systems[J]. Chemical Engineering Research and Design, 83(6): 574-582. |
| [31] | Liu GF, Liu H, Meng X H, et al. 2012. Frequency-related factors analysis in frequency domain waveform inversion[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1345-1353, doi: 10.6038/j.issn.000133.2012.04. 030. |
| [32] | Liu H, He L, Liu G F, et al. 2008. Derivation and generalization of the stratigraphic filtering formula via Lie algebraic integral[M]// The paper collection in memory of 80th anniversary of Academician Liu Guangding (in Chinese). Beijing: Ocean Press, 412-422. |
| [33] | Liu H, Liu G F, Li B, et al. 2009. The travel time calculation method via lateral derivative of velocity and its application in pre-stack time migration[J]. Geophysical Prospecting for Petroleum (in Chinese), 48(1): 3-10. |
| [34] | Liu H, Wang X M, Zeng R, et al. 2007. Symbol description to integral solution of one-way wave operator[J]. Progress in Geophysics (in Chinese), 22(2): 463-471. |
| [35] | Liu H W, Li B, Liu H, et al. 2012. The issues of prestack reverse time migration and solutions with Graphic Processing Unit implementation [J]. Geophysical Prospecting, 60(6): 906-918, doi: 10.1111/j.1365-2478.2011.01032.x. |
| [36] | Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2447-2451, doi: 10. 6038/cjg20130730. |
| [37] | Magnus W. 1954. On the exponential solution of differential equations for a linear operator[J]. Comm. Pure Appl. Math. , 7(4): 649-673. |
| [38] | National Lab of Multi-phase Complex Systems, Project of Discrete Multi-scale Simulating. 2009. Discrete multi-scale simulating parallel computation via GPU (in Chinese)[M]. Beijing: Science Press. |
| [39] | O’Doherty R F, Anstey N A. 1971. Reflections on amplitudes[J]. Geophys. Prospect. , 19(3): 430-458. |
| [40] | Qin M Z, Wang Y S. 2011. Structure Preserved Algorithm for Partial Differential Equation[M]. Hangzhou: Zhejiang Science & Technology Press. |
| [41] | Rokhlin V. 1990. Rapid solution of integral equations of scattering theory in two dimensions[J]. J. Comput. Phys. , 86(2): 414-439. |
| [42] | Shapiro S A, Zien H. 1993. The O’Doherty-Anstey formula and localization of seismic waves[J]. Geophysics, 58(5): 736-740. |
| [43] | Shi X D, Liu H, Ding R W, et al. 2013. Elimination of multiple scattering for thin layers based on the Lie algebra integral[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2437-2446, doi: 10. 6038/cjg20130729. |
| [44] | Stovas A, Roganov Y, Duffaut K, et al. 2013. Low-frequency layer-induced anisotropy[J]. Geophysics, 78(5): WC3-WC14. |
| [45] | Wen L, Helmberger D V. 1998. Ultra-low velocity zones near the core-mantle boundary from broadband PKP precursors [J]. Science, 279(5357): 1701-1703, doi: 10.1126/science.279.5357. 1701. |
| [46] | Xia J L, Chandrasekaran S, Gu M, et al. 2010. Fast algorithms for hierarchically semiseparable matrices[J]. Numerical Linear Algebra with Applications, 17(6): 953-976. |
| [47] | Xia J L, Chandrasekaran S, Gu M, et al. 2009. Superfast multifrontal method for large structured linear systems of equations[J]. SIAM Journal on Matrix Analysis and Applications, 31(3): 1382-1411. |
| [48] | Xia J L, Gu M. 2010. Robust approximate Cholesky factorization of rank-structured symmetric positive definite matrices[J]. SIAM Journal on Matrix Analysis and Applications, 31(5): 2899-2920. |
| [49] | Yang T H, Tang C A, Xu T, et al. 2004. Seepage Characteristic in Rock Failure-Theory, Model and Applications (in Chinese)[M] Beijing: Science Press. |
| [50] | Ying L X, Biros G, Zorin D. 2004. A kernel-independent adaptive fast multipole algorithm in two and three dimensions[J]. J. Comput. Phys. , 196(2): 591-626. |
| [51] | 程代展, 洪奕光, 陈翰馥,等. 1997. 非线性控制系统的层次化与机械化-关于新方向的探索[J]. 控制理论与应用, 14(5): 617-622. |
| [52] | 多相复杂系统国家重点实验室、多尺度离散模拟项目组. 2009. 基于GPU的多尺度离散模拟并行计算[M]. 科学出版社. |
| [53] | 冯康, 秦孟兆. 2003. 哈密顿系统的辛几何算法[M]. 杭州: 浙江科学技术出版社. |
| [54] | 冯端. 2004. 冯康的科学生涯--我的回忆[Z]. http://blog.sina.com.cn/s/blog_542dafc80100bmcb. html. |
| [55] | 刘洪, 何利, 刘国峰,等. 2008. 地层滤波公式的李代数积分证明和推广[M]. //中国地质地球物理研究进展-庆贺刘光鼎院士八十华诞. 北京: 海洋出版社, 412-422. |
| [56] | 刘洪, 刘国峰, 李博,等. 2009. 基于横向导数的走时计算方法及其在叠前时间偏移中的应用[J]. 石油物探, 48(1): 3-10. |
| [57] | 刘洪, 王秀闽, 曾锐,等. 2007. 单程波算子积分解的象征表示[J]. 地球物理学进展, 22(2): 463-471. |
| [58] | 刘国峰, 刘洪, 孟小红,等. 2012. 频率域波形反演中与频率相关的影响因素分析[J]. 地球物理学报, 55(4): 1345-1353. |
| [59] | 刘璐, 刘洪, 张衡,等. 2013. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 56(7): 2447-2451. |
| [60] | 秦孟兆, 王雨顺. 2011. 偏微分方程中的保结构算法[M]. 杭州: 浙江科学技术出版社. |
| [61] | 史小东, 刘洪, 丁仁伟,等. 2013. 基于李代数积分的薄层多重散射消除技术[J]. 地球物理学报, 56(7): 2437-2446. |
| [62] | 杨天鸿, 唐春安, 徐涛,等. 2004. 岩石破裂过程的渗流特性-理论、模型与应用[M]. 北京: 科学出版社. |
 2014, Vol. 29
2014, Vol. 29


