2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266237
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science, Qingdao 266237, China
凭借着较高的分辨率以及丰富的探测信息,阵列侧向测井被广泛用于大斜度井/水平井的油气藏评价(Rasmus, 1982; Itskovich et al., 1998; 邓少贵等, 2010).然而在致密性储层电阻率评价过程中,由于地层裂缝和薄互层发育以及沉积颗粒的大小、磨圆不一等因素,导致储层各向异性特征明显,测井响应复杂,为油气层的识别与评价带来一定的难度(Salazar and Torres-Verdín, 2009; 高杰等, 2010; Gao et al., 2013).因此,如何从测井响应中准确提取地层真实电阻率成为电测井领域亟待解决的难题之一.
非线性反演技术可以充分考虑井眼、侵入等因素对测井响应的影响,成为大斜度井/水平井井旁电阻率剖面重构的有效手段(Nam et al., 2010; Wang, 2011; 潘克家等, 2013).其算法包括确定性算法和随机类算法.其中,确定性算法主要基于最小二乘理论,其核心在于通过不断迭代模型参数的方式使得模拟数据与观测数据的偏差最小(Osman and Laporte, 1996; Habashy and Abubakar, 2004; Madsen et al., 2004; 姚东华等, 2010; Hu and Fan, 2018),该类算法包括最速下降法、高斯牛顿法以及列文伯格马奎特法等(Anderson, 2001).由于能够有效消除围岩、层厚和侵入等因素的影响,确定性算法被广泛用于2D阵列侧向测井资料的快速处理(Wang et al., 2009; 王磊等, 2018).然而对于斜井各向异性等三维地层环境而言,正演效率过低,导致反演迭代过程中雅可比矩阵或海森矩阵求取耗时,同时该类算法对初值依赖性强,易陷于局部极小值,不利于阵列侧向测井资料的快速精确处理(Pardo et al., 2007; Dubourg et al., 2017; Wu et al., 2020). 不同于确定性算法,随机类算法由单点或多点启发,搜索步长和方向具有随机性,可以在求解域内全空间搜索,全局寻优能力强,进而能够提高资料处理精度,此类算法包括粒子群优化算法、模拟退火算法以及差分进化算法等(Eiben et al., 1994; Yang and Torres-Verdín, 2011; Li et al., 2020).然而,两类算法在寻优过程中皆要不断调用正演,尤其对于三维地层环境而言,正演速度仍是制约反演效率的关键因素.
近年来,随着智能算法的兴起,有研究学者将深度学习技术引入地球物理反演当中(林年添等, 2018; Shahriari et al., 2020; Wu and Fan, 2021; Zhang et al., 2021),以期能够解决反演策略中正演效率低的难题.其中,反向传播神经网络(BPNN)作为一种强大的监督类学习架构,自从提出以来被广泛用于特征识别以及函数逼近领域(Rumelhart and McClelland, 1986; Xu et al., 2018).然而,面对复杂输入输出问题,BPNN存在超参数优化困难、迁移性差、训练参数过多以及不易收敛等缺点.为此,深层卷积神经网络(CNN)凭借着局部连接和权重共享的优点逐渐代替BPNN(Fukushima, 1980; LeCun et al., 1998; Krizhevsky et al., 2017). 在测井领域,Zhu等(2018)通过建立五层卷积神经网络实现了地层岩性特征的快速识别;Li等(2019)基于1D模型和多层卷积神经网络实现了大斜度井/水平井随钻电磁波测井的快速反演;Jin等(2019)通过优化卷积神经网络的损失函数实现了随钻测井领域的实时地质导向.然而,上述研究皆是针对简单输入输出问题,而对于阵列侧向测井3D反演问题,国内外尚无研究.因此,针对阵列侧向测井资料处理,如何提升高维正演效率,如何保证反演精度是当前智能测井领域亟需解决的难题.
为此,本文从三维有限元技术(3D-FEM)出发,首先对斜井各向异性地层参数进行敏感性分析,确定侵入、各向异性和地层倾角对阵列侧向测井的敏感性大小;其次,建立三维阵列侧向测井响应数据库,引入二维卷积神经网络(2D-CNN)技术,并基于二进制转换将地层模型转为网络输入层所需的2D图像,提高网络识别局部特征的能力;接着,建立深层2D-CNN结构,并引入"丢弃"(Dropout)和"填充"(Padding)机制,实现三维阵列侧向快速正演;最后,基于敏感性分析和快速正演,将多种群遗传算法与列文伯格马奎特算法相结合(MPGA-LM),对倾斜各向异性地层的电阻率剖面进行了快速精确重构.
1 阵列侧向测井数值模拟 1.1 三维有限元数值模拟本文以斯伦贝谢研发的高分辨率阵列侧向测井仪HRLA为例,仪器包括一个主电极A0、六对屏蔽电极A1-A6(A1′-A6′)及两对监督电极M1、M2(M1′、M2′),屏蔽电极和监督电极关于主电极对称,通过改变不同电极间的收发组合方式,可以形成6种具有不同探测深度的视电阻率曲线,探测深度由浅及深分别命名为RLA0,RLA1,RLA2,RLA3,RLA4,RLA5.
不同探测模式视电阻率可以通过测量监督电极电位进行计算,其中浅探测模式RLA0需要测量同侧两个监督电极的电势差值ΔUM1M2(RLA0),其他探测模式只需测量任意监督电极上电势,其视电阻率计算公式如下:

|
(1) |

|
(2) |
式中,i为1~5,分别代表上述5种工作方式;Ki为第i种测井模式的电极系数,可在均匀地层条件下获得;RRLAi为第i种测井模式的视电阻率;UM1(RLAi)为第i种测井模式的主电极电位;I0(RLAi)为第i种测井模式的主电极电流.
可以看出,求解阵列侧向测井视电阻率的关键在于得到监督电极上的电势,为此必须将整个空间的电位分布函数求出.由于阵列侧向测井用的是低频交流电,故可视为稳定电流,进而该问题转为稳流场电势分布函数的求解问题.
根据边界条件和变分原理,阵列侧向测井响应可归结为求取泛函极值问题,泛函构造式如下:
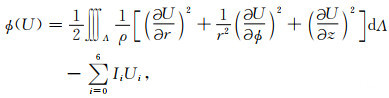
|
(3) |
式中,Λ为除去电极部分的求解区域,Ii和Ui分别代表仪器每个电极的电流和电势大小.
在电阻率不同的子空间交界面上,电流、电位具有连续性,满足如下边界条件:
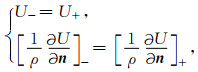
|
(4) |
式中,"-"表示交界面左侧(上侧),"+"表示交界面右侧(下侧);n为交界面单位法向量.
在无穷远边界和绝缘电极表面还需满足Dirichlet和Neumann边界条件,如下所示:
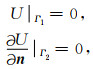
|
(5) |
式中,Γ1和Γ2分别为无穷远边界和绝缘电极表面.
在主电极和屏蔽电极表面,满足等值面边界条件:

|
(6) |
式中,UAi为电极表面电势,Γ3主电极或屏蔽电极表面,n为电极表面单位法向量,Ii为电极发射电流,i为0~5.
为求解上述泛函的最小值,一般采用三维有限元方法(3D-FEM),最后采用前线解法求取含有大型稀疏矩阵的线性方程组,如式(7),该方法由于可以在求解过程中对刚度矩阵边消元边安装,可有效提升正演计算速度(张庚骥, 2009).
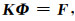
|
(7) |
其中,
阵列侧向测井受泥浆侵入、地层倾角以及各向异性等多种因素影响,因此,确定各因素对测井响应影响强弱对于反演初值选取、约束条件施加具有重要意义.本节系统分析了侵入深度、各向异性和地层相对倾角等因素对阵列侧向测井响应的敏感性,定义敏感因子S如下:
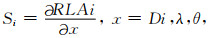
|
(8) |
其中,i为阵列侧向探测模式,此处取1~5,x为地层参数,分别代表侵入深度Di,各向异性系数λ和地层倾角θ.
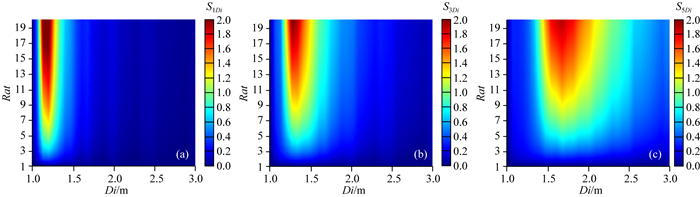
首先,分析侵入对阵列侧向测井响应的影响.以无限厚一层模型为例,地层为各向同性,侵入带电阻率为2 Ωm,侵入深度Di变化范围为0~3 m,侵入带与原状地层电阻率对比度范围Rat为1~20.敏感性分布图如图 1所示,横纵坐标分别为侵入深度和电阻率对比度.可以看出,阵列侧向测井对侵入深度敏感因子最大约为2,且随着探测深度的增大,对侵入深度的敏感区间也随之增大:浅、中、深探测模式RLA1、RLA3和RLA5的敏感区域分别为0.2~0.5 m、0.3~1.0 m和0.6~2.3 m.
|
图 1 HRLA对侵入深度的敏感性 (a)∂RLA1/∂Di;(b)∂RLA3/∂Di;(c)∂RLA5/∂Di Fig. 1 The sensitivity of HRLA to invasion depth |
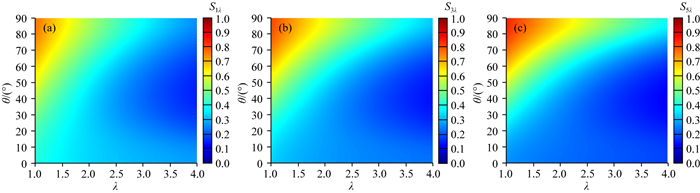
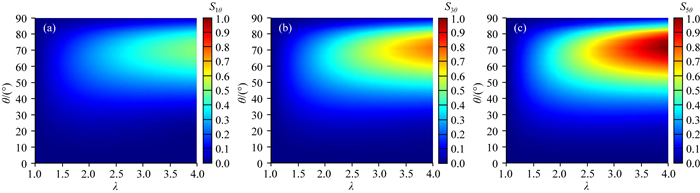
接着,分析各向异性和地层倾角对阵列侧向测井的影响.以无限厚模型为例,地层为各向异性,地层水平电阻率为2 Ωm,各向异性系数变化范围为1~4,地层相对倾角变化范围为0°~90°.图 2和图 3分别表示各向异性和地层相对倾角的敏感性分布图,横纵坐标分别为各向异性系数和地层相对倾角.可以看出:(1)阵列侧向测井对各向异性系数和地层相对倾角的敏感因子最大约为1;(2)阵列侧向测井在高角度地层(60°~90°)对各向异性最为敏感,且探测深度较深的测井模式对各向异性的敏感性较大,原因在于当地层相对倾角逐渐增大时,仪器电极发射电流方向逐渐朝着垂直电阻率方向倾斜.因此,垂直电阻率对测井响应贡献变大,各向异性敏感性增强,而深探测曲线因探测范围最广,受其影响最大;(3)阵列侧向测井在中高角度(50°~80°)对地层相对倾角最为敏感,且不同测井模式对相对倾角的敏感性与各向异性相似,皆是探测深度较深的测井模式对其敏感性较大,原因在于地层倾角对阵列侧向曲线的影响本质是因为地层各向异性的影响,因为地层倾角增大,导致垂直电阻率的影响增大,进而使得阵列侧向五条曲线出现变化.
|
图 2 HRLA对各向异性的敏感性 (a)∂RLA1/∂λ;(b)∂RLA3/∂λ;(c)∂RLA5/∂λ. Fig. 2 The sensitivity of HRLA to anisotropy |
|
图 3 HRLA对地层相对倾角的敏感性 (a)∂RLA1/∂θ;(b)∂RLA3/∂θ;(c)∂RLA5/∂θ. Fig. 3 The sensitivity of HRLA to dipping angle |
深层卷积神经网络凭借着强大的泛化特性以及学习能力被广泛用于图像分类、语音检测以及物体识别等复杂特征识别领域.一般而言,卷积神经网络包括输入层、卷积层、汇聚层(池化层)、全连接层和输出层,本文以经典二维卷积神经网络——LeNet-5为例,其结构如图 4所示.其中,输入层为三通道RGB图像或者单通道灰度图像,卷积层包含多个卷积核,不同的卷积核相当于不同的特征提取器,结构为一个二维矩阵,图像经过卷积层可提取多个局部特征并保存;汇聚层的作用在于特征选择,降低特征数量,从而减少参数数量,其核心思想在于步长间隔的选择,达到"降维"的作用;全连接层与全连接前馈神经网络相同,不再赘述.
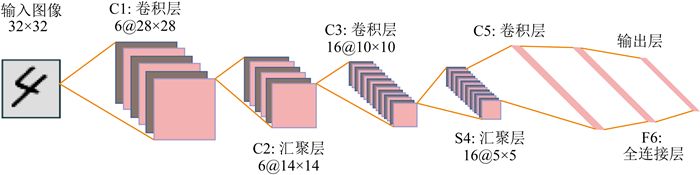
|
图 4 LeNet-5网络结构 Fig. 4 The architecture of LeNet-5 |
相较于全连接神经网络,卷积神经网络最大的特点在于局部连接和权重共享,如图 5所示,图 5a为传统的二层全连接神经网络,包括3个输入,5个输出,需训练参数包括15个权重和1个偏置共16个参数;图 5b为二层卷积神经网络,包括3个输入,5个输出,由于输入层每个神经元只需要与下层局部窗口内的神经元连接,且每个窗口内权重共享,若卷积核大小为3,则需训练参数包括3个权重和1个偏置共4个参数,可大大减少训练参数的数量,提高训练效率.
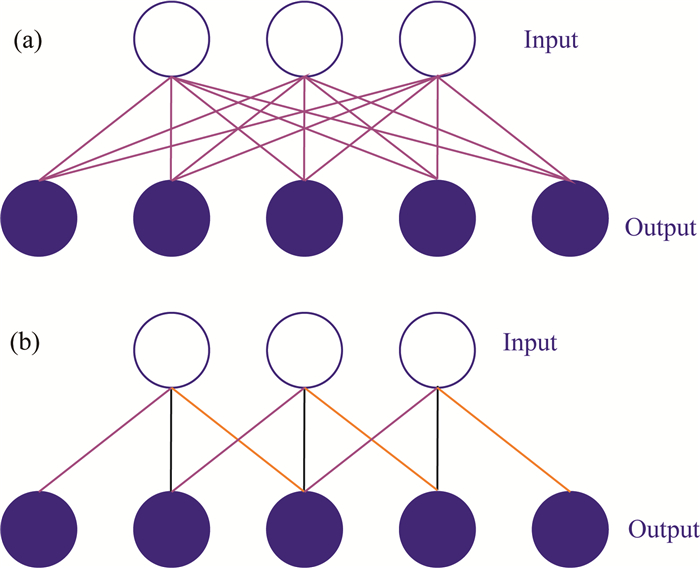
|
图 5 神经网络结构 (a) 全连接层;(b) 卷积层. Fig. 5 The connection feature of network (a) Fully connected layer; (b) Convolution layer. |
同时,为提高深层神经网络的训练效率,通常卷积层和全连接层分别引入填充(Padding)和丢弃(Dropout)机制,如图 6所示,通过在图像卷积之前填充一层像素,使卷积之后的图片与原图尺寸相同,进而使得卷积层得以加深,提高训练精度,如图 6a;另外通过随机丢弃部分神经元,可有效防止网络过拟合,加快训练进程,如图 6b.

|
图 6 神经元连接机制 (a) "Padding"机制;(b) "Dropout"机制. Fig. 6 Neuronal connection mechanism (a) "Padding" mechanism; (b) "Dropout" mechanism. |
神经网络模型的可靠性和稳定性很大程度上依赖于训练数据的精度,因此,本文基于严格三维有限元算法,构建大型数据集,并将其载入深层2D-CNN进行训练,以此建立快速回归模型.考虑围岩和层厚对阵列侧向测井响应的影响,数据集基于三层地层模型构建,如图 7a所示,该模型亦作为2D-CNN的输入.具体地,令两侧围岩为各向同性地层,电阻率相同,中间层为有侵各向异性地层,模型参数范围如下:各向异性系数λ为1~4,分为13组,间隔0.25;侵入深度Di为0~1 m,分为11组,间隔0.1 m;围岩电阻率Rs、冲洗带水平电阻率Rxoh和目的层水平电阻率Rth范围皆为0.1~500 Ωm,将其以对数形式各分为20组,对数间隔为0.19;两侧围岩为半无限厚地层;目的层厚度H为0~5 m,分为16组,间隔0.33 m;测量点为以目的层中点为中心,上下各取两个点,共5个测量点,采样点间隔为0.1 m.需要注意的是,为简化数据库构建流程,将其按地层倾角分为10个子库,每个子库地层倾角间隔10°.因此,每个子库有13×11×203×16,共18, 304, 000个样本,每个样本包括六个模型参数,共109, 824, 000个模型数据,将其储存至变量M中,大小为18304000×6;同时每个样本含有五个测量点,每个测量点包括五个电阻率值(RLA1~RLA5),因此,每组共包含457, 600, 000个数据点,将数据点作为输出储存至变量D中,大小为18304000×25.在计算机内存中,每个数据点占8个字节,因此,每组数据大小约为0.944 GB,数据库总大小为9.44 GB.
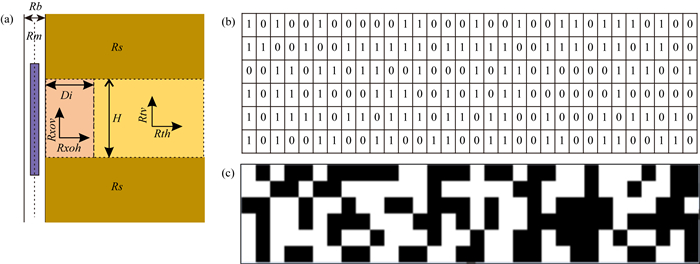
|
图 7 模型可视化过程 (a) 地层模型;(b) 模型参数对应二进制矩阵;(c) 二值图像. Fig. 7 The process of model visualization (a) Formation model; (b) The binary matrix correspond to model parameters; (c) Binary image corresponding to formation model. |
对于复杂模型回归问题,1D-CNN训练精度无法满足需求,因此,本文采用学习和泛化能力较强的2D-CNN结构.而对于2D-CNN而言,输入层普遍为2D图像,为满足网络需求,本文基于二进制转换将一系列一维模型数组转化为二维字符串,进而合成一系列二值图像(Zhong et al., 2019).具体转换过程如图 7所示,其中图 7a为三层地层模型,具体模型参数如下:两侧围岩为半无限厚各向同性地层,电阻率为2.564 Ωm,中间层层厚为3.156 m,侵入深度为0.428 m,侵入带和目的层水平电阻率分别为11.278 Ωm和47.433 Ωm,各向异性系数为1.3,图 7b为模型参数对应的二进制矩阵,图 7c为基于二进制矩阵转换为的二值图像,每个模型可唯一对应一个二值图像.由于数据库中最大数值为8000,且小数后保留3位,故确定二进制字符串长度为32,若字符串长度过长,可自动补零.
2.3 2D-CNN损失函数及数据归一化由于前馈神经网络的局限性导致训练精度偏低,为此本文将反向传播技术应用于2D-CNN网络架构中,定义损失函数如下:
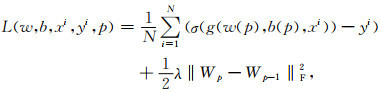
|
(9) |
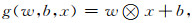
|
(10) |
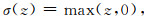
|
(11) |
式中,w和b分别为网络中的权重和偏置,xi和yi分别为训练集D={(xi, yi)}n=1N中输入二进制矩阵和输出向量,g为卷积层特征映射净输出,⊗代表互相关运算,σ为ReLu激活函数,N为训练集中样本个数,p为训练进程中的迭代次数,F代表Frobenius范数,定义如下:
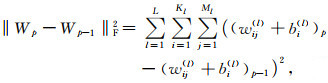
|
(12) |
式中,L为神经网络层数,Kl和Ml分别为第l层卷积核数量和卷积核尺寸.
接着,通过计算损失函数关于每层参数的梯度进行反向传播,为不失一般性,本文使用链式求导法则对卷积层第l层的参数进行求导:
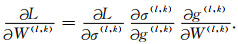
|
(13) |
由式(10)和式(11),易得
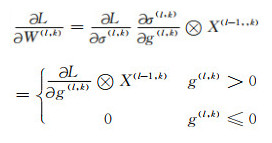
|
(14) |
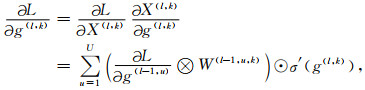
|
(15) |
式中,k为第l层第k个特征映射,U为第l+1层的卷积核数量,X(l, k)=σ(g(l, k)).
同时,由于每组样本中有5个测量点,即Y=(Y1,Y2,Y3,Y4,Y5)T,每个测量点包含五个视电阻率值,即Yi=(RLAi1, RLAi2, RLAi3, RLAi4, RLAi5)T.为提升训练精度,可将数据进行归一化处理,本文采用最小最大值归一化方法,将输出数据统一归一化至[0, 1],公式如下:
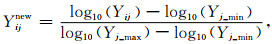
|
(16) |
式中,j为阵列侧向测井探测模式, j=1~5;Yijnew为归一化后数据,Yij为原始数据,Yij=(RLAi1, RLAi2, RLAi3, RLAi4, RLAi5)T,Yj_max为每种探测模式最大值,Yj_max=(RLA1max, RLA2max, RLA3max, RLA4max, RLA5max)T,Xj_min为每种探测模式最小值,Xj_min=(RLA1min, RLA2min, RLA3min, RLA4min, RLA5min)T.
需要注意的是,对于卷积神经网络模型预测的数据而言,需将其反归一化至正常值.
2.4 深层卷积神经网络设计及测试本文以9层卷积神经网络为例,对大型数据集进行训练测试,网络结构及超参数定义如表 1所示.网络输入为侵入深度、各向异性系数、侵入带和原状地层水平电阻率、围岩层电阻率和目的层厚度所转换为的二值图像,即Input=BImage6×32×1, 输出为阵列侧向测井归一化之后的视电阻率,即Output=RLA1×25.网格架构搭建平台为:Pycharm2020.2.3,Python3.7和Tensorflow2.0(GPU版本).为防止训练模型过拟合以及提升训练精度,引入Dropout和Padding机制,其中Dropout率为0.5,Padding选择‘same’模式,即每层输入输出维度一致,进而使得在每层输入不丢失信息的前提下将卷积层延续,达到深化卷积层、提升训练精度的目的.除此之外,由于汇聚层将卷积层提取的多个特征融合,而对于本文回归问题,每个模型特征都是唯一的,因此,为保持模型特征完整性,不使用汇聚层.同时反向传播算法采用自适应矩估计算法(Adam).训练过程中,随机选取95%的数据集为训练集,剩余5%的数据为测试集.
|
|
表 1 2D-CNN超参数定义 Table 1 The definition of hyperparameters in 2D-CNN |
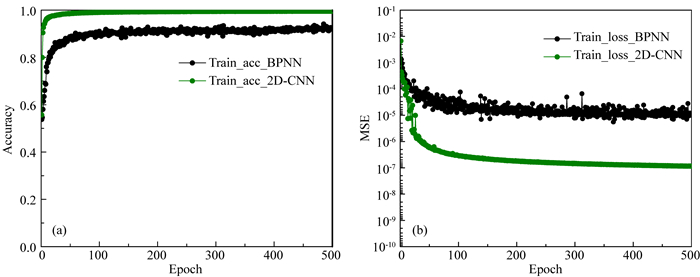
为测试2D-CNN网格训练精度,本文将其训练结果与BPNN对比分析,其中BPNN网络架构与其类似,具体为:九层神经网络结构,激活函数为ReLU,隐含层神经元个数分别为32,64,128,256,516,516,516,Dropout率为0.5,损失函数与反向传播训练算法与2D-CNN一致.图 8为其训练精度与损失函数下降量的对比结果,绿色和黑色散点线分别代表 2D-CNN和BPNN训练结果,可以看出两者收敛速度大致相同,但训练精度却相差较大,2D-CNN在100次迭代后训练精度即可达到99%左右,而BPNN为85%.除此之外,BPNN容易陷入局部极小值,精度无法随着迭代的进行而提升,相较而言,2D-CNN不仅可以快速收敛,而且训练精度随着迭代的进行逐渐接近100%.测试集与之规律类似,不再赘述.另外,通过计算2D-CNN和BPNN在测试集上的泛化误差,计算公式如式(17).我们发现,两者泛化误差分别为1.28%和16.37%,从而也佐证了2D-CNN算法的高效性.

|
(17) |
|
图 8 神经网络训练结果 (a) BPNN和2D-CNN预测精度;(b) BPNN和2D-CNN损失函数. Fig. 8 Neural network training results (a) Prediction accuracy of BPNN and 2D-CNN; (b) Loss function of BPNN and 2D-CNN. |
式中,ntest为测试集样本数,此处为211200;RLAij_2D-CNN为2D-CNN计算结果,RLAij_3D-FEM为3D-FEM计算结果.
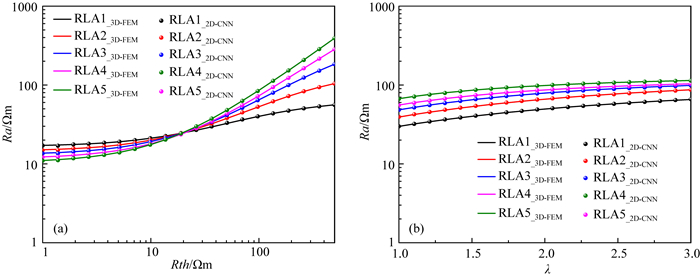
除此之外,为验证训练模型的精度,我们随机选取20个样本点,分别测试中间层原状地层水平电阻率与各向异性系数对模型预测精度的影响,如图 9所示,实线代表 3D-FEM计算结果,散点表示2D-CNN预测结果.样本点模型皆为三层模型:Rs为2 Ωm,H为4 m,Di为0.5 m,Rxoh为20 Ωm.其中图 9a λ为1.5,Rth变化范围为1~500 Ωm;图 9b中Rth为100 Ωm,λ变化范围为1~3.从对比结果可以看出,两者吻合度极高,最大相对误差分别为0.81%和0.24%.因此,基于深层卷积网络的快速正演模型满足精度需求,为斜井各向异性地层的快速反演提供有力支撑.
|
图 9 2D-CNN精度测试 (a) Rth对预测精度的影响;(b) λ对预测精度的影响. Fig. 9 Prediction accuracy testing of 2D-CNN (a) The effect of Rth on the prediction accuracy; (b) The effect of λ on the prediction accuracy. |
大斜度井/水平井阵列侧向测井是典型的非线性反演问题,确定性算法L-M算法由于结合高斯牛顿算法和最速下降法的特性,能够弥补全局寻优能力不强或收敛性差的缺陷,反演过程中采用的代价函数如下:
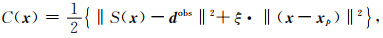
|
(18) |
式中,x为待反演参数矢量,x=(Di, Rxoh, Rth, λ, Rs)T,上标T表示矩阵的转置,S(x)为阵列侧向仪器正演响应,dobs为实际测量数据,‖·‖2表征L2范数,xp为模型已知参考矢量,通常是上一步迭代参数矢量,ξ为正则化参数,最后一项的作用是压制测量噪声,同时减小非线性反演出现的病态问题.反演的目的是得到一个x*使得代价函数最小,即x*=argmin{C(x)}.
进一步,经二阶泰勒近似,可得第k步迭代步长xk为
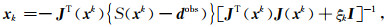
|
(19) |
式中,I为单位矩阵,J为S在xk处的雅克比矩阵,ξk为第k次迭代的正则化参数大小.
为克服传统差分方法计算雅可比矩阵耗时的缺陷,本文采用Broyden近似方法进行雅可比矩阵的迭代更新(Broyden, 2000).
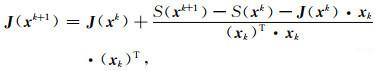
|
(20) |
式中,J(xk+1)为第k+1步的雅可比矩阵.
3.2 基于MPGA的初值优选策略由于L-M算法对初值依赖性较强,若初值选取不适,算法易困于局部极小值,反演精度低.为此,本文基于卷积神经网络快速正演模型,同时为克服标准遗传算法(GA)早熟早收敛的缺陷,利用多种群遗传算法(MPGA)优化初值选取,进而提升L-M算法全局寻优能力.
如图 10所示,多种群遗传算法的核心在于将多个种群进行初始化,即"二进制"编码,并同时进行选择、交叉和变异操作.种群间通过移民算子进行协同进化,最后通过适应度函数分析,借助人工选择算子选取种群最优个体组成精华种群.本文定义适应度函数如下:
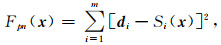
|
(21) |

|
图 10 多种群遗传算法流程 Fig. 10 The framework of multi-population genetic algorithm |
式中,p= 1, 2, …, P,P为种群数量,n=1, 2, …, N,N为每个种群个体数量,m为每个测量点数据量,此处为25.
除此之外,本文所采用的多种群遗传算法超参数选择如下:种群数目为5,个体数目为30,最大遗传代数为50,变量的二进制位数为32,交叉概率在[0.7,0.9]内随机产生,变异概率在[0.001,0.05]内随机产生.
为测试初值选取精度,以30°三层地层模型为例,两侧为各向同性围岩,中间层为有侵各向异性地层.表 2为测试模型参数分布以及多种群遗传算法初值选取结果,Mode l1-Mode l5层厚分别为1~5 m,间隔为1 m.可以看出,受层厚影响,当层厚小于3 m时,围岩电阻率可准确选取,平均相对误差为4.4%;当层厚大于3 m时,阵列侧向测井响应基本不反映围岩信息,选取误差急剧增大,而此时其他参数选取较为精确,整体而言,侵入深度平均相对误差为18.6%,各向异性系数为17.8%,侵入带和原状地层水平电阻率分别为18.7%和6.8%,选取精度满足L-M算法需求.
|
|
表 2 初值选取结果 Table 2 The selection result of initial value |
实际资料处理过程中,针对带有深度点的大型测井响应数据集,我们将其由上到下分为若干子区域,每个子区域为三层模型,中间层为有限厚,地层厚度由层界面位置决定,而层界面位置可通过视电阻率曲线拐点或伽马、自然电位等岩性曲线确定,上下地层视为无限厚地层进行处理.图 11为混合MPGA-LM反演流程图,由上节可知,经MPGA优选后的参数分布于反演代价函数真实解附近,故可将其作为L-M算法的初值,进而提升反演效率;另一方面,由于当层厚大于3 m时候,围岩对阵列侧向响应近乎无影响,此时反演参数可降为4个,即Di、Rxoh、Rth和λ.同时,为提高训练精度,反演可循环N次(本文N为2),即处理完整个井段资料后,可进行二次处理.

|
图 11 混合MPGA-LM反演流程 Fig. 11 The workflow of hybrid MPGA-LM scheme |
另外,为测试混合MPGA-LM快速反演算法的有效性,本文以三层模型为例,分别采用简单初始模型与MPGA提供的初始模型进行反演对比,反演算法皆为LM算法.地层倾角选择30°,模型参数分布如表 3所示.其中,在简单初始模型中分别将深、浅测井响应RLA1和RLA5作为Rxoh和Rth的初始值,Di和λ的初始值分别为0.5 m和1.5,表 3为两者方法反演结果及相对误差,可以看出,较之简单初始模型的LM算法,MPGA-LM可以更好的将地层剖面重构,反演精度更高.以中间地层反演结果为例,基于简单初始模型的LM算法反演后Di、λ、Rxoh和Rth的相对误差(RE)分别为36.67%、33%、84.10%和23.08%;MPGA-LM反演后Di、λ、Rxoh和Rth的相对误差分别为3.33%、0.50%、6.40%和2.86%,精度可以提高数倍至数十倍,由此本文提出的混合MPGA-LM快速反演算法的有效性得到了验证,为下文数值模拟实例的分析提供了保障.
|
|
表 3 LM与MPGA-LM算法反演结果对比 Table 3 The inverted results comparison between LM and MPGA-LM algorithm |
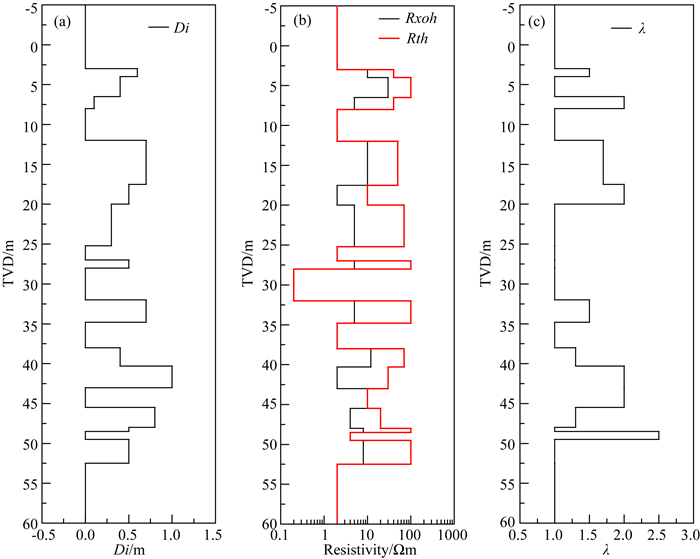
本节通过建立21层俄克拉荷马模型,进一步验证上述反演方案的有效性.模型参数如下:井径为8 inch,泥浆电阻率为0.1 Ωm,地层相对倾角分别为0°、30°和60°,侵入深度范围0~1.0 m,侵入带水平电阻率分布范围为0.2~30 Ωm,原状地层水平电阻率范围为0.2~100 Ωm,各向异性系数范围为1~2.5 Ωm.图 12为该模型参数分布示意图,纵坐标为真实垂直深度(TVD).图 13为地层相对倾角分别为0°、30°和60°时阵列侧向测井响应.本文将地层界面位置作为已知条件,仅反演侵入深度、侵入带电阻率以及原状地层电阻率.
|
图 12 俄克拉荷马模型参数分布 (a) 侵入深度;(b) 侵入带和原状地层水平电阻率;(c) 各向异性系数. Fig. 12 The Oklahoma model parameters (a) Di; (b) Rxoh and Rth; (c) λ. |
|
图 13 阵列侧向测井响应结果 (a) 0°;(b) 30°;(c) 60°. Fig. 13 The responses of array laterolog |
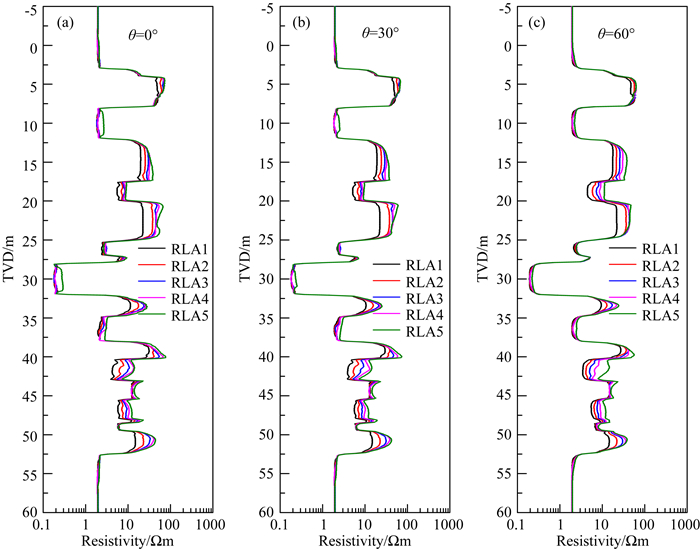
从测井响应结果可以看出,泥浆滤液侵入对其影响严重,如模型第八层,该层为各向同性地层,厚度为5.2 m,侵入深度为0.3 m,地层真实电阻率为70 Ωm,而视电阻率值在0°、30°和60°时与地层电阻率的最大偏离度,即max(RLA/Rth),分别为32.16%、31.81%和31.03%,远远偏离地层真实电阻率;除此之外,由于受地层各向异性的影响,导致响应结果介于水平和垂直电阻率之间,如模型第16层,该层无侵入,地层水平和垂直电阻率分别为5 Ωm和20 Ωm,测井响应在0°、30°和60°时的视电阻率大小分别在12 Ωm、13 Ωm和15 Ωm附近,可以看出,60°地层对各向异性更为敏感,由此验证了2.3部分的结论.由上述可知,单单从测井曲线无法提取地层真实电阻率,因此需借助反演手段对地层真实电阻率剖面进行重构.本文基于运行内存为8 GB的英特尔i7-9700处理器对60 m测井数据进行反演处理,数据采样间隔为0.1 m,循环反演次数为2次,反演总耗时约6.8 min.图 14是基于本文提出的反演策略对测井资料处理后的结果.
|
图 14 混合MPGA-LM反演结果 (a) 侵入深度;(b) 侵入带和原状地层水平电阻率;(c) 各向异性系数. Fig. 14 The inverted results using hybrid MPGA-LM algorithm (a) Di; (b) Rxoh and Rth; (c) λ. |
从图 14反演结果及图 15反演误差曲线可以看出,就反演精度而言,地层水平电阻率>侵入深度>各向异性系数,三者的相对误差范围分别为0~8.38%、0.11%~6.98%和0~14.35%,该现象可由1.3节结论解释,即测井响应对侵入深度的敏感性大于地层各向异性;另一方面,地层倾角对侵入深度和地层水平电阻率的反演精度影响较小,而对地层各向异性影响较大,可以看出,三个角度下各向异性的反演相对误差最大值分别为14.35%、7.79%和3.85%,该现象亦可由1.3节结论解释,即高角度条件下阵列侧向测井响应对各向异性的敏感性较强.
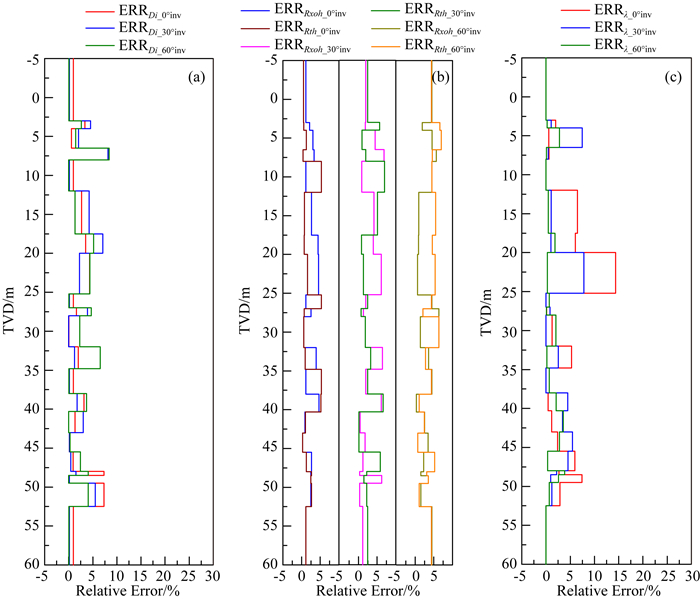
|
图 15 反演结果相对误差 (a) 侵入深度反演误差;(b) 侵入带和原状地层水平电阻率反演误差;(c) 各向异性系数反演误差. Fig. 15 The relative error of inverted results (a) The relative error of inverted Di; (b) The relative error of inverted Rxoh and Rth; (c) The relative error of inverted λ. |
另外,由于在反演过程中调用的正演模型是2D-CNN快速计算模型,而非3D-FEM算法,而2D-CNN模型缺乏对各向异性围岩层的考虑.因此,为进一步分析反演误差产生原因,我们将2D-CNN与3D-CNN的计算结果进行误差分析,平均相对误差(MRE)计算公式如式(22)所示,具体结果如表 4所示.

|
(22) |
|
|
表 4 2D-CNN与3D-FEM计算结果平均相对误差 Table 4 The mean relative error between the responses calculated by 2D-CNN and 3D-FEM |
式中,RLAi_2D-CNN为2D-CNN计算结果,RLAi_3D-FEM为3D-FEM计算结果.
可以发现,整体而言,两者平均相对误差小于10%,对于大多数层而言,相对误差小于3%,满足精度要求.然而在薄层处,由于受到围岩层厚、侵入和各向异性的影响,平均相对误差普遍大于5%,如第2层、第10层和第18层等.该现象正是造成反演结果精度较低的原因之一.为此,在后续研究中,我们将继续完善训练模型,提升神经网络算法对围岩层特征的拾取能力.
值得注意的是,本文所采用的反演模型均为侵入模型,由于多解性问题的存在,会使得无侵地层的侵入深度反演结果不为0,但侵入带电阻率和原状地层电阻率的反演结果一致性较高,如模型第五层和第九层.整体而言,该方案可有效提升算法克服反演多解性的能力,进而提高倾斜各向异性地层阵列侧向测井反演精度,给阵列侧向测井实际资料处理提供一种新思路.
5 结论针对倾斜各向异性地层,本文基于3D-FEM,分析了侵入深度、各向异性以及地层倾角等因素对阵列侧向测井响应的影响;接着,引入2D-CNN网络架构,针对侵入深度小于1.0 m,各向异性系数小于4,层厚小于5 m,围岩和地层水平电阻率位于0.1~500 Ωm的地层,通过建立大型数据集以及将模型可视化,使得2D-CNN训练精度和计算速度能够满足正反演需求,训练精度达到99%左右,计算一个测井点仅需0.36 ms;在此基础上,通过引入全局寻优能力较强的MPGA算法,可为L-M反演算法提供较为精确的初值,进而基于区域分解技术使得斜井各向异性地层电阻率反演精度达到90%以上.
不可否认的是,在更为复杂的三维地层条件下,例如碳酸盐岩地层,存在裂缝和溶洞发育、地层各向异性强以及电阻率大等特征,本文提供的数据库及网络架构将不再适用,读者仅需将其进行扩充与完善即可.另外,复杂三维地层的测井响应会使得反演多解性更为强烈,为此,在今后研究中,应进一步丰富和完善神经网络架构以及反演方案,以期为油气田开发提供更为便捷可靠的处理方案.
Anderson B I. 2001. Modeling and inversion methods for the interpretation of resistivity logging tool response. Delft: Delft University Press.
|
Broyden C G. 2000. On the discovery of the 'good Broyden' method. Mathematical Programming, 87(2): 209-213. DOI:10.1007/s101070050111 |
Deng S G, Li Z Q, Fan Y R, et al. 2010. Numerical simulation of mud invasion and its array laterolog response in deviated wells. Chinese Journal of Geophysics (in Chinese), 53(4): 994-1000. DOI:10.3969/j.issn.0001-5733.2010.04.024 |
Dubourg I, Leech R, Luling M G. 2017. The paradox of anisotropy and the Array-Laterolog anisotropy response. //SPWLA 58th Annual Logging Symposium. Oklahoma, USA.
|
Eiben A E, Raué P E, Ruttkay Z. 1994. Genetic algorithms with multi-parent recombination. //Davidor Y, Schwefel H P, Männer R, eds. Parallel Problem Solving from Nature-PPSN Ⅲ. PPSN 1994. Lecture Notes in Computer Science, vol. 866. Berlin, Heidelberg: Springer, 78-87.
|
Fukushima K. 1980. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36(4): 193-202. DOI:10.1007/BF00344251 |
Gao J, Ke S Z, Wei B J, et al. 2010. Introduction to numerical simulation of electrical logging and its development trend. Well Logging Technology (in Chinese), 34(1): 1-5. |
Gao J, Xu C H, Xiao J Q. 2013. Forward modelling of multi-component induction logging tools in layered anisotropic dipping formations. Journal of Geophysics and Engineering, 10(5): 054007. DOI:10.1088/1742-2132/10/5/054007 |
Habashy T, Abubakar A. 2004. A general framework for constraint minimization for the inversion of electromagnetic measurements. Progress In Electromagnetics Research, 46: 265-312. DOI:10.2528/PIER03100702 |
Hu X F, Fan Y R. 2018. Huber inversion for logging-while-drilling resistivity measurements in high angle and horizontal wells. Geophysics, 83(4): D113-D125. DOI:10.1190/geo2017-0459.1 |
Itskovich G B, Mezzatesta A G, Strack K M, et al. 1998. High-definition lateral log-resistivity device: basic physics and resolution. //SPWLA 39th Annual Logging Symposium. Keystone, Colorado.
|
Jin Y C, Wu X Q, Chen J F, et al. 2019. Using a physics-driven deep neural network to solve inverse problems for LWD azimuthal resistivity measurements. //SPWLA 60th Annual Logging Symposium. The Woodlands, Texas, USA.
|
Krizhevsky A, Sutskever I, Hinton G E. 2017. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 60(6): 84-90. DOI:10.1145/3065386 |
LeCun Y, Bottou L, Bengio Y, et al. 1998. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11): 2278-2324. DOI:10.1109/5.726791 |
Li H, Liu G, Yang S S, et al. 2019. Automated resistivity inversion and formation geometry determination in high-angle and horizontal wells using deep learning techniques. //SPWLA 60th Annual Logging Symposium. The Woodlands, Texas, USA.
|
Li H, Wang H, Wang L, et al. 2020. A modified Boltzmann Annealing Differential Evolution algorithm for inversion of directional resistivity logging-while-drilling measurements. Journal of Petroleum Science and Engineering, 188: 106916. DOI:10.1016/j.petrol.2020.106916 |
Lin N T, Zhang D, Zhang K, et al. 2018. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network. Chinese Journal of Geophysics (in Chinese), 61(10): 4110-4125. DOI:10.6038/cjg2018J0775 |
Madsen K, Nielsen H B, Tingleff O. 2018. Methods for Non-Linear Least Squares Problems. 2nd ed. Informatics and Mathematical Modelling, Technical University of Denmark. |
Nam M J, Pardo D, Torres-Verdín C. 2010. Simulation of triaxial induction measurements in dipping, invaded, and anisotropic formations using a Fourier series expansion in a nonorthogonal system of coordinates and a self-adaptive hp finite-element method. Geophysics, 75(3): F83-F95. DOI:10.1190/1.3431041 |
Osman I H, Laporte G. 1996. Metaheuristics: A bibliography. Annals of Operations Research, 63(5): 511-623. DOI:10.1007/BF02125421 |
Pan K J, Wang W J, Tang J T, et al. 2013. Mathematical model and fast finite element modeling of high resolution array lateral logging. Chinese Journal of Geophysics (in Chinese), 56(9): 3197-3211. DOI:10.6038/cjg20130932 |
Pardo D, Torres-Verdín C, Paszynski M. 2007. Numerical simulation of 3D EM borehole measurements using an hp-adaptive goal-oriented finite-element formulation. //77th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 653-657.
|
Rasmus J C. 1982. Determining the type of fluid contained in the fractures of the twin creek limestone by using the dual laterolog (TM) tool. Journal of Petroleum Technology, 34(11): 2673-2682. DOI:10.2118/9857-PA |
Rumelhart D E, McClelland J L. 1986. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge: The MIT Press.
|
Salazar J M, Torres-Verdín C. 2009. Quantitative comparison of processes of oil- and water-based mud-filtrate invasion and corresponding effects on borehole resistivity measurements. Geophysics, 74(1): E57-E73. DOI:10.1190/1.3033214 |
Shahriari M, Pardo D, Picon A, et al. 2020. A deep learning approach to the inversion of borehole resistivity measurements. Computational Geosciences, 24(3): 971-994. DOI:10.1007/s10596-019-09859-y |
Wang G L, Torres-Verdín C, Salazar J M, et al. 2009. Fast 2D inversion of large borehole EM induction data sets with an efficient Fréchet-derivative approximation. Geophysics, 74(1): E75-E91. DOI:10.1190/1.3033213 |
Wang H N. 2011. Adaptive regularization iterative inversion of array multicomponent induction well logging datum in a horizontally stratified inhomogeneous TI formation. IEEE Transactions on Geoscience and Remote Sensing, 49(11): 4483-4492. DOI:10.1109/TGRS.2011.2142187 |
Wang L, Fan Y R, Yuan C, et al. 2018. Selection criteria and feasibility of the inversion model for azimuthal electromagnetic logging while drilling (LWD). Petroleum Exploration and Development (in Chinese), 45(5): 914-922. |
Wu Y Z, Fan Y R. 2021. Fast hierarchical inversion for borehole resistivity measurements in high-angle and horizontal wells using ADNN-AMLM. Journal of Petroleum Science and Engineering, 203: 108662. DOI:10.1016/j.petrol.2021.108662 |
Wu Z G, Fan Y R, Wang J W, et al. 2020. Application of 2.5-D finite difference method in logging-while-drilling electromagnetic measurements for complex scenarios. IEEE Geoscience and Remote Sensing Letters, 17(4): 577-581. DOI:10.1109/LGRS.2019.2926740 |
Xu Y K, Sun K L, Xie H, et al. 2018. Borehole resistivity measurement modeling using machine-learning techniques. Petrophysics, 59(6): 778-785. |
Yang Q S, Torres-Verdín C. 2011. Efficient 2D Bayesian inversion of borehole resistivity measurements. //2011 SEG Annual Meeting. San Antonio, Texas.
|
Yao D H, Wang H N, Tao H G, et al. 2010. Iterative Tikhonov regularization inversion for dual-laterolog in horizontally stratified media. Chinese Journal of Geophysics (in Chinese), 53(9): 2227-2236. DOI:10.3969/j.issn.0001-5733.2010.09.024 |
Zhang G J. 2009. Electrical Logging Algorithm (in Chinese). Beijing: Petroleum Industry Press.
|
Zhang P, Hu Y Y, Jin Y C, et al. 2021. A Maxwell's equations based deep learning method for time domain electromagnetic simulations. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 6: 35-40. DOI:10.1109/JMMCT.2021.3057793 |
Zhong Z, Carr T R, Wu X M, et al. 2019. Application of a convolutional neural network in permeability prediction: A case study in the Jacksonburg-Stringtown oil field, West Virginia, USA. Geophysics, 84(6): B363-B373. DOI:10.1190/geo2018-0588.1 |
Zhu L P, Li H Q, Yang Z G, et al. 2018. Intelligent logging lithological interpretation with convolution neural networks. Petrophysics, 59(6): 799-810. |
邓少贵, 李智强, 范宜仁, 等. 2010. 斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟. 地球物理学报, 53(4): 994-1000. DOI:10.3969/j.issn.0001-5733.2010.04.024 |
高杰, 柯式镇, 魏宝君, 等. 2010. 电法测井数值模拟现状及发展趋势分析. 测井技术, 34(1): 1-5. DOI:10.3969/j.issn.1004-1338.2010.01.001 |
林年添, 张栋, 张凯, 等. 2018. 地震油气储层的小样本卷积神经网络学习与预测. 地球物理学报, 61(10): 4110-4125. DOI:10.6038/cjg2018J0775 |
潘克家, 王文娟, 汤井田, 等. 2013. 高分辨率阵列侧向测井的数学模型及有限元快速正演. 地球物理学报, 56(9): 3197-3211. DOI:10.6038/cjg20130932 |
王磊, 范宜仁, 袁超, 等. 2018. 随钻方位电磁波测井反演模型选取及适用性. 石油勘探与开发, 45(5): 914-922. |
姚东华, 汪宏年, 陶宏根, 等. 2010. 水平层状介质中双侧向测井资料的迭代Tikhonov正则化反演. 地球物理学报, 53(9): 2227-2236. DOI:10.3969/j.issn.0001-5733.2010.09.024 |
张庚骥. 2009. 电测井算法. 北京: 石油工业出版社.
|
 2021, Vol. 64
2021, Vol. 64


