2. 吉林大学地球探测科学与技术学院, 长春 130026;
3. 北京桔灯地球物理勘探股份有限公司, 北京 102200;
4. 安徽省勘查技术院, 合肥 230031
2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China;
3. Beijing Orangelamp Geophysical Exploration Company Limited, Beijing 102200, China;
4. Geological Exploration Technology Institute of Anhui Province, Hefei 230031, China
随着重力梯度测量技术的发展,越来越多的重力梯度全张量数据被应用到数据处理中.重力梯度全张量数据是重力位的二阶偏导数,由9个张量数据组成,较重力数据包含有更高频率的信息.对重力梯度全张量数据进行处理,可以得到更全面,更准确的地质信息.
边界识别在位场数据处理中有着重要的作用(Cooper and Cowan, 2006;马国庆等,2011;Archibald et al., 1999;鲁宝亮等,2020),其方法种类有很多,常用的有:垂向导数(Evjen,1936)、总水平导数法(THDR)(Verduzco et al., 2004)、解析信号(ASM)(Hsu et al., 1996)、倾斜角法(Miller and Singh, 1994)、倾斜角水平导数法(王明等,2013)、Theta图法(Wijns et al., 2005)以及其他方法(段杰翔和徐亚,2020;王丁丁等,2021),这些方法都是在传统的重力数据基础上提出的.随着重磁勘探方法的多样化和高精度勘探仪器的发展,梯度仪可以测量所有的重磁张量分量.许多经典的边缘检测方法被应用于梯度张量数据(郑强等,2019).Zhang等(2000)提出张量-欧拉反褶积方法,提高了地质体水平位置的分辨率(Mikhailov et al., 2007).Beiki(2010a, b)利用重力张量数据的方向解析信号振幅来确定地质体位置.朱自强等(2015)通过对重力梯度张量解析信号应用欧拉反褶积,提高了反演结果的可靠性.Yuan和Yu(2015)定义了二阶方向解析信号,提出了几种基于水平方向解析信号和二阶水平方向解析信号的新边界识别方法.Oruç和Keskinsezer(2008)使用倾斜角法,利用重力梯度张量数据对简单模型的边缘进行检测.另外,重力梯度张量的特征值也被用来描绘地质体的边缘.Beiki和Pedersen(2010)利用重力梯度张量数据的特征向量来估计场源的位置和走向.Sertcelik和Kafadar(2012)提出了一种利用结构张量特征值来识别地质体边缘的方法.Yuan等(2014a)提出了三种平衡结构张量最大特征值的方法,并重新定义了结构张量.Zhou等(2017)提出了基于三维结构张量方向总水平导数的边缘检测新方法.Oruç等(2013)利用重力梯度张量数据曲率的最大特征值圈定了地质构造的边缘.一些学者基于Oruç等提出的方法进行了相关改进(Zhou et al., 2013;Wang et al., 2015;Zuo and Hu, 2015).Yuan等(2016)提出了方向Theta方法,并利用水平方向Theta组合(ThetaX与ThetaY相加)的最大值定义了一种新的边缘检测方法(ED)来描绘重力梯度张量数据的边界.当地质体同时存在正异常和负异常时,该方法可以避免产生虚假边缘,但该方法受地质体走向的影响.本文针对其受地质体走向影响的问题,提出了一种改进的边界识别方法(IED),替换原方法中的加法运算,通过选择合适的阈值来削弱虚假边界的识别.模型试验表明,该方法不再受地质体走向的影响,在实际数据处理中取得了良好的效果.
1 ED方法及存在问题重力梯度全张量(GGT)数据是重力位U的二阶偏导数,其矩阵形式为
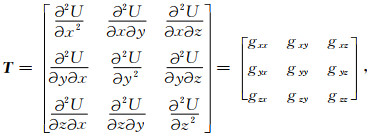
|
(1) |
由位场理论可知,地质体外的引力位满足拉普拉斯方程(Beiki et al., 2010):

|
(2) |
T为对称矩阵,它只包括5个独立张量,gxy、gxz、gyz、gxx和gzz.方向解析信号的振幅为

|
(3) |
Yuan和Geng(2014b)、Yuan和Yu(2015)定义了方向总水平导数.基于Theta方法的定义,提出了GGT数据的方向Theta方法(Yuan et al., 2016),可以表示为
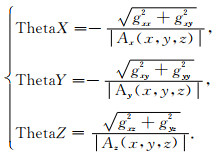
|
(4) |
并在此基础上,将ThetaX与ThetaY得到的结果进行叠加,提出了ED方法,该方法用极大值识别边界:
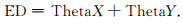
|
(5) |
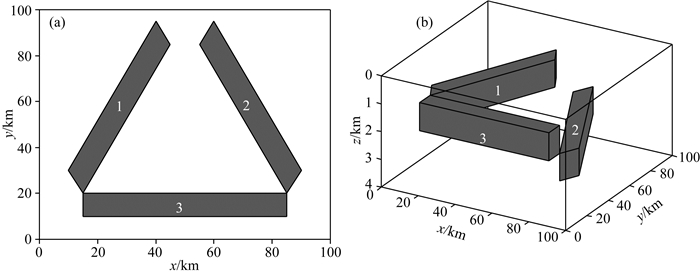
本文设计了模型试验(图 1).图 1a、b分别是模型的平面图和三维视图.测区范围为100 km×100 km,点距为0.5 km,模型参数见表 1.
|
图 1 模型位置图 (a) 平面图;(b) 立体图. Fig. 1 Positions of models (a) Planar view; (b) 3D view. |
在模型试验中,当重力梯度张量用于边界识别时,可能会受到地质体走向的影响,因此模型体设计成与坐标轴成一定角度.此外,模型的设计考虑了不同深度地质体及正负异常相间对边界识别的影响. 图 2和图 3分别为模型的重力异常图和理论重力张量图.

|
图 2 模型重力异常图 Fig. 2 Gravity anomalies of models |

|
图 3 模型理论张量 (a)gxx; (b) gyy; (c) gzz; (d) gxz; (e) gyz; (f) gxy. Fig. 3 Synthetic gravity gradient tensors of models |
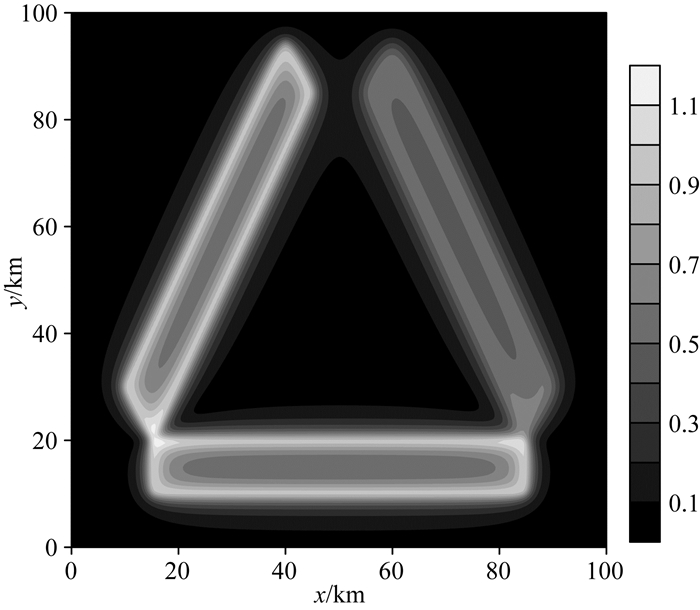
本文将总水平导数(THDR)方法的边界识别效果(图 4)与ED方法的边界识别效果(图 5)进行对比,其中THDR方法为重磁数据处理中常用的边界识别方法,该方法受深度影响.图 4中,模型2较模型1、3深度大,所以模型2的边界识别效果较模型1、3差,边界模糊.
|
图 4 THDR方法边界识别结果 Fig. 4 Edge detection resultby THDR |
|
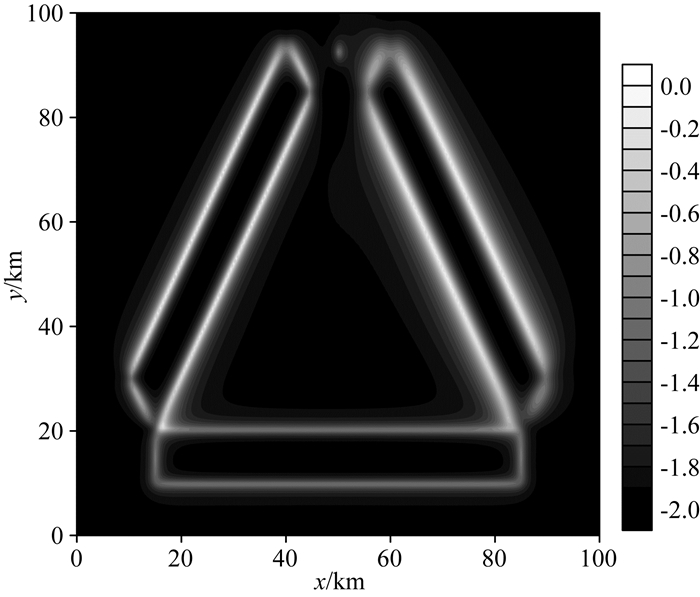
图 5 ED方法边界识别结果 Fig. 5 Edge detection result by ED |
图 5是ED方法边界识别效果,Yuan等(2016)等已经验证该方法不受正负异常梯度带的影响.与THDR方法识别结果进行比较,其中模型2的边界识别效果与模型1的相同,并且比THDR方法识别出的边界清晰,说明该方法不受深度的影响.图 5中模型3与模型1的深度相同,但是识别出的边界清晰程度不同,考虑到只有模型3边界垂直于x轴或y轴,所以推测该方法受地质体走向的影响.
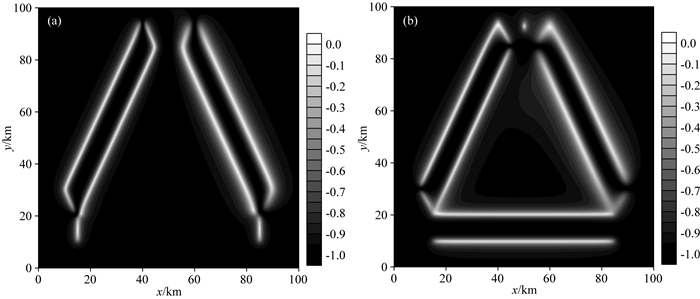
从ThetaX和ThetaY的等值线图(图 6)中可以看出,模型体1,2的边界在ThetaX和ThetaY中分别对应极大值,且大小相近.而模型体3,在ThetaX的图中只能识别出垂直于x轴的边界,在ThetaY的图中只能识别出垂直于y轴的边界,对ThetaX和ThetaY进行叠加后,模型体1, 2边界的数值绝对值会达到模型体3边界的2倍左右,因此模型体3的边界较为模糊.因此,ED方法识别边界的结果中,当待识别区域内存在垂直或平行于坐标轴的地质体和与坐标轴成一定角度的地质体时,与坐标轴垂直或平行的地质体的边界较模糊,不利于边界信息的提取.
|
图 6 边界识别结果 (a) ThetaX;(b) ThetaY. Fig. 6 Edge detection results |
为了减小地质体走向对ED方法的影响,本文提出IED方法,表达式为
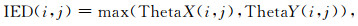
|
(6) |
式中,i、j分别为点线号,将ThetaX和ThetaY逐点对比,取较大的值赋给IED.这样可以避免与坐标轴成一定角度的边界叠加两次.但这样运算会使ThetaX和ThetaY中的较弱的虚假异常凸显出来.为了减弱这种效应,本文根据ThetaX和ThetaY各自的最小值TXmin和TYmin,定义了阈值T:
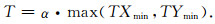
|
(7) |
由于ThetaX和ThetaY都为负值,T也为负值,α取值的范围为0~1.设定判定条件:当测点的ThetaX和ThetaY的值都小于T,则IED取二者较小的值;其他情况,IED取二者较大的值,即:
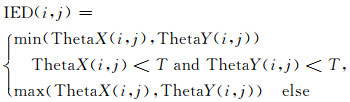
|
(8) |
将其应用到模型试验中,令α分别为0.9、0.6、0.3,并与EI方法及常用的斜导数法、Theta法进行对比(图 7).

|
图 7 几种常用方法及不同α值的IED方法边界识别结果 (a) 斜导数法;(b) Theta角法;(c) ED法;(d) IED of α=0.9;(e) IED of α=0.6;(f) IED of α=0.3. Fig. 7 Edge detection results of several commonly used methods and IED with different values of α (a) Tilt derivative method; (b) Theta angle method; (c) ED method; (d) IED with α=0.9; (e) IED with α=0.6; (f) IED with α=0.3. |
由图 7,对比几种常用方法及α分别为0.9、0.6、0.3的IED方法边界识别结果,可以看出,斜导数法和Theta方法都会在正负异常之间产生虚假边界,从而影响边界识别效果.IED方法对三个模型体的边界识别效果都较明显,一定程度上改善了ED方法中模型体3相比于模型体1、2边界模糊的现象,而且随着α值的减小,虚假异常也逐渐减弱,但是当α值减小到一定程度,边界的有用信息也开始有一定的损失,通过实验对比分析得到当α值取0.6~0.8时效果较好.根据图 1中虚线位置提取斜导数方法,Theta方法,ED方法及α值为0.6的IED方法边界识别结果剖面图如图 8所示.

|
图 8 几种方法边界识别结果剖面图 (a) 斜导数法;(b) Theta角法;(c) ED法;(d) IED α=0.6. Fig. 8 Edge detection resultsby methods shown by profile (a) Tilt derivative method; (b) Theta angle method; (c) ED method; (d) IED with α=0.6. |
图 8a是斜导数方法边界识别结果的剖面图,该方法用零值线(图中虚线)识别边界,图中零值点与地质体边界对应较好,但是在正负异常之间有多余的零值点d,该点显示为虚假边界.图 8b是Theta角法边界识别结果的剖面图,与图 8a类似,在正负异常之间也有虚假边界存在(f点).图 8c是ED方法边界识别结果的剖面图,从图中可以看出该方法能够较好的识别出地质体边界,且没有虚假边界产生,但是左侧异常体边界处的值是右侧异常体边界处值的2倍以上,如果地下地质构造情况较复杂,有些地质体的边界可能无法识别出来.图 8d是IED方法边界识别结果的剖面图,可以看出该方法能够较好的识别出地质体边界,没有虚假异常产生,且异常体边界处的值几乎相等.为进一步讨论该方法的实用性,设计了加干扰的复杂模型,模型参数如表中所示.
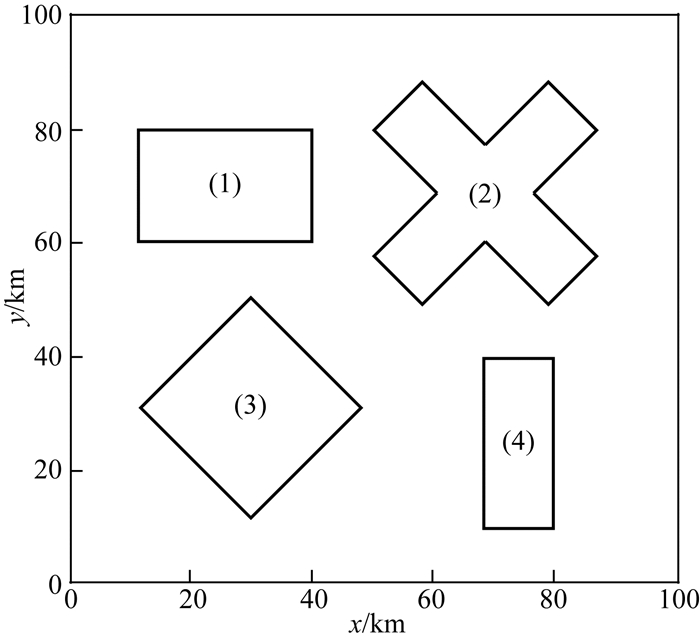
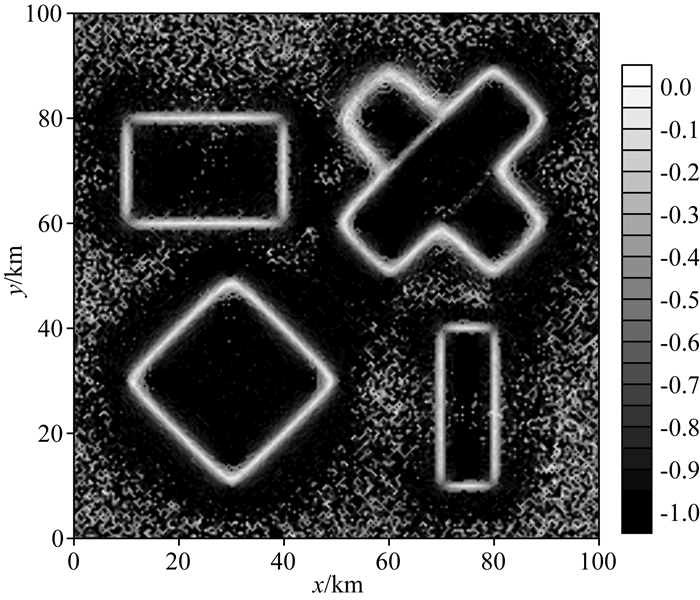
图 9为复杂模型的示意图,表 2为复杂模型参数.在模型试验中加入异常最大幅值1%的随机噪声.用IED方法进行边界识别,结果如图 10所示.
|
图 9 复杂模型示意图 Fig. 9 Schematic diagram of complex model |
|
|
表 2 复杂模型参数 Table 2 Parameters of complex model |
|
图 10 IED方法边界识别结果(α=0.6) Fig. 10 Edge detection result of IED(α=0.6) |
从图 10的处理结果可以看出,对于加入噪声的复杂模型,IED方法也能较好地识别出边界.边界识别结果在模型体边界位置受噪声影响最小,则该方法在地质体边界处对干扰的压制作用最强,这一特点在边界识别中是有利的.
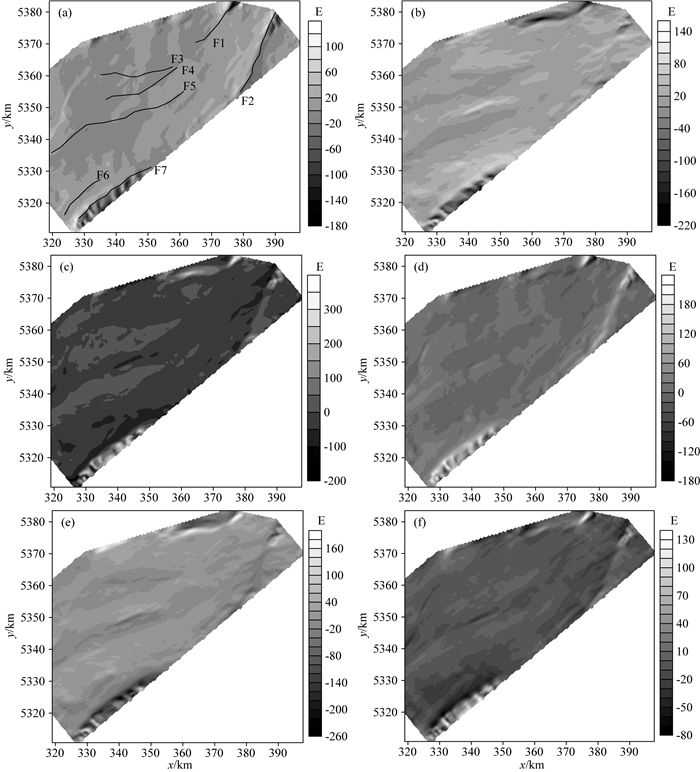
3 实际数据处理本文实际数据是加拿大自然资源部(Natural Resources Canada)提供的圣乔治湾的(St.George′s Bay)全张量重力梯度测量数据(Miller and Singh, 1994),包含88条测线,线距为400 m,总飞行长度为6602 km,测区覆盖面积为3056 km2,飞行高度为80 m,联络线距为5000 m.该地区测得的重力全张量数据,如图 11所示图,其中黑色实线是已知的地质边界.
|
图 11 圣乔治湾地区重力全张量 (a) gxx; (b) gyy; (c) gzz; (d) gxz; (e) gyz; (f) gxy. Fig. 11 Fullgravity tensors in St. George′s Bay, Canada |
测区位于圣劳伦斯在纽芬兰岛西南海岸的海湾,测区包含了圣乔治湾的大面积石炭系凹陷,石炭系和上泥盆统的沉积岩在北、东、南三个方向出露,覆盖在前寒武纪基底上.测区中分布着不同时代的地层,可以通过重力梯度全张量数据对不同密度的地质边界进行边界识别.图 12为利用ED方法(图 12a、b)和α值为0.7时的IED方法(图 12c、d)进行边界识别的图像.

|
图 12 圣乔治湾重力梯度全张量数据处边界识别效果 (a)和(b) ED方法;(c)和(d) IED方法. Fig. 12 Edge detection results of full tensor gravity gradient data in the St. George′s Bay (a) and(b) ED method; (c) and(d) IED method. |
对比图 12a、c,可以看出两种方法都能识别出该地区大的构造边界.ED法和IED法在对断裂F1、F2、F4、F6、F7的识别效果是相近的,因为这5条断裂与水平方向存在一定的夹角,而对于断裂F3与F5,对比图中红色虚线圈闭框(B和C)标示出来的区域(即F5断裂),会发现ED方法一些边界由于受走向的影响在图中只有较弱的显示,边界不连续,点状分布,而IED方法能清楚地分辨出边界的位置;对比红色虚线框(A)标示出来的区域(即断裂F3位置),可以看出一些边界通过ED方法甚至无法识别出来,但通过IED方法却能得到清楚连续的边界,可以对F3断裂进行更好的解释.通过对实际数据的处理发现,与ED方法对比,IED方法在实际数据处理中边界识别更加清晰,细节处更加明显,处理结果更加可靠.
4 结论为了解决地质构造走向对边界识别的影响,本文提出了一种改进的ED方法(IED),通过理论研究、模型试验及实际数据的处理验证了该方法的可靠性.得出以下结论:
(1) ED方法在边界识别中,会受到地质体走向的影响,对于平行或者垂直于坐标轴方向的边界识别效果较差,导致这种现象的原因是原方法中叠加项对于识别这种走向的地质体较该坐标轴成一定角度的地质体的能力弱.
(2) 改进后IED方法,摒弃了原方法中的叠加项,选择合适的阈值来减少虚假异常,从而使该方法不受地质体走向的影响,进一步提高边界识别效果.
(3) 在实际数据处理中IED方法比ED方法识别出的边界细节更多,同时边界也更连续,为地质解释提供了更详细的信息.
致谢 感谢加拿大自然资源部(Natural Resources Canada)提供圣乔治湾(St.George′s Bay)全张量重力梯度测量数据,并允许发表数据处理结果.
Archibald N, Gow P, Boschetti F. 1999. Multiscale edge analysis of potential field data. Exploration Geophysics, 30(1-2): 38-44. DOI:10.1071/EG999038 |
Beiki M. 2010a. Analytic signals of gravity gradient tensor and their application to estimate source location. Geophysics, 75(6): I59-I74. DOI:10.1190/1.3493639 |
Beiki M. 2010b. Analytic signals of the gravity gradient tensor and their application to Euler deconvolution. //EGM 2010 International Workshop. Capri, Italy: European Association of Geoscientists & Engineers.
|
Beiki M, Pedersen L B. 2010. Eigenvector analysis of gravity gradient tensor to locate geologic bodies. Geophysics, 75(6). |
Cooper G R J, Cowan D R. 2006. Enhancing potential field data using filters based on the local phase. Computers & Geosciences, 32(10): 1585-1591. |
Duan J X, Xu Y. 2020. Method and application of edge enhancement of tilt angle based on moving small sub-domain filtering. Progress in Geophysics (in Chinese), 35(6): 2315-2322. DOI:10.6038/pg2020DD0504 |
Evjen H M. 1936. The place of the vertical gradient in gravitational interpretations. Geophysics, 1(1): 127-136. DOI:10.1190/1.1437067 |
Hsu S H, Sibuet J C, Shyu C T. 1996. High-resolution detection of geologic boundaries from potential-field anomalies; an enhanced analytic signal technique. Geophysics, 61(2): 373-386. DOI:10.1190/1.1443966 |
Lu B L, Ma T, Xiong S Q, et al. 2020. A new recognition method for source locations and attributes based on correlation analysis of gravity and magnetic anomalies. Chinese Journal of Geophysics (in Chinese), 63(4): 1663-1674. DOI:10.6038/cjg2020N0355 |
Ma G Q, Du X J, Li L L. 2011. Edge detection of potential field data using correlation coefficients of horizontal and vertical derivatives. Journal of Jilin University (Earth Science Edition) (in Chinese), 41(S1): 345-348. |
Mikhailov V, Pajot G, Diament M, et al. 2007. Tensor deconvolution: A method to locate equivalent sources from full tensor gravity data. Geophysics, 72(5): 161-169. |
Miller H G, Singh V. 1994. Potential field tilt-a new concept for location of potential field sources. Journal of Applied Geophysics, 32(2-3): 213-217. DOI:10.1016/0926-9851(94)90022-1 |
Oruç B, Keskinsezer A. 2008. Structural setting of the northeastern Biga Peninsula (Turkey) from tilt derivatives of gravity gradient tensors and magnitude of horizontal gravity components. Pure and Applied Geophysics, 165(9): 1913-1927. DOI:10.1007/s00024-008-0407-8 |
Oruç B, Sertcelik I, Kafadar Ö, et al. 2013. Structural interpretation of the Erzurum Basin, eastern Turkey, using curvature gravity gradient tensor and gravity inversion of basement relief. Journal of Applied Geophysics, 88: 105-113. DOI:10.1016/j.jappgeo.2012.10.006 |
Sertcelik I, Kafadar O. 2012. Application of edge detection to potential field data using eigenvalue analysis of structure tensor. Journal of Applied Geophysics, 84: 86-94. DOI:10.1016/j.jappgeo.2012.06.005 |
Verduzco B, Fairhead J D, Green C M, et al. 2004. New insights into magnetic derivatives for structural mapping. The Leading Edge, 23(2): 116-119. DOI:10.1190/1.1651454 |
Wang D D, Wang W Y, Zhu Y J, et al. 2021. Extraction methods and application of feature points of edge recognition for potential field. Chinese Journal of Geophysics (in Chinese), 64(4): 1401-1411. DOI:10.6038/cjg2021O0055 |
Wang J, Meng X H, Li F. 2015. Improved curvature gravity gradient tensor with principal component analysis and its application in edge detection of gravity data. Journal of Applied Geophysics, 118: 106-114. DOI:10.1016/j.jappgeo.2015.04.013 |
Wang M, Guo Z H, Luo Y, et al. 2013. Extended tilt angle and total horizontal derivatives. Progress in Geophysics (in Chinese), 28(3): 1453-1463. DOI:10.6038/pg20130340 |
Wijns C, Perez C, Kowalczyk P. 2005. Theta map: edge detection in magnetic data. Geophysics, 70(4): L39-L43. DOI:10.1190/1.1988184 |
Yuan Y, Gao J Y, Chen L N. 2016. Advantages of horizontal directional Theta method to detect the edges of full tensor gravity gradient data. Journal of Applied Geophysics, 130: 53-61. DOI:10.1016/j.jappgeo.2016.04.009 |
Yuan Y, Geng M X. 2014b. Directional total horizontal derivatives of gravity gradient tensor and their application to delineat the edges. //84th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Yuan Y, Huang D N, Yu Q L, et al. 2014a. Edge detection of potential field data with improved structure tensor methods. Journal of Applied Geophysics, 108: 35-42. DOI:10.1016/j.jappgeo.2014.06.013 |
Yuan Y, Yu Q L. 2015. Edge Detection in potential-field gradient tensor data by use of improved horizontal analytical signal methods. Pure and Applied Geophysics, 172(2): 461-472. DOI:10.1007/s00024-014-0880-1 |
Zhang C Y, Mushayandebvu M F, Reid A B, et al. 2000. Euler deconvolution of gravity tensor gradient data. Geophysics, 65(2): 512-520. DOI:10.1190/1.1444745 |
Zheng Q, Guo H, Zhang G B, et al. 2019. Research and application of edge detection based on full tensor magnetic gradient direction Theta method. Progress in Geophysics (in Chinese), 34(4): 1568-1576. DOI:10.6038/pg2019CC0328 |
Zhou S, Huang D N, Jiao J. 2017. Total horizontal derivatives of potential field three-dimensional structure tensor and their application to detect source edges. Acta Geodaetica et Geophysica, 52(3): 317-329. DOI:10.1007/s40328-016-0171-7 |
Zhou W N, Du X J, Li J Y. 2013. The limitation of curvature gravity gradient tensor for edge detection and a method for overcoming it. Journal of Applied Geophysics, 98: 237-242. DOI:10.1016/j.jappgeo.2013.09.008 |
Zhu Z Q, Wang C, Lu G Y, et al. 2015. Euler deconvolution of analytic signals of gravity gradient tensor. Journal of Central South University (Science and Technology) (in Chinese), 46(1): 217-222. |
Zuo B X, Hu X Y. 2015. Edge detection of gravity field using eigenvalue analysis of gravity gradient tensor. Journal of Applied Geophysics, 114: 263-270. DOI:10.1016/j.jappgeo.2015.01.013 |
段杰翔, 徐亚. 2020. 基于滑动小子域滤波的倾斜角边界增强方法及应用. 地球物理学进展, 35(6): 2315-2322. DOI:10.6038/pg2020DD0504 |
鲁宝亮, 马涛, 熊盛青, 等. 2020. 基于重磁异常相关分析的场源位置及属性识别方法. 地球物理学报, 63(4): 1663-1674. DOI:10.6038/cjg2020N0355 |
马国庆, 杜小娟, 李丽丽. 2011. 利用水平与垂直导数的相关系数进行位场数据的边界识别. 吉林大学学报(地球科学版), 41(S1): 345-348. |
王丁丁, 王万银, 朱莹洁, 等. 2021. 位场边缘识别特征点提取方法及应用. 地球物理学报, 64(4): 1401-1411. DOI:10.6038/cjg2021O0055 |
王明, 郭志宏, 骆遥, 等. 2013. 扩展的倾斜角和倾斜角总水平导数方法. 地球物理学进展, 28(3): 1453-1463. DOI:10.6038/pg20130340 |
郑强, 郭华, 张贵宾, 等. 2019. 基于全张量磁梯度方向Theta法进行边界识别的研究与应用. 地球物理学进展, 34(4): 1568-1576. DOI:10.6038/pg2019CC0328 |
朱自强, 王灿, 鲁光银, 等. 2015. 重力梯度张量解析信号的欧拉反褶积. 中南大学学报(自然科学版), 46(1): 217-222. |
 2021, Vol. 64
2021, Vol. 64


