2021, Vol. 64
2. 中国石油天然气集团有限公司油藏描述重点实验室, 兰州 730020
2. Key Laboratory of Petroleum Resources of CNPC, Lanzhou 730020, China
波动方程数值模拟是逆时偏移(Baysal et al., 1983; Virieux et al., 2011; 陈生昌和周华敏, 2018)和全波形反演(Tarantola, 1984; Pratt et al., 1998; 董良国等, 2015)的重要基础.有限元法(Marfurt, 1984; Moczo et al., 2010, 2011)、虚谱法(Reshef et al., 1988; 黄建平等, 2016)和有限差分法(Alterman and Karal, 1968; Liu and Sen, 2011a; 梁文全等, 2013)是求解波动方程的三大主流数值算法(皮红梅等，2009；胡恒山，2018).相比其他两类方法，有限差分法占用内存更小，计算效率更高，因而成为应用最普遍的波动方程数值模拟算法(蒋韬等，2008；张志禹等，2017；姜占东等，2021).但是，有限差分法采用差分算子近似波动方程中的时间和空间偏微分算子，导致时间和空间数值频散，降低了模拟精度(Alford et al., 1974; Dablain, 1986)；同时，逆时偏移和全波形反演巨大的计算量，发展高精度和高效率的有限差分模拟算法具有重要意义.
Dablain(1986)研究指出，时间和空间高阶差分格式能够有效压制数值频散、提高模拟精度.然而，时间高阶差分格式占用内存过大，稳定性降低(Chen, 2007, 2011).针对标量波动方程，常规高阶差分方法采用时间2阶和空间高阶(2M)差分格式，并利用空间域频散关系和泰勒级数展开求解差分系数，本文称为常规空间域高阶有限差分法(简称为CSD-FDM).CSD-FDM的差分系数算法仅衡量了空间差分算子(Laplace差分算子)的精度，而没有考虑差分离散波动方程的精度，空间差分算子虽然能达到2M阶精度，但差分离散波动方程仅具有2阶精度.实际上，有限差分法通过迭代求解差分离散波动方程实现波动方程数值模拟，差分离散波动方程的差分精度才能更准确地描述有限差分法的模拟精度.Liu和Sen (2009)保持CSD-FDM的差分格式不变，提出利用时空域频散关系改进差分系数算法，本文称为时空域高阶有限差分法(简称为TSD-FDM).TSD-FDM比CSD-FDM具有更高的模拟精度和更强的稳定性.TSD-FDM在二维和三维标量波动方程模拟中，差分离散波动方程分别沿8个和48个传播方向具有2M阶差分精度，其他传播方向只能达到2阶差分精度，存在数值各向异性.基于相同思路，Liu和Sen(2011b)提出了面向应力-速度声波方程的时空域高阶交错网格差分法，同样有效提高了模拟精度和稳定性.严红勇等进一步推广应用于声波、VTI介质、黏声介质逆时偏移中，有效压制了数值频散造成的成像假象(严红勇和刘洋, 2013；Yan and Liu, 2013a，b).基于泰勒级数展开的差分系数算法计算效率高，通常低波数成分具有较高的模拟精度，但高波数模拟精度迅速降低.为了提高高波数成分的模拟精度，Zhang和Yao(2012, 2013)、Liu(2013, 2014)通过最小二乘优化频散误差，改进差分系数算法提高模拟精度.
除了改进差分系数算法，设计更合理的差分格式是提高模拟精度的另一重要途径.针对二维和三维应力-速度声波方程，Tan和Huang(2014a)利用坐标轴网格点和非坐标轴网格点构建空间差分算子近似一阶空间微分算子，提出了混合交错网格差分方法，并利用时空域频散关系和泰勒展开求解差分系数，差分离散波动方程沿任意传播方向可达到4阶、6阶差分精度，并具有更强的稳定性.Tan和Huang(2014b)利用最小二乘法优化差分系数，模拟精度进一步提高.Ren和Li(2017)针对二维弹性波方程，构建了更具一般性的混合交错网格差分格式，弹性波差分离散方程沿任意传播方向可达到2N(N＜5)阶差分精度.混合交错网格差分格式，应力和速度的空间一阶偏导算子，各坐标轴相互独立计算，因此2D可较易推广到3D.
针对二维标量波动方程，Liu和Sen(2013)、张保庆等(2016)、胡自多等(2016)和Wang等(2016)先后提出将二维Laplace微分算子近似为常规笛卡尔坐标系中坐标轴网格点构建的M个Laplace差分算子和旋转笛卡尔坐标系中坐标轴网格点构建的N个Laplace差分算子的加权平均，构建了不同的混合网格差分格式，利用时空域频散关系和泰勒展开求解差分系数，差分离散波动方程沿任意传播方向理论上可达到任意偶数阶差分精度，明显提高了二维标量波动方程有限差分法的模拟精度，稳定性进一步增强，还能采用更大的时间采样间隔以获得更高的计算效率.不同于混合交错网格差分格式，标量波动方程压力对空间的2阶偏导(Laplace算子)作为一个整体计算，2D混合网格差分格式不能直接推广到3D.而地震勘探的对象通常是三维介质，发展三维混合网格差分格式更具实际意义.
如何利用三维笛卡尔坐标系中非坐标轴网格点构建Laplace差分算子是建立三维混合网格差分格式需要解决的关键问题.本文将三维笛卡尔坐标系中的非坐标轴网格点分为两类：坐标平面内的非坐标轴网格点和坐标平面外的非坐标轴网格点，并系统推导出了这两类非坐标轴网格点构建三维Laplace差分算子的方法.在此基础上，将三维Laplace微分算子近似为坐标轴网格点构建的M个Laplace差分算子和非坐标轴网格点构建的N个Laplace差分算子的加权平均，提出了一种面向三维标量波动方程的混合网格M+N型差分方法(简称为MG-FDM)，并根据时空域频散关系和泰勒级数展开建立了差分系数求解方程组，推导出差分系数的通解.增大N的取值，三维MG-FDM给出的差分离散波动方程沿任意传播方向能够达到4阶、6阶、甚至任意偶数阶差分精度.频散分析表明，相比三维CSD-FDM和TSD-FDM，计算效率基本相同时，MG-FDM的数值频散压制效果更好，模拟精度更高；模拟精度基本相当时，MG-FDM能采用更大的时间采样间隔，计算效率更高.稳定性分析表明，MG-FDM稳定性更强，为其采用更大的时间采样间隔以提高计算效率奠定了基础.三维数值模拟实验进一步证实了MG-FDM在提高模拟精度和计算效率方面的优越性.
1 三维混合网格差分格式构建方法 1.1 三维常规空间域高阶(CSD-FDM)和时空域高阶(TSD-FDM)差分格式常密度介质中，三维标量波动方程为：
|
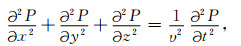
(1) |
其中P=P(x, y, z, t)为压力场，υ=υ(x, y, z)为压力场的传播速度，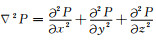
有限差分法数值求解波动方程普遍采用2阶时间差分方案，式(1)右边的时间偏微分可差分表示为：
|
(2) |
其中Pm, l, nj=P(x+mh, y+lh, z+nh, t+jτ)，h和τ分别为空间和时间采样间隔，P0, 0, 00=P(x, y, z, t)表示任意空间位置(x, y, z)和时刻t的压力值.
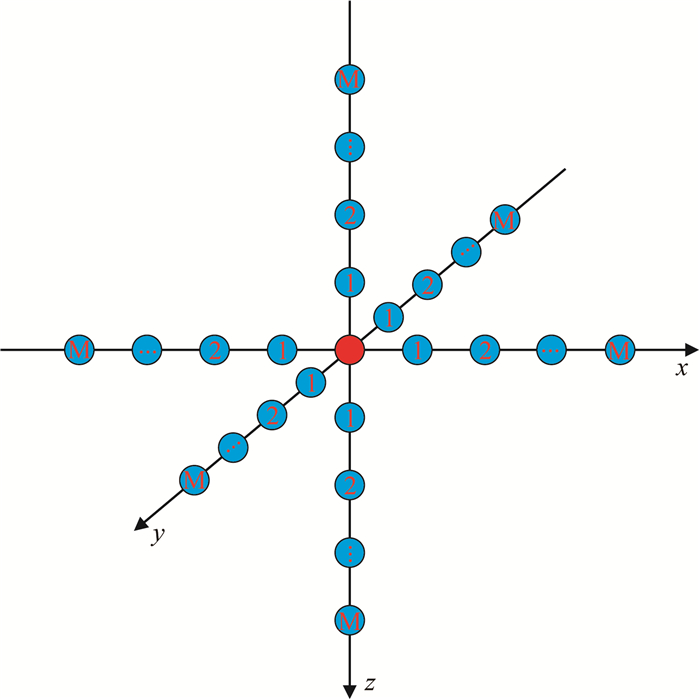
三维常规空间域高阶差分(CSD-FDM)和三维时空域高阶差分(TSD-FDM)，均采用图 1所示的差分格式，波动方程(1)中的三维Laplace微分算子可差分近似为：
|
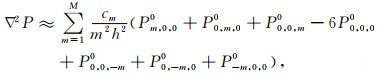
(3) |
|
图 1 三维CSD-FDM和TSD-FDM的差分格式 Fig. 1 FD stencil of 3D CSD-FDM and TSD-FDM |
其中cm(m=1, 2, …, M)为权系数；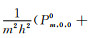
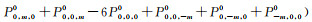
式(3)、(2)代入式(1)：
|
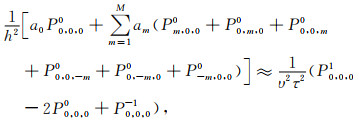
(4) |
其中
构建三维混合网格M+N型差分格式(MG-FDM)的基本思想是联合利用坐标轴网格点和非坐标轴网格点一起差分近似三维Laplace算子.如何利用非坐标轴网格点构建Laplace差分算子是建立三维MG-FDM需要解决的关键问题.
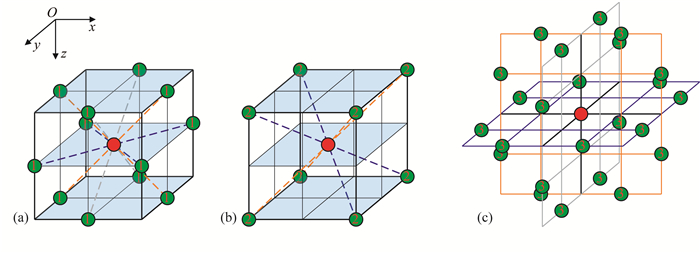
图 2a-c给出了三维笛卡尔坐标系中与差分中心点距离相等的三组非坐标轴网格点，这三组网格点与差分中心点的距离依次增大.由于无法将任意一组非坐标轴网格点置于坐标原点位于差分中心点的三维旋转笛卡尔坐标系的坐标轴上，导致不能直接利用非坐标轴网格点构建三维Laplace差分算子.为了利用非坐标轴网格点构建三维Laplace差分算子，本文将非坐标轴网格点分成两类：坐标平面内的非坐标轴网格点(如图 2a、c)和坐标平面外的非坐标轴网格点(如图 2b).
|
图 2
三维坐标系中非坐标轴网格点构建的差分格式
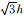(a) 坐标平面内的非坐标轴网格点构建的差分格式(网格点与中心点的距离是 )；(b) 坐标平面外的非坐标轴网格点构建的差分格式(网格点与中心点的距离是 )；(c) 坐标平面内的非坐标轴网格点构建的差分格式(网格点与中心点的距离是 ).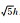
Fig. 2
FD stencils constructed by off-axial grid nodes in the 3D Cartesian coordinate system
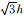(a) FD stencil constructed by the off-axial grid nodes in the coordinate plane (distance between grid node and center grid node is ); (b) FD stencil constructed by the off-axial grid nodes outside the coordinate plane (distance between grid node and center grid node is ); (c) FD stencil constructed by the off-axial grid nodes in the coordinate plane (distance between grid node and center grid node is ).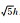
|
针对坐标平面内的非坐标轴网格点，在三维笛卡尔坐标系中的三个坐标平面内，借用二维旋转坐标系的概念，即可导出坐标平面内非坐标轴网格点构建的三维Laplace差分算子.图 2a为一组坐标平面内的非坐标轴网格点，与差分中心点距离等于
|
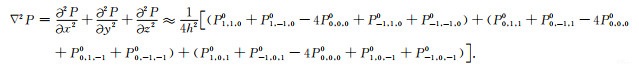
(5) |
针对坐标平面外的非坐标轴网格点，本文提出利用三元函数泰勒级数展开，推导出坐标平面外的非坐标轴网格点构建三维Laplace差分算子的方法.图 2b为一组坐标平面外的非坐标轴网格点，与差分中心点距离等于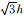
|
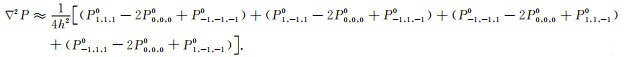
(6) |
将三维坐标系中坐标轴网格点差分格式(图 1)与非坐标轴网格点差分格式(图 2)进行组合，构建出三维MG-FDM的差分格式(图 3).图 1与图 2a中的差分格式组合，可构建出三维MG-FDM(N=1)的差分格式(图 3a).式(3)与式(5)加权求和：
|
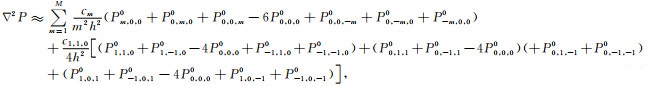
(7) |
|
图 3 三维MG-FDM的差分格式 (a) MG-FDM(N=1)；(b) MG-FDM(N=2)；(c) MG-FDM(N=3). Fig. 3 FD stencils of 3D MG-FDM |
其中cm(m=1, 2, …, M)和c1, 1, 0为权系数.
式(7)表明，三维MG-FDM(N=1)是将三维Laplace微分算子近似为坐标轴网格点构建的M个Laplace差分算子和非坐标轴网格点构建的1个Laplace差分算子的加权平均.式(7)和(2)代入(1)：
|
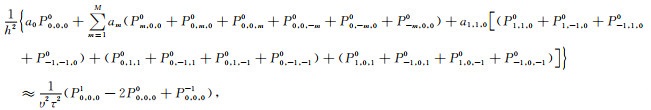
(8) |
其中，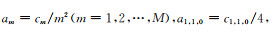
式(8)是三维MG-FDM(N=1)的差分离散波动方程，附录B给出了三维MG-FDM(N=2, 3)对应的差分离散波动方程，同理可导出N取任意值时三维MG-FDM的差分离散波动方程.MG-FDM实质上是将三维Laplace微分算子近似为坐标轴网格点构建的M个Laplace差分算子和非坐标轴网格点构建的N个Laplace差分算子的加权平均.
2 差分系数计算方法和差分精度分析三维CSD-FDM和TSD-FDM的差分系数计算，分别利用空间域频散关系和时空域频散关系.为了阐述三维MG-FDM差分系数计算方法和差分精度对比，我们首先列出三维CSD-FDM和TSD-FDM的差分系数算法，进而推导出三维TSD-FDM和MG-FDM差分系数的通解.
2.1 三维CSD-FDM的差分系数算法在均匀介质中，三维标量波动方程具有如下离散形式的平面波解：
|
(9) |
其中kx=ksinϕcosθ, ky=ksinϕsinθ, kz=kcosϕ，ω为角频率，k为波数，ϕ和θ为平面波的传播方向角.
将式(9)代入式(3)中，得到CSD-FDM的Laplace差分算子频散关系，即空间域频散关系：
|
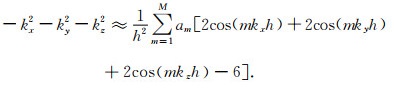
(10) |
对余弦函数进行泰勒展开，可导出三维CSD-FDM的差分系数通解为：
|
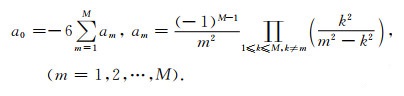
(11) |
三维CSD-FDM差分系数计算，利用空间域频散关系，仅考虑空间差分算子(Laplace差分算子)的差分精度.
2.2 三维TSD-FDM的差分系数算法三维TSD-FDM差分系数计算，考虑了差分离散波动方程的差分精度.将平面波解式(9)代入差分离散方程式(4)，得到差分离散波动方程的频散关系，即时空域频散关系：
|
(12) |
|
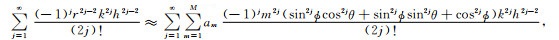
(13) |
其中r=υτ/h为Courant条件数，表示单位时间采样间隔(τ)内波传播的距离与空间采样间隔(h)之比.
令方程(13)中k2jh2j-2左右两边的系数相等，并考虑到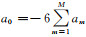
|
(14) |
其中f(j, ϕ, θ)=sin2jϕ(cos2jθ+sin2jθ)+cos2jϕ.可以看出，三维TSD-FDM的差分系数am(m=0, 1, 2, …, M)是地震波传播方向角ϕ和θ的函数.Liu和Sen(2009)计算差分系数时，取ϕ=π/2, θ=π/8，分析出三维TSD-FDM的差分离散波动方程沿48个传播方向具有2M阶差分精度.
取ϕ=0, θ=0，式(14)可简化得到TSD-FDM差分系数通解的一个特殊形式：
|
(15) |
取ϕ=0, θ=0，三维TSD-FDM的差分离散波动方程仅沿6个传播方向(3个坐标轴的正负方向)具有2M阶差分精度. 因此，取ϕ=π/2, θ=π/8计算的差分系数，TSD-FDM的差分离散波动方程能达到更高的模拟精度.
2.3 三维MG-FDM的差分系数算法借鉴时空域频散关系和泰勒展开求解差分系数的方法，本文推导出了MG-FDM的差分系数通解.
将平面波解式(9)代入三维MG-FDM(N=1)的差分离散波动方程式(8)，得到：
|
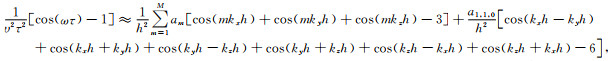
(16) |
式(16)描述了三维MG-FDM(N=1)的差分离散波动方程的时空域频散关系，泰勒展开余弦函数可得：
|
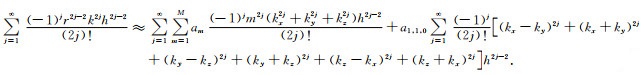
(17) |
令方程(17)中
|
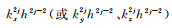
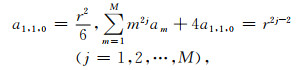
(18) |
考虑到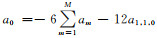
|
|
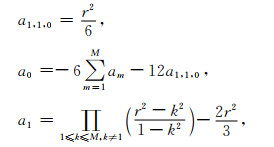
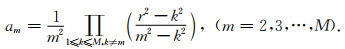
(19) |
差分精度是一种定量描述有限差分法模拟精度的传统方法，通常将误差函数关于时间采样间隔τ或者空间采样间隔h的最小幂指数称为差分精度阶数.根据频散关系式(10)，定义三维CSD-FDM的Laplace差分算子的误差函数εCSD-FDM为：
|
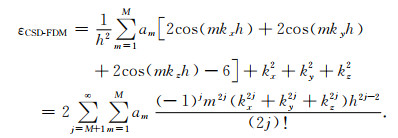
(20) |
根据频散关系式(12)，定义三维CSD-FDM的差分离散波动方程的误差函数ECSD-FDM为：
|
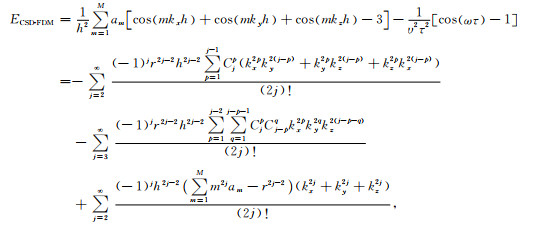
(21) |
其中Cjp和Cj-pq为组合数.式(20)表明，三维CSD-FDM的Laplace差分算子具有2M阶差分精度；式(21)表明三维CSD-FDM的差分离散波动方程仅具有2阶差分精度.综合分析可以看出，三维CSD-FDM的Laplace差分算子虽然能够达到2M阶差分精度，但差分离散波动方程仅具有2阶差分精度.然而，有限差分法通过迭代求解差分离散波动方程实现波动方程数值模拟，因此，差分离散波动方程的差分精度才能准确描述有限差分法的模拟精度.
根据三维TSD-FDM差分离散波动方程的频散关系式(12)，结合式(13)，TSD-FDM的差分离散波动方程的误差函数：
|
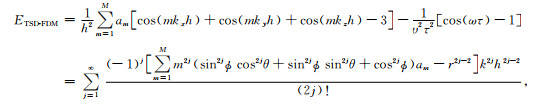
(22) |
计算差分系数时，取ϕ=π/2, θ=π/8，三维TSD-FDM的差分离散波动方程，沿特定的48个传播方向可达到2M阶差分精度，但沿其他传播方向仅具有2阶差分精度.整体来讲，三维TSD-FDM的差分离散波动方程仅具有2阶差分精度.
根据三维MG-FDM(N=1)的差分离散波动方程的频散关系式(16)，定义MG-FDM(N=1)的差分离散波动方程的误差函数EMG-FDM(N=1)为：
|
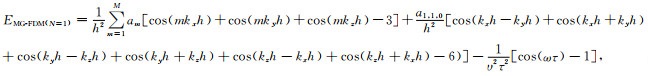
(23) |
结合式(17)、(18)，误差函数EMG-FDM(N=1)可表示为：
|
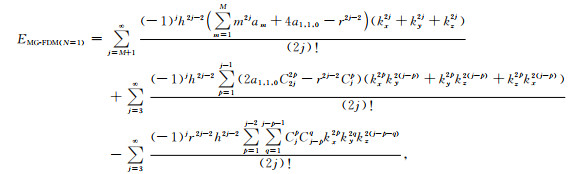
(24) |
其中Cjp、C2j2p和Cj-pq为组合数.式(24)表明，误差函数EMG-FDM(N=1)中空间采样间隔h的最小幂指数为4，因此三维MG-FDM(N=1)的差分离散波动方程沿任意传播方向可达到4阶差分精度.
同理，可分析出三维MG-FDM(N=2, 3)的差分精度.表 1给出了三维CSD-FDM、TSD-FDM和MG-FDM(N=1, 2, 3)的差分精度，可以看出，相比三维CSD-FDM和TSD-FDM，MG-FDM能够有效提高差分离散波动方程的差分精度.增大N的取值，MG-FDM的差分离散波动方程理论上可达到任意偶数阶差分精度.
|
表 1 三维CSD-FDM、TSD-FDM和MG-FDM(N=1, 2, 3)的差分离散波动方程的差分精度 Table 1 Difference accuracy of the discrete difference wave equation for 3D CSD-FDM, TSD-FDM and MG-FDM (N=1, 2, 3) |
数值频散使得相速度υph与地震波的真实传播速度不相等，并且随地震波的传播方向变化，呈现数值各向异性特征.本文采用归一化相速度δ(ϕ, θ)=υph/υ描述相速度的数值频散特性，根据相速度定义υph=ω/k和三维MG-FDM(N=1)的差分离散波动方程的频散关系式(16)，可得出MG-FDM(N=1)的归一化相速度δ(ϕ, θ)的表达式：
|
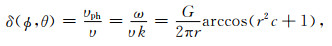
(25) |
|
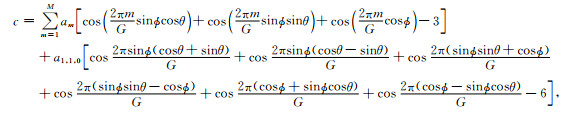
(26) |
其中，G=λ/h，λ为波长，G为波长与空间采样间隔之比，则G值越大，1/G越小，表示空间采样越密，反之，空间采样越稀疏.
归一化相速度δ(ϕ, θ)的值越接近1，相速度数值频散越小；δ(ϕ, θ)＞1，相速度偏大，称为时间数值频散；δ(ϕ, θ)＜1，相速度偏小，称为空间数值频散.另外, δ(ϕ, θ)随地震波传播方向角ϕ和θ变化越小，数值各向异性越弱，反之，数值各向异性越强.相速度数值频散越小，数值各向异性越弱，则数值模拟精度越高；相反，相速度数值频散越大，数值各向异性越强，则数值模拟精度越低.
同样地，可导出三维CSD-FDM、TSD-FDM和MG-FDM(N=2, 3)的归一化相速度δ(ϕ, θ)的表达式.δ(ϕ, θ)是传播方向角ϕ和θ的函数，分析相速度频散特性时给出了8个传播角度(ϕ=π/2;θ=0, π/16, 2π/16, 3π/16, 4π/16)和(ϕ=π/12, 2π/12, 3π/12;θ=2π/16)的相速度频散曲线.
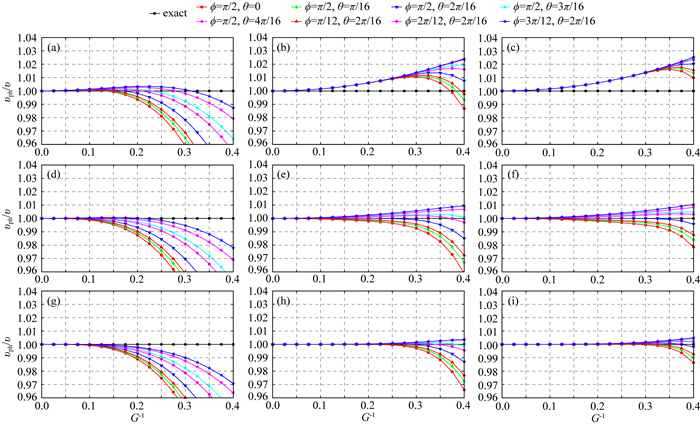
图 4给出了三维CSD-FDM(M=2, 6, 10)、TSD-FDM(M=2, 6, 10)和MG-FDM(M=2, 6, 10;N=1)的相速度频散曲线，Courant条件数r的取值均为r=0.3.分析对比相速度频散曲线特征，可以得出：
|
图 4 三维CSD-FDM、TSD-FDM和MG-FDM(N=1)的相速度频散曲线(r=0.3) (a)(b)(c) CSD-FDM(M=2, 6, 10); (d)(e)(f) TSD-FDM(M=2, 6, 10); (g)(h)(i) MG-FDM(M=2, 6, 10;N=1) Fig. 4 Phase velocity dispersion curves of 3D CSD-FDM, TSD-FDM and MG-FDM (N=1) with r=0.3 |
(1) 三维CSD-FDM(M=2)、TSD-FDM(M=2)和MG-FDM(M=2;N=1)的相速度频散特征相似，均具有明显的空间数值频散，模拟精度都很低.
(2) 三维CSD-FDM(M=6, 10)具有明显的时间数值频散；TSD-FDM(M=6, 10)的相速度频散曲线较发散，同时存在空间和时间数值频散，表现出明显的数值各向异性(数值频散特征随地震波的传播方向变化)；MG-FDM(M=6, 10;N=1)的相速度频散曲线收敛，数值各向异性明显减弱，数值频散幅值也明显减小.
综合(1)和(2)可以看出：相比三维CSD-FDM和TSD-FDM，M取值较小时(M=2左右)，MG-FDM在压制相速度数值频散方面无明显优势；M取值较大时(M≥6)，MG-FDM的相速度数值频散和数值各向异性均明显减小，因而具有更高的模拟精度.
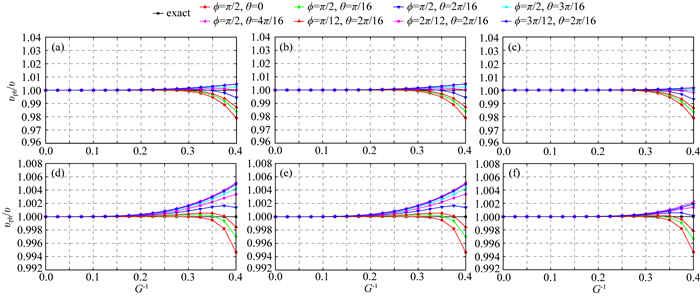
图 5给出了三维MG-FDM(M=8, 15;N=1, 2, 3)的相速度频散曲线(r=0.3).需要注意，图 5a、b、c和图 5d、e、f两组频散曲线具有不同的纵轴刻度.
|
图 5 三维MG-FDM的相速度频散曲线(r=0.3) (a)(b)(c) MG-FDM(M=8;N=1, 2, 3)；(d)(e)(f) MG-FDM(M=15;N=1, 2, 3). Fig. 5 Phase velocity dispersion curves of 3D MG-FDM with r=0.3 |
(1) 三维MG-FDM(M=8;N=1, 2, 3)的相速度数值频散特征基本相同；相比MG-FDM(M=15;N=1, 2)，MG-FDM(M=15;N=3)的相速度频散曲线更收敛，数值频散幅值和数值各向异性均明显减小.因此，三维标量波动方程数值模拟对精度要求较高时，建议采用MG-FDM(N=1)，且M取值为8左右；对模拟精度要求极其苛刻时，可采用MG-FDM(N=3)，且M取值为15左右；N取值大于4，同时M取值更大的三维MG-FDM因为数值计算量巨大，计算效率极低而很少采用.三维MG-FDM可根据模拟精度要求选择适当的M和N值.
(2) 三维MG-FDM(M=8;N=1, 2)的相速度数值频散特征基本相同，同样地，MG-FDM(M=15;N=1, 2)的相速度数值频散特征也基本相同，和三维MG-FDM(N=1, 2)的差分离散波动方程均具有4阶差分精度的结论一致(见表 1).
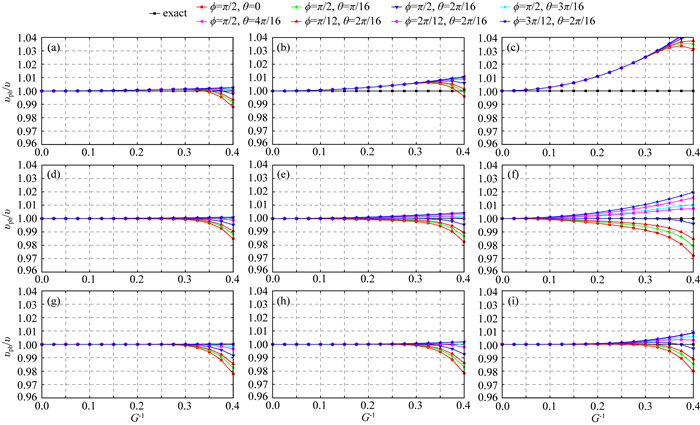
图 6给出了r取值分别为r=0.1, 0.2, 0.4时，三维CSD-FDM(M=10)，TSD-FDM(M=10)和MG-FDM(M=8;N=1)的相速度频散曲线. 根据r=υτ/h，空间采样间隔h保持不变时，r取值从0.1增大至0.2和0.4，相应的时间采样间隔τ将分别增大至2倍和4倍.
|
图 6 三维CSD-FDM(M=10)，TSD-FDM(M=10)和MG-FDM(M=8;N=1)的相速度频散曲线 (a)(b)(c) 分别为r=0.1, 0.2, 0.4时CSD-FDM(M=10)的相速度频散曲线；(d)(e)(f) 分别为r=0.1, 0.2, 0.4时TSD-FDM(M=10)的相速度频散曲线；(g)(h)(i) 分别为r=0.1, 0.2, 0.4时MG-FDM(M=8;N=1)的相速度频散曲线. Fig. 6 Phase velocity dispersion curves of 3D CSD-FDM (M=10), TSD-FDM (M=10) and MG-FDM (M=8; N=1) (a), (b) and (c) CSD-FDM (M=10) with r=0.1, 0.2, 0.4; (d), (e) and (f) TSD-FDM (M=10) with r=0.1, 0.2, 0.4; (g), (h) and (i) MG-FDM (M=8;N=1) with r=0.1, 0.2, 0.4. |
(1) r取值为0.1，三维CSD-FDM表现出轻微的时间频散，具有较高的模拟精度；r取值增大至0.2和0.4，时间频散显著增强，模拟精度低.
(2) r取值为0.1和0.2时，三维TSD-FDM的相速度频散曲线较收敛，表现出轻微的空间和时间频散，具有较高的模拟精度；r取值增大至0.4时，频散曲线严重发散，数值频散的幅值明显增大，数值各向异性显著增强，模拟精度低.
(3) 当r取值为0.1、0.2和0.4时，三维MG-FDM的相速度频散曲线收敛性均较好，数值频散微弱，模拟精度高.
综合可知，三维MG-FDM(M=8;N=1)可以比CSD-FDM(M=10)和TSD-FDM(M=10)取更大的r值(速度模型υ和空间采样间隔h相同时，r取值越大等价于时间采样间隔τ越大)，同时数值频散大小基本相当.因此，MG-FDM(M=8;N=1)能采用较大的时间采样间隔以提高计算效率，同时保持较高的模拟精度.
3.2 稳定性分析有限差分法通过迭代求解差分离散波动方程模拟地震波的传播过程，必须确保迭代过程稳定.根据式(16)可得出：
|
(27) |
取空间波数kx=ky=kz=π/h，并且0≤1-cos(ωτ)≤2，则可得到：
|
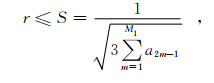
(28) |
其中，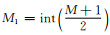
图 7给出了三维CSD-FDM、TSD-FDM和MG-FDM(N=1, 2, 3)的稳定性曲线，描述了稳定性条件约束下的最大r取值随M的变化关系.稳定性条件约束前提下，r取值越小，稳定性越弱；相反，r取值越大，稳定性越强.分析图中的稳定性曲线可以看出：
|
图 7 三维CSD-FDM，TSD-FDM和MG-FDM(N=1, 2, 3) 的稳定性曲线 Fig. 7 Stability curves of 3D CSD-FDM, TSD-FDM and MG-FDM (N=1, 2, 3) |
(1) M的取值增大，三维CSD-FDM、TSD-FDM和MG-FDM(N=1, 2, 3)的稳定性均下降.
(2) N的取值增大，MG-FDM的稳定性增强，但差分离散波动方程的差分精度相同时，稳定性基本相同，MG-FDM(N=1, 2)的差分离散波动方程均为4阶差分精度，稳定性基本一致.
(3) 三维CSD-FDM的稳定性最弱，TSD-FDM的稳定性明显增强，MG-FDM(N=1, 2, 3)的稳定性进一步增强.MG-FDM(N=1, 2, 3)的强稳定性为数值模拟采用更大的时间采样进而提高计算效率奠定了基础.
4 计算效率分析计算效率是衡量有限差分格式优劣的另一项重要指标.图 6中的相速度频散曲线表明，三维CSD-FDM和TSD-FDM均可采用较小的时间采样间隔来减小数值频散，以获得较高的模拟精度，但计算量会显著增加.MG-FDM的相速度频散曲线收敛性好，模拟精度高，稳定性强，可采用更大的时间采样间隔以提高计算效率，同时保持较高的模拟精度.
下面以三维CSD-FDM(M=10)、TSD-FDM(M=10)和MG-FDM(M=8;N=1)为例分析三种差分格式具有基本相同的模拟精度条件下的计算效率.这三种差分格式均包含61个网格点，单次时间迭代的浮点运算量基本相同，模拟时间长度相等时，计算效率之比约等于时间采样间隔之比.
分析图 6中的相速度频散曲线，可以认为CSD-FDM(M=10)取r=0.1，TSD-FDM(M=10)取r=0.2和MG-FDM(M=8;N=1)取r=0.4基本能保持同样高的模拟精度.根据r=vτ/h, 在速度v和空间采样间隔h保持不变的条件下，时间采样间隔τ之比等价于r之比.此分析表明，模拟精度基本相当的前提下，TSD-FDM可采用2倍于CSD-FDM的时间采样间隔，MG-FDM可采用4倍于CSD-FDM的时间采样间隔.因此，TSD-FDM的计算效率是CSD-FDM的2倍；MG-FDM的计算效率是CSD-FDM的4倍，是TSD-FDM的2倍.表 2列出了模拟精度基本相当时，三种差分格式采用的时间采样间隔和理论加速比.
|
|
表 2 三维CSD-FDM、TSD-FDM和MG-FDM三种差分格式的计算效率分析 Table 2 Analysis of computational efficiency for 3D CSD-FDM, TSD-FDM and MG-FDM |
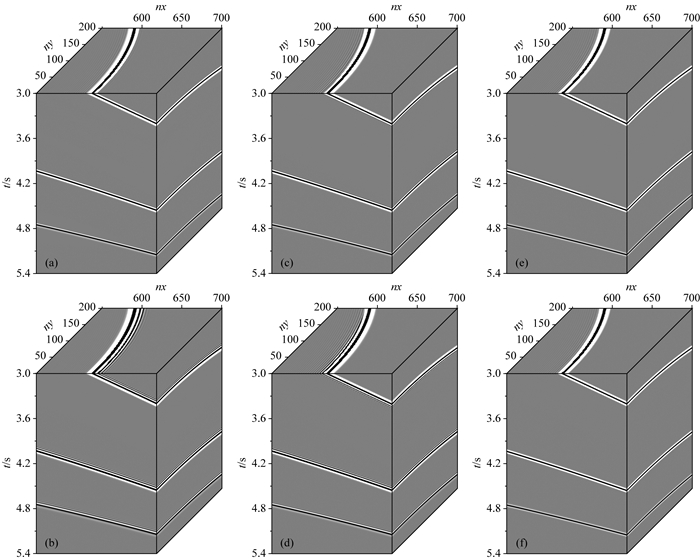
图 8a给出了一个8 km×3 km×6 km的三层模型：v1=2000 m·s-1, h1=3.0 km; v2=2450 m·s-1, h2=1.2 km; v3=2680 m·s-1, h3=1.8 km.空间采样间隔Δx=Δy=Δz=h=10 m，模型网格数为nx×ny×nz=801×301×601，主频25 Hz的Ricker子波作为震源，位于网格点(51, 21, 3).三维CSD-FDM(M=10)、TSD-FDM(M=10)和MG-FDM(M=8;N=1)分别采用不同的时间采样间隔进行数值模拟.图 8b给出了MG-FDM(M=8;N=1)采用时间采样间隔τ=1.5 ms进行数值模拟得到的炮集，为了便于对比分析，图 9给出了三维CSD-FDM(M=10)采用时间采样间隔τ=0.5 ms(图 9a)和τ=1.0 ms(图 9b)，TSD-FDM(M=10)采用τ=1.0 ms(图 9c)和τ=1.5 ms(图 9d)，MG-FDM(M=8;N=1)采用τ=1.0 ms(图 9e)和τ=1.5 ms(图 9f)进行数值模拟得到的局部炮集，局部区域范围由坐标标出.
|
图 8 三维层状速度模型及数值模拟炮集 (a) 层状速度模型；(b) MG-FDM(M=8;N=1)数值模拟炮集，时间采样间隔τ=1.5 ms. Fig. 8 3D layered velocity model and numerical modeling seismogram (a) 3D layered velocity model; (b) Numerical modeling seismogram using MG-FDM(M=8;N=1) with τ=1.5 ms. |
|
图 9 三维层状介质模型数值模拟的局部炮集 (a)(b) CSD-FDM(M=10), 时间采样间隔τ=0.5 ms和τ=1.0 ms; (c)(d) TSD-FDM(M=10), 时间采样间隔τ=1.0 ms和τ=1.5 ms; (e)(f) MG-FDM(M=8;N=1), 时间采样间隔τ=1.0 ms和τ=1.5 ms. Fig. 9 Local parts of the numerical modeling seismograms on 3D layered model (a) and (b) CSD-FDM(M=10) with τ=0.5 ms and τ=1.0 ms; (c) and (d) TSD-FDM(M=10) with τ=1.0 ms and τ=1.5 ms; (e) and (f) MG-FDM(M=8;N=1) with τ=1.0 ms and τ=1.5 ms. |
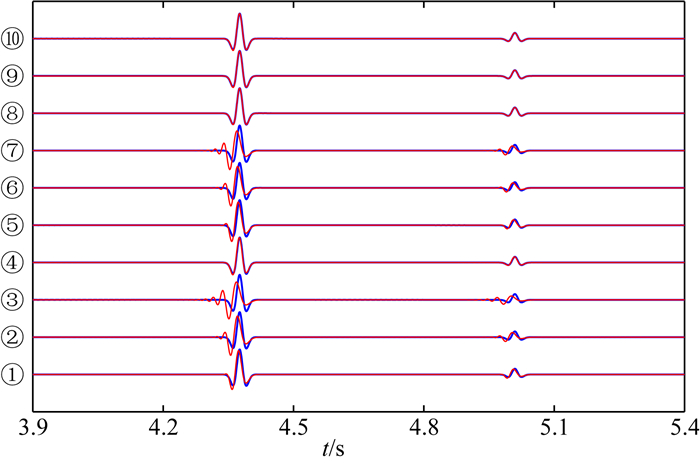
图 10给出了三维CSD-FDM(M=10)采用τ=0.5 ms, 0.75 ms, 1.0 ms，TSD-FDM(M=10)采用τ=0.5 ms, 1.0 ms, 1.25 ms, 1.5 ms和MG-FDM(M=8;N=1)采用τ=1.0 ms, 1.25 ms, 1.5 ms进行数值模拟得到的单道波形图，检波器位于网格点(650, 3, 3).
|
图 10 三维层状介质模型数值模拟单道波形对比图 检波器位于(650, 3, 3)，蓝色为参考波形, CSD-FDM(M=10)采用极小时间采样间隔τ=0.1 ms得到；红色为不同差分格式模拟波形. ①②③分别为CSD-FDM(M=10), 时间采样间隔τ=0.5 ms, 0.75 ms, 1.0 ms；④⑤⑥⑦分别为TSD-FDM(M=10)，时间采样间隔τ=0.5 ms, 1.0 ms, 1.25 ms, 1.5 ms; ⑧⑨⑩分别为M2M+N-FD(M=8;N=1), 时间采样间隔τ=1.0 ms, 1.25 ms, 1.5 ms. Fig. 10 Comparison of numerical modeling single trace waveforms on 3D layered model The geophone is located at (650, 3, 3), and the blue line is the reference waveform which is obtained by CSD-FDM (M=10) with a very small time sampling interval τ=0.1 ms; The red lines are the modeling waveform with different FD schemes. ①②③CSD-FDM(M=10) with τ=0.5 ms, 0.75 ms, 1.0 ms; ④⑤⑥⑦TSD-FDM(M=10) with τ=0.5 ms, 1.0 ms, 1.25 ms, 1.5 ms; ⑧⑨⑩ M2M+N-FD(M=8; N=1) with τ=1.0 ms, 1.25 ms, 1.5 ms. |
从图 9和图 10可以看出：CSD-FDM采用时间采样间隔τ=0.5 ms，未出现明显数值频散，采用τ=0.75 ms, 1.0 ms，出现明显的时间频散；TSD-FDM采用τ=0.5 ms, 1.0 ms，未出现明显的数值频散，采用τ=1.25 ms, 1.5 ms，出现较明显的数值频散；MG-FDM采用τ=1.0 ms和τ=1.5 ms，均未出现明显的数值频散.表 3给出了层状介质模型单炮模拟时，三种差分格式采用不同时间采样间隔的计算机耗时和加速比，数值模拟均采用Inter Xeon CPU E5-2670处理器.
|
|
表 3 三维层状介质模型CSD-FDM、TSD-FDM和MG-FDM数值模拟计算效率对比 Table 3 Comparison of computational efficiency for numerical modeling on 3D layered model with CSD-FDM, TSD-FDM and MG-FDM |
层状模型数值模拟结果表明：确保不出现明显数值频散，实现高精度数值模拟，MG-FDM(M=8;N=1)可达到CSD-FDM(M=10)的计算效率的3.31倍，可达到TSD-FDM(M=10)的计算效率的1.5倍.
5.2 盐丘模型
图 11a给出了利用公式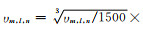
|
图 11 修改的三维SEG/EAGE盐丘速度模型及数值模拟炮集 (a) 三维盐丘速度模型；(b) MG-FDM(M=8;N=1)数值模拟炮集，时间采样间隔τ=1.5 ms，顶部显示了3.0 s时刻的切片. Fig. 11 Revised 3D SEG/EAGE salt model and numerical modeling seismogram (a) Revised 3D SEG/EAGE salt model; (b) Numerical modeling seismogram using MG-FDM(M=8;N=1) with τ=1.5 ms. The top shows the slice at 3.0 s. |
图 11b给出了MG-FDM(M=8;N=1)采用时间采样间隔τ=1.5 ms进行数值模拟得到的炮集，同样为了分析对比方便，图 12仅给出三种差分格式数值模拟的两个局部炮集.图 12a、b给出了CSD-FDM采用时间采样间隔τ=1.0 ms，图 12c、d给出TSD-FDM采用τ=1.25 ms，图 12e、f给出MG-FDM采用τ=1.5 ms进行数值模拟得到的两个局部炮集.图 13给出了CSD-FDM采用τ=0.5 ms, 1.0 ms，TSD-FDM(M=10)采用τ=1.0 ms, 1.25 ms和MG-FDM采用τ=1.25 ms, 1.5 ms的两个单道波形记录，两个检波器分别位于网格点(3, 650, 3)和(560, 650, 3).
|
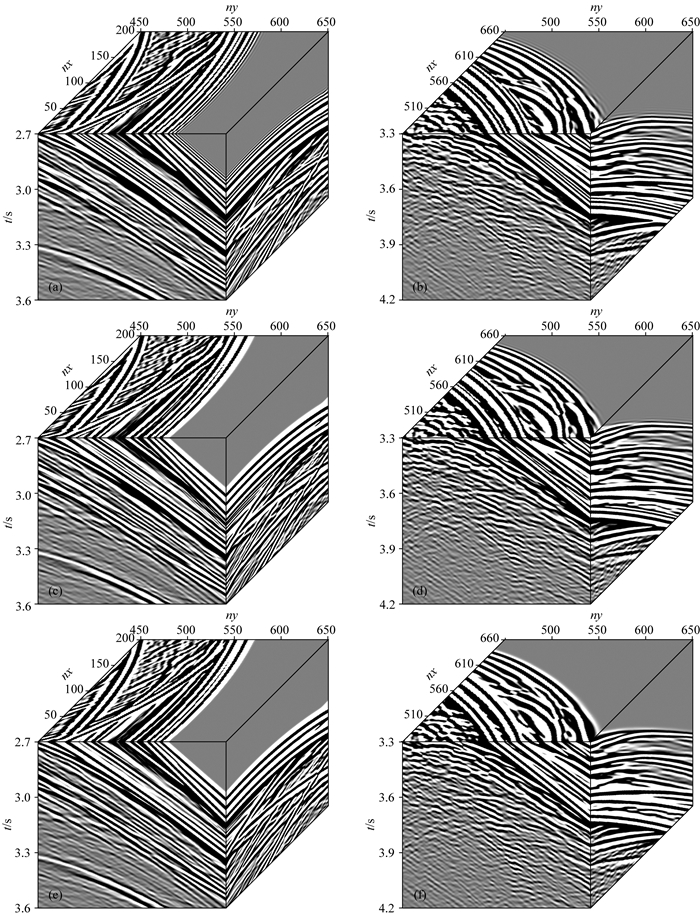
图 12 修改的三维SEG/EAGE盐丘模型数值模拟的两个局部炮集 (a)(b) CSD-FDM(M=10), 时间采样间隔τ=1.0 ms; (c)(d) TSD-FDM(M=10), 时间采样间隔τ=1.25 ms; (e)(f) MG-FDM(M=8;N=1), 时间采样间隔τ=1.5 ms. Fig. 12 Two local parts of the numerical modeling seismogram on the revised 3D SEG/EAGE salt model (a) and (b) CSD-FDM(M=10) with τ=1.0 ms; (c) and (d) TSD-FDM(M=10) with τ=1.25 ms; (e) and (f) MG-FDM(M=8;N=1) with τ=1.5 ms. |
从图 12和图 13可以看出：CSD-FDM采用τ=1.0 ms，表现出明显的时间数值频散；TSD-FDM采用τ=1.25 ms，表现出较明显的数值频散；MG-FDM采用τ=1.5 ms，未出现明显的数值频散.表 4给出了盐丘模型单炮模拟时，三种差分格式采用不同时间采样间隔的计算机耗时和加速比.
|
图 13 修改的三维SEG/EAGE盐丘模型数值模拟单道波形对比图 (a)(b)检波器分别位于(3, 650, 3)和(560, 650, 3)，蓝色为参考波形, CSD-FDM(M=10)采用极小时间采样间隔τ=0.1 ms得到；红色为不同差分格式模拟波形. ①②分别为CSD-FDM(M=10), 时间采样间隔τ=0.5 ms, 1.0 ms；③④分别为TSD-FDM(M=10)，时间采样间隔τ=1.0 ms, 1.25 ms; ⑤⑥分别为M2M+N-FD(M=8;N=1), 时间采样间隔τ=1.25 ms, 1.5 ms. Fig. 13 Numerical modeling single trace waveform on the revised 3D SEG/EAGE salt model (a) and (b) Geophone at (3, 650, 3) and (560, 650, 3). ① and ② CSD-FDM(M=10) with τ=0.5 ms, 1.0 ms; ③ and ④ TSD- FDM(M=10) with τ=1.0 ms, 1.25 ms; ⑤and ⑥ M2M+N-FD(M=8;N=1) with τ=1.25 ms, 1.5 ms. |
|
|
表 4 修改的三维SEG/EAGE盐丘模型CSD-FDM、TSD-FDM和MG-FDM数值模拟计算效率对比 Table 4 Comparison of computational efficiency for numerical modeling on revised 3D SEG/EAGE Salt model with CSD-FDM, TSD-FDM and MG-FDM |
盐丘模型数值模拟结果表明，三维MG-FDM(M=8;N=1)能采用更大的时间采样间隔以提高计算效率，同时能更有效地减小数值频散，获得更高的模拟精度.
6 结论与讨论本文提出了一种面向三维标量波动方程数值模拟的混合网格有限差分方法(MG-FDM)，将三维Laplace微分算子近似表示为坐标轴网格点构建的M个Laplace差分算子和非坐标轴网格点构建的N个Laplace差分算子的加权平均，充分利用了与差分中心点距离更近的非坐标轴网点，有效减小数值频散和数值各向异性，获得更高的模拟精度.通过对比分析，得出以下结论：
(1) 三维CSD-FDM的空间差分算子(Laplace差分算子)虽然能达到2M阶差分精度，但其差分离散波动方程仅具有2阶差分精度；TSD-FDM的差分离散波动方程沿特定的48个传播方向可达到2M阶差分精度，但沿其他传播方向仅具有2阶差分精度；MG-FDM的差分离散波动方程沿任意传播方向可达到4阶、6阶、甚至任意偶数阶差分精度.
(2) 相比三维CSD-FDM和TSD-FDM，计算效率基本相同时，MG-FDM的数值频散压制效果更好，模拟精度更高；模拟精度基本相同时，MG-FDM可以采用更大的时间采样间隔以提高计算效率；稳定性分析表明，MG-FDM稳定性更强，为采用更大的时间采样间隔以提高计算效率奠定了基础.
(3) 数值模拟实例进一步证实了三维MG-FDM在模拟精度和计算效率方面的优越性，也验证了其普遍适用性.
但是，本文提出的三维MG-FDM也具有一定的局限性，推导过程隐含了三个方向的空间采样间隔相等，即MG-FDM要求采用立方体网格.适用于长方体网格的更具一般性的MG-FDM，有待进一步研究.
附录A 三维坐标系中非坐标轴网格点构建Laplace差分算子
图 2a中的12个绿色网格点为与差分中心点距离等于
|
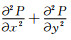
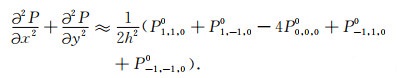
(A1) |
同样地，在坐标平面yOz和zOx内，可导出二维Laplace算子
|
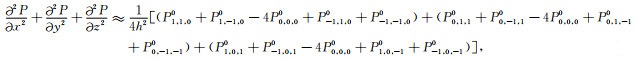
(A2) |
式(A2)给出了图 2a中12个坐标平面内的非坐标轴网格点构建三维Laplace差分算子的表达式.
图 2c中的24个绿色网格点为与差分中心点距离等于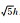
|
(A3) |
|
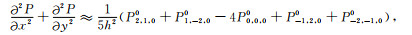
(A4) |
|
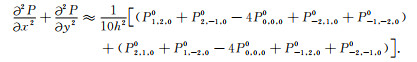
(A5) |
同样地，在坐标平面yOz和zOx内，可导出二维Laplace算子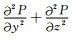
|
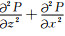
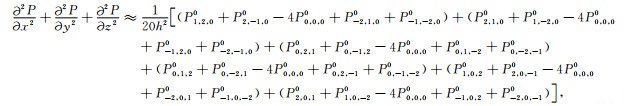
(A6) |
式(A6)给出了图 2c中24个坐标平面内的非坐标轴网格点构建三维Laplace差分算子的表达式.
图 2b中的8个绿色网格点为与差分中心点距离等于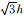
|
(A7) |
同样地，对其余7个网格点(P-1, -1, -10, P1, -1, 10, P-1, 1, -10, P-1, -1, 10, P1, 1, -10, P-1, 1, 10, P1, -1, -10)进行泰勒级数展开，可得到相应的泰勒级数展开表达式.8个网格点的泰勒级数展开表达式相加，可以得到：
|
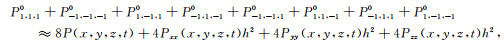
(A8) |
正文已经约定P0, 0, 00=P(x, y, z, t)，整理式(A8)可得到：
|
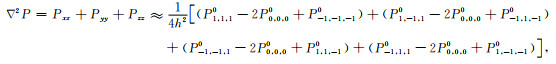
(A9) |
式(A9)给出了图 2b中8个坐标平面外的非坐标轴网格点构建三维Laplace差分算子的表达式.
附录B 三维MG-FDM(N=2, 3)的差分离散波动方程和差分系数通解图 3b中三维MG-FDM(N=2)的差分格式由图 1和图 2a、b中的差分格式组合构建，三维MG-FDM(N=2)的差分离散波动方程可表示为：
|
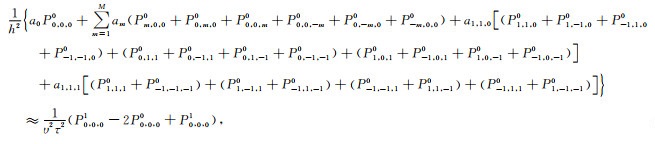
(B1) |
其中a0, a1, a2, …aM, a1, 1, 0, a1, 1, 1为差分系数，且满足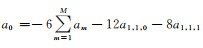
三维MG-FDM(N=2)的差分系数通解为：
|
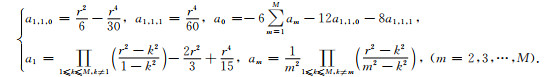
(B2) |
图 3c中三维MG-FDM(N=3)的差分格式由图 1和图 2a、b、c中的差分格式组合构建，三维MG-FDM(N=3)的差分离散波动方程可表示为：
|
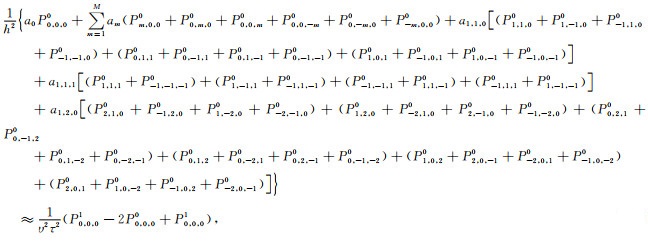
(B3) |
其中a0, a1, a2, …aM, a1, 1, 0, a1, 1, 1, a1, 2, 0为差分系数，且满足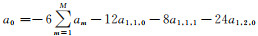
三维MG-FDM(N=3)的差分系数通解为：
|
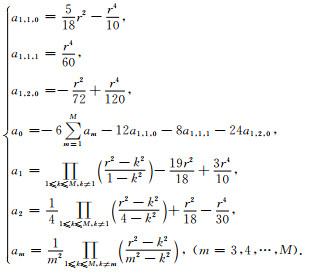
(B4) |
Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. DOI:10.1190/1.1440470 |
Alterman Z, Karal F C Jr. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of the Seismological Society of America, 58(1): 367-398. |
Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
Chen J B. 2007. High-order time discretizations in seismic modeling. Geophysics, 72(5): SM115-SM122. DOI:10.1190/1.2750424 |
Chen J B. 2011. A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation. Geophysics, 76(2): T37-T42. DOI:10.1190/1.3554626 |
Chen S C, Zhou H M. 2018. Least squares migration of seismic data with reflection wave equation. Chinese Journal of Geophysics (in Chinese), 61(4): 1413-1420. DOI:10.6038/cjg2018L0025 |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
Dong L G, Huang C, Chi B X, et al. 2015. Strategy and application of waveform inversion based on seismic data subset. Chinese Journal of Geophysics (in Chinese), 58(10): 3735-3745. DOI:10.6038/cjg20151024 |
Hu H S. 2018. Note on the Lamé constant and the reason for the presence of the shear modulus in the compressional wave speed formula. Progress in Geophysics (in Chinese), 33(1): 219-222. DOI:10.6038/pg2018BB0432 |
Hu Z D, He Z H, Liu W, et al. 2016. Scalar wave equation modeling using the mixed-grid finite-difference method in the time-space domain. Chinese Journal of Geophysics (in Chinese), 59(10): 3829-3846. DOI:10.6038/cjg20161027 |
Huang J P, Huang J Q, Li Z C, et al. 2016. Staggered grid pseudo-spectral numerical simulation of first-order quasi P-wave equation for TTI media. Oil Geophysical Prospecting (in Chinese), 51(3): 487-496, 415. DOI:10.13810/j.cnki.issn.1000-7210.2016.03.010 |
Jiang T, Fu L Y, Wang X J, et al. 2008. Target-oriented layout designing method based on wave equations. Progress in Geophysics (in Chinese), 23(02): 359-367. |
Jiang Z D, Fan C W, Li X Z, et al. 2021. Numerical simulation of marine ghost wave based on high order finite difference method with variable grids. Progress in Geophysics (in Chinese), 36(1): 365-373. DOI:10.6038/pg2021DD0485 |
Liang W Q, Yang C C, Wang Y F, et al. 2013. Acoustic wave equation modeling with new time-space domain finite difference operators. Chinese Journal of Geophysics (in Chinese), 56(10): 3497-3506. DOI:10.6038/cjg20131024 |
Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
Liu Y, Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
Liu Y, Sen M K. 2011a. 3D acoustic wave modelling with time-space domain dispersion-relation-based finite-difference schemes and hybrid absorbing boundary conditions. Exploration Geophysics, 42(3): 176-189. DOI:10.1071/EG11007 |
Liu Y, Sen M K. 2011b. Scalar Wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes. Bulletin of the Seismological Society of America, 101(1): 141-159. DOI:10.1785/0120100041 |
Liu Y, Sen M K. 2013. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation. Journal of Computational Physics, 232(1): 327-345. DOI:10.1016/j.jcp.2012.08.025 |
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. DOI:10.1190/1.1441689 |
Moczo P, Kristek J, Galis M, et al. 2010. On accuracy of the finite-difference and finite-element schemes with respect to P-wave to S-wave speed ratio. Geophysical Journal International, 182(1): 493-510. DOI:10.1111/j.1365-246X.2010.04639.x |
Moczo P, Kristek J, Galis M, et al. 2011. 3-D finite-difference, finite-element, discontinuous-Galerkin and spectral-element schemes analysed for their accuracy with respect to P-wave to S-wave speed ratio. Geophysical Journal International, 187(3): 1645-1667. DOI:10.1111/j.1365-246X.2011.05221.x |
Pi H M, Jiang X Y, Liu C, et al. 2009. Three methods of wave equation forward modeling and comparisons. Progress in Geophysics (in Chinese), 24(2): 391-397. DOI:10.3969/j.issn.1004-2903.2009.02.004 |
Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
Ren Z M, Li Z C. 2017. Temporal high-order staggered-grid finite-difference schemes for elastic wave propagation. Geophysics, 82(5): T207-T224. DOI:10.1190/geo2017-0005.1 |
Reshef M, Kosloff D, Edwards M, et al. 1988. Three-dimensional acoustic modeling by the Fourier method. Geophysics, 53(9): 1175-1183. DOI:10.1190/1.1442557 |
Tan S R, Huang L J. 2014a. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation. Geophysical Journal International, 197(2): 1250-1267. DOI:10.1093/gji/ggu077 |
Tan S R, Huang L J. 2014b. A staggered-grid finite-difference scheme optimized in the time-space domain for modeling scalar-wave propagation in geophysical problems. Journal of Computational Physics, 276: 613-634. DOI:10.1016/j.jcp.2014.07.044 |
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Virieux J, Calandra H, Plessix R É. 2011. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging. Geophysical Prospecting, 59(5): 794-813. DOI:10.1111/j.1365-2478.2011.00967.x |
Wang E J, Liu Y, Sen M K. 2016. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils. Geophysical Journal International, 206(3): 1933-1958. DOI:10.1093/gji/ggw250 |
Yan H Y, Liu Y. 2013. Acoutic prestack reverse time migration using the adaptive high-order finite-difference method in time-space domain. Chinese Journal of Geophysics (in Chinese), 56(3): 971-984. DOI:10.6038/cjg20130325 |
Yan H Y, Liu Y. 2013a. Acoustic VTI modeling and pre-stack reverse-time migration based on the time-space domain staggered-grid finite-difference method. Journal of Applied Geophysics, 90: 41-52. DOI:10.1016/j.jappgeo.2012.12.008 |
Yan H Y, Liu Y. 2013b. Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophysical Prospecting, 61(5): 941-954. DOI:10.1111/1365-2478.12046 |
Zhang B Q, Zhou H, Chen H M, et al. 2016. Time-space domainhigh-order finite-difference methods for seismic wave numerical simulation based on new stencils. Chinese Journal of Geophysics (in Chinese), 59(5): 1804-1814. DOI:10.6038/cjg20160523 |
Zhang J H, Yao Z X. 2012. Globally optimized finite-difference extrapolator for strongly VTI media. Geophysics, 77(4): T125-T135. DOI:10.1190/geo2011-0505.1 |
Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
Zhang Z Y, Hou W T, Miao Y K. 2017. Seismic wave simulation method based on variable grid step. Progress in Geophysics (in Chinese), 32(3): 1321-1330. DOI:10.6038/pg20170350 |
陈生昌, 周华敏. 2018. 地震数据的反射波动方程最小二乘偏移. 地球物理学报, 61(4): 1413-1420. DOI:10.6038/cjg2018L0025 |
董良国, 黄超, 迟本鑫, 等. 2015. 基于地震数据子集的波形反演思路、方法与应用. 地球物理学报, 58(10): 3735-3745. DOI:10.6038/cjg20151024 |
胡恒山. 2018. 拉梅常数的力学意义与剪切模量出现于纵波速度公式的原因. 地球物理学进展, 33(1): 219-222. DOI:10.6038/pg2018BB0432 |
胡自多, 贺振华, 刘威, 等. 2016. 旋转网格和常规网格混合的时空域声波有限差分正演. 地球物理学报, 59(10): 3829-3846. DOI:10.6038/cjg20161027 |
黄建平, 黄金强, 李振春, 等. 2016. TTI介质一阶qP波方程交错网格伪谱法正演模拟. 石油地球物理勘探, 51(3): 487-496, 415. DOI:10.13810/j.cnki.issn.1000-7210.2016.03.010 |
蒋韬, 符力耘, 碗学检, 等. 2008. 基于波动方程的目标导向观测系统设计方法研究. 地球物理学进展, 23(02): 359-367. |
姜占东, 范彩伟, 黎孝璋, 等. 2021. 基于变网格高阶有限差分的鬼波数值模拟研究. 地球物理学进展, 36(1): 365-373. DOI:10.6038/pg2021DD0485 |
梁文全, 杨长春, 王彦飞, 等. 2013. 用于声波方程数值模拟的时间-空间域有限差分系数确定新方法. 地球物理学报, 56(10): 3497-3506. DOI:10.6038/cjg20131024 |
皮红梅, 蒋先艺, 刘财, 等. 2009. 波动方程数值模拟的三种方法及对比. 地球物理学进展, 24(2): 391-397. DOI:10.3969/j.issn.1004-2903.2009.02.004 |
严红勇, 刘洋. 2013. 基于时空域自适应高阶有限差分的声波叠前逆时偏移. 地球物理学报, 56(3): 971-984. DOI:10.6038/cjg20130325 |
张保庆, 周辉, 陈汉明, 等. 2016. 基于新的差分结构的时-空域高阶有限差分波动方程数值模拟方法. 地球物理学报, 59(5): 1804-1814. DOI:10.6038/cjg20160523 |
张志禹, 侯文婷, 苗永康. 2017. 步长自适应的有限差分复杂地表波场数值模拟. 地球物理学进展, 32(3): 1321-1330. DOI:10.6038/pg20170350 |