在广义连续介质力学理论框架下，可以描述由介质内部微结构相互作用所导致的不均匀性(Zhu et al.，2020)，且介质内一点的应力不只与位移的一阶导数，即传统应变有关，还与位移的更高阶导数有关，这些更高阶的导数包含介质特征尺度，且与微结构相互作用有关(Askes et al.，2002；Askes and Gutiérrez，2006).Bonnell和Shao(2003)认为，考虑介质内微结构的长程相互作用(介质内一点的应力状态与整个介质中诸点的应力状态有关，本构关系是对空间积分的形式)以及考虑微结构相互作用时，经典连续介质力学理论会不适用.那是因为经典连续介质力学在给介质建模时，其假设组成介质的材料是均匀且连续分布的，没有涉及介质内部的微结构，而广义连续介质力学考虑介质内部结构、内部自由度以及内部尺度特征，可以得到力学特性是非对称的结论(赵亚溥，2016).实际上，介质的内部通常都具有极其复杂的微结构，这里的微结构是一个相对概念，对于金属介质，微结构的尺度一般在纳米量级(Trautt et al.，2012).而对于岩土介质，其微结构的尺度可以达到微毫米级甚至更高，一般指的是微夹杂/微裂缝/微孔隙/微孔洞(Ba ant，2002; Ba ant and Pang, 2007).考虑介质微结构相互作用，会使介质存在不均匀性，而这种不均匀性，则会引发新的响应.当存在剪切应变的强烈变形带时，即位移场/旋转场存在强烈空间变化时，这种由介质微结构相互作用所导致的不均匀性会愈加明显(Suiker et al.，2001).除此之外，当位移场/旋转场存在强烈时间变化时，即入射波尺度和微结构尺度愈加接近时，可以得到类似结论(Mindlin and Tiersten, 1962).

自Cosserat和Cosserat(1909)系统地建立了以考虑偶应力的作用为主要特征的连续介质模型之后，广义连续介质力学形成了多种纳入介质特征尺度的理论方法，以修正经典连续介质力学在处理考虑介质内微结构相互作用所引发的问题时的局限性，其中，应变梯度理论(Mindlin, 1964, 1965; Mindlin and Eshel, 1968；Altan and Aifantis, 1997；Ru and Aifantis, 1993；Aifantis, 1999, 2011；Askes et al.，2002；Li et al.，2015)是应用较为广泛的理论之一.应变梯度理论将位移场各阶梯度的所有分量纳入介质的应变能密度函数中，并结合介质特征尺度，以描述介质微结构相互作用所导致的不均匀性.应变梯度理论的提出可追溯至1964年，Mindlin(1964)基于Cosserat理论(Cosserat and Cosserat, 1909)提出了一个更加一般化的广义连续介质力学理论，把介质看成是由宏观物质和微观物质组成的协调变形连续体，由于该理论过于复杂，包含较多的介质特征尺度，因此，Mindlin(1965)，Mindlin和Eshel(1968)假设微观变形和宏观变形相等，分别将应变的一阶梯度以及二阶梯度引入介质的应变能密度函数，先后提出了一阶应变梯度理论和二阶应变梯度理论.为了进一步减少介质特征尺度的数量，以利于实验定量标定以及物理理解，Aifantis(1999)在本构关系中引入应变的拉普拉斯算子构建等效应力张量，提出仅含有一个介质特征尺度的应变梯度理论，且在该理论中没有定义应变梯度张量的功共轭量.Aifantis(2011)结合非局部理论，即一点的应力不仅与该点的应变有关，而且与该点一定邻域内各点的应变有关，提出非局部-梯度线弹性理论.在该理论中，如果不考虑非局部效应，非局部-梯度线弹性理论就退化为Aifantis应变梯度理论(Aifantis，1999).由于Aifantis应变梯度理论(Aifantis, 1999, 2011)是一个唯象理论(phenomenological theory)，不能清楚地表示介质特征尺度与微观结构的几何特征的联系(Askes et al.，2002)，Askes和Metrikine(2005)应用连续化方法，将小尺度下的离散不均匀介质转换为大尺度下的连续均匀介质，推导得到包含二阶应变梯度以及介质特征尺度的等效本构关系，其中，该理论中的介质特征尺度与颗粒中心的平均距离有关(假设介质为颗粒介质)(Suiker et al.，2001).

在地震勘探领域，对应变梯度理论的研究较少，缺少解析解和数值解的分析.相比于偶应力理论，由于应变梯度理论在应变能密度函数中引入了应变的二阶甚至二阶以上的高阶导数，可以描述更小尺度的微结构相互作用(偶应力理论只引入了旋转场的一阶导数)，在计算量增大的同时，也对引入的各种高阶量存在解释和实验验证困难的问题.单参数二阶应变梯度理论作为应变梯度理论的一种特例，提供了一种更加简单，灵活且易于理解的应变梯度理论(Askes and Gutiérrez，2006)，在该理论中，二阶应变梯度被视为应变能密度函数的附加影响.本文从非局部理论出发，推导单参数二阶应变梯度理论的本构方程，并基于该本构方程，结合几何方程和运动微分方程，推导得到包含独立自由项的非对称弹性波动方程.之后，应用该非对称弹性波动方程在各向同性均匀介质模型和Marmousi模型上进行数值模拟，合成地震记录.将该地震记录与传统弹性波动方程所生成的合成地震记录进行对比，研究分析应用二阶应变梯度描述介质微结构相互作用对地震记录的影响规律，为后续的介质特征尺度反演奠定理论基础.

Mindlin(1965)提出二阶应变梯度理论，将应变的一阶和二阶导数都纳入到介质的应变能密度函数中，以描述考虑介质内部微结构相互作用所导致的介质非均匀性.该理论比较复杂，介质特征尺度的数量较多，因此，Aifantis(1999)通过构建等效应力的方式提出了只含有一个介质特征尺度的二阶应变梯度理论，但该理论是一个唯象理论.Voyiadjis和Dorgan(2004)认为可以设置一个球形邻域，该邻域内各点的状态变量都可用n =0处的泰勒展开表示为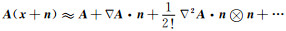, 并用该泰勒展开式替换非局部理论积分公式中的被积分项.我们基于Voyiadjis和Dorgan(2004)的思路，推导基于二阶应变梯度理论的非对称弹性波动方程.

非局部理论考虑了一点邻域内所有点的状态变量对该点的状态变量的加权影响.可用体积分公式表示为(Eringen，1972)：

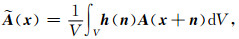
(1)

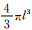
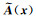
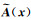
其中，V为邻域体积，一般为球形邻域，则V=，l为介质特征尺度.为一点的等效状态变量，A(x+n)为邻域内各点的状态变量.h(n)是服从归一化条件∫_Vh(n)dV=V的经验加权函数，该归一化条件确保当A(x+n)为常数时，=A(x+n).可以假设h(n)=1，则公式(1)变为公式(2)：

(2)

将A(x+n)使用泰勒展开，可近似表示为：

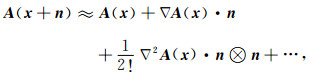
(3)

将公式(3)代入公式(2)，并将邻域积分用球体坐标r(0≤r≤l)，θ(0≤θ≤2π)，φ(0≤φ≤π)表示为：

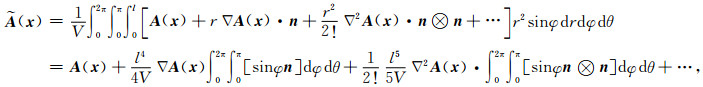
(4)

其中，n={sinφcosθ sinφsinθ cosφ}，为球面法线向量.

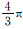
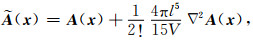
根据球面法线向量的定义，可以证明，所有涉及奇数梯度的项均为零. 同时，∫₀^2π∫₀^π[sinφn⊗n]dφdθ=，并只保留泰勒展开的二阶以下导数项，可得(Voyiadjis and Dorgan, 2004)：

(5)

将邻域体积代入式(5)可得：

(6)

公式(6)表明，邻域内任何一点的状态变量都受到邻域内其他点的影响，而且和介质特征尺度l有关，其本质上是一个等效状态变量.

我们可以令一点的状态变量A(x)为应变张量ε，等效状态变量为等效应变张量，可得：

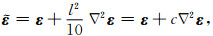
(7)

其中，c=l²/10，为二阶梯度张量的特征系数.

在弹性范围内，基于格林弹性和柯西弹性，可得本构方程的一般表达式为：

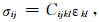
(8)

其中，σ_ij为应力张量，ε_kl为应变张量，C_ijkl为弹性系数张量.

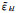
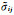
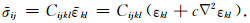
如果将公式(8)中的应变张量ε_kl替换为等效应变张量，则可得到等效应力张量的表达式为：

(9)

对于各向同性介质，公式(9)可进一步简化为

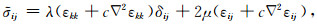
(10)

其中，λ, μ为Lame常数.

已知运动微分方程：

(11)

其中ρ为介质密度，ü_i为位移分量的二阶时间导数，F_i为体力分量，σ_{ji, j}为应力的一阶导数.

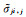
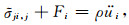
将公式(11)中应力的一阶导数σ_{ji, j}，替换为等效应力的一阶导数，则可得：

(12)

将几何方程，本构方程(公式(10))，代入运动微分方程(公式(12))可得：

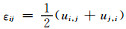
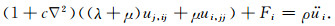
(13)

公式(13)即为基于二阶应变梯度理论的非对称弹性波动方程，当c=l²/10=0，即不考虑介质内微结构相互作用时，公式(13)即退化为传统弹性波动方程：

(14)

单参数二阶应变梯度理论推导的非对称弹性波动方程包含独立的自由项，以描述介质内微结构相互作用所导致的介质不均匀性所产生的响应.该响应与介质特征尺度l有关，而介质特征尺度l，可以表征介质内微孔缝隙结构的特征尺度，如果不考虑变形局部化问题、组成介质的颗粒几何形状以及应力集中效应等因素，其可为介质内微孔缝隙特征尺度.对于岩土介质来说，微孔缝隙特征尺度指的是岩土介质内部的微夹杂/微裂缝/微孔隙/微孔洞的尺度.具体地说，在微孔结构方面涉及多个长度尺度，例如平均颗粒直径、平均裂缝宽度、平均孔喉半径等.我们用孔缝隙特征尺度来表征平均颗粒直径，一般可以达到微毫米量级甚至更高.我们认为单参数二阶应变梯度理论可以描述更小尺度的微结构相互作用所导致的介质非均匀性，而这种更小尺度的非均匀性对地震记录的影响很小，但是，这种更小尺度的介质非均匀性可以影响纵波和横波的传播规律.另外，对地震记录的影响的大小与位移场的时间/空间变化的剧烈程度有关，即当入射波和微结构尺度越接近或者介质存在剪切带时(混凝土和岩石在围压作用下，重固结土在剪切作用下，或者金属在高速冲击下，皆可形成剪切带)，影响可增强.由于介质局部化变形带内具有很高的应变梯度影响，可以增强这种更小尺度的非均匀性对地震记录的影响，为了便于研究分析应用二阶应变梯度描述介质微结构相互作用对地震记录的影响规律，我们在之后的数值模拟时考虑了变形局部化、介质颗粒几何形状以及应力集中效应等因素的影响，即介质特征尺度l是一个综合参数，如果定义介质内微孔缝隙特征尺度为l_m，则介质特征尺度l可表示为l=γl_m，γ≥1.γ是考虑上述因素影响的加成系数，我们根据我国水利部、交通部联合制定的作为高速铁路路基填料的粗粒土的颗粒标准(0.075 mm＜d＜60 mm)，设置介质孔缝隙特征尺度，通过比较高铁实际数据与非对称弹性波动方程得到的合成数据之间的时频域特征，提取系数γ的值(王之洋等，2020)，另外，也可以通过实验获得(Roscoe，1970；Gudehus，1996；Huang et al.，2014；鲍亦兴和毛昭宙，1993).因此，公式(13)也可写为：

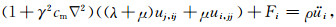
(15)

其中，c_m定义为二阶梯度张量的系数.

值得注意的是，考虑包括变形局部化等情况，可以增强这种由高阶应变梯度描述的介质微结构相互作用所导致的不均匀性响应，尽管在勘探领域，普遍存在这种情况，如果没有这种情况，本文所述的不均匀性响应虽然量级较小，但也是存在和可观测的.

综上，通过非局部理论推导的单参数二阶应变梯度理论可以通过定义一个受影响邻域，建立与介质内微结构几何特征的联系，本构关系是一个对空间积分的关系.一个很好的理解案例是，微裂缝/微孔隙都是成簇分布的，成簇的微裂缝变成成簇的中裂缝/中孔隙，进而中裂缝变成大裂缝/大孔隙，而这里说的有些裂缝/孔隙，是无法拿到实验室测量的，因为取了标本，就等于破坏了结构.

在这个部分，我们将应用推导的非对称弹性波动方程进行数值模拟，研究分析考虑微结构相互作用所导致的介质非均匀性对地震波传播的影响规律.

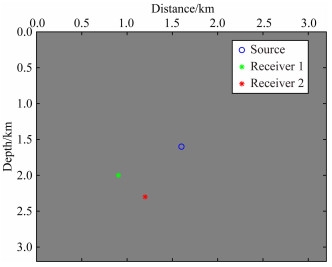
首先，在均匀各向同性介质模型上进行数值模拟. 构建的模型大小为nx=nz=401，网格间隔是dx=dz=8 m. 纵波速度和横波速度分别为2.0 km·s^-1和1.1547 km·s^-1，密度为2600 kg·m^-3.主频率为25 Hz的Ricker子波在模型的中心激发，时间步长设置为0.001 s，设置二阶梯度张量的系数c_m= 1000 μm²(即对应的介质微孔缝隙特征尺度为100 μm)，检波点设置在不同的两处，分别应用非对称弹性波动方程和传统弹性波动方程得到合成单道地震记录.图 1显示了炮点和检波器之间的相对位置关系.蓝点代表炮点位置，绿点和红点代表两个检波器的位置.

图 1

Fig. 1

图 1 炮点和检波器之间的相对位置关系 Fig. 1 The relative position relationships between shots and receivers

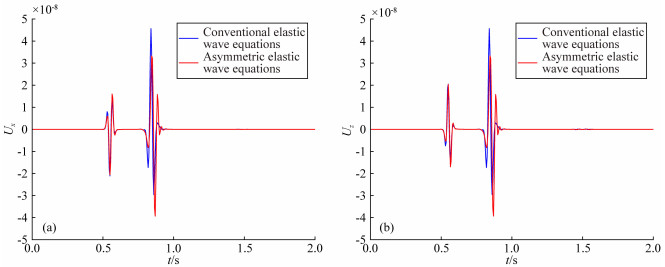
图 2和图 3分别为使用不同弹性波动方程在检波器1和检波器2的合成单道地震记录.从图 2和图 3可以看出，应用非对称弹性波动方程的数值模拟，其合成记录的x分量和z分量都出现了新的波场成分.考虑介质内微结构的相互作用，对横波的影响要明显大于纵波，横波记录出现了明显的新增信息，同时，振幅也出现了变化，甚至走时也发生了改变，而对于纵波，地震记录的变化要相对减弱很多.

图 2

Fig. 2

图 2 使用不同弹性波动方程在检波器1处的地震记录 (a) x分量；(b) z分量. Fig. 2 Shot records using different elastic wave equations at receiver 1 (a) x component; (b) z component.

图 3

Fig. 3

图 3 使用不同弹性波动方程在检波器2处的地震记录 (a) x分量；(b) z分量. Fig. 3 Shot records using different elastic wave equations at receiver 2 (a) x component; (b) z component.

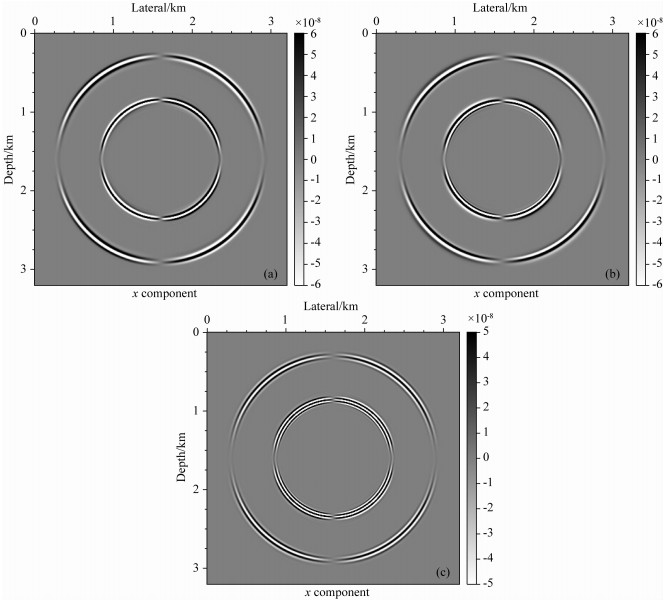
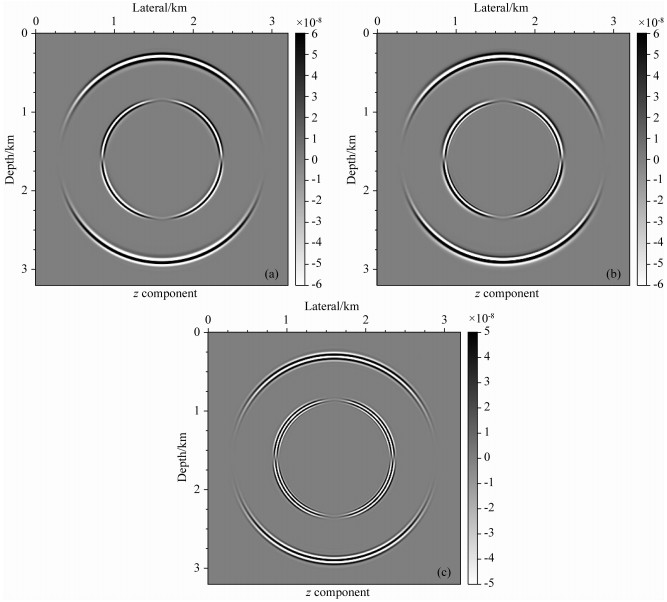
图 2和图 3是单道的地震记录分析，我们在图 4和图 5中进一步分析应用传统弹性波动方程和非对称弹性波动方程进行数值模拟所得到的波场快照x分量和z分量上的差异.从图 4和图 5可以发现，不论是x分量还是z分量，从波场快照中都是可以明显看到，非对称弹性波动方程引入应变的二阶导数和额外的介质特征尺度所描述的位移扰动对地震波传播产生的影响，即出现了新的波场成分.将图 4a和图 4b相减，可以更加清晰地观察到波场的变化，这种变化不仅体现在横波的传播上，也体现在纵波的传播上.对于图 5的波场快照z分量的分析，可以得到相同的结果.

图 4

Fig. 4

图 4 应用不同弹性波动方程得到的合成波场快照(x分量) (a) 传统弹性波动方程；(b) 非对称弹性波动方程；(c)(a)和(b)的差值. Fig. 4 Synthetic wavefield snapshots (x component) using different elastic wave equations (a) The conventional elastic wave equations; (b) The asymmetric elastic wave equations; (c) The difference between (a) and (b).

图 5

Fig. 5

图 5 应用不同弹性波动方程得到的合成波场快照(z分量) (a) 传统弹性波动方程；(b) 非对称弹性波动方程；(c)(a)和(b)的差值. Fig. 5 Synthetic wavefield snapshots (z component) using different elastic wave equations (a) The conventional elastic wave equations; (b) The asymmetric elastic wave equations; (c) The difference between (a) and (b).

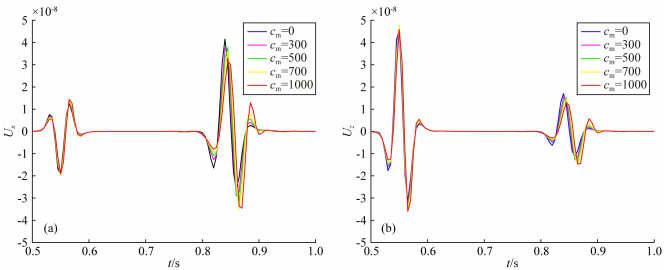
进一步，通过改变二阶梯度张量的系数c_m的数值，研究微结构相互作用所导致的不均匀性对地震记录的影响规律.依然提取点源脉冲响应的单道地震记录，检波点位于图 1中的红圈位置，即检波器2处.我们设置二阶梯度张量的系数c_m的数值分别为0 μm², 300 μm², 500 μm², 700 μm², 1000 μm²，对应的介质内微孔缝隙特征尺度分别为0 μm(不考虑介质微结构相互作用，非对称弹性波动方程退化为传统弹性波动方程)，55 μm，70 μm，100 μm.应用非对称弹性波动方程生成的单道地震记录，如图 6所示.图 6表明，设置不同的介质特征尺度，对地震记录的影响可以被清晰的观察到，无论是纵波还是横波，都出现了走时、相位和振幅的变化，而且这种变化随着介质特征尺度的数值增大而愈加明显.另外，不同介质特征尺度下，微结构相互作用所导致的介质不均匀性对横波的影响都要大于纵波.从图 6的分析也证明了，我们考虑微结构相互作用对地震波传播的影响是合理的.

图 6

Fig. 6

图 6 不同的二阶梯度张量的系数cm(单位：μm2)在检波器2处的地震记录 (a) x分量；(b) z分量. Fig. 6 Shot records with different coefficients of the second-order gradient tensors cm (unit: μm2)at receiver 2 (a) x component; (b) z component.

需要说明的是，为了能够更好的进行比较，我们全部采用高阶优化有限差分算子进行模拟，采用较厚的PML(Perfectly Matched Layer，完全匹配层)边界条件对边界问题进行处理，以排除数值频散和边界问题所带来的干扰.

之前的分析是基于均匀模型点源脉冲效应.为了在更复杂的模型上比较两种弹性波动方程进行数值模拟的差异，研究分析微结构相互作用效应，我们应用这两种弹性波动方程，在大小为767×751的Marmousi模型上进行数值模拟，其中网格间距为12 m×4 m.纵波速度与横波速度之比为v_p/v_s=1.7.主频率为25 Hz的Ricker子波在模型顶层的中心处激发，时间步长为0.0005 s，记录时长为5 s，同样设置二阶梯度张量的系数c_m=1000 μm².

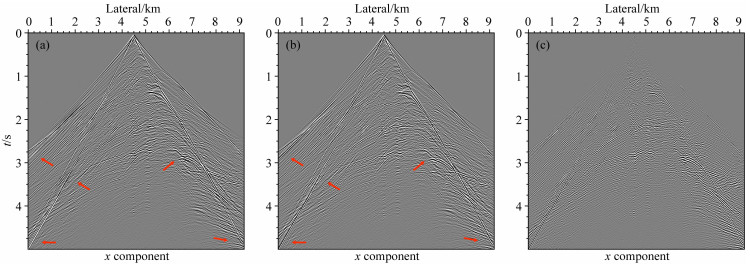
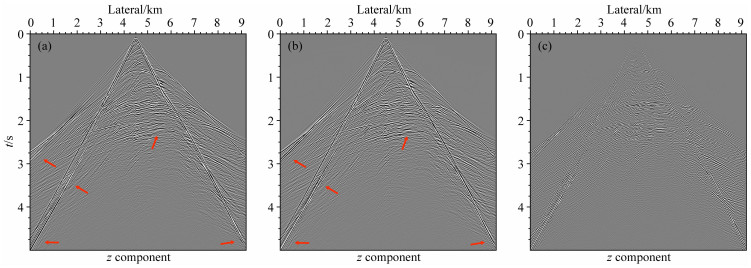
仍然采用优化20阶有限算子以及PML边界条件，以将数值频散和边界问题对结果的干扰降到一个较低的程度.图 7和图 8分别是应用传统弹性波动方程和非对称弹性波动方程对Marmousi模型进行数值模拟所得到的x分量和z分量的合成地震记录.图 7c是图 7a和图 7b相减之后的记录，图 8c是图 8a和图 8b相减之后的记录.我们注意到，即使在模型更为复杂的情况下，引入应变的二阶导数和额外的介质特征尺度所描述的微结构相互作用仍然十分明显，如图 7和图 8所示，相比于传统弹性波动方程生成的地震记录，使用非对称弹性波动方程生成的记录出现了明显的差异，如图中红色箭头标注区域所示.如图 7c和图 8c所示，我们可以从中清晰地看到，纵波、横波、面波的记录都出现了新的成分，这些新的成分是由于考虑了介质微结构相互作用所导致的不均匀性所产生的.

图 7

Fig. 7

图 7 在Marmousi模型上应用不同弹性波动方程得到的合成地震记录(x分量) (a) 传统弹性波动方程；(b) 非对称弹性波动方程；(c)(a)和(b)的差值. Fig. 7 Synthetic shot records (x component) for Marmousi model using different elastic wave equations (a) The conventional elastic wave equations; (b) The asymmetric elastic wave equations; (c) The difference between (a) and (b).

图 8

Fig. 8

图 8 在Marmousi模型上应用不同弹性波动方程得到的合成地震记录(z分量) (a) 传统弹性波动方程；(b) 非对称弹性波动方程；(c)(a)和(b)的差值. Fig. 8 Synthetic shot records (z component) for Marmousi model using different elastic wave equations (a) The conventional elastic wave equations; (b) The asymmetric elastic wave equations; (c) The difference between (a) and (b).

综上，不论是均匀介质模型还是复杂的Marmousi模型，应用非对称弹性波动方程进行数值模拟时，相比于传统弹性波动方程的数值模拟结果，合成地震记录都出现了变化，而这种变化又与介质特征尺度具有非常紧密的联系.考虑微结构相互作用所导致的不均匀性，在地震勘探频段，仍然可观察到这种由不均匀性所产生的响应.基于单参数二阶应变梯度理论所推导的非对称弹性波动方程在进行数值模拟时，可以反映更小尺度的不均匀性响应，该响应是可以考虑的.

介质微结构相互作用会使得介质存在不均匀性，引发新的响应，并且当位移场/旋转场存在强烈空间/时间变化时，这种不均匀性会更加明显.本文从非局部理论出发，推导了基于单参数二阶应变梯度理论的非对称弹性波动方程，引入应变的二阶导数项以描述更小尺度的微结构相互作用.分别应用非对称弹性波动方程和传统弹性波动方程在均匀模型和Marmousi模型上进行数值模拟，合成地震记录，通过对比分析发现，非对称弹性波动方程引入应变的二阶导数和额外的介质特征尺度，所描述的位移扰动对地震波传播产生了影响，且对横波的影响较大.同时，由于考虑了更小尺度的介质微结构相互作用，无论是在均匀模型还是复杂模型的数值模拟试验中，合成地震记录均出现了明显可辨识的新的成分，即介质更小尺度的微结构相互作用可以在地震记录中被反映出来，我们需要考虑其对地震波传播的影响.