2. 东北石油大学, 大庆 163318;
3. 中国科学院地质与地球物理研究所, 北京 100029;
4. 中国科学院地球科学研究院, 北京 100029;
5. 中国科学院油气资源研究院重点实验室, 北京 100029;
6. 中国科学院大学, 北京 100049
2. Northeast Petroleum University, Daqing 163318, China;
3. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
4. Innovation Academy for Earth Sciences, Chinese Academy of Sciences, Beijing 100029, China;
5. Key Laboratory of Petroleum Resource Research, Chinese Academy of Sciences, Beijing 100029, China;
6. Chinese Academy of Sciences, Beijing 100049, China
地震波正演模拟是地震勘探反演和成像的基础和关键,提高弹性波数值模拟的精度和效率具有非常重要的理论和工程意义.目前广泛运用于地震波数值模拟的方法主要是有限差分法(Chu and Stoffa, 2012;Di Bartolo et al., 2012;Yan et al., 2016;Yang et al., 2017;Liang et al., 2018;He et al., 2019;杜泽源等,2019;Miao et al., 2020),其适用于GPU并行计算,计算速度快并且易于编程实现.
应用有限差分算法进行弹性波数值模拟时,使用差分算子来代替微分算子,因而必然会产生数值误差,如果忽略这一误差,将会严重影响数值模拟的精度,导致弹性波数值模拟过程中出现数值频散问题(Chu and Stoffa, 2012;王之洋等,2015).为了解决差分算子频散问题,可以在数值模拟时选择主频较低的子波,较小的离散网格间距,或者优化差分算子.然而,随着子波主频的降低,高频成分缺失,由此也将导致地震反演和成像的分辨率大大降低;而减小离散网格的间距则会增加计算量,对于大模型来说,由此带来的计算量、存储量问题进一步制约勘探技术的发展(王之洋等,2015;He et al., 2019;刘立彬等,2020).优化差分算子,提高低阶数差分算子的精度,可以在不增加计算量,保证计算效率的同时,减小差分算子对微分算子的逼近误差,从而避免数值模拟过程中的数值计算误差,因此,优化有限差分算子在弹性波动方程的数值求解中具有非常重要的意义.
Chu和Stoffa(2012)指出,根据Taylor级数展开,可以使用二项式窗函数截断伪谱法的空间褶积序列推导得出有限差分算子,然而由于截断效应存在,频谱泄露不可避免,为了减弱频谱泄露,可以选择优化的窗函数.应用窗函数法优化有限差分算子,其主要目标是设计一种通带窄,阻带衰减大的窗函数,以尽可能的减弱截断所导致的频谱泄露(王之洋等,2015;Wang et al., 2017;Ren et al., 2018),然而,不可忽略的问题是,窗函数的通带宽度与阻带衰减是相互矛盾的,很难同时满足通带窄、阻带衰减大的要求.因此,另一种更常用的优化有限差分算子的方法是最优化方法(Liu,2013;Zhang and Yao, 2013;Yang et al., 2017;He et al., 2019;Miao and Zhang, 2020),通过构造包含有限差分系数的目标函数,将有限差分算子的优化问题转化为多参数优化问题,进而应用最优化算法进行优化求解.Zhang和Yao(2013)首次使用模拟退火算法优化有限差分算子.He等(2019)将Remez交换算法应用于常规网格和交错网格的有限差分算子优化.Miao和Zhang(2020)基于L1范数构造了包含有限差分系数的目标函数,并应用交替方向乘子算法(ADMM)获得了优化的有限差分算子.
应用最优化方法优化有限差分算子,其目标是在保证精度误差的同时,获得最大的谱覆盖范围(Liu,2013;Zhang and Yao, 2013;He et al., 2019),常规有限差分优化方法往往难以兼顾精度和谱覆盖范围两个方面,尤其是在高波数情况下,难以满足数值模拟精度的要求.因此,需要寻求一种更适用于高维多参数问题的快速收敛且易于跳出局部极值的高效优化算法.
启发式优化算法是目前广泛应用的一种优化算法(雷秀娟等,2012;Beheshti and Shamsuddin, 2013;Pillay,2016;Qu et al., 2015;Li et al., 2016;Hussain et al., 2018),不同于传统优化算法,启发式算法通过在解空间范围内随机搜索以获得最优结果,是一种基于概率计算的领域随机搜索算法,该类算法主要包括:模拟退火算法(SA),粒子群算法(PSO),遗传算法(GA),等等.相比于其他算法,PSO算法在迭代更新时利用了当前最优解的信息,从而可以更快收敛到最优解(Kennedy and Eberhart, 1995;Hazra and Sinha, 2011;Jadoun et al., 2015),然而,PSO算法的全局搜索能力对初始参数的要求较高,当初始参数随机性较大时,算法很容易陷入局部极值,尤其是对于一些参数维度较高的问题、多峰问题和病态问题,会出现过早收敛甚至难以收敛的问题.细菌觅食算法(BFO)是一种仿生类算法(Passino,2002;李珺等,2013;Daryabeigi and Dehkordi, 2014),其模拟大肠杆菌觅食行为,算法主体结构包括三层循环,分别对应趋化、复制、驱散三个步骤,具有较强的并行搜索能力,同时,驱散操作加强了搜索的随机性,从而有助于提高算法的全局搜索能力,然而,BFO算法包含三层循环嵌套,使得算法结构相对复杂,引入了较多参数,导致算法的收敛速度较慢.因此,结合PSO算法和BFO算法的思想,使其优势互补,提升性能,改进算法可以在快速收敛的同时搜索到全局最优解,以同时满足有限差分算子对精度和频谱覆盖范围的要求.
本文提出一种BFO-PSO算法下的有限差分优化方法,并采用优化的有限差分算子进行弹性波数值模拟.针对PSO算法全局搜索能力较弱的问题,引入BFO算法中的趋化、复制、驱散三个步骤,形成BFO-PSO混合优化算法;构造包含有限差分系数的目标函数,并运用BFO-PSO混合优化算法求取全局最优解,获得优化的有限差分算子,通过理论频散分析,比较优化性能;进而应用此优化的差分方法分别在层状介质模型和复杂模型上进行弹性波数值模拟,对比分析合成地震记录.
1 理论分析 1.1 BFO-PSO算法下的有限差分算子优化根据采样定理,连续信号f(x)的一阶空间导数可以表示为(Chu and Stoffa, 2012):
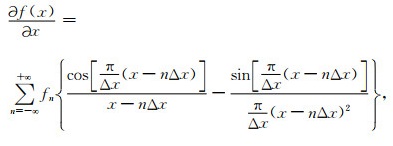
|
(1) |
其中,Δx为空间采样间隔,Δx/π为Nyquist波数,fn=f(nΔx).
将x=0代入公式(1)并截断,可推导得出一阶空间导数的有限差分算子:
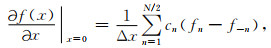
|
(2) |
其中,
对公式(2)左右两端同时应用Fourier变换,可推导出:
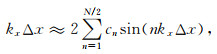
|
(3) |
其中,kx为波数.
根据公式(3),可得出有限差分算子的频散关系:
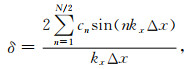
|
(4) |
式中,考虑波数趋于0的情况,满足:

|
进一步,应用最优化算法优化有限差分系数,可以构造目标函数为:
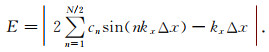
|
(5) |
根据公式(5)给出的目标函数,可以应用最优化算法搜索其全局最优解(目标函数的解即对应有限差分系数),从而得到优化的有限差分算子.综合比较多种优化算法,PSO算法对问题本身的依赖性较小,同时算法简单,易于并行实现,因此,本文选择PSO算法以优化差分系数.然而,PSO算法的全局搜索能力对初始参数的要求较高,当初始参数随机性较大时,算法很容易陷入局部极值,出现过早收敛甚至难以收敛的问题.对于低阶差分算子,其很难满足谱覆盖范围的要求;而对于高阶差分算子,由于目标函数维度较高,应用该算法很难得到较好的结果.
因此,本文结合BFO算法的全局寻优能力,将BFO算法的趋化、复制、驱散三个步骤引入PSO算法中的粒子速度和位置更新策略,以形成BFO-PSO混合优化算法,进一步应用BFO-PSO算法对包含有限差分系数的目标函数(公式(5))进行求解,从而得到精度误差较小且频谱覆盖范围较大的有限差分算子.
PSO算法是一种基于概率计算的领域随机搜索算法,种群中的每一个粒子都代表目标函数的一组解,在该算法中,每个粒子都以随机的方式向当前最优粒子的方向移动,从而使得整个种群向最优解的方向运动,进而实现在目标函数解空间范围内以随机搜索的方式求解最优解.常规PSO算法的粒子速度和位置更新策略如下:

|
(6) |
其中,xij(t)表示第t次迭代时第i个粒子在第j维的位置,vij(t)表示第t次迭代时第i个粒子在第j维的更新速度,ω为惯性系数,c1、c2为学习因子,r1、r2为取值为0~1的随机因子.pbestij(t)表示第i个粒子在前t次迭代中的历史局部最优位置,gbestj(t)当前种群最优粒子位置.
为了克服PSO算法对初始参数的高度依赖性以及难以跳出局部极值的缺陷,本文在PSO算法的粒子速度和位置更新方式中增加BFO算法的趋化、复制、驱散三种步骤,以提高算法在邻域搜索时的随机性,形成BFO-PSO混合优化算法,从而提高PSO算法的全局搜索能力,降低算法对初始参数的依赖性,同时进一步提高算法的收敛速度.
首先引入趋化步骤,在粒子速度和位置更新过程中,粒子种群向着全局最优解的方向运动,但是,对于一些参数维度较高的问题、多峰问题和病态问题,粒子种群很容易趋向局部最优,从而导致算法全局搜索能力较差.为了避免这一问题,在粒子位置更新时增加随机方向性,使粒子随机地向一个方向运动或者翻转,从而增加粒子种群在全局范围内的搜索随机性,使其具有跳出局部最优的能力,增加算法收敛到全局最优解的概率.引入趋化步骤的粒子位置更新公式为:
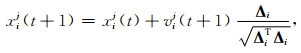
|
(7) |
其中,
其次是复制步骤,将BFO算法中细菌优胜劣汰的繁殖过程引入到PSO算法粒子速度和位置更新策略中,对种群中的每个粒子计算适应度值,并根据目标函数要求按照从优到劣的顺序对其排序,并将排序在末尾的一半种群粒子淘汰,而将剩余的种群粒子进行完全复制,使得种群大小不变.通过这一步骤,可以保证粒子种群在每一次迭代更新时都向着部分较优解的方向运动,从而有效提高粒子种群向最优解方向移动的速度,提高算法的收敛速度.
最后是驱散步骤,为了进一步放置粒子种群过早的收敛到局部最优位置,避免种群粒子聚集在局部极值位置处,按照一定的概率将种群粒子随机移动到解空间中的新区域,以此提高算法在邻域内搜索的随机性,从而增加粒子种群的随机性,避免种群过早的收敛到局部极值,提高全局搜索能力.
根据上述分析,将BFO算法的趋化、复制、驱散三种步骤引入PSO算法,改进PSO算法的粒子速度和位置更新策略,形成BFO-PSO混合优化算法,算法流程图如图 1所示.
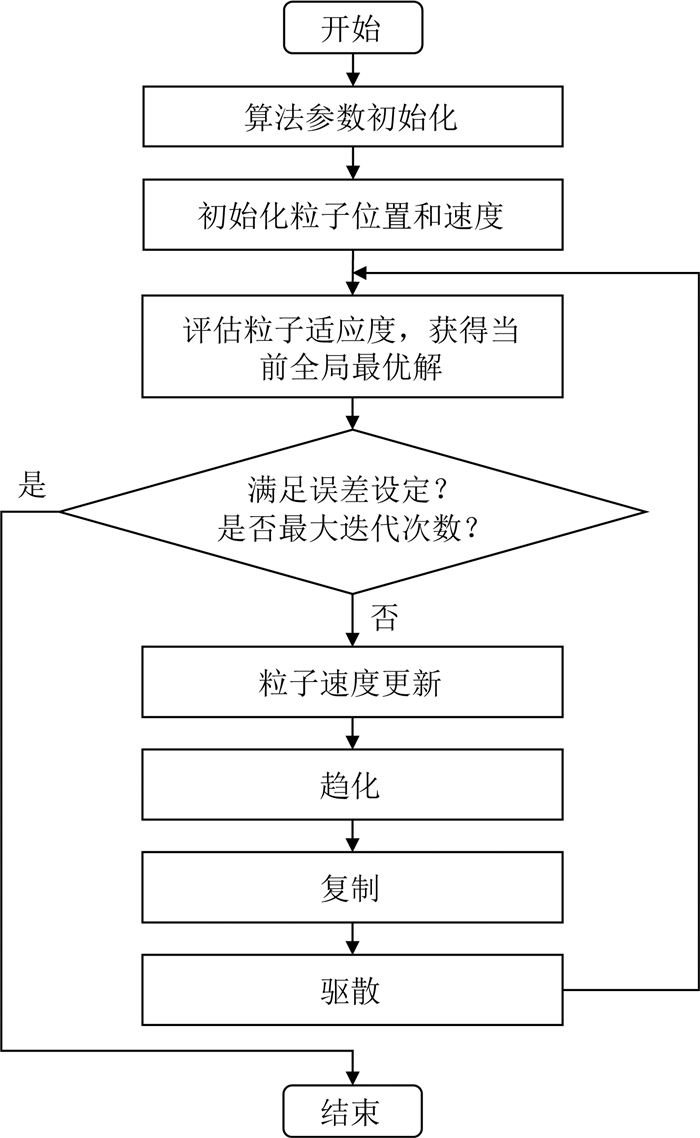
|
图 1 BFO-PSO算法流程图 Fig. 1 Flowchart of the BFO-PSO algorithm |
根据公式(3)所示有限差分算子的频散关系式,分析比较BFO-PSO算法,PSO算法以及Remez交换算法(He et al., 2019)下的优化有限差分算子的数值频散曲线,比较其精度误差.
分别应用BFO-PSO算法和PSO算法对包含有限差分系数的目标函数(公式(5))进行优化求解,以获得BFO-PSO算法下的优化有限差分算子.本文中,BFO-PSO算法和PSO算法的初始参数设定如下:粒子位置表示有限差分系数,并进行随机初始化;粒子速度表示有限差分系数的调整方向;种群大小为N=300,最大迭代次数为T=1500,权重系数为ω=0.7,粒子驱散概率为0.25.
如图 2、3所示,分别为BFO-PSO算法和PSO算法优化得到的一阶空间导数有限差分算子的数值频散曲线,其中,图 2应用BFO-PSO算法,图 3应用PSO算法,图中黑色实线表示不同阶数下常规有限差分算子的数值频散曲线.对比分析,可以明显看出,采用BFO-PSO算法得到的优化有限差分算子在保证精度误差的同时,其频谱覆盖范围远大于常规有限差分算子.8阶BFO-PSO算法优化的有限差分算子的频散曲线甚至接近16阶常规有限差分算子的频散曲线,两者的频谱覆盖范围几乎一致,而12阶BFO-PSO算法优化的有限差分算子的频散曲线则远远优于20阶常规有限差分算子的频散曲线,在12阶时就可以满足高波数的精度要求.
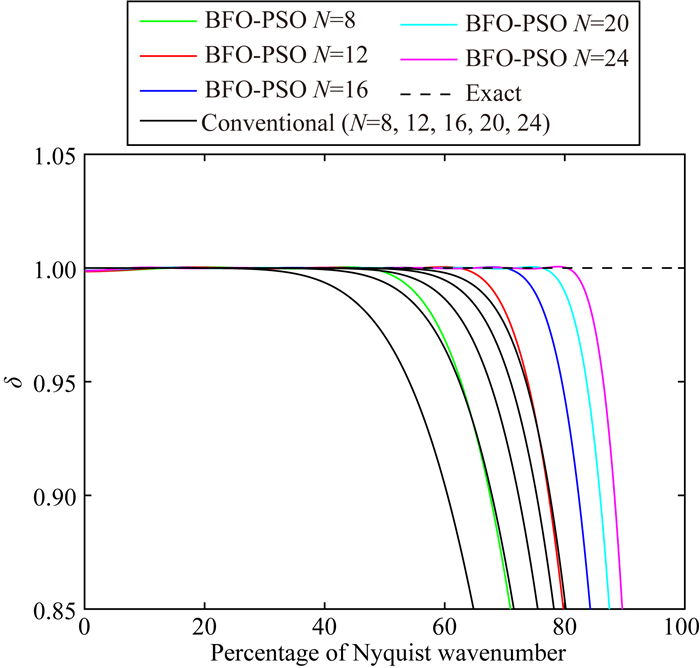
|
图 2 不同阶数的BFO-PSO算法下的优化有限差分算子的频散曲线 Fig. 2 Dispersion curves of the optimized FD operator based on the BFO-PSO algorithm for different values of N (different orders) |

|
图 3 不同阶数的PSO算法下的优化有限差分算子的频散曲线 Fig. 3 Dispersion curves of the optimized FD operator based on the PSO algorithm for different values of N (different orders) |
进一步分析比较BFO-PSO混合优化算法的全局搜索能力和收敛速度,图 4给出了BFO-PSO算法与PSO算法优化获得的有限差分算子的数值频散曲线对比.可以看出,在8阶、12阶、16阶、20阶的情况下,BFO-PSO算法和PSO算法优化得到的有限差分算子,其数值频散曲线几乎完全一致,即两种优化算法得到的有限差分算子是一致的.然而,当差分算子的阶数继续增加到24阶时,应用BFO-PSO算法得到的优化有限差分算子在保持精度误差不变的同时,具有更大的频谱覆盖范围.基于这一分析,可以说明,引入趋化、复制、驱散三种步骤后形成的BFO-PSO混合优化算法很好的结合了PSO算法的快速收敛性和BFO算法的全局搜索能力,对于多参数优化问题,BFO-PSO混合优化算法可以快速收敛到较好的全局最优解,就本文而言,应用BFO-PSO算法可以很快的获得精度误差小且适应高波数情况的优化有限差分算子.

|
图 4 BFO-PSO算法与PSO算法优化的有限差分算子的频散曲线对比 Fig. 4 Comparison of numerical dispersion curves between optimized FD operator based on the BFO-PSO algorithm and the PSO algorithm |
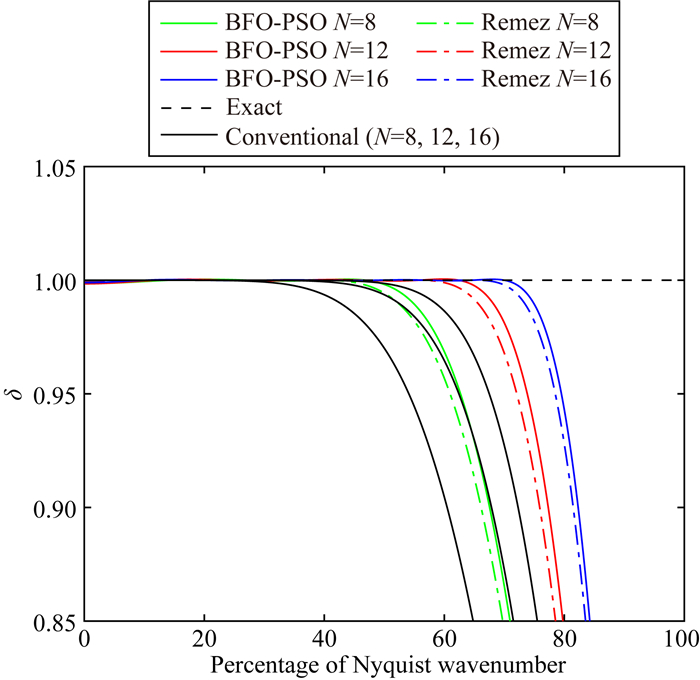
图 5为分别应用BFO-PSO算法和Remez交换算法得到的优化有限差分算子的数值频散曲线对比,其中,彩色实线分别对应不同阶数的BFO-PSO算法优化的有限差分算子的频散曲线,彩色虚线分别对应不同阶数的基于Remez交换算法的有限差分算子的频散曲线.对比可得,在保证精度误差控制在一定范围内的同时,BFO-PSO算法优化后的有限差分算子具有更大的频谱覆盖范围,更适用于高波数情况下的数值模拟.表 1列出了应用BFO-PSO算法得到的优化有限差分算子的系数.
|
图 5 BFO-PSO算法与Remez交换算法(He et al., 2019)优化的有限差分算子的频散曲线对比 Fig. 5 Comparison of numerical dispersion curves between the optimized FD operator based on the BFO-PSO algorithm and the Remez algorithm (He et al., 2019) |
|
|
表 1 BFO-PSO算法下的优化有限差分算子系数 Table 1 Optimized FD coefficients based on the BFO-PSO algorithm |
应用有限差分法进行数值模拟时,差分格式的稳定性是一个非常重要的问题.这里假定空间步长均匀,即Δx=Δz,介质最大波速为v,时间步长为Δt,给出常规网格一阶有限差分算子的简单稳定性条件(Lines et al., 1999):
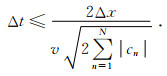
|
(8) |
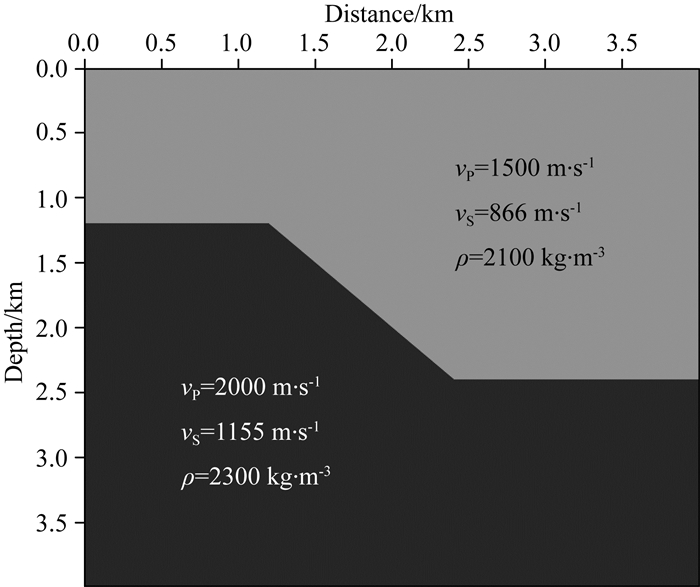
首先在应用BFO-PSO算法优化的有限差分算子在各向同性双层介质模型上进行弹性波数值模拟测试,模型示意图如图 6所示,模型上下两层的纵波速度、横波速度、密度分别在图中标出,模型宽和高均为4000 m,空间步长设置为Δx=Δz=8 m,时间采样间隔为Δt=0.0005 s.震源坐标为(2000 m, 1000 m),采用主频为25 Hz的Ricker子波.
|
图 6 双层介质模型 Fig. 6 Double-layer velocity model |
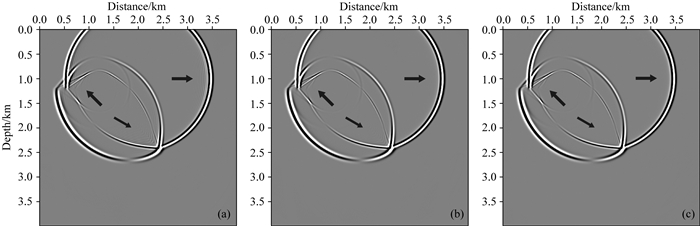
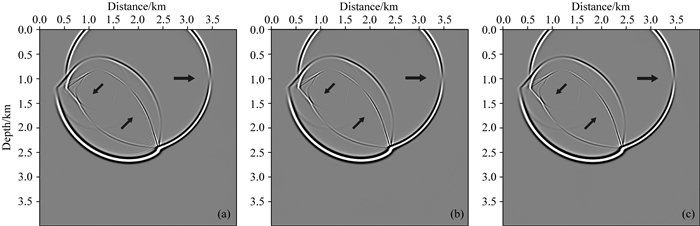
图 7和图 8为分别应用BFO-PSO算法优化得到的有限差分算子和常规有限差分算子进行弹性波数值模拟所得到的合成波场快照的X分量和Z分量,其中,图 7a和图 8a应用8阶常规有限差分算子,图 7b和图 8b应用BFO-PSO算法优化得到的8阶有限差分算子,图 7c和图 8c应用16阶常规有限差分算子.对比分析发现,应用8阶常规有限差分算子获得的合成波场快照,无论是X分量还是Z分量,均存在明显的数值频散现象,如图中黑色箭头指示.而应用BFO-PSO算法优化得到的有限差分算子进行弹性波数值模拟,所获得合成波场快照中几乎没有数值频散,数值模拟的精度甚至达到了16阶常规差分算子的效果.因此,采用BFO-PSO算法可以有效的提高有限差分算子的精度和效率,优化获得的低阶有限差分算子在逼近微分算子时就具有较小的数值误差,进而可以在不增加计算量,保证计算效率的同时,达到常规高阶有限差分算子的精度,满足高精度数值模拟的要求,有效提高弹性波数值模拟的精度和效率.
|
图 7 应用不同有限差分算子得到的合成波场快照(X分量) (a) 8阶常规有限差分算子;(b) 8阶BFO-PSO算法优化的有限差分算子;(c) 16阶常规有限差分算子. Fig. 7 Synthetic wavefield snapshots (X component) using different FD operators (a) Eighth-order conventional FD operator; (b) Eighth-order FD operator optimized based on the BFO-PSO algorithm; (c) Sixteenth-order conventional FD operator. |
|
图 8 应用不同有限差分算子得到的合成波场快照(Z分量) (a) 8阶常规有限差分算子;(b) 8阶BFO-PSO算法优化的有限差分算子;(c) 16阶常规有限差分算子. Fig. 8 Synthetic wavefield snapshots (Z component) using different FD operators (a) Eighth-order conventional FD operator; (b) Eighth-order FD operator optimized based on the BFO-PSO algorithm; (c) Sixteenth-order conventional FD operator. |
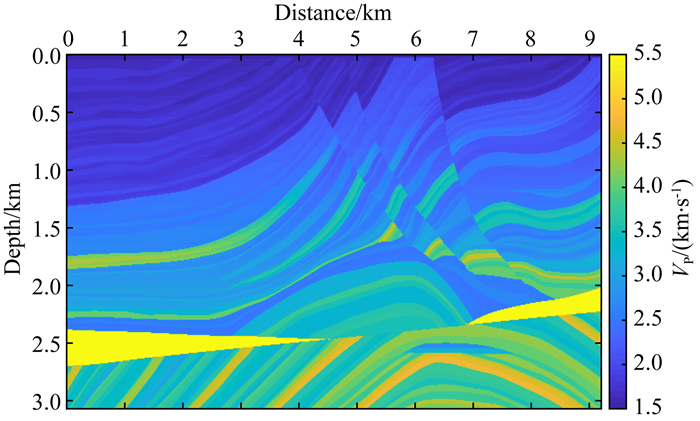
之后,我们在较为复杂的Marmousi模型上进行弹性波数值模拟,以进一步对比分析BFO-PSO算法优化得到的有限差分算子在压制数值频散、提升弹性波数值模拟效率方面的性能.如图 9所示,为Marmousi纵波速度模型,在本文数值模拟实验中,模型横波速度和纵波速度的比值为vP/vS=1.7,密度设置为ρ=2000 kg·m-3.模型空间离散网格大小设置767×376,空间步长设置为Δx=12 m, Δz=8 m,时间采样间隔为Δt=0.001 s,记录时长为t=5 s.震源坐标为(4600 m, 1 m),采用主频为25 Hz的Ricker子波.
|
图 9 Marmousi模型 Fig. 9 Marmousi model |
图 10为分别应用BFO-PSO算法优化得到的有限差分算子和常规有限差分算子在Marmousi模型上进行弹性波数值模拟所得到的合成地震记录.其中,图 10a、b、c分别为应用8阶常规有限差分算子、8阶BFO-PSO算法优化得到的有限差分算子、16阶常规有限差分算子得到的合成地震记录,图 10d、e分别为区块1和2的放大记录.根据合成地震记录的对比分析,可以发现,应用BFO-PSO算法优化的有限差分算子得到的地震记录具有更好的精度和效果,几乎与16阶常规有限差分算子的精度一致,而8阶常规算子得到的地震记录上则可以清晰看到数值频散存在.因此,通过在层状介质模型和复杂的Marmousi模型上进行的弹性波数值模拟测试,可以充分说明,BFO-PSO算法优化得到的有限差分算子具有较高的精度,可以有效压制用差分算子替代微分算子时导致的数值频散,优化后的低阶差分算子就可以达到常规高阶算子的精度,从而可以有效提高对弹性波动方程求取数值解时的计算效率,降低对于计算资源的要求.

|
图 10 在Marmousi模型应用不同有限差分算子进行弹性波数值模拟得到的合成地震记录(Z分量) (a) 8阶常规有限差分算子;(b) 8阶BFO-PSO算法优化的有限差分算子;(c) 16阶常规有限差分算子;(d) 区块1放大记录;(e) 区块2放大记录.图(d)、(e)中,左边为8阶常规有限差分算子,中间为8阶BFO-PSO算法优化的有限差分算子,右边为16阶常规有限差分算子. Fig. 10 Synthetic shot records (Z component) obtained by numerical modelling of elastic waves using different FD operators on Marmousi model (a) Eighth-order conventional FD operator; (b) Eighth-order FD operator optimized based on the BFO-PSO algorithm; (c) Sixteenth-order conventional FD operator; (d) Zoomed view of block 1; (e) Zoomed view of block 2. In (d) and (e), the left is eighth-order conventional FD operator; middle is eighth-order FD operator based on the BFO-PSO algorithm; and right is sixteenth-order conventional FD operator. |
本文提出一种BFO-PSO算法下的有限差分算子优化方法,并应用此优化的有限差分算子分别在层状介质模型和复杂模型上进行弹性波数值模拟,对比分析合成地震记录.首先,针对PSO算法对初始参数依赖性大及算法易于陷入局部极值的缺点,引入BFO算法的趋化、复制、驱散三种步骤,以改进PSO算法的粒子速度和位置更新策略,形成BFO-PSO混合优化算法.其次,构造包含有限差分系数的目标函数,并应用BFO-PSO混合优化算法求取最优解,获得优化的有限差分算子,根据理论频散曲线分析,BFO-PSO算法可以在快速收敛的同时获得较好的全局最优解,对于低阶差分算子,在保证精度误差的同时,有效扩大了频谱覆盖范围,满足弹性波数值模拟对高波数的要求;对于高阶差分算子,BFO-PSO算法优化得到的差分系数精度更好,即BFO-PSO算法更适用于复杂的多参数优化问题.最后,应用BFO-PSO算法优化后的有限差分算子进行弹性波数值模拟,对比分析合成波场快照及合成地震记录,进一步验证了BFO-PSO混合优化算法获得的优化有限差分算子在压制数值频散方面的有效性,降低了弹性波动方程数值求解的误差,提高数值模拟的精度和效率.
Beheshti Z, Shamsuddin S M H. 2013. A review of population-based meta-heuristic algorithm. International Journal of Advances in Soft Computing and its Applications, 5(1): 1-35. |
Chu C L, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics, 77(3): W17-W26. DOI:10.1190/geo2011-0336.1 |
Daryabeigi E, Dehkordi B M. 2014. Smart bacterial foraging algorithm based controller for speed control of switched reluctance motor drives. International Journal of Electrical Power & Energy Systems, 62: 364-373. |
Di Bartolo L, Dors C, Mansur W J. 2012. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation. Geophysics, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
Du Z Y, Wu G C, Li Y S. 2019. Three-dimensional elastic wave forward modeling in orthorhombic media based on least squares. Progress in Geophysics (in Chinese), 34(1): 69-79. DOI:10.6038/pg2019BB0566 |
Hazra J, Sinha A K. 2011. A multi-objective optimal power flow using particle swarm optimization. European Transactions on Electrical Power, 21(1): 1028-1045. DOI:10.1002/etep.494 |
He Z, Zhang J H, Yao Z X. 2019. Determining the optimal coefficients of the explicit finite-difference scheme using the Remez exchange algorithm. Geophysics, 84(3): S137-S147. DOI:10.1190/geo2018-0446.1 |
Hussain K, Salleh M N M, Cheng S, et al. 2018. Metaheuristic research: a comprehensive survey. Artificial Intelligence Review, 52(4): 2191-2233. |
Jadoun V K, Gupta N, Niazi K R, et al. 2015. Modulated particle swarm optimization for economic emission dispatch. International Journal of Electrical Power & Energy Systems, 73: 80-88. |
Kennedy J, Eberhart R. 1995. Particle swarm optimization.//Proceedings of ICNN′95-International Conference on Neural Networks. Perth, WA, Australia: IEEE, 4: 1942-1948.
|
Lei X J. 2012. Swarm Intelligent Optimization Algorithms and Their Applications (in Chinese). Beijing: Science Press.
|
Li J, Dang J W, Bu F. 2013. Research and improvment of bacteria foraging optimization algorithm. Computer Simulation (in Chinese), 30(4): 344-347, 415. |
Li M D, Zhao H, Weng X W, et al. 2016. A novel nature-inspired algorithm for optimization: Virus colony search. Advances in Engineering Software, 92: 65-88. DOI:10.1016/j.advengsoft.2015.11.004 |
Liang W Q, Wu X, Wang Y F, et al. 2018. A new staggered grid finite difference scheme optimised in the space domain for the first order acoustic wave equation. Exploration Geophysics, 49(6): 898-905. DOI:10.1071/EG17088 |
Lines L R, Slawinski R, Bording R P. 1999. A recipe for stability of finite-difference wave-equation computations. Geophysics, 64(3): 967-969. DOI:10.1190/1.1444605 |
Liu L B, Duan P R, Zhang Y Y, et al. 2020. Overview of mesh-free method of seismic forward numerical simulation. Progress in Geophysics (in Chinese), 35(5): 1815-1825. DOI:10.6038/pg2020DD0117 |
Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
Miao Z Z, Zhang J H. 2020. Reducing error accumulation of optimized finite-difference scheme using the minimum norm. Geophysics, 85(5): T275-T291. DOI:10.1190/geo2019-0758.1 |
Passino K M. 2002. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine, 22(3): 52-67. DOI:10.1109/MCS.2002.1004010 |
Pillay N. 2016. A review of hyper-heuristics for educational timetabling. Annals of Operations Research, 239(1): 3-38. DOI:10.1007/s10479-014-1688-1 |
Qu R, Pham N, Bai R B, et al. 2015. Hybridising heuristics within an estimation distribution algorithm for examination timetabling. Applied Intelligence, 42(4): 679-693. DOI:10.1007/s10489-014-0615-0 |
Ren Y J, Huang J P, Yong P, et al. 2018. Optimized staggered-grid finite-difference operators using window functions. Applied Geophysics, 15(2): 253-260. DOI:10.1007/s11770-018-0668-7 |
Wang J, Meng X H, Liu H, et al. 2017. Cosine-modulated window function-based staggered-grid finite-difference forward modeling. Applied Geophysics, 14(1): 115-124. DOI:10.1007/s11770-017-0596-y |
Wang Z Y, Liu H, Tang X D, et al. 2015. Optimized finite-difference operators based on Chebyshev auto-convolution combined window function. Chinese Journal of Geophysics (in Chinese), 58(2): 628-642. DOI:10.6038/cjg20150224 |
Yan H Y, Yang L, Li X Y. 2016. Optimal staggered-grid finite-difference schemes by combining Taylor-series expansion and sampling approximation for wave equation modeling. Journal of Computational Physics, 326: 913-930. DOI:10.1016/j.jcp.2016.09.019 |
Yang L, Yan H Y, Liu H. 2017. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm. Geophysics, 82(1): T27-T42. DOI:10.1190/geo2016-0171.1 |
Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
杜泽源, 吴国忱, 李雨生. 2019. 基于最小二乘的三维正交介质弹性波高精度正演模拟. 地球物理学进展, 34(1): 69-79. DOI:10.6038/pg2019BB0566 |
雷秀娟. 2012. 群智能优化算法及其应用. 北京: 科学出版社.
|
李珺, 党建武, 卜锋. 2013. 细菌觅食优化算法的研究与改进. 计算机仿真, 30(4): 344-347, 415. DOI:10.3969/j.issn.1006-9348.2013.04.078 |
刘立彬, 段沛然, 张云银, 等. 2020. 基于无网格的地震波场数值模拟方法综述. 地球物理学进展, 35(5): 1815-1825. DOI:10.6038/pg2020DD0117 |
王之洋, 刘洪, 唐祥德, 等. 2015. 基于Chebyshev自褶积组合窗的有限差分算子优化方法. 地球物理学报, 58(2): 628-642. DOI:10.6038/cjg20150224 |
 2021, Vol. 64
2021, Vol. 64


