2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
2. MOE Key Laboratory of Geospatial Environment and Geodesy, Wuhan University, Wuhan 430079, China
水下潜航器隐蔽性好、机动能力强,广泛应用于现代军事领域.其中潜艇作为一种大型的潜航器具有强大的威慑力和战斗力,成为各个国家重点发展的战略武器装备.潜艇的发展促使各国对反潜作战的高度重视(Angevine, 2005;刘腾, 2019;魏征等, 2019).反潜的前提是搜索定位潜艇即探潜,传统探潜手段主要采用声纳探测.随着潜艇隐身技术的不断进步,不管是主动声纳探测还是被动声纳探测的能力都被大幅削弱,雷达探测、磁探测、光学探测和尾迹探测等非声学探测技术受到欧美国家关注且取得了重要进展(方尔正等, 2020).
重力场信号反映了物质的空间分布特征,特别是重力梯度对密度异常反应灵敏,可用于水下目标的探测(Wu et al., 2013;胡敏章等, 2014).潜航器水下运行时一般处于中性浮力状态,其总质量等于排开水的质量,如果质量分布均匀则不会产生重力异常.实际上,潜航器的质量分布并不均匀,下半部分质量一般要大于上半部分质量,必然产生重力异常(Lanzagorta et al., 2015).重力异常信号无法隐藏或屏蔽,而且重力探测是被动式的无源探测手段,不易被发现,因此,重力探测是一种具有发展潜力的非声学探潜技术(孙岚等, 2010).
重力探潜的概念在20世纪60年代就已提出,但是受仪器观测精度所限,相关的研究进展较慢.随着重力测量仪器精度的不断提升,近年来这一领域又重新受到关注(Wu et al., 2010, 2013;Lanzagorta et al., 2015).其中,一类研究着重于利用重力和重力梯度探测与定位水下目标的反演算法(Wu and Tian, 2010; Wu et al., 2013;Tang et al., 2017, 2018).另一类是模拟研究潜艇引起的重力场信号的量级和分布特征,分析重力探潜的可行性.孙岚等将均质旋转椭球面作为潜艇的数学模型分析了垂直重力梯度沿三个轴线方向的变化特征(孙岚等, 2010),该模型将全部质量均匀分布在椭球面上.张志强等人采用头部为半球面、中段为圆柱面和尾部为圆锥面的三段式潜艇模型,并假设浮心高于重心1 m使得模型的下半部面密度大于上半部面密度,模拟计算了潜艇的垂直重力梯度,进而分析了航空重力梯度探潜的可行性(Zhang et al., 2018; 张志强等, 2019).由于难以明确潜艇真实的质量分布,只能借助几何模型进行模拟分析,前述研究都采用规则形状的几何质面模型,需要通过数值积分来计算其相应的重力和重力梯度,通用性和方便性较差.为此,本文根据潜航器特点提出一种引力偶极子模型,以简化潜航器异常重力场的计算和分析,并对重力探潜的仪器精度和平台稳定性需求进行探讨.
1 引力偶极子模型潜航器因用途不同具有不同的外形,难以用统一的几何模型来分析各类潜航器的重力场特征.但是为了航行安全,潜航器需进行质量均衡调整以保证满足水下平衡条件:重力等于浮力且重心低于浮心,以及纵倾(纵轴方向)和横倾(左右舷)引力偶极矩为零(苏玉民等, 2005).水下悬浮状态时潜航器总质量等于排开水的质量,净质量为零,故可以将其看作一个上半部为负质量、下半部为正质量的垂直引力偶极子.偶极子在引力问题中应用较少,因为实际没有负的质量,但是在磁场研究中,偶极子有许多重要的应用(王亶文, 2005;尹刚等, 2016),也有研究利用磁偶极子模型探讨探潜问题(杨日杰等, 2014).鉴于引力偶极子的相关文献较少,本节将推导偶极子引力场的相关公式,并分析其空间分布特征.
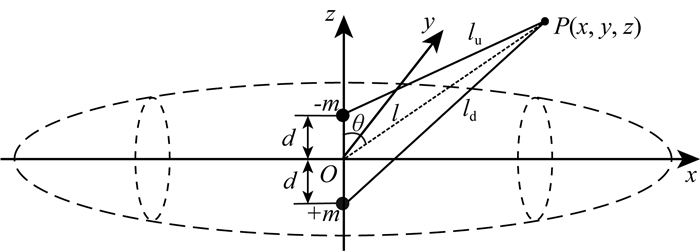
1.1 引力和引力梯度垂直分量计算公式以浮心O为原点,艇艏方向为x轴正向,左舷方向为y轴正向,z轴垂直向上为正向建立如图 1所示的坐标系,xy平面为水平面.设上极点质量为-m,下极点质量为+m,极距为2d,则偶极子产生的引力位可表示为
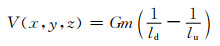
|
(1) |
|
图 1 垂直引力偶极子模型 Fig. 1 Vertical gravitational dipole |
式中,G为万有引力常数,
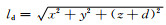
将(1)式对z求一阶、二阶偏导数,可得到引力和引力梯度垂直分量的计算公式:

|
(2) |
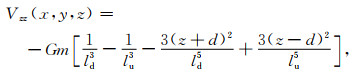
|
(3) |
类似地,将(1)式分别对x、y求偏导数可以得到引力和引力梯度的水平分量,本文只讨论垂直分量,故不作进一步讨论.
1.2 偶极场分布特征偶极子产生的引力场关于z轴旋转对称,故可选任意一个垂直面分析其空间分布特征.以xz平面为例,图 2给出了一个极距为20 m的偶极子的引力和引力梯度垂直分量的空间分布,黑色虚线为零值线.图 2a、2c为Vz/Gm、Vzz/Gm在xz面内的值,它们分别与Vz和Vzz具有完全相同的空间分布.可以看出,偶极场在上半空间被零值线划分成正负相间的三个区域,形如花朵,主信号位于偶极子正上方的区域,两侧有符号相反、强度较弱的旁瓣.由于上极为负质量,在正上方主信号区的引力垂直分量为正值,即方向向上,旁瓣区的引力垂直分量为负值.引力梯度垂直分量则刚好相反,主信号区为负值,旁瓣区为正值.

|
图 2 偶极场的空间分布 (a) Vz/Gm在xz平面内的分布(单位:m-1); (b) Vz/Gm随水平距离的变化(z=200 m, d=10 m); (c) Vzz/Gm在xz平面内的分布(单位:m-2); (d) Vzz/Gm随水平距离的变化(z=200 m, d=10 m). Fig. 2 Spatial distribution of gravitation field of vertical dipole (a) The value of Vz/Gm in xz plane (unit: m-1); (b) The change of Vz/Gm along the horizontal distance in case of z=100 m and d=10 m; (c) The value of Vzz/Gm in xz plane (unit: m-2); (d) The change of Vz/Gm along the horizontal distance in case of z=100 m and d=10 m. |
图 2b、2d给出了引力和引力梯度垂直分量随水平距离的变化曲线,均有3个极值和2个零点.其中,水平距离为零的中心点即P点位于极轴上时,引力和引力梯度均取得模最大值,这可以利用式(2)和式(3)证明.水平面内,主信号区是以零点距离为半径的圆形区域,故可以用两个零点之间的距离表示主信号区的宽度.零点位置可以利用式(2)、(3)计算得到,但是求解式(3)的零点较为困难.在极距远小于计算点距离的情况下,零点位置可以近似用下列两个公式计算:
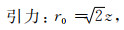
|
(4) |
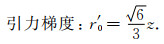
|
(5) |
这里用r0和r′0分别表示引力和引力梯度的零点距离中心的水平距离,它们随着高度增加而增大.可以看出,在同一高度处,引力的零点距离比引力梯度的大,说明引力的主信号区要比引力梯度的宽.此外,两条零值线趋近于偶极子的中心.
1.2.2 随高度的变化在不同高度的平面内,当计算点P位于极轴上时,即x=y=0,|Vz|和|Vzz|取得最大值,此时有
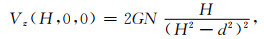
|
(6) |
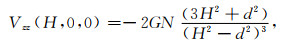
|
(7) |
式中N=2md称为偶极矩,H表示P点到中心O的垂直高度.当d≪H时,忽略式(6)、(7)中d/H的高次项,可得到极轴上引力和引力梯度垂直分量的近似估计公式:
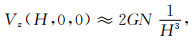
|
(8) |
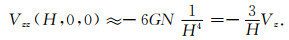
|
(9) |
由上两式可知,垂直偶极子模型产生的重力值按高度的三次方衰减,而重力垂直梯度值随高度的四次方衰减.利用这一关系可近似估计探测高度对探测仪器性能的需求.
1.2.3 随斜距的变化为了导出Vz、Vzz与斜距l的关系,利用距离倒数的展开式将1/ld、1/lu表示成d/l的级数形式(Hofmann-Wellenhof and Moritz, 2006),忽略二阶以上的项,有
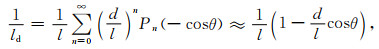
|
(10) |
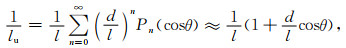
|
(11) |
式中,Pn(x)是勒让德多项式,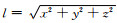
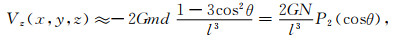
|
(12) |
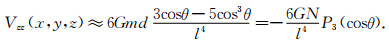
|
(13) |
不难看出,当斜距l为常数时,Vz、Vzz随极角θ变化而变化,变化曲线近似地分别与二阶、三阶勒让德多项式的曲线相同.而当θ不变时,Vz、Vzz的大小分别与斜距l的三次方、四次方成反比.特别的,当θ=0时,可导出随高度变化的近似关系式(8)、(9)两式.当cos2θ=1/3时,Vz=0,利用式(12)可导出式(4).同理,当cos2θ=3/5时,Vzz=0,利用式(13)可导出式(5).
2 潜航器异常重力场水下悬浮状态的潜航器总质量等于其置换的海水质量,故不会产生一阶异常重力场,但是由于质量分布不均匀可能产生二阶和更高阶的异常信号.将潜航器置换海水后的质量分布视为垂直分布的偶极子,由于离心力场不会发生变化,潜航器异常重力场就等于偶极子产生的引力场.从上一节知道,要确定潜航器异常重力场只需已知偶极矩即可,也就是说,只需根据潜航器的质量和几何形状确定偶极子模型的质量和极距.
设潜航器水下排水量为M,其下半部分的质量可记为αM,其中α∈(0.5, 1)为比例系数.由于上、下半部分排开水的质量均为0.5M(假设几何形状上、下对称),所以相对于原来海水的质量,上半部分置换后的质量是亏损的,亏损质量为-(α-0.5)M,而下半部分质量盈余(α-0.5)M,总净质量为零.因此,偶极子的质量大小为
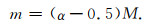
|
(14) |
极距的长度与潜航器的形状相关,它是上、下半部分形心之间的距离.如果用一个以纵倾轴为旋转轴的旋转椭球体作为潜航器几何形状的近似,则极距等于上、下半椭球形心之间的距离,根据半椭球体形心的位置可得:
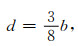
|
(15) |
式中,b为椭球的短半径.
3 实例分析以国外某级别弹道导弹核潜艇为例,其水下排水量为18750 t,长约为171 m,宽约13 m,应用本文建立的偶极子模型分析潜艇引起的异常重力场特征,并与其它模型的数值积分结果进行对比,检验本文方法的可行性.将艇体近似当作旋转椭球体,取长半径a=85.5 m,海水密度为1.03 g·cm-3,则根据排水量和椭球体积公式可计算得出短半径b=7.13 m.
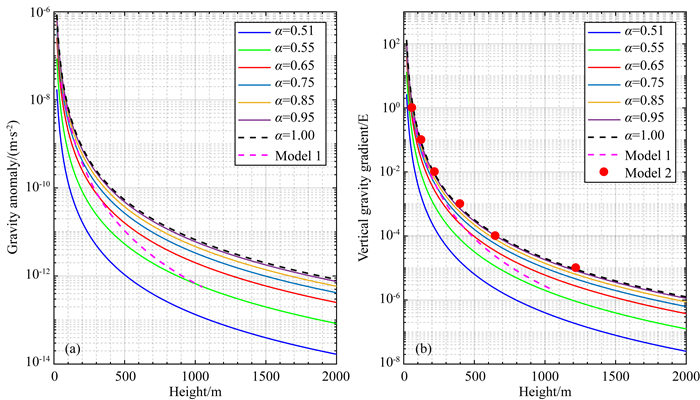
3.1 潜艇异常重力场图 3给出了α取不同值时由式(6)、(7)计算得到的潜艇重力异常和重力垂直梯度模最大值变化曲线.α值反映了潜艇上下两部分的质量差异,值越大代表质量分布越不均匀,因此随着α值的增大,异常场信号逐渐增强.α的取值对于异常场的量级有较大影响,α分别取0.51和1时,不管是重力异常还是重力垂直梯度的量级相差接近2个数量级.当α值比较接近0.5时,曲线之间的间隔较大,当α逐渐增大曲线间距逐渐缩小,直至趋近于α=1的情况(黑色虚线).因为实际中潜艇质量不可能全部集中在下半部分,显然α=1是其极限值,表 1给出了这一极限条件下信号不同量级对应的最大高度值.
|
图 3 不同α对应的重力异常(a)与重力垂直梯度(b)模最大值随高度的变化 Fig. 3 Modulus maximum of (a) gravity anomaly and (b) vertical gravity gradient varying with height for different α |
|
|
表 1 重力异常和重力垂直梯度不同量级对应的最大高度 Table 1 Maximum heights corresponding to different magnitudes of gravity anomaly and vertical gravity gradient |
从量级上看,潜艇引起的重力异常值最大可超过1 μGal(10-8m·s-2),重力垂直梯度最大超过1E(10-9s-2), 但是超过这一量级的信号只局限在潜艇附近很小的范围内.图 3显示,高度300 m时重力异常和重力垂直梯度的量级分别在10-10m·s-2、10-3E以下,2000 m时信号量级小于10-12m·s-2、10-6E.高度在500 m内时信号衰减速度很快,其中重力异常衰减了4~5个数据量,重力垂直梯度减小了5~6个数据量.高度大于500 m时,信号的衰减速度相对较为平缓.
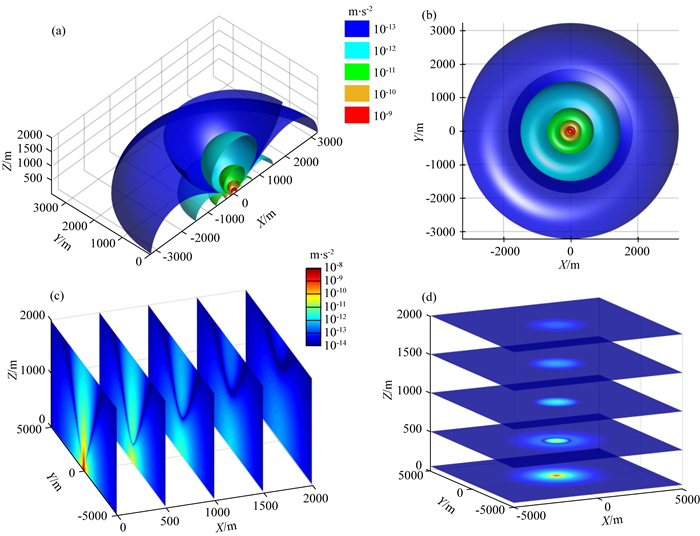
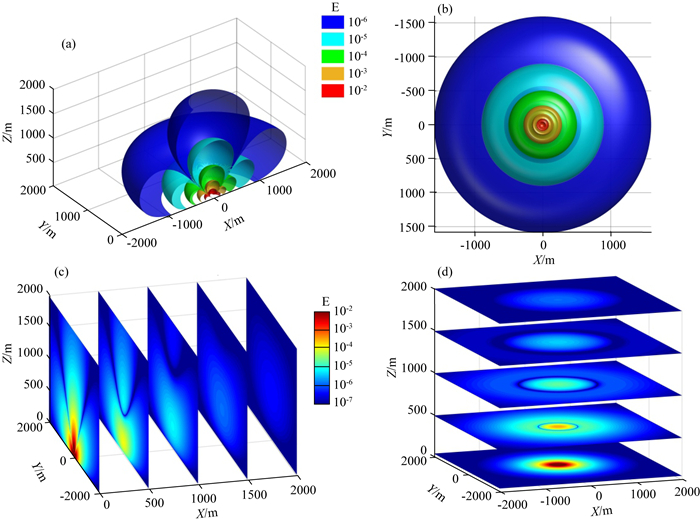
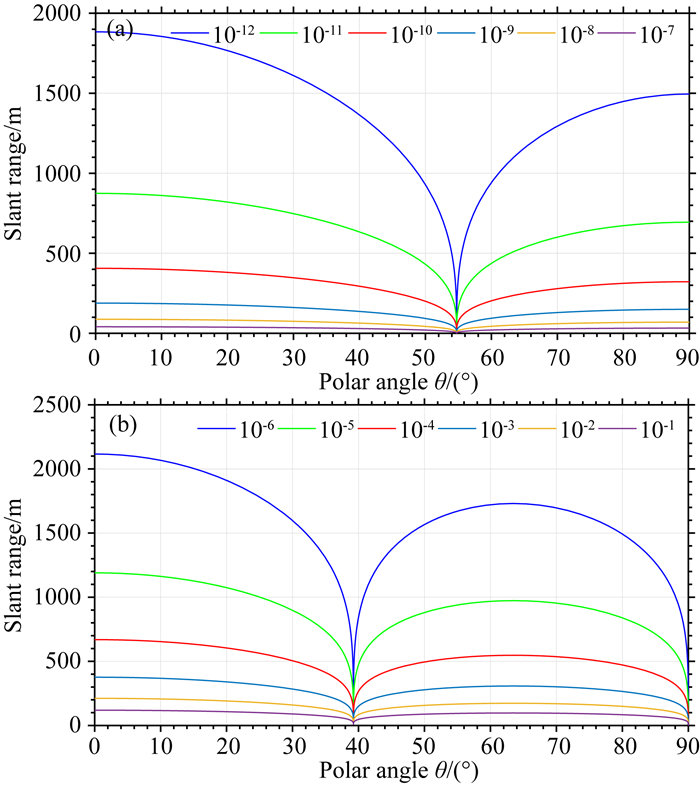
α的取值决定了异常场的强度大小(图 3),但不会改变异常场的空间分布特征.不失一般性,可以取α=1的情况分析异常场的特征.图 4和图 5是根据式(2)、(3)得到的潜艇重力异常和重力垂直梯度绝对值的三维空间分布图,其中图 4a、5a是从y=0处切开的等值面剖视图,图 4b、5b是从正下方向上观察等值面的仰视图,图 4c、5c是x方向的切片图(垂直面内的分布),图 4d、5d是z方向的切片图(水平面内的分布).图 6是重力异常和重力垂直梯度取不同固定值时斜距l随极角θ的变化情况,也可以理解为在(θ, l)平面内重力异常和重力垂直梯度绝对值的等值线分布,该结果由式(12)和(13)取绝对值后计算得到.
|
图 4 潜艇重力异常绝对值的空间分布(α=1) (a) 剖视图; (b) 仰视; (c) x轴方向切片图; (d) z轴方向切片图. Fig. 4 Spatial distribution of absolute gravity anomaly derived from the submarine in case of α=1 (a) Section view; (b) Upward view; (c) Slice map along x-axis; (d) Slice map along z-axis. |
|
图 5 潜艇垂直重力梯度绝对值的空间分布(α=1) (a) 剖视图; (b) 仰视; (c) x轴方向切片图; (d) z轴方向切片图. Fig. 5 Spatial distribution of absolute vertical gravity gradient derived from the submarine in case of α=1 (a) Section view; (b) Upward view; (c) Slice map along x-axis; (d) Slice map along z-axis. |
|
图 6 (a) 重力异常和(b)重力垂直梯度绝对值在极角θ-斜距l平面内的等值线图 Fig. 6 Contour maps in (θ, l) plane of absolute value of (a) gravity anomaly and (b) vertical gravity gradient. |
从三维视图看,重力异常和重力垂直梯度的等值面具有相似的空间结构,就像一只气球压在一个穹顶上,使穹顶中心下陷,等值面与水平面的交线是一个个同心圆.但是对比图 4a、图 5a和图 6,可以发现重力异常和重力梯度等值面的差异.对重力异常而言,等值面上的点到潜艇中心的距离随极角的增大先减小后增大,在θ=54.7°时取得极小值,在θ=0和90°时取得极大值.对重力垂直梯度,等值面上的点到潜艇中心的距离变化更为复杂,有两个极小值(θ=39.2°、90°)和两个极大值(θ=0°、63.4°).换言之,在以潜艇中心为球心的半球面上,重力异常在θ=54.7°时取得极小值,在θ=0和90°时取得极大值,重力垂直梯度则分别在θ=39.2°、90°和θ=0°、63.4°时取得极小值和极大值.它们的最大值都是在过潜艇中心的垂直轴线上(θ=0°).
3.2 与其他模型的比较模型一(Model 1)采用一个均值旋转椭球面模型来模拟潜艇,这是一种未考虑上下质量差异的理想模型,认为潜艇全部质量均匀分布在椭球面上(孙岚等, 2010).这种模型的异常场为椭球面剩余质量与椭球面内部海水质量亏损产生的异常场之和,可以通过数值积分计算得到,其最大值随高度的变化曲线如图 3中的品红色虚线所示.当高度较低时,椭球面模型的结果接近α=1的情况,而高度超过500 m时结果趋近于α=0.55的情况.椭球面模型产生的异常场信号强度未超过α=1时的偶极场.
模型二(Model 2)采用半球面+圆柱面+圆锥面的三段式组合质面模型(张志强等,2019),这一模型的异常场仍是外壳和内部质量亏损两部分引起的,但是顾及了密度不均匀性和水平方向形状不对称.他们在假设重心低于浮心1 m的条件下,确定了圆柱面上下两部分的不同密度值,再通过数值积分给出了重力垂直梯度与斜距的关系.表 1中最后一列给出了该模型与本文α=1的偶极子模型的结果对比,从图 3b可以看到两者基本一致.
3.3 重力探潜平台精度需求分析前面结果表明α=1是极限情况,产生的异常场信号最强,这里以这一极限情况的异常场来分析重力探潜对探测平台的最低精度要求.根据图 3的结果,表 2给出了几个不同高度时重力异常和重力垂直梯度的最大值,由此可以确定对应的重力探测传感器精度需求.高度为100 m时,潜艇的重力异常信号已小于微伽级,重力仪的精度至少要达到10-9m·s-2才可能探测到.当探测高度为1000 m时,对重力仪的精度要求提高3个数量级,在2000 m高度上重力仪精度需达到10-13m·s-2.重力梯度在100 m的高度上可达0.2 E,相应的重力梯度仪至少应满足0.1 E的观测精度.由于重力梯度以高度的四次方衰减,因此,探测高度每增加约0.8倍,重力梯度仪的精度需增加一个数量级.
|
|
表 2 不同高度重力探测平台的精度需求 Table 2 Accuracy requirement for the gravity detection platform |
对于探潜应用,重力传感器需要固定在飞机等运动平台上工作,载体运动产生的噪声对探测平台有严重影响,必须分析平台稳定性要求.在地球表面,地球重力加速度随高度的变化率约为-0.3086 mGal·m-1,即如果高度相差1 m,地球重力加速度将相差3.806×10-6m·s-2.要使探测平台能够探测出潜艇的重力异常信号,平台垂直位移引起的噪声必须小于潜艇产生的重力异常,因此平台稳定性要求可由下式估算:

|
(16) |
式中,mg为潜艇重力异常最大值(以m·s-2为单位),ΔH是对平台垂直位移的精度要求.如果采用重力梯度仪作为探测平台的传感器,由于地球重力垂直梯度随高度的变化率约为1.45×10-3E/m,相应的平台垂直位移量ΔH为
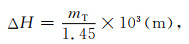
|
(17) |
式中,mT为潜艇重力垂直梯度最大值(以E为单位).
根据潜艇异常重力场信号的大小可由式(16)和式(17)估计出探测平台高程值的精度,误差必须小于ΔH,计算结果见表 2.可以看到,如果重力传感器采用重力仪,要分辨出潜艇重力异常信号对探测平台的稳定性有非常严格的要求,在高度为100 m时高度补偿精度必须优于2.17 mm,1000 m高度上补偿精度则要求微米级.如果采用重力梯度仪,对平台稳定性的要求相对较为宽松,高度为1000 m时平台的垂直位移量小于1.38 cm即可.
4 讨论通过构造几何模型来模拟分析潜航器的异常重力场,需要用数值积分的方法计算复杂的三重积分,而且积分式的形式和上、下限随几何模型和潜航器相关参数变化而变化,故这种方法通用性较差.本文给出的偶极子模型形式简单,重力场量的表达式具有解析形式,计算简便,通用性强.算例中与两种几何模型模拟结果的对比表明,利用偶极子模型来分析潜航器异常重力场结果可信、方法可行.
需要说明的是,如果潜航器上、下两部分质量相等(α=0.5),在内部质量分布不均匀的情况下仍可能产生异常重力场,由式(14)可知m=0,此时偶极子模型不适用.但是,实际舰船的设计一般不会有这种情况.
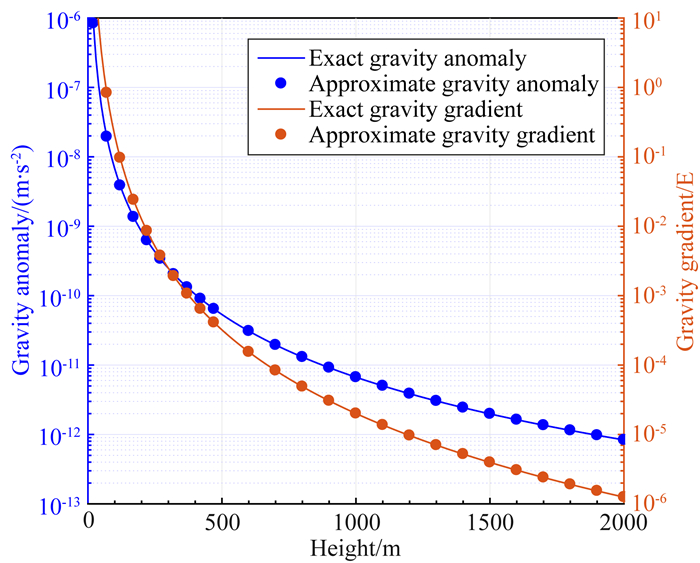
基于偶极子模型,本文还导出了重力异常和重力垂直梯度最大值与高度的近似关系式,即式(8)和式(9).利用这两个近似公式可以很方便地估算潜航器异常重力场信号的量级,分析探测平台的精度需求,或者估计给定传感器精度时的最大探测距离.仍以前文实例中的参数,由近似公式计算的近似值与精确值的对比如图 7所示.重力异常和重力垂直梯度近似估值的相对精度均优于0.1%,可见,近似公式具有很高精度,能够满足理论分析要求.
|
图 7 潜航器异常重力场量级的近似估值与精确值对比 Fig. 7 Comparison between approximate and exact magnitudes of the anomalous gravitational field induced by the underwater vehicle |
算例结果表明,如果利用重力探测例中所选级别的核潜艇,重力仪的精度至少需达到0.1 μGal,当前航空或船载重力仪的精度只有毫伽级,难以满足需求.与重力仪精度需求相比,重力探潜对平台稳定性的要求更为苛刻,探测高度为100 m时就要求毫米级的平台垂直位移补偿精度,这是仅考虑平台垂直位移影响的精度要求.由于重力仪观测值包含了载体垂直运动加速度,要从观测值中有效分离出潜艇的重力异常信号,对载体高度的测量精度要求更高.假设载体平台垂直运动是周期T=10 s的简谐运动,如果利用载体高度观测值对时间的二阶导数来计算传感器垂直运动加速度,以100 m的探测高度为例,载体高度观测值的精度必须优于
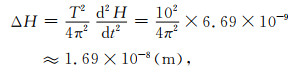
|
(18) |
这个值已经接近X射线波长的量级,显然,载体高度测量难以达到如此高的精度.
采用重力梯度仪作为探测传感器,对平台稳定性的要求低得多,实现起来相对较容易.当前,海空重力梯度测量系统已经达到10E~1E的精度水平,重力梯度仪的实验室精度可达10-4E.随着超导技术的应用,未来重力梯度仪的精度有望达到10-6E.由表 1可知,如果重力梯度仪精度达到10-2E,其探测高度可达200 m左右.如果10-4E的重力梯度仪实现工程实用化,可探测高度将超过500 m.因此,利用重力梯度探测潜航器具有较好的发展前景,有必要进一步研究相关的理论和方法.
5 结语本文基于引力偶极子模型导出了潜航器异常重力场的计算公式,并通过实例对异常重力场特征、重力探测的传感器精度和平台稳定性需求进行了定量分析.实验结果表明,相较于几何建模方法,利用偶极子模型分析潜航器异常重力场计算简单、通用性强,相应的近似关系式可方便地用于估计潜航器异常重力场的量级、分析重力探潜的精度需求和可探测范围,因此,本文提出的方法对于重力探潜的研究具有重要理论价值.
利用重力异常信号探测潜航器不具备可行性,因为即使是重力仪能满足精度要求,也无法满足平台稳定性要求,除非将重力仪安装在静止的固定平台.这是由于重力和惯性力等效,要分离出潜航器重力异常对探测平台稳定性的要求极高,在运动载体平台上几乎不可能实现.
重力梯度仪的快速发展以及重力梯度测量对平台稳定性要求较低,基于重力梯度测量的重力探潜技术具有实用化价值.然而,要使重力探潜真正达到实用化,除了仪器精度和平台稳定性补偿精度有待提高外,仍有许多问题需要解决,如高精度重力梯度背景场,潮汐、海浪等海面高频时变信息对重力梯度测量的噪声影响等.
Angevine R G. 2005. Innovation and experimentation in the US Navy: the UPTIDE antisubmarine warfare experiments, 1969-721. Journal of Strategic Studies, 28(1): 77-105. DOI:10.1080/01402390500032070 |
Fang E Z, Gui C Y, Wang H. 2020. Non-acoustic detection techniques for submarines. Defence Science & Technology Industry (in Chinese), (6): 66-68. |
Hofmann-Wellenhof B, Moritz H. 2006. Physical Geodesy. Vienna: Springer.
|
Hu M Z, Li J C, Xing L L. 2014. Global bathymetry model predicted from vertical gravity gradient anomalies. Acta Geodaetica et Cartographica Sinica (in Chinese), 43(6): 558-565, 574. |
Lanzagorta M, Uhlmann J, Venegas-Andraca S E. 2015. Quantum sensing in the maritime environment.//OCEANS 2015-MTS/IEEE Washington. Washington, DC, USA: IEEE, 1-9.
|
Liu T. 2019. Review on the current situation and development of aviation antisubmarine. China New Telecommunications (in Chinese), 21(8): 74-77. |
Su Y M, Pang Y J. 2005. Principle of Submarine (in Chinese). Harbin: Harbin Engineering University Press.
|
Sun L, Li H P, Bian S F, et al. 2010. Study on the submarine detection method based on the gravity gradient. Hydrographic Surveying and Charting (in Chinese), 30(2): 24-27, 45. |
Tang J T, Hu S G, Ren Z Y, et al. 2017. Analytical formulas for underwater and aerial object localization by gravitational field and gravitational gradient tensor. IEEE Geoscience and Remote Sensing Letters, 14(9): 1557-1560. DOI:10.1109/LGRS.2017.2722475 |
Tang J T, Hu S G, Ren Z Y, et al. 2018. Localization of multiple underwater objects with gravity field and gravity gradient tensor. IEEE Geoscience and Remote Sensing Letters, 15(2): 247-251. DOI:10.1109/LGRS.2017.2784837 |
Wang T W. 2005. The geomagnetic dipole field in the 20th century. Chinese Journal of Geophysics (in Chinese), 48(1): 52-55. |
Wei Z, Du D, Liu Y, et al. 2019. Research on the development of anti-submarine equipment and technology. Ship Science and Technology (in Chinese), 41(9): 154-157. |
Wu L, Tian J W. 2010. Automated gravity gradient tensor inversion for underwater object detection. Journal of Geophysics and Engineering, 7(4): 410-416. DOI:10.1088/1742-2132/7/4/008 |
Wu L, Tian X, Ma J, et al. 2010. Underwater object detection based on gravity gradient. IEEE Geoscience and Remote Sensing Letters, 7(2): 362-365. DOI:10.1109/LGRS.2009.2035455 |
Wu L, Ke X P, Hsu H, et al. 2013. Joint gravity and gravity gradient inversion for subsurface object detection. IEEE Geoscience and Remote Sensing Letters, 10(4): 865-869. DOI:10.1109/LGRS.2012.2226427 |
Yang R J, Xiong X, Guo X Q, et al. 2014. Research on model and simulation of airborne magnetic anomaly detection sweep width based on magnetic dipole model. Acta Armamentarii (in Chinese), 35(9): 1458-1465. |
Ying G, Zhang Y T, Li Z N, et al. 2016. Research on geometric invariant of magnetic gradient tensors for a magnetic dipole source and its application. Chinese Journal of Geophysics (in Chinese), 59(2): 749-756. DOI:10.6038/cjg20160232 |
Zhang Z Q, Shi J, Yu Z, et al. 2018. Feasibility analysis of submarine detection method based on the airborne gravity gradient.//Proceedings of the 37th Chinese Control Conference. Wuhan, China: IEEE, 4587-4591.
|
Zhang Z Q, Zheng H, Cui Y F. 2019. Research on the submarine detection method based on the airborne gravity vertical gradient. Hydrographic Surveying and Charting (in Chinese), 39(4): 6-9, 13. |
方尔正, 桂晨阳, 王欢. 2020. 潜艇的非声学探测技术. 国防科技工业, (6): 66-68. |
胡敏章, 李建成, 邢乐林. 2014. 由垂直重力梯度异常反演全球海底地形模型. 测绘学报, 43(6): 558-565, 574. |
刘腾. 2019. 航空反潜的现状和发展综述. 中国新通信, 21(8): 74-77. DOI:10.3969/j.issn.1673-4866.2019.08.062 |
苏玉民, 庞永杰. 2005. 潜艇原理. 哈尔滨: 哈尔滨工程大学出版社.
|
孙岚, 李厚朴, 边少锋, 等. 2010. 基于重力梯度的潜艇探测方法研究. 海洋测绘, 30(2): 24-27, 45. DOI:10.3969/j.issn.1671-3044.2010.02.007 |
王亶文. 2005. 二十世纪的地球偶极子磁场. 地球物理学报, 48(1): 52-55. DOI:10.3321/j.issn:0001-5733.2005.01.009 |
魏征, 杜度, 刘洋, 等. 2019. 美国反潜装备技术发展研究. 舰船科学技术, 41(9): 154-157. DOI:10.3404/j.issn.1672-7649.2019.09.031 |
杨日杰, 熊雄, 郭新奇, 等. 2014. 基于潜艇磁偶极子模型的航空磁探潜探测宽度模型与仿真. 兵工学报, 35(9): 1458-1465. DOI:10.3969/j.issn.1000-1093.2014.09.019 |
尹刚, 张英堂, 李志宁, 等. 2016. 磁偶极子梯度张量的几何不变量及其应用. 地球物理学报, 59(2): 749-756. DOI:10.6038/cjg20160232 |
张志强, 郑晗, 崔银锋. 2019. 航空重力垂直梯度探测潜艇方法研究. 海洋测绘, 39(4): 6-9, 13. |
 2021, Vol. 64
2021, Vol. 64

