微地震压裂监测是通过识别地下岩石破裂或错断引发的微小地震信号来监测水力压裂施工过程中人工裂缝发育情况的地球物理技术(Maxwell and Urbancic, 2001；Warpinski，2009；Bao and Eaton, 2016).在微地震监测资料处理中，震相识别和初至拾取作为其中两个关键步骤，是最终事件定位及压裂裂缝缝网解释的基础(Maxwell et al., 2010).井中微地震监测通常采用布置于压裂井周边邻井中的多级三分量检波器接收微地震信号，信号具有震级小、频率高、能量弱等特点，不易被准确地识别与记录，因此有效且精确的低信噪比事件识别和初至拾取至关重要.

提取并分析微地震信号和噪声的特征差异是震相识别和初至拾取的主要依据.传统人工微地震震相识别和初至拾取的工作模式容易受拾取标准不一致及人为因素干扰而产生误差，难以满足实际处理中对计算效率的要求.自动识别及拾取方法中代表性的三类方法分别是：①单道特征法，②多道互相关法，③模板匹配法.单道特征法中，基于振幅差异的STA/LTA方法(Allen，1978；Sabbione and Velis, 2010)在单道连续波形的滑动时窗内分别计算长短时窗能量比值，当比值超过设定阈值时所对应的时刻视为初至到时.该类方法计算效率高，但对低信噪比事件的敏感度较低，具有较高的漏拾/误拾率.此外，基于其他单道特征差异的偏振分析法(Deflandre and Dubesset, 1992)、高阶统计量法(Saragiotis et al., 2004)、AR-AIC方法(Sleeman and Van Eck，1999)及结合上述多种算法的单道特征法(谭玉阳等，2016)相继被提出(Akram and Eaton, 2016).多道互相关法考虑同一事件相邻道集间事件的波形相似特征，与单道方法相比，有效提高了低信噪比事件的拾取精度(De Meersman et al., 2009；Tan and He, 2016).模板匹配法利用相邻发震位置处不同事件间的波形相似特征拾取事件，以高信噪比事件波形作为模板可有效检测和拾取低信噪比事件，但其应用效果强烈依赖于模板事件的选取，容易漏拾部分有效事件(Song et al., 2010；翟尚等，2020).上述方法均需通过分析信号与噪声的特征差异，并通过建立的特征目标函数将原始波形记录转化到相应的“特征域”来拾取事件，因此拾取效果依赖于方法的特征函数等的选取，且不同方法应用于同一套实际资料的拾取效果存在偏差.针对事件间时差校正后仍存在对齐差异而产生拾取误差的问题，喻志超等(2019)利用相邻道间及事件间的波形相似特征对初至拾取结果进行了全局优化，克服了拾取标准一致性差的缺陷.

计算机运算能力的快速提高使得利用机器学习、深度学习等技术进行地震资料处理成为可能(Bergen et al., 2019)，其优势在于构建的模型本身具有自动特征提取能力，省去了人为提取信号特征的复杂过程.在地震波识别和拾取应用中，首先利用具有不同特征的波形记录样本构建模型，模型自适应地学习波形特征，建立输入波形与识别/拾取结果间的对应关系；然后，待处理的原始波形记录经简单预处理后馈入模型，即可完成地震波识别和拾取处理工作.机器学习作为深度学习技术应用的基础，可采用各种优化策略进行数据挖掘，如机器学习中的人工神经网络方法、支持向量机法等均被应用于地震波拾取工作中(Maity et al., 2014；Qu et al., 2019；蒋一然和宁杰远，2019).深度学习运用以深度神经网络参数结构为基础的模型，具备处理复杂问题的能力，其中卷积神经网络方法(Convolutional Neural Networks)(Lecun et al., 1998)利用卷积操作从离散采样数据中提取丰富特征，取得了较好的应用效果(Perol et al., 2018；Ross et al., 2018；Yuan et al., 2018；Dokht et al., 2019；Zhou et al., 2019；Duan and Zhang, 2020)，已成为近年来的研究热点.

U-Net语义分割模型最早被应用于医学图像分割任务中(Ronneberger et al., 2015)，它省去了卷积神经网络中的全连接层，增加了高维到低维的多级特征融合，使得其既能准确识别目标体，同时可对目标体边界准确定位.Zhu和Beroza(2019)、赵明等(2019)将U-Net模型应用至天然地震震相拾取领域，针对单道地震记录进行了直达P波、S波的拾取，实现了“逐采样点”的拾取效果；同样地，与U-Net类似的SegNet模型被Wu等(2019)应用于压裂监测微地震事件初至拾取中.上述方法均采用单道地震/微地震记录进行模型构建与预测(统称为ST-Net)，但对于由井中多级检波器构成的微地震观测系统而言，ST-Net在模型构建阶段存在无法利用相邻道间波形相似性的缺陷，在实际应用中容易出现低信噪比事件漏拾、震相间误拾和拾取结果偏差严重等问题.

本文基于卷积神经网络中的U-Net模型，提出一种多道联合微地震震相识别和初至拾取方法(记作MT-Net).与ST-Net不同，模型构建中将井中相邻多道的微地震波形记录同时馈入，使得相邻道的波形信息对模型形成有效约束，一方面提高了对低信噪比事件的震相识别效果，同时构建的加权交叉熵损失函数增强了模型对有效震相初至误差的敏感度，使得微地震震相识别和初至拾取工作仅利用单个深度学习模型即可完成，保证了识别和拾取处理结果的标准一致性.我们从方法原理、数据预处理、模型训练与测试等方面阐述了本文方法的操作流程，作为对比，使用本文方法与单道方法(ST-Net)处理同一套微地震资料，验证MT-Net在压裂监测实时微地震资料处理中的应用效果.

基于卷积神经网络的U-Net模型最早应用于生物医学图像分割任务中(Ronneberger et al., 2015)，其主要优点是对图像边缘部分的检测较为敏感.与图像分割任务类似，直达P波、S波的识别和初至拾取可认为是一个多分类优化问题，波形记录中的每个采样点均属于P波、S波和噪声三类中的一类，我们希望对所有采样点正确分类，并对噪声与有效震相间的边缘部分进行检测与定位，进而准确拾取P波和S波初至.本文的MT-Net首先利用具有不同特征的多道微地震记录样本构建模型，然后将待处理的多道波形记录馈入构建好的模型即可完成微地震震相识别和初至拾取工作.

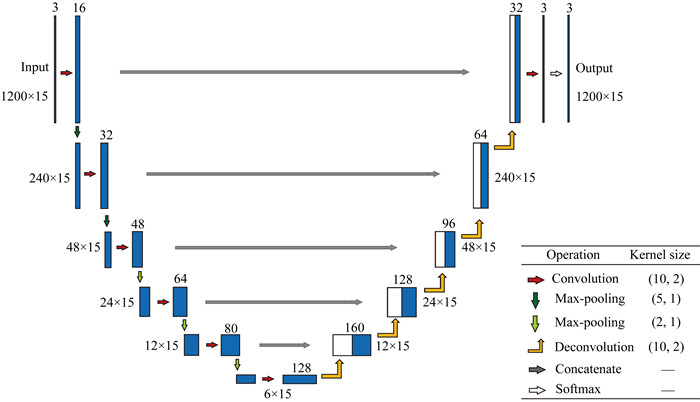
MT-Net的网络结构如图 1所示，模型输入以连续微地震记录中截取的多道分段波形为单元，三个分量(两个水平分量和一个垂直分量)分别对应三个通道；输出为与输入相同尺寸的概率分布值，三个通道分别对应P波、S波和噪声的概率分布曲线.设输入和输出均为N×M×K大小的三维数据，第一维是“道内”维度，N代表截取波形单道记录内的采样点数，理论上至少应保证截取波形段内可包含一个完整的双震相事件；第二维是“道间”维度，M代表多道联合数量，MT-Net将相邻检波器的波形记录同时作为输入，M取值与观测系统中排布的检波器数量保持一致；第三维是“通道”维度，K代表通道个数，三分量波形记录对应的K取值为3.

图 1

Fig. 1

图 1 MT-Net示意图 参数含义：采样点数N×检波道数M(标注于每层侧方)，通道数K(标注于每层上方). Fig. 1 The sketch map of MT-Net Parameters: number of sampling points×number of receivers (marked on the side of each layer), number of channels (marked on the top of each layer).

如图 1所示，MT-Net从输入层到输出层包含若干个下采样阶段和上采样阶段.下采样阶段为收缩路径，主要作用是逐层提取数据特征，每个下采样阶段包含一个卷积层和一个池化层.卷积操作(Convolution)采用多个卷积核提取特征，得到的特征图数量取决于卷积核的个数.MT-Net在第一和第二维度上进行卷积操作，可以同时提取道内和道间的波形信息，模型可以自适应地对道间初至信息进行约束.池化层对卷积层输出的所有特征图进行最大池化操作(Max-pooling)，降低特征图分辨率，减少模型参数量.上采样阶段为扩展路径，每个上采样阶段包含一个转置卷积层和一个融合层，转置卷积操作(Deconvolution)的作用是特征恢复，特征图放大倍数与对应的上采样阶段池化层保持一致.融合操作(Concatenate)将5个同级别的下采样阶段输出特征图与上采样阶段输出特征图进行融合，实现“端到端”的连接.上述卷积层和转置卷积层均采用ReLU非线性激活函数(Glorot et al., 2011).经过上采样阶段后特征图大小恢复至原始输入尺寸(N×M×K).最后经Softmax层，使输出转换为0~1之间的概率分布，本文使用的具体函数形式为

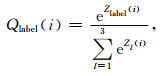
(1)

式中，Z(i)表示Softmax层第i个采样点的输入值；label取值1、2、3，分别代表P波、S波和噪声三个通道；Q即为P波、S波和噪声的输出概率分布.

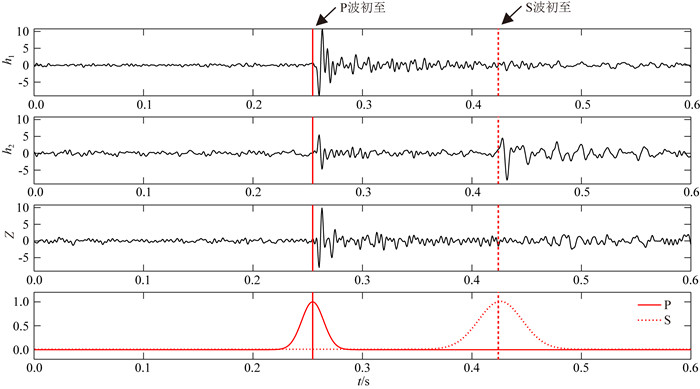
与输出概率分布Q一致，样本标签同样为P波、S波和噪声通道的概率分布.对于噪声样本(标签为T，三个通道的概率分布分别记作T_P、T_S、T_N)，我们只需将其识别正确即可，因此设置T_P、T_S均为0，T_N均为1；对于包含P波、S波的样本(标签为T'，三个通道的概率分布分别记作T′_P、T′_S、T′_N)，我们需要同时完成识别和初至拾取，因此，标签T′以手动拾取的震相初至作为参考标准进行设定.以一个典型的单道双震相样本标签(图 2)为例，考虑到手动初至拾取结果(图中红色竖线：P波初至为实线，S波初至为虚线)也并非绝对准确，设置P波和S波标签分别为以P波初至到达点(μ_P)、S波初至到达点(μ_S)为中心的高斯概率分布(图中红色实线和红色虚线)，对应标准差分别为σ_P、σ_S.T′_P、T′_S、T′_N对应第i个采样点处的计算公式如下：

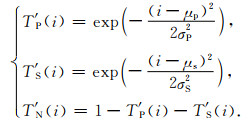
(2)

在MT-Net模型训练阶段，我们需要设定损失函数来表示模型输出的概率分布与样本标签间的差异，通过最小化损失函数得到最优化训练模型.Zhu和Beroza(2019)使用了简单的交叉熵损失函数，由于没有考虑到非震相部分在一个分段波形内所占的比例显著大于震相部分的数据特点(如图 2中0.6 s的双震相事件内：P波、S波震相部分约占10%，噪声部分约占90%)，可能导致损失函数在震相部分的误差敏感度较低.针对这一问题，我们构建了加权的交叉熵损失函数，依据震相和非震相部分在分段波形所占的比例，分别采用不同的加权因子，效果上增大了对震相部分误差的惩罚.具体形式为

(3)

图 2

Fig. 2

图 2 双震相样本标签示例 Fig. 2 The sample label of one double-phase event

式中，p_P(i)、p_S(i)、p_N(i)分别表示第i个采样点处P波、S波和噪声的真实概率分布，q_P(i)、q_S(i)、q_N(i)分别表示第i个采样点处P波、S波和噪声的模型输出概率分布，ω₀、ω₁分别表示震相部分(P波、S波)和非震相部分的加权因子，具体设置时可将震相与非震相部分分别占分段记录比例的倒数作为ω₀、ω₁的参考取值.

测试阶段根据模型输出得到震相识别和初至拾取结果.首先，对于每个样本输出的P波和S波概率分布，分别记录概率分布的最大值和其对应的位置.然后通过设定阈值识别震相，若P波和S波概率分布最大值均超过阈值，则认为该样本是双震相事件；若其中一个超过阈值，则认为是单震相事件；若均未超过阈值，则认为是噪声.对于识别出的单震相和双震相事件，其概率分布最大值所对应的位置即为模型预测的初至时刻(Zhu and Beroza, 2019).

与MT-Net相比，ST-Net中分段记录以单道波形为单元输入模型(Wu et al., 2019)，在输入和输出尺寸设置中，N、K取值与MT-Net一致，M取值为1；同时只在第一维度进行卷积操作，模型只能自动提取道内的波形特征，因此无法利用相邻道间波形的相互约束提高整体识别和拾取准确率.

本文使用胜利油田樊154区块一多段压裂水平井的微地震监测记录作为模型训练及后继测试对比的样本集(Tan and He, 2016)，数据共包含11个压裂段，连续监测时间约16小时.观测系统为布设于压裂水平井附近一口直井中的15级检波器串，检波器等间距排布，级间距为10 m，采样率为2000SPS(sample per second).我们首先需要对原始地震记录进行预处理，采用30~350 Hz的带通滤波去除原始记录低频和高频干扰信息.由于连续监测记录无法直接输入模型，需要以特定窗长将其分段截取.本文数据记录中同一双震相事件的P波和S波到时差均小于0.25 s，考虑到井中微地震监测数据资料的普遍特点，我们设定截取长度N为1200(0.6 s)，同时相邻的截取段重叠200个采样点，防止因人为截断而漏拾部分有效震相.对截取的分段记录进行去均值处理，去除波形记录中的直流成分，使振幅范围分布于0附近；并按照标准差进行归一化，在保留波形特征的前提下使振幅均衡化.

如图 1中MT-Net模型的各层参数设置，输入/输出层尺寸为1200×15×3，卷积/转置卷积核尺寸设置为(10，2)；前2个池化层压缩尺度为(5，1)，后3个池化层尺度压缩为(2，1)；原始输入先经过5个下采样阶段，单道内的采样点数N由1200减少至6，同时为了防止信息丢失，通道数K由3增加至128，后经5个上采样阶段逐渐恢复至原尺寸；在损失函数中，ω₀、ω₁分别设置为6.7、1.2.ST-Net的输入(输出)层尺寸为1200×1×3，卷积/转置卷积核尺寸设置为(10，1)，其余与MT-Net保持一致.

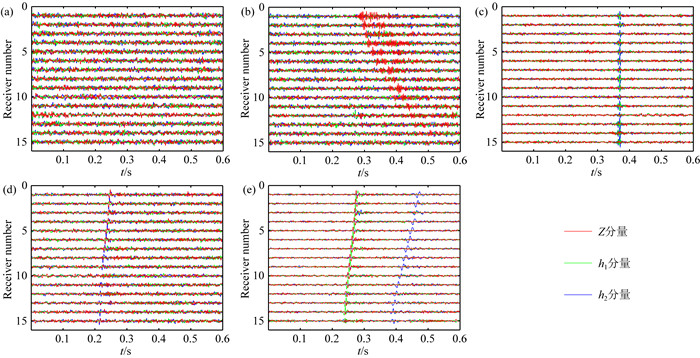
截取的分段记录经前述预处理后即可作为输入样本，在本文实际资料中，样本类型包括背景噪声、噪声事件、单震相事件和双震相事件.如图 3所示为典型的多道三分量波形记录(红色、绿色和蓝色线条分别为垂直分量Z和两个水平分量h₁、h₂).背景噪声(图 3a)的振幅变化范围较小，可认为不包含任何有效信息；典型噪声事件包括井筒波信号(图 3b)和仪器干扰信号(图 3c)，井筒波信号沿着井筒传播，Z分量上有明显振幅异常，与有效震相类似同样存在道间时差，但相邻检波道间的时差保持一致；仪器干扰信号也存在明显振幅异常，其道间时差几乎为0；有效微地震事件中包含标准的双震相事件(图 3e)和单震相事件(图 3d)，单震相事件产生的原因可能是受微地震事件震源机制及观测系统的影响，事件记录中某个震相的信噪比可能较低，影响其被有效识别.

图 3

Fig. 3

图 3 连续波形记录中截取的不同类型样本示例 (a) 背景噪声；(b) 噪声事件(井筒波信号)；(c) 噪声事件(仪器干扰信号)；(d) 单震相事件；(e) 双震相事件. Fig. 3 Samples of different types from continuous waveform records (a) Background noise; (b) Noise event (tube wave signal); (c) Noise event (tool interference signal); (d) Single-phase event; (e) Double-phase event.

在实时监测中，我们只希望准确快速地得到震相识别和初至拾取结果，因此将除单震相事件和双震相事件之外的其他样本都归类为噪声样本.如图 2所示，受实际资料中P波、S波信噪比及主频成分的影响，P波的手动拾取精度往往高于S波，因而在对含有效震相样本制作标签时本文设置T_P、T_S的标准差σ_P、σ_S分别为0.01 s(20个采样点)、0.02 s(40个采样点).

实际处理资料截取的分段记录中绝大部分是噪声样本，单震相和多震相样本只占很小的一部分.在模型训练阶段，若将连续记录中的所有样本作为输入构建模型，会产生深度学习中典型的样本不均衡问题，导致数量较少的含有效震相样本的拾取效果变差(López et al., 2013).因此，本文在保证训练样本集可以完全覆盖连续波形记录中所有类别事件的前提下，选取部分噪声样本和其余所有含震相样本作为训练样本集.最终训练样本集来源于水平井11个压裂段微地震监测记录中的前7个压裂段，单震相、双震相和噪声样本数分别为480、6540、12225，共计19245个样本.

以神经网络库Keras(http://keras.io)为基本库函数，基于Tensorflow深度学习框架(http://www.tensorflow.org)搭建并训练MT-Net模型.训练阶段采用小批量梯度下降法，以一个batch大小的分段波形记录为单元进行损失函数计算和网络参数更新，本文设置batch大小为32.采用Adam优化算法更新模型参数，同时使用动量和自适应学习率加快模型收敛速度(Kingma and Ba, 2015).整个训练样本集经过多次迭代，当损失函数不再下降时训练阶段结束.模型训练中，划分训练集中10%的样本作为验证集调整模型超参数，经调整优化的MT-Net模型即可作为最终的训练模型用于模型测试.

测试样本集为水平井11个压裂段微地震监测记录中的后4个压裂段.微地震监测记录经预处理后进行连续分段截取，共得到439605个分段记录样本.本节采用相同模型及参数设置的单道方法(ST-Net)作为对比，验证基于U-Net的多道联合方法(MT-Net)在震相识别和初至拾取中的应用效果.作为评价标准，我们对这4个压裂段的监测记录进行了人工精细事件识别与初至拾取，得到含单震相、双震相事件的样本数分别为120、1275，其余均为噪声样本.

在震相识别中，需要为P波、S波通道的输出概率分布曲线设定阈值以判别震相类型.阈值选取的大小至关重要，阈值过高可能导致部分低信噪比震相被误拾为噪声；阈值过低则可能将部分噪声事件误拾为有效事件.本文设定P波和S波的概率分布阈值均为0.5.

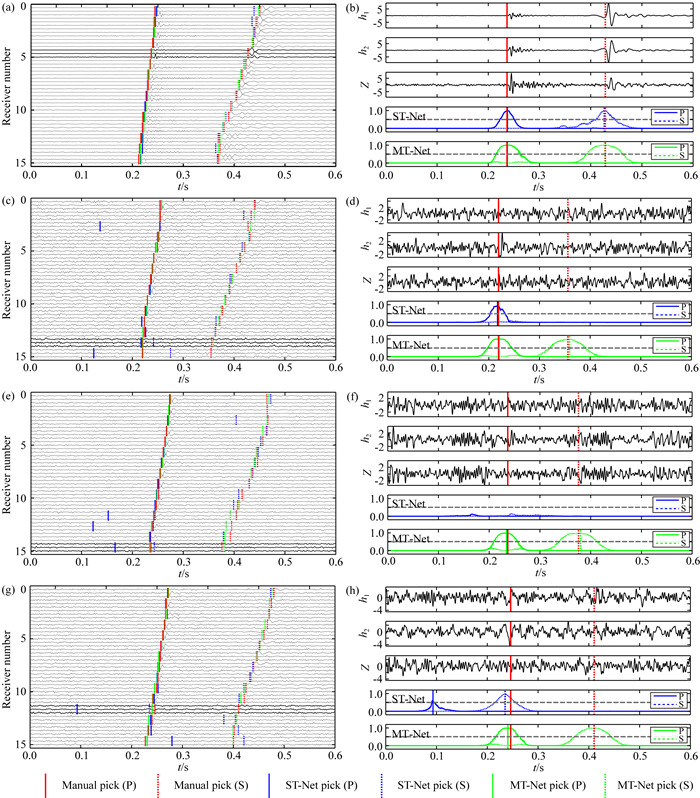
如图 4所示，从测试集中选取了4个双震相事件(图 4a、4c、4e、4g)说明MT-Net与ST-Net的识别与拾取结果.同一事件相邻15级检波器的三分量波形记录从上到下依次排列，每道记录中依次为h₁、h₂和Z三个分量；P波、S波输出概率分布的最大值对应的位置分别以短实线和短虚线标注于各道记录上.对于事件中的单道记录(图 4b、4d、4f、4h)，若概率分布最大值超过设定阈值则将其对应的位置认为是该震相的初至拾取时刻，并以竖线标注于图中；若未超过设定阈值则不进行标注.手动拾取(manual pick)、ST-Net拾取(ST-Net pick)和MT-Net拾取(MT-Net pick)的初至分别以红色、蓝色和绿色竖线表示，概率分布阈值线以黑色双划线表示.

图 4

Fig. 4

图 4 双震相事件识别与拾取结果示例 (a) 事件1的波形记录；(b) 事件1的第5道记录；(c) 事件2的波形记录；(d) 事件2的第14道记录；(e) 事件3的波形记录；(f) 事件3的第15道记录；(g) 事件4的波形记录；(h) 事件4的第12道记录.蓝色和绿色线条分别为ST-Net、MT-Net的输出概率分布. Fig. 4 Detection and arrival picking results of double-phase events (a) The waveform record of event 1; (b) The 5th trace record of event 1; (c) The waveform record of event 2; (d) The 14th trace record of event 2; (e) The waveform record of event 3; (f) The 15th trace record of event 3; (g) The waveform record of event 4; (h) The 12th trace record of event 4.The blue and green lines are the output probability distributions of ST-Net and MT-Net respectively.

图 4a为选取的一个高信噪比事件(事件1)，可以看出整体上ST-Net与MT-Net的拾取效果十分接近，与手动拾取结果之间均无显著差异；图 4b为事件1中的第5道波形记录及模型输出概率分布，ST-Net和MT-Net的概率分布曲线形态也较为接近，在P波和S波初至附近均出现了明显的概率分布高值，均显著超过了阈值0.5，表明两种方法对于高信噪比事件的拾取结果均较为理想.

图 4c为事件2的波形记录，该事件中部分单道的S波能量较弱，导致ST-Net对第3、15道两个震相的拾取结果均发生严重偏离，将第14道记录(图 4d)误拾为只包含P波的单震相事件，MT-Net可将事件中各道的两个震相正确识别，整体上MT-Net的拾取效果明显好于ST-Net.

事件3的波形记录和其中第15道波形记录如图 4e、4f所示，图 4f中由于该道内信号与噪声的特征无显著差异，ST-Net对其边界部分不敏感，导致在整个概率分布内均未超过设定阈值，无明显峰值出现；而MT-Net仍可以在大量背景干扰噪声中正确识别出两个震相.

图 4g所示事件的信噪比更低(事件4)，且各单道内的P波、S波能量逐渐减弱.整体上MT-Net较ST-Net拾取的初至更接近于手动拾取结果.在靠后几道(11-14道)中，ST-Net拾取的初至较手动拾取初至发生明显偏离，而MT-Net的拾取误差均小于0.01 s，仍在误差允许范围内.第12道波形记录中(图 4h)受背景噪声干扰，ST-Net将P波初至到达前的局部噪声误拾为P波，将P波初至误拾为S波；而MT-Net有效避免了此类震相间误拾情况的发生.

综上，MT-Net拾取效果好于ST-Net的原因是由于MT-Net中的二维卷积操作可以利用空间信息的约束，使得具有较低信噪比道的拾取结果向相邻的高信噪比道的拾取结果“靠拢”；而ST-Net为一维卷积操作，相邻各道样本间没有任何约束，对背景噪声干扰较为敏感.

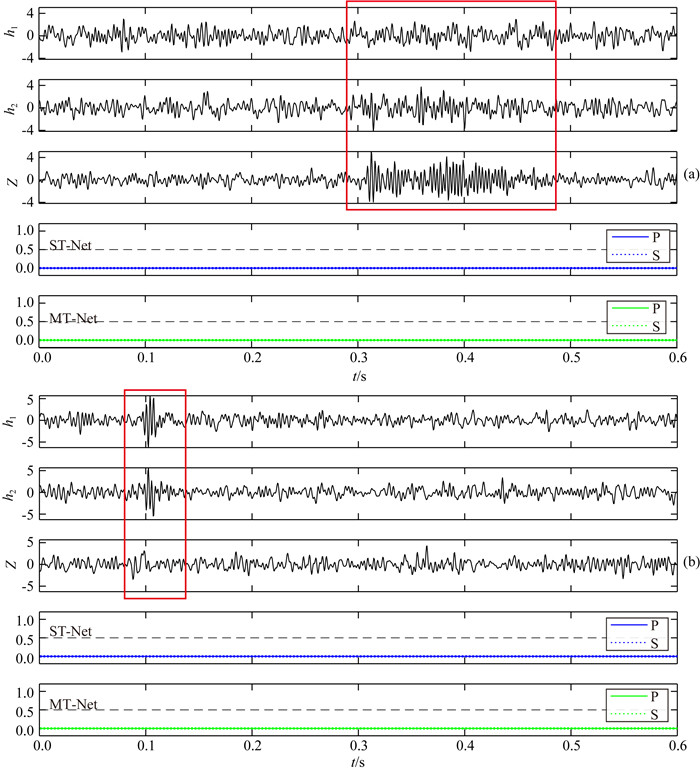
如图 5所示为两个单道噪声样本的识别结果示例，图 5a中红框位置处的Z分量振幅异常，h₁、h₂分量没有明显异常，是一个典型的沿井筒传播的井筒波事件；图 5b中红框位置处为仪器噪声，三个分量均有幅值异常，但其频谱成分明显高于有效事件震相(图 4).虽然两个噪声事件均存在振幅异常，但红框位置处对应的概率分布曲线均无峰值出现.结果表明无论ST-Net还是MT-Net，均自适应地提取到了干扰信号和有效信号间更加抽象的特征差异，有效避免了将噪声事件误拾为有效微地震事件的情况发生.

图 5

Fig. 5

图 5 噪声事件识别结果示例 (a) 井筒波信号样本；(b) 仪器干扰信号样本.图注与图 4一致. Fig. 5 Detection results of noise events (a) Sample of tube wave signal; (b) Sample of tool interference signal. The legend is consistent with that of Fig. 4.

ST-Net和MT-Net对测试集中有效事件样本(单震相和双震相样本)识别结果的统计情况如表 1，对于某类样本，我们定义识别正确率为正确识别的样本数量占实际该类样本总数的比例.由表可见，测试集中单震相样本均被MT-Net正确识别，而ST-Net漏拾了3个样本；两种方法均漏拾了部分双震相样本，但MT-Net的漏拾个数明显较少，识别正确率由ST-Net的89.88%提高至97.57%.在实时微地震监测中，我们主要利用双震相样本进行后续反演定位，可以看出MT-Net较ST-Net可以正确识别出更多的双震相样本，对这部分样本进行初至拾取和事件定位，有助于得到更加完整的压裂区域裂缝解释缝网.

表 1 (Table 1)

表 1 测试集样本的识别结果统计 Table 1 Detection result statistics of test set samples 样本类型 实际样本数 正确识别数量 识别正确率 ST-Net MT-Net ST-Net MT-Net 单震相 120 117 120 97.50% 100.00% 双震相 1275 1146 1244 89.88% 97.57%

表 1 测试集样本的识别结果统计 Table 1 Detection result statistics of test set samples

U-Net模型的输出概率分布曲线可直接用于有效事件的初至拾取，我们以手动拾取初至为参考标准，统计对比了两种方法对双震相样本的拾取误差(如图 6所示，图中ST-Net、MT-Net分别用蓝线、绿线表示)，P波、S波和P-S波到时差的误差高斯统计分别如图 6a、6b和6c所示，图中横轴表示误差值，纵轴表示对应误差值概率分布的相对大小，表 2为具体的拾取误差定量统计.分析可见，ST-Net初至拾取结果的误差分布均值(ME)与零点有较为明显的偏差，而MT-Net的误差分布均值更加接近零点，且其误差分布的标准差(SD)明显小于ST-Net，整体上具有更高的拾取精度.

图 6

Fig. 6

图 6 MT-Net与ST-Net的拾取误差高斯分布 (a) P波；(b) S波；(c) P-S波到时差. Fig. 6 Gaussian distribution of picking errors of MT-Net and ST-Net (a) P-phases; (b) S-phases; (c) Time differences between P-phases and S-phases.

在实际资料处理中，P-S波到时差是否准确对后续事件定位结果影响巨大.由图 4b、4h中ST-Net与MT-Net的输出概率分布曲线可见，与ST-Net相比，MT-Net的输出概率分布曲线峰值处相对平缓，这主要是受公式(2)中标签概率分布函数设定的影响.但由表 2的统计分析可见，对于MT-Net，P-S波到时差的误差标准差不但比ST-Net的结果降低近一个数量级，而且显著小于MT-Net对P波、S波的误差标准差.这说明MT-Net较为平缓的输出概率分布并没有降低初至拾取的准确性，反而由于多道联合的空间约束提高了某些低信噪比道的拾取效果，使得出现拾取结果与手动拾取严重偏离的概率大大降低.对于P-S波到时差结果，多道联合的MT-Net拾取误差的标准差只有0.004 s，已经可以满足实时微地震监测数据处理需求，利用其拾取结果可以得到更加准确一致的事件定位结果.

表 2 (Table 2)

表 2 拾取误差结果定量统计(均值：ME，标准差：SD) Table 2 Quantitative statistics of arrival picking errors(Mean: ME, Standard deviation: SD) 方法 P波 S波 P-S波时差 ME SD ME SD ME SD ST-Net -0.002 s 0.034 s -0.011 s 0.047 s -0.008 s 0.030 s MT-Net 0.001 s 0.012 s 0 s 0.014 s -0.001 s 0.004 s

表 2 拾取误差结果定量统计(均值：ME，标准差：SD) Table 2 Quantitative statistics of arrival picking errors(Mean: ME, Standard deviation: SD)

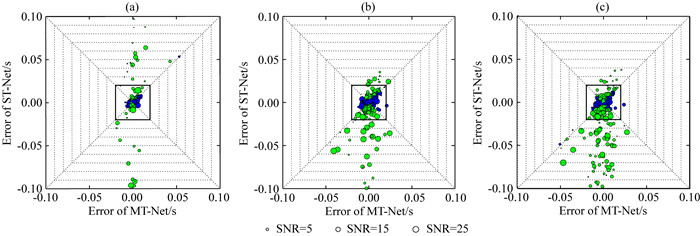
如图 7所示，我们从另一个角度观察分析双震相样本的初至拾取误差分布，图示横纵坐标分别为ST-Net、MT-Net的初至拾取结果与样本手动拾取结果之间的差值，所有样本均以实心圆圈表示，蓝色圆圈为ST-Net拾取误差绝对值小于MT-Net的样本，绿色圆圈为ST-Net大于MT-Net的样本，圆圈的相对大小与其对应微地震事件的信噪比成正比，信噪比SNR的计算公式为

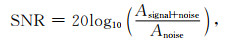
(4)

图 7

Fig. 7

图 7 双震相样本的拾取误差分布 (a) P波；(b) S波；(c) P-S波到时差.绿色圆圈：ST-Net拾取误差绝对值大于MT-Net的样本；蓝色圆圈：MT-Net拾取误差绝对值大于ST-Net的样本. Fig. 7 Arrival picking error distribution of double-phase samples (a) P-phases; (b) S-phases; (c) Time differences between P-phases and S-phases.Green circle: the absolute error of ST-Net is greater than that of MT-Net; Blue circle: the absolute error of MT-Net is greater than that of ST-Net.

A_noise和A_signal+noise分别表示初至到达前、后波形记录的均方根振幅，由于S波初至可能会受P波初至影响，我们利用P波初至(以手动拾取结果为准)前、后的波形记录计算得到信噪比SNR.

根据实际处理经验，我们认为拾取误差在0.02 s内均在可接受的范围内，在图中以黑色实线围成的正方形区域表示.在图 7a、7b、7c中，绿色圆圈的数量及分散程度远远大于蓝色圆圈，说明总体上MT-Net较ST-Net的拾取误差绝对值更小，且整体上信噪比较低(圆圈较小)的样本对应的误差绝对值更大.由图可见，蓝色圆圈基本都落在了正方形区域内，而绿色圆圈中有相当大一部分落于区域之外，说明MT-Net拾取误差较大的样本显著少于ST-Net.综上，图 6、图 7从两个方面同时验证了MT-Net可以有效避免较大拾取误差出现的概率.

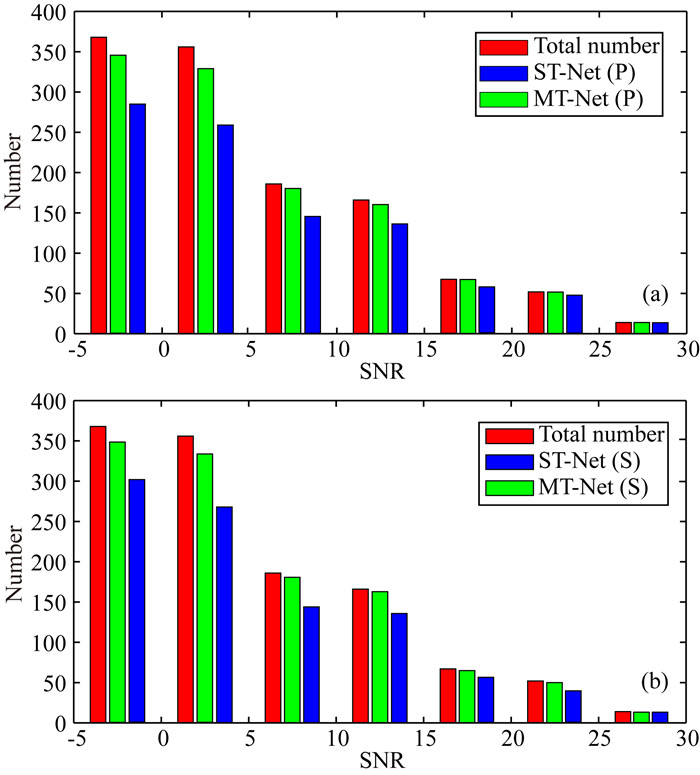
对于测试集中的有效事件样本，我们认为拾取误差约在一个震相范围内即为拾取准确，分别设置P波、S波的拾取误差小于0.01 s(20个采样点)、0.02 s(40个采样点)即为拾取准确，准确拾取的样本数量统计情况如图 8所示，红色柱形为测试集中某一信噪比范围内所有的样本数量.由图可见，在不同信噪比范围内，MT-Net(绿色柱形)相较ST-Net(蓝色柱形)准确拾取的样本数量均有增加：SNR分布于-5~0范围内样本的P波拾取准确率从77.45%提高至93.75%，S波拾取准确率从81.79%提高至94.57%；SNR分布于0~5范围内样本的P波拾取准确率从72.75%提高至92.42%，S波拾取准确率从75.28%提高至93.54%.验证了与ST-Net相比，MT-Net对低信噪比事件拾取准确率的提高效果最为显著.

图 8

Fig. 8

图 8 两种方法准确拾取的样本数量统计 (a) P波；(b) S波. Fig. 8 Quantity statistics of samples accurately picked by the two methods (a) P-phases; (b) S-phases.

水力压裂实时微地震监测需要对微地震事件进行快速识别、拾取和定位工作，一个高效、准确且无需人工经验干预的自动化处理程序是我们的最终目标.本文提出的多道联合方法MT-Net只需利用具有不同特征的波形记录样本搭建深度学习框架，模型在完成训练和验证之后即可自动建立输入微地震波形与识别/拾取结果间的对应关系，并对连续记录进行实时处理.实际数据测试结果表明MT-Net的识别和拾取结果已经与应用效果较好的多道互相关方法(Tan and He, 2016)十分接近，说明了基于U-Net的多道联合方法可满足实际微地震处理中对识别与拾取精度的要求.

本文在使用MT-Net方法扫描连续记录的过程中，将P波和S波输出概率分布的判定阈值设置为0.5，没有出现将噪声样本误拾为有效事件的情况.进一步降低阈值可能识别出更多的低信噪比事件，但同时也可能出现将噪声样本误判为有效事件的现象.在实际处理中，可根据具体的监测处理需求调整阈值大小，在漏拾和误拾情况间达到平衡.

在实时监测任务中，模型的训练样本质量直接决定了深度学习模型最终的应用效果.因此，一个人工样本质量控制与深度学习模型协同作用的现场工作流程是必不可少的.如图 9所示，在初始压裂阶段，首先利用自动微地震识别与拾取方法(如多道互相关法)快速得到疑似微地震事件，并人为对疑似微地震事件分类和排查，对有效事件进行初至拾取，并将结果作为样本标签完成MT-Net模型的构建与训练；将这一初始模型应用于第二个压裂段，对该段内的连续记录进行扫描，在得到该段内微地震事件和初至拾取结果的同时，对其质量进行人工判别，将识别和拾取效果较差的事件剔除，将剩余样本补充进训练样本集中，参与对MT-Net模型的重构与训练；在后续压裂施工中不断重复上述过程直到压裂施工结束.随着压裂施工的进展，MT-Net模型的样本集在不断扩大，模型的识别/拾取能力也相应地在不断提高.

图 9

Fig. 9

图 9 基于MT-Net的实时微地震震相识别和初至拾取流程 Fig. 9 The real-time microseismic phase detection and arrival picking process based on MT-Net

本文基于深度学习中的U-Net模型提出了一种井中多道联合微地震震相识别和初至拾取方法(MT-Net).方法根据井中微地震观测系统中多级检波器依次排列的多道数据源特点，通过U-Net中的二维卷积操作同时约束道内和道间的波形信息，提高了震相识别的有效性和初至拾取的准确性.以此为基础，结合水平井多段压裂的施工特点，本文提出了满足现场压裂微地震监测实时性与准确性要求的工作流程，通过人工样本质量控制与深度学习模型协同作用，逐段扩充样本集，达到不断修正和优化MT-Net模型的目的.基于数据驱动的深度学习技术在微地震震相识别和初至拾取工作中取得了初步的应用效果，但这并非意味着这一技术在目前阶段可以完全取代基于信号特征差异的常规处理方法；相反，一个模型驱动与数据驱动相结合的压裂微地震监测数据处理流程将展现出更大的应用潜力.