2. 山东建筑大学测绘地理信息学院, 济南 250101
2. School of Surveying and Geo-Informatics, Shandong Jianzhu University, Jinan 250101, China
地震是地壳岩层受力突破弹性极限(抗剪切强度)后快速破裂错动引起的地表振动或破坏,是对人类文明威胁最大的自然灾害之一.震源参数反演是研究地震断层错动特征、震源机制、触发关系等的重要方式,也是地震危险性评价及地震预警的基础.地表形变是地震发生时最直接的表现,是研究地震断层构造、破坏程度及地震机理等的重要资料(王乐洋等,2017).在获取地表形变数据的过程中,由于各种噪声的干扰导致形变数据的准确性和可靠性受到影响,进而导致震源参数的精度损失.因此,获取震源参数的精度信息、误差水平及可信程度显得尤为重要,对震源参数进行精度评定研究成为了提升成果质量的重要内容,对准确、深刻的理解地震也具有一定的实际意义.
由于依据弹性半空间矩形位错模型(Okada,1985)建立的关于地表形变与震源参数之间的关系为复杂多维的非线性函数,因此需要依靠搜索算法进行非线性反演.常用的搜索算法有模拟退火法(Kirkpatrick et al., 1983)、粒子群算法(Kennedy and Eberhart, 1995;冯万鹏和李振洪,2010)、神经网络法(Barradas and Vieira, 2000)、遗传算法(Genetic Algorithm,GA)(Holland,1975)等,该类方法无需获取参数的解析表达式,也无需求导计算,因此常用于非线性反演获取参数最优值.遗传算法不必明确地描述优化问题的全部特征,且不存在连续性、可导或单峰等特殊要求,因此具有通用性.此外,该搜索算法全局性性强,不易陷入局部最优,并且适合并行计算(王新洲,2002),因此较适用于数据量大的大地测量震源参数非线性反演问题研究(Nolte and Frazer, 1994;万永革等,1997;王文萍和王庆良,1999).
将震源参数反演过程视为一个非线性函数,目前已有的非线性精度评定方法有近似函数法(徐培亮,1986;Xue et al., 2015;Wang and Zhao, 2019)和近似非线性函数的概率密度分布方法(王乐洋和赵英文,2019;Wang and Yu, 2019;Wang and Zou, 2019).近似函数法需要利用泰勒级数公式对非线性模型展开,根据误差传播定律获取参数估值的方差或协方差.但由于该方法无法避免求导计算,因此在震源参数精度评定研究中适用性较差.通过采样来代替复杂求导计算的非线性精度评定方法包括蒙特卡罗(Monte Carlo, MC)方法、自适应蒙特卡罗(Adaptive Monte Carlo, AMC)方法、Jackknife方法、Sterling插值方法等.该类方法一般通过重复采样获取随机样本来近似非线性函数的概率密度分布,进而输出待统计量的精度信息,这些采样方法在一般的非线性模型精度评定问题中能够取得较好的效果.在震源参数反演精度评定方面,Monte Carlo方法得到了较为广泛的应用(Wright et al., 1999;Funning et al., 2005;Dawson and Tregoning, 2007;Xu et al., 2017),亦有学者将Jackknife方法、SUT(Scaled Unscented Transformation)方法、Sterling插值方法用于地震大地测量反演精度评估(Ichinose et al., 2003;Prieto et al., 2007;Wang and Zou, 2021;Wang and Ding, 2020).
Bootstrap方法(Johnson,2001;Chen,2018)也称为自助法,是一种用于估计和修正统计估计值的偏差或方差信息的一种统计推断方法.Efron(1979)首次提出了通过重复采样得到的自助世界的经验分布来逼近总体真实分布的思想,并给出了其基本采样策略和相关理论证明.由于Bootstrap方法通过重采样代替求导计算,只需选择采样次数并结合有放回抽样策略获取自助样本,最后解算每个样本便可求得未知统计量的均值和协方差阵,因此历年来有较多学者将该方法用于偏差分析和方差计算(Sahinler and Topuz, 2007;Kitagawa and Konishi, 2010;O′Hagan et al., 2019).目前,关于Bootstrap方法的研究成果较为丰富,主要集中于该方法在统计学上的性质(Martínez-Camblor and Corral, 2012;Pan and Politis, 2016).目前,已有部分学者将Bootstrap方法用于地球科学反演精度评估问题,Wéber(2005)利用贝叶斯方法和Bootstrap重采样对震源参数进行了误差分析;Cesca等(2014)通过Bootstrap采样来评估发震断层位置的不确定性;Jia等(2017)采用Bootstrap方法来估计质心深度的不确定性.但Bootstrap采样方法在大地测量震源参数反演精度评定方面的性能未得到较为全面的研究,尚未给出将该方法用于获取震源参数精度信息的详细采样步骤及具体实现流程,并且在震源参数中误差计算及区间估计方面的对比评价也未得到重视.
针对以上问题,本文从为了获取参数估值更为合理的精度信息出发,将Bootstrap方法用于震源参数非线性反演的精度评定研究中,通过对地表形变数据实施自助重采样并结合遗传算法,进而设计得到震源参数反演精度评定的Bootstrap方法计算流程.最后通过6个模拟地震、Amatrice地震和Visso地震,对本文精度评定方法的有效性和可靠性进行验证.
1 震源参数反演与遗传算法 1.1 震源参数反演均匀弹性半空间矩形位错模型是反演震源参数的常用有效模型(Okada,1985),本文采用Okada矩形位错模型并结合GPS台站地表形变观测资料进行震源参数反演.地表形变量观测值与震源参数之间为高度非线性关系,其函数模型可表示为
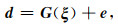
|
(1) |
式中,d为GPS观测到的地表形变量,它包含dx、dy及dz三个分量,分别表示东西、南北和垂直三个不同方向的地表形变.G(·)为利用Okada弹性位错理论模型建立的关于GPS地表形变量与震源参数的复杂非线性关系.e为GPS地表形变量观测误差.ξ为震源参数,包括发震断层位置(经度、纬度、深度),断层尺寸(长度、宽度),断层几何(走向角、倾角、滑动角)以及滑动量;本文以顶深、底深、走向角、倾角、长度、滑动角、滑动量以及断层中心位置为参数进行反演和精度评定,其中通过顶深和底深可计算获得深度,长度可联立顶深、底深及倾角获取.
1.2 遗传算法在震源参数反演中的应用由于震源参数未知向量与地表形变观测值向量之间是复杂的多维非线性关系,本文将遗传算法运用于震源参数反演问题.遗传算法最早由美国教授Holland(1975)提出,该算法是一种启发式高级全局搜索算法,它所依据的是自然界生物优胜劣汰的生存法则,是基于达尔文的进化论和孟德尔的遗传学说建立的.遗传算法仅通过目标函数而不需要其他附加条件对种群(将待求参数称之为种群,每个参数称之为个体)进行全局搜索.对提高算法的搜索效率并保证反演得到的震源参数具有物理意义,反演前通常需要给定震源参数的搜索区间作为约束.本文在使用遗传算法进行震源参数反演时,首先在全参数空间内进行全局搜索,当获取初步的反演结果后再缩减搜索空间并通过反复迭代计算最后求得稳定的最优解.
将遗传算法用于震源参数反演的大致步骤是首先使用二进制对区间内的数进行编码;其次,随机生成一组任意排列的字符串,即产生初始种群;然后根据提前设置的适应度函数判断个体的优劣性,淘汰适应度低的个体,选择复制适应度较高的个体作为父代并且进行交叉和变异操作进而生成下一代个体;最后通过不断繁殖、选择、交叉及变异,便可朝最优解的方向进化获得最优的震源参数.遗传算法实现非线性反演的具体过程总结为
1) 选择初始群体大小pop及最大迭代次数maxgen.
2) 编码:编码是将震源参数解的搜索范围转换到遗传算法所能认知的搜索空间的一种转换方式,通过编码将具体的非线性反演问题与自然界生物进化建立联系.
3) 生成初始种群:在编码区间内随机生成数量为pop的初始参数,作为遗传算法求解优化问题时的初始解的集合.
4) 个体适应度函数值的计算:适应度函数是用来评价个体优劣的指标.震源参数反演中常将残差的均方根即式(2)作为目标函数,计算每个个体的适应度函数值,区分出每个个体的优劣性.
5) 选择复制:将步骤4)所计算出的个体适应度函数值作为评价标准,选择出适应度较好的个体作为父代来繁衍后代种群.
6) 交叉:交叉是个体两两配对的过程即基因重组过程,具体实现过程为从父代中选取部分基因,并以某个交叉概率交换部分染色体进而生成新的个体.该过程的目的是为了生成新一代个体以提升算法搜索能力.
7) 变异:基因遗传算法中的变异过程是指等位基因替换引起的基因结构的变化,是自然界生物进化的必然要求.变异的目的是保证种群多样性,防止陷入局部最优.
8) 更新:将步骤7)获取到的子代作为更适应环境的父代种群,重复步骤4)~步骤7),重新计算个体适应度函数值、选择、交叉、变异,直到迭代次数大于设定的最大迭代次数即Itei>maxgen则跳出迭代.那么,最新一代中适应度函数值最小所对应的个体即为震源参数的最优参数估值.
在使用基因遗传算法反演震源参数的过程中,本文采用地表形变观测值与Okada模型预测值差值的均方根(Root Mean Square, RMS)误差作为目标函数来评估反演结果,其表达式为
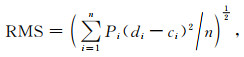
|
(2) |
式中,n为地表GPS观测点个数,Pi表示每个观测值的权值,di为形变实际观测值,ci为通过反演模型得到的地表形变预测值.
2 震源参数反演及精度评定的Bootstrap方法Bootstrap方法将原始观测值样本作为总体,利用有放回随机抽样法从总体分布函数中得到一系列独立样本(称为自助样本),并通过计算每个自助样本来获取未知统计量抽样分布的经验估计(Efron,1979;Sahinler and Topuz, 2007).该方法的优势性主要表现在它不需要对未知模型及分布做任何假设,也无需推导估计量的精确表达式,只需通过检验样本内统计量的变化便能够估计未知参数的均值和方差.Bootstrap方法通过重采样获取自助样本的方式来代替复杂的求导运算,因此本文将Bootstrap方法引入到震源参数精度评定问题,试图通过在避免求导计算的情形下依然能够获取合理的精度评定结果.
2.1 精度评定的Bootstrap方法
假设给定样本集(ux1, ux2, …, uxn; uy1, uy2, …, uyn; uz1, uz2, …, uzn)来自于独立同分布的样本,总体的分布函数为F(X, ξ),其中X为固定的GPS观测点三个方向的形变量数据样本(假设地表GPS观测点个数为n,则X的样本容量为3×n,Xi为X的样本值),ξ为未知的震源参数,其估值表示为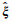
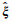
Bootstrap方法首先将原始固定的GPS观测点三个方向形变量数据样本X定义为总体,然后将1/n的概率分别设置在随机项中每个元素Xi上,并通过一个随机数生成过程来抽取一个包含某些特定GPS观测点形变量的自助样本;通过基因遗传搜索算法获取震源参数估计值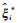
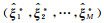
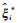

|
(3) |
式中,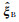
震源参数估值的方差-协方差阵计算公式为
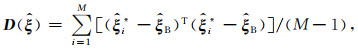
|
(4) |
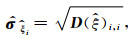
|
(5) |
式中,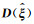
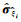
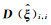
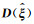
由式(3)可知,震源参数均值的Bootstrap估计值是未知参数的近似值,它未反应出该近似值的误差范围和可信程度.本文试图确定一个区间并具有较高的可靠程度相信该区间包含震源参数真值,因此引入置信区间的Bootstrap估计.最常用且最实用的Bootstrap置信区间技术有4种:百分位t法(Efron,1981)、百分位法(Efron,1982)、偏差改正百分位法(Efron,1982;Stine,1989)以及正态近似法(Efron,1981;Diciccio and Tibshirani, 1987;Sahinler and Topuz, 2007).百分位t法需要将每个自助样本获取到的参数估值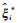
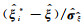


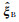

|
(6) |
式中,pr表示概率,α为显著性水平,Zα/2为对应的标准分数.
2.2 精度评定计算步骤为充分利用总体包含在样本中的先验信息和数据性质,Bootstrap方法通过有放回随机抽样将GPS观测点三个方向形变量数据采样成多个自助样本,原始样本集中的每个样本点被采样到的概率相同,每个自助样本的样本容量与原始样本相同.顾及GPS站点形变量含有误差,故对三个方向形变量数据按照其对应的观测精度进行加权处理,通常将三个方向形变量所对应的观测中误差作为定权的依据.在重采样获得自助样本的过程中,需保持自助样本中的形变观测值与其权值Pi相对应,具体表现为重采样三个方向形变量数据的中误差.形变值与对应中误差两者的采样方式一致.根据以上分析,总结得到震源参数精度评定的Bootstrap方法的完整计算步骤:
1) 假设n个GPS观测点的三个方向形变量为随机项样本N=(ux, uy, uz),其对应的观测中误差为ε=(σx, σy, σz);
2) 将1/n的概率分别设置在N中的每个样本值上;
3) 产生服从均匀分布的n个随机数(i1, i2, …in),其中1≤ij≤n, j=1, 2, 3, …, n;
4) 对N中的元素采样,获取自助样本Nr*=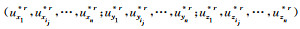
5) 对ε中的元素进行采样,获取自助样本元素对应的中误差εr*=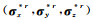
6) 根据εr*重新计算自助样本的权阵Pr*;
7) 将Nr*和Pr*代入基因遗传算法,获取震源参数的估值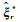
8) 循环步骤3)~步骤7)M次,得到M组参数估值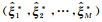
9) 分别利用式(3)、式(4)获取震源参数的均值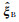
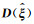
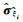
根据以上计算步骤,可得Bootstrap方法评定震源参数精度的计算流程图,如图 1所示.

|
图 1 震源参数精度评定的Bootstrap方法迭代流程图 Fig. 1 The iteration flow chart of the Bootstrap resampling method for precision estimation of fault source parameters |
由以上的震源参数精度评定的Bootstrap方法计算流程可知,本文精度评定方法获得的所有自助样本中的数据均来源于原始固定的GPS观测点三个方向形变量数据,并未根据更多的观测形变信息进行计算.Bootstrap方法的采样过程不会产生额外的模型误差,也不会改变模型态性.尽管每个自助样本的样本容量与原始样本相同,但不是改变GPS观测点三个方向形变量数据的先后排列顺序,有放回随机抽样过程使得每个自助样本中可能存在重复的数据点,而另外一些样本点则没有出现.因此,每个自助样本将随机地异于原始样本,导致每个自助样本反演得到的震源参数估值存在细微差异.
3 实验与分析为验证Bootstrap方法在震源参数非线性反演精度评定中的可靠性和有效性以及探讨该方法在实际震例中的性能,本文共设计了6个模拟实验,同时也将本文精度评定方法用于获取Amatrice地震和Visso地震的震源参数精度信息,并与Jackknife方法和Monte Carlo方法进行对比分析.当使用到遗传算法时,为同时保证较高的反演精度和反演效率,初始群体大小取值为450,最大迭代次数选择200次,交叉概率为0.85,变异概率选择0.1.Bootstrap采样次数的选择取决于统计量的具体研究问题并且依赖于需要做的检验(例如方差或置信区间)(Efron,1981),诸多统计学家给出了抽样次数的经验取值,若要获取未知参数较为合理的方差或中误差,采样次数应为50~200之间,当采样次数超过200时,方差近似值的改进很小(Efron,1981;Efron and Tibshirani, 1986;Léger et al., 1992).经实验,通过增加自助采样次数在一定程度上能够提升精度评定结果质量,但随着采样次数的增加,中误差结果趋于较为稳定的值,而其计算量将成倍递增.本文依据已有研究的经验取值并顾及复杂多维的地震非线性反演实际问题,在保证较高的反演精度条件下,同时考虑较高的反演效率,因此本文将Bootstrap方法的采样次数设置为300.
本文对照实验中,Jackknife方法用于非线性模型精度评定的重采样策略及计算步骤借鉴Wang和Yu(2019)的研究成果.Wang和Yu(2019)研究发现,Jackknife-1方法获取的精度信息结果和Jackknife-d方法的结果基本一致,且Jackknife-d方法通常需要比Jackknife-1方法多Cnd-n次的计算量,随着d值的增大,其计算量也会迅速增加,因此本文采用Jackknife-1方法进行精度评定对比实验.震源参数置信区间的Jackknife估计公式及求取步骤见Sahinler和Topuz(2007).在计算震源参数置信区间时,显著性水平取值为0.05.其中Monte Carlo方法获取震源参数中误差的大致计算过程为:首先利用遗传算法获取的参数代入Okada模型正演出GPS地表形变;然后在正演出的形变数据中施加均值为0、单位权中误差为3 mm的正态分布随机噪声;循环构建300组模拟形变数据并分别利用遗传算法进行非线性反演;最后求取震源参数的统计均值及中误差.
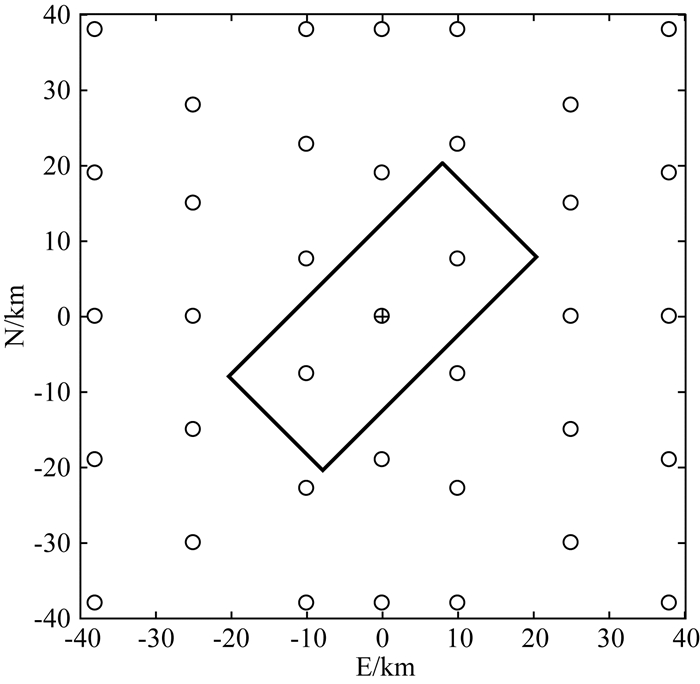
3.1 模拟地震通过仿真获取某一地震区域GPS观测点三个方向的形变量资料(仿真设置1):断层面的几何中心位于坐标系原点,37个GPS观测点分布在断层面几何中心的40 km范围内,模拟断层平面位置及GPS观测点分布如图 2所示(其中横坐标E为东方向,纵坐标N为北方向,矩形框表示断层投影平面);断层面几何参数的仿真设置为:断层顶深为2 km、底深为18 km、走向角为45°、倾角为60°、断层长度为40 km,滑动角为70°、滑动量为1.5 m;将GPS观测点坐标及参数模拟真值代入Okada模型正演获取形变量真值;最后在形变值真值上施加服从均值为0、单位权中误差为3 mm的随机正态分布噪声进而获取模拟形变量.仿真设置1的GPS同震形变场在水平方向和垂直方向的模拟形变值如图 3所示.
|
图 2 仿真设置1的断层平面位置及观测点位分布 Fig. 2 The fault plane position and observation point positions of the first simulation setting |
|
图 3 仿真设置1的GPS同震形变场 (a) 水平位移场;(b) 为垂直位移场. Fig. 3 The coseismic displacement fields of the first simulation setting obtained by GPS (a) The horizontal displacement field; (b) The vertical displacement field. |
在获取GPS形变量数据后,分别采用Jackknife方法和Bootstrap方法对地表形变值进行采样并获取震源参数均值和中误差;为推断总体均值,利用Bootstrap方法计算震源参数的置信区间,并与Jackknife方法的结果进行对照.各方法获取仿真设置1的震源参数结果、置信上下限及区间间隔列于表 1.
|
|
表 1 仿真设置1的震源参数搜索区间、参数估值及置信水平为95%情况下的置信区间计算结果 Table 1 Search ranges, inversion values, and confidence intervals with 95% confidence level of source parameters in the first simulation setting |
由表 1中的震源参数估值可以看出,使用遗传算法搜索到的震源参数估值与参数模拟真值基本一致,表明本文采用遗传算法进行非线性反演是正确且可靠的.Jackknife方法和Bootstrap方法得到的震源参数在符号和量级上与遗传算法的结果相同,且Bootstrap方法的结果与真值的差值二范数小于遗传搜索算法和Jackknife方法的结果;根据遗传算法、Jackknife方法和Bootstrap方法获取的震源参数得到的矩震级均为MW6.97,与模拟的矩震级MW6.98的差异仅在小数点后第2位.这表明基于重采样的Bootstrap方法能够适用于震源参数非线性反演,也说明该方法通过对形变量数据实施自助采样在一定程度上能够降低反演估值的偏差,因此其震源参数反演值比遗传算法和Jackknife方法的结果更加靠近模拟真值.
根据表 1中各参数的置信上限、置信下限及区间间隔可以看出,在95%置信水平下,Jackknife方法获取的震源参数置信区间均比Bootstrap方法获取的置信区间更宽,说明Jackknife方法反演得到的震源参数的可靠性较弱,因此Bootstrap方法的反演精度较高.这表明在震源参数非线性反演问题中,Bootstrap方法获取的参数估值比Jackknife方法的结果更具可信度.由于置信区间的计算公式取决于所用的统计量,Jackknife方法的样本量为总观测个数,而Bootstrap方法的样本量可根据模型复杂度或样本容量进行调整.因此,与Jackknife方法相比,Bootstrap方法在震源参数反演中更具可靠性和适用性.
为评估在不同随机噪声水平及不同GPS观测个数情况下,Bootstrap方法获取震源参数估值精度信息的性能,本文在仿真设置1的基础上增加了5个不同的模拟实验.仿真设置2:参数真值及GPS观测点个数不变,在形变量真值上施加服从均值为0、单位权中误差为5 mm的正态分布随机噪声;仿真设置3:模拟参数真值不变,GPS观测点个数增至49个,形变量中的随机噪声满足均值为0、单位权中误差为3 mm的正态分布;仿真设置4:参数真值不变,GPS观测点个数为49个,在形变量真值上添加均值为0、单位权中误差为5 mm的正态分布随机噪声.为进一步验证观测点数量对Bootstrap方法精度评定结果的影响,本文增设了仿真设置5,即随机误差水平同为N(0, 32mm)情况下,使得仿真设置1的GPS观测点个数增加一倍.为评价Bootstrap方法在GPS站点分布不均匀情况下的精度评定性能,本文设计了仿真设置6实验:震源参数真值、形变量的随机误差水平及GPS观测点个数与仿真设置1相同,站点在断层面几何中心(坐标系原点)的40 km范围内不均匀分布.本文获取不均匀分布的GPS站点坐标的大致过程为:首先采用MATLAB中的rand函数产生2组范围在(0, 1)之间的均匀分布随机数(x1, x2, …, xn)和(y1, y2, …, yn),然后分别将其转换化为在(-40, 40)之间的随机数(x1*, x2*, …, xn*)和(y1*, y2*, …, yn*),最后进行组合获取模拟站点坐标(xi*, yi*).为直观表示,将仿真设置6的GPS同震形变场在水平方向和垂直方向的模拟形变值绘于图 4;各仿真设置异同及相应说明列于表 2.

|
图 4 仿真设置6的GPS同震形变场 (a) 水平位移场;(b) 垂直位移场. Fig. 4 The coseismic displacement fields of the sixth simulation setting obtained by GPS (a) The horizontal displacement field; (b) The vertical displacement field. |
|
|
表 2 六种实验方案及其说明 Table 2 The six experimental schemes and their explanations |
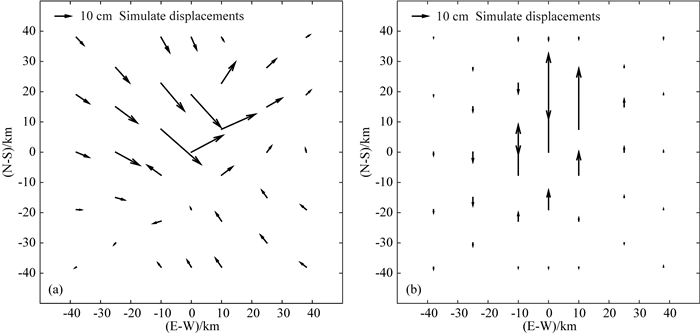
在获取以上6个仿真设置的形变量数据后,分别利用Bootstrap方法、Jackknife方法和Monte Carlo方法获取震源参数的中误差,3种精度评定方法的计算结果列于表 3,并将6个不同仿真设置的中误差可视化绘于图 5((a—f)所绘中误差分别表示仿真设置1~6的结果).
|
|
表 3 六种不同仿真设置下震源参数的中误差计算结果 Table 3 The standard errors of source parameters under the six different simulation settings |
|
图 5 不同仿真设置情况下的震源参数中误差图 图中,“TD”表示顶深(Top Depth)、“BD”表示底深(Bottom Depth)、“Strike”表示走向角(Strike)、“Dip”表示倾角(Dip)、“Length”表示长度(Length)、“Rake”表示滑动角(Rake)、“Slip”表示滑动量(Slip) Fig. 5 The standard error of source parameters under the six different simulation settings Let "TD" denote the Top Depth, and "BD" indicate the Bottom Depth. "Strike", "Dip", "Length", "Rake" and "Slip" corresponding to the source parameters Strike, Dip, Length, Rake and Slip, respectively. |
通过表 3中的参数中误差结果可以看出,Bootstrap方法在6个不同的仿真设置下所获得的震源参数中误差与Monte Carlo方法的结果在符号和量级上相同、在数值上相近,表明基于重采样的Bootstrap方法能够对反演得到震源参数进行有效的精度评定.从计算结果上看,相比于Monte Carlo方法所获得的震源参数中误差,Jackknife方法得到的结果偏离较大,是由于Jackknife法易受原始样本容量大小的影响且其重采样过程获取的刀切样本较少所致.表明Jackknife方法的结果可能会低估震源参数反演估值的精度,因此无法反映参数估值的真实精度.Bootstrap方法获取的震源参数中误差小于Jackknife法的结果且与Monte Carlo方法的结果较为接近.从图 5也可直观看出,在不同仿真设置情况下,Jackknife方法获取的参数中误差总是表现出较多深色,而Bootstrap方法的结果与Monte Carlo方法所得中误差颜色较为相近且浅色居多,这表明将Bootstrap方法用于解决震源参数精度评定问题是可行的,也表明Bootstrap方法在获取震源参数精度信息方面较Jackknife方法更加精确有效.
通过表 3中仿真设置1和仿真设置2的结果对比、以及仿真设置3和仿真设置4的结果对比可以看出,在GPS观测点个数相同的情况下,正态分布随机噪声越大,通过执行不同的采样方法获取的震源参数的中误差也均相应增大.对比图 5a与5b、图 5c与5d也可以直观看出,单位权中误差为5 mm的随机噪声情况下得到的震源参数中误差比3 mm情况下误差颜色更深,表明不同误差水平对震源参数精度的影响不同:随机误差越大,震源参数的精度越低.
对比表 3中仿真设置1、3、5的结果可以看出,当GPS观测点三个方向形变量数据的随机噪声为同分布情况下,将仿真设置1中的GPS观测点个数增加一倍,并未对仿真设置5的参数中误差结果造成较大的影响.并且随着观测点个数的增加,参数中误差并未呈现出较明显的递减趋势.通过对比仿真设置2、4的结果,图 5a、5c、5e,以及图 5b与5d的中误差也可发现,当误差水平相同条件下,观测点的个数对震源参数的中误差影响较小.因此,若试图通过增加GPS观测点数量来提升震源参数的精度可能并不十分显著.
从表 3中仿真设置6的结果可以看出,在GPS站点随机分布情况下,Bootstrap方法依然能够估出合理的震源参数中误差,而Jackknife方法的结果与Monte Carlo方法结果偏离较大.这表明Bootstrap方法同样适用于站点分布不均匀的普遍情况,并且能够获取比Jackknife方法更加合理的震源参数精度信息.对比仿真设置1与仿真设置6的结果可以看出,在相同的随机误差水平及GPS观测点个数的条件下,通过执行不同采样方法获取的不均匀分布站点情况下的震源参数中误差较均匀分布情况下的结果更大,这可能是因为不均匀分布站点对断层面的约束力不及均匀分布情况,进而导致更大的震源参数中误差.
3.2 Amatrice地震2016年8月24日,意大利中部阿马特里斯地区发生一次MW6.2地震,造成约300人伤亡且震中附近大量房屋被毁.美国地质调查局(United States Geological Survey, USGS)发布该地震的震中位置为(13.188°E,42.723°N),震源深度为4.4 km,属于浅层地震.震后,许多研究机构和学者快速对该地震进行了研究,分析了地震的震源机制、触发关系以及库仑应力(Wang et al., 2018);亦有学者对该地震进行了震源参数反演和精度评估(Xu et al., 2017),但针对不同的重采样精度评定方法的性能评估对比、以及Jackknife方法和Bootstrap方法区间估计的对比分析未得到深入的研究.
本文获取了Amatrice地震的106个GPS观测台站的形变量数据(https://ring.gm.ingv.it/),将Amatrice地震GPS同震形变场在水平方向和垂直方向的实际形变值、利用Okada模型正演得到的预测值及其对应残差分别绘于图 6(a、b、c).GPS形变整体拟合较好,水平方向的拟合残差RMS为0.11 cm,垂直方向的拟合残差RMS为0.36 cm,略小于Wang等(2018)得到的结果.水平方向的拟合精度整体上高于垂直方向,仅在主要形变区域的南侧及西北侧存在少量较大垂直残差.
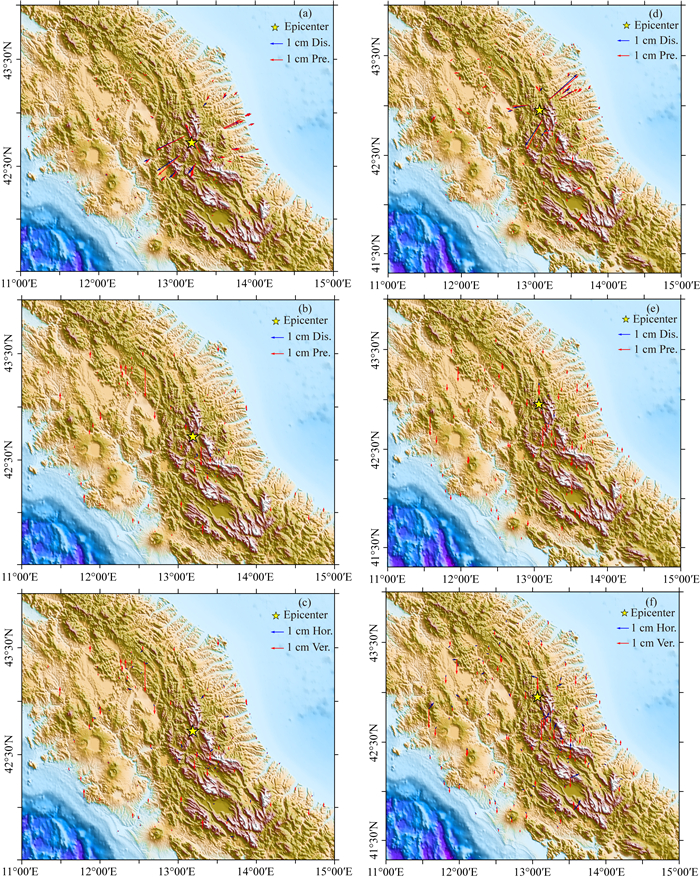
|
图 6 Amatrice地震和Visso地震GPS同震形变场及残差 (a) Amatrice地震水平位移场;(b) Amatrice地震垂直位移场;(c) Amatrice地震的残差图;(d) Visso地震水平位移场;(e) Visso地震垂直位移场;(f) Visso地震的残差图;“Dis.”为实际形变值(Displacement),“Pre.”为模型预测值(Prediction),“Hor.”为水平方向残差,“Ver.”为垂直方向残差. Fig. 6 The coseismic displacement fields and the corresponding residuals of Amatrice earthquake and Visso earthquake obtained by GPS (a) The horizontal displacement field of Amatrice earthquake; (b) The vertical displacement field of Amatrice earthquake; (c) The corresponding residuals of Amatrice earthquake; (d) The horizontal displacement field of Visso earthquake; (e) The vertical displacement field of Visso earthquake; (f) The corresponding residuals of Visso earthquake; "Dis." is the actual displacement, "Pre." is the model prediction; "Hor." is the horizontal residual, and "Ver." is the vertical residual. |
在获取形变量数据后,经过坐标转换将原始数据中的经纬度坐标转换为以USGS发布的震中位置为原点的大地坐标;在均匀位错模型和遗传算法的基础上,利用Bootstrap方法对该地震的形变量数据进行重采样,通过遗传算法搜索震源参数并获取断层参数的置信区间;再采用Bootstrap方法获取参数的中误差并与Jackknife方法和Monte Carlo方法的计算结果进行对比评估.参数的搜索区间、部分已有文献研究结果、Monte Carlo方法获取的中误差,以及Jackknife方法和Bootstrap方法的反演估值、置信上下限、区间间隔和参数中误差均列于表 4.
|
|
表 4 Amatrice地震震源参数搜索区间、反演估值、95%置信区间及参数中误差计算结果 Table 4 Search ranges, inversion values, and confidence intervals with 95% confidence level of source parameters for the Amatrice earthquake |
根据表 4中的震源参数估值可以看出,遗传算法、Jackknife方法及Bootstrap方法获取的Amatrice地震震源参数较为接近.由于各研究者采用的反演方法和数据的不同,这3种方法得到的震源参数与已有文献的研究成果有所差异.通过对比各研究所得的矩震级可以发现,Bootstrap方法获取的震源参数得到的矩震级与已有研究成果较为接近,之间的差异在仅在小数点后第2位.这证明了将Bootstrap重采样与遗传算法相结合、并用于解决Amatrice地震的震源参数反演问题是可行的.
由表 4中Jackknife获取的震源参数置信区间的上下限可以看出,顶深、底深及滑动量的Jackknife置信区间的下限均为负值.其中滑动量的Jackknife置信区间为(-4.15551, 5.86072)即存在95%的概率相信该区间包含滑动量的真值,因此该结果说明Jackknife方法求取的顶深、底深及滑动量的置信区间包含的均值信息是模糊的或不精确的.通过对比Jackknife方法和Bootstrap方法获取到的震源参数置信区间的区间间隔可知,在置信水平同为95%的情况下,采用Bootstrap方法获取的区间间隔与Jackknife方法获取的结果相差较大,Bootstrap方法获取的9个震源参数置信区间均比Jackknife方法获取的区间更窄.这表明与Bootstrap方法相比,Jackknife方法反演得到的震源参数的精确度较低,而Bootstrap方法获取的参数估值更加可靠.
通过表 4中的震源参数中误差结果可以看出,Jackknife方法获取的震源参数中误差与Monte Carlo方法所得结果偏离较大,是因为Jackknife方法的重采样过程仅仅能够得到等于总观测数的少量刀切样本量所致,因此Jackknife方法会低估Amatrice地震的震源参数精度,无法提供反演估值的有效精度信息.Bootstrap方法获取的震源参数中误差小于Jackknife方法的结果,尽管Bootstrap方法获取的震源参数中误差比Monte Carlo方法的结果略大,但这两种方法得到的结果仍在符号和数量级上均保持一致、在数值上也较为接近.造成Bootstrap方法的中误差结果略大的原因可能是方法采样的随机性以及非线性反演算法自身无法避免的不稳定性.实验结果说明了本文震源参数精度评定的Bootstrap方法的有效性,也表明Bootstrap方法在获取震源参数精度信息方面较Jackknife方法更加精确.从9个参数的中误差数值结果可以看出,对于Amatrice地震,走向角、倾角、滑动角的中误差比其他6个震源参数更大,这可能是由于本文所采用的106个GPS观测台站的形变量数据中的随机噪声对角度量的反演产生较大影响所致,该现象也从侧面反映出本文给出的震源参数精度评定的Bootstrap方法能够合理反映Amatrice地震各个震源参数的精度信息.
3.3 Visso地震Amatrice地震发生的两个月后,震中30km范围内于2016年10月26日又发生一次6.1级地震.根据USGS消息,此次地震的震中位于13.067°E、42.956°N的维索西部约3km地区.地震触发后,许多学者和机构采用不同的数据和方法对该地震展开深入研究,分析了该地震的触发机制和周边断层的应力变化(Wang et al., 2018),反演了该地震的震源参数并获取了参数精度(Xu et al., 2017).
本文获取了127个GPS台站形变数据(https://ring.gm.ingv.it/)生成Visso地震同震形变场,GPS水平方向的拟合效果较好,残差RMS为0.17 cm,垂直方向残差RMS为0.44 cm,与Wang等(2018)的计算结果较为一致.残差的主要来源是GPS台站的观测误差,而垂直方向残差偏大是由于垂直观测精度较水平方向精度低造成的.各台站观测得到的水平方向和垂直方向的实际形变值、模型正演得到的预测值及其对应残差绘于图 6(d、e、f).
依据Okada弹性半空间位错模型理论及遗传算法,利用本文设计的精度评定方法对该地震进行震源参数搜索、置信区间计算及震源参数精度信息获取;并与Jackknife方法得到的参数置信区间和震源参数中误差、Monte Carlo方法得到的中误差进行对比分析,从而验证Bootstrap方法在实际地震的震源参数精度评定问题中的广泛适用性.参数搜索区间和部分已有文献研究结果,Jackknife方法和Bootstrap方法的反演估值、置信上下限、区间间隔和参数中误差,以及Monte Carlo方法获取的中误差均列于表 5.
|
|
表 5 Visso地震震源参数搜索区间、反演估值、95%置信区间及参数中误差计算结果 Table 5 Search ranges, inversion values, and confidence intervals with 95% confidence level of source parameters for the Visso earthquake |
对比表 5中的遗传算法、Jackknife方法及Bootstrap方法获取的Visso地震矩震级可以发现,Bootstrap方法的结果为MW6.04,略小于USGS提供的结果(MW6.10)及Xu等(2017)的结果(MW6.08),且比遗传算法和Jackknife方法更加接近已有的文献成果.由表 5中的震源参数95%置信区间结果可以发现,USGS提供的震源参数及Xu等(2017)的研究结果均在本文Bootstrap方法求取的置信区间内.由Jackknife方法计算得到的倾角置信下限为-31.34522、置信上限为107.78006.而Okada弹性半空间位错模型中的倾角是断层面与水平面的夹角,其范围仅为(0, 90].说明Jackknife方法获取的倾角置信区间内包含了一些无物理意义的信息,因此可信程度较低.由表中数据也可看出,Jackknife方法获取的滑动量置信区间为(-8.68948, 11.53444),区间长度达20.22392,说明Jackknife方法求取的滑动量置信区间过宽因此可靠性较弱.对比Jackknife方法和Bootstrap方法获取的Visso地震震源参数置信区间能够发现,Jackknife方法得到的9个参数置信区间宽度均比Bootstrap方法的结果偏大较多.以上分析说明了Bootstrap方法获取的震源参数可信程度更高.
表 5中的震源参数中误差显示,Jackknife方法获取的震源参数中误差与Monte Carlo方法所得结果差异较大,甚至出现量级不相等的情况.导致该现象是因为Jackknife重采样容易受原始样本影响,对于Visso地震,通过Jackknife方法重采样仅能够获取127个少量刀切样本,使得Jackknife方法获取的震源参数中误差因受样本量的影响进而偏离参数的真实精度信息,因此Jackknife方法在实际震例的震源参数精度评定问题中可能不适用.Bootstrap方法获取的震源参数中误差小于Jackknife方法的结果,并且与Monte Carlo方法所获结果在量级上一致、在数值上相近,说明Bootstrap方法能够有效地起到对震源参数精度评定的作用,表现出比Jackknife方法更强的优势.实验结果证明了本文方法用于Visso地震震源参数精度评定的可行性和有效性,也证明了本文方法具有广泛的适用性.从参数的中误差数值结果可以看出,在Visso地震精度评定研究中,分别使用Bootstrap方法和Monte Carlo方法获取的走向角、倾角、滑动角的中误差比其它6个参数的中误差更大,可能是因为本文采用的127个GPS台站形变量数据中的随机噪声对Visso地震的角度量参数反演产生较大影响所致.该现象也再次从侧面反映了Bootstrap方法的确能够合理反映实际震例的各个震源参数的精度信息.
4 结论为获取震源参数在统计意义上更加合理的精度信息,若采用传统的泰勒级数展开方法在计算过程中无法获取复杂多维非线性函数的偏导数.本文在Okada弹性半空间矩形位错模型及非线性反演遗传算法的基础上,引入了基于重采样的Bootstrap方法,定义了一种通过实施自助采样并解算自助样本便可获取震源参数中误差的精度评定方法,并给出了具体的采样步骤和迭代流程图.最后将震源参数精度评定的Bootstrap方法用于模拟地震、Amatrice地震和Visso地震实验中,通过对震源参数进行非线性反演、置信区间计算以及参数中误差获取,并与Jackknife方法计算得到的置信区间和中误差、Monte Carlo方法获取的中误差进行对比,对本文方法进行了验证.
模拟实验结果显示,采用本文方法获取的震源参数均值与模拟真值更为接近;同时,在不同的随机噪声水平、观测点个数以及GPS站点分布情况下,本文方法均能得到合理的精度信息.这表明将基于重采样的Bootstrap方法用于震源参数非线性反演及精度评定问题是可行且有效的.在Amatrice地震和Visso地震实验中,本文对比的已有研究结果均在Bootstrap方法求取的置信区间内,且Bootstrap方法获取的震源参数95%置信区间均比Jackknife方法得到的区间长度更窄.与Monte Carlo方法获取的震源参数中误差相比,Jackknife方法得到的参数中误差与之差异较大.尽管Bootstrap方法获取的震源参数中误差略大于Monte Carlo方法的结果,但这两种方法得到的结果仍在符号和数量级上均保持一致、在数值上也较为接近.实际地震结果验证了本文震源参数精度评定的Bootstrap方法的有效性和可靠性.Monte Carlo方法的结果依赖于三个方向形变量的平差值以及模拟随机误差时的协方差阵,并且该方法必须对总体模型做出具体的假设,例如需要假设扰动项的概率分布为高斯分布,而所得的结论只适用于该特定的数据生成过程.此时,不需要对未知模型及分布做任何假设的Bootstrap方法则表现出更强的适用性.随着Bootstrap方法引入震源参数精度评定问题,将拓展该采样方法在大地测量地震反演领域中的应用,对认知震源参数反演精度也具有一定的实际意义.
致谢 感谢审稿专家对本文提出的宝贵意见.文中部分图件是采用开源软件GMT绘制.
Babu G J, Singh K. 1983. Inference on means using the bootstrap. Annals of Statistics, 11(3): 999-1003. |
Barradas N P, Vieira A. 2000. Artificial neural network algorithm for analysis of Rutherford backscattering data. Physical Review E, 62(4): 5818-5829. DOI:10.1103/PhysRevE.62.5818 |
Cesca S, Grigoli F, Heimann S, et al. 2014. The 2013 September-October seismic sequence offshore Spain: a case of seismicity triggered by gas injection?. Geophysical Journal International, 198(2): 941-953. DOI:10.1093/gji/ggu172 |
Cheloni D, De Novellis V, Albano M, et al. 2017. Geodetic model of the 2016 central Italy earthquake sequence inferred from InSAR and GPS data. Geophysical Research Letters, 44(13): 6778-6787. DOI:10.1002/2017GL073580 |
Chen X H. 2018. Gaussian and Bootstrap approximations for high-dimensional U-statistics and their applications. The Annals of Statistics, 46(2): 642-678. |
Chiaraluce L, Stefano R D, Tinti E, et al. 2017. The 2016 central Italy seismic sequence: A first look at the mainshocks, aftershocks, and source models. Seismological Research Letters, 88(3): 757-771. DOI:10.1785/0220160221 |
Dawson J, Tregoning P. 2007. Uncertainty analysis of earthquake source parameters determined from InSAR: A simulation study. Journal of Geophysical Research Solid Earth, 112(B9): B09406. DOI:10.1029/2007JB005209 |
Diciccio T, Tibshirani R. 1987. Bootstrap confidence intervals and Bootstrap approximations. Journal of the American Statistical Association, 82(397): 163-170. DOI:10.1080/01621459.1987.10478409 |
Diciccio T J, Romano J P. 1988. A review of Bootstrap confidence intervals. Journal of the Royal Statistical Society: Series B (Methodological), 50(3): 338-354. DOI:10.1111/j.2517-6161.1988.tb01732.x |
Efron B. 1979. Bootstrap methods: another look at the Jackknife. The Annals of Statistics, 7(1): 1-26. |
Efron B. 1981. Nonparametric standard errors and confidence intervals. The Canadian Journal of Statistics, 9(2): 139-158. DOI:10.2307/3314608 |
Efron B. 1982. The Jackknife, the Bootstrap and Other Resampling Plans. Philadelphia, PA: Society for Industrial and Applied Mathematics.
|
Efron B, Tibshirani R. 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statistical Science, 1(1): 54-75. |
Feng W P, Li Z H. 2010. A novel hybrid PSO/simplex algorithm for determining earthquake source parameters using InSAR data. Progress in Geophysics (in Chinese), 25(4): 1189-1196. |
Funning G J, Parsons B, Wright T J, et al. 2005. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery. Journal of Geophysical Research: Solid Earth, 110(B9): B09406. DOI:10.1029/2004JB003338 |
Hall P. 1988. Theoretical comparison of bootstrap confidence intervals. Annals of Statistics, 16(3): 927-953. |
Holland J H. 1975. Adaptation in Natural and Artificial Systems. Ann Arbor: University of Michigan Press.
|
Ichinose G A. Anderson J G, Smith K D, et al. 2003. Source parameters of eastern California and Western Nevada earthquakes from regional moment tensor inversion. Bulletin of the Seismological Society of America, 93(1): 61-84. DOI:10.1785/0120020063 |
Jia Z, Ni S D, Chu R S, et al. 2017. Joint inversion for earthquake depths using local waveforms and amplitude spectra of Rayleigh waves. Pure and Applied Geophysics, 174(1): 261-277. DOI:10.1007/s00024-016-1373-1 |
Johnson R W. 2001. An introduction to the Bootstrap. Teaching Statistics, 23(2): 49-54. DOI:10.1111/1467-9639.00050 |
Kennedy J, Eberhart R. 1995. Particle swarm optimization. Proceedings of ICNN'95-International Conference on Neural Networks. Perth, WA, Australia: IEEE, 1942-1948.
|
Kirkpatrick S, Celatt C D Jr, Vecchi M P. 1983. Optimization by simulated annealing. Science, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
Kitagawa G, Konishi S. 2010. Bias and variance reduction techniques for Bootstrap information criteria. Annals of the Institute of Statistical Mathematics, 62(1): 209-234. DOI:10.1007/s10463-009-0237-1 |
Léger C, Politis D N, Romano O P. 1992. Bootstrap technology and applications. Technometrics, 34(4): 378-398. DOI:10.1080/00401706.1992.10484950 |
Lavecchia G, Castaldo R, Nardis R D, et al. 2016. Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modeling of DInSAR measurements and structural-geological data. Geophysical Research Letters, 43(24): 12389-12398. |
Martínez-Camblor P, Corral N. 2012. A general Bootstrap algorithm for hypothesis testing. Journal of Statistical Planning and Inference, 142(2): 589-600. DOI:10.1016/j.jspi.2011.09.003 |
Nolte B, Frazer L N. 1994. Vertical seismic profile inversion with genetic algorithms. Geophysical Journal International, 117(1): 162-178. DOI:10.1111/j.1365-246X.1994.tb03310.x |
O'Hagan A, Murphy T B, Scrucca L, et al. 2019. Investigation of parameter uncertainty in clustering using a Gaussian mixture model via Jackknife, Bootstrap and weighted likelihood Bootstrap. Computational Statistics, 34(4): 1779-1813. DOI:10.1007/s00180-019-00897-9 |
Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America, 75(4): 1135-1154. |
Pan L, Politis D N. 2016. Bootstrap prediction intervals for linear, nonlinear and nonparametric autoregressions. Journal of Statistical Planning and Inference, 177: 1-27. DOI:10.1016/j.jspi.2014.10.003 |
Prieto G A, Thomson D J, Vernon F L, et al. 2007. Confidence intervals for earthquake source parameters. Geophysical Journal International, 168(3): 1227-1234. DOI:10.1111/j.1365-246X.2006.03257.x |
Sahinler S, Topuz D. 2007. Bootstrap and Jackknife resampling algorithms for estimation of regression parameters. Journal of Applied Quantitative Methods, 2(2): 188-199. |
Stine R. 1989. An introduction to bootstrap methods. Sociological Methods & Research, 18(2-3): 243-291. |
Tinti E, Scognamiglio L, Michelini A, et al. 2016. Slip heterogeneity and directivity of the ML 6.0, 2016, Amatrice earthquake estimated with rapid finite-fault inversion. Geophysical Research Letters, 43(20): 10745-10752. DOI:10.1002/2016GL071263 |
Wéber Z. 2005. Probabilistic waveform inversion for focal parameters of local earthquakes. Acta Geodaetica et Geophysica Hungarica, 40(2): 229-239. DOI:10.1556/AGeod.40.2005.2.9 |
Wan Y G, Liu R F, Li H J. 1997. Inversion of 3D crustal structure and source location in Jing-Jin-Tang-Zhang area by genetic algorithm. Acta Seismologica Sinica (in Chinese), 19(6): 623-633. |
Wang L Y, Gao H, Feng G C. 2017. InSAR and GPS inversion for source parameters of the 2016 MW6.4 Meinong, Taiwan earthquake. Chinese Journal of Geophysics (in Chinese), 60(7): 2578-2588. DOI:10.6038/cjg20170707 |
Wang L Y, Gao H, Feng G C, et al. 2018. Source parameters and triggering links of the earthquake sequence in central Italy from 2009 to 2016 analyzed with GPS and InSAR Data. Tectonphysics, 744: 285-295. DOI:10.1016/j.tecto.2018.07.013 |
Wang L Y, Zhao Y W. 2019. Second-Order approximation function method for precision estimation of Total Least Squares. Journal of Surveying Engineering, 145(1): 04018011. DOI:10.1061/(ASCE)SU.1943-5428.0000266 |
Wang L Y, Zhao Y W. 2019. Adaptive Monte Carlo method for precision estimation of nonlinear adjustment. Geomatics and Information Science of Wuhan University (in Chinese), 44(2): 206-213, 220. |
Wang L Y, Zou C Y. 2019. Accuracy analysis and applications of the Sterling interpolation method for nonlinear function error propagation. Measurement, 146: 55-64. DOI:10.1016/j.measurement.2019.06.017 |
Wang L Y, Yu F B. 2019. Jackknife resample method for precision estimation of weighted total least squares. Communications in Statistics-Simulation and Computation, 2021, 50(5), 1272-1289.
|
Wang L Y, Ding R. 2020. Inversion and precision estimation of earthquake fault parameters based on scaled unscented transformation and hybrid PSO/Simplex algorithm with GPS measurement data. Measurement, 153: 107422. DOI:10.1016/j.measurement.2019.107422 |
Wang L Y, Zou C Y. 2021. Accuracy estimation of earthquake source geometry parameters by the Sterling interpolation method in nonlinear inversion. Journal of Surveying Engineering, 147(1): 04020019. DOI:10.1061/(ASCE)SU.1943-5428.0000331 |
Wang W P, Wang Q L. 1999. Joint inversion of republican seismic dislocation parameters using Genetic Algorithm and Least Squares. Acta Seismologica Sinica (in Chinese), 21(3): 285-290. |
Wang X Z. 2002. Theories and Applications of Nonlinear Model Parameter Estimation (in Chinese). Wuhan: Wuhan University Press.
|
Wright T J, Parsons B E, Jackson J A, et al. 1999. Source parameters of the 1 October 1995 Dinar (Turkey) earthquake from SAR interferometry and seismic bodywave modelling. Earth and Planetary Science Letters, 172(1-2): 23-37. DOI:10.1016/S0012-821X(99)00186-7 |
Xu G Y, Xu C J, Wen Y M, et al. 2017. Source parameters of the 2016-2017 central Italy earthquake sequence from the Sentinel-1, ALOS-2 and GPS data. Remote Sensing, 9(11): 1182. DOI:10.3390/rs9111182 |
Xu P L. 1986. Variance-covariance propagation for a nonlinear function. Geomatics and Information Science of Wuhan University (in Chinese), 11(2): 92-99. |
Xue J, Leung Y, Ma J H. 2015. High order Taylor series expansion methods for error propagation in geographic information systems. Journal of Geographical Systems, 17(2): 187-206. DOI:10.1007/s10109-014-0207-x |
冯万鹏, 李振洪. 2010. InSAR资料约束下震源参数的PSO混合算法反演策略. 地球物理学进展, 25(4): 1189-1196. DOI:10.3969/j.issn.1004-2903.2010.04.007 |
万永革, 刘瑞丰, 李鸿吉. 1997. 用遗传算法反演京津唐张地区的三维地壳结构和震源位置. 地震学报, 19(6): 623-633. |
王乐洋, 高华, 冯光财. 2017. 2016年台湾美浓MW6.4地震源参数的InSAR和GPS反演. 地球物理学报, 60(7): 2578-2588. DOI:10.6038/cjg20170707 |
王乐洋, 赵英文. 2019. 非线性平差精度评定的自适应蒙特卡罗法. 武汉大学学报·信息科学版, 44(2): 206-213, 220. |
王文萍, 王庆良. 1999. 利用遗传算法和最小二乘联合反演共和地震位错参数. 地震学报, 21(3): 285-290. DOI:10.3321/j.issn:0253-3782.1999.03.009 |
王新洲. 2002. 非线性模型参数估计理论与应用. 武汉: 武汉大学出版社.
|
徐培亮. 1986. 非线性函数的协方差传播公式. 武汉测绘科技大学学报, 11(2): 92-99. |
 2021, Vol. 64
2021, Vol. 64