0 引言

航空Z轴倾子法(ZTEM)正在逐渐成为一种快速普查浅层电阻率结构的重要方法(Hübert et al., 2016；Wang et al., 2016；Lee et al., 2018)，该方法利用直升机在一定飞行高度测量天然场源的垂直磁场，具有测量效率高的优点.ZTEM最大的优势是不需要直升机携带发射源，然而ZTEM观测的天然场源数据易受到环境噪音的污染.因此，我们希望可以使用可控源替代天然场源.最常见的利用人工源替代天然场源的勘探法，就是可控源音频大地电磁法(CSAMT)(林昌洪等，2012；Lin et al., 2018; He et al., 2019; Wang et al., 2019).CSAMT采用有限长线源产生一个人工电磁场，在强噪音环境下，通常被用来替代音频大地电磁法(AMT).

为了改善ZTEM，一种新的航空电磁系统在2015SEG会议被首次提出(Kang et al., 2015)，实际可以认为是人工源频率域半航空电磁法.设计者在早期计划利用直升机测量垂直磁场(Nittinger et al., 2017)，地面放置发射源，而现在新的实验和分析正在使用无人机进行(Zhou et al., 2016；Gao et al., 2019；Lin et al., 2019；Liu et al., 2020).利用无人机测量空中数据已在多个领域进行了尝试(Koparan et al., 2018；Zhai et al., 2019；Kachroo et al., 2019)，而将无人机应用于半航空电磁法同样具有明显的优势：①利用无人机可以测量来自人工源更强的垂直磁场；②无人机易于操作，可以悬停在空中更好的记录数据，且发射频率可以更低；③无人机不需要携带发射源.

目前无人机频率域半航空电磁法主要还在硬件研发阶段.Zhou等(2016)与Lin等(2019)介绍了他们的硬件系统，并初步对实验数据进行了分析.Gao等(2019)描述了硬件开发中一种新的发射波形.Liu等(2020)利用COMSOL Multiphysics分析软件进一步研究了数据分布特征.可以看出，无人机频率域半航空电磁法还有待进一步发展，但相关成果已经显示出该领域广阔的前景.

本文对Liu等(2020)的系统进行了调整，两个水平的接地双极源放置在不同的坐标轴上.为了更好的提高无人机半航空电磁法的反演效果，我们将它与大地电磁法进行联合反演，并引入交叉梯度实现结构约束.首先，大地电磁具有更低的频率，适当的增加大地电磁测深点，可以极大的提升勘探深度.利用大地电磁增加勘探深度已在其它领域有了诸多研究，比如Lee等(2018)实现了大地电磁与ZTEM的联合反演，Amatyakul et al.(2017)研究了大地电磁与直流电法的联合反演.其次，交叉梯度结构约束可以进一步提高电磁法的分辨能力，交叉梯度理论是Gallardo和Meju(2003)首次提出，并且他们很快就实现了直流电法与地震的二维联合反演(Gallardo and Meju, 2004)，取得了不错的效果.从此交叉梯度逐渐成为提高反演分辨率的重要方法，彭淼等(2013)实现了大地电磁与地震走时资料三维联合反演，Wang等(2017)实现了CSAMT与磁法的二维联合反演，闫政文等(2020)与张镕哲等(2019)实现了多个方法的联合反演，吴萍萍等(2020)实现了电阻率法和背景噪声法三维联合反演.从这些研究可以看出，交叉梯度可以有效提高反演分辨率.

为了实现上述目标，本文正演采用交错网格有限差分，反演采用有限内存拟牛顿法(LBFGS)，对于结构约束我们使用的方式不需要进行泰勒展开与近似，可以快速实现基于交叉梯度的结构约束方案.最后，本文通过建立四个理论模型验证三维反演的效果.

1 接收系统与正演模拟 1.1 无人机半航空电磁法装置

图 1展示了本文的发射与接收系统，两个正交的接地双极源被放置在不同的坐标轴上.发射源1放置在Y轴上，并平行于X轴，发射源2放置在X轴上，且平行于Y轴.当发射源1工作时，关闭发射源2，无人机悬停在空中采集垂直磁感应强度Bz₁.当发射源2工作时，关闭发射源1，无人机悬停在空中采集垂直磁感应强度Bz₂.图 1所示的系统与Liu等(2020)有一定的不同，此外我们在图 1中还显示了地面的大地电磁观测台站，目的就是要进一步拓展整个系统的勘探深度.

1.2 正演模拟

对于图 1的无人机系统，这里采用一次场与二次场分离的办法实现正演，二次场方程如下：

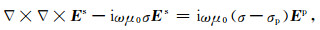
(1)

其中，ω为圆频率，μ₀为真空磁导率，σ为介质电导率，σ_p为背景电导率，E^s为二次场，E^p为背景场.针对大地电磁法，使用总场法计算：

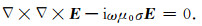
(2)

对于方程(1)与方程(2)，我们采用交错网格有限差分进行模拟计算.方程(1)的背景场采用解析解获得，边界条件设为电场的切向分量为零.方程(2)的边界条件来自于二维大地电磁正演，计算速度快，具体的离散过程可以参考作者之前的论文(Wang et al., 2019；罗威等，2019).

2 反演实现 2.1 无人机反演目标函数及梯度式

本文采用LBFGS法进行反演迭代计算，设目标函数为

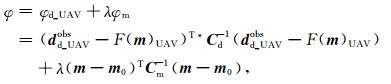
(3)

其中，obs代表观测数据，F代表正演算子，UAV代表无人机数据，*代表复数共轭，λ为正则化因子，C_d^-1与C_m^-1代表数据与模型协方差矩阵，m及m₀分别为电阻率的模型参数和先验模型.

本文采用仿射线性参数变换(Egbert and Kelbert, 2012；Kelbert et al., 2014)对真实模型参数进行如下转换：

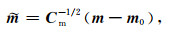
(4)

在上式变换下，最终的真实模型参数可以用以下式子获得：

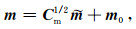
(5)

在参数变换策略下，目标函数(3)的梯度式为

(6)

针对式(6)所示的梯度计算，本文采用“拟正演”方案实现(Newman and Alumbaugh, 2000；Commer and Newman, 2008).

2.2 与大地电磁联合反演的目标函数及梯度式

为了提高无人机频率域半航空电磁法的反演深度，我们在反演中融入了大地电磁法，设联合反演目标函数为

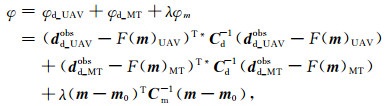
(7)

其中，MT代表大地电磁数据，其余参数与(3)式一致.

同样在参数变换的策略下，目标函数(7)的梯度表达式为

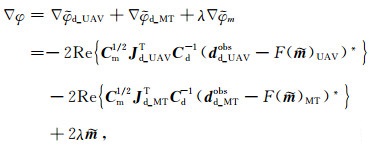
(8)

上式中的梯度计算，这里依然采用“拟正演”方案实现.

2.3 基于交叉梯度的结构耦合

在2.2节联合反演目标函数的基础上，我们希望可以进一步提高对先验结构信息的利用.基于此，本文提出在目标函数(7)的基础上进一步添加交叉梯度项：

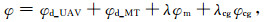
(9)

其中，φ_cg为交叉梯度项，λ_cg为交叉梯度项权重.

本文的交叉梯度项φ_cg定义如下：

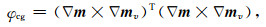
(10)

上式中，m_v为外部输入的已知结构信息，如速度结构.将上式按三个方向进一步展开，有

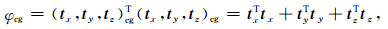
(11)

根据闫政文等(2020)，式(11)中t_x, t_y, t_z三个向量的任意元素可以表述为

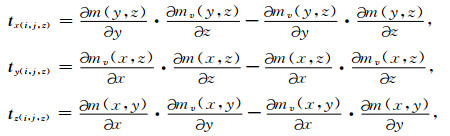
(12)

其中，m与m_v分别为某个电阻率参数和约束模型参数.

对于某个具体的t_{x(i, j, z)}计算，这里以图 2来说明，将t_{x(i, j, z)}以中心差分离散：

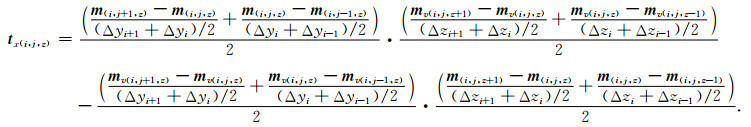
(13)

将式(13)以矩阵形式描述，则有

(14)

其中，a₁₁、a₂₂、a₃₃、a₄₄、a₅₅形式如下：

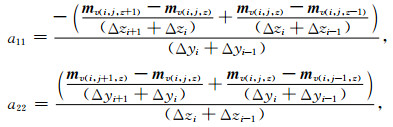
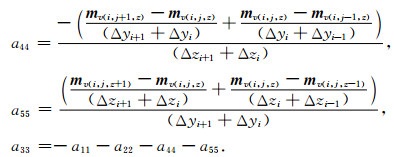
(15)

在图 2中的内部单元循环，可以完成t_x向量所有元素的计算.最终的t_x向量是由式(14)的矩阵累加形成，拓展到整个三维模型单元为

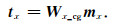
(16)

同样地，t_y, t_z以矩阵形式表述为

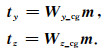
(17)

在式(16)与(17)中，矩阵W_{x_cg}, W_{y_cg}, W_{z_cg}包含了网格信息以及约束模型，因此交叉梯度以类似于模型协方差矩阵的形式对电阻率参数进行了结构约束.在式(16)与(17)的基础上，交叉梯度项φ_cg最终的矩阵形式为

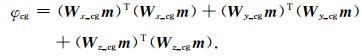
(18)

为了配合变换后的目标函数，最终含交叉梯度的总目标函数梯度式，有如下描述：

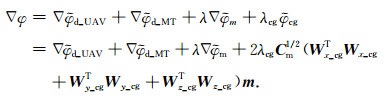
(19)

最终在目标函数(3)(7)(9)及相应的梯度表达式下，我们使用LBFGS(Nocedal and Wright, 2006)完成上述反演.

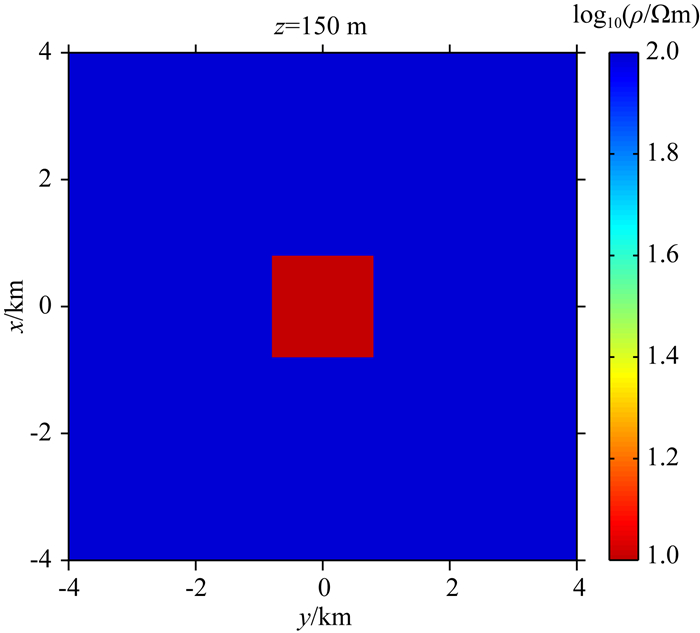
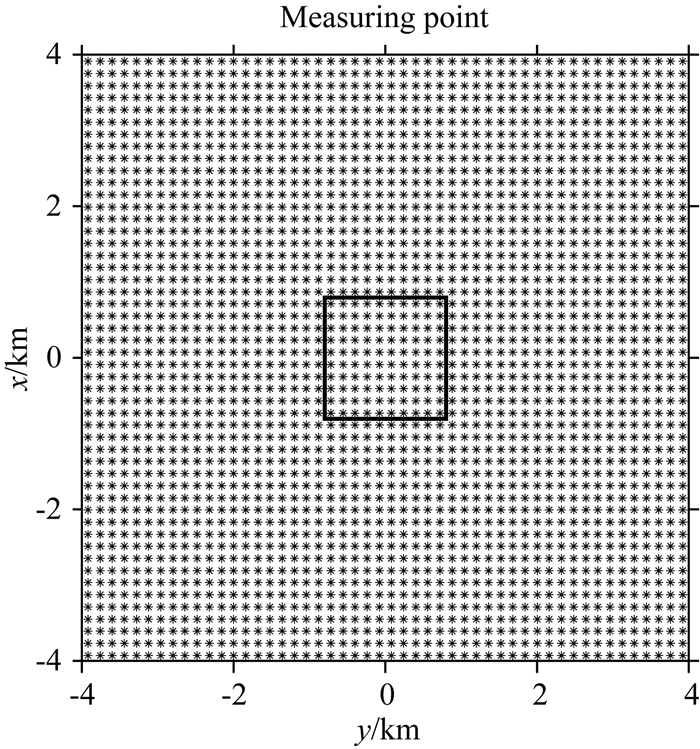
3 半航空频率域电磁法正演分析

本节建立了如图 3所示的正演模型，背景电阻率100 Ωm，低阻模型电阻率为10 Ωm.模型的顶面埋深为120 m，整体尺寸为1600 m×1600 m×200 m.根据图 1所示的系统，这里将发射源1放置在y轴负半轴(x=0 m, y=-10 km, z=0 m)，而发射源2放置在x轴负半轴(x=-10 km, y=0 m, z=0 m).整个测量范围在-3920 m到3920 m，在X和Y方向每隔160 m一个点(图 4).垂直磁感应强度Bz₁来自发射源1，垂直磁感应强度Bz₂来自发射源2，采集高度均在100 m空中，测点分布2500个.

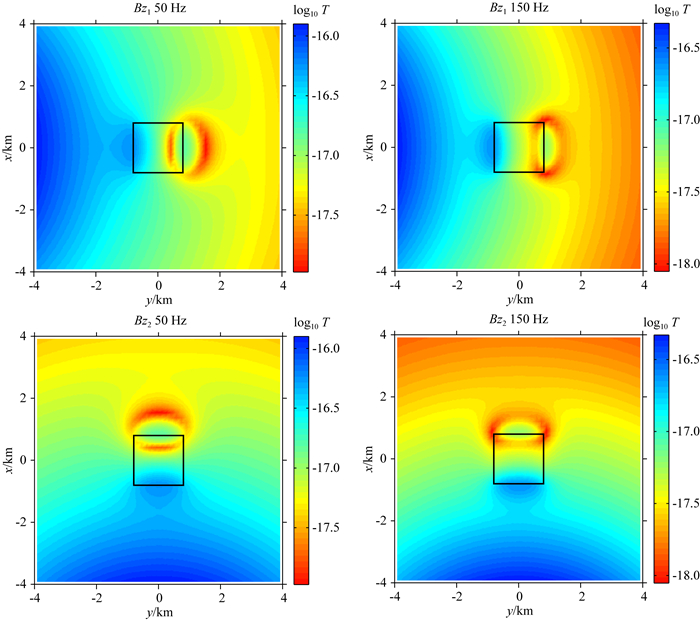
计算剖分网格为80×80×39，这里给出50 Hz和150 Hz的计算结果(图 5)，图 5中的黑色方框为异常体在地面的投影.从图 5的结果可以看到，Bz₁对Y方向的边界灵敏，Bz₂对X方向的边界灵敏.图 5的结果显示，应当使用两个正交发射源分别采集Bz₁和Bz₂可以获得最佳的分辨率，我们会在下一节反演中进一步的证实这个结论.

4 理论模型反演分析 4.1 无人机半航空频率域电磁法反演

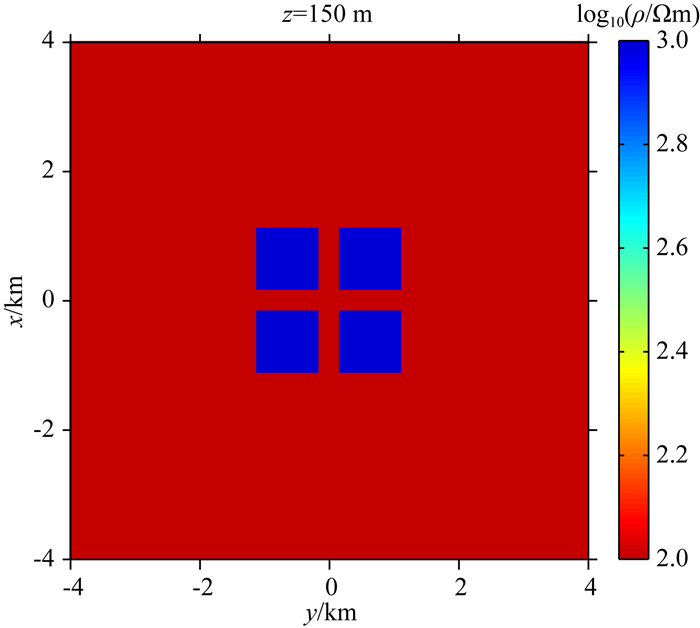
本节建立了如图 6所示的理论模型，该模型是为了进一步证明第3节正演中得出的结论.图 6模型的背景电阻率为100 Ωm，四个高阻异常体模型为1000 Ωm.异常体的顶面埋深为120 m，尺寸为960 m×960 m×200 m，四个频率(300，150，80，50 Hz)被用于反演测试.

测点位置及范围仍然沿用图 4所示的分布，两个水平正交的双极源被分别放置在X轴负半轴以及Y轴负半轴，源1的具体坐标为(x=0 m, y=-10 km, z=0 m)，源2为(x=-10 km, y=0 m, z=0 m).正演及反演网格为80×80×39，正演数据添加2%的高斯随机噪音.Bz₁和Bz₂数据的反演权重为各自振幅的2%，反演数据为Bz₁和Bz₂的实部与虚部，初始模型为100 Ωm均匀半空间.为了更好地展示Bz₁和Bz₂在反演中的作用，我们选择三组反演数据进行测试：①仅使用Bz₁反演；②仅使用Bz₂反演；③Bz₁和Bz₂同时参与反演.

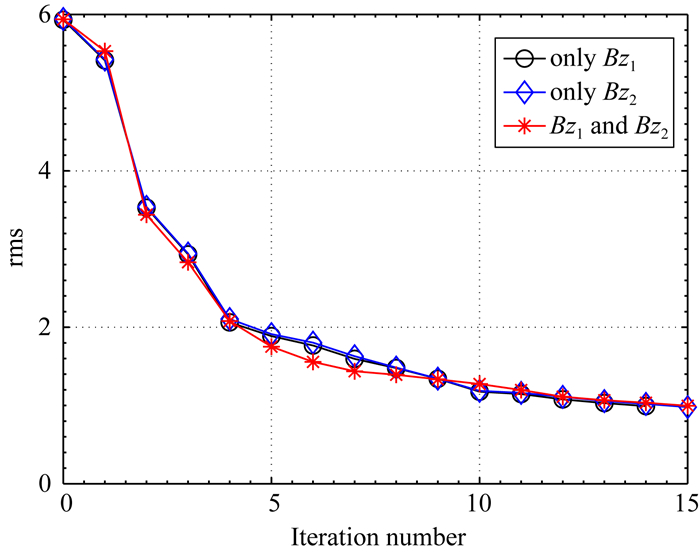
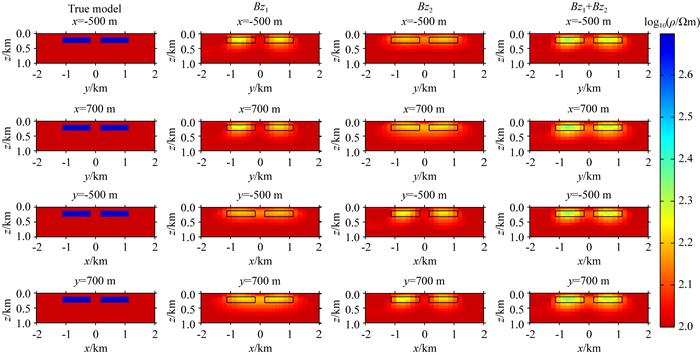
最终的反演结果如图 8和9所示，图 7给出了三种数据体的反演拟合差曲线，Bz₁、Bz₂、Bz₁+Bz₂拟合差分别为0.993，0.979，0.997，整体反演呈现出稳定收敛，证明LBFGS适用于无人机频率域半航空电磁法反演.为了更好地展示细节，这里缩小了成图范围.在图 5的正演响应特征中，我们可以看到Bz₁与Bz₂在X与Y方向的显著差异，Bz₁对Y方向边界灵敏，而Bz₂对X方向边界灵敏，这个现象在图 7和图 8的反演结果中也再一次体现，而Bz₁和Bz₂的组合反演得到了最佳的反演效果.对于无人机而言，使用两个发射源的工作量仅仅是多设置了一个发射源.尽管显著增加了无人机测量的工作量，但相比于地面测量而言，仍然有极高的效率.因此，我们认为实际情况下，应尽量使用两个发射源，以增加对复杂异常体的识别能力.

4.2 反演抗噪测试

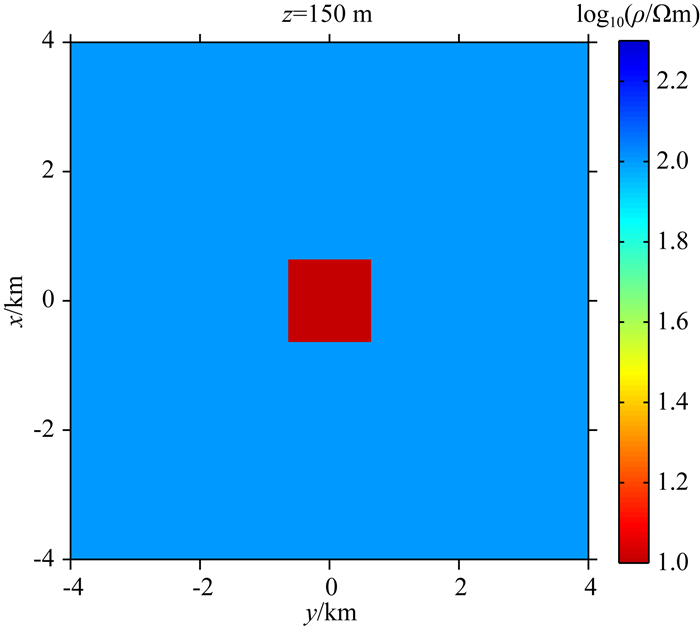
在本节我们将利用一个低阻棱柱体模型进行反演抗噪测试，在正演数据中添加不同程度的噪音，进一步验证无人机数据反演的稳定性和可靠性.如图 10所示，本节的低阻模型尺寸为1280 m×1280 m×200 m，埋深120 m.背景电阻率为100 Ωm，低阻异常体电阻率为10 Ωm.反演频率、发射源位置及测点分布与前一节一致，本节分别对正演响应添加3%、5%、10%、20%、35%、50%的随机噪音，所有反演的数据权重都选择为场值的3%.

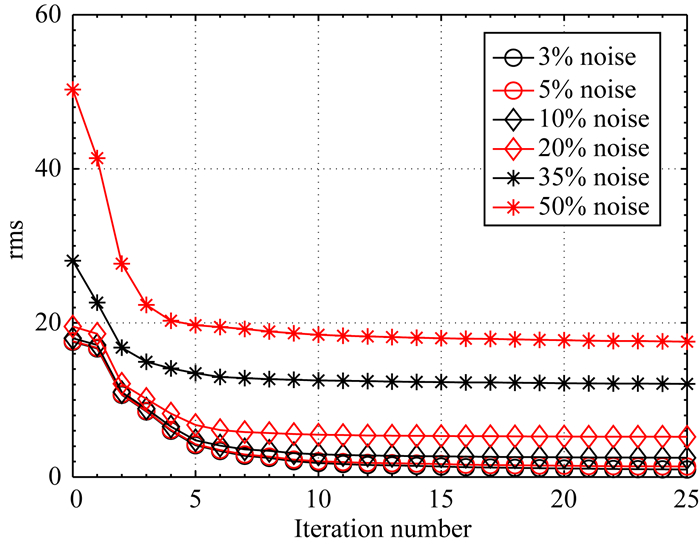
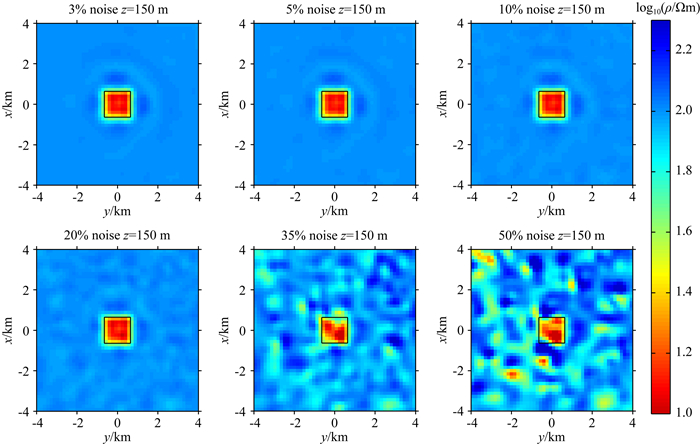
反演拟合差曲线如图 11所示，对于3%的噪音而言，由于数据权重也与之匹配，仅迭代25次就收敛，拟合差为0.984，为了防止出现严重过拟合的现象，余下反演都限制了最大迭代次数为25次.最终的反演结果如图 12所示，从图中的结果可以看到无人机数据随着噪音的逐渐增加，不仅收敛越来越难，反演结果也随之出现愈来愈多的假异常.所有的反演对于异常体都具有非常明显的反应，并且随机噪音增加至20%时，整体的反演仍然较为理想，这说明本文的无人机数据反演具有较强的抗噪性.需要指出的时，实际情况的地质结构复杂，噪音水平仍然需要做到最大程度的降低.

4.3 联合大地电磁法反演

在4.1节我们证明了同时使用Bz₁和Bz₂反演效果最佳，然而对于无人机来说接收更低的频率仍然十分困难，因此仅靠无人机还无法获得更深的电阻率结构.获得更低频率的常用做法，是与大地电磁进行联合反演，这样可以使用频率更低的观测数据.

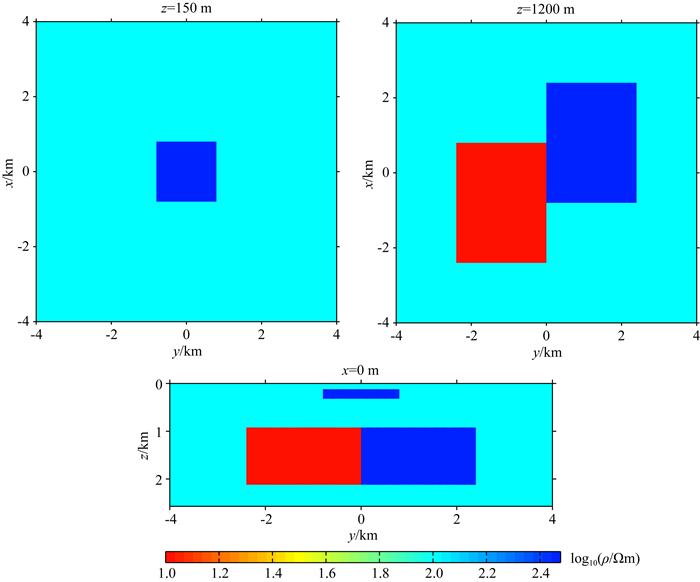
为了研究无人机数据与大地电磁法的联合反演效果，我们首先建立了如图 13所示的模型.背景电阻率为100 Ωm，浅部和深部的高阻异常体均为1000 Ωm，低阻异常体为10 Ωm.浅部的高阻异常体顶面埋深为120 m，深部的高、低阻异常体顶面埋深均为920 m.浅部低阻异常体的尺寸为1600 m×1600 m×200 m，两个深部异常体的尺寸均为3200 m×2400 m×1200 m.

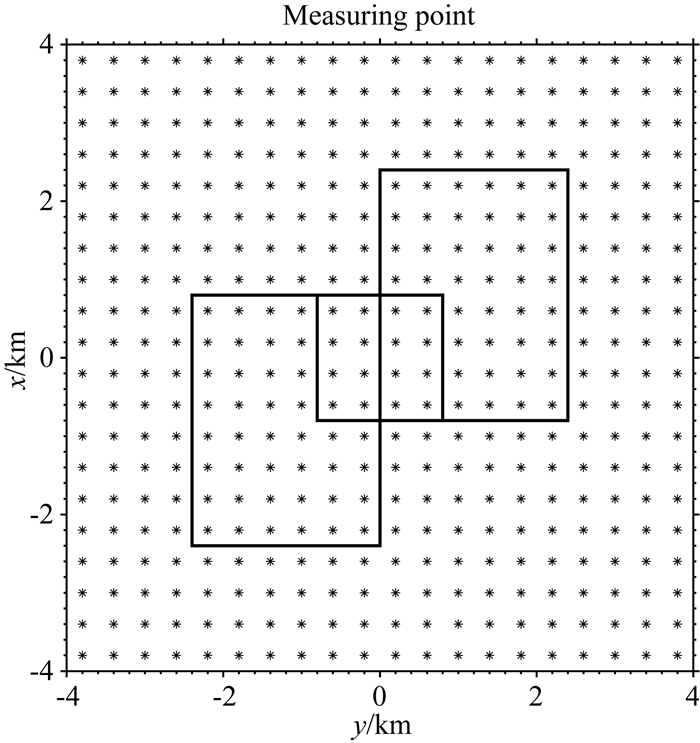
无人机的观测系统与前一节一致，测点分布如图 4所示.大地电磁的观测点远远小于无人机观测点数目，其分布如图 14，共400个大地电磁台站.因为大地电磁在这里关注的是更深的结构，因此台站整体分布相对稀疏，图 14中大地电磁台站在X和Y方向每隔400 m一个.

在本节测试中，我们使用了一个较细的网格进行正演计算，网格剖分为136×136×60.无人机的计算频率为300，150，80，50 Hz，反演数据依然是实部和虚部.大地电磁的计算频率为50，10，1，0.5，0.1 Hz，共5个频率.为了验证反演的稳健性，反演采用稀疏网格，整体剖分为80×80×50，正演数据加入了3%的高斯随机噪音，反演初始模型为100 Ωm的均匀半空间.

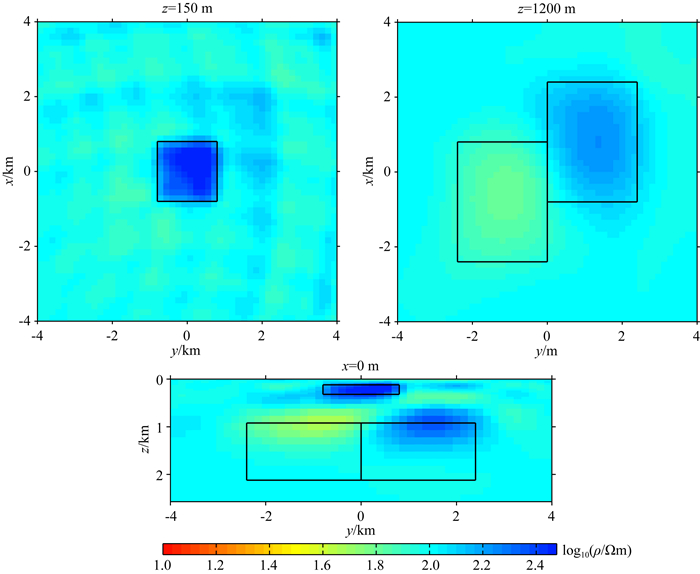
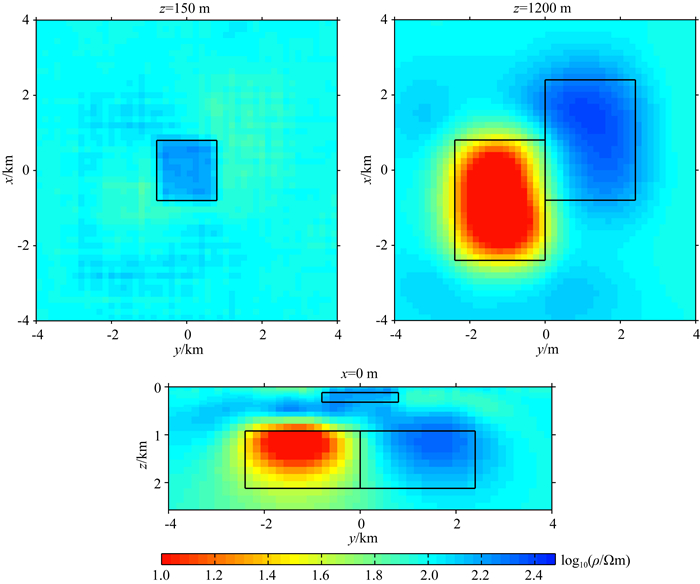
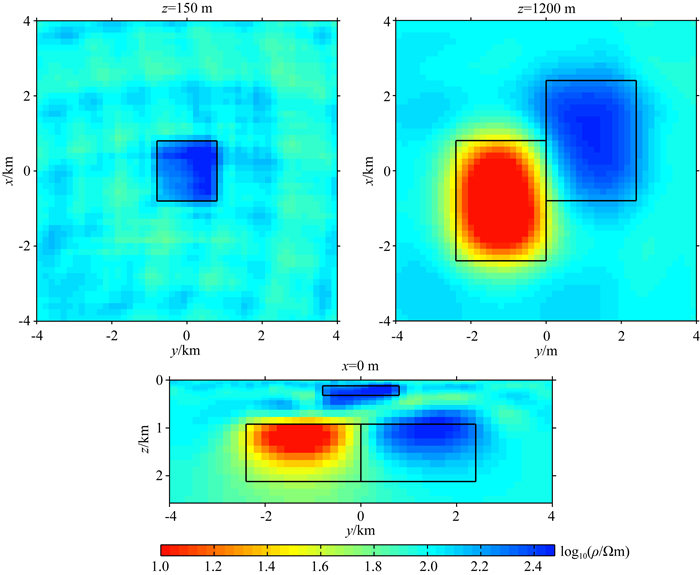
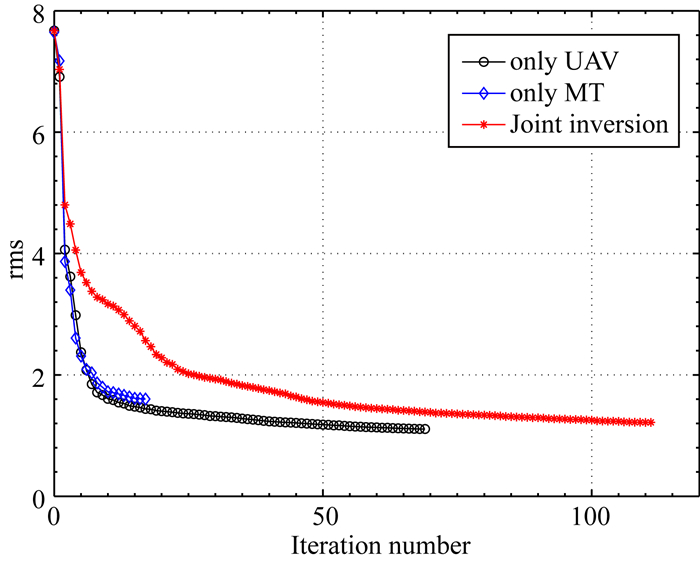
为了体现单独反演与联合反演的差异，我们首先使用无人机数据进行了反演测试，反演结果如图 15所示.从图中结果可以看到，单独的无人机数据反演可以较好地恢复浅部结构，但深部的两个高低阻异常体都未能很好地反应出来.随后，我们在图 16中给出了仅仅依靠大地电磁反演出来的结果，图 16的深部相较于图 15而言有了明显的改观，但此时图 16的浅部异常体效果不如图 15.最后，我们将无人机数据与大地电磁数据进行了联合反演，结果如图 17所示，从图中的结果可以看到，联合反演具有相对最佳的效果，既能反应浅部构造，同时也能获得深部信息.图 18展示了三个反演的拟合差曲线，从中可以看出三个反演都非常稳定.

本节的反演实验为实际勘探给出了一个可能的方案，即对于浅部结构，借助无人机的快捷，可以进行较为密集的观测.而深部信息的获得，则可在地面补充布置较为稀疏的大地电磁测点，这样可以相对快速地获得浅部和深部信息，提高野外工作效率.

4.4 基于交叉梯度结构约束的联合反演

在4.3节，我们进一步证明了无人机数据与大地电磁联合反演的有效性，可同时获得浅部和深部结构.然而，对于实际情况而言，面对更复杂的异常体，有可能这种数据体仍显不足，对真实电阻率模型的分辨能力仍然有限.因此，利用某些已知的结构(如速度结构)，约束电磁法反演逐渐成为一种流行的方式.在这种背景下，交叉梯度理论被提出和广泛使用，并且已经被证明可以有效实施结构约束反演.

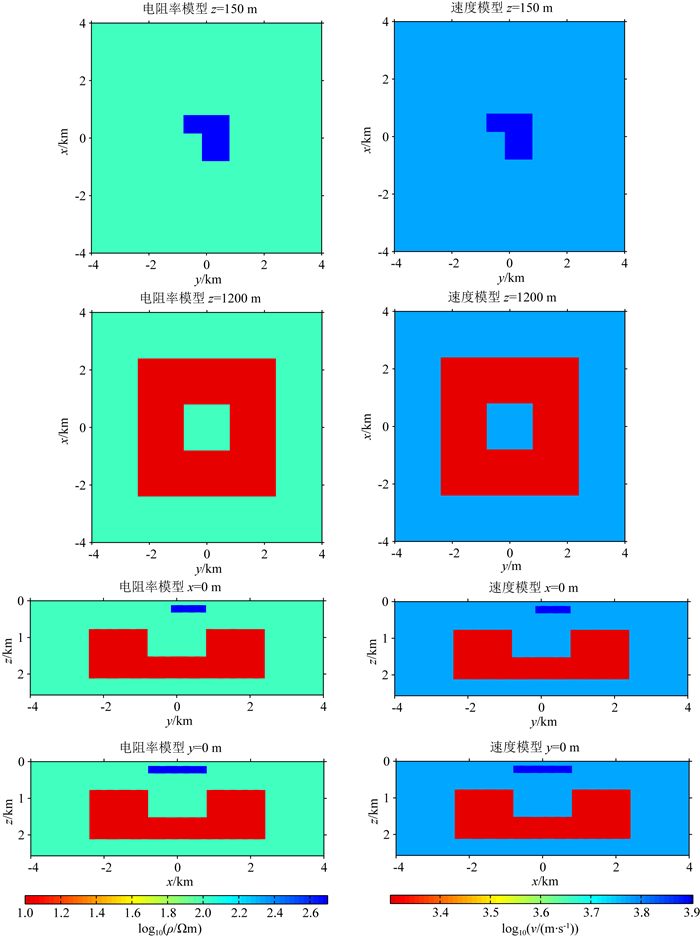
在4.3节的支撑下，本节尝试进行基于交叉梯度结构约束的无人机频率域半航空电磁法与大地电磁法的联合反演.首先建立图 19所示的电阻率模型与速度模型，这里的速度模型与电阻率模型具有相同的结构.浅部异常体的电阻率和速度分别为500 Ωm及8000 m·s^-1，深部异常体的电阻率和速度分别为10 Ωm及2000 m·s^-1，背景电阻率和背景速度分别为100 Ωm及6000 m·s^-1.无人机的观测系统与前一节一致，测点分布如图 4所示，大地电磁的观测点与图 14一致.

在本节测试中，反演网格剖分为80×80×50.无人机的计算频率为300，150，80，50 Hz，反演数据为垂直磁感应强度的实部与虚部.大地电磁的计算频率为50，10，1，0.5，0.1 Hz.正演数据加入了2%的高斯随机噪音，反演初始模型为100 Ωm的均匀半空间.

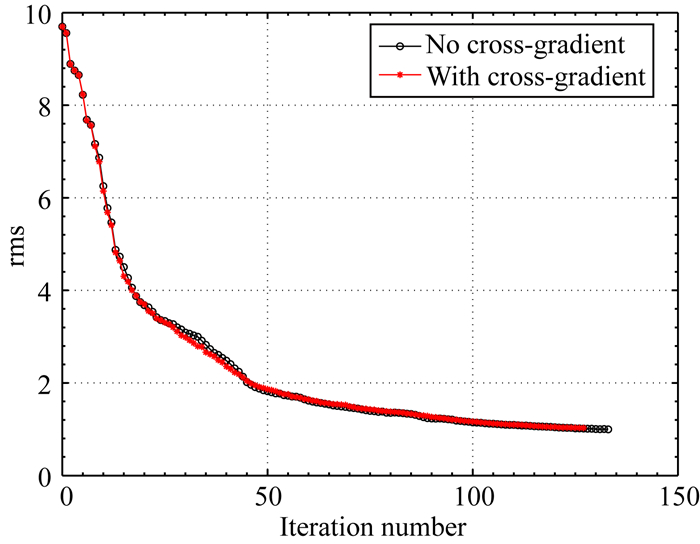
最终的反演结果如图 20所示，首先对于浅部异常体而言，由于无人机数据的密集性且异常体形态相对简单，交叉梯度并没有对浅部构造取得更明显的约束效果.然而，面对深部的低阻异常体，无交叉梯度约束的反演，对构造形态的准确识别开始变差，尤其是对低阻中间的凹槽恢复能力较弱.使用交叉梯度项进行结构约束后，深部结构开始有了明显改善，这说明交叉梯度项在联合反演中有效，同时也证明了本文程序的正确性.图 21展示了无交叉梯度与使用交叉梯度的拟合差曲线，从图中可以看到二者在局部迭代的差异，这也同时说明交叉梯度项确实是在影响整体反演的走势.

本节的反演初步尝试了使用结构约束的联合反演，对于实际勘探而言，下一步还有很多工作需要验证，比如无人机数据的准确性，联合反演的实用性，结构约束的可靠性等等.但总体而言，我们认为无人机勘探潜力巨大，值得更深入的研究.

5 结论

无人机探测效率高，在研究浅层电阻率结构方面有很大的潜力.在本文中，我们为无人机频率域半航空电磁法开发了一种有效的三维反演算法.在正演中，我们使用了交错网格有限差分法，该方法在三维电磁法中很容易实现.在反演部分，我们采用了LBFGS法，它具有较高的稳定性和效率，不需要计算和存储巨大的灵敏度矩阵.

为了进一步增强无人机勘探的反演能力，我们融入了与大地电磁的联合反演，以及基于交叉梯度方案的结构约束.在正演模拟和第一个反演测试中，我们比较了垂直磁感应强度Bz₁和Bz₂之间的分辨率差异，并证明同时使用Bz₁和Bz₂是最理想的，因为Bz₁对Y方向边界敏感，而Bz₂对X方向边界敏感.在第二个反演测试中，我们对正演响应添加了不同程度的噪音，结果显示无人机数据的反演具有较强的抗干扰能力，这在一定程度上增加了未来实测数据反演的可靠性.在第三个反演测试中，我们分别进行了三个反演试验，研究结果表明：①无人机的单独反演可以很好地恢复浅层结构；②大地电磁的单独反演可以很好地恢复深层结构；③无人机与大地电磁的联合反演可以同时获得浅部和深部的结构.最后，在第四个模型中，我们依靠交叉梯度实现了针对联合反演的结构约束.结果证明，在实际情况下若能够从其它地球物理方法获得可靠的结构信息，交叉梯度可以显著改善电磁法反演对边界的识别.