2. 北京白家疃地球科学国家野外科学观测研究站, 北京 100095
2. Beijing Baijiatuan Earth Sciences National Observation and Research Station, Beijing 100095, China
时变重力场反映地球系统内物质的分布、运动和变化,是研究地球系统内物质运动状态及其动力学机制的重要约束信息,可为解决人类面临的资源、环境和灾害等紧迫问题提供重要的基础地球物理信息(许厚泽等, 2012; 宁津生等, 2016).近十几年来,GRACE(Gravity Recovery And Climate Experiment)卫星已成功获取全球均匀覆盖的时变重力观测数据,使地球时变重力场模型在分辨率和精度上实现了重大提升(Tapley et al., 2004; Flechtner et al., 2014; 宁津生等, 2016).GRACE月时变重力场在大空间尺度上定量揭示了全球环境变化,例如:陆地水储量变化(Rodell et al., 2018)、冰川消融(Harig and Simons, 2015; 高春春等, 2019)、海洋变化(Reager et al., 2016; Jin et al., 2020)、冰后回弹(Riva et al., 2009)以及强地震(Han et al., 2006; Panet et al., 2018)等导致的地球表层质量重新分布.
GRACE重力卫星具有可重复、大范围的观测优势,但其轨道距地面约500 km,所观测到的地球重力场信号已大幅衰减,其中短波长(高频)部分衰减幅度最大(周新等, 2011; 徐新禹等, 2018).因此,GRACE对重力场信号的中长波长部分较为敏感,对短波长部分敏感性较弱,不利于恢复较高阶的时变地球重力场模型.GRACE的实际空间分辨率约400 km (Tapley et al., 2004),其数据存在空间域的南北向条带等噪声需做滤波处理(Swenson and Wahr, 2006; Chen et al., 2007),会进一步降低空间分辨率,难以满足环境保护、资源监测以及灾害预测等研究对高精度高分辨率时变重力场的需求(许厚泽等, 2012; Alley and Konikow, 2015; Feng et al., 2018).
地面重力时变观测在地表进行,通过定期同点位复测来获得重力场随时间的变化.与GRACE重力卫星相比,地面重力测量的优点在于重力信号衰减幅度小,观测结果的短波长部分更加精确(Bomfim et al., 2013),空间分辨率也更高(Van Camp et al., 2017),适于分析区域性、近地表的物质运动和迁移现象(许才军和尹智, 2014; Van Camp et al., 2017).但地面重力观测易受地理和环境等因素制约:一方面,很多区域(如南极、沙漠和冰川等)难以施测,存在数据空白区,无法像GRACE卫星观测那样实现数据全球覆盖;另一方面,在可施测区域内,测点空间位置也难以实现均匀分布.直接利用地面重力观测数据确定区域重力场模型时,由于数据仅区域覆盖且空间不均匀分布,无法满足球谐分析这样的经典重力场恢复理论对数据的要求(基函数在区域内部不满足正交性).因此,需借助局部重力场恢复理论和方法.
目前应用较为广泛的局部重力场恢复方法包括最小二乘配置法(Hwang et al., 2014; 王灼华等, 2017)、球冠谐分析法(Li et al., 1995; 王燚和姜效典, 2017)、Mascon (Mass concentration)法(Watkins et al., 2015; 邹贤才等, 2016; Ran et al., 2018)等.除上述方法外,国内外学者还发展了多种采用特殊基函数的区域重力场建模方法,如矩谐分析法、径向基函数(radial basis function)法以及Slepian局部谱分析法等.矩谐分析方法选取三角函数作为基函数,便于计算和展开到较高阶次(蒋涛等, 2014).径向基函数方法可定义多种基函数,具备在空间域和频率域局部化的特性(Klees et al., 2008; 吴怿昊等, 2016; 杨帆等, 2017).Slepian局部谱分析方法最早由Slepian(1983)提出,旨在解决一维连续情况下的时域和频域能量集中问题,随后被不断发展并引入到重力场研究领域中(Albertella et al., 1999; Simons and Dahlen, 2006; Simons et al., 2006; Simons, 2010).Slepian方法通过构建在研究区域内部的正交基函数(Simons, 2010; Slobbe et al., 2012; 朱广彬等, 2012),可使信号能量集中在研究区域内部,适用于表达区域尺度的重力场变化,例如月球区域重力场模型(Han, 2008; 孙雪梅等, 2015)和中国大陆区域重力场模型(陈石等, 2017),并且Slepian展开与相同阶次的经典球谐展开具有同样的意义(Simons, 2010; Slobbe et al., 2012; 陈石等, 2017).
本文对利用Slepian局部谱分析恢复区域重力场的方法进行了研究,并将Slepian方法应用到我国华北地区,确定了华北年尺度的区域重力场时变模型.本文分以下3个部分展开研究,第1部分主要介绍Slepian方法的基本原理,第2部分首先说明观测数据处理过程及重复测点分布,接着利用EGM2008模型和实际观测点位分布,讨论分析Slepian最佳截断数和最大展开阶数的确定,最后对多期地面实测重力观测数据进行处理,获得我国华北地区2011—2013年时变重力场模型,并与研究区域内GRACE卫星重力估计结果进行对比分析,第3部分给出讨论与结论,并对下一步工作做出展望.
1 Slepian方法基本原理
本节主要基于Simons和Dahlen (2006)、Simons等(2006)和Simons(2010),说明Slepian局部谱分析方法的基本原理.对于单位球面Ω上的一点


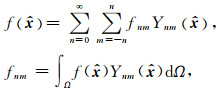
|
(1) |
其中,n, m分别为展开的阶数和次数,Ynm(

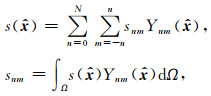
|
(2) |
其中,snm为Slepian系数.Slepian基函数在区域Γ内的集中程度由(3)式给出
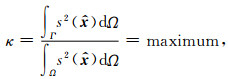
|
(3) |
其中,κ为“聚集因子”(concentration factor),取值0<κ<1.公式(3)的最大化可通过求解以下特征方程实现:

|
(4) |
κ是上述特征方程的特征值,s是特征向量,即公式(2)中的Slepian系数.矩阵D各元素由公式(5)给出
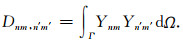
|
(5) |
由公式(4)可解得(N+1)2个特征值和特征向量,将特征向量s代入式(2),经整理可得Slepian基函数sα[α=1, …, (N+1)2]具有整个球面Ω内及区域Γ内的正交特性:
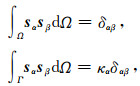
|
(6) |
其中δ为Kronecker函数.
对于聚集因子κ(0<κ<1)而言,当κ值越接近1时,表明所对应Slepian基函数较好地集中在区域Γ内,该基函数在表达区域Γ内信号时贡献越大;当κ值越接近0时则表明基函数较好地集中在Γ=Ω-Γ内,在表达区域Γ内信号时贡献越小.因此,可将(N+1)2项κ按大小进行排序,仅以κ值较接近1的前J项Slepian基函数(s1, …, sJ)来表达区域Γ内的重力场信号g(
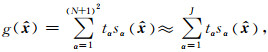
|
(7) |
其中,tα为Slepian展开系数,J为Slepian截断数.需要指出的是,对于球面区域Γ内的重力场信号表达,Slepian展开与相同阶次的经典球谐展开具有同样的意义(Simons, 2010; Slobbe et al., 2012; 陈石等, 2017).
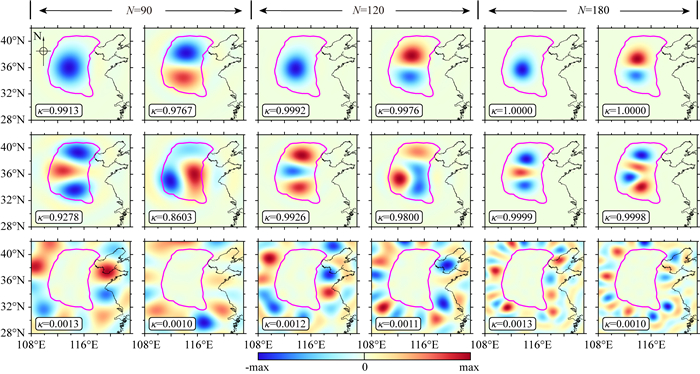
公式(7)表明Slepian方法是一种具有稀疏(sparse)特性的时空局部谱方法.以本文研究的华北地区为例,图 1直观反映了Slepian函数分别展开到90、120和180阶时聚集因子κ的稀疏分布情况.对于120阶Slepian展开,聚集因子κ的总数量为(120+1)×(120+1)=14641个,其中大于0.001的共41个,仅占总数量的0.3%,剩余14600个κ值均接近0,分布具有明显的稀疏性.

|
图 1 华北地区对应90、120和180阶Slepian展开的聚集因子分布 Fig. 1 The concentration factors of Slepian functions in North China for N=90, 120, and 180, respectively |
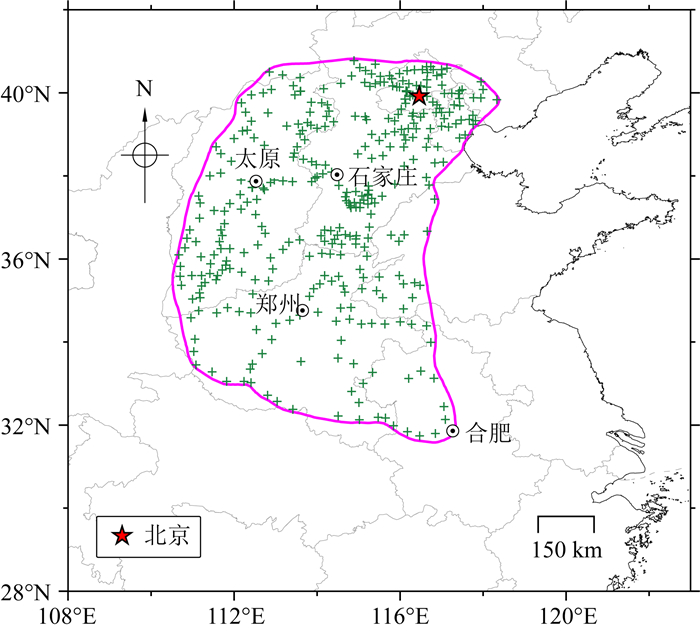
图 2进一步给出了华北地区Slepian展开到90、120和180阶时基函数的空间分布情况,其中洋红色曲线标记重力数据覆盖范围的边界,也即本文研究区域.由图 2可以看出,对于每组展开,当聚集因子κ较接近1时,所对应基函数基本都集中在研究区域内部,能量很少泄漏到区域外部;当聚集因子κ很小时(如图 2第3行中κ接近0.001的情况),所对应基函数基本集中在研究区域外部,在研究区域内部几乎没有贡献.因此,在表达研究区域内重力场信号时,可按公式(7)做截断近似处理,只采用较大的聚集因子所对应的基函数.
|
图 2 华北地区3组Slepian展开的基函数空间分布,分别对应90阶(左边2列)、120阶(中间2列)和180阶(右边2列)展开. 对于每组展开,第1和第2行为聚集因子κ最大的前4个基函数,第3行为κ接近0.001的基函数 洋红色线为研究区域边界,黑色线为陆海边界. Fig. 2 Spatial patterns of the Slepian functions with corresponding concentration factors in North China for N=90 (the left 2 columns), N=120 (the central 2 columns), and N=180 (the right 2 columns). For each group, the first and second rows show the basis functions with the 4 largest concentration factors, the third row shows the 2 basis functions with concentration factors around the value of 0.001 The magenta line denotes the boundary of the study area, while the black line indicates the land-ocean boundary. |
本文采用了华北地区重力测网2011—2013年间的实际重力观测成果,一共6期观测数据(每年上下半年各测1期).重力网平差采用基于贝叶斯平差模型的pyBACGS软件完成(Chen et al., 2019),该方法可以较好地解决多台相对重力仪器联合平差的权系数优化、非线性漂移估计和仪器格值的最优化估计等问题,6期观测平差结果的点值精度均优于10×10-8 m·s-2.图 3给出了6期数据覆盖的重复测点位置的空间分布,共有364个.以最边缘的重复观测点位置确定闭合边界(图 3中洋红色曲线),边界内部即为本文研究区域.由图 3可以看出,研究区域内部重力测点的空间分布很不均匀:京津地区最为密集,该地区约占研究区域总面积的5.5%,测点数约占全部的15.9%,相对测点密度(测点百分比/面积百分比)约2.9;河南、安徽及山东境内较为稀疏,该地区约占研究区域总面积的42.4%,测点数仅占全部的22.5%,相对测点密度约0.5.研究区域内相邻测点最小距离约0.2 km,最大距离约167.2 km,平均距离为43.5 km.
|
图 3 本文研究区域及重复测点位置分布 洋红色线为研究区域边界,绿色十字代表重复测点位置,灰色线为省界,黑色线为陆海边界. Fig. 3 The study area and the locations of the repeated gravity stations The magenta line denotes the boundary of the study area, the green crosses show the locations of the repeated gravity stations, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
在利用实测数据和Slepian方法恢复华北区域重力场前,还需解决两个问题:(1) Slepian展开最佳截断数的确定.研究区域内观测点仅有364个,应用Slepian方法时,不管最大展开阶数N如何取值,都须采用公式(7)给出的截断形式(J≤364),否则求解Slepian展开系数时会出现欠定情况;(2) Slepian最大展开阶数N的确定.研究区域内观测点分布稀疏不均,需测试基于现有测点分布对重力变化的恢复能力,以此确定Slepian的最大展开阶数N.接下来将在2.2和2.3节对以上两个问题进行详细讨论.
2.2 Slepian展开最佳截断数的确定对于不同的Slepian展开阶数,由于聚集因子和基函数的分布不同(图 1和2),在根据公式(7)确定重力场模型时选取的截断数也有所不同.假设观测点数为M,最佳截断数Jopt会在Msha和M之间变化,Msha为Shannon数,即最小截断数(Simons, 2010; Slobbe et al., 2012)

|
(8) |
其中,κα为第α个聚集因子,N为最大展开阶数,A/4π为研究区域所占球面面积的比例.
对Slepian最佳截断数Jopt的确定,目前比较常用的方法为:首先给定一个已知N阶的初始场,然后模拟测点处的观测值,接着利用模拟观测值和Slepian方法基于变化的J值(Msha≤J≤M)获得一系列N阶恢复结果,最后将恢复结果与初始场进行比较,令二者差值均方根(root mean square, RMS)最小的J即为Slepian展开最佳截断数Jopt(Slobbe et al., 2012; Plattner and Simons, 2017; 陈石等, 2017).这一确定准则虽然简便易行,但是(1)采用的已知场跟恢复结果的阶数是一致的,不适合二者阶数不同的情形.本文的解算数据为地面重力观测值,信号为全波段(可展开至无穷阶),远大于所要恢复的N阶;(2)没有顾及模型的复杂度,在实际应用中可能存在模型参数过多导致的过拟合现象.
对于确定Jopt时存在的问题(1),应用Slepian理论求解N阶模型时,观测数据中高于N阶的信号会影响解算得到的低阶系数,造成宽带泄漏(broadband leakage)(Simons and Dahlen, 2006; Slobbe et al., 2012).为削弱宽带泄漏的影响,需尽可能地移除观测数据中高于N阶的信号.本文采用Bomfim等(2013)在比较地面重力观测数据和GOCE(Gravity Field and Steady-State Ocean Circulation Explorer)卫星重力数据时采用的滤波方法,移除地面重力数据中高于N阶的高频信号.
对于问题(2),本文采用贝叶斯信息量准则(Bayesian Information Criterion, BIC)(Baur, 2012; He et al., 2019)确定最佳截断数Jopt.通过引入关于参数数量的惩罚项,BIC在提高拟合度的同时,要求尽可能少的模型参数以避免过拟合现象(Baur, 2012; He et al., 2019).对于截断数为J的恢复结果,
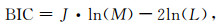
|
(9) |
其中,M为观测值个数,L为最大似然函数值.当BIC值最小时,对应的J即为最佳截断数Jopt,此时应同样满足Msha ≤Jopt≤M.
本文利用BIC准则确定了华北地区90、120和180阶(半波长空间分辨率约200 km、150 km和100 km)Slepian展开时的最佳截断数,具体步骤如下:首先选取EGM2008重力场模型(Pavlis et al., 2012)作为已知场,以模型最高2190阶自由空气重力异常模拟全波段的地面重力观测值,获得研究区域内地面重复测点处重力值.然后利用模拟观测值和Slepian方法恢复N阶重力场,最后将对应不同J值(2≤J≤364)的恢复结果与初始N阶EGM2008模型进行比较,基于公式(9)确定对应的BIC值.上述过程执行3次,N分别取90、120和180,获得3组BIC值随J值的变化趋势(图 4).从J=2开始,每组BIC曲线首先下降到达最小值,然后呈上升趋势;当J>50时,3组BIC曲线均为上升趋势,因此图 4仅列出了2≤J≤121的部分.对于华北地区90、120和180阶Slepian展开,最大截断数为M=364(即总测点数),最小截断数(Shannon数)Msha分别为8、14和32,BIC曲线的最小值分别出现在J=12、J=26和J=36处(图 4),即以上90、120和180阶Slepian展开的最佳截断数Jopt分别为12、26和36.
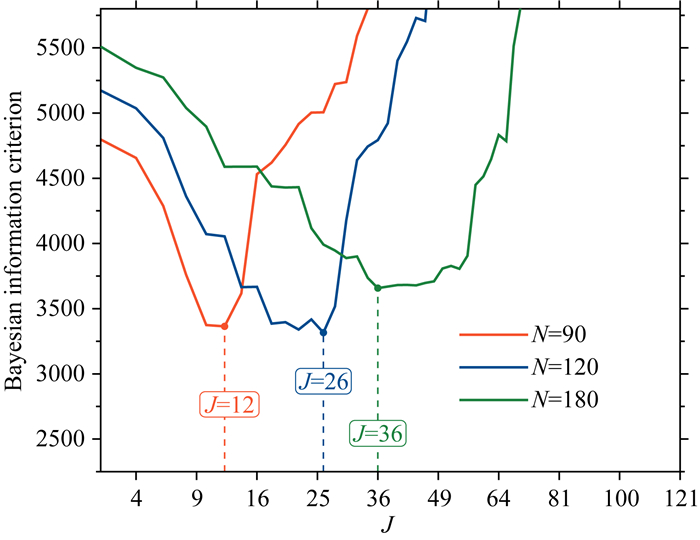
|
图 4 华北地区BIC与J取值的关系图(N=90, 120, 180),虚线指示BIC最小值对应的J值 Fig. 4 The relationship between BIC and J in North China (N=90, 120, 180), where a dashed line indicates the smallest BIC and the corresponding J value in each scenario |
表 1给出了N取90、120和180时,分别基于Msha和BIC确定的Jopt进行截断,Slepian方法对华北地区初始模型(即N阶EGM2008模型)恢复情况的统计信息.
|
|
表 1 选取不同截断数时Slepian恢复结果在研究区域内评估信息 Table 1 Quality assessment of the Slepian-recovered results based on different truncation numbers within the study area |
图 5以120阶展开为例,给出了基于不同截断数恢复结果的空间分布及其与初始模型的差异(格网间隔为0.1°×0.1°).结合表 1和图 5可以发现,采用BIC确定的Jopt截断较使用Msha截断,Slepian恢复结果有较为明显的改进:(1)基于不同N的3组测试,以BIC确定的Jopt截断时,Slepian恢复结果的精度均有较显著提升;(2)基于Jopt和Msha的120阶恢复结果在空间分布上较为接近,但与初始EGM2008模型做差后,基于Jopt恢复结果的残差在山东省西部和安徽省西北部明显减小,表明以Jopt进行截断的恢复结果更加接近初始模型.基于90阶和180阶恢复结果的空间分布可得出同样结论,相关结果不再逐一列出.
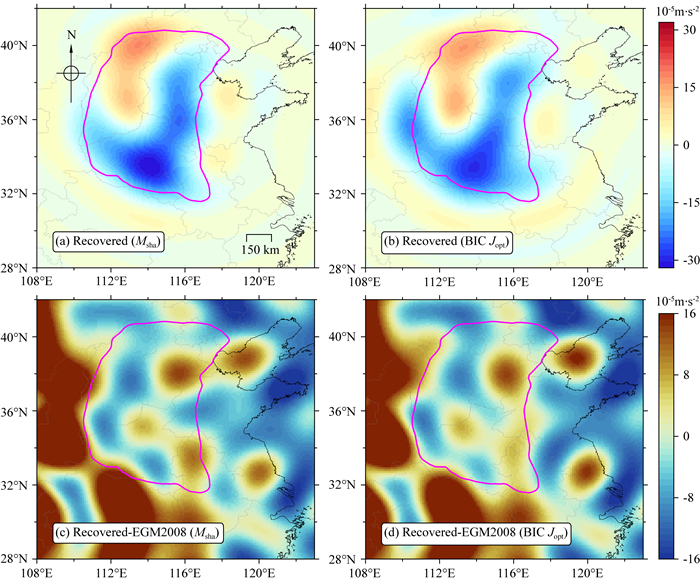
|
图 5 华北地区120阶Slepian恢复结果及其与初始EGM2008模型的差异 (a) 以Shannon数Msha进行截断的恢复结果; (b) 以BIC准则确定的最佳截断数Jopt进行截断的恢复结果; (c) 基于Msha的恢复结果与EGM2008模型的差值; (d) 基于Jopt的恢复结果与EGM2008模型的差值.洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 5 The Slepian recovered results (degree 120) and differences with the EGM2008 inputs (a) Slepian results after truncating at Msha; (b) Slepian results after truncating at BIC-derived Jopt; (c) Recovered results in (a) minus the EGM2008 inputs; (d) Recovered results in (b) minus the EGM2008 inputs. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
本节将进一步讨论基于现有测点分布和本文方法所能恢复研究区域内重力场变化的最大阶数.根据本文2.1节中统计信息,测点稀疏区域内相邻测点的最大距离约167 km,较为接近120阶重力场模型的半波长空间分辨率(约150 km),明显小于180阶的空间分辨率(约100 km),但仅从测点最大距离难以确定最大展开阶数.本文2.2节基于研究区域内现有测点分布和Slepian方法进行重复实验,给出了Slepian方法对研究区域内90、120和180阶EGM2008初始模型恢复情况的对比分析(表 1),结果表明120阶恢复结果与EGM2008初始场差值的RMS最小,即120阶恢复结果的精度最高.基于上述对比分析,本文选取研究区域内Slepian最大展开阶数为N=120.
2.4 观测点位分布对Slepian恢复结果的影响基于实际重力观测恢复区域重力场时,Slepian恢复结果受到宽频泄漏和地表重力观测点分布不均匀(疏密)程度的影响,例如2.2节中的实验结果(表 1和图 5).本节将着重讨论华北地区现有测点分布对恢复研究区域内部120阶重力场变化的影响.选取研究区域内部以0.1°×0.1°间隔均匀分布的5019个点作为“控制点”,通过比较“控制点”处的EGM2008模型值与Slepian恢复值,对Slepian方法解算的120阶模型进行评估.为了避免宽频泄漏的影响,采用120阶EGM2008重力场模型模拟地面观测值(此时Jopt=21由BIC准则确定).表 2列出了研究区域内相关评估结果,在研究区域内EGM2008已知场重力变化约58×10-5 m·s-2,Slepian解算模型的变化约55×10-5 m·s-2,与已知场吻合较好,整体偏差较小(-0.13×10-5 m·s-2),解算误差为2.50×10-5 m·s-2.模型解算误差受地表重力观测点分布不均匀(疏密)程度的影响较为显著,在观测点位最为密集的京津地区(“控制点”数为287个),相对测点密度约2.9(相对测点定义见2.1节),解算模型在此区域的误差明显减小,为2.05×10-5 m·s-2; 在观测点位较为稀疏的河南、安徽和山东(“控制点”数为2071个),相对测点密度约0.5,解算模型在此区域的误差显著增大至2.98×10-5 m·s-2.未来若能在河南、安徽和山东加密重力测网、增加更多的重复重力观测点,将较大地提高华北区域重力场的解算精度.
|
|
表 2 观测点位分布对Slepian恢复结果(N=120)的影响(单位:10-5 m·s-2) Table 2 Impact of the distribution of gravity stations on the Slepian-recovered results (N=120)(unit: 10-5 m·s-2) |
在研究区域内部364个重复测点处,将相邻两年对应测期内的重力观测做差(后一年观测减去前一年)获得1年尺度重力变化.所有比较都限定在相对应的测期内,以减弱水文变化等季节性信号的影响(祝意青等, 2012, 2013; 徐伟民等, 2016).最终得到4组1年尺度重力变化,即基于第1期观测的2013-04—2012-03、2012-03—2011-03(“—”号表示前后两组数据做差),以及基于第2期观测的2013-08—2012-08和2012-08—2011-08.获得研究区域重复测点处的重力变化后,接下来应用Slepian方法恢复华北地区120阶时变重力场模型,空间变化结果(格网间距为0.1°×0.1°)如图 6所示.
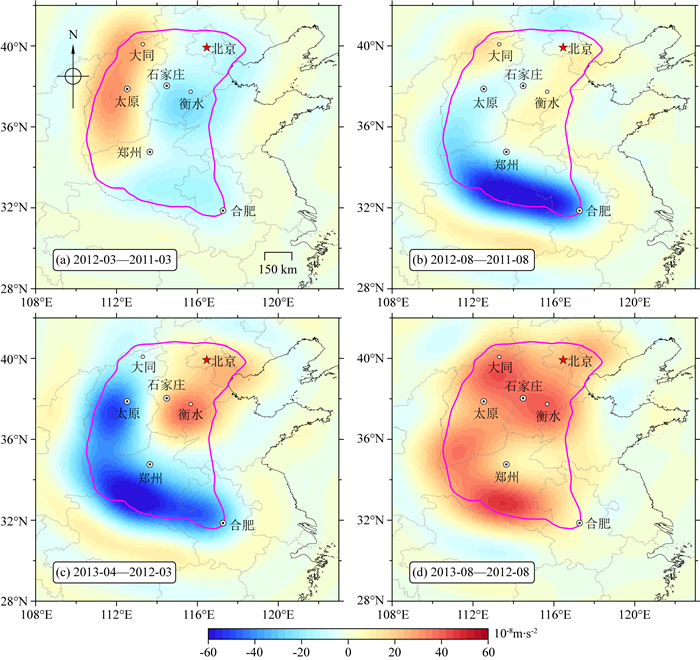
|
图 6 华北地区由Slepian方法确定的120阶1年尺度重力场变化(2011—2013)空间分布 (a) (c) 基于相邻两年第1期观测差值; (b) (d) 基于相邻两年第2期观测差值. 洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 6 Spatial pattern of the annual gravity changes up to degree 120 determined by the Slepian method in North China from 2011 to 2013 (a) (c) Based on the differences between observations from the first campaigns of two adjacent years; (b) (d) Based on the differences between observations from the second campaigns of two adjacent years. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
图 6反映了2011—2013年间华北地区较为明显的重力变化信号.图 6a中大同—太原一带正重力变化,图 6c中石家庄—北京一带的正重力变化、太原—郑州—合肥一带的负重力变化以及图 6d中大范围的正重力变化,与徐伟民等(2016)给出的结果基本一致.除Slepian解算结果外,本文还利用最小曲率插值法(Wessel et al., 2019)得到了2013-04—2012-03、2012-03—2011-03、2013-08—2012-08和2012-08—2011-08等4组重力变化的空间插值结果(格网间距为0.1°×0.1°),如图 7所示.

|
图 7 华北地区1年尺度重力场变化(2011—2013)最小曲率空间插值结果 (a) (c) 基于相邻两年第1期观测差值; (b) (d) 基于相邻两年第2期观测差值. 洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 7 Spatial pattern of the annual gravity changes obtained by minimum curvature interpolation in North China from 2011 to 2013 (a) (c) Based on the differences between observations from the first campaigns of two adjacent years; (b) (d) Based on the differences between observations from the second campaigns of two adjacent years. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
对比图 6和图 7可以发现,Slepian方法所确定的模型重力信号基本都集中在研究区域内部且较为光滑,可有效压制高频干扰,空间插值方法所得结果存在较多的高频信号.值得强调的是,Slepian方法在频率域内恢复重力场,可通过调整展开阶数从观测数据中提取所需的信号频段,这一点利用空间插值方法无法实现.
除1年尺度时变重力场模型外,本文还解算了2组华北地区120阶的2年尺度重力变化模型(最优截断数Jopt同样取26),第1组利用基于上半年观测(2013-04—2011-03)的重力变化数据解算,第2组利用基于下半年观测(2013-08—2011-08)的重力变化数据解算,解算结果如图 8所示.
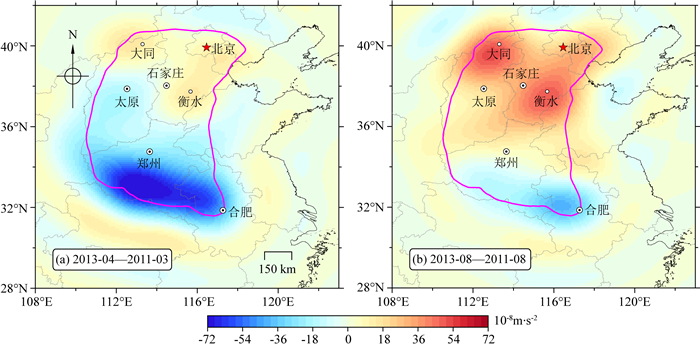
|
图 8 华北地区由Slepian方法确定的120阶2年尺度重力场变化(2011—2013)空间分布 (a) 基于2013-04和2011-03的观测差值; (b) 基于2013-08和2011-08的观测差值. 洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 8 Spatial pattern of the 2-year gravity changes (between 2011 and 2013) up to degree 120 determined by the Slepian method in North China (a) From differences between 2013-04 and 2011-03; (b) From differences between 2013-08 and 2011-08. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
在研究区域内部,图 8a和图 8b所示两组120阶结果在变化极值上存在较大差异,图 8a结果最大值和最小值分别为16.94×10-8 m·s-2、-79.04×10-8 m·s-2,而图 8b结果最大值和最小值分别为52.68×10-8 m·s-2、-41.70×10-8 m·s-2.除去重力变化极值差异外,图 8a和图 8b所示重力变化在空间分布上大致呈现“南减北增”的特征:在河南省南部和安徽省西北部(郑州—合肥连线以南区域),重力变化呈减少趋势;在河北省南部、京津和大同附近区域,重力变化呈增加趋势.
2.6 基于GRACE数据的华北2011—2013时变重力场为了与2.5节中地面结果进行对比,本文利用Slepian方法和GRACE卫星数据估计了华北地区2011—2013年间的1年尺度重力变化,结果如图 9所示.本文采用由美国德克萨斯大学空间研究中心(Center for Space Research at the University of Texas)发布的GRACE Level-2 Release 06 (RL06)月时变重力场模型,数据为球谐模型形式,完整展开到60阶.由于GRACE无法观测地心运动(球谐系数中相关1阶项数值均为0),同时2阶项系数C20也包含较大误差,本文对RL06球谐系数做了如下替换:将原始1阶项C10、C11和S11替换为Sun等(2016)基于大气海洋模型、冰后回弹模型和GRACE数据计算的结果,将原始C20项替换为卫星激光测距确定的结果(Cheng and Ries, 2017).
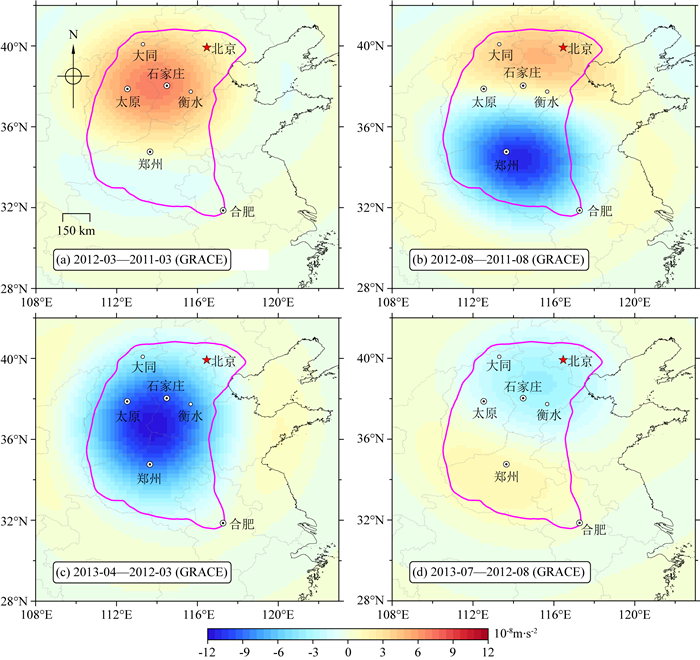
|
图 9 华北地区由Slepian方法得到的1年尺度GRACE重力变化(2011—2013)空间分布 (a), (b), (c), (d)分别为2012-03—2011-03、2012-08—2011-08、2013-04—2012-03和2013-07—2012-08结果. 洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 9 Spatial pattern of the annual gravity changes from GRACE obtained by the Slepian method in North China (2011—2013) (a), (b), (c) and (d) denote results of 2012-03—2011-03, 2012-08—2011-08, 2013-04—2012-03, and 2013-07—2012-08, respectively. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
Slepian方法由Harig和Simons(2012)引入到GRACE数据后处理中,首先将GRACE球谐系数转换为Slepian系数,然后利用Slepian系数计算重力场变化(Harig and Simons, 2012, 2015; Von Hippel and Harig, 2019; 高春春等, 2019).本文在RL06球谐系数的转换过程中,根据2.2节方法将60阶Slepian展开的最佳截断数确定为Jopt=5(Shannon数为4).为了跟图 6中地面时变重力观测时段保持一致,本文尽量选取GRACE相同时段数据;对于地面重力的2013-08—2012-08时间段,由于GRACE缺失2013-08和2013-09月数据,因此替换为最接近的2013-07—2012-08.利用Slepian方法完成对GRACE数据的处理后,本文未再扣除地壳均衡调整(Glacial Isostatic Adjustment)和水文变化的影响.
本文还利用Slepian方法计算了华北地区2011—2013年间2年尺度的GRACE重力变化(2013-04—2011-03和2013-07—2011-08),如图 10所示.

|
图 10 华北地区由Slepian方法得到的2年尺度GRACE重力变化空间分布 (a),(b)分别为2013-04—2011-03和2013-07—2011-08结果. 洋红色线为研究区域边界,灰色线为省界,黑色线为陆海边界. Fig. 10 Spatial pattern of the 2-year gravity changes from GRACE derived by the Slepian method in North China (a) From differences between 2013-04 and 2011-03; (b) From differences between 2013-07 and 2011-08. The magenta line denotes the boundary of the study area, the gray lines show the provincial borders, and the black line indicates the land-ocean boundary. |
利用Slepian方法获得华北地区2011—2013基于地面和GRACE观测的重力场变化后,本节就1年和2年尺度重力变化的空间分布对二者进行了比较.总体上看,基于地面重力观测的120阶结果(空间分辨率约150 km)给出的重力变化量级更大、细节(高频信号)更多.由于空间分辨率相差较大,基于GRACE卫星观测的结果(60阶,空间分辨率约400 km)无法给出与地面120阶结果相当的重力变化信息,但二者在时空变化的显著趋势上存在较好的对应.
对于1年尺度重力变化,首先对比时间段不完全一致的2013-08—2012-08地面结果和2013-07—2012-08 GRACE结果,前者重力变化在研究区域内呈整体增加趋势(图 6d),后者大致呈“北减南增”趋势(图 9d),二者相差较大.当地面结果与GRACE结果所取时间段完全一致时,二者出现显著变化的区域大致相同,如2012-03—2011-03(图 6a和图 9a)、2012-08—2011-08(图 6b和图 9b)和2013-04—2012-03(图 6c和图 9c).以2012-08—2011-08时间段为例,地面结果在河南与安徽西北部呈明显减少趋势(图 6b),GRACE结果在河南和安徽也呈明显减少趋势,由于分辨率原因,GRACE重力显著减小区域的范围更大、中心也偏北一些(图 9b).
对于2年尺度的重力变化,地面结果(图 8)与GRACE结果(图 10)表现出较为一致的“南减北增”空间分布特征:2013-04—2011-03时间段,GRACE结果在研究区域内部基本为减少趋势,在京津地区呈增加趋势(图 10a),地面结果在山西省南部、河南省、安徽省西北部及山东省西南部呈重力减少趋势,在京津地区、河北省以及山西省北部(大同邻近区域)呈增加趋势(图 8a);2013-08—2011-08(卫星数据为2013-07—2011-08)时间段,GRACE结果大致以太原—石家庄—衡水连线为分界,以南区域呈减少趋势、以北区域呈增加趋势(图 10b),地面结果重力减少区域出现在郑州—合肥连线以南,以北区域呈差异性增加趋势,其中山东省西南部增加幅度较小,山西省南部稍大,京津地区、河北省以及山西省北部最大(图 8b).
进一步对比图 8和图 10,可发现2年尺度的地面与GRACE卫星结果差异最大区域出现在石家庄—衡水连线一带,2011—2013年区域内地面结果为增大趋势,GRACE结果为减少趋势.该区域长期存在严重的浅层、深层地下水超量开采以及地表沉降问题(张永红等, 2016; 冯伟等, 2017; Zhao et al., 2019),这是影响区域内重力场长期变化的两个主要因素(Shen et al., 2015).对地面测量而言,地下水亏损会令重力观测减小,地表沉降会导致重力观测增加.根据Shen等(2015)的地面观测结果,2009—2013年在河北省南部(包含石家庄—衡水连线一带)由地表沉降导致的重力增加效应要大于地下水亏损带来的减小效应;由于2009—2013年间石家庄—衡水连线一带地表沉降速度基本维持不变(约-0.05 m·a-1, Zhao et al., 2019),我们推断2011—2013年区域内地表沉降的影响仍然大于地下水亏损的影响,因此地面重力结果呈增大趋势.对GRACE观测而言,在卫星轨道处地面沉降导致的重力变化已大幅衰减,此时地下水亏损导致的重力减小效应占主导地位,因此GRACE结果整体为减少趋势,冯伟等(2017)给出的2011、2012和2013年GRACE结果在该区域内的减少趋势也证实了这一点.
3 讨论与结论Slepian方法的基函数除具备整个球面上的正交性之外,同时具备在指定区域内部的正交性,适用于构建局部重力场模型.通过构建在研究区域内部的正交基函数,可使信号能量集中在区域内部,从而有效减小信号泄漏的影响,提高研究区域内恢复结果的信噪比(Harig and Simons, 2012, 2015; 高春春等, 2019),这一特点利于提取和分析较小区域内的重力信号.
Slepian基函数另一个重要的特点即具备稀疏性(Simons, 2010):以120阶Slepian展开为例,基函数共有(120+1)2=14641个,其中聚集因子大于0.001的仅有41个(占总数量的0.3%),而这41个基函数的累积能量占全部Slepian基函数能量的99.98%.根据Slepian基函数具备稀疏性这一特点,可对Slepian表达进行截断、只采用聚集因子较大的若干项基函数来表达研究区域内的重力场信号.本文2.2节基于BIC准则确定最佳截断数Jopt对Slepian展开进行近似(即只采用前Jopt项基函数),以ε1表示近似误差(包含宽频泄漏误差),当展开阶数取120时,ε1约为初始信号大小的9%.由于Slepian展开与相同阶次的经典球谐展开具有同样的意义(Simons, 2010; Slobbe et al., 2012; 陈石等, 2017),当将重力观测数据展开到N阶且Slepian方法取其全部(N+1)2个基函数时,二者的“截断误差”ε2(重力信号在N+1~∞阶之间的部分)是一致的;若Slepian方法取Jopt个基函数时,Slepian展开的“截断误差”除ε2外,还要包含近似误差ε1(Han and Razeghi, 2017).
稀疏性使得利用Slepian方法恢复区域重力场时所需的重力观测值数量大为减少,仍以构建120阶重力场为例,在不考虑测点分布的情况下,至少需要14641个观测值才能求解全部展开系数;而根据稀疏性,需要最少Jopt个观测值(Jopt远小于14641)即可求解所需的展开系数.
本文研究了基于Slepian谱分析理论的局部重力场建模方法,并利用EGM2008模型和实际观测点位分布,讨论分析了Slepian最佳截断数和最大展开阶数的确定,最后利用Slepian方法和2011—2013年间地面实测重力数据对华北区域时变重力场构建做出了尝试,获得了华北地区120阶(约150 km空间分辨率)的2011—2013年变化重力场模型,并与研究区域内基于Slepian方法和GRACE卫星数据得到的重力变化进行了比较.研究结果表明:
(1) 贝叶斯信息量准则(BIC)可作为确定Slepian展开最佳截断数的有效手段.对于90、120和180阶Slepian展开(半波长空间分辨率约200 km、150 km和100 km),基函数数量分别为8281、14641和32761个,基于BIC的最佳截断数分别为12、26和36,表明Slepian方法是一种具有稀疏特性的时空局部谱方法.
(2) 对于本文选取的3组展开阶数(90、120和180),研究区域内Slepian展开的最大阶数为120,模拟实验的解算误差为4.98×10-5 m·s-2(包含测点分布和宽频泄漏的影响).仅考虑测点分布对Slepian展开的影响时,120阶模拟实验的解算误差变为2.50×10-5 m·s-2; 在重复测点最为密集的京津地区,模型解算误差为2.05×10-5 m·s-2; 在重复测点稀疏的河南、安徽和山东区域,解算误差增大至2.98×10-5 m·s-2.若能在重复测点稀疏地区加密重力测网,可较大提高华北区域重力场模型的解算精度.
(3) 基于实测数据和Slepian方法解算的120阶重力场模型,重力变化信号基本都集中在研究区域内部,信号向研究区域外部的泄漏较小;可提供准确的信号频段,并滤除高频干扰,凸显主要的重力变化信号.
(4) 2011—2013年,研究区域内GRACE估计结果(60阶)与地面结果(120阶)在时空分布的显著趋势上存在较好的对应,证明了本文利用Slepian方法和地面数据所得重力场模型的可靠性.此外,120阶地面结果的空间差异性更强、重力变化的细节(高频信号)更多,可作为GRACE卫星模型的有效补充.
本文确定的华北地区120阶2011—2013时变重力场模型数据可由https://github.com/jchhan/TVGM-NorthChina下载.基于本文的理论方法框架和研究成果,未来如果使用华北区域包含更多测期和测点的地面数据,可在时间跨度和空间分辨率上实现对本文2011—2013年变化结果的改进,为华北构造活动分析、地震风险性评估以及水资源变化监测等研究提供持续可靠的时变重力场模型产品.此外,基于本文思路还可以实现在Slepian域内融合来自地面和卫星观测在内的多源重力数据,有望获得精度更高、适用范围更广的区域重力场模型.
致谢 感谢三位评审专家提出的宝贵修改建议.感谢美国普林斯顿大学Frederik Simons教授提供Slepian局部谱分析程序包(https://github.com/fjsimons)和德国地学中心(GeoForschungsZentrum)提供GRACE RL06 Level-2数据(ftp://isdcftp.gfz-potsdam.de/grace/).
Albertella A, Sansò F, Sneeuw N. 1999. Band-limited functions on a bounded spherical domain: the Slepian problem on the sphere. Journal of Geodesy, 73(9): 436-447. DOI:10.1007/pl00003999 |
Alley W M, Konikow L F. 2015. Bringing GRACE down to earth. Ground Water, 53(6): 826-829. DOI:10.1111/gwat.12379 |
Baur O. 2012. On the computation of mass-change trends from GRACE gravity field time-series. Journal of Geodynamics, 61: 120-128. DOI:10.1016/j.jog.2012.03.007 |
Bomfim E P, Braitenberg C, Molina E C. 2013. Mutual evaluation of global gravity models (EGM2008 and GOCE) and terrestrial data in Amazon Basin, Brazil. Geophysical Journal International, 195(2): 870-882. DOI:10.1093/gji/ggt283 |
Chen J L, Wilson C R, Tapley B D, et al. 2007. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophysical Research Letters, 34(13): L13302. DOI:10.1029/2007gl030356 |
Chen S, Xu W M, Wang Q S. 2017. The spherical harmonic model of gravity field in Mainland China by Slepian local spectrum method. Acta Geodaetica et Cartographica Sinica (in Chinese), 46(8): 952-960. DOI:10.11947/j.AGCS.2017.20150542 |
Chen S, Zhuang J C, Li X Y, et al. 2019. Bayesian approach for network adjustment for gravity survey campaign: methodology and model test. Journal of Geodesy, 93(5): 681-700. DOI:10.1007/s00190-018-1190-7 |
Cheng M K, Ries J. 2017. The unexpected signal in GRACE estimates of C20. Journal of Geodesy, 91(8): 897-914. DOI:10.1007/s00190-016-0995-5 |
Feng W, Wang C Q, Mu D P, et al. 2017. Groundwater storage variations in the North China Plain from GRACE with spatial constraints. Chinese Journal of Geophysics (in Chinese), 60(5): 1630-1642. DOI:10.6038/cjg20170502 |
Feng W, Shum C K, Zhong M, et al. 2018. Groundwater storage changes in China from satellite gravity: An overview. Remote Sensing, 10(5): 674. DOI:10.3390/rs10050674 |
Flechtner F, Sneeuw N, Schuh W-D. 2014. Observation of the System Earth from Space-CHAMP, GRACE, GOCE and Future Missions. Heidelberg: Springer.
|
Gao C C, Lu Y, Shi H L, et al. 2019. Detection and analysis of ice sheet mass changes over 27 Antarctic drainage systems from GRACE RL06 data. Chinese Journal of Geophysics (in Chinese), 62(3): 864-882. DOI:10.6038/cjg2019M0586 |
Han S-C, Shum C K, Bevis M, et al. 2006. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake. Science, 313(5787): 658-662. DOI:10.1126/science.1128661 |
Han S-C. 2008. Improved regional gravity fields on the Moon from Lunar Prospector tracking data by means of localized spherical harmonic functions. Journal of Geophysical Research: Planets, 113(E11): E11012. DOI:10.1029/2008je003166 |
Han S-C, Razeghi S M. 2017. GPS recovery of daily hydrologic and atmospheric mass variation: A methodology and results from the Australian continent. Journal of Geophysical Research: Solid Earth, 122(11): 9328-9343. DOI:10.1002/2017jb014603 |
Harig C, Simons F J. 2012. Mapping Greenland's mass loss in space and time. Proceedings of the National Academy of Sciences of the United States of America, 109(49): 19934-19937. DOI:10.1073/pnas.1206785109 |
Harig C, Simons F J. 2015. Accelerated West Antarctic ice mass loss continues to outpace East Antarctic gains. Earth and Planetary Science Letters, 415: 134-141. DOI:10.1016/j.epsl.2015.01.029 |
He X, Bos M S, Montillet J P, et al. 2019. Investigation of the noise properties at low frequencies in long GNSS time series. Journal of Geodesy, 93(9): 1271-1282. DOI:10.1007/s00190-019-01244-y |
Hsu H Z, Lu Y, Zhong M, et al. 2012. Satellite gravity and its application to monitoring geophysical environmental change. Scientia Sinica Terrae (in Chinese), 42(6): 843-853. DOI:10.1360/zd-2012-42-6-843 |
Hwang C, Hsu H J, Chang E T Y, et al. 2014. New free-air and Bouguer gravity fields of Taiwan from multiple platforms and sensors. Tectonophysics, 611: 83-93. DOI:10.1016/j.tecto.2013.11.027 |
Jiang T, Li J C, Dang Y M, et al. 2014. Regional gravity field modeling based on rectangular harmonic analysis. Science China Earth Sciences, 57(7): 1637-1644. DOI:10.1007/s11430-013-4784-1 |
Jin T Y, Li X L, Shum C K, et al. 2020. The balance and abnormal increase of global ocean mass change from land using GRACE. Earth and Space Science, 7(5): e2020EA001104. DOI:10.1029/2020ea001104 |
Klees R, Tenzer R, Prutkin I, et al. 2008. A data-driven approach to local gravity field modelling using spherical radial basis functions. Journal of Geodesy, 82(8): 457-471. DOI:10.1007/s00190-007-0196-3 |
Li J C, Chao D B, Ning J S. 1995. Spherical cap harmonic expansion for local gravity field representation. Manuscripta Geodaetica, 20(4): 265-277. |
Ning J S, Wang Z T, Chao N F. 2016. Research status and progress in international next-generation satellite gravity measurement missions. Geomatics and Information Science of Wuhan University (in Chinese), 41(1): 1-8. DOI:10.13203/j.whugis20150732 |
Panet I, Bonvalot S, Narteau C, et al. 2018. Migrating pattern of deformation prior to the Tohoku-Oki earthquake revealed by GRACE data. Nature Geoscience, 11(5): 367-373. DOI:10.1038/s41561-018-0099-3 |
Pavlis N K, Holmes S A, Kenyon S C, et al. 2012. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). Journal of Geophysical Research: Solid Earth, 117(B4): B04406. DOI:10.1029/2011jb008916 |
Plattner A, Simons F J. 2017. Internal and external potential-field estimation from regional vector data at varying satellite altitude. Geophysical Journal International, 211(1): 207-238. DOI:10.1093/gji/ggx244 |
Ran J J, Ditmar P, Klees R, et al. 2018. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. Journal of Geodesy, 92(3): 299-319. DOI:10.1007/s00190-017-1063-5 |
Reager J T, Gardner A S, Famiglietti J S, et al. 2016. A decade of sea level rise slowed by climate-driven hydrology. Science, 351(6274): 699-703. DOI:10.1126/science.aad8386 |
Riva R E M, Gunter B C, Urban T J, et al. 2009. Glacial Isostatic Adjustment over Antarctica from combined ICESat and GRACE satellite data. Earth and Planetary Science Letters, 288(3-4): 516-523. DOI:10.1016/j.epsl.2009.10.013 |
Rodell M, Famiglietti J S, Wiese D N, et al. 2018. Emerging trends in global freshwater availability. Nature, 557(7707): 651-659. DOI:10.1038/s41586-018-0123-1 |
Shen C Y, Xuan S B, Zou Z B, et al. 2015. Trends in gravity changes from 2009 to 2013 derived from ground-based gravimetry and GRACE data in North China. Geodesy and Geodynamics, 6(6): 423-428. DOI:10.1016/j.geog.2015.08.001 |
Simons F J, Dahlen F A. 2006. Spherical Slepian functions and the polar gap in geodesy. Geophysical Journal International, 166(3): 1039-1061. DOI:10.1111/j.1365-246X.2006.03065.x |
Simons F J, Dahlen F A, Wieczorek M A. 2006. Spatiospectral concentration on a sphere. SIAM Review, 48(3): 504-536. DOI:10.1137/s0036144504445765 |
Simons F J. 2010. Slepian functions and their use in signal estimation and spectral analysis. //Freeden W, Nashed M Z, Sonar T eds. Handbook of Geomathematics. Heidelberg, Germany: Springer, 891-923.
|
Slepian D. 1983. Some comments on Fourier analysis, uncertainty and modeling. SIAM Review, 25(3): 379-393. DOI:10.1137/1025078 |
Slobbe D C, Simons F J, Klees R. 2012. The spherical Slepian basis as a means to obtain spectral consistency between mean sea level and the geoid. Journal of Geodesy, 86(8): 609-628. DOI:10.1007/s00190-012-0543-x |
Sun X M, Li F, Yan J G, et al. 2015. An analysis of the applicability of Slepian function in analyzing lunar local gravity field. Acta Geodaetica et Cartographica Sinica (in Chinese), 44(3): 264-273. DOI:10.11947/j.AGCS.2015.20130728 |
Sun Y, Riva R, Ditmar P. 2016. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. Journal of Geophysical Research: Solid Earth, 121(11): 8352-8370. DOI:10.1002/2016jb013073 |
Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophysical Research Letters, 33(8): L08402. DOI:10.1029/2005gl025285 |
Tapley B D, Bettadpur S, Ries J C, et al. 2004. GRACE measurements of mass variability in the Earth system. Science, 305(5683): 503-505. DOI:10.1126/science.1099192 |
Van Camp M, De Viron O, Watlet A, et al. 2017. Geophysics from terrestrial time-variable gravity measurements. Reviews of Geophysics, 55(4): 938-992. DOI:10.1002/2017rg000566 |
Von Hippel M, Harig C. 2019. Long-term and inter-annual mass changes in the Iceland ice cap determined from GRACE gravity using Slepian functions. Frontiers in Earth Science, 7: 171. DOI:10.3389/feart.2019.00171 |
Wang Y, Jiang X D. 2017. The spherical cap harmonic analysis modeling method based on disturbing gravity gradients. Acta Geodaetica et Cartographica Sinica (in Chinese), 46(11): 1802-1811. DOI:10.11947/j.AGCS.2017.20160412 |
Wang Z H, Jin H L, Fu G Y, et al. 2017. EGM2008 model and the measured ground gravity data fusion and its application in the western Sichuan region. Progress in Geophysics (in Chinese), 32(3): 1051-1058. DOI:10.6038/pg20170314 |
Watkins M M, Wiese D N, Yuan D N, et al. 2015. Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons. Journal of Geophysical Research: Solid Earth, 120(4): 2648-2671. DOI:10.1002/2014jb011547 |
Wessel P, Luis J F, Uieda L, et al. 2019. The generic mapping tools version 6. Geochemistry, Geophysics, Geosystems, 20(11): 5556-5564. DOI:10.1029/2019gc008515 |
Wu Y H, Luo Z C, Zhou B Y. 2016. Regional gravity modeling based on heterogeneous data sets by using Poisson wavelets radial basis functions. Chinese Journal of Geophysics (in Chinese), 59(3): 852-864. DOI:10.6038/cjg20160308 |
Xu C J, Yin Z. 2014. Progress in inversion for tectonic stress-strain fields using geodetic data. Geomatics and Information Science of Wuhan University (in Chinese), 39(10): 1135-1146, 1178. DOI:10.13203/j.whugis20130748 |
Xu W M, Sun S B, Li X Y, et al. 2016. Calculation of gravity variations in North China based on Kriging gridding with variogram approach. Earthquake (in Chinese), 36(4): 171-185. |
Xu X Y, Jiang W P, Zhang X M, et al. 2018. Ability of recovering the global gravity field of a new satellite gravimetry system. Chinese Journal of Geophysics (in Chinese), 61(6): 2227-2236. DOI:10.6038/cjg2018L0270 |
Yang F, Xu H Z, Zhong M, et al. 2017. GRACE global temporal gravity recovery through the radial basis function approach. Chinese Journal of Geophysics (in Chinese), 60(4): 1332-1346. DOI:10.6038/cjg20170409 |
Zhang Y H, Wu H A, Kang Y H. 2016. Ground subsidence over Beijing-Tianjin-Hebei region during three periods of 1992 to 2014 monitored by interferometric SAR. Acta Geodaetica et Cartographica Sinica (in Chinese), 45(9): 1050-1058. DOI:10.11947/j.AGCS.2016.20160072 |
Zhao Q, Zhang B, Yao Y B, et al. 2019. Geodetic and hydrological measurements reveal the recent acceleration of groundwater depletion in North China Plain. Journal of Hydrology, 575: 1065-1072. DOI:10.1016/j.jhydrol.2019.06.016 |
Zhou X, Sun W K, Fu G Y. 2011. Gravity satellite GRACE detects coseismic gravity changes caused by 2010 Chile MW8.8 earthquake. Chinese Journal of Geophysics (in Chinese), 54(7): 1745-1749. DOI:10.3969/j.issn.0001-5733.2011.07.007 |
Zhu G B, Li J C, Wen H J, et al. 2012. Slepian localized spectral analysis of the determination of the Earth's gravity field using satellite gravity gradiometry data. Acta Geodaetica et Cartographica Sinica (in Chinese), 41(1): 1-7. |
Zhu Y Q, Liang W F, Zhan F B, et al. 2012. Study on dynamic change of gravity field in China continent. Chinese Journal of Geophysics (in Chinese), 55(3): 804-813. DOI:10.6038/j.issn.0001-5733.2012.03.010 |
Zhu Y Q, Wen X Z, Zhang J, et al. 2013. Dynamic variation of the gravity field in middle North China and its implication for seismic potential. Chinese Journal of Geophysics (in Chinese), 56(2): 531-541. DOI:10.6038/cjg20130217 |
Zou X C, Jin T Y, Zhu G B. 2016. Research on the MASCON method for the determination of local surface mass flux with Satellite-Satellite Tracking technique. Chinese Journal of Geophysics (in Chinese), 59(12): 4623-4632. DOI:10.6038/cjg20161223 |
陈石, 徐伟民, 王谦身. 2017. 应用Slepian局部谱方法解算中国大陆重力场球谐模型. 测绘学报, 46(8): 952-960. DOI:10.11947/j.AGCS.2017.20150542 |
冯伟, 王长青, 穆大鹏, 等. 2017. 基于GRACE的空间约束方法监测华北平原地下水储量变化. 地球物理学报, 60(5): 1630-1642. DOI:10.6038/cjg20170502 |
高春春, 陆洋, 史红岭, 等. 2019. 基于GRACE RL06数据监测和分析南极冰盖27个流域质量变化. 地球物理学报, 62(3): 864-882. DOI:10.6038/cjg2019M0586 |
蒋涛, 李建成, 党亚民, 等. 2014. 基于矩谐分析的区域重力场建模. 中国科学: 地球科学, 44(1): 82-89. DOI:10.1007/s11430-013-4784-1 |
宁津生, 王正涛, 超能芳. 2016. 国际新一代卫星重力探测计划研究现状与进展. 武汉大学学报·信息科学版, 41(1): 1-8. DOI:10.13203/j.whugis20150732 |
孙雪梅, 李斐, 鄢建国, 等. 2015. Slepian函数在月球局部重力场分析中的适用性分析. 测绘学报, 44(3): 264-273. DOI:10.11947/j.AGCS.2015.20130728 |
王燚, 姜效典. 2017. 扰动重力梯度的球冠谐分析建模. 测绘学报, 46(11): 1802-1811. DOI:10.11947/j.AGCS.2017.20160412 |
王灼华, 金红林, 付广裕, 等. 2017. EGM2008模型与地表观测重力数据的融合及其在川西地区的应用. 地球物理学进展, 32(3): 1051-1058. DOI:10.6038/pg20170314 |
吴怿昊, 罗志才, 周波阳. 2016. 基于泊松小波径向基函数融合多源数据的局部重力场建模. 地球物理学报, 59(3): 852-864. DOI:10.6038/cjg20160308 |
许才军, 尹智. 2014. 利用大地测量资料反演构造应力应变场研究进展. 武汉大学学报·信息科学版, 39(10): 1135-1146, 1178. DOI:10.13203/j.whugis20130748 |
许厚泽, 陆洋, 钟敏, 等. 2012. 卫星重力测量及其在地球物理环境变化监测中的应用. 中国科学: 地球科学, 42(6): 843-853. DOI:10.1360/zd-2012-42-6-843 |
徐伟民, 孙少波, 李晓一, 等. 2016. 基于变差函数的插值方法计算华北地区重力场变化. 地震, 36(4): 171-185. |
徐新禹, 姜卫平, 张晓敏, 等. 2018. 一种新型重力测量卫星系统确定全球重力场的性能分析. 地球物理学报, 61(6): 2227-2236. DOI:10.6038/cjg2018L0270 |
杨帆, 许厚泽, 钟敏, 等. 2017. 利用径向基函数RBF解算GRACE全球时变重力场. 地球物理学报, 60(4): 1332-1346. DOI:10.6038/cjg20170409 |
张永红, 吴宏安, 康永辉. 2016. 京津冀地区1992-2014年三阶段地面沉降InSAR监测. 测绘学报, 45(9): 1050-1058. DOI:10.11947/j.AGCS.2016.20160072 |
周新, 孙文科, 付广裕. 2011. 重力卫星GRACE检测出2010年智利MW8.8地震的同震重力变化. 地球物理学报, 54(7): 1745-1749. DOI:10.3969/j.issn.0001-5733.2011.07.007 |
朱广彬, 李建成, 文汉江, 等. 2012. 卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法. 测绘学报, 41(1): 1-7. |
祝意青, 梁伟锋, 湛飞并, 等. 2012. 中国大陆重力场动态变化研究. 地球物理学报, 55(3): 804-813. DOI:10.6038/j.issn.0001-5733.2012.03.010 |
祝意青, 闻学泽, 张晶, 等. 2013. 华北中部重力场的动态变化及其强震危险含义. 地球物理学报, 56(2): 531-541. DOI:10.6038/cjg20130217 |
邹贤才, 金涛勇, 朱广彬. 2016. 卫星跟踪卫星技术反演局部地表物质迁移的MASCON方法研究. 地球物理学报, 59(12): 4623-4632. DOI:10.6038/cjg20161223 |
 2021, Vol. 64
2021, Vol. 64


