2. 中国科学院油气资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Petroleum Resource Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
高温介质地震波传播是地热资源勘查、岩石圈高温结构探测和深层-超深油气勘探等领域的重要研究课题.一般而言,高温引起岩石黏弹性,快纵波波速随温度增加而降低,其理论基础是热弹性理论,即温度场弹性动力学.热弹性动力学方程由位移场波动方程和温度场扩散方程耦合构成.经典热弹性波动方程(Biot,1956a;Deresiewicz,1957)基于傅里叶抛物型热传导定律,其热平衡瞬间形成,忽略了温度变化趋于平衡需要时间,导致热弹介质中波的速度随频率无限变大的非物理现象(Savage,1966;Armstrong,1984).Lord和Shulman(1967)引入弛豫时间修正傅里叶热传导定律,简称L-S双曲型热辐射模型,解决了经典热弹波动方程的非物理解问题.本文基于L-S双曲型热辐射模型,研究热弹介质中弹性波传播特征和各种热参数对速度频散和振幅衰减的影响.
温度对岩石力学性质的影响以及热弹介质中波传播的研究由来已久.Ackerman等(1966)通过实验验证了Ward和Wilks(1951)提出的热弹性介质中存在热纵波(一种准静态慢纵波).Rudgers(1990)对含弛豫时间的L-S型热弹性动力学方程进行频散分析,从理论上预测热弹性介质中存在快纵波、横波和热波的传播,两个纵波为热耗散衰减波而横波不受介质热特性的影响.Carcione等(2018)和Wang等(2019)分别利用伪谱法和格林函数法求解L-S双曲型耦合热弹波动方程,模拟热弹介质中快纵波、热波和横波的传播行为,指出了热弹介质中的热波与孔弹介质(Biot,1956b)中的Biot慢纵波具有相似的传播特征.物理本质上,Biot波是由于孔隙介质中压力驱动形成的流体局域流传播行为;而热波则是由于P波膨-缩传播模式在介质中产生的温度梯度,形成的局域热扩散传播行为.热弹介质与孔弹介质的这两种局域行为均引起弹性波能量的耗散和衰减.上述研究侧重热弹波动方程的物理解释和数值求解方法,热参数的影响分析比较简单,仅给出了热导率简单变化的影响,证实模拟方法的有效性.
本文着重研究各种热参数对热弹性介质中弹性波传播的影响,详细分析了热导率、热膨胀系数、比热、热扩散系数等介质热参数的大范围变化(临界变化)对弹性波频散和衰减的影响.热传导是岩石圈最主要的热量传递方式,其表征参数热导率是岩石热物理性质最重要的参数;热膨胀系数表示岩石受热膨胀的幅度,与岩石热应力与热应变密切相关;热扩散率通过介质的比热和热导率计算确定.热导率、热膨胀系数和比热构成了岩石的热弹性基本系数.本文采用平面波频散分析方法,研究了这些热参数变化对热弹介质中波速频散与能量衰减的影响.然后利用热弹性动力学频率域的二阶格林函数进行波场快照数值模拟,直观展示热参数对快纵波和热波传播特性的影响.本文研究为地热资源勘查、岩石圈高温结构探测和超深层油气勘探提供理论依据,也为实验室条件下两类热耗散衰减纵波的观测提供参数依据.
1 热弹性动力学方程Biot(1956a)和Deresiewicz(1957)将弹性理论与热传导定律相结合,建立了经典的热弹性理论,表征热负荷作用下温度变化与应力应变之间的耦合关系.对于各向同性热弹性介质,其应变-位移关系和应力-应变关系定义如下:

|
(1) |
和
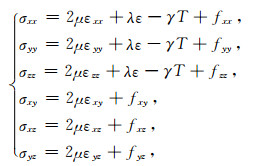
|
(2) |
式中,σij(i, j=x, y, z)、εij(i, j=x, y, z)和ui(i=x, y, z)分别为应力、应变和位移分量,T为相对于初始温度T0的温度增量,λ、μ为拉梅系数,fij(i, j=x, y, z)表示施加的外应力,γ=(3λ+2μ)αT,其中αT表示热膨胀系数.可见与常规弹性介质本构关系不同,热弹性介质中引入了温度的影响,产生热应力和热应变,其大小取决于介质的热膨胀系数.相应的动量守恒方程为:
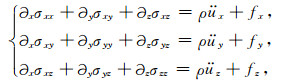
|
(3) |
式中,fi(i=x, y, z)表示体力分量,ρ表示体密度.
经典的傅里叶热传导定律可表示为:

|
(4) |
式中,k表示热导率,c表示恒应变下的比热,q表示热源,Δ为拉普拉斯算子.该定律精确描述了热流与温度差之间的关系,但由于热流密度和温度梯度同步,当介质产生温度梯度时,无穷远处瞬间感受到温度变化,从而导致热弹性介质中波以无限大速度传播,即热弹性波动方程存在非物理解,这在实际工程应用中问题比较突出(Qi and Suh, 2010;Wu et al., 2013).
Lord和Shulman(1967)引入弛豫时间修正傅里叶热传导定律,简称L-S双曲型热辐射模型,解决了经典热弹性波动方程的非物理解问题,对应的热传导方程可表示为:
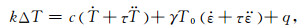
|
(5) |
式中τ表示弛豫时间,当τ=0时,(5)式退化为傅里叶热传导定律(4).将应力-应变关系带入动量守恒方程,利用应变-位移关系,得到表征位移与温度之间关系的热弹性动力学方程:

|
(6) |
而对于传统抛物型傅里叶热传导定律,经典热弹性动力学方程为:

|
(7) |
由方程(5)可知,在热传导过程中,热与应变耦合只涉及体应变,与剪切应变无关,建立的热弹性动力学方程(6)仅考虑波与热相互作用的一种机制:P波的膨-缩传播模式在介质中产生温度梯度,形成耗散衰减的慢纵波模式(T波),这是实验证实的一种热与波作用机制.因此,在此理论框架下,剪切波(S波)不受温度影响.
2 频散分析 2.1 平面波频散方程为了分析热弹介质中波的传播特征,将位移矢量u与T的变化表示为平面波形式:
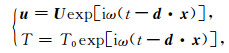
|
(8) |
其中,ω为角频率,d为慢度矢量,x为位置矢量,
为简单起见,若假定平面波为横波,其位移矢量方向与传播方向相互垂直,即Uili=0,热弹方程的频散关系简化为(Deresiewicz,1957):

|
(9) |
式中复波数s=ω/vc,得到横波的传播速度:

|
(10) |
由(10)式可知,横波的传播不受介质热特性的影响.若假定平面波为纵波,其位移矢量方向与传播方向一致,即Uili=1,得到纵波的频散关系:

|
(11) |
(11) 式的解为:

|
(12) |
令

|
(13) |
对于经典热弹性动力学方程,(12)式中M=iωa2,当ω→∞时,M→∞,由方程(10)可知会产生非物理解.而对于L-S广义热弹性理论,M=iωa2/(1+iωτ),Rudgers(1990)在晶格模型中将弛豫时间表示为:

|
(14) |
因此,当ω→∞时,M→a2/τ=vI2,两个纵波复波速为:
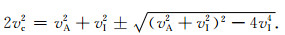
|
(15) |
当角频率ω=0时,由表达式(10)知,复速度为实数:

|
(16) |
其中,vT表示热波速度,vE表示快纵波速度.利用复速度vc,得到相速度vp与衰减因子A(Carcione, 2007):

|
(17) |
Deresiewicz(1957)引入衰减系数L,用来表示每个应力周期内,耗散的能量与总振动能量的比值:

|
(18) |
利用表 1中的热弹性介质模型参数进行频散分析,通过2.1节平面波频散方程可知,经典热弹性波动方程以抛物型热传导方程为基础,未考虑弛豫时间的影响,各向同性弹性连续体受到热扰动时,在距热扰动无穷远处会立即感受到扰动,即速度无限大,其波速和衰减频散曲线如图 1所示.可见,在热效应作用频段,快纵波随频率增加反而减小,而热波速迅速增加至无穷大,其对应的衰减为非物理的倒弛豫峰.
|
|
表 1 热弹性介质模型参数 Table 1 Parameters for a thermoelastic medium model |
|
图 1 经典热弹波动方程的(a)速度频散曲线和(b)振幅衰减曲线 Fig. 1 Velocity dispersion curves (a) and Amplitude attenuation curves (b) of classical thermoelastic wave equation |
将表 1热弹参数应用到双曲型L-S热弹理论得到的频散曲线如图 2所示,可见,考虑加入热扰动介质达到新稳态的平衡时间(弛豫时间)后,热效应作用频段热波速随频率增大趋于稳定值,避免了经典热弹性动力学中速度无限大问题.由图 2b的衰减频散曲线可知,热波在低频时表现出强衰减的扩散传播特性,而在高频时表现为弱衰减的波动传播特征.在高低频之间热效应过渡频段及其频散特征取决于热介质的特征参数.

|
图 2 L-S双曲型耦合热弹波动方程的(a)速度频散曲线和(b)振幅衰减曲线 Fig. 2 Velocity dispersion curves (a) and Amplitude attenuation curves (b) of L-S hyperbolic coupling thermoelastic equation |
利用L-S方程分析热弹介质中三种波的传播,假设平面波入射,可知热弹介质中的横波不会受到介质温度与热弹参数的影响,只与介质密度及介质的弹性剪切模量有关,但由于实际介质非常复杂,横波的传播取决于很多因素,在本文所应用的条件下,横波不发生频散,当频率约为100 MHz时,横波与热波传播速度相同,如图 3所示.

|
图 3 L-S双曲型耦合热弹波动方程快纵波、热波和横波的速度频散曲线 Fig. 3 The velocity dispersion curves of a fast longitudinal, thermal wave and shear waves of L-S hyperbolic coupling thermoelastic equation |
L-S热弹理论中位移场与温度场相互耦合,因此快纵波也受到温度场的影响,快纵波和热波的相速度和衰减系数根据平方根复速度(方程(17))计算得到,且由方程(12)可知其波速与衰减系数均涉及热弹参数.基于表 1中热弹参数作为基准量,本文着重分析表征岩石热物理性质的热导率、热膨胀系数及比热对波传播特征的影响.
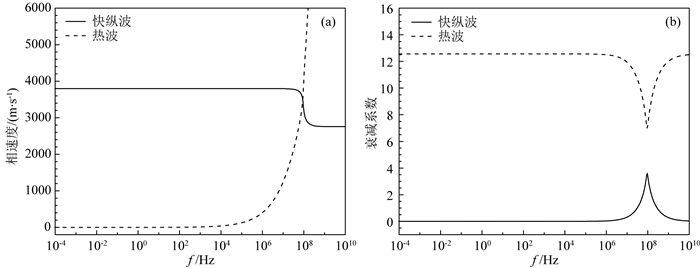
热导率表征岩石的导热能力,不仅是研究地壳、上地幔热结构及地球深部热状态的重要参数,在勘探开采等领域也得到广泛应用(沈显杰等,1988).热导率是热弹介质中波传播最重要的影响参数,其大小不仅依赖于介质的矿物组成,还取决于矿物分布、几何形状、内部结构等因素.对于大多数岩石类型,热导率随温度的升高而降低,与矿物结晶特性有关.对于孔隙介质和颗粒状材料,热导率还依赖于孔隙和晶粒尺寸等介质特征.通过经典热弹理论与L-S热弹理论对比可知,弛豫时间对热弹介质中波的传播性质有重要影响,通过分析与计算(Rudgers,1990)了解到热导率与弛豫时间有很强的相关性.图 4描述了热导率与快纵波和热波的频散与衰减的关系,数值计算过程中选取不同数量级的热导率.可见,随着热导率的增加,相速度和衰减系数的频散效应向低频移动,但其低频和高频稳态值并未发生改变,说明热导率不改变波传播的极限速度和衰减幅度;热频散过渡带的频宽也未见改变,但改变了热频散效应出现的频率,介质热导率越高,对应的热频散效应的初始频率越低.需要强调的是热波传播特征发生了较大变化,从低频慢速强衰减的扩散传播模式跨越到高频快速弱衰减的波动传播模式,热导率发挥了至关重要的作用.由方程(14)可知,弛豫时间与热导率呈正相关,高热导率情况下,介质受到热扰动后达到稳态的时间增大,即热导率的升高增加了达到平衡的弛豫时间,从而降低了扩散频率,如图 4b所示,衰减频带向低频移动.因此,在实验观测中,高热导率介质更容易观测到热波,下一节将通过格林函数数值模拟热波传播,直观观测热导率的影响.
|
图 4 不同热导率快纵波和热波的(a)速度频散曲线和(b)振幅衰减曲线 Fig. 4 Effect of thermal conductivity variety on Velocity dispersion curves (a) and Amplitude attenuation curves (b) of fast P and thermal waves |
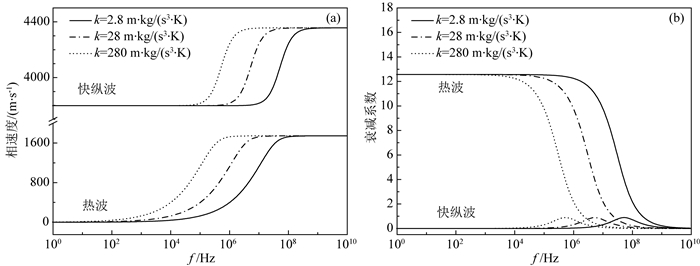
热膨胀系数表征介质的热膨胀量,不仅可以用来衡量介质的热稳定性能,还与介质受热时所产生的热应力与热应变密切相关,因此热膨胀系数对介质的结构有很大的影响,可能会导致结构破坏.与热导率影响不同,热膨胀系数对热弹介质中波传播特性的衰减影响主要表现在幅度方面.结合热导率影响,可知,当介质热导率较大时,可以观测到波状传播的热波.因此,取热导率k=280 m·kg/(s3·K)对热膨胀系数进行分析,如此大的热导率值在一般岩石材料中是没有的,在此仅作为参照值来阐述热参数变化会对弹性波传播特征产生多大的影响.图 5为不同热膨胀系数快纵波和热波的波速和衰减频散曲线,与图 4热导率影响特征相比,热膨胀系数不改变相速度及衰减热频散效应发生的起始频率及其过渡带频宽,说明热膨胀系数并不影响扩散频率,衰减频带未发生改变.由图 5a可知,热膨胀系数改变了波传播极限速度,特别是快纵波改变幅度较大.值得注意的是热膨胀系数对两纵波的影响方式相反,热膨胀系数越大,快纵波相速度在全频范围内越大,而此时介质热稳定性能较低,热波的相速度在高频段越小.热膨胀系数对热波衰减系数影响很小,而对快纵波衰减系数的峰值影响稍大.

|
图 5 不同热膨胀系数快纵波和热波的(a)速度频散曲线和(b)振幅衰减曲线 Fig. 5 Effect of thermal expansion coefficient variety on Velocity dispersion curves (a) and Amplitude attenuation curves (b) of fast P and thermal waves |
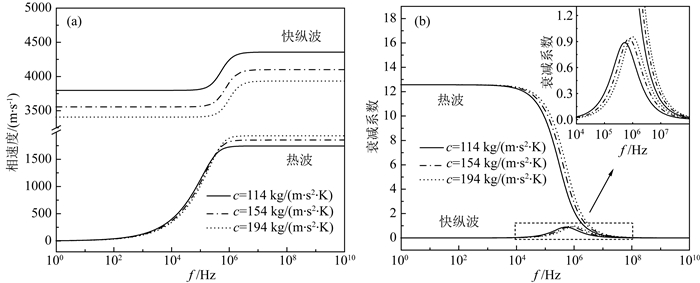
对于超高温介质热扩散率与比热是不可或缺的参数,而热扩散率可由热导率和比热计算得到.前面已经对热导率和热膨胀系数的波传播影响进行了分析,本节研究比热对热弹介质中波传播特性的影响,介质的比热由介质组成成分决定.图 6为不同比热介质快纵波和热波的频散曲线与衰减曲线,其中热导率也为280 m·kg/(s3·K).可见,比热的影响兼顾热导率和热膨胀系数的影响,既改变热频散效应发生的起始频率,又影响极限速度的大小及快纵波弛豫峰值,但影响幅度要小得多.由图 6a可知,随着比热的增大,快纵波和热波相速度的增量区均向高频方向移动,但对两纵波的影响相反.比热越大快纵波的相速度在全频范围内越小,而热波的相速度在高频段越大;相比于快纵波,比热对热波相速度影响较小.且由图可知,随着比热的增大,对纵波相速度的影响会越小.分析图 6b可知,随着比热增加,扩散频带向高频移动,此时弛豫时间减小,达到稳态的时间缩短.比热综合晶格振动和粒子热运动的贡献来表征岩石热容性,是描述介质热学性质的重要物理量,在常温及高温条件下,晶格振动影响占主导,因而对快纵波速度影响相对较大.
|
图 6 不同比热快纵波和热波的(a)速度频散曲线与(b)振幅衰减曲线 Fig. 6 Effect of specific heat variety on Velocity dispersion curves (a) and Amplitude attenuation curves (b) of fast P and thermal waves |
格林函数一般定义为偏微分方程自由空间中点源的解,是构成偏微分方程积分形式的基本解.针对L-S热弹性动力学方程的格林函数研究鲜有发表(Wang et al., 2019),其频率域的二阶格林函数张量解的简要推导见附录B,本文利用该格林函数张量进行热介质波场快照数值模拟,直观观察热弹性介质中纵波、横波和热波的传播行为,传播特征与第2节中的频散分析结果一致.本文着重分析不同力源方向对三种波的波形特征及能量衰减的影响,同时再现热弹介质参数对快纵波和热波传播特性的影响.
本节利用二阶格林函数张量模拟波动传播的快纵波和热波,模型大小为NX×NZ=200×200,纵横网格间隔均为0.1 mm,集中点源采用位于网格中点处主频为3.5 MHz的雷克子波,时间步长dt=0.1 μs.
图 7表示在表 1热弹参数条件下,即热导率为2.8 m·kg/(s3·K),3 μs时刻的波场快照,(a)表示在水平力源条件下,水平方向位移的波场快照;(b)表示在垂直力源条件下,垂直方向位移的波场快照;(c)表示在热源条件下,温度场的波场快照.为了研究热导率对快纵波和热波传播特征的影响,图 8中热导率k=280 m·kg/(s3·K).由图 7和图 8可知,在力源作用下的波场快照中观察到快纵波与横波,在热源作用下的温度位移场中观察到快纵波与热波.由图 4可知,在该主频下,当k=2.8 m·kg/(s3·K)时,热波表现为慢速强衰减的扩散传播模式,而k=280 m·kg/(s3·K)时,热波以快速弱衰减的波动模式传播,对于快纵波,高热导率比低热导率的传播速度更快,而对于横波,热弹性介质参数不影响其传播特性,均与格林函数数值模拟结果一致.
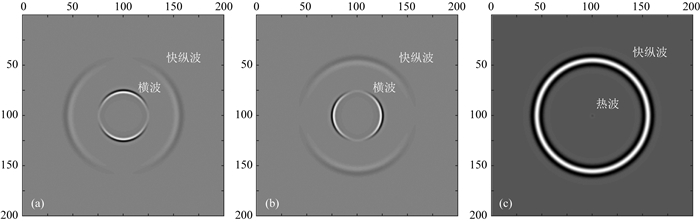
|
图 7 热导率k=2.8 m·kg/(s3·K),3 μs时刻的波场快照,震源分别为(a)水平力源,(b)垂直力源和(c)热源 Fig. 7 Snapshots at 3 μs for k=2.8 m·kg/(s3·K), the source are a horizontal elastic force (a), a vertical elastic force (b) and a heat source (c), respectively |

|
图 8 热导率k=280 m·kg/(s3·K),3 μs时刻的波场快照,震源分别为(a)水平力源,(b)垂直力源和(c)热源 Fig. 8 Snapshots at 3 μs for k=280 m·kg/(s3·K), the source are a horizontal elastic force (a), a vertical elastic force (b) and a heat source (c), respectively |
为了研究热膨胀系数与比热对快纵波和热波传播特性影响,在热源条件下,热导率k=280 m·kg/(s3·K)时,分别观察介质热膨胀系数不同和介质比热不同时的波场快照.图 9a为热膨胀系数αT=4.0×10-6K-1,对比图 8c和图 9a波场快照图可知,热膨胀系数对两纵波的影响方式相反,在该主频条件下,热膨胀系数越大,快纵波速度越大,而热波速度越小,与频散分析结果(图 5)相符合.图 9b为比热c=194 kg/(m·s2·K),3 μs时刻的波场快照,通过与图 8c对比可知,比热增大时快纵波速度减小,而热波传播速度增加,与图 6中的频散分析结果一致.

|
图 9 热源条件下(a)热膨胀系数αT=4.0×10-6K-1和(b)比热c=194 kg/(m·s2·K)时的波场快照 Fig. 9 Snapshots for c=194 kg/(m·s2·K) (a) and αT=4.0×10-6K-1 (b), where source is a heat source, respectively |
地震波在热弹介质中的传播是岩石圈高温结构探测、地热资源勘查和深层-超深油气勘探等领域的重要研究课题.基于傅里叶抛物型热传导定律的经典热弹性动力学理论,由于忽略了温度分布趋于平衡需要时间而导致波速随频率无限增大的非物理现象.基于L-S双曲型热传导方程的热弹性动力学理论,由于引入弛豫时间修正项而解决了这一非物理现象问题,本文通过对比这两种热弹性动力学理论的频散曲线,分析了弛豫时间对热弹介质中波传播特征的影响.
含弛豫时间修正项的L-S双曲型热耦合热弹波动方程,从理论上预测了在热弹性介质中存在两种热耗散衰减纵波(即快纵波和热波)和横波,本文利用平面波频散分析和数值模拟再现了这些波的传播特征.热波与孔弹介质中的Biot慢纵波(如,Ba et al., 2017, 2019;Zhang et al., 2019)具有相似特征,两种波分别为压力和温度的局部差异而产生的流体和热流局域流,其频散和衰减特征分别受制于介质的热导率和流体黏度.两种波低频时呈现慢速高衰减的扩散特征,而高频时表现为高速弱衰减的波动模式.本文的数值模拟表明,高热导率材料在高频实验条件下可以观测到热波.Ackerman等(1966)在固体氦中观测到热波,McNelly等(1970)和Jackson等(1970)在NaF晶体中观察到热波.作为热弹性问题不可分割的理论组成部分,热波的客观存在具有重要的科学意义(Gueguen,2013).
鉴于热弹参数对热弹介质中弹性波传播的重要影响,本文详细分析了热导率、热膨胀系数和比热三个基本参数的变化对波速频散和振幅衰减的影响.结果表明,热导率决定了两种热耗散纵波波速频散与能量衰减的临界变化;热膨胀系数主要影响快纵波的波速和热波衰减的幅度,而比热既影响波速和衰减的临界变化,又影响变化的幅度.格林函数方法数值模拟展现了热弹介质中横波、快纵波和热波的波场快照,热参数(热导率、热膨胀系数和比热)对快纵波和热波传播特征的影响与平面波频散分析结果一致.本文研究为地热资源勘查、岩石圈高温结构探测和超深层油气勘探提供理论依据,也为实验室条件下两类热耗散衰减纵波的观测提供参数依据.
附录A 文中涉及的符号列表|
|
关于热弹问题的格林函数,前人做了大量研究,主要涉及热静力学问题格林函数(Kupradze et al., 1976)和时间域及频率域的经典热弹性耦合热弹波动方程的格林函数(Nowacki, 1975;Tosaka, 1985;Tosaka and Suh, 1991;Norris, 1994;Scarpetta et al., 2014),未考虑弛豫时间,存在非物理解问题. Wang等(2019)推导了含弛豫时间修正项的L-S双曲型热耦合热弹波动方程,得到了均匀各向同性材料中点载荷(力或热源)对应的二阶张量格林函数.
若不考虑热流的影响,方程(6)简化为:
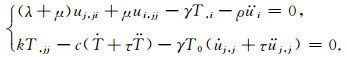
|
(B1) |
对耦合系统运用傅里叶变换进行求解,傅氏变换为:

|
(B2) |
得到热弹性动力学方程在频率域的双曲型微分控制方程(为了方便,在下面的公式表达中去掉-):
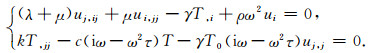
|
(B3) |
将(B3)式写成矩阵方程形式:LijUj=0,考虑二维情况,经过数学计算得到系数算子Lij:

|
其中Di=∂/∂xi(i=1, 2).
下面分析基本解张量Vij*,对于Vij*满足方程:

|
(B4) |
式中lij为Lij的代数余子式,因此系数lij为:
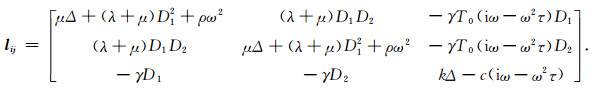
|
利用βij与标量函数Φ*构建基本解张量Vij*:

|
(B5) |
式中βij为lij的余子式.将(B5)式代入方程(20)得到:

|
(B6) |
式中微分算子Λ为:

|
(B7) |
系数hi2(i=1, 2, 3)为:

|
(B8) |
其中:
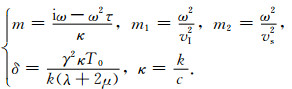
|
(B9) |
由方程(B8)知h1和h2是弛豫时间τ的函数. 综上所述,得到热弹性介质系统动力学方程在频率域内的基本解张量Vij*:

|
(B10) |
其中:
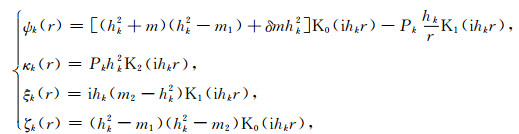
|
(B11) |
K0,K1,K2分别为修正的零阶、一阶和二阶贝塞尔函数,并且:

|
(B12) |
Ackerman C C, Bertman B, Fairbank H A, et al. 1966. Second sound in solid helium. Physical Review Letters, 16(18): 789-791. DOI:10.1103/PhysRevLett.16.789 |
Armstrong B H. 1984. Models for thermoelastic attenuation of waves in heterogeneous solids. Geophysics, 49(7): 1032-1040. DOI:10.1190/1.1441718 |
Ba J, Xu W H, Fu L Y, et al. 2017. Rock anelasticity due to patchy saturation and fabric heterogeneity: A double double-porosity model of wave propagation. Journal of Geophysical Research: Solid Earth, 122(3): 1949-1976. |
Ba J, Ma R P, Carcione J M, et al. 2019. Ultrasonic wave attenuation dependence on saturation in tight oil siltstones. Journal of Petroleum Science and Engineering, 179: 1114-1122. DOI:10.1016/j.petrol.2019.04.099 |
Biot M A. 1956a. Thermoelasticity and irreversible thermodynamics. Journal of Applied Physics, 27(3): 240-253. DOI:10.1063/1.1722351 |
Biot M A. 1956b. The theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. The Journal of the Acoustical Society of America, 28(2): 168-178. DOI:10.1121/1.1908239 |
Carcione J M. 2007. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media. Amsterdam: Elsevier Science.
|
Carcione J M, Wang Z W, Ling W C, et al. 2018. Simulation of wave propagation in linear thermoelastic media. Geophysics, 84(1): 1-37. |
Deresiewicz H. 1957. Plane waves in a thermoelastic solid. The Journal of the Acoustical Society of America, 29(2): 204-209. DOI:10.1121/1.1908832 |
Gueguen Y. 2013. Wave propagation and attenuation in rocks from poroelasticity and thermoelasticity. //Poromechanics V: Proceedings of the Fifth Biot Conference on Poromechanics, 2391-2394.
|
Jackson H E, Walker C T, McNelly T F. 1970. Second sound in NaF. Physical Review Letters, 25(1): 26-28. DOI:10.1103/PhysRevLett.25.26 |
Kupradze V D, Gegelia T G, Basheleishvili M O, et al. 1976. Three-dimensional Problems of the Mathematical Theory of Elasticity and Thermoelasticity. Amsterdam: Elsevier.
|
Lord H W, Shulman Y. 1967. A generalized dynamical theory of thermoelasticity. Journal of the Mechanics and Physics of Solids, 15(5): 299-309. DOI:10.1016/0022-5096(67)90024-5 |
McNelly T F, Rogers S J, Channin D J, et al. 1970. Heat pulses in NaF: onset of second sound. Physical Review Letters, 24(3): 100-102. DOI:10.1103/PhysRevLett.24.100 |
Norris A N. 1994. Dynamic Green's functions in anisotropic piezoelectric, thermoelastic and poroelastic solids. Proceedings of the Royal Society A: Mathematical: Physical and Engineering Sciences, 447(1929): 175-188. |
Nowacki W. 1975. Dynamic Problems of Thermoelasticity. Netherlands: Springer Science & Business Media.
|
Qi X L, Suh C S. 2010. Generalized thermo-elastodynamics for semiconductor material subject to ultrafast laser heating. Part Ⅰ: Model description and validation. International Journal of Heat and Mass Transfer, 53(1-3): 41-47. DOI:10.1016/j.ijheatmasstransfer.2009.10.010 |
Rudgers A J. 1990. Analysis of thermoacoustic wave propagation in elastic media. The Journal of the Acoustical Society of America, 88(2): 1078-1094. DOI:10.1121/1.399856 |
Savage J C. 1966. Thermoelastic attenuation of elastic waves by cracks. Journal of Geophysical Research, 71(16): 3929-3938. DOI:10.1029/JZ071i016p03929 |
Scarpetta E, Svanadze M, Zampoli V. 2014. Fundamental solutions in the theory of thermoelasticity for solids with double porosity. Journal of Thermal Stresses, 37(6): 727-748. DOI:10.1080/01495739.2014.885337 |
Tosaka N. 1985. The integral equation formulation for boundary-value problems by the coupled system of differential equations. Japan NCTAM: 323-324. |
Tosaka N, Suh I G. 1991. Boundary element analysis of dynamic coupled thermoelasticity problems. Computational Mechanics, 8(5): 331-342. DOI:10.1007/BF00369891 |
Wang Z W, Fu L Y, Wei J, et al. 2019. On the Green function of the Lord-Shulman thermoelasticity equations. Geophysical Journal International, 220(1): 393-403. |
Ward J C, Wilks J. 1951. The velocity of second sound in liquid helium near the absolute zero. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 42(326): 314-316. DOI:10.1080/14786445108561271 |
Wu S C, Peng X, Zhang W H, et al. 2013. The virtual node polygonal element method for nonlinear thermal analysis with application to hybrid laser welding. International Journal of Heat and Mass Transfer, 67: 1247-1254. DOI:10.1016/j.ijheatmasstransfer.2013.08.062 |
Zhang L, Ba J, Fu L Y, et al. 2019. Estimation of pore microstructure by using the static and dynamic moduli. International Journal of Rock Mechanics and Mining Sciences, 113: 24-30. DOI:10.1016/j.ijrmms.2018.11.005 |
沈显杰, 杨淑贞, 张文仁. 1988. 岩石热物理性质及其测试. 北京: 科学出版社.
|
 2021, Vol. 64
2021, Vol. 64


