陆地水包括了地表水(湖泊、河流和水库蓄水)、土壤水、地下水、冰雪以及树冠水等(Famiglietti et al., 2011)，它们在人类的日常生活、农业灌溉、工业生产等领域都扮演着至关重要的角色.中国是一个极度缺水的国家，水资源短缺已经成为我们国家社会经济发展面临的一个重大资源问题(孙冬营等，2020).川云渝地区作为南水北调西线工程的重要源头(张金良等，2020)，监测和量化当地陆地水的变化对地方政府进行干旱与洪涝的预防、气候变化分析甚至国家水资源管理政策的制定等都着有重大意义.目前多种现代空间大地测量技术和水文同化建模已广泛应用于监测陆地水的变化.

全球尺度下的水文模型主要包含陆面模型和水文水资源模型，当前应用最为广泛的是美国国家航空航天局NASA (Nation Aeronautics and Space Administration)发布的全球陆面数据同化系统GLDAS(Global Land Data Assimilation System)，该模型的优点是能提供全球高时空分辨率的多种陆地表状态和通量场，例如降水、蒸散、地表径流和地下径流等(Rodell et al., 2004).Wang和Zeng(2012)利用青藏高原地区的63个气象站点观测资料验证了GLDAS能提供较为准确降水数据，同时气温的描述也较好.李霞等(2014)利用水文站观测数据验证了模型在黄河源区的适用性，发现GLDAS数据能较好地体现黄河源区的流量特征.但GLDAS数据也存在着一些缺陷，例如Noah模型缺乏部分地表水和深层地下水数据(Jin and Zhang, 2016)，不能完整地监测区域陆地水变化.同时部分地区存在径流与蒸散结果不够精确.例如，王文等(2017)研究表明GLDAS低估了中国外流区的径流以及高估了蒸散作用的影响，且该模型简化了物理过程，只考虑了气候因素作用，没有考虑流域内人为因素对水储量造成的影响(Tatsumi and Yamashiki, 2015).因此，GLDAS数据很难以精确反映实际的陆地水变化.

重力恢复与气候试验GRACE(Gravity Recovery and Climate Experiment) 是美国国家航空航天局和德国航空航天中心于2002年3月17日发射的重力卫星.其主要目标是获取每月的时变地球重力场来探究水圈、冰层和海洋中的质量变化(Tapley et al., 2004).当前GRACE提供的时变重力场数据已广泛应用于研究全球范围内季节和年际尺度上的陆地水储量变化、地下水储量变化、冰层质量再分布等(Seo et al., 2006; Tiwari et al., 2009; Velicogna, 2009).除此之外，GRACE对局部地区较为明显的质量变化也有良好的响应，例如有学者研究利用GRACE探测三峡水坝以及巴贡大坝的蓄水量变化(Wang et al., 2011; Tangdamrongsub et al., 2019). 但GRACE一方面由于条带误差和高频误差的原因解算时需要进行滤波处理(Swenson and Wahr, 2006)，这在一定程度上抑制真实信号特征，另一方面，GRACE在全球范围内只能保持一个月的时间分辨率和约300 km的空间分辨率，导致小范围内的高频质量变化的监测受到限制.此外，在GRACE与后期的GRACE Follow-on任务衔接期间有着接近一年的观测空缺，因此需要一种代替手段来弥补这部分空缺.

地表季节性的陆地水变化会导致弹性地球由于负荷作用产生周期性的形变.Van Dam and Wahr(1998)发现单个GPS站点的位移时间序列包含了地表负荷对地球造成的显著位移，Bevis等(2005)认为GPS观测技术能对周围100 km内的负荷变化有着较好的灵敏度，后续也有许多学者将GPS位移时间序列与GRACE计算的位移数据进行对比，发现GPS时间序列中的季节性成分主要与陆地水变化有关(Van Dam et al., 2001; Davis et al., 2004; 王林松等，2014; Gu et al., 2017; 丁一航等，2018). 于是有学者探索利用GPS垂直位移时间序列来研究陆地水储量变化，例如Argus等(2014)与Fu等(2015)基于GPS站垂直位移时间序列，应用圆盘负荷格林函数的方法分别反演计算了美国加利福利亚地区以及美国西部地区的陆地水储量变化，Borsa等(2014)基于GPS监测的地表隆起计算了美国西部2013年干旱时期流失的水质量.国内也有学者根据GPS监测的地表形变来研究了云南境内的水储量变化以及干旱特征(何思源等，2018; Jiang et al., 2017).Hsu等(2020)基于GPS垂直形变反演了台湾地区2005至2016年间的陆地水储量变化，并分析了降雨模式、入渗率、土壤饱和度和径流等多种因素对陆地蓄水的影响.他们的结论表明除了GRACE与水文模型以外，GPS可以作为一种独立的数据源来监测陆地水变化.且相较于GRACE而言，GPS时间序列时间分辨率高(达到天或天以下)，监测时间长(部分站点观测时长达二十余年)，使得GPS在小尺度上的反演计算上有着独特的优势.

然而格林函数方法对区域内GPS站点的分布和密度有着较高的要求，不适合用于大尺度陆地水储量的反演工作(Han and Razeghi, 2017).为了能够使GNSS用于大尺度水储量的研究工作，将其转为与GRACE类似的空间谱是一种有效的分析方法.本文探究应用局部Slepian函数将负荷位移信号转换为Slepian空间谱，并以此反演地表质量变化.Slepian问题最早的提出，主要用于解决有限信号截断问题和提高信号功率谱密度的估算等应用(Slepian, 1983)，后来进一步完善后逐渐开始应用于地球科学等各个领域.Slepian函数与GRACE所使用的球谐系数法类似，是用一定阶数的Slepian基函数表示局部区域的地球物理信号场.Simons等(1997)基于该方法研究了金星的重力地形构造.Han等用该方法研究了2004年苏门答腊地震的震后局部重力场变化以及局部月球重力场的优化(Han et al., 2008; Han, 2008).Harig和Simons(2012)将该方法应用于监测冰川消融现象，利用重力卫星跟踪数据计算了格陵兰岛地区2002到2011年间的质量变化趋势.在国内该方法也已普遍应用于地月重力场方面的相关研究(朱广彬等，2012；孙雪梅等，2015；陈石等，2017).在反演陆地水方面，Han和Razeghi(2017)使用Slepian函数反演了澳大利亚大陆地区质量变化，结果显示该方法可以适当降低区域内站点空间覆盖率的要求，实现更大尺度的陆地水储量变化的反演计算.

川云渝三省位于我国西南地区，地处青藏高原东南部，地势西高东低，是青藏高原向东挤压的构造单元中活动性最强的一个，其内部结构具有明显的空间变异性(Jin et al., 2019).气候由西部青藏高原的高原季风气候向东逐渐过渡为亚热带季风气候，区域内水资源丰富，有着较强的季节性现象且空间差异明显.本文目标是开发基于Slepian基函数的GNSS陆地水反演方法并验证该方法在川云渝地区的适用性.文中将GPS垂直位移信号应用局部Slepian基函数结合地表质量负荷理论反演得到2011—2015年川云渝三省陆地水储量变化，并在空间和时间上与GRACE、水文模型和降雨数据进行对比来分析该方法的可行性.

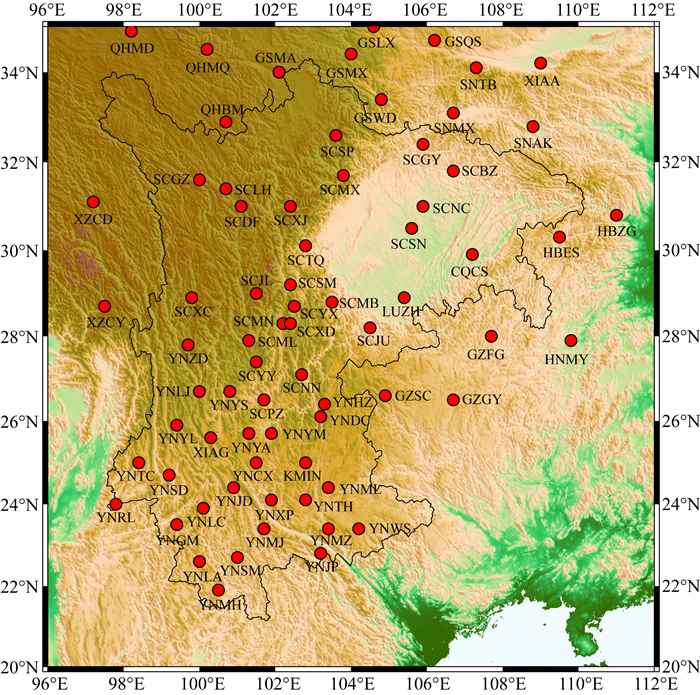
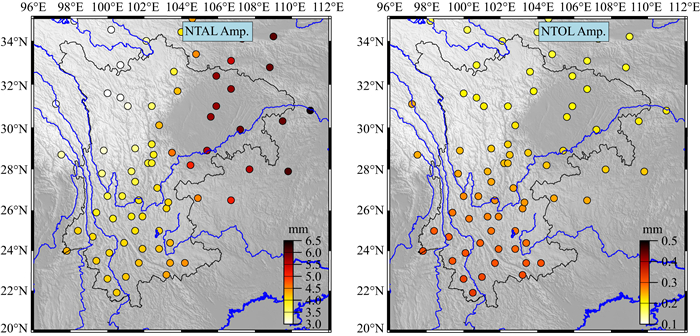
本文采用国家地震科学数据共享中心提供的单天解坐标时间序列(http://www.eqdsc.com/data/pgv-sjxl.htm)，选取了川云渝地区分布较均匀的72个GPS站，站点分布如图 1所示.本文选取的数据时间跨度为2011—2015年，且在研究时段内具有较好的完整性.数据解算使用麻省理工学院提供的GAMIT软件，采用IGS提供的轨道和钟差信息，先验对流层延迟采用GMF模型改正，固体潮和极潮改正使用IERS03模型，海潮使用FES2004模型进行改正.为了能精确地提取陆地水变化所造成的地表形变信号，本实验在后续的时间序列处理中，使用国际质量负荷服务(http://massloading.net/)所提供的大气负荷(Merra2模型)和非潮汐海洋负荷(OMTC05模型)的垂向位移改正产品.图 2为两者产生的垂向位移在站点处的周年振幅大小.由图可知，川云渝地区受到大气负荷的影响较为明显，垂向周年振幅可达6.5 mm，受到非潮汐海洋负荷的影响较小，最大约为0.4 mm.在站点原始坐标时间序列中将这两种负荷信号扣除得到主要由陆地水变化所产生的位移信号.最后为了准确获取季节性位移，本文拟合并去除了时间序列中的线性趋势以及跳变，以减小构造运动，地震以及仪器更换等其他因素的影响.拟合公式如下：

(1)

图 1

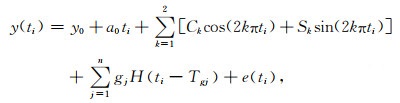
Fig. 1

图 1 西南地区GPS站分布图 Fig. 1 Distribution of GPS stations in Southwest China

图 2

Fig. 2

图 2 站点处大气负荷(Non-tidal atmospheric loading: NTAL)与非潮汐海洋负荷(Non-tidal ocean loading: NTOL) 垂直位移周年振幅 Fig. 2 Annual vertical displacement amplitude of atmospheric loading and non-tidal oceanic loading at GPS station

式中，t_i为观测时间，y为观测序列，a₀为线性项，H(t_i- T_gj) 为地震与仪器更换所造成的阶跃项，C_k与S_k表示待估的正余弦振幅，e(t_i)为残差.当k为1，2时，时间序列分别拟合周年变化与半周年变化.

为了保证反演计算时数据的完整性，本文采用了Kriging-Kalman-Filter模型补齐缺失的GPS数据(Liu et al., 2018)，该方法插值时考虑了GPS站之间的空间相关性，可以更好地恢复GPS时间序列中的地球物理信号.

本文使用的GRACE时变重力场数据来自美国德克萨斯大学空间研究中心(Center of Space Research，CSR) 提供的RL06 v02 Mascon数据，本文选取数据的时间跨度为2011年至2015年，共47个月.这些Mascon解纯粹由GRACE与GRACE-FO信息进行正则化约束计算得到，为了便于分析重采样为0.25°×0.25°的格网形式.数据解算时采用卫星激光测距的估计值替代C₂₀项和C₃₀项(仅GRACE-FO解)，并根据Swenson等(2008)计算的估计值校正了地心改正项以及基于ICE6G-D模型修正冰川均衡调整.Mascon数据较好地解决了条带误差，不需要再附加滤波以及缩放因子等处理过程，相较于GRACE球谐解能更好地保留真实的质量变化特征.

水文模型使用美国航天航空局提供的全球陆地数据同化模型GLDAS-Noah(http://daac.gsfc.nasa.gocv)，数据为格网形式.文中选择空间分辨率为1°×1°，时间分辨率为一个月的L4表面陆地模型，GLDAS中主要体现了浅层土壤水以及冰雪等成分的变化，将模型中的积雪量、树冠总蓄水和四层(0~2 m)土壤含水量累加就可得到陆地总水储量. 再去均值后即可得到研究时段内的陆地水储量变化.

球谐函数法是在保证全局正交性的条件下将球面上全球分布的地球物理信号用一系列不同阶次的球谐系数表示.但研究时常有目标信号只集中于某一特定区域内的情况，Slepian函数原理是寻找带边界限制的局部球谐函数，函数的信号能最佳地集中在单位球表面上的某个封闭部分，进而可以表示特定区域内的局部物理场(Simons and Dahlen, 2006)，Slepian函数只与研究区域与选取的最大阶数有关.基于最大阶数L解算第a项Slepian基函数g_a的公式为

(2)

θ为余纬，λ为经度，Y_lm为l阶m次的表面球谐函数，g_{α, lm}为第α项Slepian函数的l阶m次球谐膨胀系数，它可以由球面Ω上某个封闭区域R内的能量集中度γ来确定.

(3)

Slepian函数的目的在于得到γ接近于1的一系列g_{α, lm}值来求得信号集中于R内的基函数g_α.方法是用各阶次两个球谐函数积的积分构造矩阵D_{lm, l′m′}

(4)

解上式中的特征值与特征向量即可得到能量集中度γ与g_{α, lm}.本文选择封闭积分区域为西南地区川云渝三省边界，最大阶数由积分区域内GPS站点密度决定，试验后本文选择60阶，计算得到特征值和特征向量分别为γ与g_{α, lm}.图 3为60阶Slepian函数下求得的3721个能量集中度γ.

图 3

Fig. 3

图 3 各阶次下Slepian函数能量集中度 Fig. 3 Concentration ratio of each Slepian function

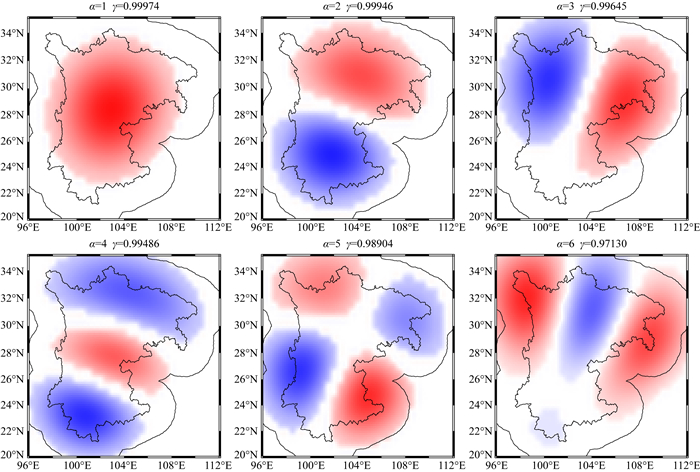
从图 3可以得出越靠前的项Slepian函数能量集中度越接近于1，即信号在指定区域所占的比重越大.图 4为前六项基函数信号在积分区域的空间分布.其中红色表示信号为正，蓝色表示信号为负，颜色的深浅表示信号的大小，内轮廓为实际研究区域边界，外轮廓是为了能让信号能充分覆盖区域周围，将研究区域向外扩充一定缓冲区后的积分边界.结合图 3和图 4也可以得到γ越接近于1时，信号越集中于积分区域内.随着项数α的增大，基函数信号逐渐往积分区域外扩散，当能量集中度减少至0时，表明信号主要集中于实验区域以外.因此一般只需要选择γ大于一定阈值的前J项基函数，使其能充分覆盖积分区域即可有效转换内部所有地球物理信号.本文中的实验选择γ大于0.1以上的Slepian基函数.

图 4

Fig. 4

图 4 前6项Slepian基函数信号分布 α为基函数项数，γ表示能量集中度.内轮廓为川云渝三省边界，外轮廓为扩充后积分边界. Fig. 4 Signal distribution of the first 6 Slepian basis functions α is the number of base function items, γ represents the energy concentration.The inner contour is the boundary of Sichuan, Yunnan and Chongqing, and the outer contour is the extended boundary for integral calculation.

根据上节中Slepian函数的特性，我们可以将地球表面局部位移场信号用一组Slepian基函数来表示.各个站点处的垂向位移信号u可以近似为

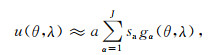
(5)

s_a为前J项Slepian函数下的位移基函数系数.又根据地表弹性负荷理论(Farrell, 1972)，可将区域内位移基函数系数转化为质量负荷基函数系数s_β^ewh

(6)

ρ_e为地球密度，ρ_w为水密度，h′_l为负荷勒夫数，最后得到区域内(θ, λ)处等效水高形式的质量负荷为

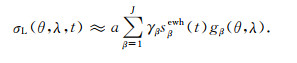
(7)

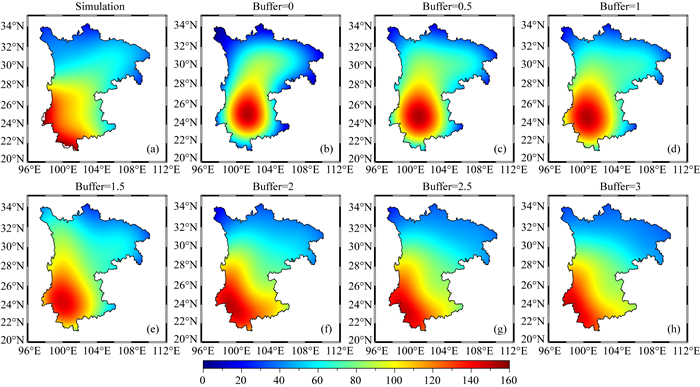
由于Slepian基函数是从中心向外平滑扩散的，边界附近远离积分区域中心的Slepian基函数灵敏度会有所降低(Harig and Simons, 2012).因此为了保证有足够的灵敏度来响应边界附近的站点信号，也为了验证该方法反演水储量变化的可靠性.本文进行了恢复川云渝三省质量变化趋势的实验来确定缓冲区的大小.实验首先将2012年的GLDAS水储量变化转化为类似于GRACE的60阶球谐系数，并以此计算了区域内站点处相应的垂直位移时间序列，用来进行不同缓冲区下的信号恢复实验.实验选择最大阶数为60，缓冲区边界在0°至3°之间，分别计算了各缓冲区下水储量变化恢复情况如图 5所示.图中第一幅(Simulation)为GLDAS数据2012年水储量周年振幅，后面为不同缓冲区下恢复的区域内水储量变化图像.可以发现当缓冲区小于2°时，由于边界附近Slepian基函数信号灵敏度较低，边界会有明显的信号缺失现象，同时信号大量集中于区域中央部分.随着缓冲区的增大，边界信号浓度逐渐提升，当缓冲区为2°至3°时趋势逐渐稳定且较好地恢复了模拟数据的水储量变化，当缓冲区为3°时可恢复90%以上的模拟水储量变化.分析模拟实验中的误差来源一是Slepian函数的截断误差的影响，二是由于站点分布不均匀，导致无法完全恢复部分地区的质量变化信号.针对这个问题，陈石等(2017)的相关实验表明在站点覆盖的空白区容易产生较大的剩余误差，而均匀分布的站点对Slepian函数恢复信号效果有着较好的提升.

图 5

Fig. 5

图 5 不同缓冲区下模拟信号恢复实验 (a) GLDAS模拟的陆地水变化; (b)—(h) 不同扩充缓冲区下恢复的信号变化. Fig. 5 Experiment of signal recovery under different buffers The first sub-picture is the land water change simulated by GLDAS, and the follow pictures are the signal changes recovered under different expansion buffers.

基于积分区域大小内站点分布密度，本文最终选择最大阶数60，缓冲区为3°，γ＞0.1的前31项Slepian函数将处理后GPS垂向位移时间序列通过式(5)转换为区域内的Slepian位移场，转换后的GPS空间位移场的周年振幅如图 6所示.图 6a为川云渝区域内空间插值后的垂直位移周年振幅，图 6b为用Slepian函数转化的空间位移场周年振幅.图中显示川云渝地区陆地水造成的垂向季节性变化有着明显的从西南至东北减少的趋势，具体表现为云南以及四川西南部地区位移周年变化较为明显，往四川盆.地方向开始变化逐渐减小，最大位于云南西部山地可达13 mm，最小位于重庆地区约为4 mm.图 6a和图 6b比较发现Slepian函数能有效地将位移信号展开到了整个区域，图 6b相比图 6a信号过渡更加平滑.分析认为这是由于两种方法恢复的信号成分不同，空间插值侧重对空间局部点值变化的拟合，而Slepian函数是从空间谱频率上合成地球物理信号，该方法对局部的高频干扰具有明显的压制作用.

图 6

Fig. 6

图 6 (a) 空间插值后的周年振幅与(b)Slepian函数合成的周年振幅 Fig. 6 (a) Annual amplitude obtained by spatial interpolation and (b) Slepian function synthesis

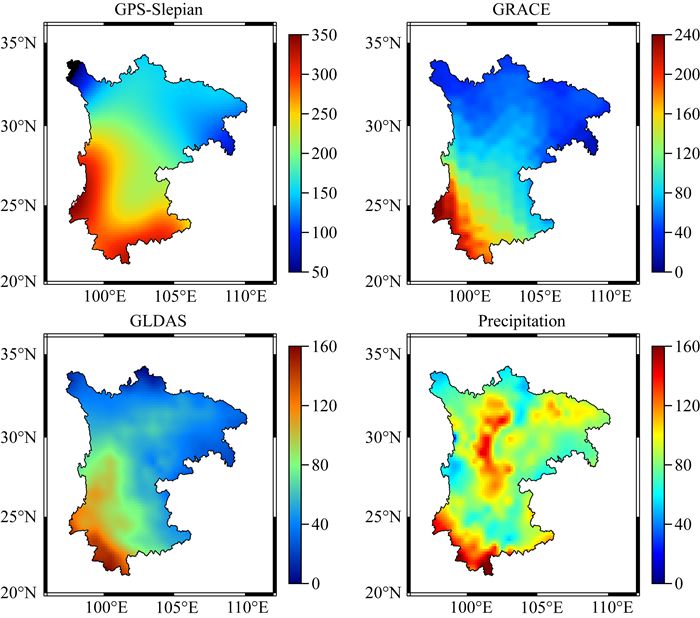
将时变Slepian位移谱场通过式(6)、(7)转换为时变质量负荷分布，在计算过程中用高斯滤波抑制不稳定的高频噪声信号，得到区域等效水高形式的地表质量变化.为了更好分析陆地水的季节性变化，本文利用中国气象数据网(http://data.cma.cn/) 提供的中国地面降水数据计算了区域平均降水量.采用该降水量与GPS-Slepian、GRACE和GLDAS计算的川云渝地区陆地水储量周年振幅进行比较，结果如图 7所示.从图中可以发现在空间分布上GPS-Slepian，GRACE和GLDAS结果有较好的一致性，三种数据在区域内分布都表现为南北分化的趋势，质量变化最大均为云南西部地区，GPS结果周年振幅达300 mm左右，大于GRACE的230 mm和GLDAS的160 mm.往川渝地区开始逐渐减少，最小在四川北部和重庆地区GPS结果为70 mm左右，GRACE和GLDAS分别为40 mm和25 mm，结合降雨数据可以发现川云渝地区降雨最大位于云南西南部山区，最大高达160 mm，这点与前面数据结果保持一致，表明在云南地区季节性降水是陆地水变化的一个重要驱动因子.而在川西高原处降水丰富却没有造成明显的陆地水周年变化，推测原因是区域内地形及地质条件不利于降水的存储.

图 7

Fig. 7

图 7 川云渝地区2011—2015年陆地水储量和降雨数据周年振幅 Fig. 7 Annual amplitude of terrestrial water storage and precipitation data in Southwest China from 2011 to 2015

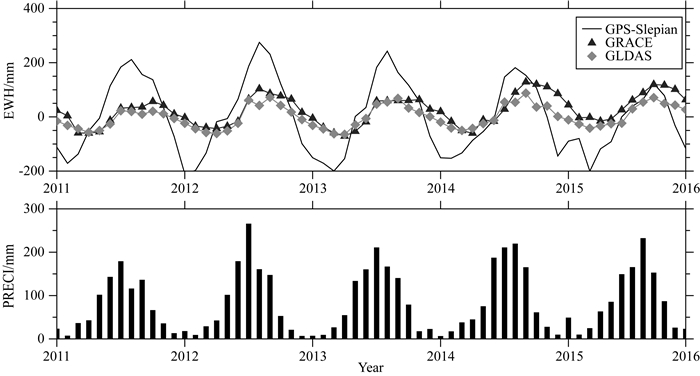
为了体现川云渝地区整体陆地水随时间的变化，本文分别计算了GPS-Slepian、GRACE和GLDAS结果在地区内的平均等效水高，并结合区域内平均降水量进行了综合对比(图 8).图中可以看出，在随时间变化特征上GPS与GRACE和GLDAS都有着很强的一致性，表现为在每年夏季的8至10月份出现高峰，在冬季的1月至3月达到低谷.对比降雨数据可知川云渝地区降水集中于夏季，冬季降雨全年最少，这与前面三种数据结论一致.但在峰值出现时间上，GPS结果要比GRACE与GLDAS要早一定时间，这点在冬季特别明显，分析原因为西南地区冬季降雨较少，陆地水变化主要受区域内径流和蒸散的影响，而GPS对周围轻微的水文变化更为灵敏，因此造成GPS结果与GRACE和GLDAS之间存在延迟.姚朝龙等(2019)在西南地区干旱的研究中也有类似现象.在时间序列大小上，GPS得到的陆地水变化与降雨数据相关性较好，同时发现在2015年1—2月GPS-Slepian结果表现出了小幅度的上升，降雨数据在2015年1月也出现了异常增大，经查询资料发现这是由于该时期南方地区大范围强降水过程的影响(李妍和李春，2019).但这点在GRACE与GLDAS上没有明显体现，表明GPS-Slepian结果能反映更为真实的局部陆地水变化，而GRACE与GLDAS都在一定程度上抑制了时空信号特征.

图 8

Fig. 8

图 8 区域内平均陆地水储量变化及降雨时间序列 Fig. 8 Variation of average terrestrial water storage and precipitation time series

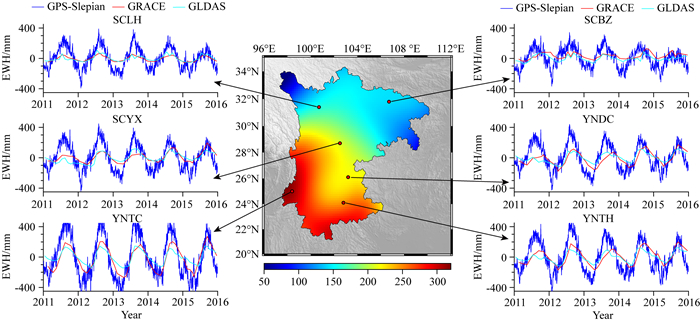
为了观察GPS反演结果在区域内各个部分的时间变化趋势，本文选取了位于四川炉霍、巴中、越西以及云南东川、腾冲、通海的六个站进行分析.各站反演的等效水高时间序列如图 9所示.比较各个站等效水高时间序列，位于云南西部山区的腾冲站(YNTC)变化幅度最大，云南东部云贵高原处的东川站(YNDC)与通海站(YNTH)次之，位于四川盆地的巴中站(SCBZ)振幅最小，总体上站点处GPS反演得到的等效水高变化与GRACE和GLDAS之间较为一致，GPS振幅比其余两种数据要大. SCYX、YNDC和YNTH站点处2011年5月至2012年1月之间GLDAS结果与GRACE和GPS结果出现较大差异，存在明显的水储量减少现象，对比图 8并查阅资料认为可能是由于该时期四川南部云贵高原附近出现的局部干旱，降水相较于往年有所减少(周莉等，2018).而降雨量大小对GLDAS计算陆地水储量的影响更为明显，且王文等学者分析过GLDAS高估了中国区域内流域蒸散作用，综合导致了GLDAS数据在发生极端气候时期精度较低.

图 9

Fig. 9

图 9 站点处等效水高时间序列 Fig. 9 Time series of equivalent water height at GPS stations

为了体现各站点处GPS结果与其他数据时间序列上的一致性，本文计算了站点处互相关系数来判断三种数据间的相关性.由于地球物理信号类似于红噪声，具有显著的自相关现象(Grinsted et al., 2004)，因此文中采用了高春春等(2019)分析南极冰盖地区所使用的Monte Carlo模拟法进行了互相关函数的显著性检验.

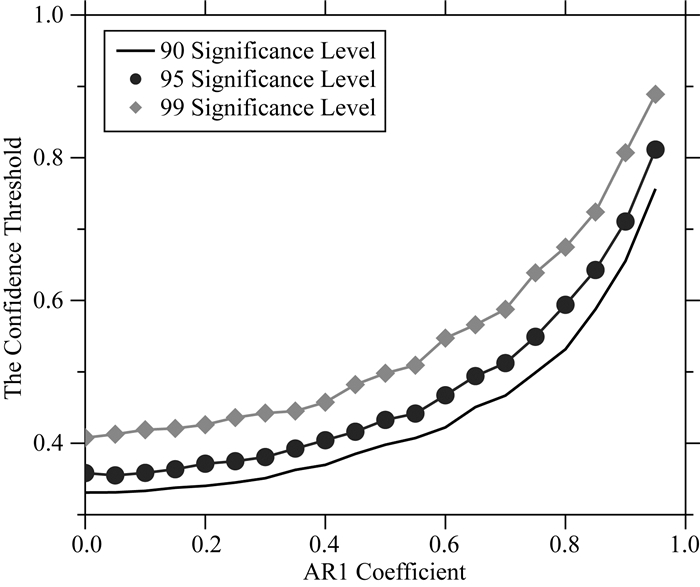
本文将2011—2015年内GPS反演的等效水高进行月平均，GRACE缺失的数据采用三次多项式插值方法补齐后，分别计算各个站点处GPS与GRACE，GPS与GLDAS，GRACE与GLDAS三种等效水高时间序列间的互相关系数，同时拟合每个站点三种数据等效水高的一阶自相关系数，采用一阶自回归模型(Autoregressive model：AR)来模拟地球物理信号中的红噪声信号，模拟的时间序列与站点处等效水高的长度一致，Monte Carlo模拟次数为5000.如图 10，本文计算了在不同AR1系数下90%、95%和99%置信水平的相关显著临界值进行Monte Carlo模拟来计算相关显著的临界值，比较互相关系数与临界值来判断各个站点处三种数据的相关程度.

图 10

Fig. 10

图 10 Monte Carlo模拟的不同AR1模型在90%、95%和99%置信度检验时相关显著的临界值 Fig. 10 The cross-correlation 90%, 95% and 99% confidence threshold from different AR1 model derived by Monte Carlo experiments

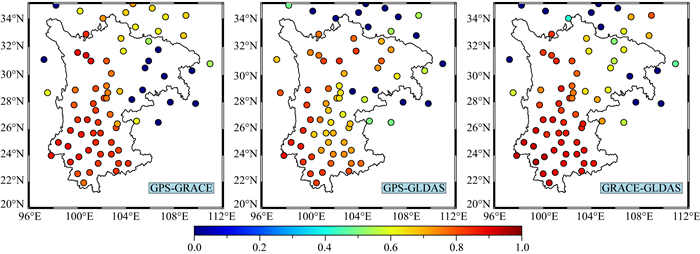
文中选取90%置信水平的临界值作为标准，为了对比明显，将未达到临界值的站点互相关系数置为0.由此得到各站点处三种数据间的互相关系数如图 11所示.比较三幅子图发现，GPS、GRACE和GLDAS之间互相关系数在云南地区和四川西部地区大于四川东部以及重庆地区，分析是因为川西和云南地区站点密集且有较明显的季节性信号.比较GPS与其他两种数据间的相关程度，发现GPS与GRACE在整体上相关性更强，站点互相关系数平均为0.77.而GPS与GLDAS之间的相关系数普遍要小，平均互相关系数为0.72.其中GPS和GRACE主要在四川东部以及重庆地区相关性较差，区域内的有10个站没有通过90%置信度检验，推测是由于该区域陆地水季节性较弱，GPS结果反映的是站点附近局部范围的陆地水变化，而GRACE反映的是分辨率300 km左右的整体变化特征，因此在季节性变化较小的地区两种数据反映的站点处陆地水变化会有不同.在该区域GPS与空间分辨率较高的GLDAS相关性明显更好也可以验证这一点.子图三中GRACE与GLDAS之间在云南以及四川西部地区相关性最好，根据图 9分析，这是因为两者的陆地水变化时间序列上都有着相似的相位以及振幅，使得两者的等效水高变化特征更为相近.比较分析三幅子图，发现GLDAS与GPS和GRACE之间在四川以北的陕甘青地区相关性都较差，分析原因可能是这些地区水资源匮乏，径流与降雨较少导致GLDAS反映的水文变化不够精确，且GLDAS不能探测到完整的陆地水变化，导致在部分地区与另外两者有差异.

图 11

Fig. 11

图 11 GPS，GRACE与GLDAS数据之间的互相关系数，图中值为0表示站点处互相关系数小于90%置信水平的相关显著临界值 Fig. 11 The cross-correlation coefficient between GPS, GRACE and GLDAS, and value is 0 means that the cross-correlation coefficient is less than 90% confidence level

本文应用Slepian函数反演了西南地区川云渝三省内的陆地水储量变化，基于GPS坐标时间序列数据反演得到区域内2011年至2015年的等效水高时间序列.实验中选择川云渝三省边界解算60阶的Slepian函数，为了保证对边界站点有足够的灵敏性，本文实验模拟了将边界扩充0°至3°的条件下对Slepian函数恢复质量变化的影响.最后通过对比区域内GPS、GRACE、GLDAS得到的等效水高和降雨数据的空间分布和时间序列变化来分析反演结果.本文的主要研究结论如下：

(1) 局部Slepian函数可以将空间上离散的GPS位移信号转化为位移空间谱.实验表明Slepian函数合成的空间位移场能很好的反映实际的位移分布，与插值得到的结果相比之间的空间过渡更加平滑.川云渝地区位移周年振幅有着从西南至东北减少的趋势，表现为四川南部青藏高原、云南地区位移周年变化较为明显，往四川平原方向开始变化逐渐减小，最大位于云南西部山区可达13 mm，最小位于重庆地区约为4 mm.

(2) 川云渝地区陆地水储量周年变化在空间分布上体现为南部的云南地区大于北部的川渝地区.其中云南西部山地陆地水周年变化最大，四川北部以及重庆地区总体变化最小.GPS得到的陆地水周年振幅约为7~30 cm，而GRACE和GLDAS仅为GPS的76%和53%左右，这是因为GPS结果分辨率高且在监测局部区域环境质量变化上更为灵敏，而Mascon数据实际分辨率仅为300 km左右，解算时的正则化约束也与200 km高斯滤波效果相当(Save et al., 2016)，GLDAS则缺乏了部分地表水以及深层地下水信息，因此两者振幅相较于GPS偏小.在平均水储量变化和站点处变化趋势中可以发现，GPS结果与降雨数据在时间上更为接近，GPS能得到近实时的监测陆地水变化，而GRACE与GLDAS在冬季存在一定的延迟.在极端气候的监测上，GPS结果与降雨数据均能体现出2015年1月的强降雨事件，而GRACE与GLDAS则没有表现出明显特征.在时间分辨率上，GPS能监测以天为单位的陆地水储量变化，而GRACE与GLDAS只能反映月变化，所以GPS在监测高频的水文特征上有着一定优势.

(3) GPS反演的站点处等效水高时间序列与GRACE和GLDAS结果具有较好的互相关性，均有80%以上的站点通过90%的置信度检验.在空间上相关程度为南部云南地区强于北部川渝地区，四川西部地区强于四川东部以及重庆地区，原因是云南和四川西部地区站点更为密集且季节性现象较明显.整体来看GPS结果在时空上与GRACE更为相似，GPS-GRACE之间的互相关系数平均为0.77，强于GPS-GLDAS之间的0.72.GPS与GRACE之间主要在四川东部和重庆地区相关性较差，分析是因为地区内陆地水的季节性变化较小且GPS结果主要反映站点周围局部的陆地水变化，而GRACE反映的是300 km左右的整体变化特征.GRACE-GLDAS整体相关性最优，但在四川以北的陕甘青地区效果较差，推测是由于地区内降雨与径流较少，且GLDAS缺乏地下水等因素综合导致GLDAS反映的水文变化不精确.

实验证明GPS站网也可以作为独立观测量来有效的监测陆地水储量变化，是GRACE与水文模型之外的另一种可行方案.在反演计算中，Slepian函数在GPS站分布相对均匀的条件下可以适当降低站点密集程度且能应用于面积更大的地区.反演结果可以得到区域内随时间变化的等效水高时间序列，结合学者利用GRACE探测干旱的方法(Thomas et al., 2014)，本文认为此结果可同样用于监测西南区域内的干旱事件.在目前GRACE和GRACE Follow-on之间任务衔接导致出现大量数据空缺的情况下，该方法可以对应用GPS手段填补数据空缺以及联合多种大地测量手段监测全球各地区陆地水储量变化提供一定的研究和参考.