2. 清华大学数学科学系, 北京 100084;
3. 中国地质大学地球物理与空间信息学院, 武汉 430074;
4. 中国科学院地质与地球物理研究所, 岩石圈演化国家重点实验室, 北京 100029
2. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China;
3. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China;
4. State Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
基于地震波运动方程的地震成像方法越来越受到研究者的关注(Tape et al., 2009; Tan and Huang, 2014; Liu et al., 2018; Lei et al., 2020). 在此类地震成像原理中, 无论是伴随成像方法(Tromp et al., 2005), 还是逆时偏移方法(Dai et al., 2012), 由于都需要反复数值求解地震波运动方程, 因此数值算法的计算效率直接关系到地震成像效率. 经过四十余年的发展, 研究者已开发出多种数值方法用于地震波运动方程的直接求解, 如:有限差分法(FDM)(Madariaga, 1976; Graves, 1996; Zhang and Yao, 2013), 伪谱法(PSM)(Kosloff and Baysal, 1982; Furumura et al., 1998; Wang and Takenaka, 2011), 有限元法(FEM)(Marfurt, 1984; Padovani et al., 1994; Liu et al., 2014a), 谱元法(SEM)(Seriani and Priolo, 1994; Komatitsch and Vilotte, 1998; Liu et al., 2017a)等.
在以上提到的数值算法中, FDM使用最为广泛(Yang et al., 2013).通过对地震波方程直接离散, FDM的优点在于算法较为直观、程序易于实现和并行(Graves, 1996).但FDM的不足也较为明显, 其缺点主要表现在三个方面.首先, 传统FDM在使用低阶算子时数值频散明显(Zhang and Yao, 2013), 其较强的数值频散必然降低算法精度.虽然高阶插值能减弱FDM的数值频散, 但是高阶插值不仅会增加计算量, 同时差分算子半径过长造成并行计算时通信量的增加, 降低了FDM并行计算效率(宋国杰等, 2012).其次, FDM网格不灵活, 难以运用于复杂模型中的地震波场模拟(Shragge, 2014).虽然可通过坐标变换的方式将伪正交网格变换成正交网格(Rao and Wang, 2013; Zhang et al., 2014), 然后在正交网格上采用常规差分格式求解地震波运动方程, 实现复杂不规则模型中的地震波场模拟.但当模型复杂程度高时会造成网格严重畸变, 使得曲线网格FDM稳定性变差, 以至于影响地震波模拟效率.第三, FDM较难处理自由地表边界条件(Ruud and Hestholm, 2001).虽然通过设置虚拟层的方式可方便满足自由地表边界条件, 但该处理方式对自由地表边界条件近似程度较低(苏波等, 2019).针对FDM存在的缺陷或不足, 研究者做出了许多有益研究(Yang et al., 2003; Zhang and Yao, 2013; 刘少林等, 2013;Liu, 2014), 例如:Yang等(2003)引入质点位移的梯度信息, 联合质点位移用于空间微分算子的数值近似, 该方法有效解决了FDM数值频散大的弊端, 但FDM网格的不灵活性以及自由边界不易处理等问题依然存在.
FEM可采用非结构化网格离散复杂模型, 具有很强的网格灵活性(Cohen, 2002), 同时, 将FEM形成的地震波运动方程弱形式所包含的边界积分项直接令为零, 即可方便实现自由地表边界条件.虽然FEM具有一定的优越性, 但是FEM计算量和存储量较大(Bielak et al., 2005), 在大尺度地震波场模拟时对计算机的计算性能要求较高.此外, FEM在单元上插值逼近时, 往往只能采用低阶插值, 因此精度较低, 在采用高阶插值时出现Runge现象, 造成精度的损失(Fichtner, 2011).尽管研究者在提升FEM计算效率方面做出了许多改进, 例如:通过构造集中质量矩阵的方式减少FEM的计算量(Padovani et al., 1994), 采用存储核矩阵的方式减少FEM的存储量(Liu S L et al., 2014; Meng and Fu, 2017), 但FEM的计算与存储量都明显高于FDM.
在简单模型中, 傅里叶PSM具有较高的计算精度, PSM算法的核心在于通过快速Fourier变换对空间微分算子逼近(Kosloff and Baysal, 1982), 其理论精度可达到FDM无穷阶时的精度(龙桂华等, 2009).在相同空间网格采样的条件下, PSM的数值频散小于FDM.但PSM由于使用全局长算子, 一方面较难适用于复杂分层、固液耦合模型(Wang et al., 2001); 另一方面长算子用于空间微分近似, 有悖于微分算子局部性的特点(Li et al., 2011).此外, 与FDM类似, PSM难以具备网格的灵活性也较难处理自由地表边界条件.
相对而言, SEM是较为高效的地震波模拟方法, 该方法不仅具有谱方法的高精度性也具有FEM网格的灵活性.在20世纪80年代, SEM最早在流体力学领域提出并得到应用(Patera, 1984).随后, Seriani和Priolo(1994)将SEM引入到地震学领域, 并模拟了二维非均匀介质中声波传播.Seriani和Priolo(1994)的数值模拟结果表明, 在相同空间网格采样条件下, 谱元法的精度要高于FEM, 例如:在空间插值阶数为8阶、地震波的最短波长采样点数为4.5时SEM即可以获得高精度模拟结果(Seriani and Priolo, 1994).早期的SEM在正交多项式的选取上往往采用Chebyshev正交多项式(Seriani and Priolo, 1994; Seriani, 1997, 1998), 虽然基于Chebyshev正交多项式的SEM取得了较好的数值模拟结果, 但Chebyshev多项式带权正交(Wang et al., 2007), 以至于该类SEM无法形成对角质量矩阵, 在求解线性方程组时占用较大计算资源(Seriani, 1998).虽然该类SEM可采用类似于FEM质量集中的方式形成对角质量矩阵, 但这必然造成SEM精度损失(Seriani and Oliveira, 2007).
为了保证SEM的计算精度, 同时避免求解大型线性方程组, 基于Legendre正交多项式的SEM被发展起来, 并被运用于地震波场的数值模拟(Komatitsch and Vilotte, 1998).该类SEM的优势在于积分点与插值点重合, 使得质量矩阵为对角矩阵, 从而避免求解大型线性方程组.基于Legendre正交多项式的谱元法已被广泛应用于区域尺度和全球尺度的地震波模拟与成像之中(Komatitsch et al., 2002; Dong et al., 2019; Lei et al., 2020).
刚度矩阵与解向量的乘积为谱元法计算量的主要来源.在并行计算时, 由于模型的复杂性, 不规则网格剖分模型会导致分配到每个计算核心的单元数不同, 使得每个计算核心所分配的刚度矩阵数量不同, 最终导致计算核心负载不均衡, 影响了并行计算效率.为了提升SEM的并行计算效率, Liu等(2017a)提出逐元并行谱元法, 其思想是将谱元单元平均分配到每个计算核心, 在单元上进行刚度矩阵与解向量相乘.数值实验表明, 逐元并行策略能有效提升SEM的并行计算效率.逐元并行SEM除了提升并行效率以外, 还将刚度矩阵的存储转化为64个子矩阵的存储, 大幅降低了SEM的存储量.
需要注意的是, 本文作者前期对逐元并行SEM的研究中计算核心之间通信采用的是主从(Master-Slave)通信模型(Liu et al., 2017a), 虽然主从通信模式程序上容易实现(Komatitsch and Tromp, 1999), 但计算核心通信等待时间较长.为了减少通信等待时间, 本文采用缓存通信模式, 在计算核心对之间通信, 大幅减少SEM的通信时间.此外, 本文不再采用存储子矩阵的方式用于重建单元刚度矩阵, 而是存储单元雅克比矩阵的逆及其行列式的值, 再结合插值多项式直接对空间微分算子数值近似, 因此避免了重建稠密单元刚度矩阵, 减少了计算量.为了消除边界截断而引起的虚假反射, 本文在模型边界上利用逐元并行SEM求解二阶位移形式的PML吸收边界条件.
1 逐元谱元法地震波在震源处激发, 向三维空间辐射能量, 地震波的传播满足以下运动方程:
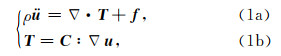
|
其中u为质点位移, T为应力张量, f为震源项, C为四阶弹性张量, ρ为密度, ∇ 为空间梯度算子.任意测试向量v乘以公式(1a)并在空间积分, 利用分部积分和散度定理, 得到地震波运动方程的弱形式:
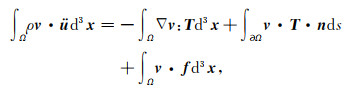
|
(2) |
其中n为边界外法向, Ω为研究区域.考虑自由地表处法向应力为0, 即T·n=0, 认为地震波在无限半空间中传播, 即无穷远处边界上应力为0, 即T=0, 公式(2)可简化为:

|
(3) |
公式(3)自动满足自由地表边界条件.将研究区域Ω离散成N个非重叠六面体单元, 假设每个单元的控制点数为n, 物理空间中的每个六面体单元都可变换成标准参考单元, 同样每个参考单元可变换回至六面体单元, 物理域与参考域之间的坐标满足以下关系(Komatitsch and Tromp, 1999):
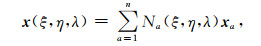
|
(4) |
其中xa为控制点在物理域中的坐标, Na(ξ, η, λ)(-1≤ξ≤1, -1≤η≤1, -1≤λ≤1)为单元形函数.在参考单元上求解如下方程确定每个方向上插值节点的坐标:
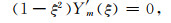
|
(5) |
其中Ym为m阶Legendre多项式, 其上标表示一阶导数.公式(5)可确定m+1个根ξi(i=0, …, m), 即在每个方向上插值节点数为m+1, 三维情况下一共有(m+1)3个插值节点.在每个单元上利用Lagrange多项式近似函数值, 对u和v的近似可表示为:
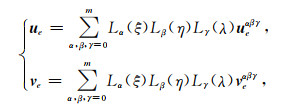
|
(6) |
其中L为Lagrange插值多项式, α, β和γ为单元e上三个方向GLL(Gauss-Lobatto-Legendre)节点索引.由公式(6)可知, 单元上的插值多项式由三个方向上的Lagrange插值多项式组合而成.利用公式(6), 公式(2)等号左边积分可以表示为:
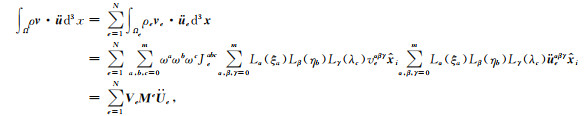
|
(7) |
其中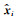
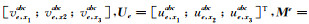
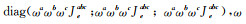
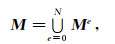
|
(8) |
其中∪为矩阵组装算子.定义Γe算子将总体质量矩阵投影至单元上:

|
(9) |
在同一个单元上Me′和Me不相等, 原因在于相邻单元共享GLL节点, 与共享节点对应的质量矩阵元素需累加, 使得Me′中共享节点对应的质量矩阵元素值要大于Me中的元素值.
与公式(7)类似, 公式(3)中等号右边第一式也可写成离散形式:
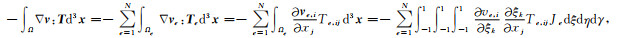
|
(10) |
其中(ξ1, ξ2, ξ3)=(ξ, η, λ). 为了实际计算简便, 仿照Komatitsch和Tromp(1999)中的组合方式, 将
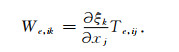
|
(11) |
将(6)和(11)式代入(10)式并利用GLL数值求积, (10)式可离散为:
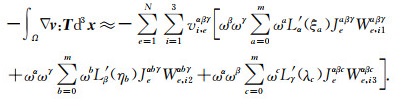
|
(12) |
(12) 式可进一步写成矩阵的形式:
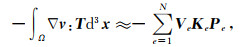
|
(13) |
其中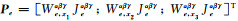
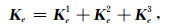
|
(14) |
其中Ke1、Ke2和Ke3的具体形式为:

|
(15) |
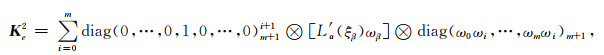
|
(16) |
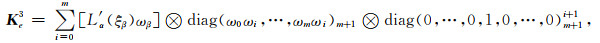
|
(17) |
其中⊗表示矩阵张量积运算符(Seriani, 1998), 对角矩阵的下标表示矩阵维度, 对角矩阵的上标表示非零元所在的位置.(13)式需要用到GLL点上的Weαβγ, 而Weαβγ由Teαβγ在GLL点上的值通过坐标变换系数线性组合得到, 因此得到Teαβγ之后就可计算Weαβγ. 由公式(1b)和公式(6)可计算Teαβγ, 即:
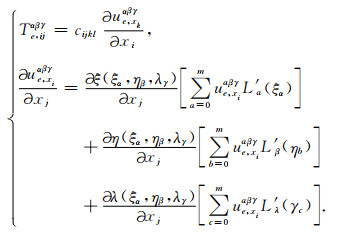
|
(18) |
假设地震震源为点源, 且可以写成关于矩张量的形式, 公式(1)中的体力f可表示为:

|
(19) |
其中M为地震矩张量(Aki and Richards, 1980), S(t) 为震源时间函数, xs为震源坐标.将(19)式代入(3)式, 公式(3)等式右边第二项可表示为:
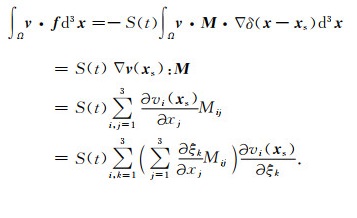
|
(20) |
推导(20)式过程中用到关系式v·M·∇δ(x-xs)=∇·(v·Mδ(x-xs))-∇v: Mδ(x-xs), 并利用到散度定理与Delta函数的积分性质.记Gik= 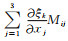

|
(21) |
其中(ξs, ηs, λs)为震源坐标xs所对应的局部坐标, 下标es表示震源所在的单元.(21)式可写成向量相乘的形式:
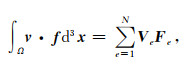
|
(22) |
其中单元上的载荷向量Fe具体形式为:
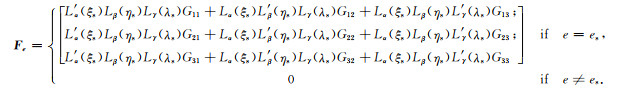
|
(23) |
由(21)—(23)式不难看出, 震源项离散以后所形成的载荷向量Fe只在一个单元上有值, 在其他单元上均为零.如果震源恰好位于单元表面而被多个单元共享, 此时Fe可在多个单元上有值.为了简化程序设计, 可在震源位置施加以小的扰动(如单元尺寸的1/100,本文算例中选择1/300),将震源放置到单元内部, 保证Fe只在一个单元上有值.数值算例显示该处理方式不会造成明显误差, 关于精度的讨论本文将在第4节数值算例部分具体给出.需要注意的是, 本文公式(21)—(23)与Komatitsch和Tromp(1999)的表述不同, Komatitsch和Tromp(1999)的处理方式是将点源平滑至单元的每个GLL节点上, 本文公式(21)—(23)仍将震源当成点源.当单元尺寸远小于地震波长时, Komatitsch和Tromp(1999)的震源处理方式不会产生较大误差; 当单元尺寸和地震波长相当时, 该处理方式可能产生明显误差.Komatitsch和Tromp(1999)震源处理存在的问题已超出本文范围, 本文不再讨论.
由(7)、(13)和(22)式可知, 以下等式成立:
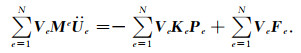
|
(24) |
由于测试向量v的任意性, (24)式等价为:

|
(25) |
单元上的质点加速度向量可组装成质点总体加速度向量, 即: 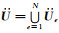
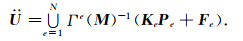
|
(26) |
从公式(26)容易看出, 本文先在每个单元上做矩阵Ke和向量Pe相乘运算, 再将单元上的加速度向量组装获得总体加速度向量.因为公式(26)采用逐元(element-by-element)的方式计算地震波场, 所以本文称之为逐元SEM.该计算方式与前人在合成总体刚度矩阵以后再做矩阵与向量相乘不同(Padovani et al., 1994; Liu Y S et al., 2014), (26)式所体现的优势主要表现在三方面.首先, 极大简化了并行程序设计.SEM的计算量主要来源于单元上的矩阵与向量乘积, 将单元上的矩阵与向量乘积分配到计算核心就可以方便实现SEM的并行计算.其次, 节省了存储空间.由(7)、(15)—(17)式不难看出, 逐元SEM不需要存储稠密的单元刚度矩阵, 只用存储单元GLL点上的雅克比矩阵(Jacobian matrix)行列式的值以及雅克比矩阵的逆(计算单元雅克比矩阵逆的过程见附录A), 也就是需要存储元素的个数为GLL点数的10倍, 因此逐元SEM的存储量和FDM的存储量在同一数量级(为FDM的5倍左右).最后, 节省了计算量.由(12)式可知逐元SEM充分利用到GLL积分与插值重合的特点, 一个方向上的空间微分数值近似, 只保留对应方向的非零元, 因此极大减少了浮点运算次数.如果空间GLL点的个数为H, 插值阶数为m, 那么逐元SEM的浮点运算次数大约为O(18(m+1)H), 其计算量与FDM的计算量大致相同.
2 逐元并行策略在关于SEM的并行程序设计中, 研究者往往采用主从(master-slave)通信模式(Komatitsch and Tromp, 2002; Liu et al., 2017a)完成每个时间迭代步的数据通信.SEM的主从通信过程分为三步, 首先, 一个计算核心作为主计算核心收集从计算核心需要通信的信息(如加速度向量); 然后, 主计算核心对通信信息处理(如不同计算核心共有的GLL节点对应的加速度相加); 最后, 主计算核心将处理好的信息分发给从计算核心.显然这三步中主要通信和计算任务都由主计算核心完成, 而从计算核心承担的通信和计算任务远小于主计算核心, 较多时间浪费在通信等待上, 以至于降低了SEM的并行计算效率.
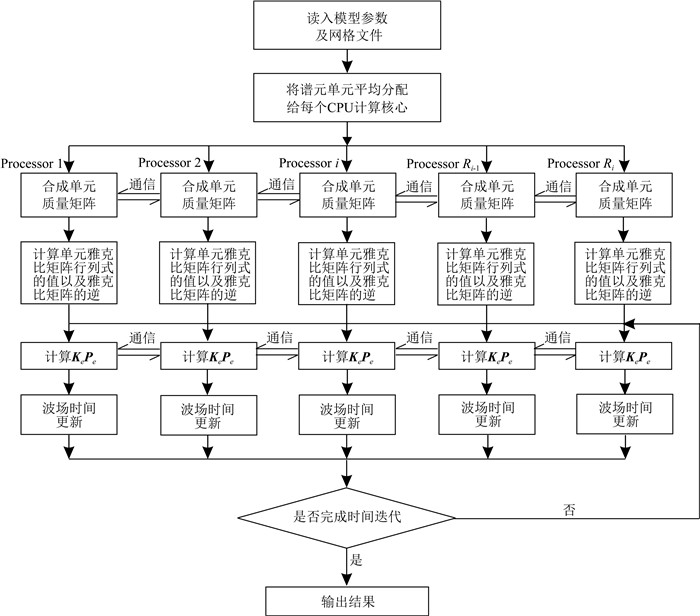
为了提升SEM的并行效率, 本文采用缓存通信模式(Gropp et al., 1996), 在需要通信的计算核心对之间两两通信, 具体通信过程如图 1所示, 为了计算流程更加完整, 图 1也显示了通信以外的其他过程.由图 1可知, 在合成单元质量矩阵以后, 需要在计算核心之间通信完成之后获得Γe(M). 在每一个时间步, 每个单元上需要计算KePe, 然后将计算核心之间共享GLL点上的加速度在通信之后累加得到完整的质点加速度.从图 1不难看出, 与主从通信模式不同, 本文的通信方式将总的通信量分配给计算核心对, 有效减少了通信等待时间.此外, 在主从通信模式中主计算核心的数据处理任务(共享GLL点上加速度累加求和)被分配给各个计算核心, 有效平衡了计算核心的数据计算加载.因此, 本文通信模式有效提升了SEM的并行计算效率.有关并行计算效率, 本文将在第4节进一步讨论.
|
图 1 逐元并行SEM地震波场模拟流程图 Fig. 1 Schematic showing the processes of seismic wave modeling using element-by-element parallel spectral-element method |
需要指出的是, 为了讨论方便, 图 1只显示相邻计算核心之间通信.事实上, 任何计算核心可能与其他多个计算核心构成通信对进行通信.至于如何构成通信对, 取决于模型复杂程度以及模型剖分以后生成的网格.
3 PML吸收边界条件PML吸收边界条件已被广泛应用于地震波数值模拟之中(罗玉钦和刘财, 2020), 为了本文的完整性本节简要介绍本文所采用的二阶位移形式PML吸收边界条件.有限的计算资源难以模拟高频(>2 Hz)地震波在整个地球中的传播(Tong et al., 2014).实际地震波场模拟时往往将模型截断, 然后在小规模模型中模拟高频地震波传播.在使用SEM模拟地震波传播时, 直接将模型截断不做任何处理, 相当于在截断边界处引入自由地表边界条件, 此时必然造成强烈的虚假反射而干扰模型内部地震波场的可靠性.为了防止边界截断而引入的虚假反射, 本文在边界截断处引入PML吸收边界条件(Liu Y S et al., 2014; Liu et al., 2017a).
构造PML吸收边界条件的思想是在频率域PML吸收层中做坐标变换而引入衰减因子使得波场沿着垂直截断边界方向指数衰减.PML吸收层中的坐标变换公式如下(Komatitsch and Tromp, 2003):
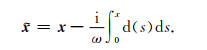
|
(27) |
将(27)式代入(1)式, 忽略震源项, 得到:
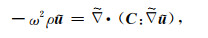
|
(28) |
其中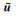
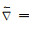
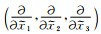
本节通过两个数值算例讨论本文发展的逐元并行SEM在三维地震波场模拟时的有效性和高效性.数值算例采用二阶中心差分用于时间离散(Liu et al., 2017b); PML吸收层厚度为5个谱单元.
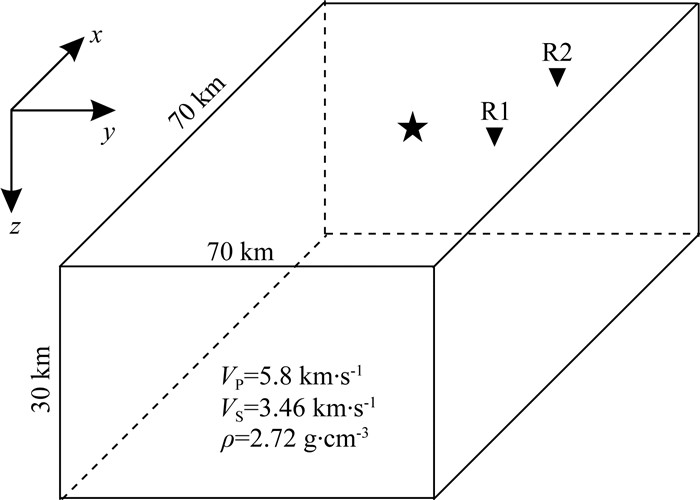
4.1 理论测试为了测试逐元并行SEM的有效性, 选择如图 2所示的均匀各向同性介质模型.模型水平尺度为70 km, 深度为30 km.模型介质参数由P波速度(5.8 km·s-1)、S波速度(3.46 km·s-1)和密度(2.72 g·cm-3)描述.笛卡尔坐标原点位于模型上表面中心.如图 2所示x轴正向指向正北, y轴正向指向正东, z轴正向垂直向下.震源为爆炸源位于(0 km, 0 km, 0.5 km)处, 其对应的矩张量只在对角线上有值, 对角线上的值都为2×1016N·m.两个台站R1和R2分别位于(0 km, 20 km, 0 km)和(20 km, 20 km, 0 km)处.震源时间函数选择Ricker子波, 其主频为1 Hz, 时间函数最高频率约为2.5 Hz.采用正方体离散图 2中规则模型, 正方体的边长为1 km.在每个单元上采用4阶多项式插值.波形模拟结果如图 3所示.
|
图 2 均匀介质模型用于测试逐元并行SEM的有效性 坐标原点位于模型上表面中心, 五角心表示震源, 坐标为(0 km, 0 km, 0.5 km), 三角形表示台站, 两个台站为R1和R2, 分别位于(0 km, 20 km, 0 km)和(20 km, 20 km, 0 km)处.介质参数P波速度为5.8 km·s-1, S波速度为3.46 km·s-1, 密度为2.72 g·cm-3. Fig. 2 3D homogeneous model for the benchmark test of EBE-SEM The origin of the Cartesian coordinates is located at the center of the top surface of the model. The star denotes an explosive source, and is placed at (0 km, 0 km, 0.5 km). The triangles represent two stations R1 and R2, which are at (0 km, 20 km, 0 km) and (20 km, 20 km, 0 km), respectively. The media parameters are described by VP, VS, and ρ, which are 5.8 km·s-1, 3.46 km·s-1, 2.72 g·cm-3, respectively. |
|
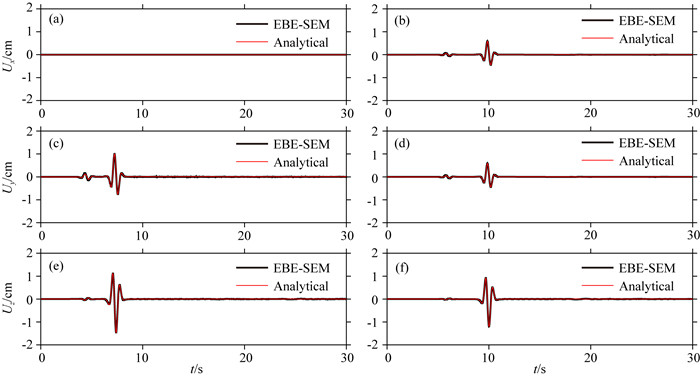
图 3 逐元并行SEM合成波形与理论波形对比 (a)、(c)和(e)分别为台站R1处位移的x、y和z分量; (b)、(d)和(f)分别为台站R2处位移的x、y和z分量. 黑线由逐元并行SEM计算得到; 红色线由解析解计算得到. Fig. 3 Synthetic waveforms at stations R1 (a, c, e) and R2 (b, d, f) computed by EBE-SEM (black lines) and analytical method (red lines) (a) and (b) are for x component of displacement; (c) and (d) are for y component of displacement; (e) and (f) are for z component of displacement. |
从图 3可以看出, 逐元并行SEM得到的合成波形与解析解(由Cagniard-de Hoop(De Hoop, 1959)方法得到)得到的波形几乎完全重合, 两者之间并未出现明显差别.无论是振幅较小的直达P波还是振幅较大的Rayleigh面波都得到了精确模拟, 说明逐元并行SEM用于地震波模拟的有效性.两个台站R1和R2靠近模型边界, 但从合成地震图上并未发现来自模型边界的虚假反射波, 说明地震波传播至PML吸收层时已被有效吸收.
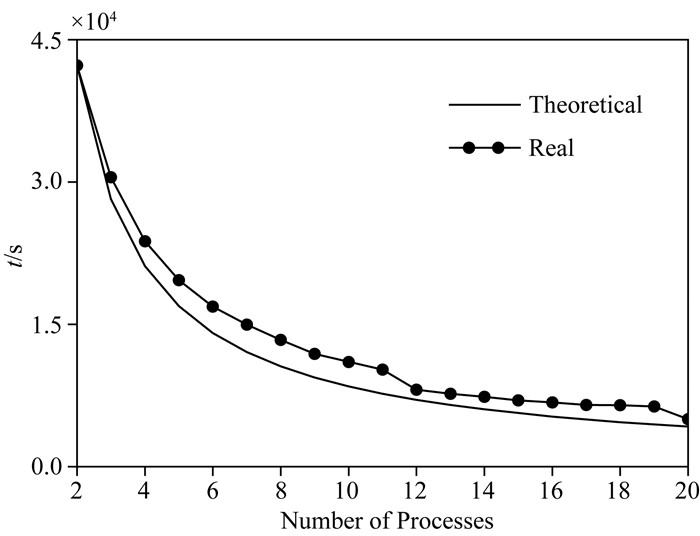
同样采用图 2中的模型用于测试逐元并行SEM的并行计算效率.逐元并行SEM最少需要2个计算核心进行并行计算, 在使用2个计算核心计算时总耗时为t2, 由于计算核心之间通信时间远小于用于矩阵与向量乘积的计算时间, 此时可忽略通信耗时, 当使用i个计算核心计算时, 理论计算时间为ti=2t2/i.由于计算核心增多时, 通信量随之增加, 因此实际计算时间要大于理论计算时间ti.如果并行计算时间越靠近ti说明并行性越好.逐元并行SEM的并行计算效率如图 4所示.从图 4可看出, 实际并行计算时间接近理论并行时间.当计算核心数为素数(如11、19)时每个计算核心所分配的空间网格较为复杂, 使得通信量相对增加, 以至于实际并行计算时间出现异常(图 4).即便出现并行计算时间异常(如计算核心数为11和19), 也未出现在主从通信模式中计算核心增多而计算时间增加的情况(Liu et al., 2017a), 说明本文采用的计算核心对通信方式能有效平衡分配给计算核心的计算和通信任务.事实上, 将本文的通信模式换成主从通信模式, 在使用20个计算核心并行计算时耗时增加约2倍, 使用3至20个计算核心平均计算时间增加1倍左右.
|
图 4 逐元并行SEM并行效率曲线 图中黑点为实际计算时间, 黑色曲线为理论计算时间. Fig. 4 The parallel efficiency of the EBE-SEM The black line with solid circles shows the real computing time, while the black line is the theoretical computing time. |
应该指出的是, 逐元并行SEM除了并行效率提升以外, 在节省内存方面具有巨大优势.与本文作者前期工作利用64个单元子矩阵重建单元刚度矩阵(Liu et al., 2017a)不同, 本文的逐元SEM不再需要重建单元刚度矩阵((12)式, (15)—(17)式), 而只用存储GLL点上雅克比矩阵的逆及行列式的值(一共10个元素), 因此比Liu等(2017a)的方法节省约6倍的存储.对于图 2中的三维模型, 单元个数为196875, 每个单元上的GLL点数为125, 存储雅克比矩阵的逆及行列式的值一共消耗0.23 GB内存, 本次模拟一共消耗约2 GB内存(额外需要存储当前时刻位移三分量、上一时刻位移三分量、加速度三分量、空间GLL点坐标、空间GLL点编号等).
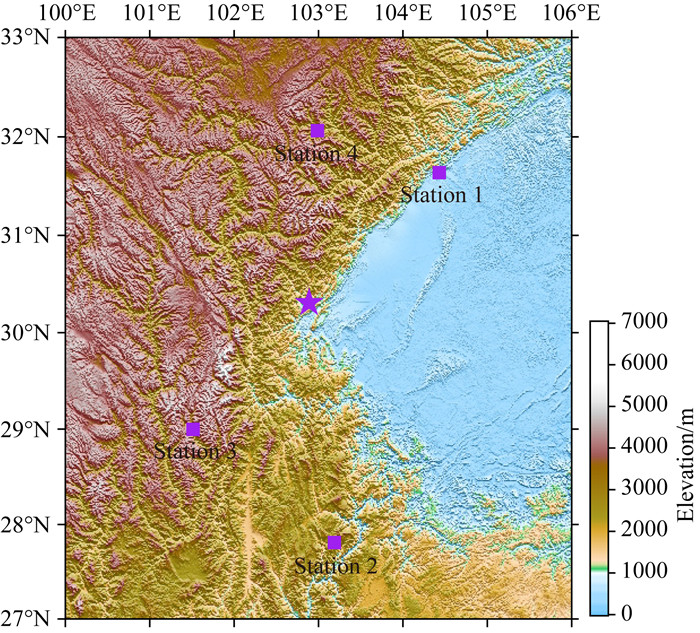
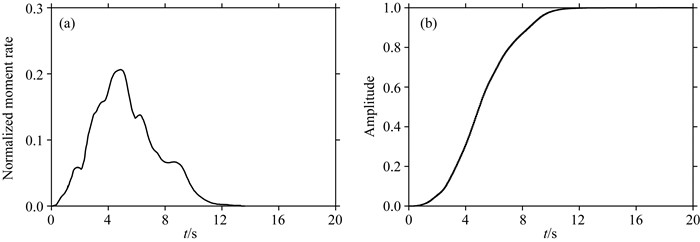
4.2 实际地震波场模拟为了验证逐元并行SEM在实际地震模拟时的有效性, 本节模拟2013年芦山MW6.6地震波场传播.芦山地震震中区及周边地形如图 5所示.从图中可看出, 模型存在较大的地形起伏.模型西部为青藏高原隆起区, 海拔较高; 东部主要为四川盆地, 海拔较低.从全球地形网格文件(Tozer et al., 2019)中提取研究区域内的高程, 然后将高程文件导入到Hypermesh剖分软件(仅限学术用途使用)中.除了地表地形以外, 模型的其他界面(Conrad、Moho面等)由CRUST1.0模型(Laske et al., 2013)提供, 模型深度到120 km.由Hypermesh剖分软件生成的网格如图 6所示, 离散模型采用六面体单元, 其平均尺寸为4 km.本文采用张小艳等(2020)给出的震源机制解得到震源矩张量以及矩张量释放率函数(图 7a).通过对矩张量释放率函数做时间积分得到震源时间函数S(t) (图 7b).实际地震波场模拟结果如图 8和图 9所示.
|
图 5 2013年四川芦山MW6.6地震震中及周边地形图 五角心表示震中, 其经纬度坐标为(102.888°E, 30.308°N) (USGS提供, http://www.usgs.gov).小方块表示震中附近国家测震台网的4个固定台. Fig. 5 Topography of the area around the epicenter of 2013 Lushan MW6.6 earthquake The star denotes the epicenter of the earthquake, the coordinates of which are (102.888°E, 30.308°N) (http://www.usgs.gov). The squares are broadband seismic stations from China National Seismic Network. |

|
图 6 2013年芦山地震震源区网格化模型 地表地形高程从全球地形网格中提取得到.模型内部界面从CRUST1.0中提取得到.模型深度为120 km. Fig. 6 Mesh for the model of the area around the 2013 Lushan Earthquake Topography is derived from the global topography grid. The subsurface is extracted from the CRUST1.0. The depth of the model is 120 km. |
|
图 7 (a) 矩张量释放率随时间变化; (b) 震源时间函数 Fig. 7 (a) Moment rate function; (b) Source time function |
|
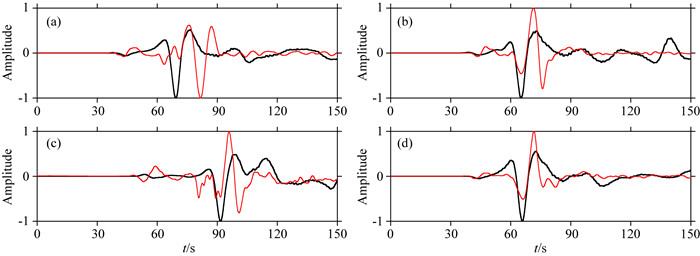
图 8 合成波形与实际观测波形对比 图(a)—(d)中波形分别由台站1—4记录.红色线为观测波形; 黑线为合成波形. Fig. 8 Waveform comparison The waveforms in plots (a)—(d) are recorded by stations 1—4, respectively. The red lines are the real observed seismograms, while the black lines are the synthetic seismograms. |
|
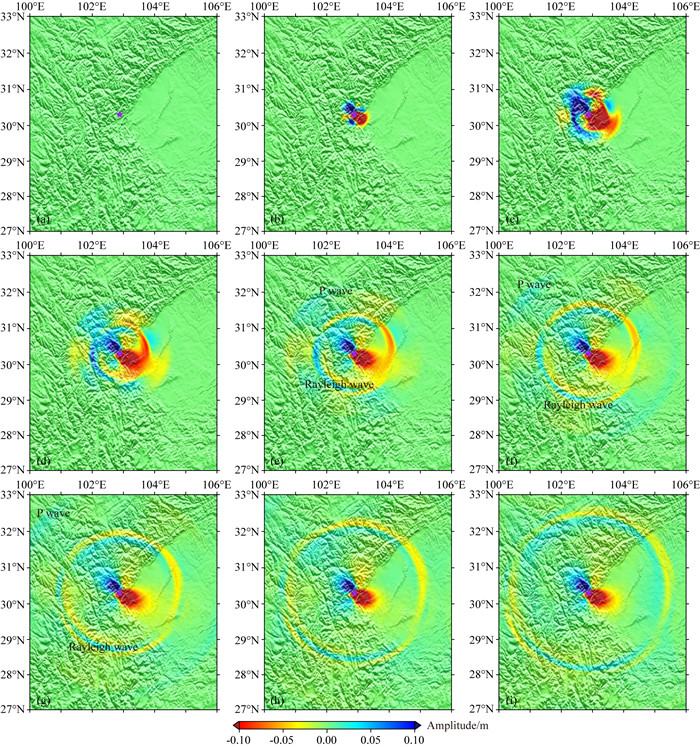
图 9 2013年芦山地震地表波场快照 图(a)—(i)分别为t=1 s、10 s、20 s、30 s、40 s、50 s、60 s、70 s和80 s时的地表垂直位移. Fig. 9 Wavefield snapshots of the 2013 Lushan Earthquake. The seismic wavefields of vertical component are on the free surface The snapshots in plots (a)—(i) are taken at t=1 s, 10 s, 20 s, 30 s, 40 s, 50 s, 60 s, 70 s, and 80 s, respectively. |
图 8中红色线为实际地震仪记录的波形经过去仪器响应、低通滤波(最高截止频率为0.2 Hz)以后的波形, 图中黑色线为逐元并行SEM的合成波形.总体而言, 数值方法能较好模拟直达P波和Rayleigh面波初至到时, 但相位有较大差别.需要注意的是, 图 8a中数值解显示Rayleigh面波主要能量到时要早于观测到时, 主要原因在于模型速度不准.模型浅部(图 6, 深度小于20 km)S波速度为3.55 km·s-1, 而四川盆地浅部(深度小于20 km)S波平均速度约为2.5 km·s-1(Laske et al., 2013), 如果利用S波速度近似面波速度, 模拟的面波到时约比观测早20 s, 这与图 8a中的结果基本一致.另外, 为了模拟得到更准确的波形, 在震源近似上需要采用有限断层近似(公式(23)是对点源的离散而不是有限断层的离散)以及采用更加精确的地震波速度结构模型.图 9展示的是9个时刻的地面波场(垂直分量)快照.当t=1 s时(图 9a), 地震波主要能量还未传播至地表, 地表位移几乎为0.当t=10 s时(图 9b), 震中处表现出较强的位移.除了震中处较强的位移以外, 图 9也显示地表传播的直达P波和Rayleigh面波成分, 其中Rayleigh面波振幅远大于P波.图 9f显示地震波传播到PML吸收层时被很好地吸收而未见来自模型边界的反射波.
5 结论和讨论本文发展了一种高效的逐元并行SEM用于地震波场模拟.并在边界处构造二阶位移形式的PML吸收边界条件避免边界截断而产生的虚假反射.通过公式推导、数值实验、分析与对比, 证实本文给出的逐元并行SEM主要表现出三方面的优点: (1)并行性强; (2)计算量小; (3)内存消耗少.此外, 基于逐元并行SEM原理, 我们开发出一套三维地震波模拟软件包, 将其称之为EBE-SEM3D.
通过逐元并行SEM求解地震波场和伴随波场(Tromp et al., 2005), 可在EBE-SEM3D的基础上发展一套伴随层析成像软件包, 通过构造远震入射边界条件(Liu et al, 2017a)也可方便开发出一套远震伴随成像软件包.关于区域地震和远震的伴随成像软件包本文作者将另文介绍和给出.
本文的EBE-SEM3D软件包可无偿用于学术用途, 为了获得软件包请与本文第一作者邮件联系.
致谢 感谢两位审稿专家提出的宝贵修改意见.感谢Julien Diaz教授关于解析解的交流、讨论以及为本研究提供解析解源代码.感谢中国地震局地球物理研究所国家测震台网数据备份中心(doi:10.11998/SeisDmc/SN)为本研究提供地震波形数据.本文图由开源软件GMT(Generic Mapping Tools) (Wessel et al., 2013)绘制而成.逐元并行SEM软件包中并行通讯库采用的是开源库MPICH (http://www.mpich.org).
附录A由公式(4)知, 通过物理坐标对局部坐标求偏导可计算雅克比矩阵行列式的值, 即:
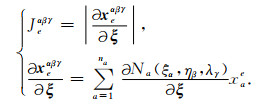
|
(A1) |
由(A1)式可获得单元雅克比矩阵在每个GLL点处行列式的值.对雅克比矩阵求逆, 可得到局部坐标对物理坐标偏导数的值, 即:
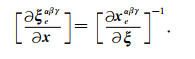
|
(A2) |
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods. New York: W. H. Freeman & Co.
|
Bielak J, Ghattas O, Kim E J. 2005. Parallel octree-based finite element method for large-scale earthquake ground motion simulation. Computer Modeling in Engineering and Sciences, 10(2): 99-112. |
Cohen G C. 2002. Higher-Order Numerical Methods for Transient Wave Equation. Berlin Heidelberg: Springer-Verlag.
|
Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration. Geophysical Prospecting, 60(4): 681-695. DOI:10.1111/j.1365-2478.2012.01092.x |
De Hoop A T. 1959. The surface line source problem. Applied Scientific Research, 8(4): 349-356. |
Dong X P, Yang D H, Niu F L. 2019. Passive adjoint tomography of the crustal and upper mantle beneath Eastern Tibet with a W2-norm misfit function. Geophysical Research Letters, 46(12): 12986-12995. |
Fichtner A. 2011. Full Seismic Waveform Modelling and Inversion. Berlin Heidelberg: Springer-Verlag.
|
Furumura T, Kennett B L N, Takenaka H. 1998. Parallel 3-D pseudospectral simulation of seismic wave propagation. Geophysics, 63(1): 279-288. DOI:10.1190/1.1444322 |
Graves R. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bulletin of the Seismological Society of America, 86(4): 1091-1106. |
Gropp W, Lusk E, Doss N, et al. 1996. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Computing, 22(6): 789-828. DOI:10.1016/0167-8191(96)00024-5 |
Komatitsch D, Vilotte J P. 1998. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88(2): 368-392. |
Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional Seismic wave propagation. Geophysical Journal International, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
Komatitsch D, Tromp J. 2002. Spectral-element simulations of global seismic wave propagation-Ⅰ. Validation. Geophysical Journal International, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x |
Komatitsch D, Ritsema J, Tromp J. 2002. The spectral-element method, Beowulf computing, and Global seismology. Science, 298(5599): 1737-1742. DOI:10.1126/science.1076024 |
Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
Laske G, Masters G, Ma Z T, et al. 2013. Update on CRUST1.0-A 1-degree global model of earth's crust.//EGU General Assembly Conference Abstracts. Vienna, Austria: AGU.
|
Lei W, Ruan Y Y, Bozdağ E, et al. 2020. Global adjoint tomography-model GLAD-M25. Geophysical Journal International, 233(1): 1-21. |
Li X, Li Y, Zhang M, et al. 2011. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method. Bulletin of the Seismological Society of America, 101(4): 1710-1718. DOI:10.1785/0120100266 |
Liu S L, Li X F, Wang W S, et al. 2013. Optimal symplectic scheme and generalized discrete convolutional differentiator for seismic wave modeling. Chinese Journal of Geophysics (in Chinese), 56(7): 2452-2462. DOI:10.6038/cjg20130731 |
Liu S L, Li X F, Wang W S, et al. 2014. A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modelling. Journal of Geophysics and Engineering, 11(5): 055009. DOI:10.1088/1742-2132/11/5/055009 |
Liu S L, Yang D H, Dong X P, et al. 2017a. Element-by-element parallel spectral-element methods for 3-D teleseismic wave modeling. Solid Earth, 8(5): 969-986. DOI:10.5194/se-8-969-2017 |
Liu S L, Yang D H, Lang C, et al. 2017b. Modified symplectic schemes with nearly-analytic discrete operators for acoustic wave simulations. Computer Physics Communications, 213: 52-63. DOI:10.1016/j.cpc.2016.12.002 |
Liu S L, Lang C, Yang H, et al. 2018. A developed nearly analytic discrete method for forward modeling in the frequency domain. Journal of Applied Geophysics, 149: 25-34. DOI:10.1016/j.jappgeo.2017.12.007 |
Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
Liu Y S, Teng J W, Lan H Q, et al. 2014. A comparative study of finite element and spectral element methods in seismic wavefield modeling. Geophysics, 79(2): T91-T104. DOI:10.1190/geo2013-0018.1 |
Long G H, Li X F, Zhang M G. 2009. The application of staggered-grid Fourier pseudospectral differentiation operator in wavefield modeling. Chinese Journal of Geophysics (in Chinese), 52(1): 193-199. |
Luo Y Q, Liu C. 2020. On the stability and absorption effect of the multiaxial complex frequency shifted nearly perfectly matched layers method for seismic wave propagation. Chinese Journal of Geophysics (in Chinese), 63(8): 3078-3090. DOI:10.6038/cjg2020N0028 |
Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. |
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. DOI:10.1190/1.1441689 |
Meng W J, Fu L Y. 2017. Seismic wavefield simulation by a modified finite element method with a perfectly matched layer absorbing boundary. Journal of Geophysics and Engineering, 14(4): 852-864. DOI:10.1088/1742-2140/aa6b31 |
Padovani E, Priolo E, Seriani G. 1994. Low and high order finite element method: Experience in seismic modeling. Journal of Computational Acoustics, 2(4): 371-422. DOI:10.1142/S0218396X94000233 |
Patera A T. 1984. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. Journal of Computational Physics, 54(3): 468-488. DOI:10.1016/0021-9991(84)90128-1 |
Rao Y, Wang Y H. 2013. Seismic waveform simulation with pseudo-orthogonal grids for irregular topographic models. Geophysical Journal International, 194(3): 1778-1788. DOI:10.1093/gji/ggt190 |
Ruud B, Hestholm S. 2001. 2D surface topography boundary conditions in seismic wave modelling. Geophysical Prospecting, 49(4): 445-460. DOI:10.1046/j.1365-2478.2001.00268.x |
Seriani G, Priolo E. 1994. Spectral element method for acoustic wave simulation in heterogeneous media. Finite Elements in Analysis and Design, 16(3-4): 337-348. DOI:10.1016/0168-874X(94)90076-0 |
Seriani G. 1997. A parallel spectral element method for acoustic wave modeling. Journal of Computational Acoustics, 5(1): 53-69. DOI:10.1142/S0218396X97000058 |
Seriani G. 1998. 3-D large-scale wave propagation modeling by spectral element method on Cray T3E multiprocessor. Computer Methods in Applied Mechanics and Engineering, 164(1-2): 235-247. DOI:10.1016/S0045-7825(98)00057-7 |
Seriani G, Oliveira S P. 2007. Optimal blended spectral-element operators for acoustic wave modeling. Geophysics, 72(5): SM95-SM106. DOI:10.1190/1.2750715 |
Shragge J. 2014. Reverse time migration from topography. Geophysics, 79(4): 1-12. DOI:10.1190/2014-0519-TIOGEO.1 |
Song G J, Yang D H, Tong P, et al. 2012. Parallel WNAD algorithm for solving 3D elastic equation and its wavefield simulations in TI media. Chinese Journal of Geophysics (in Chinese), 55(2): 547-559. DOI:10.6038/j.issn.0001-5733.2012.02.017 |
Su B, Li H L, Liu S L, et al. 2019. Modified symplectic scheme with finite element method for seismic wavefield modeling. Chinese Journal of Geophysics (in Chinese), 62(4): 1440-1452. DOI:10.6038/cjg2019M0538 |
Tan S R, Huang L J. 2014. Reducing the computer memory requirement for 3D reverse-time migration with a boundary-wavefield extrapolation method. Geophysics, 79(5): S185-S194. DOI:10.1190/geo2014-0075.1 |
Tape C, Liu Q Y, Maggi Q, et al. 2009. Adjoint tomography of the Southern California crust. Science, 325(5943): 988-992. DOI:10.1126/science.1175298 |
Tong P, Komatitsch D, Tseng T L, et al. 2014. A 3-D spectral-element and frequency-wave number hybrid method for high-resolution seismic array imaging. Geophysical Research Letters, 41(20): 7025-7034. DOI:10.1002/2014GL061644 |
Tozer B, Sandwell D T, Smith W H F, et al. 2019. Global bathymetry and topography at 15 Arc Sec: SRTM15+. Earth and Space Science, 6(10): 1847-1864. DOI:10.1029/2019EA000658 |
Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels. Geophysical Journal International, 160(1): 195-216. |
Wang X M, Seriani G, Lin W J. 2007. Some theoretical aspects of elastic wave modeling with a recently developed spectral element method. Science in China Series G: Physics, Mechanics and Astronomy, 50(2): 185-207. DOI:10.1007/s11433-007-0022-1 |
Wang Y B, Takenaka H, Furumura T. 2001. Modelling seismic wave propagation in a two dimensional cylindrical whole earth model using the pseudospectral method. Geophysical Journal International, 145(3): 689-708. DOI:10.1046/j.1365-246x.2001.01413.x |
Wang Y B, Takenaka H. 2011. SH-wavefield simulation for a laterally heterogeneous whole-Earth model using the pseudospectral method. Science China Earth Sciences, 54(12): 1940-1947. DOI:10.1007/s11430-011-4244-8 |
Wessel P, Smith W H F, Scharroo R, et al. 2013. Generic mapping tools: Improved version released. Eos, 94(45): 409-410. |
Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly-analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2): 882-890. DOI:10.1785/0120020125 |
Yang D H, Wang M X, Ma X. 2013. Symplectic stereomodelling method for solving elastic wave equations in porous media. Geophysical Journal International, 196(1): 560-579. |
Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
Zhang X, Hao J, Gao X, et al. 2020. Evaluation of investigating magnitude, source mechanism and rupture process based on restored seismic data-Taking the 2013 Lushan MW6.6 earthquake in Sichuan as an example. Chinese Journal of Geophysics (in Chinese), 63(6): 2262-2273. DOI:10.6038/cjg2020N0402 |
Zhang Z G, Zhang W, Chen X F. 2014. Three-dimensional curved grid finite-difference modelling for non-planar rupture dynamics. Geophysical Journal International, 199(2): 860-879. DOI:10.1093/gji/ggu308 |
刘少林, 李小凡, 汪文帅, 等. 2013. 最优化辛格式广义离散奇异核褶积微分算子地震波场模拟. 地球物理学报, 56(7): 2452-2462. DOI:10.6038/cjg20130731 |
龙桂华, 李小凡, 张美根. 2009. 错格傅里叶伪谱微分算子在波场模拟中的应用. 地球物理学报, 52(1): 193-199. |
罗玉钦, 刘财. 2020. 地震波模拟中多轴复频移近似完全匹配层的吸收效果及稳定性. 地球物理学报, 63(8): 3078-3090. DOI:10.6038/cjg2020N0028 |
宋国杰, 杨顶辉, 童平, 等. 2012. 求解3D弹性波方程的并行WNAD方法及其TI介质中的波场模拟. 地球物理学报, 55(2): 547-559. DOI:10.6038/j.issn.0001-5733.2012.02.017 |
苏波, 李怀良, 刘少林, 等. 2019. 修正辛格式有限元法的地震波场模拟. 地球物理学报, 62(4): 1440-1452. DOI:10.6038/cjg2019M0538 |
张小艳, 郝金来, 高星, 等. 2020. 基于恢复地震数据获取震级、震源机制及破裂过程的评价-以2013年四川芦山MW6.6地震为例. 地球物理学报, 63(6): 2262-2273. DOI:10.6038/cjg2020N0402 |
 2021, Vol. 64
2021, Vol. 64


