2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
黏弹性和各向异性是当前地球物理学中的研究热点,这是因为它们不仅会导致地震波能量衰减(McDonal et al., 1958; Carcione et al., 1990), 还会产生速度的各向异性和频散(Thomsen, 1986; Tsvankin, 1997).这些效应的存在会影响后续反演和成像的精度(石星辰等, 2019), 例如能量衰减引起AVO分析的误差(Blangy, 1994).因此对黏弹性各向异性介质中波传播特征的研究将会给后续地震数据处理提供有价值的信息.
岩石各向异性的成因有很多, Crampin等(1984)将其总结为三种类型: 固有各向异性, 裂缝诱导各向异性和长波长各向异性,这导致地震波在地下介质中传播时表现出速度和衰减各向异性(Picotti et al., 2010, 2012),在两者之间速度各向异性引起了更多的关注.Thomsen参数的提出奠定了描述TI介质速度各向异性的基础(Thomsen, 1986),随后, Tsvankin(1997)将其推广到正交各向异性介质,然而一些物理实验和现场测量的结果表明在一些情况下衰减各向异性更加明显(Prasad and Nur, 2003),这二者之间的差异被Zhu和Tsvankin(2006, 2007)进行了仔细区分,他们先后提出了类比于Thomsen参数和Tsvankin参数的衰减各向异性参数来表征衰减各向异性Q矩阵, 并分析了平面波在衰减横向各向同性和衰减正交各向异性介质中的传播特征.然而, 这些研究只关注了介质的弹性性质, 没有涉及黏弹性对波传播的影响, 这与实际情况是有区别的.
除了各向异性之外, 岩石的黏弹性对地震波传播的影响同样显著,为了量化影响的程度, 我们通常使用品质因子参数Q来估计能量的衰减.在地震勘探频带内, 品质因子Q通常被认为是恒定不变的.为了描述这种Q行为, Carcione(1990)首先提出了基于广义标准线性固体的黏弹性各向异性介质模型,这个模型通过在时域中叠加标准线性固体来模拟一定频率范围内近似恒定的品质因子Q, 因此又被称为近似常Q模型.随后Carcione(1992, 1994)将其推广到频率域, 推导出均匀平面波在介质中传播时的不同物理速度、品质因子等多个量的计算公式, 并和纯弹性各向异性介质进行了对比.近似常Q模型被广泛地应用于地震模拟(Robertsson et al., 1994; Hestholm, 1999; Picotti et al., 2010, 2012; Zhu et al., 2013; Yang et al., 2015; 巴晶等, 2008; 赵海波等, 2011; 严红勇和刘洋, 2012).然而, 它在计算时间和内存上要求较高, 限制了在地震数据处理中的应用.
相比于近似常Q模型, Kjartansson(1979)提出的常Q模型可以在所有频率范围内精准描述恒定Q行为而受到关注.该模型在时域波动方程中引入了分数阶时间导数, 即时间导数的非整数幂(Caputo, 1967).Carcione等(2002)使用Grünwald-Letnikov近似对分数阶波动方程数值求解,由于这种方法需要存储每一时刻的历史波场, 因此对内存的消耗量巨大.为了解决这个问题, 人们提出了使用分数阶拉普拉斯算子来模拟常Q介质中的波传播(Chen and Holm, 2004; Carcione, 2009; Zhu and Carcione, 2014; Zhu and Harris, 2014; 吴玉等, 2017; 陈汉明, 2017; Wang et al., 2018, 2020; Qiao et al., 2019; Li et al., 2016, 2019).分数拉普拉斯采用分数阶傅里叶伪谱法计算, 通过常Q频散关系将分数阶时间导数转换成分数阶空间导数, 有效避免了分数阶时间导数所需的额外内存.
目前对于常Q模型的研究大多关注于地震波场模拟以及定性分析波场特征, 很少对地震波传播进行定量描述, 而且只涉及到介质的速度各向异性, 并没有考虑衰减各向异性给波传播带来的影响, 这与实际情况存在一定偏差.本文的研究从常Q模型出发, 旨在构建更加符合实际地下介质的模型, 通过平面波理论定量分析地震波响应和模型参数之间的关系.为此,本文首先建立了包含衰减和速度各向异性的黏弹性衰减VTI介质模型,其中, 衰减各向异性通过Zhu和Tsvankin(2006)提出的参数表示, 速度各向异性则通过Thomsen参数来描述.通过使用分数阶时间导数, 我们推导出相应的本构关系和波动方程.然后运用均匀平面波分析得到在(x, z)平面中传播的准压缩波qP、准剪切波qSV和纯剪切波SH的复速度、相速度以及品质因子解析表达式.在黏弹性介质中, 波前面需要由能量速度表示,因此, 为了获得表示波前面的正确公式, 我们引用Poynting定理来计算能量速度.最后通过数值试验验证了模型的正确性, 计算了相速度、能量速度以及品质因子关于传播角度、速度和衰减各向异性等参数的变化.通过对模拟结果的详细分析, 我们对地震波在黏弹性衰减VTI介质模型中的传播特征进行了总结.
为了叙述方便, 我们对本文的符号和变量进行统一约定: 空间变量x, y和z分别由指标i, j=1, 2, 3表示, 关于空间变量x, y和z的偏导数分别表示为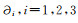

在地震勘探频带范围内, 通常认为品质因子Q值大小不随频率变化.为了描述这种品质因子Q行为, Kjartansson提出了一种常Q介质模型.该模型通过将松弛函数中时间整数幂因子替换为非整数幂因子, 可以在整个频率范围内展现恒定Q值的特征.Kjartansson(1979)给出了如下的松弛函数来模拟常Q介质的线性衰减特性:
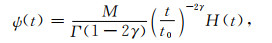
|
(1) |
其中M=ρv02cos2(πγ/2) 是体积模量, ρ是密度, v0是参考频率为ω0时的相速度, t为时间变量, t0为参考时间(它对应参考频率ω0=1/t0), Γ是伽马函数, H(t)是Heaviside阶跃函数.参数γ是一个无量纲量, 其表达式为
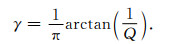
|
(2) |
对于任意的品质因子Q, γ的取值范围为0<γ<0.5.
传统黏弹性模型假设衰减是各向同性的,即模型衰减特性只由P波和S波分别对应的品质因子Qp和Qs决定.然而, 实际介质可能呈现衰减各向异性的特征.因此, 建立一个同时包括速度和衰减各向异性的黏弹性模型十分必要.针对真实地层中常见的VTI介质, 我们将构建基于常Q模型的黏弹性衰减VTI介质模型.
黏弹性衰减VTI介质的速度各向异性可以通过Thomsen参数εv, γv和δv表示(Thomsen, 1986):

|
(3) |
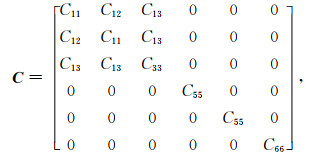
其中CIJ是弹性刚度张量C的分量.在VTI介质中, 弹性刚度张量C有如下形式(Thomsen, 1986):
|
(4) |
其中C12=C11-2C66.如果cp和cs分别是P波和S波沿着垂直对称轴的相速度, 则弹性刚度分量C33和C55可以表示为

|
(5) |
从式(3)和(5)可以看出, 当已知垂直对称轴方向上P波和S波的相速度cp和cs, 介质密度ρ, 以及Thomsen参数εv, γv和δv, 黏弹性衰减VTI介质的弹性刚度张量C就可以被确定.
黏弹性衰减VTI介质的衰减各向异性可以通过参数εQ, γQ和δQ表示(Zhu and Tsvankin, 2006):
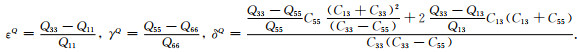
|
(6) |
衰减各向异性参数是通过类比Thomsen参数得到, εQ和γQ分别是定义qP波和SH波衰减各向异性强度的参数, 它们度量了水平方向和垂直方向的衰减系数之间的差异; δQ描述了垂直对称轴附近qP波衰减系数的各向异性强度.在式(6)中, QIJ是品质因子矩阵Q的分量.黏弹性衰减VTI介质的品质因子矩阵Q具有和弹性刚度张量C相同的对称性, 可以表示为(Zhu and Tsvankin, 2006)

|
(7) |
其中

|
(8) |
这里分量Q11和Q33分别决定了水平方向和垂直方向上的qP波品质因子(其中Q33和衰减各向同性的P波品质因子Qp等效), Q55是S波垂直方向上的品质因子(Q55和衰减各向同性的S波品质因子Qs等效).在VTI介质情况下, 垂直方向的衰减一般要强于水平方向, 这意味着Q33<Q11.由式(6)可知衰减VTI介质的εQ小于0.观察式(6)和(8)可知, 若给出品质因子矩阵Q的分量Q33和Q55, 以及衰减各向异性参数εQ, γQ和δQ, 就可以得到黏弹性衰减VTI介质品质因子矩阵Q的各个分量.
常Q模型中无量纲参数γ由品质因子Q决定.类比于品质因子矩阵Q, 在黏弹性衰减VTI介质中我们定义一个无量纲参数矩阵γ.γ的分量γIJ可以通过矩阵Q的分量QIJ计算出:

|
(9) |
同理, 我们定义体积模量张量M, 它的分量MIJ可以被表示为
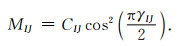
|
(10) |
张量M结合了介质的Thomsen和衰减各向异性参数.结合式(1), (9)和(10), 我们可以类比得到黏弹性衰减VTI介质的松弛函数张量ψ(t), 其分量ψIJ(t) 表示为
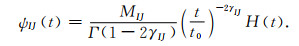
|
(11) |
相比于传统的常Q介质松弛函数, 松弛函数张量ψ(t) 同时包含了介质的速度和衰减各向异性信息, 为下一步构建黏弹性衰减VTI介质的本构关系和波动方程奠定了基础.
由松弛函数张量ψ(t) 诱导出的黏弹性衰减VTI介质模型可以通过衰减各向异性参数来控制衰减各向异性的强度.当参数εQ=γQ=δQ=0时, 介质从衰减各向异性退化为衰减各向同性.传统的衰减各向同性黏弹性模型的品质因子只是由Qp和Qs(即Q33和Q55)表示, 并不能体现介质的衰减各向异性特征.因此, 引入衰减各向异性是对传统黏弹性模型一个很好的补充.
1.2 基于分数阶时间导数的本构关系和波动方程通过上节所建立的松弛函数张量, 我们将推导黏弹性衰减VTI介质的本构关系和波动方程.各向异性线性黏弹性介质的应力张量和应变张量满足本构关系(Carcione, 1990):

|
(12) |
其中符号‘*’表示时间卷积,
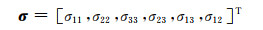
|
(13) |
是包含分量σij的应力张量, 以及
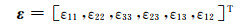
|
(14) |
是包含分量εij的应变张量.应变张量可以表示为关于位移向量u=[u1, u2, u3] 的形式:
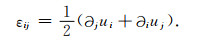
|
(15) |
将松弛函数张量式(11)应用到式(12), 并利用分数阶导数的性质(Caputo, 1967; Zhu and Harris, 2014), 可以得到黏弹性衰减VTI介质模型的本构关系:
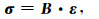
|
(16) |
其中B为六阶张量.张量B与弹性刚度张量C具有相同的对称性, 其分量可以表示为
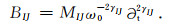
|
(17) |
本构关系式(16)可以改写为分量形式:
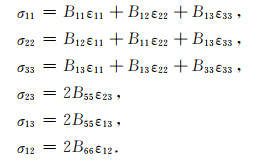
|
(18) |
各向异性黏弹性介质的运动方程可以表示为应力张量的空间偏导数和位移向量的时间偏导数:

|
(19) |
其中fi是体力向量的分量.将式(15)代入式(18)并联立(19)式得到黏弹性衰减VTI介质的波动方程:
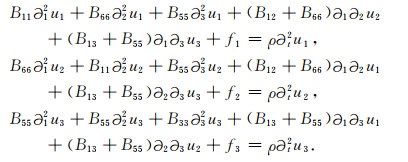
|
(20) |
本小节所构建的本构关系(16)和波动方程(20)均包含时间分数阶导数, 对应的分数阶矩阵γ由衰减各向异性参数表示的品质因子矩阵Q决定.当分数阶矩阵γ趋近于零矩阵时(即Q33和Q55趋近于无穷大), 本构关系(16)和波动方程(20)将退化为弹性各向异性介质的情形.黏弹性衰减VTI介质本构关系和波动方程的建立是研究地震波传播特征的前提.
1.3 黏弹性衰减VTI介质模型的平面波理论研究地震波在介质中传播的方法通常可以分为两类: 一类是地震波场的正演模拟; 另一类是基于平面波理论.前者可用于定性分析波场特征, 后者可以通过求取解析表达式对地震波传播特征进行定量描述.基于上节给出的本构关系和波动方程, 本节将利用平面波理论推导在黏弹性衰减VTI介质中复速度、相速度以及品质因子的解析表达式.
平面波的位移可以表示为
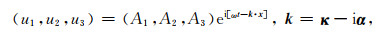
|
(21) |
其中ω是角频率, A=[A1, A2, A3]T代表偏振向量, x是位置向量, k是复波数向量, κ和α分别是k的实部和衰减向量, 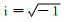
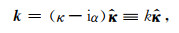
|
(22) |
其中
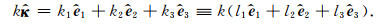
|
(23) |
式(23)中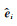
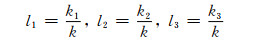
|
(24) |
为复波数方向的方向余弦, 在均匀波传播的情况下它们对应着传播方向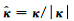
在不失一般性的前提下, 我们假定平面波在包含垂直对称轴的(x, z)坐标平面上传播.定义平面波传播方向和z轴之间的夹角为传播角度θ, 于是
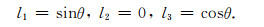
|
(25) |
通过方向余弦表达式(25), 式(21)可以改写为
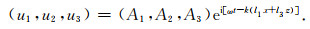
|
(26) |
在零体力的情况下, 将式(26)代入波动方程(20)可以得到Christoffel方程:
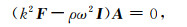
|
(27) |
其中I是三阶单位矩阵, F是Christoffel矩阵,
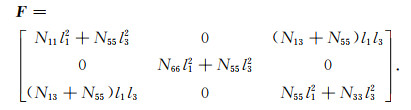
|
(28) |
式(28)中六阶张量N的分量NIJ可以表示为

|
(29) |
为了使齐次方程(27)中偏振向量A有非零解, 系数矩阵(k2F-ρω2I) 必须满足行列式为0, 即
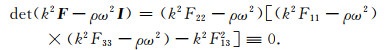
|
(30) |
式(30)包含一个线性因子
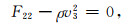
|
(31) |
以及一个二次因子

|
(32) |
式(31)和(32)中v1, v2和v3表示复速度,
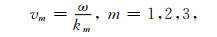
|
(33) |
分别对应于qP, qSV和SH波情形(在没有特殊说明的情况下, 后文将继续沿用这一对应关系).需注意的是, 纯剪切波SH的偏振方向垂直于(x, z)平面, 与qP和qSV波的传播方向不耦合.通过求解式(31)和(32)并结合Christoffel矩阵分量(28), 我们可以得到qP, qSV和SH波复速度的解析表达式:

|
(34) |
其中
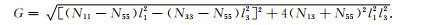
|
(35) |
通过给出的复速度, 我们可以得到每个波的品质因子qm和相速度vmp(Carcione, 1990).它们可以表示为
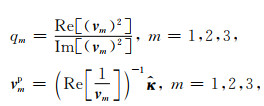
|
(36) |
其中Re[·]和Im[·] 分别表示取实部和虚部.观察式(36)可知, 相速度的方向和传播方向是一致的.由于复速度的方向取决于传播方向, 因此品质因子具有各向异性.
1.4 黏弹性衰减VTI介质模型的能量速度地震波的波前面为某时刻波前能量到达的空间位置, 可以通过能量速度精确表示(Carcione, 1994).在弹性介质中, 群速度和能量速度是等价的, 由于群速度的计算相对于能量速度较为简单, 因此波前面通常由群速度给出.在黏弹性介质中, 频散效应将根据黏弹性程度使波前面传播到更大或更小的空间范围(Carcione, 1992).在这种情况下, 群速度将不能准确表示波前面.为了得到在黏弹性衰减VTI介质中波前面的正确计算公式, 我们需要推导能量速度的解析表达式.
能量速度通常被定义为平均功率流密度与平均能量密度之比, 其中平均功率流密度是复Poynting矢量的实部(Carcione, 1990).于是, 我们将黏弹性衰减VTI介质中能量速度ve表示为
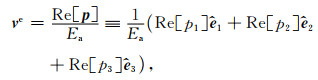
|
(37) |
其中Ea是平均能量密度, 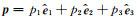

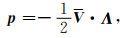
|
(38A) |
其中矩阵Λ有如下形式

|
(38B) |
平均能量密度Ea等于平均应变能密度Es和平均动能密度Ev之和的一半, 即
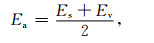
|
(39) |
这里, Es与应变张量ε和松弛函数张量ψ(t)有关,
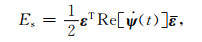
|
(40) |
Ev可以由介质密度ρ和速度向量V表示为
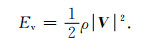
|
(41) |
利用以上给出的表达式, 我们可以推导出在(x, z)平面中传播的qP波能量速度v1e的分量(v1e)1和(v1e)3, 以及qSV波能量速度v2e的分量(v2e)1和(v2e)3为(详细的计算过程由附录A给出)
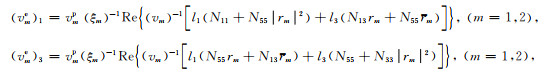
|
(42) |
其中变量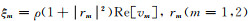
SH波能量速度v3e可以用类似的方法推导出, 它可以表示为(推导细节见附录C):
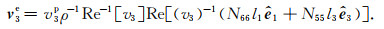
|
(43) |
qP、qSV和SH波的能量速度与相速度具有不同的物理意义, 其中相速度是等相位面沿垂直波前面方向的传播速度, 能量速度是波前面的传播速度.两个速度之间存在一个几何关系, 即相速度可以视为能量速度在传播方向的投影(Carcione, 1994).因为相速度的方向和传播方向一致, 所以能量速度和波前面并不正交.通过推导qP, qSV和SH波的品质因子、相速度和能量速度的解析表达式, 我们建立了地震波速度和能量与模型的Thomsen参数、衰减各向异性参数以及传播角度之间的联系, 为定量分析模型参数对地震波传播特征的影响提供了理论基础.
2 数值试验为了分析平面波在黏弹性衰减VTI介质模型中的传播特点, 本节模拟了三个例子.首先, 我们验证模型的正确性.然后, 我们分析速度各向异性对qP, qSV和SH波相速度和能量速度的影响.最后, 衰减各向异性对三种波的品质因子和速度的影响被详细讨论.本节所有例子的参考角频率是30 Hz, 介质密度为ρ=2100 kg·m-3.
2.1 验证模型为了验证黏弹性衰减VTI介质模型的正确性, 我们计算了几个曲线来分析模型的Q行为, 黏弹性差异导致频散效应的变化, 以及介质的速度和衰减各向异性.表 1显示了模型的介质属性, 即Thomsen参数和衰减各向异性参数, 以及在垂直方向上qP和S波的品质因子和相速度, 其中衰减各向异性参数参考了Zhu和Tsvankin(2006)使用的参数值.由于VTI介质在垂直方向上衰减大于水平方向上衰减, 所以我们采用εQ<0.
|
|
表 1 黏弹性衰减VTI介质属性 Table 1 Material properties of the viscoelastic attenuative VTI media |
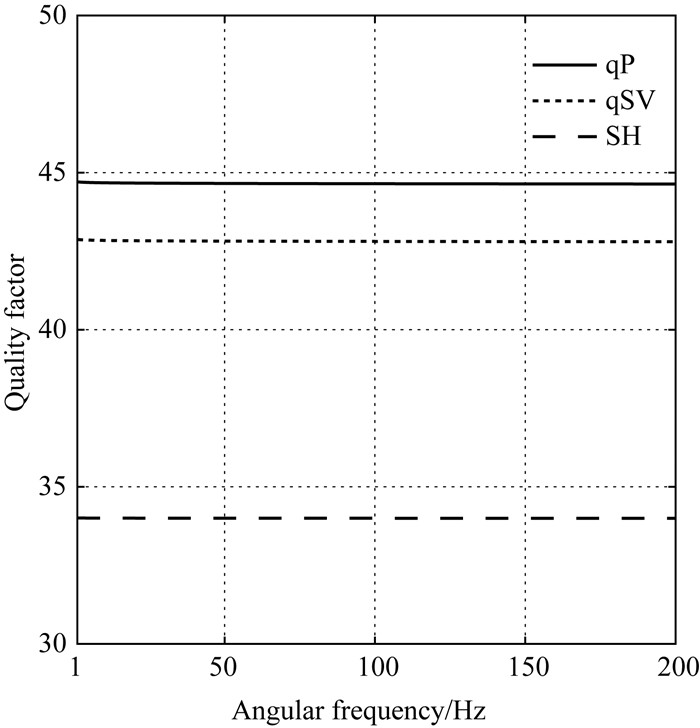
图 1显示了在(x, z)平面中传播的qP、qSV和SH波品质因子与频率的关系, 其中传播角度为π/8, 介质属性在表 1中给出.从图 1可以看出即使是在非常低的频率时,三种波的品质因子在地震勘探频带仍保持了理想恒定Q行为, 相比之下, 近似常Q模型的品质因子在低频率范围(1~5 Hz)随频率变化较大, 并不能达到常Q模型的这种效果.
|
图 1 qP, qSV和SH波品质因子关于频率的变化, 介质属性在表 1中定义 Fig. 1 Quality factors of the qP, qSV, and SH waves as a function of the angular frequency for the medium defined in Table 1 |
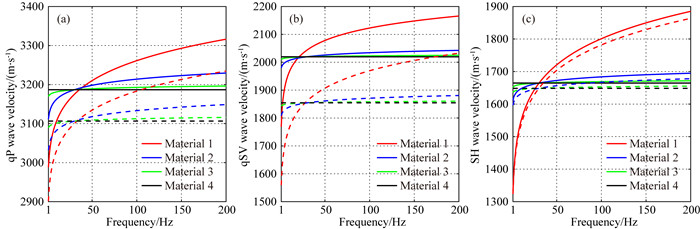
为了验证黏弹性对速度频散效应的影响, 图 2展示了在4个不同黏弹性属性介质中相速度和能量速度关于频率的变化, 其中(a), (b)和(c)分别对应于qP、qSV和SH波, 图中每个颜色的实线和虚线分别代表能量速度和相速度.4个介质属性的区别在于Q33和Q55不同, 其分别在表 2中所示, 第四个介质的Q33和Q55取较大值是为了使介质退化为弹性各向异性介质, 其他属性参数和表 1相同.图 2显示出黏弹性程度的差异导致三个波的频散曲线显著不同.对于强黏弹性介质(即低Q值), 相速度和能量速度随着频率变化剧烈.相比之下, 弱黏弹性介质的频散效应相对较弱, 特别是弹性介质4, 两个速度几乎不受频率影响, 它们之间的差也几乎恒定.此外, 在低频率段, 强黏弹性介质的能量速度和相速度均低于弱黏弹性介质的, 随着频率升高, 强黏弹性介质的速度会大于弱黏弹性介质的.
|
图 2 能量速度和相速度关于频率的变化, 其中每个介质的品质因子在表 2中给出, 实线代表能量速度, 虚线代表相速度 (a) qP波; (b) qSV波; (c) SH波. Fig. 2 The energy and phase velocities as a function of the angular frequency, where the quality factors of the four materials are given in Table 2, and the solid and dotted line represent the energy and phase velocities, respectively (a) qP wave; (b) qSV wave; (c) SH wave. |
|
|
表 2 四个介质的品质因子 Table 2 Quality factors of the four materials |
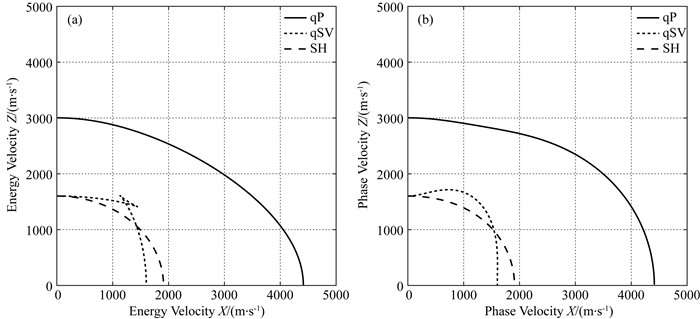
图 3a和3b分别为qP、qSV和SH波能量速度与相速度的极坐标表示, 其中介质属性如表 1所示.由于介质的对称性, 这里仅显示四分之一平面.能量速度能够表示波前面, 因此它的曲线可以看做是波前面的截面.相比较相速度曲线, 波前面曲线的形态完全不同, 特别是qSV波曲线在大约角度π/4的方向上有一个尖端三角形, 这是由于Thomsen参数εv和δv两者值相差较大导致.此外, 图 3a和3b印证了在传播角度为0和π/2时能量速度与相速度相等.
|
图 3 在35 Hz频率时qP、qSV和SH波的能量速度(a)和相速度(b)的极坐标表示, 介质属性如表 1中所示 Fig. 3 Polar representations of the energy (a) and phase velocities (b) of the qP, qSV, and SH waves for a angular frequency 35 Hz. The material properties are shown in the Table 1 |
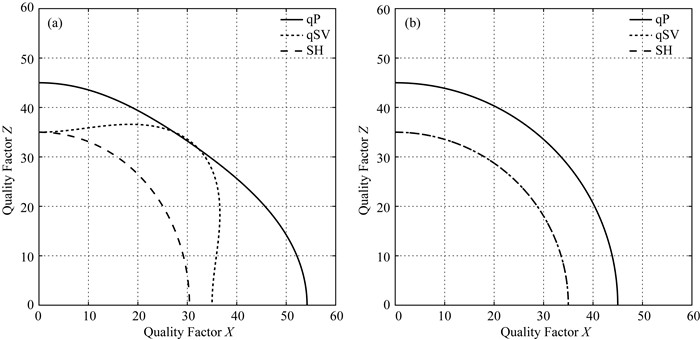
为了验证模型的衰减各向异性, 我们设计了两个介质.两个介质的性质差异是衰减各向异性参数值.对于第一个, 衰减各向异性参数如表 1所示; 对于第二个, 衰减各向异性参数εQ=γQ=δQ=0, 这使介质退化成衰减各向同性.为了避免速度各向异性对品质因子的影响, 我们使两个介质的Thomsen参数εv=γv=δv=0.其他属性参数取表 1中的值.图 4为在两个介质中qP、qSV和SH波品质因子曲线的极坐标表示.图 4a显示了衰减各向异性导致品质因子曲线形态不是圆形的, 表现出明显的各向异性特征.作为对比, 衰减各向同性介质的品质因子曲线是一个标准的圆形(看图 4b), 其中qSV和SH波的品质因子曲线重合在一起了, 这是由于S波在各向同性介质中不发生横波分裂.通过对比可知, 衰减各向异性造成了品质因子的各向异性, 因此模型的衰减各向异性特征被证明.
|
图 4 qP, qSV和SH波品质因子的极坐标表示, 频率为35 Hz (a) 衰减VTI介质; (b) 衰减各向同性介质. Fig. 4 Polar representations of the quality factors of the qP, qSV, and SH waves. The angular frequency is 35 Hz (a) Attenuative VTI media; (b) Attenuative isotropic media. |
为了分析模型的速度各向异性, 我们计算了能量速度、相速度以及两个速度的差关于Thomsen参数和传播角度θ的变化曲线.观察式(34), (42)和(43)可知, 参数εv和δv只作用于qP和qSV波速度, 参数γv只影响SH波速度.因此, 对于qP和qSV波, 我们计算了速度关于参数εv和δv变化的曲线; 对于SH波, 我们计算了速度关于参数γv变化的曲线.所有曲线对应的频率是35Hz, 介质属性中除了所研究的变量外均取表 1中的值.
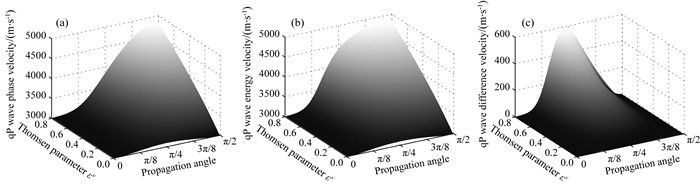
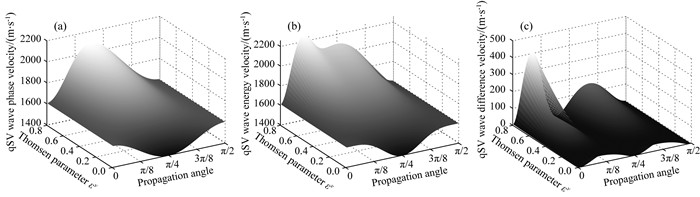
图 5和6分别显示了参数εv和传播角度θ对qP波与qSV波速度的影响, 其中(a)是相速度, (b)是能量速度, (c)是能量速度和相速度的差(后续简称差速度).对比图 5a和5b中可知, qP波相速度与能量速度关于εv和传播角度的变化一致, 同时εv值的大小会导致两个速度随传播角度呈现不同的变化.例如, 当εv较小时两个速度随着传播角度变化会出现一个极大值; 随着εv增大, 两个速度会随着传播角度增大而单调递增, 而且εv越大变化越剧烈.两个速度的差速度在εv较小时几乎为0; 当εv变大, 差速度将在中间角度处取得极大值(看图 5c).相比之下, 图 6a和6b显示出qSV波相速度与能量速度关于εv和传播角度变化可能会出现不一致的情况, 其中能量速度在εv较大时会随着传播角度变化出现两个极大值, 这导致差速度也出现了两个极值(看图 6c).此外, qSV波能量速度和相速度在εv较小时与较大时关于传播角度的变化趋势完全相反.
|
图 5 qP波的相速度(a)、能量速度(b)以及两个速度的差速度(c)关于参数εv和传播角度的变化 Fig. 5 The phase velocity (a), energy velocity (b), and the difference of the two velocities (c) of the qP wave versus the parameter εv and propagation angle |
|
图 6 qSV波的相速度(a)、能量速度(b)以及两个速度的差速度(c)关于参数εv和传播角度的变化 Fig. 6 The phase velocity (a), energy velocity (b), and the difference of the two velocities (c) of the qSV wave versus the parameter εv and propagation angle |
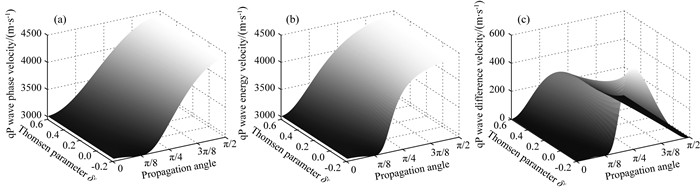
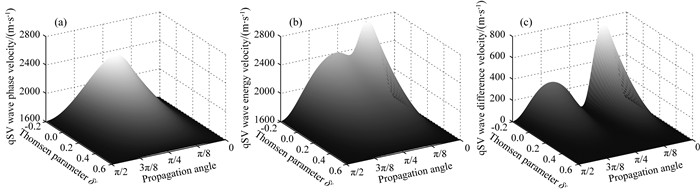
图 7和图 8分别给出参数δv和传播角度对qP与qSV波速度的影响.其中(a), (b)和(c)分别对应相速度, 能量速度和差速度.图 7a, 7b, 8a和8b同样体现出了两个波速度变化的差异性, 这一点和上个例子是相同的, 即qP波能量速度与相速度具有相同的变化趋势, 而在δv向负值移动时qSV波能量速度与相速度产生显著的变化差异.图 7c和8c显示出当δv向负值移动时, 两个波的差速度都会逐渐增大, qP波的差速度始终在中间角度取得极大值, 而qSV波的差速度会出现两个极大值.
|
图 7 qP波的相速度(a)、能量速度(b)以及两个速度的差速度(c)关于参数δv和传播角度的变化 Fig. 7 The phase velocity (a), energy velocity (b), and the difference of the two velocities (c) of the qP wave versus the parameter δv and propagation angle |
|
图 8 qSV波的相速度(a)、能量速度(b)以及两个速度的差速度(c)关于参数δv和传播角度的变化 Fig. 8 The phase velocity (a), energy velocity (b), and the difference of the two velocities (c) of the qSV wave versus the parameter δv and propagation angle |
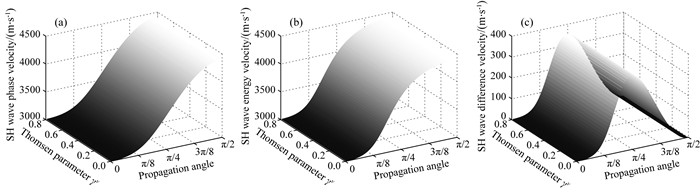
图 9a, 9b和9c分别显示了SH波相速度, 能量速度以及差速度关于参数γv和传播角度的变化.从图中可以看出, 在任意γv值的介质中, SH波能量速度和相速度均随传播角度的增大而增大, 差速度在中间角度取得极大值.此外, 差速度关于传播角度的变化较为显著, 而γv值的变化对差速度影响较小.
|
图 9 SH波的相速度(a)、能量速度(b)以及两个速度的差速度(c)关于参数γv和传播角度的变化 Fig. 9 The phase velocity (a), energy velocity (b), and the difference of the two velocities (c) of the SH wave versus the parameter γv and propagation angle |
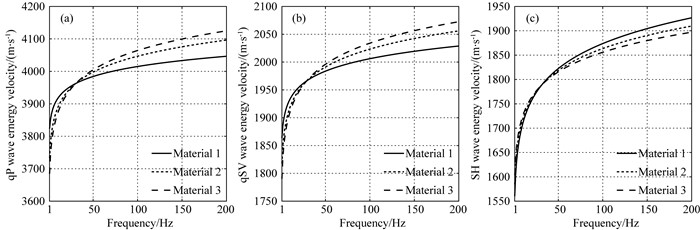
为了研究衰减各向异性对速度频散效应的影响, 我们计算了在三个不同衰减各向异性强度介质中能量速度关于频率的变化, 结果在图 10所示, 其中(a), (b)和(c)分别对应于qP、qSV和SH波, 波传播角度为π/4.三个介质的衰减各向异性参数在表 3中给出, qP和S波在垂直方向上具有相同的品质因子, 其中Q33=15, Q55=10.观察图 10可知, 衰减各向异性强度的变化会导致频散曲线变化.对于qP和qSV波, 随着衰减各向异性增强, 能量速度关于频率的变化会更加平缓.与之相比, SH波呈现出相反趋势, 即在强衰减各向异性介质中速度变化越剧烈.此外, 一个有意思的现象是每个波在三个介质中的能量速度在参考频率30 Hz处几乎相等.当频率小于参考频率时, qP和qSV波在强衰减各向异性介质中能量速度较大, 而SH波在强衰减各向异性介质中能量速度较小.当频率超过参考频率后, 这种关系发生了反转.从这可知, 参考频率是一个关键量, 它会影响能量速度对于衰减各向异性强度的响应.
|
图 10 在三个不同衰减各向异性强度介质中关于频率变化的能量速度曲线 (a) qP波; (b) qSV波; (c) SH波. Fig. 10 The energy velocities curves in the three material as a function of the frequency, where these materials have the different levels of the attenuation anisotropy (a) qP wave; (b) qSV wave; (c) SH wave. |
|
|
表 3 三个介质的衰减各向异性参数 Table 3 Attenuation anisotropic parameters of the three materials |
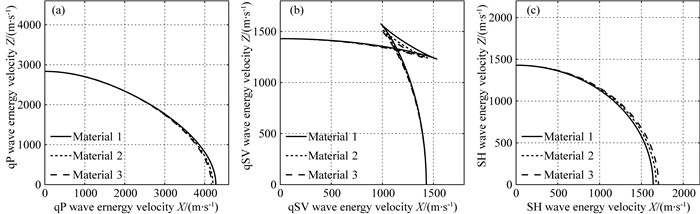
为了进一步分析衰减各向异性对波前面形态的影响, 图 11a, 11b和11c分别给出了qP, qSV和SH波能量速度在5 Hz频率时的极坐标表示.这里沿用了上个例子的三个介质.因为能量速度表示波前面的截面, 所以从图中可以看出衰减各向异性强度变化会导致波前面扩散到更大或者更小的空间, 其中耦合的两个波qP和qSV的波前面变化一致, 即随着衰减各向异性强度提升扩散到更大的空间, 这与SH波的波前面变化相反.结合上个例子, 我们可知: 当衰减各向异性强度变化时, 耦合在一起的qP和qSV波频散曲线和波前面具有相同变化, 而SH波与qP和qSV波呈现出的变化相反.
|
图 11 在三个不同衰减各向异性强度介质中能量速度曲线的极坐标表示 (a) qP波; (b) qSV波; (c) SH波. Fig. 11 Polar representations for the energy velocities curves in the three material at 5 Hz, where these materials have the different levels of the attenuation anisotropy (a) qP wave; (b) qSV wave; (c) SH wave. |
除了对速度的影响外, 衰减各向异性对品质因子的影响同样显著.因此, 我们计算了品质因子曲线, 它是关于衰减各向异性参数和传播角度θ的函数.类似于速度各向异性的分析, 因为εQ和δQ只作用于qP和qSV波品质因子, γQ只决定SH波品质因子, 所以qP和qSV波只计算了关于参数εQ和δQ变化, SH波只计算了关于参数γQ变化.所有曲线对应的频率均为35Hz, 介质属性中除了所研究的变量外均和表 1相同.
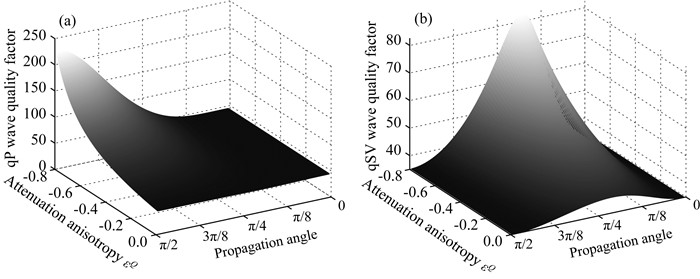
图 12a和12b分别给出了qP和qSV波品质因子关于参数εQ和传播角度的变化.从图中可以看出, 对于任意的εQ值, qP波始终在平行于对称轴方向时衰减最强(即品质因子最小), 在垂直于对称轴方向衰减最小; qSV波在垂直和平行对称轴方向衰减均很强, 而在中间角度时衰减最小.随着εQ向负值方向增大时, qP和qSV波的衰减均逐渐减弱.
|
图 12 品质因子关于参数εQ和传播角度的变化 (a) qP波; (b) qSV波. Fig. 12 The quality factors versus the parameter εQ and propagation angle (a) qP wave; (b) qSV wave. |
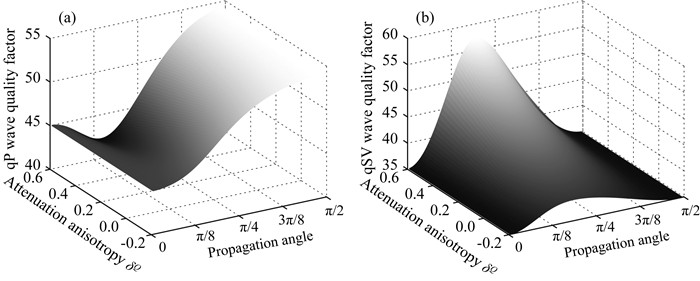
图 13显示了参数δQ和传播角度对品质因子的影响, 其中(a)和(b)分别对应于qP和qSV波.图 13a和13b表明在δQ增大的情况下, qP波品质因子逐渐减小, 衰减最强的角度将从平行于对称轴向中间角度移动, 而衰减最弱的角度依然保持在与对称轴垂直的方向; qSV波品质因子随着δQ的增大而增大, 同时依然在中间角度有较小衰减.
|
图 13 品质因子关于参数δQ和传播角度的变化 (a) qP波; (b) qSV波. Fig. 13 The quality factors versus the parameter δQ and propagation angle (a) qP wave; (b) qSV wave. |
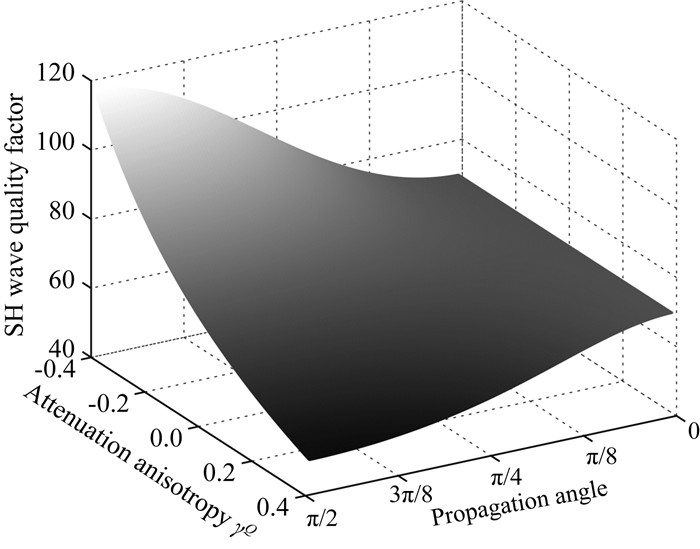
图 14给出了SH波品质因子关于参数γQ和传播角度的变化.观察图可知, γQ值对品质因子关于角度的变化有着直接影响.当γQ大于0时, SH波品质因子会随着角度增大而减小, 在垂直于对称轴方向产生最大衰减; 当γQ小于0时, SH波品质因子会随着角度增大而增大, 在垂直于对称轴方向有最小衰减.这和Zhu和Tsvankin(2006)在弹性衰减各向异性介质中得出的结论一致.此外, SH波品质因子会随着γQ向负值增大而增大.
|
图 14 SH波的品质因子关于参数γQ和传播角度的变化 Fig. 14 The quality factor of the SH wave versus the parameter γQ and propagation angle |
本文将衰减各向异性和速度各向异性与常Q模型相结合, 建立了一个更接近于实际介质的黏弹性衰减VTI介质模型, 可以通过类比于Thomsen参数(εv, δv和γv)的衰减各向异性参数εQ, δQ和γQ来控制衰减各向异性强度.基于分数阶时间导数, 我们推导出黏弹性衰减VTI介质的本构关系和波动方程.在均匀平面波的假设下, 利用Christoffel方程计算出在(x, z)平面中传播的qP, qSV和SH波复速度, 相速度以及品质因子解析表达式.由于介质黏弹性的影响, 我们运用Poynting定理给出了能够表示波前面的能量速度计算公式.
根据推导出的公式进行了数值试验, 试验结果验证了模型的正确性, 即在地震勘探频带上实现理想的恒定Q行为, 黏弹性强度差异导致频散效应的变化, 以及速度和品质因子表现出各向异性特征.此外, 对模型的速度和衰减各向异性进行了模拟计算, 数值结果表明:
(1) qP波能量速度与相速度关于Thomsen参数和传播角度变化是一致的, 差速度一般在中间角度取得极大值.对于任意黏弹性衰减VTI介质, qP波品质因子在垂直于对称轴方向取到最大值; 当εQ向负值方向增大时, qP波的品质因子逐渐增大; 随着δQ增大, 使品质因子取得最小值的传播角度会从平行于对称轴的零角度逐渐移动到中间角度.
(2) qSV波能量速度与相速度在εv较大或者δv为负值的介质中会出现关于传播角度变化不一致的情况, 这导致差速度在传播角度上出现两个极大值.qSV波品质因子始终在平行和垂直于对称轴的方向取得最小值, 而在中间角度取得最大值; 在εQ向负值方向增大和δQ向正值方向增大的情况下, qSV波品质因子均增大.
(3) SH波能量速度和相速度均随传播角度增大而增大, 差速度在中间角度取得极大值.SH波品质因子关于角度变化取决于γQ的正负性; 当γQ为正值时, 品质因子会随着角度增大而减小; 当γQ为负值时, 品质因子会随着角度增大而增大; 随着γQ从负值增大为正值, SH波品质因子将逐渐减小.
(4) 衰减各向异性强度的变化会导致qP, qSV和SH波的频散曲线和波前面发生显著变化, 其中耦合在一起的qP和qSV波变化趋势相同, 而SH波呈现与它们相反的变化.
本文提出的黏弹性衰减VTI介质模型是对传统常Q模型一个很好的补充.虽然正文理论推导部分都是针对具有垂直对称轴的均匀TI介质展开, 但是通过类比可以推广到任意对称轴方向的均匀TI介质.通过平面波理论和Poynting定理推导出相速度、能量速度和品质因子表达式, 为分析地震波传播特征提供了一个有用工具, 其数值模拟结果为研究衰减各向异性黏弹性介质奠定了理论基础.本文的分析只针对均匀平面波情形, 即复波数的实部和衰减向量方向一致, 且均与传播方向相同; 相比于由非均匀介质和有界面的地层导致的非均匀波传播来说, 这是一个特例; 在下一步研究工作中将考虑非均匀波传播的情形.
附录A qP和qSV波的能量速度计算-Ⅰ在本附录中我们考虑均匀平面波在(x, z)平面中传播且传播角度θ的范围为0°<θ<90°, 这意味着qP和qSV波的应变张量ε中只有分量ε11, ε33, 以及ε13不等于0. 将式(26)代入式(15)可得到应变分量关系式:
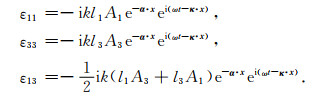
|
(A1) |
类似地, 将式(26)代入黏弹性衰减VTI介质的本构关系(16)可以得到应力分量关系式:

|
(A2) |
根据式(38), 复Poynting矢量可以写为
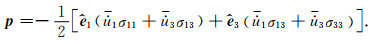
|
(A3) |
结合式(A3)和(A2), 我们可以得到qP和qSV波的复Poynting矢量的两个分量:
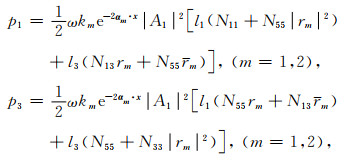
|
(A4) |
其中rm=A3/A1, m=1和2分别对应于qP和qSV波.比例因子rm可以通过Christoffel方程(27)得到:

|
(A5) |
从式(41)可知, 平均动能密度可以写为
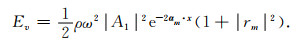
|
(A6) |
根据式(40), 平均应变能密度被表示为
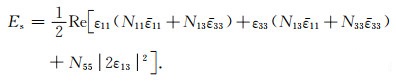
|
(A7) |
将式(A1)带入式(A7)并联立式(A5), 可以得到
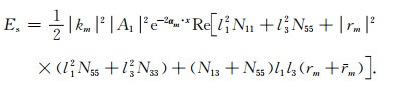
|
(A8) |
利用Christoffel分量(28), 式(A8)可以改写为
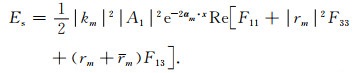
|
(A9) |
结合式(A5)和(33), 式(A9)可以被简化为
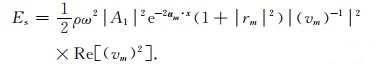
|
(A10) |
结合式(A6)和(A10)并联立式(39), 平均能量密度Ea可以表示为

|
(A11) |
利用复数的性质, 式(A11)可以进一步表示为
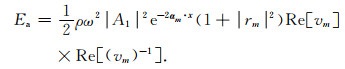
|
(A12) |
将式(A4)和(A12)代入方程(37), 可以得到qP和qSV波能量速度的两个分量(vme)1和(vme)3:

|
(A13) |
其中ξm=ρ(1+|rm|2)Re[vm].
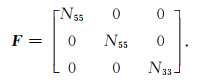
附录B qP和qSV波的能量速度计算-Ⅱ本附录是对附录A的一个补充推导, 即计算当传播角度θ为0°和90°时qP和qSV波能量速度. 首先我们考虑传播角度为0°时的情形. 在此情形下, l1=0和l3=1, Christoffel矩阵(28)可以改写为
|
(B1) |
结合式(B1)和Christoffel方程(27), qP和qSV波的复速度v1和v2分别表示为

|
(B2) |
当传播角度为0°时, qP波偏振方向和传播方向一致, 以及qSV波偏振方向和传播方向垂直. 因此qP波偏振向量A=[A1, A2, A3]T中只有分量A3不为0, qSV波偏振向量A=[A1, A2, A3]T中只有分量A1不为0. 类似于附录A的推导, 此时qP和qSV波的复Poynting矢量p1和p2分别为
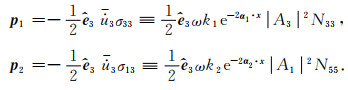
|
(B3) |
联立式(33), (B2)和(B3), 复Poynting矢量p1和p2可以分别通过复速度v1和v2表示为
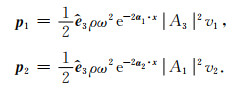
|
(B4) |
利用式(41), 我们可以计算出qP和qSV波的平均动能密度Ev1和Ev2:
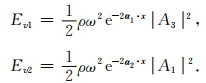
|
(B5) |
根据式(40), qP和qSV波的平均应变能密度Es1和Es2分别表示为
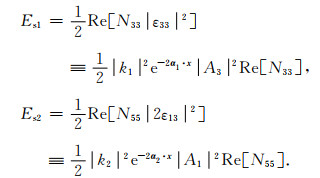
|
(B6) |
结合式(39), (B2), (B5)以及(B6)并利用式(33), 我们可以得到qP和qSV波的平均能量密度:
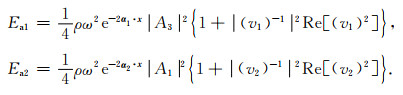
|
(B7) |
根据复数的性质, 式(B7)可以写为
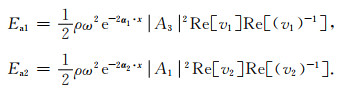
|
(B8) |
将式(B4)和(B8)代入式(37)并利用式(23), 可以计算出在传播角度为0°时qP和qSV波分别对应的能量速度v1e和v2e:
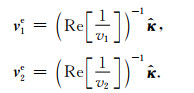
|
(B9) |
对比式(36B)和(B9)可知, 当传播角度为0°时, qP和qSV波的能量速度与相速度将大小相等且方向相同.
传播角度为90°时, qP和qSV波能量速度的计算可以类比得到, 这里不再赘述. 在此情况下, qP和qSV波的能量速度与相速度依然保持大小相等且方向相同的关系.
附录C SH波的能量速度计算由正文分析可知, SH波偏振方向垂直于(x, z)平面, 与qP和qSV波不耦合. 在这种情况下, 偏振向量A=[A1, A2, A3]T的分量只有A2不为0.结合式(15)可知, SH波应变张量ε只有分量ε23和ε12不为0, 且可以表示为
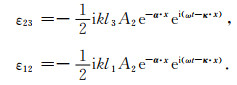
|
(C1) |
对应的SH波应力分量为
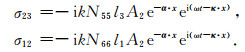
|
(C2) |
根据式(38), (40)和(41), SH波的复Poynting矢量, 平均动能和应变能密度可以分别写为
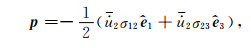
|
(C3) |
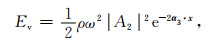
|
(C4) |
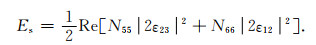
|
(C5) |
类似附录A的分析, 我们可以计算出复Poynting矢量和平均能量密度:
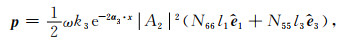
|
(C6) |
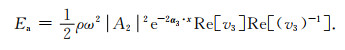
|
(C7) |
结合式(37), SH波能量速度v3e可以表示为
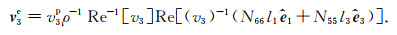
|
(C8) |
Ba J, Lu M H, Hu B, et al. 2008. The skeleton-relaxed model for poroviscoelastic media. Chinese Journal of Geophysics (in Chinese), 51(5): 1527-1537. DOI:10.3321/j.issn:0001-5733.2008.05.027 |
Blangy J P. 1994. AVO in transversely isotropic media-An overview. Geophysics, 59(5): 775-781. DOI:10.1190/1.1443635 |
Caputo M. 1967. Linear models of dissipation whose Q is almost frequency independent-Ⅱ. Geophysical Journal of the Royal Astronomical Society, 13(5): 529-539. DOI:10.1111/j.1365-246X.1967.tb02303.x |
Carcione J M. 1990. Wave propagation in anisotropic linear viscoelastic media: theory and simulated wavefields. Geophysical Journal International, 101(3): 739-750. DOI:10.1111/j.1365-246X.1990.tb05580.x |
Carcione J M. 1992. Anisotropic Q and velocity dispersion of finely layered media. Geophysical Prospecting, 40(7): 761-783. DOI:10.1111/j.1365-2478.1992.tb00551.x |
Carcione J M. 1994. Wavefronts in dissipative anisotropic media. Geophysics, 59(4): 644-657. DOI:10.1190/1.1443624 |
Carcione J M, Cavallini F, Mainardi F, et al. 2002. Time-domain modeling of constant-Q seismic waves using fractional derivatives.//Seismic Waves in Laterally Inhomogeneous Media. Birkhäuser, Basel: Springer, 1719-1736.
|
Carcione J M. 2009. Theory and modeling of constant-Q P-and S-waves using fractional time derivatives. Geophysics, 74(1): T1-T11. DOI:10.1190/1.3008548 |
Chen H M. 2017. Study on numerical simulation of wave equations and viscoacoustic full waveform inversion[Ph. D. thesis] (in Chinese). Beijing: China University of Petroleum (Beijing).
|
Chen W, Holm S. 2004. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. The Journal of the Acoustical Society of America, 115(4): 1424-1430. DOI:10.1121/1.1646399 |
Crampin S, Chesnokov E M, Hipkin R G. 1984. Seismic anisotropy-the state of the art: Ⅱ. Geophysical Journal International, 76(1): 1-16. DOI:10.1111/j.1365-246X.1984.tb05017.x |
Hestholm S. 1999. Three-dimensional finite difference viscoelastic wave modelling including surface topography. Geophysical Journal International, 139(3): 852-878. DOI:10.1046/j.1365-246x.1999.00994.x |
Kjartansson E. 1979. Constant Q-wave propagation and attenuation. Journal of Geophysical Research: Solid Earth, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
Li Q Q, Zhou H, Zhang Q C, et al. 2016. Efficient reverse time migration based on fractional Laplacian viscoacoustic wave equation. Geophysical Journal International, 204(1): 488-504. DOI:10.1093/gji/ggv456 |
Li Q Q, Fu L Y, Zhou H, et al. 2019. Effective Q-compensated reverse time migration using new decoupled fractional Laplacian viscoacoustic wave equation. Geophysics, 84(2): S57-S69. DOI:10.1190/geo2017-0748.1 |
McDonal F J, Angona F A, Mills R L, et al. 1958. Attenuation of shear and compressional waves in Pierre shale. Geophysics, 23(3): 421-439. DOI:10.1190/1.1438489 |
Picotti S, Carcione J M, Santos J E, et al. 2010. Q-anisotropy in finely-layered media. Geophysical Research Letters, 37(6): L06302. DOI:10.1029/2009GL042046 |
Picotti S, Carcione J M, Santos J E. 2012. Oscillatory numerical experiments in finely layered anisotropic viscoelastic media. Computers & Geosciences, 43: 83-89. |
Prasad M, Nur A. 2003. Velocity and attenuation anisotropy in reservoir rocks.//73rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1652-1655.
|
Qiao Z H, Sun C Y, Wu D S. 2019. Theory and modelling of constant-Q viscoelastic anisotropic media using fractional derivative. Geophysical Journal International, 217(2): 798-815. DOI:10.1093/gji/ggz050 |
Robertsson J O A, Blanch J O, Symes W W. 1994. Viscoelastic finite-difference modeling. Geophysics, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
Shi X C, Mao W J, Li X L. 2019. Viscoelastic Q-compensated Gaussian beam migration based on vector-wave imaging. Chinese Journal of Geophysics (in Chinese), 62(4): 1480-1491. DOI:10.6038/cjg2019L0797 |
Thomsen L. 1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
Tsvankin I. 1997. Anisotropic parameters and P-wave velocity for orthorhombic media. Geophysics, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
Wang N, Zhou H, Chen H M, et al. 2018. A constant fractional-order viscoelastic wave equation and its numerical simulation scheme. Geophysics, 83(1): T39-T48. DOI:10.1190/geo2016-0609.1 |
Wang N, Zhu T Y, Zhou H, et al. 2020. Fractional Laplacians viscoacoustic wavefield modeling with k-space-based time-stepping error compensating scheme. Geophysics, 85(1): T1-T13. DOI:10.1190/geo2019-0151.1 |
Wu Y, Fu L Y, Chen G X. 2017. Forward modeling and reverse time migration of viscoacoustic media using decoupled fractional Laplacians. Chinese Journal of Geophysics (in Chinese), 60(4): 1527-1537. DOI:10.6038/cjg20170425 |
Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media. Chinese Journal of Geophysics (in Chinese), 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
Yang R H, Mao W J, Chang X. 2015. An efficient seismic modeling in viscoelastic isotropic media. Geophysics, 80(1): T63-T81. DOI:10.1190/geo2013-0439.1 |
Zhao H B, Chen B J, Li K Z, et al. 2011. VSP record numerical modeling in viscoelastic media and its application in the study of Q-value estimation method. Chinese Journal of Geophysics (in Chinese), 54(2): 329-335. DOI:10.3969/j.issn.0001-5733.2011.02.008 |
Zhu T Y, Carcione J M, Harris J M. 2013. Approximating constant-Q seismic propagation in the time domain. Geophysical Prospecting, 61(5): 931-940. DOI:10.1111/1365-2478.12044 |
Zhu T Y, Harris J M. 2014. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians. Geophysics, 79(3): T105-T116. DOI:10.1190/geo2013-0245.1 |
Zhu T Y, Carcione J M. 2014. Theory and modelling of constant-Q P-and S-waves using fractional spatial derivatives. Geophysical Journal International, 196(3): 1787-1795. DOI:10.1093/gji/ggt483 |
Zhu Y P, Tsvankin I. 2006. Plane-wave propagation in attenuative transversely isotropic media. Geophysics, 71(2): T17-T30. DOI:10.1190/1.2187792 |
Zhu Y P, Tsvankin I. 2007. Plane-wave attenuation anisotropy in orthorhombic media. Geophysics, 72(1): D9-D19. DOI:10.1190/1.2387137 |
巴晶, 卢明辉, 胡彬, 等. 2008. 黏弹双相介质中的松弛骨架模型. 地球物理学报, 51(5): 1527-1537. DOI:10.3321/j.issn:0001-5733.2008.05.027 |
陈汉明. 2017. 波动方程数值模拟与粘滞波形反演方法研究[博士论文]. 北京: 中国石油大学(北京).
|
石星辰, 毛伟建, 栗学磊. 2019. 矢量黏弹性衰减补偿高斯束偏移. 地球物理学报, 62(4): 1480-1491. DOI:10.6038/cjg2019L0797 |
吴玉, 符力耘, 陈高祥. 2017. 基于分数阶拉普拉斯算子解耦的黏声介质地震正演模拟与逆时偏移. 地球物理学报, 60(4): 1527-1537. DOI:10.6038/cjg20170425 |
严红勇, 刘洋. 2012. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟. 地球物理学报, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
赵海波, 陈百军, 李奎周, 等. 2011. 黏弹性介质VSP记录模拟及在估算Q值研究中应用. 地球物理学报, 54(2): 329-335. DOI:10.3969/j.issn.0001-5733.2011.02.008 |
 2021, Vol. 64
2021, Vol. 64


