岩石的核磁共振(NMR)弛豫性质分析在孔隙度、孔隙结构、渗透率、润湿性、流体饱和度及黏度等岩石物理参数评价方面发挥着重要作用(Coates et al., 1999;邓克俊和谢然红,2010;Wang et al., 2018;Liang et al., 2019;王迪等,2019;党海龙等,2020;王香增等,2020).核磁共振弛豫信号是由流体的分子动力学和所处的物理化学环境共同决定.在连通的孔隙中,流体分子的布朗运动会导致其所处的环境发生变化,这种变化会反映在核磁共振弛豫信号上.因此,只要通过一定的脉冲序列和量子相干,基于核磁共振技术就可以得到孔隙的连通性信息.目前,利用核磁共振评价孔隙连通性有两种方法:一种是Song等(2000)提出通过探测孔隙内部梯度磁场的分布(DDIF方法)得到孔隙尺寸分布,结合压汞实验的孔喉分布,评价孔隙连通性.Zhang等(2018)利用DDIF方法结合CPMG测量弛豫信息,获取多孔介质的孔隙尺寸,评价样品的非均质性.但是,DDIF方法的应用存在一定门槛.首先要求外部磁场较高并且非常均匀;其次,该方法是基于曲线形态的差异定性分析,无法定量评价孔隙连通性.第二种方法是通过探测孔隙间的扩散耦合现象,得到孔隙中流体分子的弛豫交换速率,以此表征孔隙的连通性.主要思路分两种:一种是分析扩散耦合对一维T2谱形态的影响.一些学者通过建立含大孔和小孔(Ramakrishnan et al., 1999)或含裂缝和基质孔(Chi and Heidari, 2015)的数字岩心模型,运用数值模拟的方法得到岩石的核磁共振响应特征,证实了不同尺度的连通孔隙间存在扩散耦合现象.Anand和Hirasaki(2007)、Anand等(2008)通过实验分析发现温度升高会加剧孔隙的扩散耦合程度,岩石内部黏土的赋存状态不同会产生不同程度的扩散耦合现象.这类方法的缺点是无法直接得到孔隙流体的弛豫交换速率,很难建立起与连通性的定量关系;第二种是基于二维核磁共振方法观测扩散耦合现象,定量计算弛豫交换速率.Lee等(1993)最早提出利用拉普拉斯变换方法反演得到二维的横向弛豫时间谱,观测到玻璃状聚合物的弛豫交换现象.McDonald等(2005)首次设计出T2-T2脉冲序列(REXSY),用该方法成功观测到水泥的弛豫交换现象,实验证实只要流体分子在测量期时的孔隙尺寸环境发生变化,在二维谱上就会出现非对角峰.之后,一些学者陆续将其应用到砂岩(Washburn and Callaghan, 2006)、碳酸盐岩(Fleury and Soualem, 2009)、生物膜(Codd et al., 2011)等存在多尺度孔隙特征的天然样品的扩散耦合现象的测量分析中.Schwartz等(2013)、Johnson和Schwartz (2014)基于Ramakrishnan等(1999)建立的双重孔隙数字岩心模型,运用数值模拟的方法得到了岩石的T2-T2二维谱,结合双孔弛豫交换模型的解析公式,分析弛豫交换速率与混合时间的相关性.Song等(2016)提出一种基于时域的数据处理方法分析孔隙扩散耦合现象,避免了常规反演的不确定性.Yu等(2019)基于T2-T2脉冲序列提出一种直接表征多孔介质平均孔径的方法,能够有效地提取不满足快扩散条件下的孔隙尺寸,有望提升碳酸盐岩孔径表征的准确性.
针对存在多尺度孔隙的岩石,特别是碳酸盐岩,受到沉积环境和成岩作用的影响,储层具有强非均质性,孔隙结构复杂多样,常常表现出微裂缝、粒间孔、粒内孔和溶蚀孔洞同时发育的特点,孔隙的特征尺寸从几十纳米到几厘米不等.在这种复杂的多尺度孔隙结构背景下,流体分子在孔隙间的核磁共振弛豫交换会产生显著的扩散耦合现象.因此,充分挖掘岩石的核磁共振扩散耦合现象与孔隙连通性之间的关系,对于深入认识复杂孔隙结构对渗透率、有效孔隙度等岩石物理参数的影响具有重要意义.目前,利用核磁共振评价孔隙连通性还处于早期探索阶段,一些学者尝试将非对角峰强度与混合时间ts建立关系,给出了耦合参数或者弛豫交换速率的定义.但是,关于非对角峰能量与混合时间ts的定量关系仍然存在争议.本文的主要目的有两点:(1)基于双孔弛豫交换模型和多尺度孔隙数字岩石模型,分析T2-T2脉冲序列作用下非对角峰产生机制及影响因素;(2)计算表征孔隙间扩散耦合强度的弛豫交换速率,分析扩散耦合与孔隙连通性的相关性,为后续建立扩散耦合参数与孔隙连通性及渗透率之间的定量关系作铺垫工作.
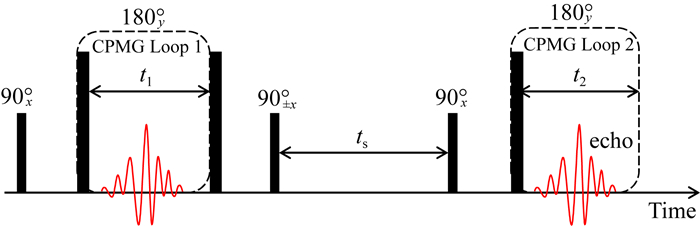
1 核磁共振扩散耦合探测原理 1.1 脉冲序列及其探测原理利用T2-T2脉冲序列测量扩散耦合现象.如图 1所示,序列由三部分组成,第一部分及第三部分为CPMG脉冲序列,第二部分为一个90°射频脉冲.基于Torrey-Bloch方程(Bloch, 1946;Torrey, 1956)推导T2-T2脉冲序列的磁化矢量演化过程,说明测量原理.
|
图 1 T2-T2脉冲序列 Fig. 1 T2-T2 pulse sequence |
磁化矢量的变化受到流体分子扩散和分子与孔隙-骨架接触面碰撞导致能量吸收的共同作用.在孔隙流体和固体颗粒表面之间满足部分吸收边界条件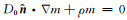

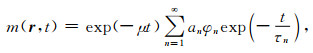
|
(1) |
其中, μ为体弛豫速率,φn为特征函数,τn为特征值.根据本征模的正交性,本征模系数an可表示为:
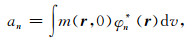
|
(2) |
对整个孔隙空间进行积分,得到总的磁化强度为:
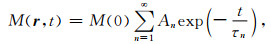
|
(3) |
其中,An为不同弛豫模态的相对强度.当T2-T2脉冲序列测量时,磁化矢量先后经历编辑期t1、混合期ts及测量期t2等三个过程.假设编辑前流体分子已经完全极化,在第一阶段编辑期t1内,孔隙流体经历横向弛豫过程,磁化强度为:
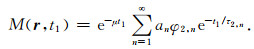
|
(4) |
第二阶段为混合期ts, 该时期施加另一个90°射频脉冲将磁化矢量搬转到纵向平面,在混合时间ts内,磁化矢量经历纵向弛豫T1过程.第三阶段为测量期t2,该部分的CPMG序列将采集记录回波信号,磁化强度的演化为:
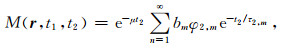
|
(5) |
其中:
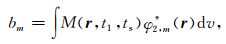
|
(6) |
使用量子力学中的bra-ket符号〈|〉将标量积定义为:
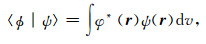
|
(7) |
信号
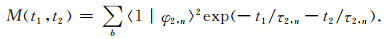
|
(8) |
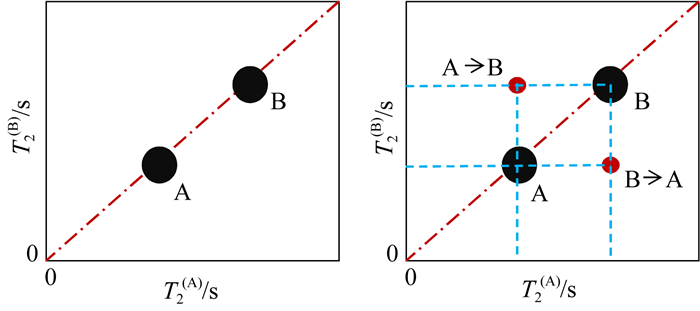
采集二维数据时,根据样品特征,设定好混合时间ts、回波间隔TE,以及测量期的180°射频脉冲个数m后,通过改变编辑期CPMG的180°射频脉冲个数n,循环测量,得到n个信号长度为m的回波串数据.采取SVD方法压缩数据,BRD方法反演回波串数据(程晶晶等,2014),得到T2(A)-T2(B)二维谱,如图 2所示,当不发生扩散耦合时,T2(A)-T2(B)二维谱只会出现与孔隙尺寸对应的对角峰,如果在测量过程中,流体分子扩散进入了不同的孔隙环境,则会出现非对角峰.在孔隙连通性确定的情况下,非对角峰的强度与混合时间有关,因此,通过改变混合时间的长短,得到非对角峰能量的变化趋势,可以计算弛豫交换速率,进而分析孔隙连通性和渗透性.
|
图 2 T2-T2谱示意图 Fig. 2 Sketch map of T2-T2 spectra |
孔隙介质中流体的横向弛豫T2包括表面弛豫、扩散弛豫和体弛豫三部分.总的磁化强度M(t)随时间的变化可表示为(Toumelin et al., 2007; 邹友龙等,2015;郭江峰等,2016):
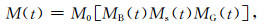
|
(9) |
式中M0为初始磁化强度,MB(t)、MS(t)、MG(t)分别代表t时刻与体弛豫、表面弛豫和扩散弛豫相关的磁化矢量信号强度.
采用随机游走(Random Walk)方法模拟大量自旋粒子在受限空间内的布朗运动求解扩散方程(1).模型假设孔隙中饱和水,背景磁场为均匀场,回波间隔较小,可忽略扩散弛豫项MG(t)的影响.由公式(9)可知,总的磁化矢量随时间t的变化可通过模拟表面弛豫和体弛豫的信号衰减进行表征.
初始时,随机在孔隙空间内分布大量游走粒子, 假设所有粒子均完全极化.设定粒子的游走步长为ε,其对应的时间步长为:

|
(10) |
其中,D0为流体的自由扩散系数,反映流体的布朗运动.设粒子的位置坐标为R=(xold, yold, zold)经过时间步长Δt后,粒子的新位置为:
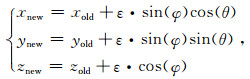
|
(11) |
其中,φ的取值范围为[0,π],θ的取值范围为[0,2π],在范围内随机取值,确保粒子运动的随机性.
粒子在扩散过程中,会不断地和孔隙与骨架的界面发生碰撞,磁化矢量会被界面部分吸收,该过程造成的衰减代表公式(9)中的表面弛豫MS(t)的变化,也指边界条件.磁化矢量被吸收的强度与表面弛豫率ρ的大小有关.通常有两种模拟算法,一种是粒子以一定的概率被“杀死”,若没被杀死,则粒径反弹回原位置或镜像对应位置,反弹的概率可表示为:
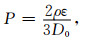
|
(12) |
在数据采集过程中,通过计算时刻t没被“杀死”的粒子数与初始状态时的粒子总数的比值来表征表面弛豫过程产生的磁化矢量信号的衰减.
另一种则不“杀死”,而是认为只要粒子碰到边界,磁化矢量就会衰减,衰减速率由与表面弛豫率ρ有关的指数函数给出,表面弛豫时间T2s可以由经验公式给出:

|
(13) |
体弛豫产生的信号衰减与孔隙结构无关,只受流体本身性质的影响,温度一定时,水的体弛豫时间T2B是固定值,本文设定为3.0 s.模拟过程中,通过乘以一个与T2B相关的指数衰减项就可表征体弛豫MB(t)造成的信号衰减.
1.3 扩散耦合模型建立基于T2-T2脉冲序列的探测原理,分别建立两种模型:第一个是双孔弛豫交换模型(Two-site Relaxation Exchange Model),该模型由Zimmerman和Brittin(1957)以及McConnell(1958)提出,模型假设孔隙间是孤立的,满足快扩散条件,单个孔隙只表现出一种弛豫模态,所以,基于该模型的T2(A)-T2(B)二维谱模拟结果等效于理想状态下的解析解结果.实际上,针对天然的多孔介质,受孔隙结构或者内部磁场梯度等因素影响,单个孔隙可能会出现多种弛豫模态,非对角峰的影响因素更加复杂.因此,为更加真实地反映天然多孔介质的扩散耦合现象,使结果更具一般性,本文引入第二种模型,即Micro-Grain Consolidation模型(简称μGC模型),该模型具有三维的孔隙结构特征,最早由Schwartz(1990)、Ramakrishnan等(1999)建立,将其等效为碳酸盐岩中大孔隙和小孔隙共存的简化的数字岩石模型,用来研究碳酸盐岩粒间孔和粒内孔之间扩散耦合对T2谱的影响.本文通过两种模型的交叉验证,分析非对角峰信号产生机制及影响因素,为定量评价扩散耦合强度奠定理论基础.
μGC模型如图 3所示,是具有双峰孔径分布特征的三维模型,模型大小设置为300 μm×300 μm×300 μm.采用实体球的空间堆积产生,实体的球形颗粒半径为7.5 μm,图中白色小圆点所示.通过均匀排列堆积实体的球形颗粒,形成一个立方体,这样球形颗粒之间产生小尺寸孔隙,图中黑色小圆点所示.为形成另外一种大尺寸孔隙,设置8组球心在立方体顶点,半径为175 μm的大球,通过空间集合运算,保留大球范围内的小球形颗粒,舍弃范围外的小球形颗粒,得到立方体中心的大尺寸孔隙,图中间黑色斑块部分.建模主要参数设置如表 1所示.

|
图 3 μGC模型及其切片(黑色为孔隙,白色为骨架) Fig. 3 μGC model and its slice(black is pore. white is matrix) |
|
|
表 1 μGC模型参数设置 Table 1 Parameter settings of μGC model |
双孔介质弛豫交换模型是理论模型,只存在两个弛豫模态,公式推导相对简单,可以用解析解方式描述.模型假设满足快扩散条件,即认为孔隙内的磁化矢量总是均匀分布.小孔A的磁化矢量大小为SA,大孔B的磁化矢量大小为SB,初始时,总磁化矢量可表示为:
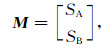
|
(14) |
纵向和横向弛豫衰减速率可分别表示为RA1(2)=1/TA1(2)和RB1(2)=1/TB1(2),在快扩散条件下,磁化矢量的解析表达式为(van Landeghem et al., 2010):
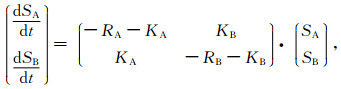
|
(15) |
其中,KA和KB表示孔隙间的等效弛豫交换速率.
假设孔隙A和B的体积分别为VA和VB,当自旋密度SA/VA=SB/VB时,孔隙A到B的弛豫交换量与孔隙B到A的弛豫交换量相等,故可定义弛豫交换速率为:
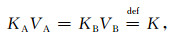
|
(16) |
方程的特征值(Schwartz et al., 2013)可以表示为:
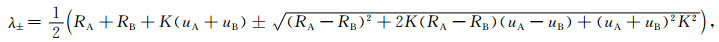
|
(17) |
其中,uA, B=1/VA, B.在弱扩散耦合机制下,即弛豫交换速率K趋近于0时:
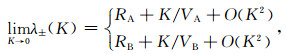
|
(18) |
在强扩散耦合机制下:
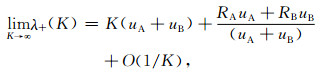
|
(19) |
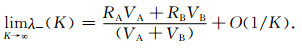
|
(20) |
公式(17)给出了特征值与弛豫交换速率之间的理论关系.公式(18)—(20)分别给出了弱扩散机制和强扩散机制的两个特征值与弛豫交换速率之间的关系.根据特征值与弛豫交换速率之间的关系建立解释图版,通过反演从T2(A)-T2(B)二维谱中得到特征值,在图版中插值就可得到弛豫交换速率.
2 模拟结果分析与讨论实验方案设计:假设μGC模型中所有孔隙空间内饱和水,流体扩散系数D0和表面弛豫率设置见表 1.脉冲序列测量参数设置为:回波间隔TE为0.4 ms,测量期CPMG的180°脉冲数m为3000,编辑期的180°脉冲数n在1到3000内对数取值,共30步,则一次实验形成的二维数据量为30×3000.每次实验,通过改变混合时间ts,得到一组实验数据,反演得到T2(A)-T2(B)二维谱.分别对非对角峰和对角峰信号进行积分,分析峰信号强度与混合时间的相关性,计算弛豫交换速率.根据表 1的μGC模型的相关参数,建立对应的双孔弛豫交换模型,参数设置见表 2,采用公式(15)计算双孔弛豫交换模型的回波串信号,反演得到T2(A)-T2(B)二维谱.通过比较两种模型的结果,阐明T2(A)-T2(B)二维谱中非对角峰产生原因及影响因素,评价数值模拟方法表征扩散耦合强度的可靠性及弛豫交换速率计算的准确性.
|
|
表 2 双孔弛豫交换模型参数设置 Table 2 Parameter settings of two-site model |
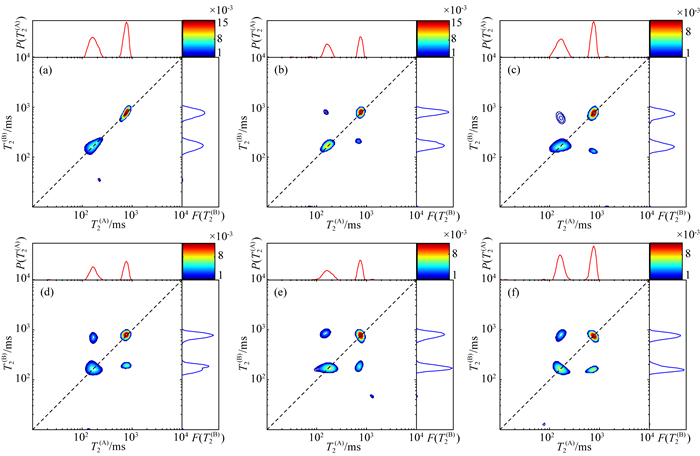
基于μGC模型采取随机游走方法模拟T2-T2脉冲序列作用下的核磁共振响应,如图 4所示,图 4a—f分别代表混合时间为0 ms、100 ms、300 ms、600 ms、800 ms、1000 ms条件下的T2(A)-T2(B)二维谱.在图中对角峰上,位于600~1000 ms之间的长弛豫信号来自大孔隙中水分子的贡献,位于110~220 ms之间的短弛豫信号来自小孔隙中水分子的贡献.当混合时间为0时,T2(A)-T2(B)二维谱上未出现非对角峰,此时孔隙间没有发生弛豫交换;当混合时间增加到100 ms时,出现非对角峰,表明部分大孔隙的水分子扩散进入小孔隙中,为保持物质平衡,同时小孔隙中部分水分子扩散进入大孔隙,所以出现两个对称的非对角峰信号.随着混合时间的不断增加,孔隙间的扩散耦合逐渐增强,非对角峰的强度逐渐增加.图 5是基于双孔弛豫交换模型的T2(A)-T2(B)二维谱,大孔隙的信号位于700~1000 ms之间,小孔隙信号位于120~200 ms之间,处于非对角上的峰值信号随混合时间增加逐渐增强.对比发现,两种方法中,二维谱上大孔和小孔的对角峰所处位置基本一致,非对角峰随混合时间的变化趋势相同,可对比性强,表明应用双孔弛豫交换模型推导的理论公式对比验证数值模拟数据具备可行性.
|
图 4 基于μGC模型的六组混合时间不同的T2(A)-T2(B)二维谱结果 (a) 0 ms;(b) 100 ms;(c) 300 ms;(d) 600 ms;(e) 800 ms;(f) 1000 ms. Fig. 4 T2-T2 maps of μGC model with different mixing time |

|
图 5 基于双孔弛豫交换模型的六组混合时间不同的T2(A)-T2(B)二维谱结果 (a) 0 ms;(b) 100 ms;(c) 300 ms;(d) 600 ms;(e) 800 ms;(f) 1000 ms. Fig. 5 T2-T2 maps of two-site model with different mixing time |
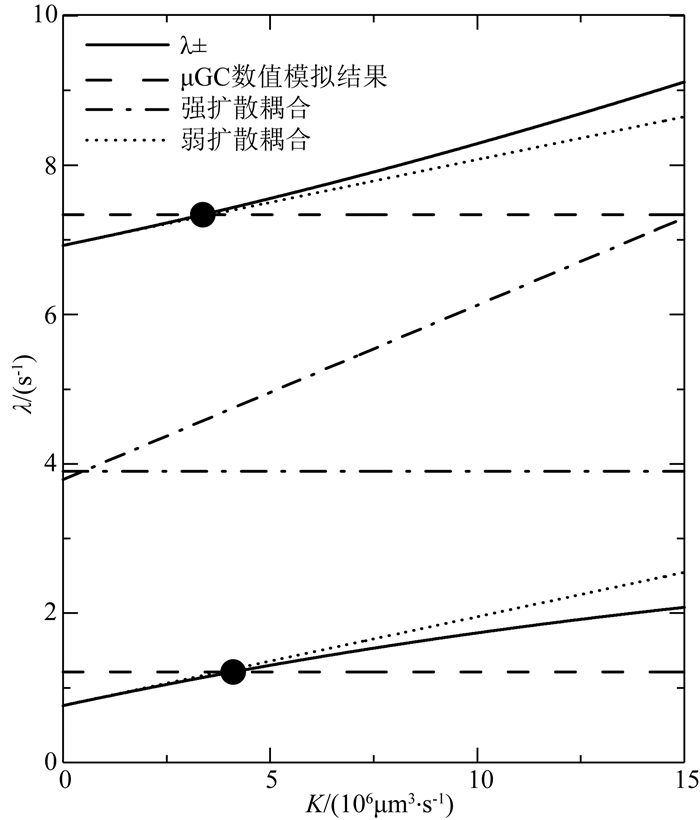
通过公式(17)—(20)建立弛豫交换速率计算图版,如图 6所示,实线由公式(17)计算得到,代表扩散耦合条件下,横向弛豫T2的特征值随弛豫交换速率K的变化趋势;短点线代表弱扩散机制下,由公式(18)得到的特征值与弛豫交换速率K的关系;点划线代表强扩散机制下,由公式(19)和(20)得到的特征值与弛豫交换速率K的关系.解释应用时,首先由μGC模型模拟得到T2(A)-T2(B)二维谱结果(图 4),计算出μGC模型的大、小孔对应的横向弛豫T2的特征值λ1和λ2,然后在图版中纵坐标上读取相应位置,作与横坐标平行的线,得到图中长虚线,长虚线与实线交点位置为插值点,即图中圆点处,将其投影到横坐标,读取μGC模型中大、小孔所对应的弛豫交换速率分别为KA=2.76×106 μm3·s-1和KB=2.09×106 μm3·s-1,为便于计算,取平均值为K=2.43×106 μm3·s-1.基于图版评价,μGC模型的弛豫交换速率值与弱扩散耦合曲线较为接近,更偏向于弱扩散耦合机制.
|
图 6 弛豫交换速率K的计算方法 Fig. 6 Calculation of relaxation exchange rate K |
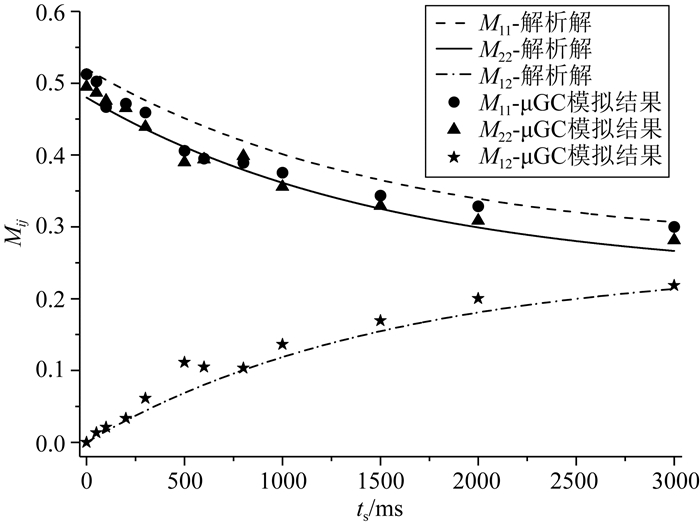
μGC模型的弛豫交换速率K确定后,可基于双孔弛豫交换模型计算出对角峰和非对角峰信号强度随混合时间ts变化的解析解.如图 7所示,连续的线代表解析解,其中,长虚线M11为对角峰上小孔隙信号强度,实线M22为对角峰上大孔隙信号强度,点划线M12为两个非对角峰总的信号强度.对于实际模拟数据,将图 4中T2(A)-T2(B)二维谱的对角峰和非对角峰信号分别进行积分,得到对角峰和非对角峰的信号强度,图中与线对应的点符号代表μGC模型数值模拟结果.当混合时间为0时,非对角峰信号强度M12为0,小、大孔的信号强度M11和M22为0.5左右,随着混合时间增加,M11和M22单调递减,M12单调递增.数值模拟结果与解析解变化趋势一致,符合度较高.通过解析解验证,随机游走算法能够准确模拟多尺度孔隙数字岩心的核磁共振扩散耦合现象.同时,也表明μGC模型的弛豫交换速率计算结果准确可靠.本文提出的弛豫交换速率计算图版简单易用,对于评价具有双尺度孔隙特征岩石的核磁共振扩散耦合现象时,具有一定的推广应用价值.
|
图 7 μGC模型二维峰值强度与混合时间之间的关系 Fig. 7 The relationship between the 2D peak intensities and mixing time of μGC model |
图 7中,相比解析解,数字岩石模型的对角峰强度偏小,非对角峰强度偏大.分析发现,这种趋势一致性的偏差与扩散条件有关.在双孔弛豫交换模型中,假设自旋扩散处于快扩散限制下,自旋密度处处相等.而针对μGC模型,采用随机游走算法模拟水分子的受限扩散时,当表面弛豫率ρ2=10 μm·s-1,D0=2×103 μm2·s-1时,小孔内满足快扩散条件,自旋扩散速度快,自旋密度是均匀分布的;但是,在大孔内,ρ2a/D0≈0.5(a为孔隙的特征半径),不满足快扩散条件,同一个孔隙内,M(t)包括多种衰减模式.T2-T2脉冲序列测量时,在编辑时期t1,由于表面弛豫的影响,大孔处的自旋密度分布不均匀,孔隙中心处自旋密度较大,靠近固-液界面处自旋密度较小.在混合时期ts,分子通过扩散会使得自旋密度的分布更加均匀,这种孔隙内的扩散平均效应导致M(r, t1)和M(r, t1+ts)的特征函数不同,该不同会对T2(A)-T2(B)二维谱的非对角峰的信号强度产生影响.
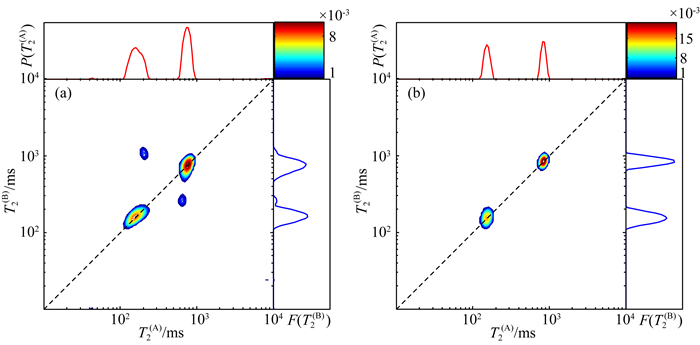
为此,设计一组实验验证上述分析.通过实验控制混合时期内孔隙间不连通,即不发生扩散耦合作用. 针对μGC模型,给大孔和小孔界面设置一层非渗透性的隔膜,阻止孔隙之间的分子扩散.针对双孔弛豫交换模型,通过设置弛豫交换速率K的值实现(设置K=0).保持其他实验条件不变,模拟混合时间ts为300 ms时的T2(A)-T2(B)二维谱.结果见图 8,图 8a是μGC模型的结果,图 8b是双孔弛豫交换模型的结果,从T2(A)-T2(B)二维谱可以发现,当混合时期扩散耦合通道关闭时,双孔弛豫交换模型中只有对角峰,而μGC模型中仍然出现非对角峰.结果表明,μGC模型中的非对角峰与混合时期的扩散耦合作用无关.
|
图 8 扩散耦合通道关闭时的T2(A)-T2(B)二维谱 (a) μGC模型;(b) 双孔弛豫交换模型. Fig. 8 T2-T2 maps when the diffusional coupling channels closed (a) μGC model; (b) Two-site model. |
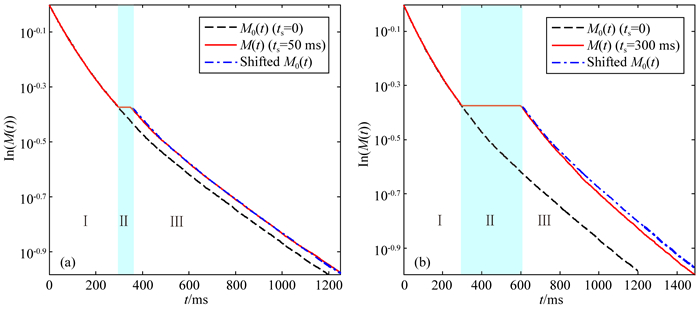
进一步分析μGC模型中非对角峰产生原因,保持上述实验条件不变,考察在T2-T2脉冲序列作用整个过程中磁化矢量的演化.分别模拟混合时间ts为0 ms、50 ms、300 ms的回波串信号,如果在混合期过后,磁化矢量发生额外衰减,则证实出现与扩散耦合不相关的扩散平均效应.图 9中长虚线代表混合时间为0的回波信号,实线代表混合时间不为0的回波信号.横折线前为编辑期的回波信号,横折线处为混合期,磁化强度不变.横折线后为测量期,即T2-T2脉冲序列的数据采集期.将测量期的混合时间为0的回波信号平移,使其与混合时间不为0的回波信号在测量期开始处重合(图中点划线),通过对比混合时间不为0的回波信号是否发生额外衰减,验证孔隙内部是否产生扩散平均效应.
|
图 9 不同混合时间的回波串信号对比 Fig. 9 Comparison of echo train signals with different mixing time |
图 9a是ts为50 ms与0 ms的对比图,图 9b是300 ms与0 ms对比图.在编辑期,孔隙流体发生正常的横向弛豫过程,流体分子总的磁化强度不受混合时间长短影响,实线与长虚线重合,衰减速率一样;在混合时期内,由于孔隙间的通道关闭,不会发生扩散耦合,流体分子只在孔隙内部运动,发生孔隙内部的扩散平均效应.由于不考虑纵向弛豫作用,所以该阶段总的磁化强度保持不变;进入测量期时,孔隙流体重新开始横向弛豫过程,ts为300 ms的回波串信号的衰减明显加快,而ts为50 ms的回波串信号衰减不明显.这是因为,相比50 ms, 混合时间为300 ms时,自旋粒子充分扩散,导致整体上大孔内的自旋密度分布更为平均,扩散平均效应更显著.因此,最终导致非对角峰的信号有一部分来自于该部分的贡献,出现对角峰信号比理论值偏小,非对角峰偏大的现象.在孔隙尺度跨度大的岩石中,特别是碳酸盐岩中,部分大孔隙处于慢扩散的范畴,这种情况比较常见,在研究扩散耦合现象时需要注意.
3 碳酸盐岩实例采用基于沉积过程的数字岩石建模方法(田志等,2019)建立含多尺度孔隙特征的碳酸盐岩数字岩石模型,探索不同尺度孔隙间的扩散耦合现象,分析其对NMR横向弛豫分布测量的影响,评价孔隙连通性.该建模方法通过模拟矿物颗粒在重力、内摩擦力及浮力等作用下发生沉积作用,建立微观尺度数字岩石模型.建模过程中,采取粒径分布为双峰特征的矿物颗粒模拟地层的沉积过程,粒径范围为40~110 μm,初始沉积完成后,进行压实和随机溶蚀算法处理,处理后部分区域发育较大尺度的溶蚀孔,同时采取自仿射分形插值算法模拟裂缝的形成,在模型中加入部分微裂缝,最后对数据体离散化,形成碳酸盐岩数字岩石模型(图 10),图中浅色代表固体骨架,黑色部分代表孔隙空间,包括微裂缝、粒间小孔、溶蚀大孔等三种类型孔隙,总孔隙度为20.8%.从图 11a的一维T2谱可以看出,孔径分布具有多峰特征,微裂缝的孔隙度较小,粒间孔和溶蚀孔的孔隙度相当.

|
图 10 碳酸盐岩数字岩石模型 Fig. 10 Digital rock model of carbonate rock |
|
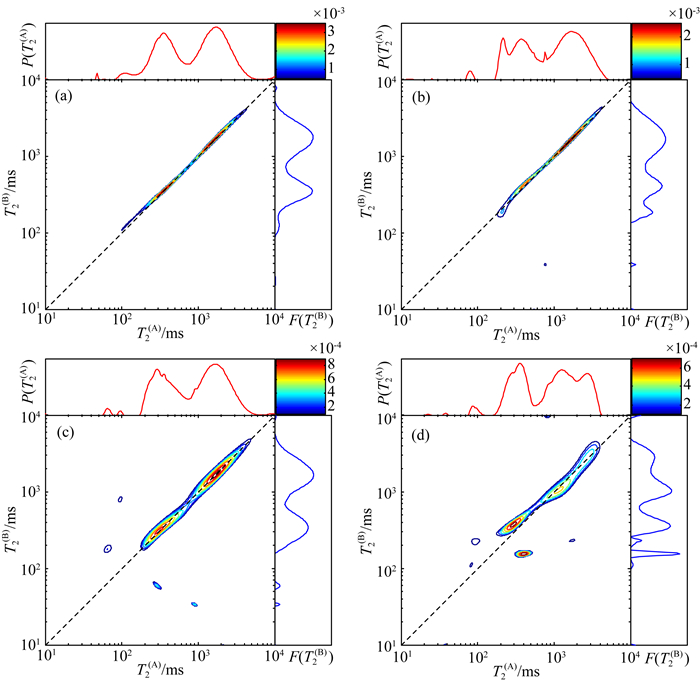
图 11 碳酸盐岩数字岩心模型的四组混合时间不同的T2(A)-T2(B)二维谱结果 (a) 0 ms;(b) 100 ms;(c) 200 ms;(d) 300 ms. Fig. 11 T2(A)-T2(B) maps of carbonate rock model with different mixing time |
实验方案设计:假设碳酸盐岩饱和水,扩散系数为D0=2×103 μm2·s-1.回波间隔TE为0.4 ms,测量期的180°脉冲个数为3000个,记录的回波个数NE也为3000个,为满足二维核磁谱的测量要求,第一阶段的180°脉冲个数在3~3000范围内对数采样30组.采用随机游走算法,依次模拟混合时间ts为0 ms、100 ms、200 ms、300 ms的T2(A)-T2(B)二维谱.
图 11是反演结果,从一维T2谱上看,微裂缝的信号位于120 ms附近,粒间小孔的信号位于350 ms附近,溶蚀大孔的信号位于2000 ms附近.当ts为0时,T2(A)-T2(B)二维谱上所有的峰均位于对角线上,不存在任何的非对角峰,说明此时不同尺度孔隙之间未发生水分子交换;当ts为100 ms时,信号依旧集中在对角线上,但是峰的能量表现出略微展宽的现象,此时已经出现轻度扩散耦合现象,不同尺度孔隙之间发生了水分子的交换,但是交换量比较小;当ts增加到200 ms和300 ms时,对角峰的能量进一步减弱,非对角峰的能量显著增强,表现出十分明显的扩散耦合现象.从T2(A)-T2(B)二维谱的变化趋势上看,代表微裂缝和小孔的短弛豫部分的对角峰强度减少的十分显著,非对角峰的增加量也相对较大,说明微裂缝和小孔隙之间的水分子的交换比较充分,连通性更好,大孔中的对角峰的能量也存在一定的损失,体现出大孔和小孔存在一定的连通性.另外,对连通性较好多孔介质,扩散耦合现象会对T2谱的分布造成一定的影响,随着混合时间的增加,图中碳酸盐岩的一维T2谱发生畸变的程度越来越高.
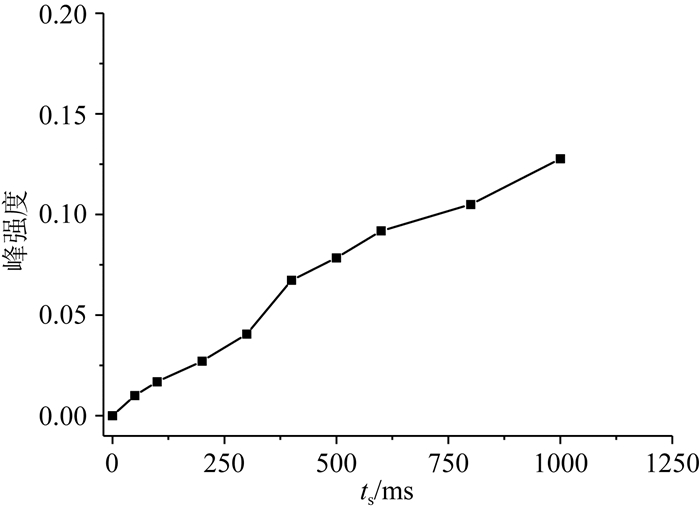
由于该模型的孔径分布十分连续,所以对角峰与非对角峰无法显著分开,给定量解释造成一定困难.当混合时间ts为0时,不发生扩散耦合,将其作为数据解释模板,认为处于该区域范围内的能量代表对角峰信号.通过与之对比,当混合时间不为0时,统计T2(A)-T2(B)二维谱上处于该范围外的信号量,代表非对角峰信号强度.如图 12所示,得到非对角峰信号强度与混合时间的关系.随混合时间增加,非对角峰的能量逐渐增加,扩散耦合的现象比较明显,证实该碳酸盐岩数字岩石模型不同尺度孔隙间的连通性较好.由于碳酸盐岩孔隙尺度跨度大,存在多个弛豫模态,应用双孔弛豫交换模型计算弛豫交换速率适用效果一般,定量评价连通性还存在瓶颈.针对该情况,后续研究中,探索适用于多弛豫模态的弛豫交换速率计算模型,建立针对复杂孔隙结构的连通性定量评价方法将是重点攻关方向.
|
图 12 碳酸盐岩模型二维非对角峰值强度与混合时间之间的关系 Fig. 12 The relationship between the intensities of 2D non-diagonal peaks and mixing time of the carbonate rock model |
结果表明,T2-T2脉冲序列可以定量评价多尺度孔隙介质的扩散耦合现象.通过理论推导、数值模拟验证得到如下结论:
(1) 针对双尺度孔隙岩石模型,孔隙间的扩散耦合强度与混合时间呈正相关性,本文提出的弛豫交换速率计算图版评价扩散耦合强度准确可靠,具有一定的推广应用价值.
(2) 当孔隙尺寸不满足快扩散条件时,自旋密度分布不均匀会导致T2(A)-T2(B)二维谱中对角峰强度偏小,非对角峰强度偏大,该现象来自于大孔隙内的扩散平均效应,与扩散耦合无关,在解释应用时需要注意.
(3) 针对孔隙尺寸跨度大的碳酸盐岩模型,模拟结果表明微裂缝、小孔隙和大孔隙之间均存在扩散耦合现象.随混合时间的增加,代表不同类型孔隙的弛豫组分在T2-T2二维谱上信号能量的变化趋势不同,同时T2谱的分布形态畸变程度加重,反映了孔隙间的连通性.
本文提出的T2-T2二维谱数据解释方法对孔隙尺寸差异显著的双尺度孔隙岩石应用效果较好,对孔径连续分布或孔隙尺寸差异较小的岩石,定量计算弛豫交换速率存在一定困难.后续研究工作,将针对实际岩心设计实验,改进数据的解释方法,有效地提取扩散耦合信息,进一步探索弛豫交换强度与孔隙连通性及岩心渗透率之间的定量关系.
致谢 感谢两位匿名评审专家的宝贵意见!
Anand V, Hirasaki G J. 2007. Diffusional coupling between micro and macroporosity for NMR relaxation in sandstones and grainstones. Petrophysics, 48(4): 289-307. |
Anand V, Hirasaki G J, Fleury M. 2008. NMR diffusional coupling: effects of temperature and clay distribution. Petrophysics, 49(4): 362-372. |
Bloch F. 1946. Nuclear induction. Physical Review, 70(7-8): 460-474. DOI:10.1103/PhysRev.70.460 |
Cheng J J, Wu L, Song G P. 2014. A study of regulation inversion method in 2D NMR logging based on SVD and BRD. Chinese Journal of Geophysics (in Chinese), 57(10): 3453-3465. DOI:10.6038/cjg20141031 |
Chi L, Heidari Z. 2015. Diffusional coupling between microfractures and pore structure and its impact on nuclear magnetic resonance measurements in multiple-porosity systems. Geophysics, 80(1): D31-D42. DOI:10.1190/geo2013-0467.1 |
Coates G R, Xiao L Z, Prammer M G. 1999. NMR Logging Principles and Applications. Texas: Gulf Publishing Company.
|
Codd S L, Vogt S J, Hornemann J A, et al. 2011. NMR relaxation measurements of biofouling in model and geological porous media. Organic Geochemistry, 42(8): 965-971. DOI:10.1016/j.orggeochem.2011.03.014 |
Dang H L, Wang X F, Cui P X, et al. 2020. Research on the characteristics of spontaneous imbibition oil displacement with the low permeability tight-sandstone oil reservoir using the Nuclear Magnetic Resonance (NMR) technology. Progress in Geophysics (in Chinese), 35(5): 1759-1769. DOI:10.6038/pg2020DD0441 |
Deng K J, Xie R H. 2010. NMR Logging Theory and Applications (in Chinese). Dongying: Press of China University of Petroleum.
|
Fleury M, Soualem J. 2009. Quantitative analysis of diffusional pore coupling from T2-store-T2 NMR experiments. Journal of Colloid & Interface Science, 336(1): 250-259. |
Guo J F, Xie R H, Zou Y L. 2016. Simulation of NMR responses in sandstone and restricted diffusion. Chinese Journal of Geophysics (in Chinese), 59(7): 2703-2712. DOI:10.6038/cjg20160733 |
Johnson D L, Schwartz L M. 2014. Analytic theory of two-dimensional NMR in systems with coupled macro- and micro pores. Physical Review E, 90(3-1): 032407. |
Lee J H, Labadie C, Springer C S Jr, et al. 1993. Two-dimensional inverse Laplace transform NMR: altered relaxation times allow detection of exchange correlation. Journal of the American Chemical Society, 115(17): 7761-7764. DOI:10.1021/ja00070a022 |
Liang C, Xiao L Z, Zhou C C, et al. 2019. Two-dimensional nuclear magnetic resonance method for wettability determination of tight sand. Magnetic Resonance Imaging, 56: 144-150. DOI:10.1016/j.mri.2018.09.020 |
McConnell H M. 1958. Reaction rates by nuclear magnetic resonance. Journal of Chemical Physics, 28(3): 430-431. DOI:10.1063/1.1744152 |
McDonald P J, Korb J P, Mitchell J, et al. 2005. Surface relaxation and chemical exchange in hydrating cement pastes: a two-dimensional NMR relaxation study. Physical Review E, 72(1): 011409. DOI:10.1103/PhysRevE.72.011409 |
Ramakrishnan T S, Schwartz L M, Fordham E J, et al. 1999. Forward models for nuclear magnetic resonance in carbonate rocks. Log Analyst, 40(4): 260-270. |
Schwartz L M. 1990. Modeling transport in granular porous media.//SPWLA 31st Annual Logging Symposium Transactions. Lafayette, Louisiana: Society of Petrophysicists and Well-Log Analysts.
|
Schwartz L M, Johnson D L, Mitchell J, et al. 2013. Modeling two-dimensional magnetic resonance measurements in coupled pore systems. Physical Review E, 88(3): 032813. DOI:10.1103/PhysRevE.88.032813 |
Song R B, Song Y Q, Vembusubramanian M, et al. 2016. The robust identification of exchange from T2-T2 time-domain features. Journal of Magnetic Resonance, 265: 164-171. DOI:10.1016/j.jmr.2016.02.001 |
Song Y Q, Ryu S, Sen P N. 2000. Determining multiple length scales in rocks. Nature, 406(6792): 178-181. DOI:10.1038/35018057 |
Tian Z, Xiao L Z, Liao G Z, et al. 2019. Study on digital rock reconstruction method based on sedimentological process. Chinese Journal of Geophysics (in Chinese), 62(1): 248-259. DOI:10.6038/cjg2019L0457 |
Torrey H C. 1956. Bloch equations with diffusion terms. Physical Review, 104(3): 563-565. DOI:10.1103/PhysRev.104.563 |
Toumelin E, Torres-Verdín C, Sun B Q, et al. 2007. Random-walk technique for simulating NMR measurements and 2D NMR maps of porous media with relaxing and permeable boundaries. Journal of Magnetic Resonance, 188(1): 83-96. DOI:10.1016/j.jmr.2007.05.024 |
van Landeghem M, Haber A, De Lacaillerie J B D, et al. 2010. Analysis of multisite 2D relaxation exchange NMR. Concepts in Magnetic Resonance Part A, 36(3): 153-169. |
Wang D, Chen M, Wang J W, et al. 2019. New method of permeability calculation based on classification conversion of T2 spectrum and capillary pressure curves. Progress in Geophysics (in Chinese), 34(5): 1900-1909. DOI:10.6038/pg2019CC0280 |
Wang J, Xiao L Z, Liao G Z, et al. 2018. Theoretical investigation of heterogeneous wettability in porous media using NMR. Scientific Reports, 8: 13450. DOI:10.1038/s41598-018-31803-w |
Wang X Z, Zhao X S, Dang H L, et al. 2020. Research on the characteristics of spontaneous imbibition and displacement of the tight reservoir with the NMR method. Progress in Geophysics (in Chinese), 35(5): 1870-1877. DOI:10.6038/pg2020DD0386 |
Washburn K E, Callaghan P T. 2006. Tracking pore to pore exchange using relaxation exchange spectroscopy. Physical Review Letters, 97(17): 175502. DOI:10.1103/PhysRevLett.97.175502 |
Yu Z, Zhang Y, Xiao L Z, et al. 2019. Characterization of porous media by T2-T2 correlation beyond fast diffusion limit. Magnetic Resonance Imaging, 56: 19-23. DOI:10.1016/j.mri.2018.10.008 |
Zhang Y, Xiao L Z, Liao G Z. 2018. Spatially resolved pore-size-T2 correlations for low-field NMR. Microporous & Mesoporous Materials, 269: 142-147. |
Zimmerman J R, Brittin W E. 1957. Nuclear magnetic resonance studies in multiple phase systems: lifetime of a water molecule in an adsorbing phase on silica gel. Journal of Physical Chemistry, 61(10): 1328-1333. DOI:10.1021/j150556a015 |
Zou Y L, Xie R H, Guo J F, et al. 2015. Reconstruction of digital core of tight reservoir and simulation of NMR response. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 39(6): 63-71. |
程晶晶, 吴磊, 宋公仆. 2014. 基于SVD和BRD的二维核磁共振测井正则化反演算法研究. 地球物理学报, 57(10): 3453-3465. DOI:10.6038/cjg20141031 |
党海龙, 王小锋, 崔鹏兴, 等. 2020. 基于核磁共振技术的低渗透致密砂岩油藏渗吸驱油特征研究. 地球物理学进展, 35(5): 1759-1769. DOI:10.6038/pg2020DD0441 |
邓克俊, 谢然红. 2010. 核磁共振测井理论及应用. 东营: 中国石油大学出版社.
|
郭江峰, 谢然红, 邹友龙. 2016. 砂岩核磁共振响应模拟及受限扩散. 地球物理学报, 59(7): 2703-2712. DOI:10.6038/cjg20160733 |
田志, 肖立志, 廖广志, 等. 2019. 基于沉积过程的数字岩石建模方法研究. 地球物理学报, 62(1): 248-259. DOI:10.6038/cjg2019L0457 |
王迪, 陈敏, 王健伟, 等. 2019. 基于T2和毛管压力分类转换的渗透率计算新方法. 地球物理学进展, 34(5): 1900-1909. DOI:10.6038/pg2019CC0280 |
王香增, 赵习森, 党海龙, 等. 2020. 基于核磁共振的致密油藏自发渗吸及驱替特征研究. 地球物理学进展, 35(5): 1870-1877. DOI:10.6038/pg2020DD0386 |
邹友龙, 谢然红, 郭江峰, 等. 2015. 致密储层数字岩心重构及核磁共振响应模拟. 中国石油大学学报(自然科学版), 39(6): 63-71. DOI:10.3969/j.issn.1673-5005.2015.06.008 |
 2021, Vol. 64
2021, Vol. 64

