2. 中国地质调查局广州海洋地质调查局, 广州 510760;
3. 长春工程学院, 长春 130021
2. Guangzhou Marine Geological Survey, China Geological Survey, Guangzhou 510760, China;
3. Changchun Institute of Technology, Changchun 130021, China
重力探勘具有轻便、快捷、成本低等优点,已经广泛应用于研究地壳内部结构、探明固体矿产和油气资源分布等领域(Last and Kubik, 1983;Guillen and Menichetti, 1984;Li and Oldenburg, 1998;Portniaguine and Zhdanov, 1999;Nabighian et al., 2005;Silva and Barbosa, 2006;Zhdanov,2009;Commer,2011). 随着重力梯度全张量仪(FTG)的问世,人们不仅可以测量重力数据,还可以测量重力梯度数据. 重力数据是通过测量重力位的垂直一阶导数获得,而重力梯度数据是通过测量重力位在三个方向的二阶导数获得. 重力梯度数据包含多个分量信息,每个梯度分量包含的信息量不同,综合利用各个分量信息有助于提高地质解释的准确性(Vasco and Taylor, 1991;Zhdanov et al., 2004;Martinez et al., 2013;陈闫等,2014;耿美霞等,2016;Zhang and Li, 2019).
反演技术是地球物理勘探最为重要的定量解释手段之一,它是通过地球物理异常场反推地下场源的空间分布情况,提供目标地质构造的物性和几何形态等特征信息.在频率域中重力数据包含更多的低频信息,对反映深层异常体细节方面具有更高的分辨率,而重力梯度数据包含更多的高频信息,对反映浅层异常体细节方面具有更高的分辨率.根据两种数据各自的特点,结合两种数据共同进行反演计算,势必会降低反演多解性和提高地质解释的可信性.Wu等(2013)将重力和重力梯度数据结合起来,通过自适应权值估计物体的质量、方向和距离.Capriotti和Li(2014)针对重力和重力梯度数据核函数随深度衰减速率不同的情况,在模型平滑约束项中加入权重平衡两种衰减速率,实现了重力和重力梯度数据的平滑联合反演.秦朋波和黄大年(2016)采用一种空间深度加权函数,用来克服重力和重力梯度数据的趋肤效应,并通过有限内存BFGS拟牛顿法求解重力和重力梯度数据的联合反演.Qin等(2016)采用非线性共轭梯度法对重力和重力梯度数据开展联合反演研究,并将该算法应用到美国墨西哥湾海岸盐丘调查中.李红蕾等(2017)提出了一种数据加权矩阵,实现了最小二乘迭代法的重力和重力梯度数据联合反演,并应用到青藏高原及邻区岩石圈三维密度结构预测中.高秀鹤等(2019)采用阈值约束的协克里金法对重力和重力梯度数据进行了联合反演研究.根据上述研究发现,目前重力和重力梯度联合反演算法仍存在以下几点问题,首先,采用平滑约束模型矩阵得到的反演结果过于模糊发散,不能很好地恢复出真实模型的尖锐边界;然后,引入依赖先验信息的深度加权函数,需要人为经验来确定参数变量的大小,具有一定的不确定性;其次,采用传统的最小二乘迭代法需要计算和存储灵敏度矩阵,尤其在三维大数据情况下,灵敏度矩阵会占用大量的内存空间,而共轭梯度法会出现连续搜索小步长的现象,增加反演的迭代次数,从而降低反演的计算效率.最后,在模型空间下求解三维联合反演时,求解的线性方程组维度较大,势必会增加大量的计算时间和内存消耗量,并对计算机的性能提出挑战.
针对上述问题,本文提出了基于数据空间和稀疏约束的重力和重力梯度数据联合反演算法.首先,我们从基于几何格架的重力快速正演算法出发,推导出多分量重力梯度数据的快速正演算法.然后,构建了重力和重力梯度数据联合反演目标函数,目标函数中包含了重力和重力梯度数据拟合项、L0范数正则化模型约束项,模型约束项中摒弃了依赖先验信息的深度加权函数,引入了自适应模型积分灵敏度矩阵来克服趋肤效应.其次,将模型计算从模型空间通过恒等式转换到数据空间下,采用一种改进的共轭梯度算法进行反演求解,可以降低反演求解方程的维度和避免存储大型的灵敏度矩阵.最后,通过模型试算和实测数据验证本文提出算法的准确性和有效性.
1 快速正演计算理论将地下目标空间划分为一系列大小相同的长方体网格单元,且每个长方体单元的密度均匀, 此时地表重力数据或重力梯度张量数据与地下密度分布可以表示为如下线性关系:
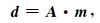
|
(1) |
其中:d为重力或重力梯度数据;A为重力数据或重力梯度数据的正演核函数,是一个Nd×Nm的矩阵,其中Nd为观测点个数,Nm为地下模型网格剖分个数;m为网格单元的剩余密度.
重力或重力梯度正演计算需要完成的积分次数为Nd×Nm,当地下网格剖分过大时,正演计算将面临巨大的挑战.为了提高正演的计算效率,本文采用姚长利等(2003)提出的几何格架的快速计算策略,通过分析地下模型单元与观测点之间的位置关系,可以发现同一层各模型单元与观测点之间的相对位置关系存在等价性,利用这个等价关系,只对每一层第一个模型单元进行几何格架核函数计算,得到该单元的核函数矩阵,而该层其他模型单元的核函数矩阵可以通过几何格架的等效性进行查找获得.通过上述方法,原本反演过程中需要多次重复进行的正演计算就变成了物性参数与对应的几何格架之间简单的乘积运算,每层模型单元只计算第一个模型单元,从而大大的提高了正演的计算效率.具体思想如下:
地下模型均匀剖分,观测点位于模型单元中心正上方的地表处,如图 1所示.假设地表观测面上任意一个观测点p(u, v)(u=1, 2, 3, …, Nx; v=1, 2, 3, …, Ny,Nx和Ny分别为x轴和y轴方向上的观测点个数)与地下第kk层模型单元Qkk(u, v)对应(kk=1, 2, 3, …, L,L为地下模型的层数).首先需要求取第kk层第一个模型单元Qkk(1, 1)在观测点p(u, v)处的几何格架核矩阵Akk(1, 1, u, v),然后根据几何格架的平移等效性、对称互换性可以得到第kk层其他模型单元Qkk(i, j)(i=1, 2, 3, …, Nx; j=1, 2, 3, …, Ny)在观测点p(u, v)处的几何格架核函数矩阵Akk(i, j, u, v).

|
(2) |
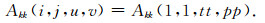
|
(3) |

|
图 1 三维模型网格剖分图 Fig. 1 3D model meshing |
为了简约起见,将公式(3)改写为一维列向量:
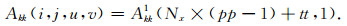
|
(4) |
上述几何格架计算策略仅适用于重力的核函数计算,而将上述方法应用到重力梯度多分量时,非对角线重力梯度分量(Vxy, Vzy, Vzx)将得不到正确的核函数矩阵.通过实验模拟分析,模型单元的位置与观测点的位置处于特殊关系时,公式(4)将不再成立.我们将几何格架等效关系式进行修改, 重力梯度非对角线分量的几何格架关系式可表示为:
对于分量Vzx:
if u<i,
Akk(i, j, u, v)=-Akk1(Nx×(pp-1)+tt, 1)
else Akk(i, j, u, v)=Akk1(Nx×(pp-1)+tt, 1)
end
对于分量Vzy:
if v<j,
Akk(i, j, u, v)=-Akk1(Nx×(pp-1)+tt, 1)
else Akk(i, j, u, v)=Akk1(Nx×(pp-1)+tt, 1)
end
对于分量Vxy:
if u<i‖v<j
if u<i && v<j,
Akk(i, j, k, l)=-Akk1(Nx×(pp-1)+tt, 1)
else Akk(i, j, u, v)=-Akk1(Nx×(pp-1)+tt, 1)
end
else Akk(i, j, u, v)=Akk1(Nx×(pp-1)+tt, 1)
end
2 反演计算理论 2.1 目标函数为了避免因求解病态反问题所引起的不稳定性和多解性等问题,本文采用Tikhonov和Arsenin(1977)正则化方法求解反演线性方程.首先,我们构建重力和重力梯度数据联合反演目标函数,其表达式如下:
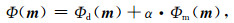
|
(5) |
其中,Φd(m)为数据拟合项,Φm(m)为稳定器构成目标函数中的模型约束项,α为正则化因子.
目标函数中数据拟合项包括两部分,
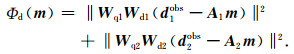
|
(6) |
将数据拟合项进行简化,
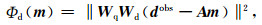
|
(7) |
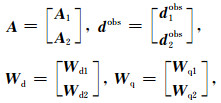
|
(8) |
其中,A1和A2分别表示重力和重力梯度的灵敏度矩阵.d1obs和d2obs分别表示重力和重力梯度观测数据.Wd1和Wd2分别表示重力和重力梯度数据噪声误差对角逆矩阵,没有噪声干扰时,表示单位对角矩阵.Wq1为重力数据加权项,Wq2为重力梯度数据加权项,数据加权项能够改善不同种类数据的拟合问题.
L0范数正则化模型约束项的表达式如下:
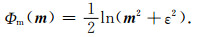
|
(9) |
求解公式(9)可以将L0范数最小化近似为迭代重加权L2范数最小化问题(Wolke and Schwetlick, 1988).
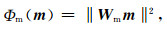
|
(10) |
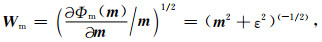
|
(11) |
其中,ε是很小的常数,该参数决定了反演结果的尖锐程度.与传统的平滑反演方法相比,基于稀疏约束的L0范数反演方法可以获得边界更清晰、对比度更强的模型.将L0范数作为模型约束项,目标函数表达式可以表示为:

|
(12) |
其中,mref为参考模型.利用公式(12)求解的反演结果会出现异常体集中在地表的现象,是由于重力和重力梯度数据的核函数随深度增加而衰减,因此会引起反演结果的趋肤效应.为了改善趋肤效应的影响,传统的方法是在模型约束项中加入深度加权函数(Li and Oldenburg, 1996;Commer,2011),但是重力和重力梯度核函数衰减速率不同,采用相同的深度加权函数势必会得到不准确的反演结果,况且深度加权函数中存在未知的变量,需要人为经验来定义变量的大小,具有一定的不确定性和不稳定性.针对上述问题,Zhdanov (2002)提出了模型积分灵敏度矩阵,它可以消除不同模型参数对观测数据的贡献是不同的,观测数据对不同模型参数的积分灵敏度也是不同所带来的影响,使得观测数据对不同模型参数的积分灵敏度变化一致.目前该方法已经应用在重力梯度三维反演中(陈闫,2014;Capriotti and Li, 2014;高秀鹤和黄大年,2017).本文也采用模型积分灵敏度矩阵,用来消除因重力和重力梯度核函数衰减速率不同引起的趋肤效应.因此,仍然是形成一个权重,平衡重力和重力梯度两个核函数衰减速率不同的问题.
首先分析模型参数mk的微扰对数据的影响.观测数据与模型参数变化的关系可表示为:

|
(13) |
数据灵敏度对模型参数mk的积分可表示为:
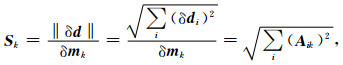
|
(14) |
故模型积分灵敏度矩阵可表示为:
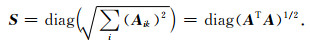
|
(15) |
将式(15)加入到目标函数中,最终得到重力梯度和重力数据联合反演的目标函数表达式如下:
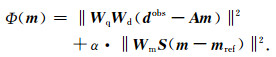
|
(16) |
通常目标函数最优化方法是采用最小二乘法,即目标函数对模型参数的求导为零,得到反演模型结果.但最小二乘法存在一定的缺陷,很容易陷入局部极小,求解不准确,所以一些非线性优化方法经常被使用,例如,牛顿法、梯度法、高斯牛顿法、共轭梯度法等.共轭梯度法对初始模型要求较少,具有存储量小、收敛速度快等优势.传统的共轭梯度法迭代求解过程是在同一个循环内完成,而本文采用内外双循环的迭代过程进行目标函数的求解,该方法可以减少迭代次数,提高计算效率.
2.2.1 传统共轭梯度法反演对目标函数公式(16)求梯度,得到第k次迭代的梯度表达式:
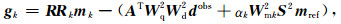
|
(17) |
其中,RRk=ATWq2Wd2A+αkWmk2S2.
准备观测数据dobs,数据加权矩阵Wd,初始模型m0,模型积分灵敏度矩阵S和数据加权项Wq,初始正则化参数α0.
计算目标函数初始梯度g0和RR0;
计算初始搜索方向:d0=g0;计算初始搜索步长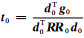
While k<k_max或misfit<σ
k=k+1;
更新模型参数:mk=mk-1-tk-1dk-1;
计算数据拟合差:
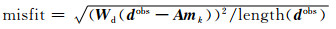
|
计算目标函数对模型mk的梯度gk和RRk;
计算第k次迭代的搜索方向:dk=gk+βkdk-1,βk=gkTgk/gk-1Tgk-1
计算第k次迭代的搜索步长: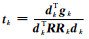
end While
输出mk.
2.2.2 改进的共轭梯度法反演对目标函数公式(16)求极值,得到第k次迭代的高斯-牛顿法模型改变量表达式:
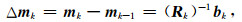
|
(18) |
其中,
准备观测数据dobs,数据加权矩阵Wd,初始模型m0,模型积分灵敏度矩阵S和数据加权项Wq,初始正则化参数α0.
While k<k_max或misfit>σ(外部循环)
计算Rk和bk;
令x0=0, r0=d0=bk;
计算初始步长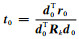
While i<i_max或sqrt(riTri)>10-6(内部循环)
i=i+1;
更新参数:xi=xi-1+ti-1di-1;
ri=ri-1-ti-1Rkdi-1;
计算第i次迭代的搜索方向:di=ri+βidi-1,βi=riTri/ri-1Tri-1
计算第i次迭代的搜索步长: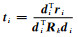
end While
k=k+1;
mk=mk-1+xi;
计算数据拟合差:

|
end While
输出mk.
2.3 数据空间共轭梯度法数据空间法(Siripunvaraporn and Egbert, 2000; Siripunvaraporn et al., 2005)是将模型计算从模型空间通过恒等式转换到数据空间下进行求解.由于模型个数Nm远远大于数据个数Nd,反演计算属于欠定问题,采用模型空间法进行反演计算需要求解一个Nm×Nm的方程组,而在数据空间中只需要求解一个Nd×Nd的方程组,因此可以有效地降低反演计算的内存占用量和计算时间(Pilkington, 2009; 李泽林, 2015; Zhang and Li, 2019; Zhang et al., 2020).本文将模型空间下的模型改变量表达式(18)转换为数据空间下的模型改变量表达式:
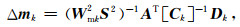
|
(19) |
其中,Ck=A(Wmk2S2)-1AT+αk(Wq2Wd2)-1,Dk=dobs-Amk-1.为了提高反演计算的收敛性和稳定性,将每次反演迭代的模型作为下次反演迭代的参考模型.
对高斯-牛顿法推导出的模型改变量表达式(19)直接求解,虽然可以降低反演计算的维度,但是需要存储灵敏度矩阵A,在三维情况下势必也会产生大量的计算内存和时间.本文采用改进的共轭梯度反演方法求解数据空间下的模型改变量,令Rk=Ck,bk=Dk.为了获得模型改变量需要对求解的变量xi再乘(Wmk2S2)-1AT,如公式(19)所示.该算法中仅仅需要形成矩阵向量的乘积Rkp,p是任意数据空间向量,而不是实际形成矩阵Rk.因此可以避免形成和存储灵敏度矩阵A, 只需要计算Ap和ATq,这两个矩阵向量乘积都可以通过一个正演问题求取. 其中,p和q分别为Nm维和Nd维的列向量.将数据空间和改进的共轭梯度法有机的结合可以降低反演计算的维度,避免存储灵敏度矩阵,进一步改善了反演的计算效率和内存消耗量.
正则化因子的选取与Portniaguine和Zhdanov(2002)采用的方法相同,初始正则化因子α0=0.1. 随着迭代的增加,模型约束项可能会增加,为了确保目标函数的收敛在全区最小,此时需要修正正则化因子,表达式如下:
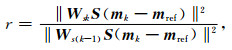
|
(20) |

|
(21) |
为了保障联合反演迭代收敛,我们会在拟合差增大或拟合差变化缓慢时,按比例减小正则化因子.
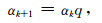
|
(22) |
其中,q为缩放因子,设q= 0.6.
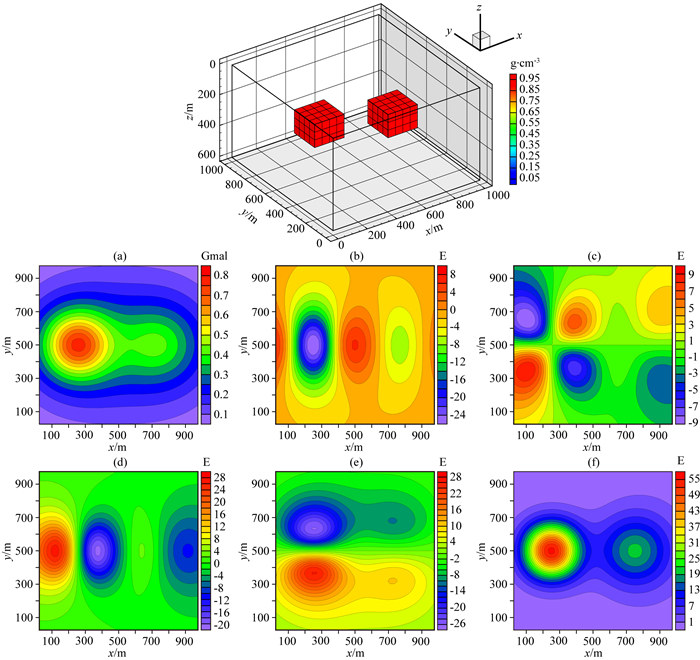
3 模型试算 3.1 单独和联合反演对比为了证明重力与重力梯度数据联合反演优于单独重力数据反演,我们设计了一个不同高度相同大小的双异常体组合模型,如图 2所示.异常体的大小都为200 m×200 m×150 m,剩余密度为1 g·cm-3.地下模型空间尺度x, y, z为1000 m×1000 m×600 m,将地下模型剖分为20×20×12个紧密排列的规则立方体单元,每个单元大小为50 m×50 m×50 m,背景剩余密度为0 g·cm-3.地面观测点个数为20×20,观测点位于网格中心,正演计算的观测重力和重力梯度数据如图 2所示.
|
图 2 模型一的理论模型和正演响应等值线图 (a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz. Fig. 2 Theoretical model and forward response contour map of model 1 (a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. |
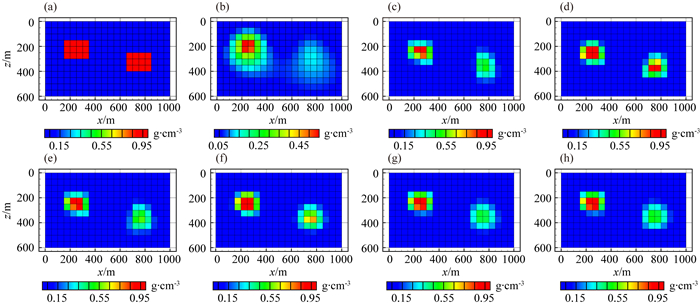
分别进行了重力数据单独反演和重力与不同重力梯度分量数据联合反演计算,初始模型均采用半空间为0 g·cm-3的剩余密度模型.第10次迭代的反演结果如图 3所示,可以发现,重力数据单独反演结果出现了严重的模糊现象,尤其深部异常体无法恢复出真实模型的几何形态和物性参数值.然而,重力与不同重力梯度分量的联合反演均可以获得较好的反演结果,分辨出深部异常体尖锐的边界,但是不同重力梯度分量包含的信息量不同,导致反演结果存在差异.为了更好的定量分析不同分量的反演效果,我们计算了所有反演模型与理论模型的均方根误差,如表 1所示.均方根误差计算公式为
|
图 3 不同观测数据反演结果对比图 (a) 理论模型; (b) gz反演结果; (c) gz和Vxx联合反演结果; (d) gz和Vxy联合反演结果; (e) gz和Vzx联合反演结果; (f) gz和Vzy联合反演结果; (g) gz和Vzz联合反演结果; (h) gz和全张量联合反演结果; 垂向切片位于y=550 m处. Fig. 3 Comparison of different observation data inversion results (a) Theoretical model; (b) gz inversion results; (c) gz and Vxx joint inversion results; (d) gz and Vxy joint inversion results; (e) gz and Vzx joint inversion results; (f) gz and Vzy joint inversion results; (g) gz and Vzz joint inversion results; (h) gz and full tensor joint inversion results; The cross section is located at y=550 m. |
|
|
表 1 反演模型和理论模型的均方根误差 Table 1 The root mean square error of each inversion model and the theoretical model |
为了验证改进的共轭梯度法更适合应用于重力和重力梯度数据的联合反演,我们建立了一个双异常体组合模型,如图 4所示.模型中包含了两个大小相同的异常体,两个异常体的大小为200 m×200 m×200 m,剩余密度为1 g·cm-3,埋深均为150 m,相距300 m.地下空间网格剖分和观测方式与模型一完全相同,正演计算的观测重力和重力梯度数据如图 4所示.

|
图 4 模型二的理论模型和正演响应等值线图 (a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz. Fig. 4 Theoretical model and forward response contour map of model 2 (a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. |
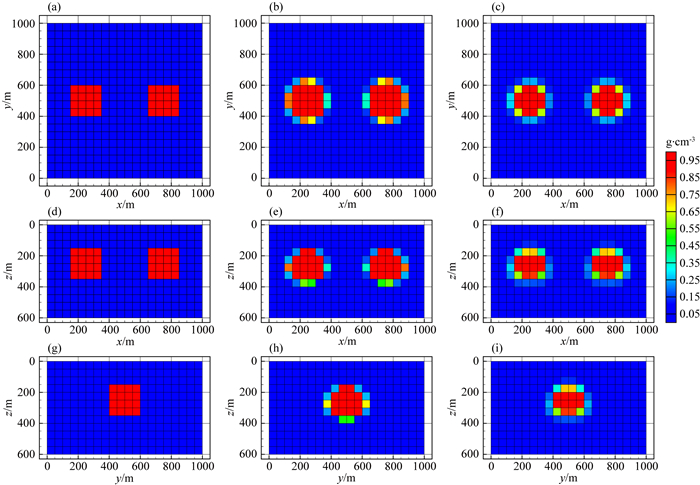
分别对传统和改进共轭梯度算法进行重力和重力梯度数据联合反演计算,两种方法都选择模型积分灵敏度矩阵,初始模型均采用半空间为0 g·cm-3的剩余密度模型.为了获得更稳定的反演结果,传统共轭梯度法反演需要在加权模型参数域下求解,反演经过48次迭代达到拟合差阈值1以下,耗时290 s,获得的反演结果切片如图 5(b, e, h)所示.而改进共轭梯度法反演经过4次迭代达到拟合差阈值1以下, 耗时70 s,获得的反演结果切片如图 5(c,f,i)所示.可以发现,两种方法都可以恢复出异常体的中心位置和几何大小,但是传统共轭梯度法反演结果边界更模糊,而改进的共轭梯度法反演结果聚焦程度更高,异常体边界更清晰.无论是在计算时间方面,还是在反演结果分辨率方面,改进的共轭梯度法反演都具有明显的优势,更适合于三维重力和重力梯度联合反演计算.
|
图 5 传统和改进的共轭梯度法反演结果对比图 (a, d, g) 理论模型; (b, e, h) 传统的共轭梯度法反演结果; (c, f, i) 改进的共轭梯度法反演结果; (a, b, c) z=300 m处的横向切片; (d, e, f) y=500 m处的垂向切片; (g, h, i) x=250 m处的垂向切片图. Fig. 5 Comparison of traditional and improved conjugate gradient inversion results (a, d, g) Theoretical model; (b, e, h) Traditional conjugate gradient inversion results; (c, f, i) Improved conjugate gradient inversion results; (a, b, c) In the z=300 m depth section; (d, e, f) In the y=500 m cross section; (g, h, i) In the x=250 m cross section. |
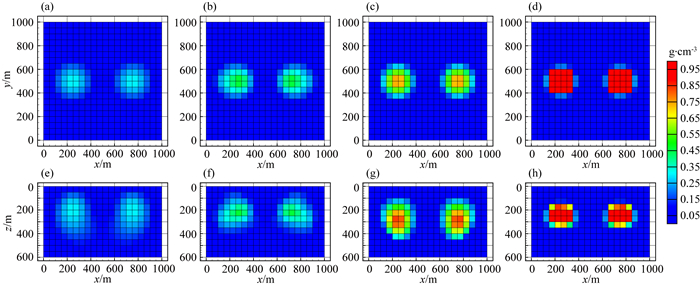
为了验证模型积分灵敏度矩阵相比于深度加权矩阵,可以更有效的消除因重力和重力梯度核函数衰减速率不同引起的趋肤效应,我们继续选用模型二进行重力和重力梯度数据联合反演试算.将公式(16)中的S矩阵选取深度加权矩阵(Li and Oldenburg, 1996)和模型积分灵敏度矩阵分别进行平滑和稀疏约束反演.所有反演方法最终的拟合差均收敛到阈值0.1以下,反演结果如图 6所示.图 6(a,e)和图 6(b,f)分别为加入深度加权矩阵后的平滑和稀疏约束反演结果切片图,可以发现,反演异常体的中心位置与真实异常体存在一定的差异,由于趋肤效应,中心位置有上移的趋势,并且异常体的物性参数值要远小于真实值.图 6(c,g)和图 6(d,h)分别为加入模型积分灵敏度矩阵后的平滑和稀疏约束反演结果切片图,由于模型积分灵敏度矩阵的加入,反演异常体物性参数值得到了明显地改善,并且异常体中心下移,有效地克服了核函数衰减引起的趋肤效应.模型积分灵敏度矩阵与稀疏约束反演相结合,反演得到的结果无论是几何形态还是物性参数值方面,都与真实模型基本吻合,尤其在纵向分辨率方面得到了明显地改善.稀疏约束反演相比于平滑反演能有效地捕捉反演解的小尺度细节,增强稀疏性以保持尖锐的边界.模拟试算验证了采用模型积分灵敏度矩阵和稀疏约束算法,可以有效地消除因重力和重力梯度核函数衰减速率不同引起的趋肤效应,将该方法应用到重力和重力梯度数据的联合反演中可以提高纵向分辨率,降低反演多解性,获得更加准确的反演结果.
|
图 6 不同S矩阵的平滑和稀疏约束反演结果的对比图 (a, b, c, d) z=250 m处的横向切片; (e, f, g, h) y=500 m处的垂向切片; (a, e) 深度加权平滑反演结果; (b, f) 深度加权稀疏约束反演结果; (c, g) 模型积分灵敏度平滑反演结果; (d, h) 模型积分灵敏度稀疏约束反演结果. Fig. 6 Comparison of smooth and sparse constraint inversion results of different S matrices (a, b, c, d) In the z=250 m depth section; (e, f, g, h) In the y=500 m cross section; (a, e) The depth weighted smooth inversion results; (b, f) The depth weighted sparse inversion results; (c, g) The model integral sensitivity smooth inversion results; (d, h) The model integral sensitivity sparse inversion results. |
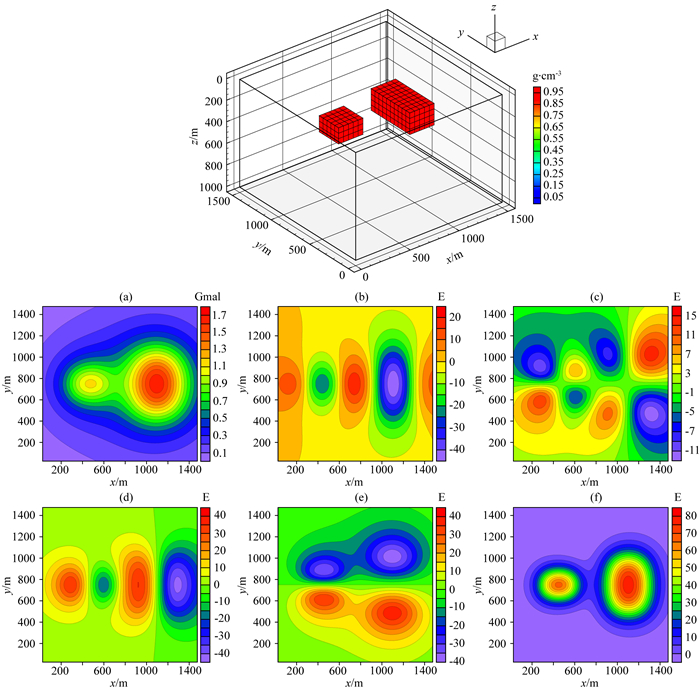
为了证明本文提出的算法在计算时间和内存占用量方面的优势,我们首先设计了一个地下网格剖分数量较大的简单模型,如图 7所示.模型中包含了两个大小不同的异常体,异常体的大小分别为300 m×200 m×150 m和300 m×500 m×200 m,剩余密度均为1 g·cm-3,顶部埋深分别为150 m和200 m,相距350 m.地下模型空间尺度x, y, z为1500 m×1500 m×1000 m,将地下模型剖分为30×30×20个紧密排列的规则立方体单元,每个单元大小为50 m×50 m×50 m,背景剩余密度为0 g·cm-3.地面观测点个数为30×30,观测点位于网格中心,正演计算的观测重力和重力梯度数据如图 7所示.
|
图 7 模型三的理论模型和正演响应等值线图 (a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz. Fig. 7 Theoretical model and forward response contour map of model 3 (a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. |
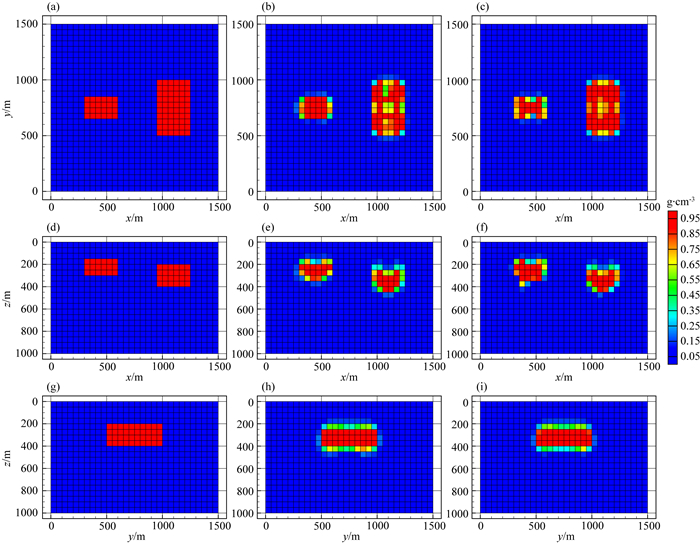
本文在改进的共轭梯度法反演基础上,分别采用模型空间和数据空间法对重力和重力梯度数据进行联合反演计算(计算机配置:Intel(R) Core(TM) i7-8750H CPU @ 2.20 GHz 2.21 GHz, 内存16 GB).所有反演的初始模型均采用均匀半空间剩余密度为0 g·cm-3的模型.模型空间法反演经过6次迭代,最终获得的拟合差为0.99,反演结果如图 8(b,e,h)所示;数据空间法反演经过6次迭代,最终获得的拟合差为1.03,反演结果如图 8(c,f,i)所示.可以发现,两种算法得到的反演结果相似,都可以较好地恢复出异常体的边界位置、几何大小和物性参数值,从而证明本文提出的算法具有一定的准确性.在反演计算时间方面,模型空间法耗时2061.85 s,而数据空间法耗时527.25 s,可以说明改进的共轭梯度法结合数据空间法有效地提高了计算效率;在内存消耗方面,模型空间法占用的最大内存约为12 GB,而数据空间法占用的最大内存只需要约0.03 GB.在这个例子中,数据空间法内存最大占用量相比于传统模型空间法减小了约百分之几.
|
图 8 模型空间和数据空间联合反演结果对比图 (a, d, g) 理论模型; (b, e, h) 模型空间法反演结果; (c, f, i) 数据空间法反演结果; (a, b, c) z=300 m处的横向切片; (d, e, f) y=750 m处的垂向切片; (g, h, i) x=1150 m处的垂向切片图. Fig. 8 Comparison of model space and data space joint inversion results (a, d, g) Theoretical model; (b, e, h) The model space inversion results; (c, f, i) The data space inversion results; (a, b, c) In the z=300 m depth section; (d, e, f) In the y=750 m cross section; (g, h, i) In the x=1150 m cross section. |
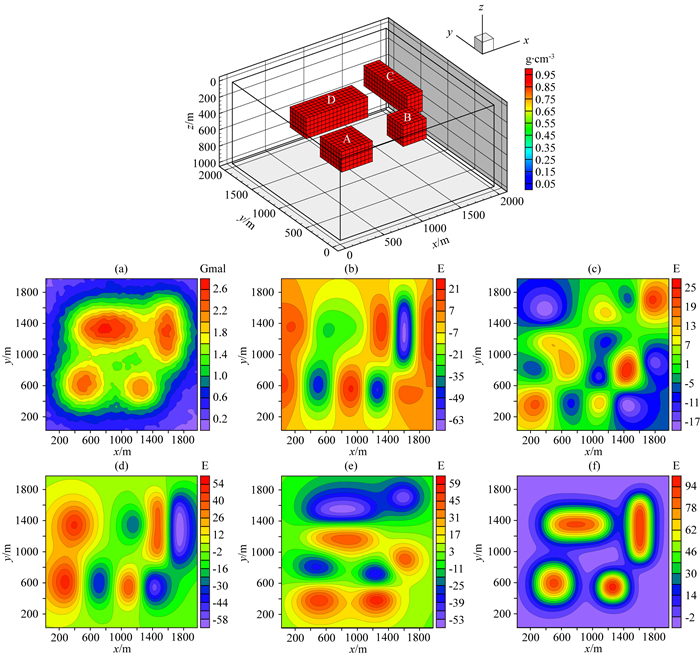
为了进一步验证本文提出算法的准确性、抗噪性和有效性,我们又设计了一个多异常体组合复杂模型,如图 9所示,由四个不同大小的长方体组成,镶嵌在剩余密度为0 g·cm-3的地下均匀半空间中.地下模型空间大小为2000 m×2000 m×1000 m,将地下剖分为40×40 ×20个紧密排列的直立立方体单元,每个单元大小为50 m×50 m×50 m.地面观测点个数为40×40,观测点位于网格中心,加入5%高斯随机噪声的理论模型正演响应如图 9所示.异常体的物性值、几何大小和顶部埋深情况如表 2所示.
|
图 9 模型四的理论模型和正演响应等值线图 (a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz. Fig. 9 Theoretical model and forward response contour map of model 4 (a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. |
|
|
表 2 理论模型异常体属性情况 Table 2 Theoretical model anomaly attributes |
由于网格剖分个数的增加,采用模型空间法进行反演计算所需要的内存空间已经超过计算机的承受范围,而数据空间法反演经过17次迭代,最终获得的拟合差为0.97,反演结果如图 10所示.可以发现,加入噪声后本文提出的算法仍然能够准确地恢复出地下异常体的几何形态和物性参数值大小,与真实模型基本吻合,表现出一定的准确性和抗噪性.反演计算耗时2206.26 s,占用的最大内存约为0.039 GB.在这个例子中,数据空间法反演内存最大占用量相比于传统模型空间法减小了约百分之几,可以证明改进的共轭梯度法结合数据空间法有效地降低了计算内存消耗量,表现出一定的有效性,更适合应用于大数据量的重力和重力梯度数据联合反演计算.

|
图 10 数据空间共轭梯度法联合反演结果图 (a, b, c, d) 理论模型; (e, f, g, h) 联合反演结果; (a, e) z=300 m处的横向切片; (b, f) x=600 m处的垂向切片; (c, g) y=550 m处的垂向切片; (d, h) x=1600 m处的垂向切片. Fig. 10 The data space conjugate gradient method joint inversion results (a, b, c, d) Theoretical model; (e, f, g, h) Joint inversion results; (a, e) In the z=300 m depth section; (b, f) In the x=600 m cross section; (c, g) In the y=550 m cross section; (d, h) In the x=1600 m cross section. |
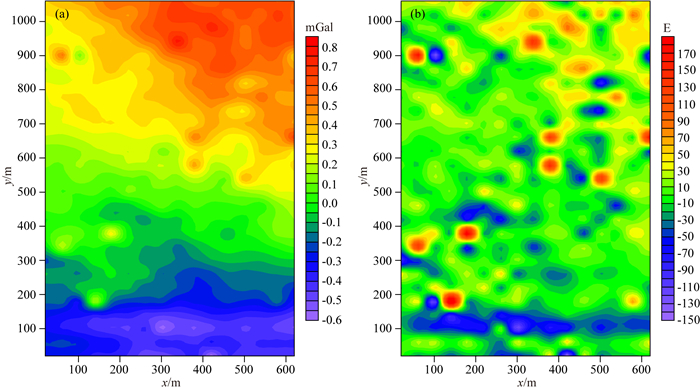
为了进一步说明本文提出算法的有效性和实用性,我们将反演算法应用于黑龙江省大兴安岭呼中区碧水镇铅锌多金属矿区的重力和重力梯度数据解释中.在碧水镇铅锌多金属矿区内共采集了27条测线,测线间距40 m,每条测线上分布16个观测点,测点间距40 m,将实测布格剩余重力异常数据网格化,网格化后的重力异常数据等值线如图 11a所示.利用傅里叶变换计算得到布格剩余重力异常的重力梯度数据,网格化后的重力梯度异常数据如图 11b所示.方便起见,实测数据应用中只考虑重力和重力梯度Vzz分量数据进行联合反演计算.
|
图 11 实测重力和重力梯度数据等值线图 (a) 重力数据; (b) 重力梯度数据Vzz. Fig. 11 Contour plots of measured gravity and gravity gradient data (a) The gravity data; (b)The gravity gradient data Vzz. |
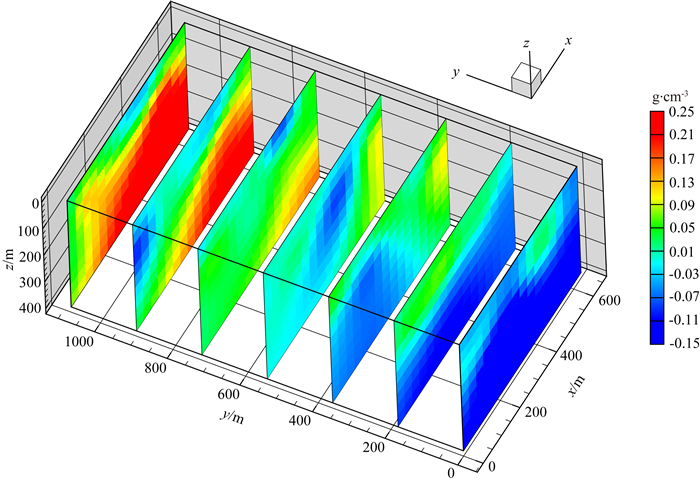
观测区域大小为640 m×1040 m,将反演目标区域的地下空间划分为16×27×10个紧密排列的直立长方体单元,每个单元的大小为40 m×40 m×40 m.我们对重力和重力梯度数据进行联合反演,反演初始模型采用剩余密度为0 g·cm-3的均匀半空间模型.反演经过5次迭代收敛到拟合差阈值以下,反演结果沿测线方向的密度分布切片如图 12所示,不同深度的密度分布切片如图 13所示.我们发现,本文提出的反演方法可以快速地分辨出地下不同密度的分布情况,密度异常分布从南到北逐渐升高,高密度异常区域主要出现在研究区的东北方向,由于铅锌多金属矿床具有较高的密度,因此可以通过反演高密度分布情况有效地圈定多金属矿床的区域位置和划分矿体与围岩的边界.同时,该反演算法获得最终模型结果耗时约434.5 s,占用内存约0.028 GB.进一步说明了所提出的算法适用于实测数据处理,可以在普通计算机下快速获得地下密度分布模型,为精准矿产勘探提供重要依据.
|
图 12 重力和重力梯度数据联合反演获得的密度分布垂向切片图 Fig. 12 Cross section of density distribution obtained by joint inversion of gravity and gravity gradient data |

|
图 13 重力和重力梯度数据联合反演获得的密度分布横向切片图 (a) z=100 m处的横向切片; (b) z=200 m处的横向切片; (c) z=300 m处的横向切片. Fig. 13 Depth section of density distribution obtained by joint inversion of gravity and gravity gradient data (a) In the z=100 m depth section; (b) In the z=200 m depth section; (c) In the z=300 m depth section. |
本文将数据空间法和改进的共轭梯度算法结合应用到重力和重力梯度数据处理中,开发出计算速度更快、占用内存更小的高分辨率三维重力和重力梯度数据联合反演算法.理论模型试算表明相比于传统的共轭梯度反演算法,改进的算法可以有效地降低反演的迭代次数,提高反演的收敛速度,获得更接近于真实模型的反演结果;联合反演采用自适应模型积分灵敏度矩阵,可以有效地消除因重力和重力梯度核函数衰减速率不同引起的趋肤效应,相比于依赖先验信息的深度加权方法,可以自适应调解矩阵大小,有效提高反演结果的纵向分辨率;稀疏约束反演方法相比于传统平滑反演方法能有效地捕捉反演解的小尺度细节,增强稀疏性以保持尖锐的边界;将数据空间法和改进的共轭梯度算法结合,可以更好地降低联合反演求解方程的维度,避免存储灵敏度矩阵,有效地提高了计算效率和大幅度的降低内存占用空间.野外实例表明,本文提出的算法可以在普通计算机下快速地获得地下密度分布模型,有效地圈定多金属矿床的区域位置和划分矿体与围岩的边界,表现出较强的稳定性和实用性.
致谢 感谢匿名评审专家为本文提出的宝贵意见.
Capriotti J, Li Y G. 2014. Gravity and gravity gradient data: Understanding their information content through joint inversions.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1329-1333.
|
Chen Y, Li T L, Fan C S, et al. 2014. The 3D focusing inversion of full tensor gravity gradient data based on conjugate gradient. Progress in Geophysics (in Chinese), 29(3): 1133-1142. DOI:10.6038/pg20140317 |
Commer M. 2011. Three-dimensional gravity modelling and focusinginversion using rectangular meshes. Geophysical Prospecting, 59(5): 966-979. |
Gao X H, Huang D N. 2017. Research on 3D focusing inversion of gravity gradient tensor data based on a conjugate gradient algorithm. Chinese Journal of Geophysics (in Chinese), 60(4): 1571-1583. DOI:10.6038/cjg20170429 |
Gao X H, Zeng Z F, Sun S Y, et al. 2019. Joint inversion of gravity and gravity gradient data based on Cokriging method with the threshold constraint. Chinese Journal of Geophysics (in Chinese), 62(3): 1037-1045. DOI:10.6038/cjg2019L0622 |
Geng M X, Huang D N, Yu P, et al. 2016. Three-dimensional constrained inversion of full tensor gradiometer data based on cokriging method. Chinese Journal of Geophysics (in Chinese), 59(5): 1849-1860. DOI:10.6038/cjg20160528 |
Guillen A, Menichetti V. 1984. Gravity and magnetic inversion with minimization of a specific functional. Geophysics, 49(8): 1354-1360. DOI:10.1190/1.1441761 |
Last B J, Kubik K. 1983. Compact gravity inversion. Geophysics, 48(6): 713-721. DOI:10.1190/1.1441501 |
Li H L, Fang J, Wang X S, et al. 2017. Lithospheric 3-D density structure beneath the Tibetan plateau and adjacent areas derived from joint inversion of satellite gravity and gravity-gradient data. Chinese Journal of Geophysics (in Chinese), 60(6): 2469-2479. DOI:10.6038/cjg20170634 |
Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics, 61(2): 394-408. DOI:10.1190/1.1443968 |
Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data. Geophysics, 63(1): 109-119. DOI:10.1190/1.1444302 |
Li Z L, Yao C L, Zheng Y M, et al. 2015. 3D data-space inversion of magnetic amplitude data. Chinese Journal of Geophysics (in Chinese), 58(10): 3804-3814. DOI:10.6038/cjg20151030 |
Martinez C, Li Y G, Krahenbuhl R, et al. 2013. 3D inversion of airborne gravity gradiometry data in mineral exploration: A case study in the Quadrilátero Ferrífero, Brazil. Geophysics, 78(1): B1-B11. DOI:10.1190/geo2012-0106.1 |
Nabighian M N, Ander M E, Grauch V J S, et al. 2005. Historical development of the gravity method in exploration. Geophysics, 70(6): 63ND-89ND. DOI:10.1190/1.2133785 |
Pilkington M. 2009. 3D magnetic data-space inversion with sparseness constraints. Geophysics, 74(1): L7-L15. DOI:10.1190/1.3026538 |
Portniaguine O, Zhdanov M S. 1999. Focusing geophysical inversion images. Geophysics, 64(3): 874-887. DOI:10.1190/1.1444596 |
Portniaguine O, Zhdanov M S. 2002. 3-D magnetic inversion with data compression and image focusing. Geophysics, 67(5): 1532-1541. DOI:10.1190/1.1512749 |
Qin P B, Huang D N. 2016. Integrated gravity and gravity gradient data focusing inversion. Chinese Journal of Geophysics (in Chinese), 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
Qin P B, Huang D N, Yuan Y, et al. 2016. Integrated gravity and gravity gradient 3D inversion using the non-linear conjugate gradient. Journal of Applied Geophysics, 126: 52-73. DOI:10.1016/j.jappgeo.2016.01.013 |
Silva J B C, Barbosa V C F. 2006. Interactive gravity inversion. Geophysics, 71(1): 696-699. |
Siripunvaraporn W, Egbert G. 2000. An efficient data-subspace inversion method for 2-D magnetotelluric data. Geophysics, 65(3): 791-803. DOI:10.1190/1.1444778 |
Siripunvaraporn W, Egbert G, Lenbury Y, et al. 2005. Three-dimensional magnetotelluric inversion: data-space method. Physics of the Earth and Planetary Interiors, 150(1-3): 3-14. DOI:10.1016/j.pepi.2004.08.023 |
Tikhonov A N, Arsenin V Y. 1977. Solution of ill-posed problems. Mathematics of Computation, 32(144): 491. |
Vasco D W, Taylor C. 1991. Inversion of airborne gravity gradient data, southwestern Oklahoma. Geophysics, 56(1): 90-101. DOI:10.1190/1.1442961 |
Wolke R, Schwetlick H. 1988. Iteratively reweighted least squares: algorithms, convergence analysis, and numerical comparisons. SIAM Journal on Scientific and Statistical Computing, 9(5): 907-921. DOI:10.1137/0909062 |
Wu L, Ke X P, Hsu H, et al. 2013. Joint gravity and gravity gradient inversion for subsurface object detection. IEEE Geoscience and Remote Sensing Letters, 10(4): 865-869. DOI:10.1109/LGRS.2012.2226427 |
Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics (in Chinese), 46(2): 252-258. |
Zhang R Z, Li T L. 2019. Joint inversion of 2D gravity gradiometry and magnetotelluric data in mineral exploration. Minerals, 9(9): 541. DOI:10.3390/min9090541 |
Zhang R Z, Li T L, Deng X H, et al. 2020. Two-dimensional data-space joint inversion of magnetotelluric, gravity, magnetic and seismic data with cross-gradient constraints. Geophysical Prospecting, 68(2): 721-731. DOI:10.1111/1365-2478.12858 |
Zhdanov M S. 2002. Geophysical Inverse Theory and Regularization Problems. Amsterdam: Elsevier.
|
Zhdanov M S, Ellis R, Mukherjee S. 2004. Three-D regularized focusing inversion of gravity gradient tensor component data. Geophysics, 69(4): 1-4. |
Zhdanov M S. 2009. New advances in regularized inversion of gravity and electromagnetic data. Geophysical Prospecting, 57(4): 463-478. DOI:10.1111/j.1365-2478.2008.00763.x |
陈闫, 李桐林, 范翠松, 等. 2014. 重力梯度全张量数据三维共轭梯度聚焦反演. 地球物理学进展, 29(3): 1133-1142. DOI:10.6038/pg20140317 |
高秀鹤, 黄大年. 2017. 基于共轭梯度算法的重力梯度数据三维聚焦反演研究. 地球物理学报, 60(4): 1571-1583. DOI:10.6038/cjg20170429 |
高秀鹤, 曾昭发, 孙思源, 等. 2019. 基于阈值约束的协克里金法联合反演重力与重力梯度数据. 地球物理学报, 62(3): 1037-1045. DOI:10.6038/cjg2019L0622 |
耿美霞, 黄大年, 于平, 等. 2016. 基于协同克里金方法的重力梯度全张量三维约束反演. 地球物理学报, 59(5): 1849-1860. DOI:10.6038/cjg20160528 |
李红蕾, 方剑, 王新胜, 等. 2017. 重力及重力梯度联合反演青藏高原及邻区岩石圈三维密度结构. 地球物理学报, 60(6): 2469-2479. DOI:10.6038/cjg20170634 |
李泽林, 姚长利, 郑元满, 等. 2012. 数据空间磁异常模量三维反演. 地球物理学报, 58(10): 3804-3814. DOI:10.6038/cjg20151030 |
秦朋波, 黄大年. 2016. 重力和重力梯度数据联合聚焦反演方法. 地球物理学报, 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
 2021, Vol. 64
2021, Vol. 64


