重力反演的目的是由地表观测的重力数据恢复出未知地下空间的密度分布,是矿产资源勘查部署的重要手段(Paterson and Reeves, 1985;Oldenburg et al., 1997;管志宁等,1998;Portniaguine and Zhdanov, 1999;姚长利等,2003;孟小红等,2012).重力反演首先需要对三维地下半空间进行离散化剖分,通常采用的方式是六面体网格方式(Li and Oldenburg, 1998).但与地震、电法等地球物理技术相比,随着深度的增加,相同大小的密度体所产生的重力异常幅值及频率衰减更快,导致重力正演核函数矩阵条件数较大,同时受到观测噪声及异常处理精度的影响,反演结果分辨率较低、多解性更强.
在保证重力异常数据拟合的前提下,合理地施加模型约束项是降低重力反演多解性问题、获得可靠密度反演结果的有效手段.不同的模型约束方法采用了不同的模型假设,以满足不同勘探目标解释工作的需求.Li和Oldenburg(1996)利用深度加权矩阵和L2范数约束以降低反演结果的趋肤效应;Last和Kubik(1983)引入了基于最小体积约束,Portniaguine和Zhdanov(1999)、Zhdanov(2002)、Zhdanov等(2004)引入最小支撑约束来获得具有聚焦特征的反演结果;Bertete-Aguirre等(2002)引入了最小梯度支撑和总变差(TV)约束来保证锐化模型反演结果的边界梯度;秦朋波和黄大年(2016)、高秀鹤和黄大年(2017)利用聚焦反演方法对重力及重力梯度数据进行联合反演,通过融合多维度观测信息提高反演结果可靠性;Farquharson和Oldenburg(1998)、Farquharson(2008)、Vatankhah等(2017)利用L1范数来提高反演分辨率;Sun和Li(2014)、李泽林等(2019)利用Lp范数来改善重力反演结果;彭国民等(2018)采用柯西分布约束来保证模型反演结果的稀疏性.相比来说,具有稀疏特征或稀疏边界特征的模型约束方法能得到更高的解释分辨率,在实际勘探应用中更具吸引力.
对于稀疏或聚焦反演方法来说,获得可靠的结果需具备较强的前提条件:一是网格剖分与地质体间的匹配性,二是重力剩余异常求取的准确性.在实际应用中,上述条件很难得到满足,首先地质体发育模式复杂、形态多样,准确的网格剖分方案难以确定;其次总的重力异常为地下半空间密度体产生重力异常的叠加,背景异常难以准确剥离,获得与聚焦密度体对应的剩余重力异常存在极大的不确定性.这些问题都会导致聚焦或稀疏约束反演密度值和空间分布与真实情况间存在较大的偏差.为此,通常可引入测井资料或添加光滑、能量最小等多种约束方式(刘展等,2011;朱自强等,2014;Utsugi,2019)来增强反演结果的可靠性,获得介于光滑与聚焦的密度反演结果.但往往研究区测井资料有限,而且光滑与聚焦(稀疏)的联合约束也难以描述复杂的密度空间分布.可以看出,要想满足高精度重力反演应用需求,还需开展更深入的模型约束方法研究.
本文提出了一种新的基于密度模型稀疏表征的重力反演方法,引入了可描述典型地质体发育模式及几何特征的特征模型,并介绍了利用特征模型构建模型特征矩阵的流程,在此基础上,重新推导了重力反演求解方程,将直接求解密度转换为求解与模型特征矩阵对应的分解系数稀疏求解问题,以保证利用最少的、最具有代表性的特征模型组合构成期望反演得到的密度模型,从而获得分辨率更高、可靠性更强的三维密度反演结果.
1 方法原理 1.1 重力反演方法首先简要回顾一下重力反演方法.在笛卡尔坐标系下,将地下半空间剖分为三维离散网格,则重力正演可表达为如下线性方程:
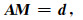
|
(1) |
其中,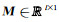
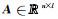
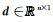
重力反演是正演的逆过程,为了减少反演多解性,通常会施加定量的模型约束,可分为线性和非线性模型约束算子两大类.前者中最为常用的包括用于保证密度模型能量最小的单位矩阵算子和保证密度模型光滑的拉普拉斯算子等;后者则在迭代反演过程中因模型的改变而改变,如最小支撑、最小梯度支撑等非线性算子.上述两类模型约束可归纳至统一的重力反演目标函数中,形式如下:
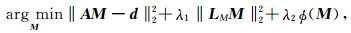
|
(2) |
其中‖·‖22为L2范数;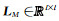

|
(3) |
其中,Mk为当前第k次迭代求解得到的密度模型,Mk-1为第k-1次迭代求解得到的密度模型,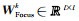
第k次迭代的密度模型Mk满足的目标函数形式如下:
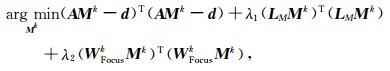
|
(4) |
求解该目标函数的等价形式为:
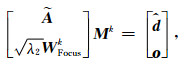
|
(5) |
其中,
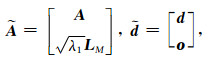
|
聚焦反演的目标是将密度反演结果集中在部分网格中,追求的是利用最少的密度网格模型来拟合重力数据.但异常分离不准确时,会有一定成分的区域背景异常干扰,而这部分异常对应的密度体并不符合聚焦算法的应用前提.即使异常分离结果较为准确,网格剖分过小或过大,也难以保证反演结果的可靠性.
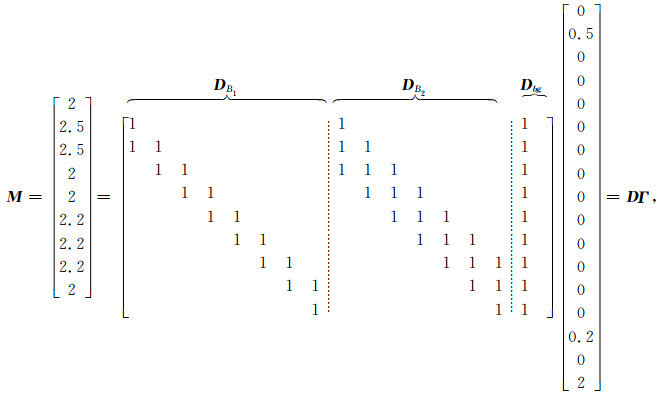
1.2 模型特征矩阵构建流程针对现有方法存在的问题,本文利用模型特征矩阵和分解系数来对密度模型进行稀疏表征.下面首先通过一维模型来阐述密度模型稀疏表征的含义.如图 1所示,该一维密度模型可分解为三个特征模型,一是数值为2 g·cm-3的区域背景密度模型,二是数值为0.5 g·cm-3的密度体B1剩余密度模型,三是数值为0.2 g·cm-3的密度体B2剩余密度模型.

|
图 1 一维密度模型分解示意图 Fig. 1 Diagram of 1D density model decomposition |
该一维密度模型M的分解过程可表达为模型特征矩阵和分解系数向量的矩阵相乘:
|
(6) |
其中,将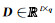
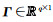
矩阵D包含了三个子矩阵,即
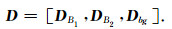
|
(7) |
根据公式(6)的矩阵形式与图 1所示三个特征模型的对应关系可看出,矩阵DB1每一列包含了块体B1的几何形态特征,矩阵DB2每一列包含了块体B2的几何形态特征,矩阵Dbg包含了背景信息.为了保证利用最少的特征模型来组成密度模型,分解向量Γ应是稀疏的,其非零点处数值的大小和位置表示特征模型的密度值大小和空间赋存位置.
模型特征矩阵的构建原则来自于先验地质假设,为更加清晰的描述模型特征矩阵构建过程,下面以二维模型(假设待反演区域沿X、Z方向剖分为9×7个网格)为例进行具体说明:
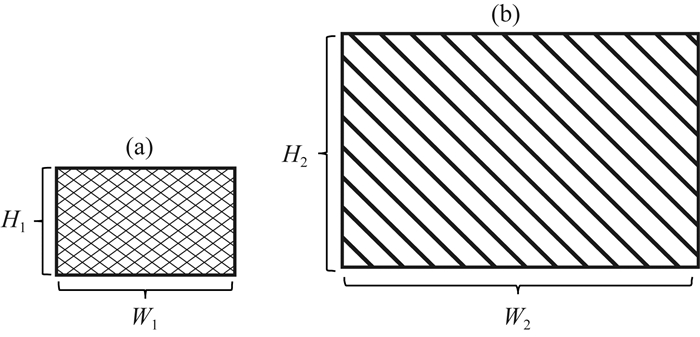
(1) 根据已知资料分析,假设地质体发育模式包含以下两类矩形块体特征模型,具体参数为:特征模型Ⅰ(图 2a):宽W1m、高H1m;特征模型Ⅱ(图 2b):宽W2m、高H2m;
|
图 2 构建模型特征矩阵的特征模型 (a) 特征模型Ⅰ;(b) 特征模型Ⅱ. Fig. 2 Feature models for building model feature matrix (a) Feature model Ⅰ; (b) Feature model Ⅱ. |
(2) 首先计算特征模型Ⅰ对应的索引向量Index_I.将特征模型I的中心点坐标置于二维剖分网格左上角第一个网格(图 3a),以此为起始点进行第1次搜索,计算特征模型I所占反演剖分的索引,索引Index_I_1位置的参数记为整数1,其余为0(图 3b);向右平移一个网格的距离至左上角第2个网格,计算特征模型I所占反演网格的索引,并将其记录为Index_I_2,索引Index_I_2位置的参数记为整数1,其余为0;以此类推,计算完第一层之后,从第二层的左侧第一个网格点为起始点计算特征模型I的所占网格位置,并进行索引标记;之后,逐层计算,设平移至第22个网格(X=4、Z=3)(图 3c)进行第22次搜索,索引Index_I_22标记如图(图 3d)所示;按此步骤直到遍历所有网格;
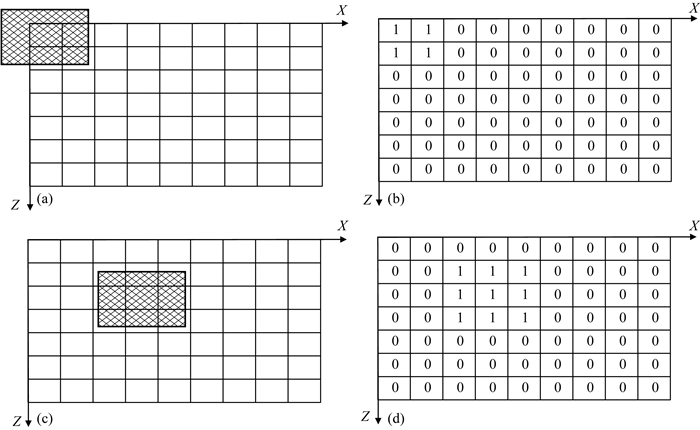
|
图 3 特征模型Ⅰ对应的模型特征矩阵构建过程 (a) 第1次搜索位置; (b) 第1次的索引; (c) 第22次搜索位置; (d) 第22次的索引. Fig. 3 Building process of model feature matrix corresponding to feature model Ⅰ (a) The first search location; (b) The first index; (c) The 22nd search location; (d) The 22nd index. |
(3) 将步骤(2)得到的索引Index_I_k(k=1, …, n),n为剖分网格个数,此次为63,展开为列向量并进行组合得到特征模型I对应的模型特征矩阵DB1;
(4) 特征模型Ⅱ的模型特征矩阵构建.重新执行第(2)、(3)步,计算特征模型Ⅱ下的索引向量,并将其进行组合得到特征模型Ⅱ对应的特征矩阵DB2;
(5) 背景模型特征矩阵.类似特征模型Ⅰ、Ⅱ的方式,选择具有趋势特征的模型作为特征模型,将其生成背景模型特征矩阵Dbg;
(6) 完成上述步骤,便可生成二维反演所需的模型特征矩阵D=[DB1, DB2, Dbg].
上述构建流程同样适用于反演不等间隔网格剖分的情况.三维模型特征矩阵的构建流程与二维类似,在后文三维模型反演实验中将举例说明,在此不做过多赘述.
模型特征矩阵所采用的特征模型不限于规则的长方体等几何形态,也适用于倾斜(岩脉)、球体(孤立火山岩体)等复杂地质模式特征.在实际应用过程中,可根据研究区的先验地质认识或其他物探资料来构建模型特征矩阵.在缺少先验地质认识的地区,也可利用重力异常分析来计算特征模型的水平和垂向上的尺寸大小及倾角信息.
相比常规反演,本文将模型特征矩阵D作用于重力正演核函数A的过程具有两大优势,一是相当于对原始剖分网格按照特征模型的样式进行了重新组合,在组合后的多套网格中分别进行分解系数的稀疏求解,更加符合期望的稀疏假设条件;二是特征模型可以更高效的将期望满足的地质模式的定性假设定量化,使得重力反演的过程更具倾向性,无论是块状、层状还是倾斜状等复杂形态的地质体发育特征都可以被引入进来.
1.3 目标函数及求解算法将公式(6)代入公式(2),将原重力反演问题的目标函数写为:

|
(8) |
其中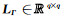
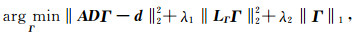
|
(9) |
其中,‖·‖1代表L1范数稀疏约束.
稀疏求解问题在目前信号处理领域得到了广泛的应用,求解算法包括基追踪(Chen et al., 2001)、交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)(Boyd et al., 2010)、正交匹配追踪(orthogonal matching pursuit)(Sahoo and Makur, 2015)等.为了获得更加高的稀疏度、更加准确的分解系数,本文采用了Majorization-Minimization(优化最小化,简称MM)优化框架来加速稀疏分解系数Γ的求解过程.MM框架(Figueiredo et al., 2007;Selesnick and Bayram, 2014;Nguyen,2017)是用来求解非凸函数的一种性能良好的优化算法框架.MM算法通过将原来的复杂优化问题分解为一系列简单优化问题,对于分解系数进行稀疏求解(具体推导过程见附录A),其第k次迭代的Γk公式如下:

|
(10) |
其中,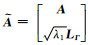
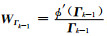
WΓk-1为第k-1次迭代求解结果Γk-1对应的对角加权矩阵;ϕ′(Γk-1)为模型约束函数ϕ(Γ)关于Γk-1的一阶偏导,其计算公式为:
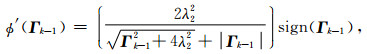
|
(11) |
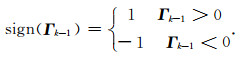
|
为避免反演出现严重的趋肤现象,对公式(10)中的重力异常正演核函数进行深度加权,则:
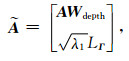
|
(12) |
其中,
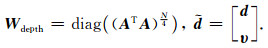
|

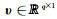
由于期望获得Γ是稀疏的,即Γ中必然会出现一定数量的0值,而WΓk-1中的Γk-1位于分母位置,易出现奇异值,可对公式(10)中的求逆项进行重新推导得到如下公式.
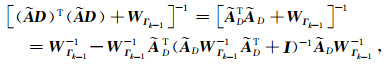
|
(13) |
其中,
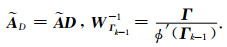
|
综合前文所述的模型特征矩阵构建及分解系数求解过程,基于密度模型稀疏表征的重力反演方法主要包含以下步骤:
(1) 根据实际需求剖分原始反演网格,计算重力正演核函数矩阵A;
(2) 根据工区实际情况、重力异常形态等信息设置特征模型(可包括块体、倾斜状岩脉、球体等各类典型地质体),根据1.2节介绍的过程构建模型特征矩阵D;
(3) 设置正则化参数λ1、λ2及深度加权参数N(一般N=4),设置最大迭代次数IterMax;
(4) 根据模型特征矩阵列向量个数设置稀疏分解系数初始模型向量Γk-1=ΓInit(k=1),注意ΓInit不要含有0值;
(5) 根据公式(11),计算稀疏约束迭代加权矩阵WΓk-1-1;
(6) 利用公式(10)和(13)计算第k次的分解系数Γk;
(7) 利用公式(6)得到第k次迭代对应的密度模型Mk=WdepthDΓk;
(8) 获得公式(9)的计算结果,若满足目标函数收敛条件则执行步骤(9);若不满足,重复步骤(5)—(7),修改反演参数;
(9) 评价(8)获得的反演结果,若符合地质认识,则执行步骤(10);若不满足,重复(2)—(8),修改特征模型,重新构建模型特征矩阵并求取反演结果;
(10) 最终的密度反演结果输出.
2 理论模型实验分析为了验证本文所提重力反演方法的有效性,分别开展了二维及三维模型实验,并与聚焦反演算法进行了对比分析.在实验过程中均未加入密度阈值约束,即不在反演过程中限定密度的最大值和最小值.
2.1 二维模型二维反演包括三个模型实验,分别是无背景模型干扰的两个地质体、存在背景模型干扰的两个地质体和存在背景模型干扰的倾斜状地质体.三个模型实验均采用相同的观测系统,具体参数为:观测点个数为30个,间距为200 m,观测点均位于海拔0 m.反演网格采用长方形剖分,X、Z方向剖分的个数为30×28个,网格大小为200 m×50 m,从海拔0 m向下剖分,观测点位于第一层网格的中心位置.
(1) 模型一:无背景模型干扰的两个地质体
该模型包括两个孤立的、不同大小的长方体(图 4b),参数见表 1.假设构造背景异常被彻底分离,即反演区域的背景密度为0 g·cm-3,模型参数见表 1.观测数据加入了3%的高斯噪声(图 4a).
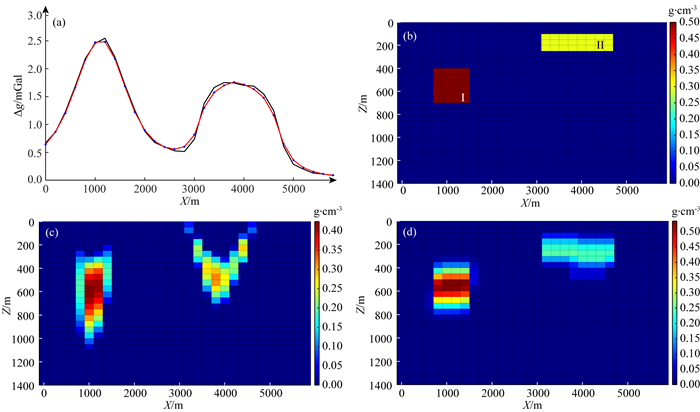
|
图 4 反演结果对比 (a) 重力异常(黑线)及拟合数据(红线); (b) 密度模型; (c) 常规聚焦反演结果; (d) 本文反演结果. Fig. 4 Comparison of inversion results (a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper. |
|
|
表 1 二维密度模型参数 Table 1 Parameters of 2D density model |
构建模型特征矩阵采用了两类模型特征矩阵构建方式,一类是选择一个特征模型,X、Z方向尺寸为600 m×200 m的矩形密度体;另一类是选择三个几何形态差异较大的特征模型,X、Z方向尺寸分别为200 m×200 m,600 m×200 m,1600 m×100 m时.设置反演参数(λ1=0.1、λ2=2,最大迭代次数IterMax=150).
从该模型实验可看出,在没有密度阈值约束前提条件下,常规聚焦反演结果(图 4c)虽然可以较好地反映地质体质心的埋深,但是聚焦程度的控制比较难以施加,易导致反演结果过于聚焦而出现较大的密度值.利用本文所提方法进行反演,采用两类模型特征矩阵构建方式都会得到相同的结果,如图 4d所示.可见,即使采用第二类模型特征矩阵构建方式,在分解系数稀疏约束的控制下,仍在三个特征模型中选择了(600 m×200 m)特征模型作为待反演密度异常体的主要构成单元,与稀疏分解系数进行组合,共同恢复出了形态与密度值更接近于真实密度模型的反演结果.
(2) 模型二:存在背景模型干扰的两个地质体
该模型包括三个密度体(图 5b),其中两个为孤立的、不同大小、不同埋深的长方形密度体,另外一个为埋深较大的地质体(密度为0.2 g·cm-3)作为背景干扰.与模型一不同的是,两个长方形的剩余密度体值有正、有负,具体参数见表 1.在模型正演数据中加入了3%的高斯噪声作为观测数据(图 5a).
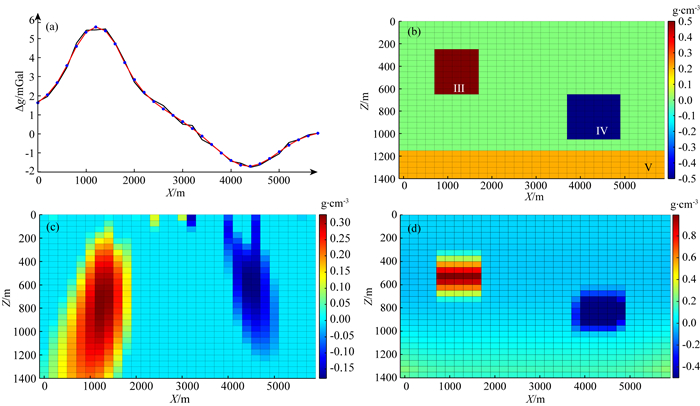
|
图 5 反演结果对比 (a) 重力异常(黑线)及拟合数据(红线); (b) 密度模型; (c) 常规聚焦反演结果; (d) 本文反演结果. Fig. 5 Comparison of inversion results (a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper. |
构建模型特征矩阵采用了四个几何形态差异较大的特征模型,X、Z方向尺寸分别为200 m×200 m,600 m×150 m,1000 m×250 m,15000 m×100 m.设置反演参数(λ1=0.2、λ2=2,最大迭代次数IterMax=150).
从该模型实验可看出,利用公式(5)求解得到的常规聚焦反演结果(图 5c)与原始模型偏差较大,原因主要是由于深部地质体产生的背景异常起到了干扰作用,聚焦后左侧的正密度体埋深加大,结果偏向与深层背景地质体与浅层地质体之间,而右侧的负密度体反演结果较浅;而从本文方法获得反演结果(图 5d)可看出,由于模型特征矩阵构建过程中包含了水平方向长条形特征模型(15000 m×100 m)的引入,在对应的分解系数求解过程中一定程度上抵消了背景异常的干扰,相当于一个异常自动分离的过程,而其余的部分又由于包含了更接近于原始模型中块体特征的特征模型(1000 m×250 m),虽然结果的密度值较原有模型略大,但反演结果的空间分布更加逼近于原始模型.
(3) 模型三:存在背景模型干扰的倾斜状地质体
该模型包括一个倾斜状的地质体,具体参数见表 1.同时,与模型二类似,模拟剩余异常仍包含一定的深层信息的情形,在深部(埋深在1150~1400 m范围内的网格)加入一个密度沿着X方向变化的横向非均匀地质体(密度值介于0.2~0.35 g·cm-3).在模型正演数据中加入了3%的高斯噪声作为观测数据.
构建模型特征矩阵采用了两种特征模型,一是倾斜地质体(图 6),另外一类是长方形(X、Z方向尺寸为5000 m×100 m).设置反演参数(λ1=0.2、λ2=2,最大迭代次数IterMax=150).
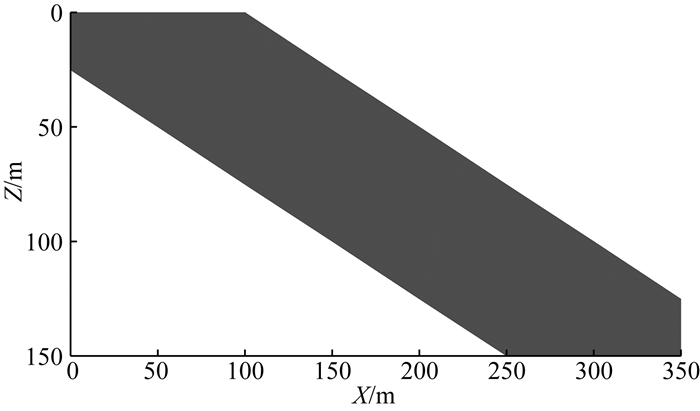
|
图 6 构建模型特征矩阵的二维特征模型 Fig. 6 2D feature model for building model feature matrix |
从该模型实验可看出,利用公式(5)获得的常规反演结果(图 7c)虽然在一定程度上体现了倾斜状地质体的特征,但由于深部地质体产生的背景异常的干扰,为同时保证异常的拟合以及反演模型的连续聚焦目标,使得结果埋深较大;而反观利用本文方法得到的反演结果(图 7d),在层状特征模型的模型特征矩阵的联合控制下,背景密度异常体的位置得到较好的恢复.同时,具有倾斜形状的特征模型(与模型大小并不相同)的引入又大大增加了逼近原始模型的可能性,使得即使没有在反演过程中控制密度阈值范围,恢复的浅层倾斜状地质体密度值及空间分布也与原始模型十分接近.
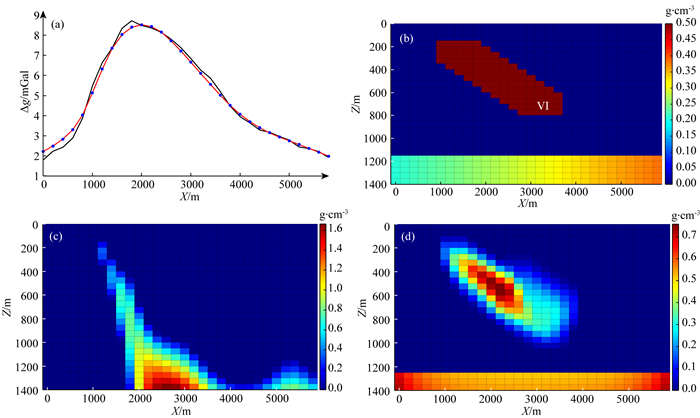
|
图 7 反演结果对比 (a) 重力异常(黑线)及拟合数据(红线); (b) 密度模型; (c) 常规聚焦反演结果; (d) 本文反演结果. Fig. 7 Comparison of inversion results (a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper. |
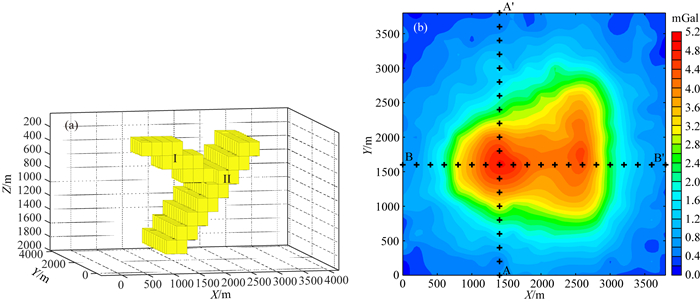
三维模型反演实验中,重力观测系统在X、Y方向的间距为200 m,观测网格X、Y方向的个数为20×20=400个.反演网格采用长方体剖分,剖分网格在X、Y、Z方向的大小为200 m×200 m×200 m,反演网格在X、Y、Z方向剖分为20×20×10=4000个网格单元.三维模型形态呈“Y”字型,由2个倾斜状地质体构成,如图 8a所示,参数见表 2.三维密度模型正演模拟获得的数据添加了3%的噪声作为观测数据,如图 8b所示.
|
图 8 三维密度模型及重力异常 (a) 三维密度模型;(b) 重力正演异常(含3%高斯噪声). Fig. 8 3D density model and gravity anomaly (a) 3D density model; (b) Gravity forward anomaly (including 3% Gaussian noise). |
|
|
表 2 “Y”字型地质体密度模型参数 Table 2 Parameters of Y-type geological body density model |
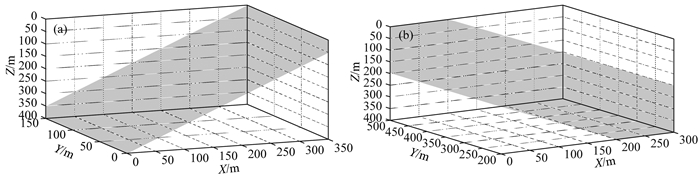
构建模型特征矩阵采用了两个三维特征模型,一是沿X轴正方向的向上右倾的三维特征模型a,如图 9a所示,另一个是沿X轴反方向的向上左倾的三维特征模型b,如图 9b所示.设置反演参数(λ1=1、λ2=1,最大迭代次数IterMax=200).
|
图 9 构建模型特征矩阵的三维特征模型 (a) 三维特征模型a;(b) 三维特征模型b. Fig. 9 3D feature model for building model feature matrix (a) 3D feature model a; (b) 3D feature model b. |
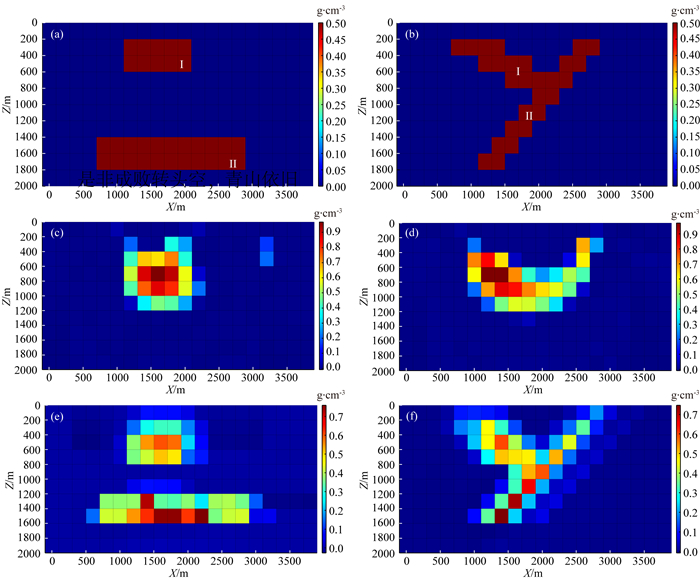
从该模型实验可看出,利用公式(5)获得的常规反演结果(图 10c、图 10d)虽然在中心埋深上与模型比较接近,且一定程度上体现了“Y”字型特征,但反演结果分辨率较低,且倾斜体II的形态与埋深均得不到较好的恢复;而观察本文方法得到的反演结果(图 10e、图 10f),虽然构建模型特征矩阵的两类倾斜形状特征模型并非与真实模型的倾斜异常体大小相同,但包含接近的倾斜状发育特征,该约束信息的引入使得反演过程中更加注重倾斜状密度异常体的生成,使得反演结果逼近原始模型的可能性大大增加,即便没有施加密度阈值约束,模型的分辨率与形态特征都与原始模型保持更高的一致性.
|
图 10 反演结果对比 (a) 理论模型A-A′垂直剖面;(b) 理论模型B-B′垂直剖面;(c) 聚焦反演A-A′垂直剖面;(d) 聚焦反演B-B′垂直剖面;(e) 本文方法A-A′垂直剖面;(f) 本文方法B-B′垂直剖面. Fig. 10 Comparison of inversion results (a) A-A′ profile of theoretical model; (b) B-B′ profile of theoretical model; (c) A-A′ profile of focus inversion; (d) B-B′ profile of focus inversion; (e) A-A′ profile of proposed method; (f) B-B′ profile of proposed method. |
通过二维及三维模型实验可看出,相比常规反演方法,利用本文所提方法得到的反演结果在分辨率和可靠性方面都得到了有效提升.
虽然在进行分解系数求解时,未知数的个数会有所增加,但是特征模型的引入反而在一定程度减少了密度模型的求解空间,这是由于期望获得的密度模型不仅需要考虑正演结果与实测数据的拟合,还需要满足由尽可能少的特征模型来组合得到;而且从重力异常解释效率的角度来看,本文所提方法可更加灵活、快速地施加密度模型约束信息,无需反复调整网格剖分方案及过多地调整重力异常分离参数,在一定程度上克服了求解分解系数带来的计算量增加的问题.
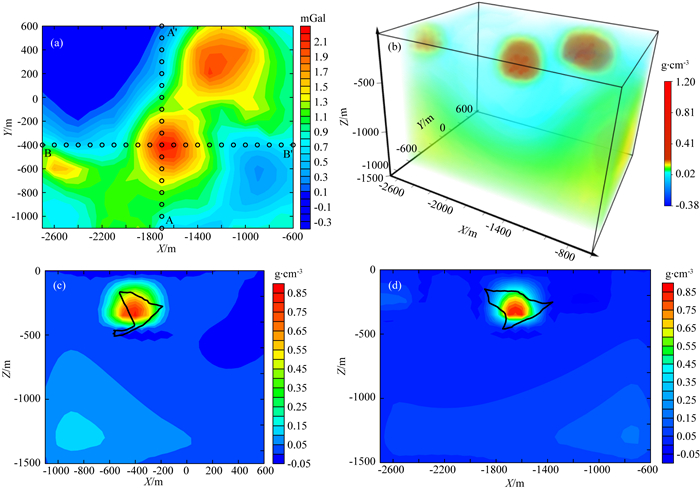
3 实际资料应用测试现将本文方法应用于墨西哥萨卡特卡斯州圣尼古拉斯硫化物铜锌矿区的重力实际资料.研究区的矿床赋存于镁铁质和长英质火山岩中,根据钻井及岩心资料可知该硫化物矿床具有高密度、高磁化率、高极化率和低电阻率的特点(Phillips et al., 2001),其中密度可达3.5 g·cm-3,较围岩大概有1.1~1.4 g·cm-3的密度差,且埋深较浅,便于利用重力勘探技术预测矿床的空间分布.工区重力测点数为198个,将其利用克里金插值为均匀网格异常(图 11a),X(东西,-2700~-600 m)、Y(南北-1100~600 m)方向间距分别为100 m、100 m,观测网格X、Y方向的个数为22×18=396个.
|
图 11 实际资料反演结果 (a) 剩余重力异常; (b) 密度三维反演结果; (c) A-A′垂直剖面反演结果;(d) B-B′垂直剖面反演结果. (c)—(d)中黑色多边形代表硫化物矿床的位置. Fig. 11 Inversion results of actual data (a) Residual gravity anomaly; (b) 3D inversion result of density; (c) The result of A-A′ vertical profile; (d) The result of B-B′ vertical profile.The sulphide location is indicated by the black polygon in (c)—(d). |
利用本文方法开展重力三维反演.首先将地下半空间沿X、Y、Z三个方向剖分为22×18×15=4000个网格单元,尺寸为100 m×100 m×100 m.第一个网格的位置X、Y、Z坐标位于(-2750 m,-1150 m,0 m).构建模型特征矩阵采用了三个长方体特征模型,在X、Y、Z方向的尺寸分别为300 m×300 m×300 m、800 m×200 m×400 m和1800 m×1200 m×200 m,前两个特征模型用于构建局部密度异常体,第三个特征模型用于拟合均匀的背景剩余密度.给定的分解系数初始模型为0.1,设置反演参数(λ1=1、λ2=1,最大迭代次数IterMax=200).
利用本文方法获得的密度反演三维结果如图 11b所示,经过矿床的南北A-A′的垂向剖面如图 11c所示,东西向垂直剖面B-B′如图 11d所示,密度反演结果与根据钻井资料获得的硫化物矿床地质认识(Phillips et al., 2001)十分吻合.对比国内外研究学者在该矿区开展的工作(Lelivere and Oldenburg, 2009;李泽林等,2019),反演结果在其他区域也恢复出了具有较高分辨率且更易解释的密度分布,有效验证了本文方法的适用性.分析原因,模型特征矩阵中引入的背景特征模型使得在三维反演结果中产生了较为合理的背景密度模型,在一定程度上消除了区域异常分离不准确的问题.与此同时,在分解系数的稀疏求解过程中,不同尺寸的特征模型得到优选,并用来逼近目标密度体,使得反演的可靠性得到了保证.进一步的,在实际资料应用中,针对不断细化的勘探工作需求,可尝试构建更精细的特征模型及模型特征矩阵,从而不断提升重力反演分辨率,逐步恢复出更符合真实情况的地质体密度空间分布.
4 结论本文提出了一种基于密度模型稀疏表征的重力反演方法.首先,将密度模型表征为模型特征矩阵和分解系数的乘积,其次,给出了由特征模型构建模型特征矩阵的技术流程,再次,重新构建重力反演目标函数,将直接求解密度模型问题转换为求解分解系数,最后,给出了分解系数的稀疏求解方法,实现了可有效融合地质模式信息、提高重力反演分辨率和可靠性的目的.理论模型实验和实际资料应用测试表明,相比常规聚焦反演算法,在反演目标包含多个地质体或剩余异常无法准确求取时,本文方法都可取得较好的应用效果.此外,本文所提出的模型约束方法并不仅限于重力反演,也为磁力、电法、地震等其他地球物理反演方法提供了一种灵活添加地质约束信息的有效途径.
附录A 基于Majorization-Minimization优化框架的分解系数稀疏求解根据正文1.3节中公式(8),原重力反演问题的目标函数写为关于分解系数Γ的最优化目标函数:
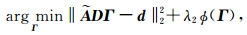
|
(A1) |
其中,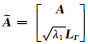
由于在稀疏求解时,ϕ(Γ)通常为一不可微的凸函数,现定义函数G(Γ)形式为:
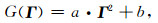
|
(A2) |
其中,a、b为常数.
可知函数G(Γ)是关于Γ的严格凸函数.
根据MM框架理论,可知在待求的Γ=Γv处,G(Γv)应满足如下假设:
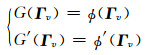
|
(A3) |
其中,Γv表示第v次迭代所对应的Γ值.
将公式(A3)代入公式(A2),则
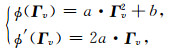
|
(A4) |
其中,a和b为常数项.
求解方程组(A4),可得a和b.
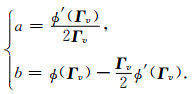
|
(A5) |
将公式(A5)代入公式(A2),G(Γ)可写为:
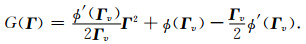
|
(A6) |
若Γ、Γv都为大小为q×1的向量,则根据MM思想:
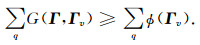
|
(A7) |
设
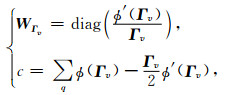
|
(A8) |
其中,WΓv为与第v次迭代求解结果对应的对角加权矩阵,c为与Γv有关的数值.
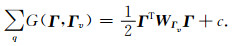
|
(A9) |
因此,原目标函数(A1)可表示为:
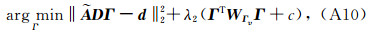
|
(A10) |
对其求最小二乘解,可得:
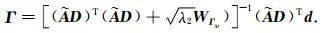
|
(A11) |
Bertete-Aguirre H, Cherkaev E, Oristaglio M. 2002. Non-smooth gravity problem with total variation penalization functional. Geophysical Journal International, 149(2): 499-507. DOI:10.1046/j.1365-246X.2002.01664.x |
Boyd S, Parikh N, Chu E, et al. 2010. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 3(1): 1-122. DOI:10.1561/2200000016 |
Chen S S, Donoho D L, Saunders M A. 2001. Atomic decomposition by basis pursuit. SIAM Review, 43(1): 129-159. DOI:10.1137/S003614450037906X |
Farquharson C G, Oldenburg D W. 1998. Non-linear inversion using general measures of data misfit and model structure. Geophysical Journal International, 134(1): 213-227. DOI:10.1046/j.1365-246x.1998.00555.x |
Farquharson C G. 2008. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics, 73(1): K1-K9. DOI:10.1190/1.2816650 |
Figueiredo M A T, Bioucas-Dias J M, Nowak R D. 2007. Majorization-minimization algorithms for wavelet-based image restoration. IEEE Transactions on Image Processing, 16(12): 2980-2991. DOI:10.1109/TIP.2007.909318 |
Gao X H, Huang D N. 2017. Research on 3D focusing inversion of gravity gradient tensor data based on a conjugate gradient algorithm. Chinese Journal of Geophysics (in Chinese), 60(4): 1571-1583. DOI:10.6038/cjg20170429 |
Guan Z N, Hou J S, Huang L P, et al. 1998. Inversion of gravity and magnetic anomalies using pseudo-BP neural network method and its application. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 41(2): 242-251. |
Last B J, Kubik K. 1983. Compact gravity inversion. Geophysics, 48(6): 713-721. DOI:10.1190/1.1441501 |
Lelièvre P G, Oldenburg D W. 2009. A comprehensive study of including structural orientation information in geophysical inversions. Geophysical Journal International, 178(2): 623-637. DOI:10.1111/j.1365-246X.2009.04188.x |
Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics, 61(2): 394-408. DOI:10.1190/1.1443968 |
Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data. Geophysics, 63(1): 109-119. DOI:10.1190/1.1444302 |
Li Z L, Yao C L, Zheng Y M. 2019. 3D inversion of gravity data using Lp-norm sparse optimization. Chinese Journal of Geophysics (in Chinese), 62(10): 3699-3709. DOI:10.6038/cjg2019M0430 |
Liu Z, Yu H Z, Chen T. 2011. 3D inversion method of density based on double constraint. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 35(6): 43-50. |
Meng X H, Liu G F, Chen Z X, et al. 2012. 3-D gravity and magnetic inversion for physical properties based on residual anomaly correlation. Chinese Journal of Geophysics (in Chinese), 55(1): 304-309. DOI:10.6038/j.issn.0001-5733.2012.01.030 |
Nguyen H D. 2017. An introduction to Majorization-Minimization algorithms for machine learning and statistical estimation. WIREs Data Mining and Knowledge Discovery, 7(3): e1198. |
Oldenburg D W, Li Y G, Ellis R G. 1997. Inversion of geophysical data over a copper gold porphyry deposit: A case history for Mt. Milligan. Geophysics, 62(5): 1419-1431. DOI:10.1190/1.1444246 |
Paterson N R, Reeves C V. 1985. Applications of gravity and magnetic surveys: The state-of-the-art in 1985. Geophysics, 50(12): 2558-2594. DOI:10.1190/1.1441884 |
Peng G M, Liu Z, Yu H Z, et al. 2018. 3D gravity inversion based on Cauchy distribution constraint and fast proximal objective function optimization. Chinese Journal of Geophysics (in Chinese), 61(12): 4934-4941. DOI:10.6038/cjg2018L0776 |
Phillips N, Oldenburg D, Chen J P, et al. 2001. Cost effectiveness of geophysical inversions in mineral exploration: Applications at San Nicolas. The Leading Edge, 20(12): 1351-1360. DOI:10.1190/1.1487264 |
Portniaguine O, Zhdanov M S. 1999. Focusing geophysical inversion images. Geophysics, 64(3): 874-887. DOI:10.1190/1.1444596 |
Qin P B, Huang D N. 2016. Integrated gravity and gravity gradient data focusing inversion. Chinese Journal of Geophysics (in Chinese), 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
Sahoo S K, Makur A. 2015. Signal recovery from random measurements via extended orthogonal matching pursuit. IEEE Transactions on Signal Processing, 63(10): 2572-2581. DOI:10.1109/TSP.2015.2413384 |
Selesnick I W, Bayram İ. 2014. Sparse signal estimation by maximally sparse convex optimization. IEEE Transactions on Signal Processing, 62(5): 1078-1092. DOI:10.1109/TSP.2014.2298839 |
Sun J J, Li Y G. 2014. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model. Geophysical Journal International, 197(2): 882-899. DOI:10.1093/gji/ggu067 |
Utsugi M. 2019. 3-D inversion of magnetic data based on the L1-L2 norm regularization. Earth, Planets and Space, 71(1): 73. DOI:10.1186/s40623-019-1052-4 |
Vatankhah S, Renaut R A, Ardestani V E. 2017. 3-D Projected L1 inversion of gravity data using truncated unbiased predictive risk estimator for regularization parameter estimation. Geophysical Journal International, 210(3): 1872-1887. DOI:10.1093/gji/ggx274 |
Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics (in Chinese), 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
Zhdanov M S. 2002. Geophysical Inverse Theory and Regularization Problems. Methods in Geochemistry and Geophysics. Amsterdam: Elsevier Science, 36: 3-609.
|
Zhdanov M S, Ellis R, Mukherjee S. 2004. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics, 69(4): 925-937. DOI:10.1190/1.1778236 |
Zhu Z Q, Cao S J, Lu G Y. 2014. 3D gravity inversion with bound constraint based on hyper-parameter regularization. The Chinese Journal of Nonferrous Metals (in Chinese), 24(10): 2601-2608. |
高秀鹤, 黄大年. 2017. 基于共轭梯度算法的重力梯度数据三维聚焦反演研究. 地球物理学报, 60(4): 1571-1583. DOI:10.6038/cjg20170429 |
管志宁, 侯俊胜, 黄临平, 等. 1998. 重磁异常反演的拟BP神经网络方法及其应用. 地球物理学报, 41(2): 242-251. DOI:10.3321/j.issn:0001-5733.1998.02.013 |
李泽林, 姚长利, 郑元满. 2019. 基于Lp范数稀疏优化算法的重力三维反演. 地球物理学报, 62(10): 3699-3709. DOI:10.6038/cjg2019M0430 |
刘展, 于会臻, 陈挺. 2011. 双重约束下的密度三维反演. 中国石油大学学报(自然科学版), 35(6): 43-50. |
孟小红, 刘国峰, 陈召曦, 等. 2012. 基于剩余异常相关成像的重磁物性反演方法. 地球物理学报, 55(1): 304-309. DOI:10.6038/j.issn.0001-5733.2012.01.030 |
彭国民, 刘展, 于会臻, 等. 2018. 基于柯西分布约束和快速近端目标函数优化的三维重力反演方法. 地球物理学报, 61(12): 4934-4941. DOI:10.6038/cjg2018L0776 |
秦朋波, 黄大年. 2016. 重力和重力梯度数据联合聚焦反演方法. 地球物理学报, 59(6): 2203-2224. DOI:10.6038/cjg20160624 |
姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
朱自强, 曹书锦, 鲁光银. 2014. 基于混合正则化的重力场约束反演. 中国有色金属学报, 24(10): 2601-2608. |
 2021, Vol. 64
2021, Vol. 64

