2. 中国石油天然气股份有限公司勘探开发研究院西北分院, 兰州 730000
2. The Research Institute of Petroleum Exploration and Development, Northwest Branch, Lanzhou 730000, China
速度分析是常规地震资料处理中的重要环节之一,主要包括叠加速度分析、偏移速度分析和速度层析反演等几种主要方法.其中,叠加速度作为速度分析中的重要内容,不但是地震资料常规叠加处理和时间偏移的必要过程,也是层析反演、叠前偏移、阻抗反演和全波形反演等初始速度模型建立的基础(杜启振等,2011;Zhang et al., 2015;Du et al., 2017;徐文君等,2017;Yuan et al., 2019).为了获得叠加速度场,需要在每个共中心点(CMP)道集对应的速度谱上进行拾取,现在普遍应用的方法是人工拾取.但是,人工拾取需要花费大量的时间,成本高昂,拾取效率较低,且拾取精度易受到人为经验的影响.这些问题在宽方位、高密度地震资料处理时显得更为突出.因此,在保证速度拾取精度的前提下,有必要研究一种快速且有效的自动拾取速度谱的方法,以减少地震资料处理人员的人工操作,提高速度拾取效率.
随着地震勘探程度的不断深入和技术条件的不断改善,自动拾取速度的研究有了一定的进展.目前发展的方法大部分可以分为优化搜寻和机器学习这两类.优化搜寻速度自动拾取方法本质上是一种反演类方法,主要是利用最优化算法和最大相似度量准则,设定一定的速度约束条件,对初始速度模型加以扰动,自动寻找速度谱中叠加能量的最优解.在自动拾取发展的早期,优化搜寻类方法发展迅速.Toldi(1989)最先提出了一种基于速度谱叠加能量的自动速度拾取方法,以最大化叠加能量和作为目标函数,反演得到速度场,但该方法假设模型线性化,也很难很好处理信噪比低的地区,需要进一步的约束.Zhang和Claerbout(1990)将非线性优化方法应用于速度拾取中;Zhang(1991)后续又对此方法做了进一步的优化.Lumley(1997)提出了一种利用蒙特卡洛随机扰动方法进行自动层速度的拾取.Meshbey等(2002)和Fomel(2009)将速度拾取视为一个变分问题,Almarzoug和Ahmed(2012)在其基础上发展了自动地震速度拾取方法.这些方法在获取相对简单地质体的速度时已经取得了一定的效果,但大部分方法依赖于初始层速度模型,并对于横向速度突变的地区,拾取准确性相对不高.还有些方法从振幅随偏移距变化(AVO)分析中挖掘速度信息,Swan(2001)在叠前道集中通过AVO分析提取特定属性特征,构建剩余速度指示器,从而迭代更新速度场.由于其方法的稳定性欠佳,适用范围有限,Ratcliffe和Roberts(2003)在此基础上增添了监控收敛准则,从而更能适应实际生产要求.基于叠前AVO分析的这类方法需要部分道准确速度作为初始模型,只能部分解决速度自动拾取问题.
近年来,由于计算机性能的显著提高,机器学习也被应用于速度自动拾取,主要有深度学习和聚类分析方法.根据不同特征的神经网络学习能力,Ma等(2018)及Park和Sacchi(2020)分别提出了基于卷积神经网络的叠加速度拾取方法;Biswas等(2018)及Fabien-Ouellet和Sarkar(2020)发展了基于循环神经网络的速度拾取方法;Zhang等(2019)利用长短期记忆网络(LSTM)算法提出了一种深度学习拾取速度方法.现有的深度学习拾取速度方法主要思路是通过学习大数据,用人工神经网络来建立CMP道集或速度谱数据(输入)和速度模型(输出)之间的非线性映射关系,模拟CMP道集或速度谱数据到速度的逆过程.在部分地区中能获得较高精度的速度场,但要学习大量且丰富的样本标签数据,对预测的输入数据质量和采样间隔等要求较高,且其预测过程和结果目前仍很难可解释.
聚类分析是无监督机器学习算法中的一种,可以挖掘数据中的隐含结构,对具有相同特征的数据进行分组,从而得到数据的大致分布.相比于深度学习方法,聚类算法不需要标签及训练网络,算法简洁,可解释性强.Smith(2017)利用多种属性特征划分出速度范围,并首次将聚类方法应用于速度谱自动拾取.K均值聚类算法是聚类分析方法中一种基本的划分式方法(MacQueen,1967;Hung et al., 2013;Ahmad and Hashmi, 2016),该算法简便易实现,且计算速度较快,通常被作为大样本聚类分析的首选算法,近年来也常被用于地震勘探中(Galvis et al., 2017;Araya-Polo et al., 2017).Song等(2018)提出了一种固定K值的智能速度拾取方法,以邻近道人工拾取速度作为筛选聚类范围的约束,并应用K均值算法进行聚类,能减少人工挑选的时间,从而降低处理数据集的成本.针对难以选取固定K值的问题,密度聚类等其他无监督方法也被应用到自动拾取速度方法中(Bin Waheed et al., 2019;Zhang and Lu, 2016).而Chen和Schuster(2018)则提出了一种自底向上的策略来实现K均值迭代过程,一定程度上解决了不同CMP道集选择不同K值的问题.但仍有两个问题需要解决:一是对于不同深度反射能量差异大的道集,如煤系地层沉积时,往往造成煤层和目标储层存在上下叠置关系,从而导致有效砂体反射信息淹没于煤层反射(田忠斌等,2016;李勤等,2019),容易会忽视弱反射的速度拾取;二是聚类范围的筛选至关重要,经典的K均值聚类算法容易受到噪声和离群点的影响,使得聚类中心偏离主要数据区域,从而使得速度拾取精度受到影响.
因此,本文提出了一种基于自适应阈值约束的无监督聚类智能速度拾取方法,减少人工劳动,提高速度拾取效率并确保其拾取精度.根据速度谱中不同深度的能量团聚焦特征,采用时窗方法在速度谱中计算自适应阈值,从而识别出一次反射波速度能量团作为速度拾取的候选区域.然后,根据K均值算法将不同的速度能量团聚类,并将聚类中心作为拾取的叠加速度,实现速度的自动拾取.同时,根据人工拾取经验设计了离群速度处理环节,以获得更为光滑的速度场.最后,数值模型和实际地震数据验证了该方法的可行性,并获得了较高的拾取精度.
1 方法原理首先,我们简单介绍地震资料处理中人工拾取叠加速度的基本过程:根据CMP道集计算速度谱,识别出不同时间位置的速度能量团,拾取能量团中心点(中浅层的速度能量团一般为峰值点),对拾取的时间速度对进行插值即得到叠加速度曲线.不难发现识别速度能量团和拾取中心点是从速度谱中拾取叠加速度的关键.因此,无监督聚类智能速度拾取的思路主要是围绕这两项内容类比并模拟人工速度拾取过程.一是在速度谱中,根据一定的规则识别出一次反射速度能量团作为速度拾取的候选区域,二是应用聚类算法对此区域样本进行聚类,并拾取中心点.为了避免噪声等因素的影响,根据叠加速度的基本变化规律和人工拾取经验,加入了离群速度处理环节.
1.1 自适应确定速度拾取候选区任何地下地层之间存在的波阻抗差异均会引起地震反射,而不同岩性的地层界面引起的反射能量可能会存在较大差异(马水平等,2010),导致在同一CMP道集中强弱反射相间存在,进而不同深度的速度能量团能量有较大的变化.而目前的聚类速度自动拾取方法(Chen and Schuster, 2018)是在整个速度谱的基础上,设定统一的阈值确定速度拾取候选区,固定的阈值使得其拾取精度不仅一定程度上受到速度能量团聚焦性的制约,且拾取时容易忽视弱反射速度能量团.为了尽可能识别到所有有效的一次反射速度能量团,同时保留强反射和弱反射,我们设计了一种滑动窗方法对速度谱进行处理.先定义速度谱矩阵S(从上至下对应时间增加,而从左至右对应速度增大),即
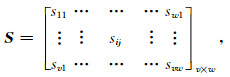
|
(1) |
其中,sij为速度谱矩阵S中第i行第j列的速度能量团幅值,i=1, 2, …, v表示时间位置,j=1, 2, …, w表示速度位置.对速度谱矩阵S进行加窗处理,定义为窗速度谱Sσi为
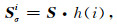
|
(2) |
其中,h(i)为一给定的窗函数,随着时间变化而向下滑动,得到一系列的窗速度谱,即每个时间点处都有对应的窗速度谱矩阵Sσi.在本文中,选取窗长为dwin的矩阵窗作为窗函数,具体形式如下
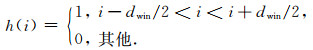
|
(3) |
将式(2)中得到的一系列窗速度谱矩阵Sσi作为计算阈值σ(i)的输入,由于窗速度谱内仅涵盖了在时间点i附近的局部速度能量团幅值,因此选取的阈值仅与窗内的局部速度能量团幅值相关,从而避免其他时间位置的能量团的干扰.阈值σ(i)可定义为第i个时间点处的窗内速度谱Sσi的上分位数,即
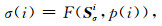
|
(4) |
其中,p(i)为阈值百分比,F(X, y)为求上分位数函数,表示对矩阵X中找到某一数值,使得在矩阵内有y%的数据小于此数值,从而式(4)表示窗速度谱Sσi内有p(i)%的速度能量值sij小于阈值σ(i).因此,阈值σ(i)的物理意义可表示为以速度能量值作为划分原则,在窗内速度谱中区分速度拾取候选区与噪声的分界值.速度谱中大于阈值σ(i)的sij被视为速度拾取候选区,小于阈值σ(i)的sij被视为噪声.加窗后计算的阈值σ(i)并不是某一固定值,随着局部速度能量团幅值的变化可以自适应变化,从而对应的速度拾取候选区一定程度上能提高弱反射的识别几率,缩小强反射的速度拾取候选区范围.
根据反射波双曲线的几何特征,速度和深度是影响其双曲线形态的主要因素.常规速度谱的生成本质上是一个应用不同时间速度对扫描进行动校正并计算叠加能量的过程(Neidell and Taner, 1971).然而不同深度的双曲线走时对速度变化敏感度不一,在相同的速度变化中位于中浅层的双曲线走时变化幅度更剧烈,从而导致其不同时窗间的叠加能量差异大,最终计算的该位置速度能量团聚焦性高,即速度谱中浅层对速度变化敏感.因此在深度和速度的共同影响下,实际数据中速度能量团聚焦性逐渐下降,横向宽度增大,速度分辨率降低.根据这一特点,实际应用中浅层速度的拾取精度要求高,而深层速度能量团聚焦性差,拾取精度要求相对较低.我们结合这一特征设计阈值百分比p(i)为

|
(5) |
其中,pmin为最小百分比阈值,pmax为最大百分比阈值.pmin和pmax的取值遵循的基本原则是p=pmax时需要能筛选出较为聚焦的浅层能量团,而p=pmin需要能筛选出有一定宽度且有递增趋势的深层能量团,具体取值可以根据速度谱能量团的分布试验而定.从上式可以看出,p(i)与深度呈负相关,深度增加,阈值百分比减小,从而降低了阈值门槛,扩大了深层速度拾取候选区范围,这基本符合实际速度谱中能量团的变化特征.同时,在浅层动校正对速度误差敏感,较小的阈值百分比p可以提高浅层速度拾取精度;而在深层人工拾取的速度并不一定在能量团峰值处,较大的阈值百分比p扩大了拾取候选区范围,更符合人工拾取经验.
最后,用自适应阈值σ(i)对速度谱Sσi进行二值化处理,得到速度拾取候选区xij为
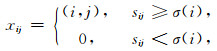
|
(6) |
其中,xij表示大于阈值时,速度谱中能量团sij对应的时间速度对的位置坐标.经过阈值门槛的筛选,将速度谱矩阵降维,仅保留非零时间速度对xij作为速度拾取候选区.
1.2 K均值聚类速度拾取在识别速度能量团后,我们应用聚类算法降维后的侯选区进行聚类,并拾取能量团中心点.在本文中,选取应用广泛的K均值算法进行聚类.将速度拾取候选区X={xij}作为聚类的输入数据集,并选取速度初始类别K及初始聚类中心mk0,其中k=1, 2, …, K表示聚类的序号.每个数据点xij与K个聚类中心mk0的距离为

|
(7) |
其中,dk表示欧氏距离.按照距离最小原则进行划分,将数据点划分到与其距离最近的聚类中心所在的类.所有数据点分类后,重新计算k个聚类中每个聚类的全部数据点的平均值,该平均值所在的数据点成为新的聚类中心.其中,新的聚类中心可写为
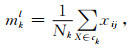
|
(8) |
其中,ck为第k类的所有数据点的合集,Nk为第k类中的总数据点数,上标l=1, 2, …, L为迭代次数.在确定新的聚类中心后,计算每个类别中数据点与聚类中心的距离和,其目标函数J为
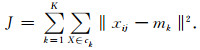
|
(9) |
然而在实际数据中,不同叠前道集中的速度谱所需拾取的能量团个数不一致,针对这一问题,我们选取一种自底向上的迭代策略来求取目标函数最佳解.即先给定一个初始类别数K0,按照初始聚类中心的分布,将数据点初步分为K0类,并逐步迭代找到聚类类别最少的聚类分布,聚类中心个数在迭代过程中逐步减小.其具体迭代过程如下:
(1) 参数初始化,给定初始类别K0值及聚类中心mk0;
(2) 由式(7)计算距离,按照最小距离原则将数据点进行重新分类.对于未分配到数据点xij的类别ck,剔除所在类别对应的聚类中心,不参与下次迭代,同时总聚类数相应减小;
(3) 根据式(8)逐个类别重新计算新的聚类中心;
(4) 重复步骤(2)和步骤(3),直到目标函数满足收敛要求.
多次迭代后,所有数据对象聚类完毕,最终得到KL个聚类中心,其对应的聚类中心M ={m1L,m2L,…, mKLL}对应的速度值即为拾取的叠加速度.因此,不同的CMP道集只需确定初始K0值,最终聚类中心个数不唯一,由此能一定程度上避免K值选取问题.最后,将拾取的速度点插值即为拾取的叠加速度曲线.
1.3 离群速度处理K均值聚类算法中每个聚类的中心都由每个聚类里所有数据点求均值得到.当存在一定噪声(如多次波、野值等)时,聚类中心易受干扰,偏离速度能量团峰值,影响聚类效果.因此,为了获得更接近人工拾取的速度场,在实际应用时我们对离群速度进行了后处理.人工拾取速度经验指出,一般情况下叠加速度会随着时间的增加而增大,即使在速度倒转的情况下,速度倒转也有一定范围(Han et al., 2007;Yan et al., 2016;Sun and Zhang, 2020).基于速度谱的以上两个特征,判断速度是否倒转的准则qk如下:

|
(10) |
其中,ymk为拾取速度mk处的位置纵坐标,xmk为拾取速度mk处的位置横坐标,将拾取的速度点与邻近点相比较,判断出是否为速度倒转点.若mk为速度倒转点且速度倒转变化范围大于判断值,则去除速度异常点.
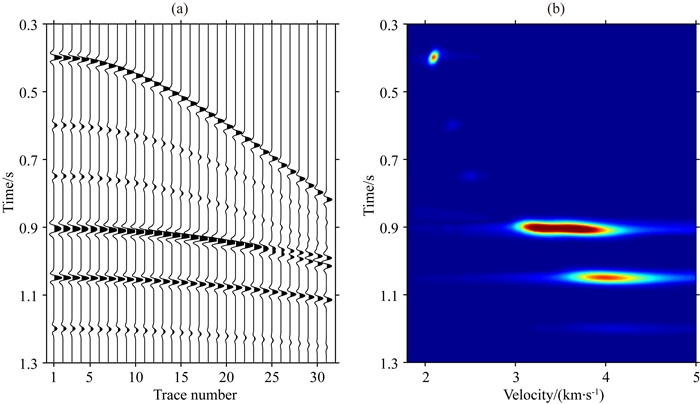
2 例子 2.1 一维数值模型测试为了测试提出方法的可行性,首先使用一维数值模型进行测试.如图 1a为一个预定义速度模型创建的CMP道集.该道集由主频为30 Hz的零相位雷克子波经射线追踪方法数值模拟获得,共包含了1300个时间采样点和31道,采样间隔为1 ms,道间距为50 m.为了测试本方法对弱反射的速度拾取能力,模型中设计了3个弱反射同相轴(0.6 s、0.75 s和1.2 s)和4个强反射同相轴相间分布.在0.9 s及0.91 s处有两个位置相近的同相轴,用于测试该方法在子波干涉时的速度拾取准确性.对图 1a中的CMP道集进行速度分析,得到速度谱(图 1b).从图 1b可以看出,弱反射的速度能量团能量远小于其他同相轴,而两个干涉同相轴(0.9 s和0.91 s)的速度能量团混叠在了一起.此外,由于不同深度速度敏感性不同,相比于浅层的能量团,深层的能量团速度方向分辨率更低.
|
图 1 一维数值模型 (a) CMP道集;(b) 速度谱. Fig. 1 One dimensional model (a) CMP gather; (b) Velocity spectrum. |
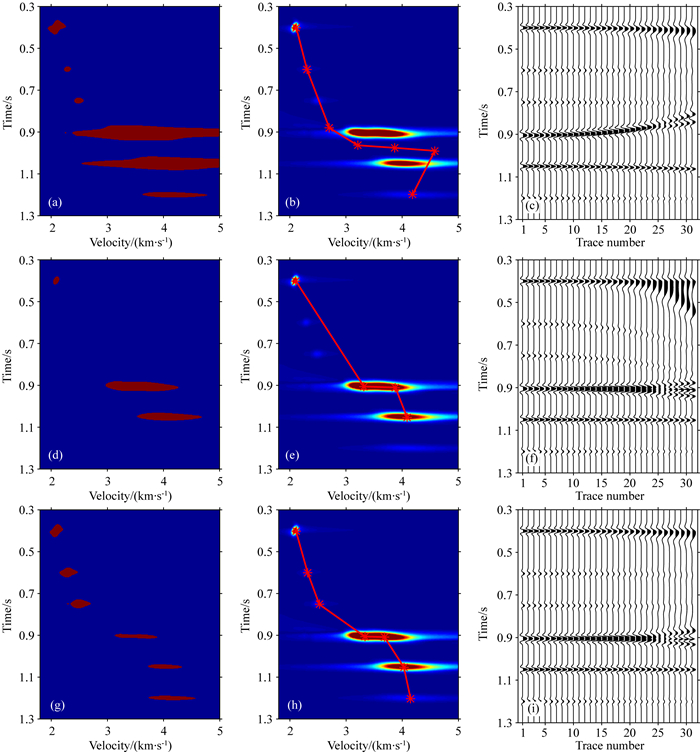
应用自适应阈值和固定阈值的无监督聚类方法(Chen and Schuster, 2018)进行智能速度拾取,并将拾取的速度进行动校正.根据速度谱能量团的大致分布,两种方法均选定初始类别K0为12,由于速度谱中能量团分布较为稀疏,在自适应阈值方法中选取较大的滑动窗窗长dwin为100 ms,而为了进一步说明常规聚类方法的局限性,比较了两种不同固定阈值(p=90%和p=95%)对聚类效果的影响.图 2(a—f)为常规聚类方法中两种阈值情况下的速度拾取候选区、速度拾取结果和动校正后的道集.在常规聚类方法中,为了拾取到弱反射速度能量团,先测试了较小的固定阈值百分比(p=90%)进行速度拾取,较小的p其对应阈值偏小,增大了深层能量团样本量(图 2a中红色部分),从而增加了后续智能速度拾取的运算量.同时,K均值算法易于将密集的、球状或团状的数据聚类,筛选的速度拾取候选区也需要符合这一特征,而p偏小时筛选的深层候选区范围并不聚焦,由此易拾取到多个聚类中心,显著降低深层速度拾取准确性(图 2b),经动校正后0.9 s及0.91 s处同相轴显著向上弯曲.当选取较大的固定阈值百分比(p=95%)时,较大的p其对应阈值偏大,只能兼顾能量较强的速度能量团,筛选速度拾取候选区时忽视了弱反射能量团(图 2d),浅层的2个弱反射和深层的1个弱反射都未能拾取到速度(图 2e),不利于速度曲线的精细刻画,也降低了拾取精度.从而0.8s以上的浅层同相轴明显校正不足,同相轴向下弯曲严重(图 2f).图 2(g—i)为自适应阈值方法的速度拾取及动校正结果,自适应阈值在识别能量团时,强度不同的速度能量团均能被识别(图 2g),所有反射的速度能量团均被包含在候选区内.因此,本文方法仍能拾取到正确速度(图 2h),即使在0.9 s处左右两个干涉同相轴情况下,且动校正后同相轴基本被拉平(图 2i).需要注意的是,由于K均值算法其划分准则是欧氏距离,本质上更适用于密集的、球状或团状的数据聚类,而速度能量团并不是标准的圆,处于深层的能量团形状更接近于椭圆,因此同一能量团可能被分为两类.而在0.9 s处左右两个干涉同相轴的速度能量团在此情况下,综合初始模型影响拾取到两个聚类中心.
|
图 2 不同方法拾取速度比较 (a) 常规聚类方法确定的速度拾取候选区(p=90%);(b) 在(a)中拾取的叠加速度;(c) 应用(b)中速度动校正后道集;(d) 常规聚类方法确定的速度拾取候选区(p=95%);(e) 在(d)中拾取的叠加速度;(f) 应用(e)中速度动校正后道集;(g) 自适应阈值方法确定的速度拾取候选区;(h) 自适应阈值方法拾取的叠加速度;(i) 应用(h)中速度动校正后道集. Fig. 2 Comparison of velocities picked by different methods (a) Candidate set selected by the conventional method (p=90%); (b) Stacking velocity curve picked on (a); (c) NMO gather corrected by the velocity picked in (b); (d) Candidate set selected by the conventional method (p=95%); (e) Stacking velocity curve picked on (d); (f) NMO gather corrected by the velocity picked in (e); (g) Candidate set selected by the proposed method; (h) Stacking velocity curve picked by the proposed method; (i) NMO gather corrected by the velocity picked in (h). |
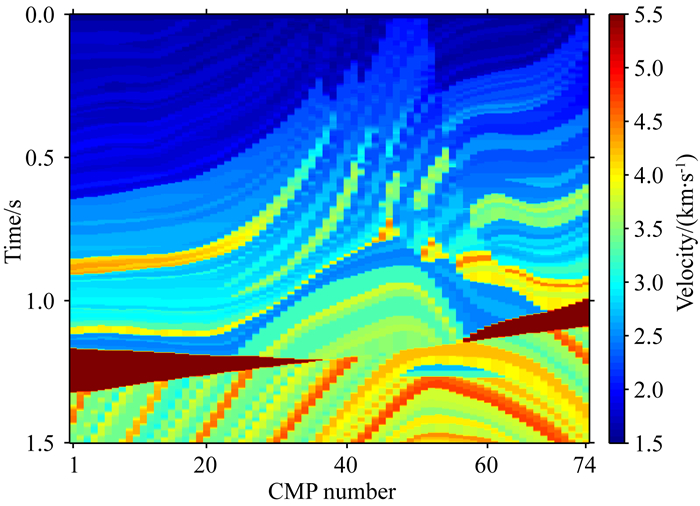
为了进一步证明本文方法复杂模型中的有效性,我们对二维的Marmousi模型(Martin et al., 2006)进行测试.在Marmousi模型中等间隔抽取了74道作为本次测试的真实层速度场(图 3),进而由速度模型和Gardner密度公式正演得到一系列CMP道集.根据速度谱能量团的大致分布规律(能量团个数,单个能量团延续时长等),两种方法均选定初始类别K0为15,并通过多次试验,在自适应阈值方法中选取滑动窗窗长dwin为40ms,最小阈值百分比pmin=85%,最大阈值百分比pmax=95%,而在常规聚类方法选取了固定阈值百分比p=90%.
|
图 3 层速度场模型 Fig. 3 Interval velocity model |
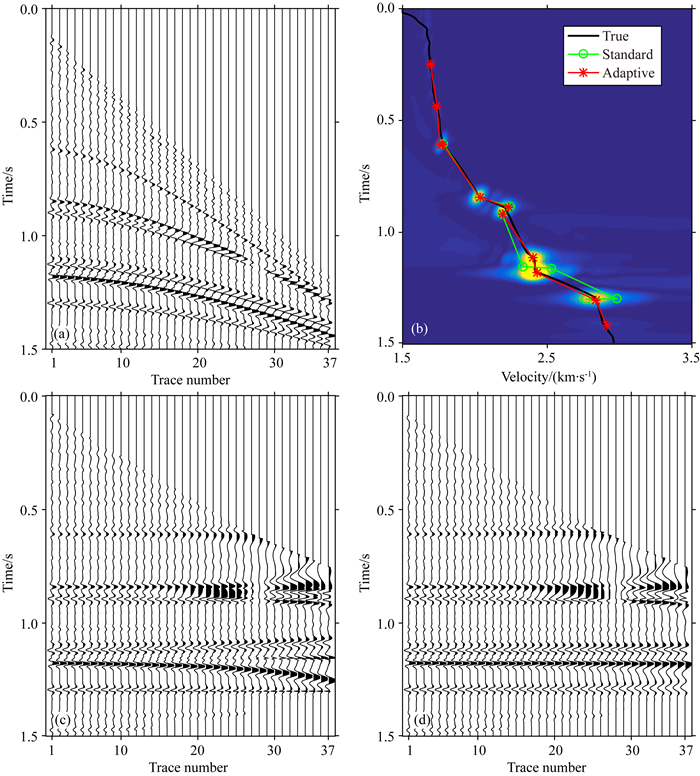
图 4(a, b)分别展示了Marmousi模型中第10道的CMP道集及常规聚类方法拾取的叠加速度(绿线)、本文方法拾取的叠加速度(红线)和真实均方根速度(黑线)的对比.在CMP道集中,浅层和深层反射波能量差异大,速度谱中不同深度的能量团间幅值相差较大,深层反射波能量强,0.5 s以上存在若干弱反射.在此情况下,本文方法拾取的速度仍与真实值基本一致,且相较于常规聚类方法,在深层(约1.2 s)和弱反射(约0.4 s)处拾取的速度均准确性更高.应用两种方法所拾取的速度场进行动校正,如图 4(c, d)所示.从动校正后的道集中可以看出,本文拾取的速度拉平了所有同相轴,证明了算法的有效性,也验证了速度拾取的正确性.而常规方法拾取的速度偏离真实值,其动校正后道集在深层约1.2 s处同相轴出现上翘现象.
|
图 4 Marmousi模型中的单道CMP拾取结果 (a) CMP道集;(b) 两种方法自动拾取的速度曲线;(c) 常规聚类方法后动校正;(d) 本文方法拾取速度动校正. Fig. 4 CMP gathers and the corresponding velocity curves picked by two different methods (a) CMP gather; (b) Automatic estimated stacking velocity curves corresponding to two methods; (c) NMO gather corrected by the conventional automatic estimated stacking velocity; (d) NMO gather corrected by the proposed automatic estimated stacking velocity. |
对整个Marmousi模型重复上述单道的处理流程,得到了两种不同方法自动拾取的叠加速度场.图 5展示了Marmousi模型真实均方根速度场(图 5a)、常规聚类方法拾取的速度场(图 5b)和自适应阈值方法拾取的速度场(图 5c).总体上看,常规方法在两侧楔状体等构造位置拾取精度较低(如蓝色箭头所示),且速度场横向上连续性差,如黑色箭头指示的CMP道拾取到速度异常值,与相邻道差异大.而自适应阈值方法拾取的速度场在构造走势上基本与真实值一致,在大部分道上比常规聚类方法的拾取精度更高,对于楔状体等构造细节刻画地更为准确,速度场变化较为连续.为了更直观看到两种方法速度拾取精度上的差异,我们应用图 5中的三个速度场进行叠加,其叠加剖面如图 6所示.与常规聚类方法(图 6b)相比,本文方法的叠加剖面(图 6c)能更清晰地反映出主要地质构造,尤其是在速度拾取精度更高的位置(如红色椭圆内),动校正后同相轴被拉平同相叠加,清晰地成像出了在1.3 s处的楔状体.

|
图 5 拾取的速度场与真实速度场比较 (a) 真实速度场;(b) 常规聚类方法拾取的速度场;(c) 自适应阈值方法拾取的速度场. Fig. 5 Comparisons of picked stacking velocity structures and the true reference (a) True stacking velocity structure; (b) Velocity structure picked by the conventional method; (c) Velocity structure picked by the adaptive threshold method. |

|
图 6 Marmousi模型叠加剖面 (a) 真实速度场叠加;(b) 常规聚类方法速度场叠加;(c) 自适应阈值方法速度场叠加. Fig. 6 Stacked sections of picked stacking velocity structures and the true reference (a) Stacked section obtained by true velocity field; (b) Stacked section obtained by the conventional method; (c) Stacked section obtained by the adaptive threshold method. |
最后,采用了一条陆上的二维实际测线对本文方法进行测试,该测线共包含500个CMP道集.每个CMP道集的偏移距及道数不等,数据的时间总长度2.5 s,采样间隔为1 ms.根据速度谱能量团的大致分布,两种方法均选取初始类别K0为12,自适应阈值方法中选取滑动窗窗长dwin为300 ms,而在常规聚类方法选取了固定阈值百分比为90%.由于实际数据噪声较多,为了保证速度模型具有一定光滑性,在速度拾取后对离群速度进行了处理,去除了大于5%的速度倒转异常值.
图 7展示了CMP 100和225道集的速度拾取结果及动校正道集.图 7(a—d)展示了在CMP 100道集中,三种方法拾取速度曲线比较以及常规聚类方法和自适应阈值方法的动校正后道集.从叠前CMP道集可以看出,浅层信噪比高,深层信噪比较低,因而本文方法在浅层拾取精度更高.从速度谱可以看出,在0.5 s处均存在高速速度异常,常规方法速度拾取范围包含了部分高速异常值,而最终的聚类的中心是本类中所有数据点的均值,受部分高速值影响,导致拾取的聚类中心向异常值靠拢,降低了拾取精度.而本文中的阈值是随时间深度变化而变化,在同一时间位置能对异常速度能量有一定的抑制作用,避开了高速速度异常.动校正后,本文中的方法(图 7c)在0.6 s左右,反射同相轴被拉平,而常规聚类方法0.6 s处校正不足,同相轴向下弯曲.图 7(e—h)分别为三种方法对CMP 225道集进行拾取的速度曲线比较,以及常规聚类方法和自适应阈值方法的动校正后道集比较.相比于CMP 100道集,CMP 225道集(图 7e)的反射波能量从浅到深差异小,常规聚类方法与本文方法在主要反射处拾取的速度精度相近(图 7f).但常规聚类方法在0.2 s处拾取的速度远偏离人工拾取值(图 7f),其对应的同相轴也未被拉平(图 7h).而本文方法浅层未拾取到速度异常值,且在弱反射(2s左右)处拾取的速度更接近人工拾取值,基本拉平了同相轴(图 7g).

|
图 7 实际数据CMP道集速度拾取及动校正结果 (a) CMP 100道集;(b) CMP 100道集的速度拾取结果;(c) 本文方法拾取速度对(a)进行动校正后道集;(d) 常规聚类方法拾取速度对(a)进行动校正后道集;(e) CMP 225道集;(f) CMP 225道集的速度拾取结果;(g) d本文方法拾取速度对(e)进行动校正后道集;(h) 常规聚类方法拾取速度对(e)进行动校正后道集. Fig. 7 Velocity picking and NMO results of field data (a) CMP 100 gather; (b) Estimated stacking velocity of CMP 100; (c) NMO result of (a) using velocity picked by the proposed method; (d) NMO result of (a) using velocity picked by the conventional method; (e) CMP 225 gather; (f) Estimated stacking velocity of CMP 225; (g) NMO result of (e) using velocity picked by the proposed method; (h) NMO result of (e) using velocity picked by the conventional method. |
在构建速度场时,由于拾取工作量较大,因此仅人工拾取了20道,CMP间隔为25,而智能方法可以逐点进行拾取,考虑到速度场光滑性问题,最终选择以5个CMP点为间隔进行拾取.图 7展示了人工拾取速度场(图 8a)、常规聚类方法拾取的速度场(图 8b)和本文方法拾取的速度场(图 8c)的比较.从图可看出,受噪声等因素的影响,常规聚类方法拾取速度场(图 8b)横向上连续性差,且在0.5~1 s处部分道拾取到了高速异常值,准确度较低.图 8c为本文方法拾取的速度场,速度变化趋势与人工拾取的速度场基本一致,与人工拾取结果(图 8a)基本吻合,但总用时是人工拾取的约0.1倍,平均单道拾取用时是人工拾取的0.02倍,拾取效率高.

|
图 8 实际数据速度场对比 (a) 人工拾取速度场;(b) 常规聚类方法拾取速度场;(c) 自适应阈值方法拾取速度场. Fig. 8 Comparisons of picked stacking velocity structures from field data (a) Velocity structure picked by the manual picking; (b) Velocity structure picked by the conventional method; (c) Velocity structure picked by the adaptive threshold method. |
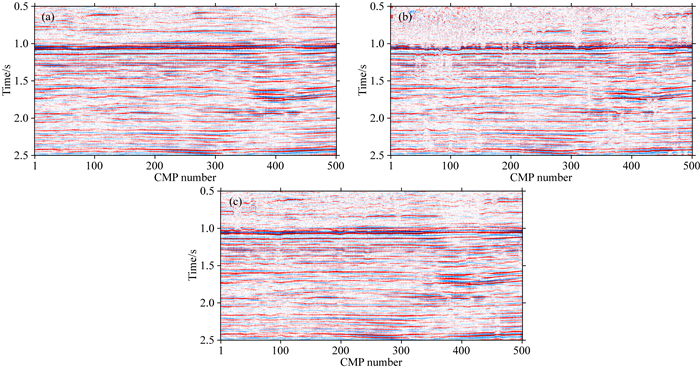
为了进一步检验拾取结果的正确性,应用图 7中三种方法拾取的速度场进行动校正和叠加处理.从叠加剖面(图 9)可以看出,本文方法的叠加剖面(图 9c)与人工结果(图 9a)相近,在0.7 s及1 s处的同相轴明显比常规聚类方法(图 9b)更连续,成像更清晰.
|
图 9 三种方法实际数据叠加剖面 (a) 人工拾取速度的叠加剖面;(b) 常规聚类方法拾取速度的叠加剖面;(c) 自适应阈值方法拾取速度的叠加剖面. Fig. 9 Stacked sections corresponding to three methods (a) Stacked section obtained by the manual picking; (b) Stacked section obtained by the conventional method; (c) Stacked section obtained by the adaptive threshold method. |
本文通过类比人工速度谱拾取过程,提出了一种基于自适应阈值约束的无监督聚类智能速度拾取方法.该方法利用时窗方法在速度谱中计算自适应阈值,从而识别出一次反射速度能量团作为速度拾取的候选区域.随后K均值聚类方法将不同的速度能量团聚类,并拾取叠加速度.最后,依据人工拾取速度的经验,对离群速度点进行后处理,为解决地震资料速度谱自动拾取问题提供了一种新的方案.
例子表明本文方法整体与人工拾取的精度相当,对速度变化的跟踪较为准确,能够快速拾取叠加速度曲线,比人工拾取快约50倍数量级,提高了拾取效率,降低了人工成本,为多维数据体逐点拾取速度场提供了可能.同比常规聚类智能拾取方法,自适应阈值的引入提高了识别速度能量团精度,主要体现在识别弱反射,适用于拾取同一CMP道集内能量强弱相间的反射波速度.离群速度处理这一步骤能规避部分速度异常值,以获得更光滑的速度场,更符合人工解释常识,避免加剧动校正子波拉伸现象.但本文方法在一定程度上仍受到速度谱精度以及逐个CMP道集处理方式的限制,下一步工作是从CMP道集角度以及多个CMP同时处理角度出发建立速度场,从而进一步提高实际速度拾取精度.
Ahmad A, Hashmi S. 2016. K-Harmonic means type clustering algorithm for mixed datasets. Applied Soft Computing, 48: 39-49. DOI:10.1016/j.asoc.2016.06.019 |
Almarzoug A M, Ahmed F Y. 2012. Automatic seismic velocity picking.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1-5.
|
Araya-Polo M, Dahlke T, Frogner C, et al. 2017. Automated fault detection without seismic processing. The Leading Edge, 36(3): 208-214. DOI:10.1190/tle36030208.1 |
Bin Waheed U, Al-Zahrani S, Hanafy S M. 2019. Machine learning algorithms for automatic velocity picking: K-means vs. DBSCAN.//89th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 5110-5114.
|
Biswas R, Vassiliou A, Stromberg R, et al. 2018. Stacking velocity estimation using recurrent neural network.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2241-2245.
|
Chen Y Q, Schuster G. 2018. Automatic semblance picking by a bottom-up clustering method.//SEG Maximizing Asset Value Through Artificial Intelligence and Machine Learning, SEG Global Meeting Abstracts, 44-48.
|
Du Q Z, Li F, Hou B, et al. 2011. Angle-domain migration velocity analysis based on elastic-wave Kirchhoff prestack depth migration. Chinese Journal of Geophysics (in Chinese), 54(5): 1327-1339. DOI:10.3969/j.issn.0001-5733.2011.05.022 |
Du Q Z, Guo C F, Zhao Q, et al. 2017. Vector-based elastic reverse time migration based on scalar imaging condition. Geophysics, 82(2): S111-S127. DOI:10.1190/geo2016-0146.1 |
Fabien-Ouellet G, Sarkar R. 2020. Seismic velocity estimation: A deep recurrent neural-network approach. Geophysics, 85(1): U21-U29. DOI:10.1190/geo2018-0786.1 |
Fomel S. 2009. Velocity analysis using AB semblance. Geophysical Prospecting, 57(3): 311-321. DOI:10.1111/j.1365-2478.2008.00741.x |
Galvis I S, Villa Y, Duarte C, et al. 2017. Seismic attribute selection and clustering to detect and classify surface waves in multicomponent seismic data by using k-means algorithm. The Leading Edge, 36(3): 239-248. DOI:10.1190/tle36030239.1 |
Han D H, Zhao H Z, Yao Q L, et al. 2007. Velocity of heavy-oil sand.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1619-1623.
|
Hung C H, Chiou H M, Yang W N. 2013. Candidate groups search for K-harmonic means data clustering. Applied Mathematical Modelling, 37(24): 10123-10128. DOI:10.1016/j.apm.2013.05.052 |
Li Q, Li Y B, Li Q C. 2019. Seismic response of anisotropic coal beds with vertical cracks. Chinese Journal of Geophysics (in Chinese), 62(1): 306-315. DOI:10.6038/cjg2019M0006 |
Lumley D E. 1997. Monte Carlo automatic velocity picks. Stanford Exploration Project, 75(17): 1-25. |
Ma S P, Wang Z H, Tian Y L, et al. 2010. Studies on geological meaning of seismic reflection events. Journal of Geophysics and Engineering (in Chinese), 45(3): 454-457. |
Ma Y, Ji X, Fei T W, et al. 2018. Automatic velocity picking with convolutional neural networks.//88th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2066-2070.
|
MacQueen J. 1967. Some methods for classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1: 281-297. |
Martin G S, Wiley R, Marfurt K J. 2006. Marmousi2:an elastic upgrade for Marmousi. The Leading Edge, 25(2): 156-166. DOI:10.1190/1.2172306 |
Meshbey V, Ragoza E, Kosloff U E, et al. 2002. Three-dimensional travel-time calculation based on Fermat's principle. Pure and Applied Geophysics, 159(7-8): 1563-1582. DOI:10.1007/s00024-002-8697-8 |
Neidell N S, Taner M T. 1971. Semblance and other coherency measures for multichannel data. Geophysics, 36(3): 482-497. DOI:10.1190/1.1440186 |
Park M J, Sacchi M. 2020. Automatic velocity analysis using convolutional neural network and transfer learning. Geophysics, 85(1): V33-V43. DOI:10.1190/geo2018-0870.1 |
Ratcliffe A, Roberts G. 2003. Robust, automatic, continuous velocity Analysis.//73rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2080-2083.
|
Smith K. 2017. Machine learning assisted velocity autopicking.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 5686-5690.
|
Song W, Ouyang Y L, Zeng Q C, et al. 2018. Unsupervised machine learning: K-means clustering velocity semblance auto-picking.//80th EAGE Annual International Meeting, Extended Abstracts, doi: https://doi.org/10.3997/2214-4609.201800919.
|
Sun M Y, Zhang J. 2020. The near-surface velocity reversal and its detection via unsupervised machine learning. Geophysics, 85(3): U55-U63. DOI:10.1190/geo2019-0025.1 |
Swan H W. 2001. Velocities from amplitude variations with offset. Geophysics, 66(6): 1735-1743. DOI:10.1190/1.1487115 |
Tian Z B, Zhang Y B, Wang J Q, et al. 2016. Study on the pre-stack seismic inversion prediction method for rich coal-bed-gas reservoirs: a case in southeastern Shanxi province. Chinese Journal of Geophysics (in Chinese), 59(12): 4494-4504. DOI:10.6038/cjg20161212 |
Toldi J L. 1989. Velocity analysis without picking. Geophysics, 54(2): 191-199. DOI:10.1190/1.1442643 |
Xu W J, Yin J F, Wang H Z, et al. 2017. Automatic estimation of stacking velocity based on sparse inversion. Chinese Journal of Geophysics (in Chinese), 60(7): 2791-2800. DOI:10.6038/cjg20170724 |
Yan F Y, Han D H, Yao Q L, et al. 2016. Seismic velocities of halite salt: Anisotropy, heterogeneity, dispersion, temperature, and pressure effects. Geophysics, 81(4): D293-D301. DOI:10.1190/geo2015-0476.1 |
Yuan S Y, Wang S X, Luo Y N, et al. 2019. Impedance inversion by using the low-frequency full-waveform inversion result as an a priori model. Geophysics, 84(2): R149-R164. DOI:10.1190/geo2017-0643.1 |
Zhang H, Zhu P M, Gu Y, et al. 2019. Automatic velocity picking based on deep learning.//89th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2604-2608.
|
Zhang L, Claerbout J. 1990. Automatic dip-picking by non-linear optimization. Stanford Exploration Project, 67: 123-138. |
Zhang L. 1991. Automatic picking and its applications. Stanford Exploration Project, 70: 275-292. |
Zhang P, Lu W K, Zhang Y Q. 2015. Velocity analysis with local event slopes related probability density function. Journal of Applied Geophysics, 123: 177-187. DOI:10.1016/j.jappgeo.2015.10.010 |
Zhang P, Lu W K. 2016. Automatic time-domain velocity estimation based on an accelerated clustering method. Geophysics, 81(4): U13-U23. DOI:10.1190/geo2015-0313.1 |
杜启振, 李芳, 侯波, 等. 2011. 角度域弹性波Kirchhoff叠前深度偏移速度分析方法. 地球物理学报, 54(5): 1327-1339. DOI:10.3969/j.issn.0001-5733.2011.05.022 |
李勤, 李永博, 李庆春. 2019. 垂向裂隙各向异性煤层地震波响应. 地球物理学报, 62(1): 306-315. DOI:10.6038/cjg2019M0006 |
马水平, 王志宏, 田永乐, 等. 2010. 地震反射同相轴的地质含义. 石油地球物理勘探, 45(3): 454-457. |
田忠斌, 张胤彬, 王建青, 等. 2016. 富含煤层气储层的叠前地震反演预测方法研究——以山西晋东南测区为例. 地球物理学报, 59(12): 4494-4504. DOI:10.6038/cjg20161212 |
徐文君, 殷俊锋, 王华忠, 等. 2017. 基于稀疏反演理论的自动叠加速度反演方法. 地球物理学报, 60(7): 2791-2800. DOI:10.6038/cjg20170724 |
 2021, Vol. 64
2021, Vol. 64


