2. 中国石油勘探开发研究院西北分院, 兰州 730020;
3. 中国石油勘探开发研究院, 北京 102258
2. Northwest Branch of China Petroleum Exploration and Development Institute, Lanzhou 730020, China;
3. China Petroleum Exploration and Development Institute, Beijing 102258, China
为了理清孔隙度以及复杂的孔隙结构类型对碳酸盐岩弹性性质的影响,国内外许多学者都对碳酸盐岩的地震岩石物理特征进行了大量的实验和理论研究.从岩石物理实验研究的角度出发,Anselmetti和Eberli(1993)、Agersborg(2008)、以及Zhang等(2015)通过对碳酸盐岩超声速度测量与微观结构观察,指出孔隙类型差异是造成相同孔隙度下碳酸盐岩样品表现出明显速度差异的主要原因;Baechle等(Baechle et al., 2007; Baechle et al., 2008)的实验结果亦表明,在相同孔隙度下含有近球形铸模孔隙的碳酸盐岩样品出现速度超过2500 m·s-1的差异;Weger等(2004)利用岩石微观结构的数字分析技术研究了高孔隙碳酸盐岩样品孔隙结构差异对速度的影响;Verwer等(2010)分析了碳酸盐岩样品中孔隙结构差异所造成的流体与岩石相互作用不同对其动态剪切模量的影响,指出具有较高比表面的岩石样品表现出更为强烈的流体-岩石骨架的相互作用,从而使岩石剪切模量明显降低;Sharma等(2013)利用CT技术系统讨论了碳酸盐岩样品微观结构不均匀造成的介质中流体流动差异,以及这种流动差异引起的岩石样品中速度随饱和度变化方式的差异.
在岩石物理理论模型方面,为了考虑孔隙结构类型对碳酸盐岩弹性性质的影响,现有的理论模型都是利用不同纵横比的夹杂体来表示碳酸盐岩中的各类孔隙,比如,在一些经典的等效介质模型——KT模型(Kuster and Toksoz′s)、自洽模型(SCA)、以及微分等效介质模型(DEM)中,利用高纵横比夹杂体表示岩石中的铸模或者孔洞类型孔隙,该类孔隙具有比粒间或者晶间孔隙更多的颗粒接触边界,因此在相同的孔隙度下会使岩石介质具有更高的弹性模量或者速度;利用低纵横比夹杂体表示岩石中的微裂隙和粒间孔隙,相同孔隙度下此种裂隙会体现出更低的弹性模量与速度.然而,KT模型、SCA模型、以及DEM模型都有一些各自的假设条件与前提,比如,KT模型仅适用于岩石骨架中具有稀疏含量的包含物;微分等效介质模型(DEM)通过往固体矿物相中逐渐加入包含物相来模拟双相或多相混合物,对于多种包含物形状或多种包含物成分,其等效模量不仅依赖于最终的各成分体积含量,还依赖于包含物加入的次序.为了克服KT模型仅适用于有稀疏含量包含物的限制,Xu与White(2010)合并了KT与DEM模型,在表征特定孔隙类型的碳酸盐岩孔隙度对速度等弹性性质的影响方面取得一定的效果.Xu和Payne(2009)将碳酸盐岩中的孔隙类型分为黏土孔隙、粒间孔隙、微裂隙和刚性孔隙(孔洞等),利用不同纵横比的椭球体分别表示上述四类孔隙,进而利用DEM模型表征其地震弹性性质与孔隙类型及其含量的关系.这些模型在研究孔隙结构类型对碳酸盐岩弹性性质的影响方面发挥了一定的作用,但是仍然存在巨大的局限性.此外,纵横比参数对孔径大小并不敏感,因此,试图利用这些模型表征具有不同孔隙结构类型的碳酸盐岩储层弹性性质仍然停留在定性的层面.
在联合岩心、测井及地震数据进行碳酸盐岩孔隙类型的储层预测方面,国内外也有学者做出努力与贡献.Anselmetti和Eberli(1999)将声波、中子-孔隙度、密度等三种测井手段相结合,可得到“速度偏差测井曲线”(velocity-deviation log),利用该技术可以获得井下碳酸盐岩主要孔隙类型信息.其研究的主要思路为:(1)通过对大量碳酸盐岩样品进行实验室速度测定,发现很难找到一个比较好的函数关系来描述这种“速度-孔隙度”的变化.也就是说在“速度-孔隙度”交会图中,孔隙度固定为某一个具体的值时,速度值分散严重;(2)提出了所谓的速度偏差的概念“velocity-deviation”来度量这种速度的散布现象.具体做法是利用Wyille时间平均公式绘制“速度-孔隙度”的理论曲线,然后在每一个具体的孔隙度点计算实际测量速度与理论曲线的偏差,这种偏差可以是正偏差、负偏差或者是0偏差,这种偏差的大小以及正负说明了碳酸盐岩孔隙结构类型的差别,比如正偏差说明了碳酸盐岩的孔隙结构主要以生化孔以及铸模孔为主,而负偏差说明了碳酸盐岩的孔隙结构主要以微裂隙为主,0偏差主要是晶间孔、粒间孔为主.(3)将如上思路应用到测井数据上,获得“速度偏差测井”曲线,由此获得定性的碳酸盐岩孔隙类型评价.国内学者也在基于岩石物理模型(如Xu-Panye模型、DEM模型等)描述碳酸盐岩储层弹性性质,以及在此基础上建立针对碳酸盐岩储层的孔隙度、流体饱和度、以及孔隙结构的半定量解释方面,做了有益的尝试并取得了很大的进展(Zhao et al., 2013; 李宏兵,2019).
为了更加精确地进行碳酸盐岩孔隙类型分析,孙跃峰(Sun, 2000, 2004)基于孔弹性Biot理论推导了一个新的岩石物理参数——孔隙结构参数(γ),这个模型可以用来定量表征碳酸盐岩储层的孔隙结构特征,因此可用于刻画不同的孔隙空间类型.另外,在地震尺度上,通过叠前地震资料获取纵横波及密度后,由于孔隙结构参数可以由孙氏模型计算获得,因此碳酸盐岩储层可以获得一个新的属性体——孔隙结构参数(γ)属性体,这使得在地震尺度上预测碳酸盐岩储层的孔隙结构类型及利用地震数据在孔隙结构参数表征与分类下的碳酸盐岩储层反演精度的提高成为可能.
总之,前人针对碳酸盐岩储层研究的特点与不足如下:(1)国内外学者基于岩石物理实验研究已经认识到复杂孔隙结构是影响碳酸盐岩弹性性质的主控因素之一;(2)针对于复杂孔隙结构的碳酸盐岩储层岩石物理建模有一定的进展,但仍不成熟;(3)利用测井数据评价井壁周围碳酸盐岩孔隙结构类型的研究已有进展,但仍停留在定性阶段;(4)利用地震数据体获取孔隙结构类型属性体的研究鲜有涉猎.本文从数字岩心技术与孙氏模型相结合的角度入手,以碳酸盐岩储层预测为目标,综合利用岩心、测井与地震数据探究获得孔隙结构因子地震属性体的解决方案.数字岩心技术可以通过CT扫描成像来建立真实岩石模型,可视化地描述碳酸盐岩孔隙结构类型,在此基础上进行弹性模拟将更加准确.除此而外,数字岩心技术也使得定量化分析孔隙结构类型对碳酸盐岩弹性性质的影响成为可能.前期的研究工作已经建立了一套针对于碳酸盐岩的合适的图像处理技术,并建立准确可信的二值化数字岩心模型;同时也通过物理实验验证了一套基于数字岩心数据体进行弹性性质模拟方法的有效性.本文尝试在基于数字岩心数据体弹性性质模拟基础上,利用孙氏模型得到每一个数字岩心数据体所代表岩石的孔隙结构因子γ,从而最终得到利用该孔隙结构因子γ表征与分类下的弹性性质与孔隙度的交会关系,以此作为解释量版,最终可以获得地震尺度下的孔隙结构因子的地震属性体.本文为两篇系列文章的第二篇,第一篇主要阐述针对碳酸盐岩二值化图像处理的建立流程与验证,以及数字岩心静态弹性模拟的理论方面,这两方面是基于数字岩心获得精确的碳酸盐岩弹性性质模拟结果的关键所在;第二篇(即本文)主要阐述利用数字岩心数据获得孔隙结构因子的思路、理论与流程,和以碳酸盐岩储层预测为目标而获得孔隙结构因子的地震属性体的实际应用方面.
1 数字岩心数据体的建立与薄片分析本文所测试的7块白云岩样品直径为38 mm,CT扫描成像分辨率为每体素20.7678 μm.我们对取自同柱塞下的碎块进行X射线衍射(XRD)分析,结果表明该样品含有7.4%的石英和92.6%的白云石.由于本文所测试的样品主要由白云石组成,因此我们在以下的研究中将不同尺度下的样品均视作只含白云石这一单一矿物.在上篇“图像处理与弹性性质模拟”一文中,我们已经针对碳酸盐岩建立图像处理与二值化的处理流程,这包括:(1)对比度增强;(2)各向异性扩散滤波;(3)边缘增强;(4)基于Otsu法的二值化图像分割.我们以3-1白云岩样品为例展示了该图像处理流程的详细实施过程,并通过物理实验证明了所建立的针对于碳酸盐岩的数字岩心图像处理流程的可靠性.图 1为利用如上所述数字岩心图像处理流程对7块白云岩样品构建的三维数字岩心数据体.第一排为白云岩样品实物图,其下为实验室氦气测量孔隙度值;第二排为获得的三维数据体,进一步的弹性性质模拟以及孔隙结构因子表征与提取均基于此三维数据体;第三排为从各三维数字岩心数据体中提取的孔隙网络结构,此种类型图件中相同颜色代表了相互连通的孔隙,与此同时我们也给出了通过三维数字岩心计算而得的孔隙度,表 1中列出了实测与计算孔隙度的比较.如第一篇文章中的分析与讨论,由于CT分辨率所限,可以看到三维数字岩心数据体计算孔隙度均小于各自的实测孔隙度.需要指出由于CT分辨率导致的孔隙度误差实际上可以认为是一种系统误差,这对进一步基于三维数字岩心数据体进行弹性性质模拟、孔隙结构因子的提取与表征以及在此基础上的岩石物理规律研究影响不大.
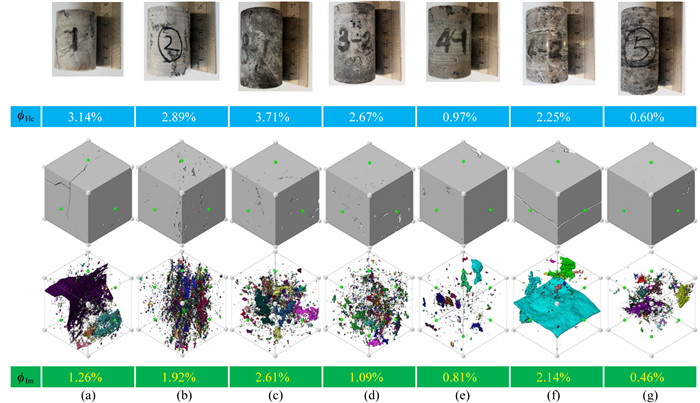
|
图 1 7块白云岩样品数字岩心数据体的构建 (a) 1#; (b) 2#; (c) 3-1#; (d) 3-2#; (e) 4-1#; (f) 4-2#; (g) 5#. Fig. 1 Reconstruction on digital core data of seven dolomite samples |
|
|
表 1 样品基本信息 Table 1 Sample description |
图 2为三种分析手段所显示的7块样品孔隙结构细节,三排图像分别为CT扫描切片、铸体薄片、以及小视域下的扫描电镜分析.我们利用CT扫描切片图像与镜下薄片分析,对所选7块样品进行从地质特征到孔隙结构类型的描述(表 2),有如下的特点:

|
图 2 7块白云岩样品的孔隙结构描述与分析 (a) 1#; (b) 2#; (c) 3-1#; (d) 3-2#; (e) 4-1#; (f) 4-2#; (g) 5#. Fig. 2 Pore structure description and analysis of seven dolomite samples |
|
|
表 2 7块样品镜下矿物学描述与孔隙类型分析 Table 2 Microscopic analysis of mineralogy and pore types for seven samples |
(1) 镜下观测可以看到,对于所有样品主要矿物为白云石,对于大部分样品有少量硅质胶结物,其中3-2#样品硅质胶结物可达25%;
(2) 从白云石不同粒径晶体含量进行分类,1#与2#样品的岩石结构与地质结构特征为粉晶-细晶结构,镜下定名均为粉-细晶白云岩;3-1#与3-2#样品分别为粉晶结构与细晶结构,镜下定名分别为粉晶白云岩与硅质细晶白云岩;4-1#与4-2#样品均为颗粒结构,主要为藻团块藻类颗粒白云石晶体与亮晶白云石颗粒,镜下定名均为亮晶藻白云岩;5#样品的岩石结构与地质结构特征为含藻泥-粉晶结构,镜下定名为含藻泥-粉晶白云岩;
(3) 联合CT及镜下薄片可以看到,1#与5#为微裂隙型孔隙结构类型的白云岩;3-1#与3-2#为仅含有晶间孔的孔隙类型白云岩;4-1#与4-2#样品为晶间孔与面缝率 < 1%的微裂隙共存的孔隙结构类型,4-1#与4-2#样品中的晶间孔含量较少;2#样品也为晶间孔与微裂隙共存的孔隙结构类型.此外,需要说明的面缝率越大代表晶间孔的粒径越大,2#、3-1#、以及3-2#样品有不同大小的晶间孔孔隙结构.
附录A给出了7块样品详细的镜下描述.为了进一步对所选7块白云岩样品进行详尽的孔隙结构分析与描述,我们在对样品进行CT扫描与薄片分析的基础上进行了小视域下的高精度扫描电镜分析,有如下的特点:
(1) 对于所有样品在100 μm视野下均可见从30~80 μm直径不等、从形态学上定义的自生孔;
(2) 样品1和3-1的扫描电镜结果可以看到清楚的结晶棱角,存在白云石晶间孔,为早期白云质重结晶的产物;
(3) 样品2和3-2的扫描电镜结果可以观测到典型石英晶体结构,明显的溶蚀面,亦可见部分小孔形成后经受溶蚀作用扩大孔径,认为是过饱和碳酸盐溶液重结晶作用形成的自生孔与后期溶蚀孔并存;
(4) 样品4-1和4-2均可以看到清楚的结晶棱角以及典型石英晶体结构,认为是白云石晶间孔,为早期白云质重结晶产物;样品4-2还可以看到丝线状胶结物胶结于白云石晶体间,丝线状结构应该是后期沸石胶结填充;
(5) 样品5可以看到清楚的结晶棱角以及典型石英晶体结构,初步分析可以认为是过饱和碳酸盐溶液重结晶作用形成的自生孔.
扫描电镜结果的视域比较小,因而对于白云岩样品孔隙结构类型分类角度而言不如相对大尺度的CT扫描成像与铸体薄片分析更好,然而,从地质角度来分析白云岩的成因时,扫描电镜优势明显,也对联系白云岩弹性性质与白云岩的地质成因与沉积类型预期有更好的作用.
2 数字岩心数据体子网格弹性性质模拟基于数字岩心图像处理及弹性模拟技术,我们设计的数字岩心孔隙结构分类与表征量版的技术流程整体如图 3所示.流程图中的五步构成两篇系列文章的主体内容,第一步是所钻取岩心CT扫描之前的物理测量,包括为得到干岩石骨架的岩心洗盐洗油预处理、XRD矿物分析、实验室孔隙度测量、薄片分析、以及实验室变围压超声实验,其中薄片分析的目的是联合后面的CT扫描图像,描述与分析岩心孔隙结构,变围压超声实验用来对数字岩心的弹性性质模拟做标定,这一步由于是物理实验部分,在本文中不做展开.第二步是CT扫描成像及图像处理,这一步详细实现过程为系列文章第一篇(上篇)所阐述的主体.图像处理所涉及的内容包括对比度增强、滤波去噪、以及边缘检测等的各步骤;二值化处理指的是数字岩心数据的二值化图像分割,经二值化处理后就得到了明确的骨架与孔隙信息,所以该步骤中的孔隙度指的是三维数字岩心二值化处理后的计算孔隙度——即由图像中孔隙像素与图像总像素占比计算而来的,三维孔隙结构模型提取指的是二值化处理后的三维数字岩心数据体,如上篇文中图 8所示.第三步是图像子块化及FEM网格,流程第三步的详细实现过程为图 4所展示的内容,三维数字岩心图像数据体建立好后,可以切出(数学上为简单的矩阵操作)任意大小图像网格,这个过程叫做子网格技术.此时,每一个小的子网格图像可以进行有限元网格剖分(如上篇文中图 10所示),至此,完成了有限元网格剖分,准备下一步的静态弹性性质模拟.流程第四步是FEM弹性性质模拟,该步骤是在上一步剖分好的有限元网格上,对每个网格单元进行弹性性质赋值,然后利用上篇文中的理论与流程进行弹性性质模拟.流程第五步为孔隙结构参数表征及分类,该部分是本文第3节所阐述的详细内容(见公式(1)—(6)),主要内容为利用孙氏模型在孔隙结构参数表征与分类下,获得弹性性质与孔隙度交会关系,并以此作为量版进行下一步的地震孔隙结构解释.
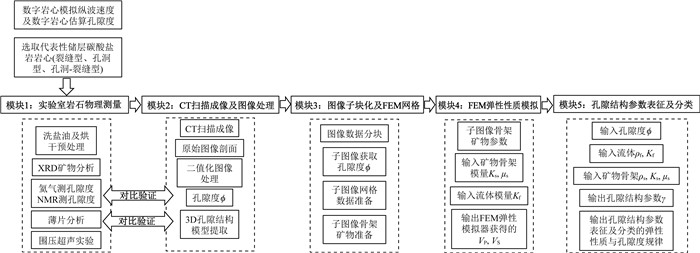
|
图 3 孔隙结构参数表征与分类下弹性性质与孔隙度关系获取流程图 Fig. 3 Flowchart of analysis on elastic properties vs porosity under pore structure characterization and classification |
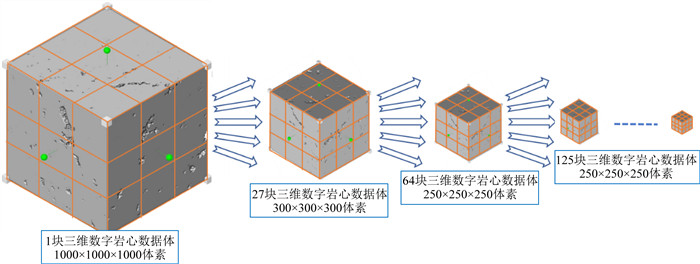
|
图 4 三维数字岩心数据体子网格化 Fig. 4 Subgridding of a 3D digital core data |
本研究中,按照如图 4所示的思路,我们对数字岩心数据进行子块化及子网格化的弹性性质模拟,由于在上篇中已经验证了该模拟的可靠性,因此我们对所有的样品通过同样的基于数字岩石物理模拟的方法计算得到了子数据集的弹性参数,模拟时基质模量为白云石KDolomite=80 GPa,GDolomite=58 GPa,孔隙流体为空气KAir=0.000131 GPa,GAir=0 GPa.特别地需要指出,本研究岩心样品只有7块,且孔隙度大都在3%以下,然而正是由于使用图 4所示的子网格技术——即切子块的方式,所以某个数字岩心数据体的局部子块其孔隙度是可以小于0.6%,也可以是很大(大于3.14%),甚至是大于20%以上,这样就可以拓展样品的孔隙度分布范围到一个很宽的范围,从而可以方便地研究弹性性质随孔隙度变化的趋势与规律.图 5展示了这些样品数字岩心模拟得到的纵波速度随孔隙度变化的交会关系.碳酸盐岩由于成岩次生改造作用强烈形成的孔隙结构极其复杂,而这些形态各异的孔隙结构对碳酸盐岩弹性性质影响不可忽略.在图 5可以看到孔隙度为10%时纵波速度差异可以达到2.5 km·s-1,数据点非常分散,于是我们下面尝试通过一定的孔隙结构分类方法来解决碳酸盐岩这种速度值分散性强的现象,并进行分析.
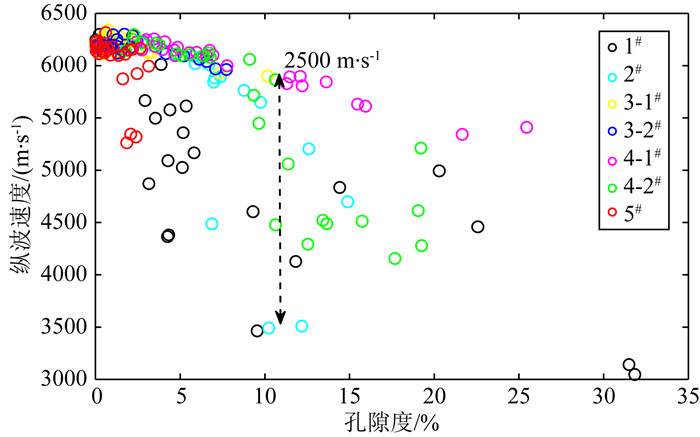
|
图 5 基于数字岩心模拟的纵波速度随孔隙度交会图 Fig. 5 Digital core simulated P-wave velocity vs porosity |
Sun(2000)基于孔弹性的Biot理论的拓展提出了孙氏模型,该模型中定义了一个等效孔隙结构参数叫做结构柔度因子γ,用于定量化描述孔隙结构对岩石弹性性质的影响:
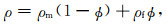
|
(1) |
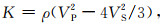
|
(2) |
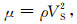
|
(3) |
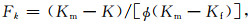
|
(4) |
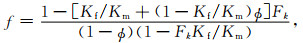
|
(5) |
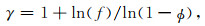
|
(6) |
式中m指代基质相,f指代流体相,γ是结构柔度因子.通过孙氏模型可以同时反演孔隙度和γ这两个参数,而γ可以有效地对岩心、测井资料或者地震数据的孔隙结构类型进行很好地分类(Dou et al., 2011, Zhang et al., 2015).下面我们尝试使用孙氏模型中的结构柔度因子γ来对数字岩心模拟数据进行孔隙类型分类分析.
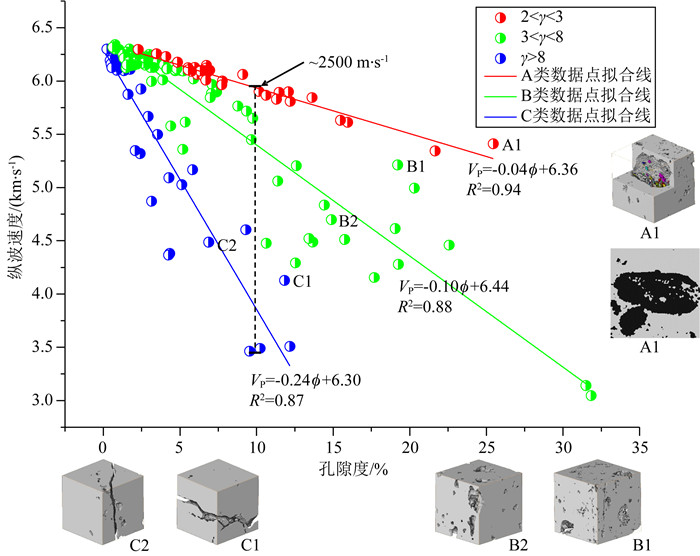
3.2 孔隙结构因子表征的弹性性质与孔隙度关系将7块白云岩的数字岩心模拟得到的弹性参数作为孙氏模型的输入,计算得到每个子数据集对应的结构柔度因子γ.借助结构柔度因子γ的数值分布范围,可将图 5杂乱无章的散点分布数据点分别聚类为不同特征的三类,并由红、绿、蓝三色区分表示见图 6.
|
图 6 基于数字岩心模拟的孔隙结构表征与分类下的纵波速度与孔隙度交会分析 Fig. 6 Digital core based analysis on P-wave velocity vs porosity under pore structure characterization and classification |
图 6中红色数据点表示其γ值小于3,该数据点表示子数据集主要含铸模孔.铸模孔是碳酸盐岩中典型的后期次生改造形成的孔隙类型,源自于海相沉积时藻类形成的鲕粒经过后期溶蚀,A1点显示了其三维结构.铸模孔在三维空间上的几何结构类似于岩石物理理论中常用的椭球状,其纵横比一般很大.孔型为铸模孔的岩石结构很硬,抗压缩系数大,因此体积模量大,其在图 6上主要表现为纵波速度随孔隙度变化不明显,即便在孔隙度高于20%时纵波速度仍维持在5.5 km·s-1以上的高值.图 6中的蓝色数据点代表岩石主要裂缝或微裂缝发育,其γ值大于6 (见图 6中C1与C2点的三维数字岩心结构).岩石若含较多的裂缝或微裂缝会导致岩石骨架较软,纵波速度会比那些含更多大孔(铸模孔或晶间孔)的岩石要低.图 6中绿色数据点代表主要孔型为溶蚀性晶间孔的岩石,其γ值介于3到6之间,白云岩样品中晶间孔的三维几何形状如图上B1和B2所示.晶间孔为主的数字岩心子数据集的纵波速度在同一孔隙度下介于含裂缝岩石与含铸模孔岩石数据之间.通过孔隙类型的划分,可以得到考虑不同孔型的更好的碳酸盐岩声波速度随孔隙度变化的相互关系.这样基于数字岩石物理知识的储层反演可使我们能够对碳酸盐岩储层预测有更深刻的认识.
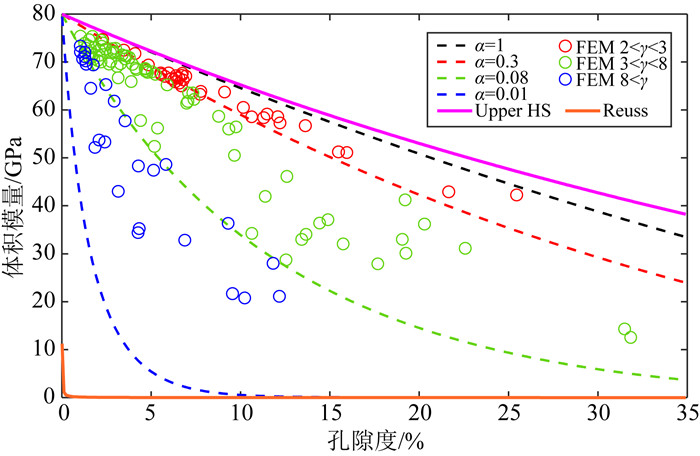
在对白云岩数字岩心模拟数据成功进行孔隙类型分类分析后,我们接下来分析体积模量随孔隙度变化关系的孔型分类结果,并尝试从岩石物理理论的角度来再次验证该分类方法的理论合理性.图 7比较了数字岩心模拟的数据与一些岩石物理等效介质模型的预测结果,其中红、绿、蓝三种实心圆点是孔型分类后的数字岩心模拟的体积模量数据,分类效果非常好,与图 6中的情况相似.在图 7中最上方的粉色实线是Hashin-Shtrikman上界限,橙色的是Reuss下界限(Reuss, 1929).这里笔者没有给出Hashin-Shtrikman下界限是因为Reuss下界限与Hashin-Shtrikman下界限重合了.造成这种Reuss下界限(Hashin-Shtrikman下界限)都紧贴零值的现象是因为基质体积模量(白云石80 GPa)与孔隙流体(空气0.000131 GPa)数量级相差过大所导致.下面阐述微分等效介质模型(DEM)计算结果(图 7虚线部分),DEM模型输入参数如下(Berryman, 1992):基质模量为白云石KDolomite=80 GPa,GDolomite=58 GPa,孔隙流体为空气KAir=0.000131 GPa,GAir=0 GPa.从左下方开始,蓝色虚线表示假定DEM模型中所有孔隙的孔隙纵横比(α)均为0.01的计算结果.我们可以看到蓝色虚线主要含这种裂缝型的软孔,因此在孔隙度为0到5%之间体积模量下降得非常快,孔隙度5%之后马上趋近于零.由此可以看出含裂缝型孔隙会使岩石弹性模量急剧下降.往右是绿色虚线为α=0.08的DEM计算结果,可以看到绿色虚线所在的位置正好是γ>8的模拟数据与3 γ 8的模拟数据的分界线.再往右是红色虚线为α=0.3的DEM理论预测结果,成功地将3 γ 8的模拟数据与2 γ 3的模拟数据分开.最后黑色虚线是α=1的DEM理论预测结果.因为孙氏模型可以看成是使用弹性信息与物性信息反演孔隙结构参数的一种方法,但反演出来的孔隙结构参数与传统岩石物理里面常用的孔隙纵横比还缺乏定量对应关系.而通过DEM的拟合标定,我们从图 7发现γ>8的数据点对应的是0.01 α 0.08的白云石样品,3 γ 8的数据点对应的是0.08 α 0.3的样品,2 γ 3的数据点则对应的是0.3 α 1的样品.这样就建立了各孔型的临界γ值与α之间的定量关系,并从岩石物理理论建模的角度验证了这种碳酸盐岩模拟数据孔型分类方法的合理性与有效性.
|
图 7 基于数字岩心模拟(散点)与差分等效介质理论(虚线)的体积模量随孔隙度变化 Fig. 7 Digital core-simulated (scatter) and DEM theory-based (dashed line) bulk modulus versus porosity |
以基于数字岩心构建的孔隙结构表征下的纵波速度-孔隙度交会量版(图 6)为前提,我们结合测井数据建立了地震孔隙结构预测的解决方案,见流程图 8.主要分为:(1)对于和数字岩心相同工区的地震数据进行精确的叠前AVO三参数反演以得到纵、横波速度以及密度参数;(2)使用神经网络的机器学习方法建立连接测井纵波速度、密度与测井孔隙度之间的模型,并使用反演得到的地震纵波速度、密度来预测地震孔隙度属性;(3)将地震工区内每一位置的纵波速度、孔隙度投影在图 6的孔隙结构量版中,根据该点在量版中所在的位置确定其对应的孔隙结构.
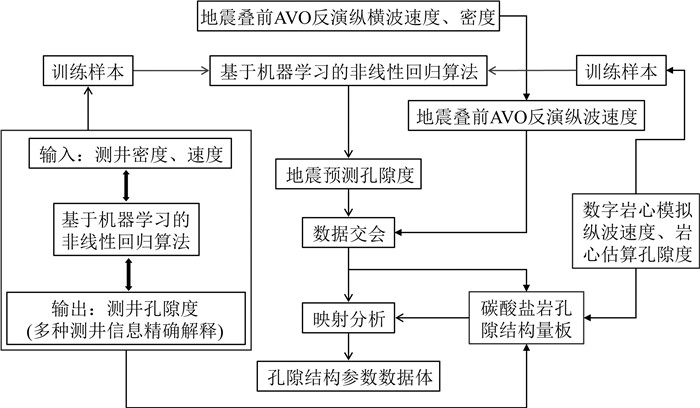
|
图 8 基于地震数据的孔隙结构属性体预测流程 Fig. 8 Workflow on seismic data-based pore structure attribute prediction |
地震孔隙度预测通常只能通过地震反演得到的纵横波速度、密度来进行,因此使用和声波、密度测井孔隙度计算相同的方法以及Wyllie时间平均方程等经验关系是最直接的.但是这些方法缺乏与孔隙结构间的联系,并且需要能够准确地预测地震响应位置的矿物分布信息,对于孔隙结构较复杂的碳酸盐岩这都会导致预测的孔隙度变得非常不可靠.而真正的测井孔隙度在计算时除了使用声波(纵波速度)、密度以外,还会通过常规中子测井、热中子测井等孔隙度计算方法一起进行孔隙度交会分析,并且在测井中每个深度的矿物分布也能够通过多种测井曲线得到,因此测井孔隙度是比较准确的.而在同一工区中只要测井数据量足够大,孔隙度足够准确,那么必定存在一个能够反映该区域纵波速度、密度与孔隙度之间规律的近似关系式,实质上这种关系式已经包含了孔隙结构对速度的影响规律.而在寻找该关系式时,神经网络相比常用的非线性拟合算法,更容易加入数据集,并且能够表征的映射关系也更加复杂,理论上只要孔隙度与纵波速度、密度间存在关联,神经网络总能找到.当然,除了使用神经网络以外也可以使用随机森林、支持向量机等机器学习方法来建立孔隙度预测模型,但是由于神经网络可以自行控制网络层数与节点数,从而能够描述更加复杂的映射关系,因此在研究中我们应用神经网络与测井数据来进行地震孔隙度的预测.
神经网络通常能够解决分类与回归两类问题,使用测井纵波速度、密度作为网络的输入数据,孔隙度作为输出数据,为回归问题.在研究中我们使用了全连接反向传播神经网络,最终得到了一个能够表征输入与输出数据两者关系的网络模型.我们使用了该工区内3口井中的测井纵波速度、密度与孔隙度数据,见图 9所示.在训练时将这些数据集分成训练集与验证集,训练过程使用训练集进行,占总数据的80%.
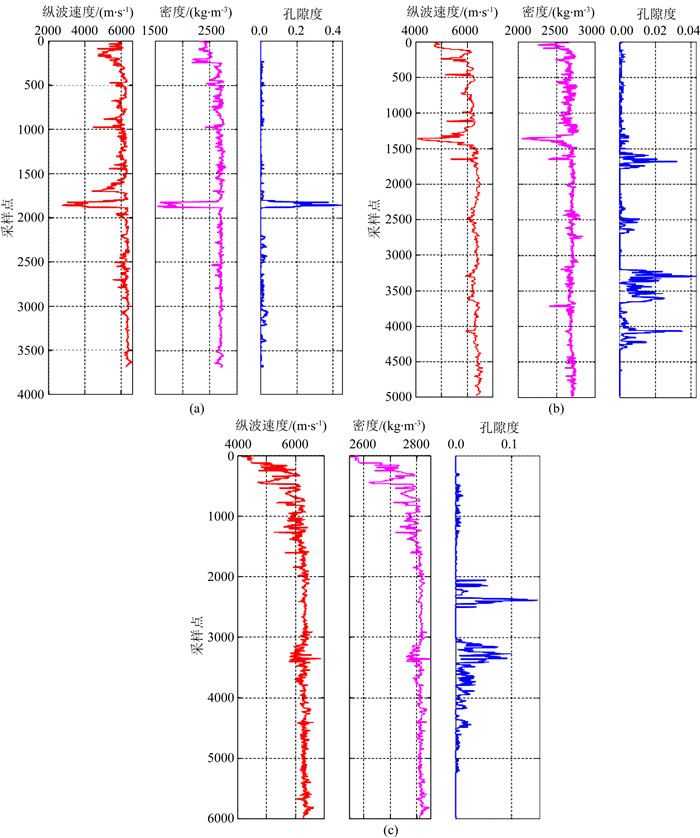
|
图 9 测井数据 (a)井1数据;(b)井2数据;(c)井3数据. Fig. 9 Well logging data (a) Well 1 data; (b) Well 2 data; (c) Well 3 data. |
训练完成后将验证集的纵波速度与密度输入网络得到预测孔隙度,和真实孔隙度对比,结果见图 10,结果表明训练的网络可以较好的预测孔隙度,并且具有一定的泛化能力.
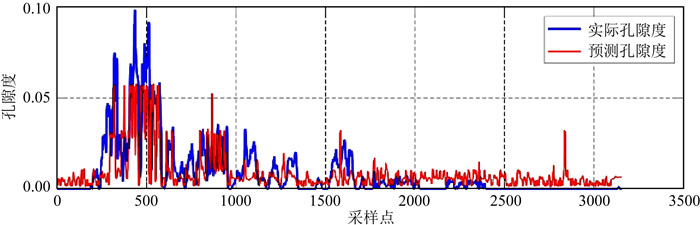
|
图 10 基于机器学习的预测孔隙度与测井孔隙度的比较 Fig. 10 Comparison between machine learning-predicted and logging-interpreted porosities |
为了展示图 8所示的工作流程,我们选择了一条过井的二维测线数据进行地震孔隙结构的解释,并基于测井数据进行一定的验证工作.将地震反演的纵波速度、密度(图 11,过井二维测线数据)输入上述训练完成的神经网络就能够得到预测的地震孔隙度数据体(如图 12所示).
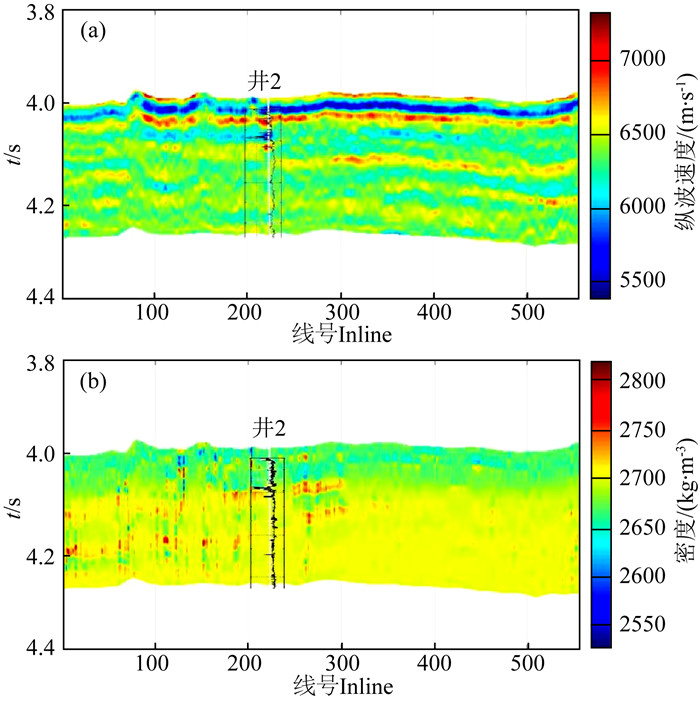
|
图 11 叠前反演结果 (a)反演纵波速度;(b)反演密度. Fig. 11 Pre-stack seismic inversion results (a) P-wave velocity attribute; (b) Density attribute. |
|
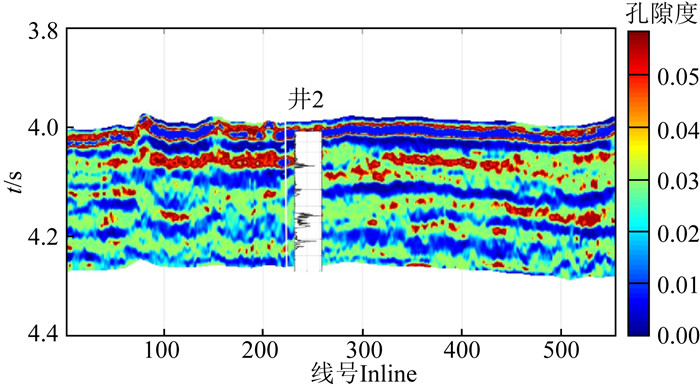
图 12 预测孔隙度剖面 Fig. 12 Predicted porosity profile |
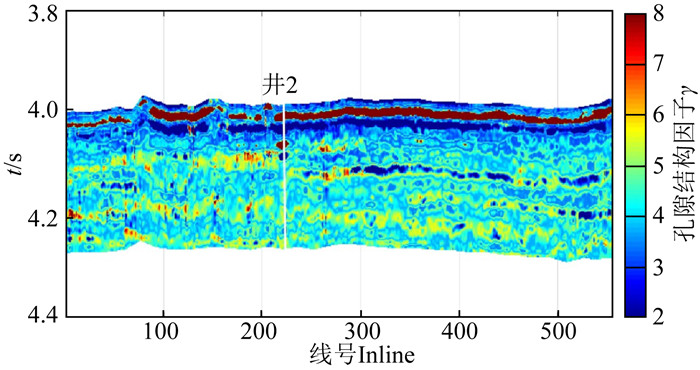
然后,将上述纵波速度与孔隙度数据进行交会分析,并将数据点投影在孔隙结构因子分类下的纵波速度-孔隙度关系量版中,在量版中我们的孔隙结构因子在2~8之间,超出该范围的点令其等于边界值,最终得到了图 13中的地震孔隙结构,其中γ因子越大对应裂隙,而越小对应于孔洞.对比图 12,可以发现高孔隙度的位置大多对应孔洞,而低孔隙度位置对应裂隙.
|
图 13 地震预测孔隙结构剖面 Fig. 13 Seismic prediction based pore structure profile |
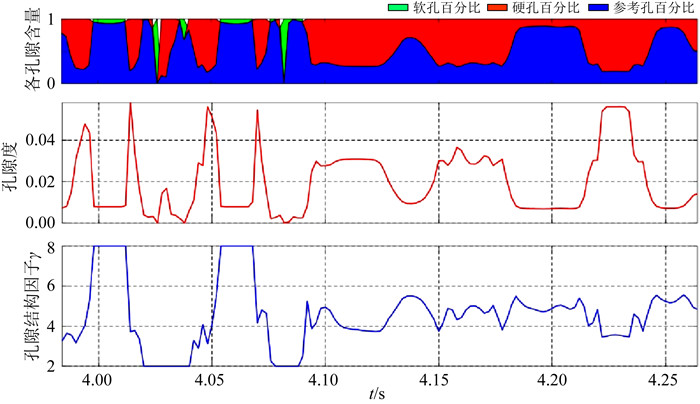
为了验证地震孔隙结构预测的准确性,通常最直接有效的技术应该是电阻率成像测井,通过成像测井我们可以清楚地观测到沿着井壁孔隙结构类型(缝、洞等)及分布等,这样能够在一定程度上验证本研究中地震孔隙结构预测的结果.遗憾的是本研究区块中未收集到成像测井数据,无法采用此方案进行孔隙结构因子的验证工作.因此,我们采用了另外一种替代的研究思路作为验证的方案,即Kumar和Han(2005)提出的可以获取碳酸盐岩孔隙结构的研究思路,利用该技术可得到过井地震道的参考孔、硬孔、软孔的孔隙纵横比大小及各种孔的体积含量,并可以与本研究中所使用的γ因子表征的孔隙结构进行对比.如图 14中彩色条带状图所示,其中蓝色表示中等尺度孔隙所占百分比,绿色表示软空隙所占百分比,红色表示硬孔隙所占百分比.硬孔隙可以对应小γ因子、大纵横比型的孔洞,软孔隙对应大γ因子、小纵横比型的裂缝,中等孔隙遵循上述规律.可以发现基于井数据,利用Kumar和Han的方法预测的孔隙结构变化,与研究中由γ因子表征的孔隙结构变化趋势基本相同,红色的硬孔隙含量较高处对应于蓝色曲线γ因子较小的位置(大纵横比孔洞),并且孔隙度总体较高(红色曲线);硬孔隙含量较少的位置(中等孔隙含量高)对应γ因子(蓝色曲线)处于中间值的位置;而出现绿色软孔隙的位置,对应于γ因子(蓝色曲线)较大处,为软孔隙,且孔隙度总体较小.此处Kumar和Han方法对孔隙形状的预测与γ因子方法具有一定的吻合度,且都表现出裂缝处孔隙度较小,孔洞处孔隙度较大的现象.
|
图 14 井旁地震道γ因子孔隙结构预测与各孔隙含量预测对比 Fig. 14 Pore structure factor (γ) and different pore types-based volume fraction estimated from a borehole-side seismic trace |
总体而言,本研究所提出的基于数字岩心构建孔隙结构定量解释量版的研究思路,与传统的基于岩石物理模型(如Xu-Panye模型,DEM模型)构建的定性半定量孔隙结构解释量版相比,是一种更加全新与相对更加定量的解决方案,这主要体现在由于大量的数字岩心数据体的存在,我们可以通过观察数字岩心图像(有时也需结合岩心薄片分析)使得基于定量解释量版获得的孔隙结构类型比较容易地得到验证(如图 6所示).然而,在将数字岩心与孙氏模型相结合获取的孔隙结构定量解释量版应用于地震孔隙结构预测时(如图 8所示流程图),一个至关重要的问题是如何准确地求取基于地震数据的孔隙度属性体,这个问题直接决定了地震孔隙结构预测的准确与否.已有很多学者结合多种机器学习算法与地震多属性分析对孔隙度属性体预测开展了大量研究(Hampson et al., 2001),但是对于这种具有复杂孔隙结构类型的碳酸盐岩储层,孔隙度预测的精度还有待提高.因此,要么在孔隙度预测技术方面,要么在利用孔隙度参数以外的其他参数进行交会来构建孔隙结构量版方面,两个方面的深入研究将有助于增强孔隙结构预测的准确性,这也是未来本项工作中需要深入研究的两个关键方向.
然而,尽管仍然存在不足,本文的工作为结合数字岩心-测井-地震数据三者的联合提供了一种新的思路与解决方案,对借助数字岩心这一新的地球物理手段来指导地震解释做出了尝试.
5 结论我们在前期的研究工作中已经建立了一套适用于碳酸盐岩的图像处理技术,并建立准确可信的二值化数字岩心模型;同时也通过物理实验验证了基于数字岩心数据体弹性性质模拟的有效性.本研究综合数字岩心技术与孙氏模型,首先在孔隙结构类型分类分析方面做了深入研究,将模拟的弹性参数作为孙氏模型中的输入,计算出各子样品的结构柔度因子γ来进行孔隙结构类型划分.经过γ可定量地将模拟数据划分为三类,每一类代表着岩石主要含某一特定孔隙类型,在此基础上可得到拟合度更好的弹性参数随孔隙度变化关系.同时本文使用岩石物理理论中的DEM模型对孔型划分结果进行验证,并建立了结构柔度因子γ与孔隙纵横比α间对应的定量关系.
基于如上研究思路,可以获取孔隙结构因子表征与分类下的弹性性质与孔隙度的交会关系,并以此作为解释量版,综合利用岩心、测井与地震数据,最终可以获得地震尺度下的孔隙结构因子的地震属性体,本研究对碳酸盐岩储层孔隙结构类型的预测与分类有重要的意义,这项技术也具有提高叠前地震反演孔隙度准确率的潜力.
附录A 7块样品的镜下观测结果样品1:光镜下观测区域为白云石,中间有少量硅质物填充.从岩石结构及构造特征上分析样品1主要是粉晶-细晶结构.从矿物组分特征上分析样品1岩石中矿物成分主要是白云石.白云石晶粒粒径多在0.2~0.3 mm,约80%左右,以细晶为主,粒径在0.1 mm以下为粉晶约15%,少数可达0.5 mm,达中晶约5%左右.镜下定名为粉-细晶白云岩.
孔隙类型为微裂隙,岩石中只见有两条宽均在0.01~0.025 mm之间的微裂缝,在石英脉中有一条宽在0.01 mm左右的微裂缝,面缝率 1%.
样品2:光镜下观测区域为白云石,从岩石结构及构造特征上看为粉晶-细晶结构.从矿物组分特征上看岩石中矿物成分主要是白云石100%.白云石晶粒粒径多在0.2~0.3 mm,约80%左右,以细晶为主,粒径在0.1 mm以下为粉晶约15%,少数可达0.5 mm,达中晶约5%左右.镜下定名为粉-细晶白云岩.
孔隙类型为晶间孔,晶间孔宽多在0.1 mm以下,形态各异大小不等.岩石中见有两个较大的孔洞,大小分别约为0.7 mm×0.2 mm和0.8 mm×0.2 mm.面孔率2%.
样品3-1:光镜下观测区域为白云石,从岩石结构及构造特征看为粉晶结构.从矿物组分特征可见岩石中矿物成分主要是白云石97%,白云石晶粒粒径多在0.1 mm以下,多为粉晶白云石.岩石中局部可见少数由重结晶作用形成可达0.1~0.2 mm晶体略大的细晶白云石晶体,另见有微量1%左右的硅质物和2%左右的黑色有机质物.镜下定名为粉晶白云岩.
孔隙类型为晶间孔,晶间孔宽多在0.05~0.1 mm,形态各异大小不等.岩石中见有两个略大的孔洞,大小分别约为0.5 mm×0.25 mm和0.4 mm×0.2 mm.面孔率约3%左右.
样品3-2:光镜下观测区域为白云石,中间有少量硅质物填充.岩石结构及构造特征为细晶结构,矿物组分特征分析可见岩石中矿物成分主要是白云石74%,硅质物25%,黑色有机质物1%.白云石晶粒粒径多在0.2~0.3 mm,多为细晶白云石,个别可达0.5 mm.岩石中局部富集0.1~0.2 mm的硅质物,镜下定名为硅质细晶白云岩.
孔隙类型为晶间孔,晶间孔宽多在0.1~0.2 mm,形态各异大小不等.岩石中见有两个略大的孔洞,大小分别约为0.5 mm×0.6 mm和1 mm×1 mm.面孔率约4%左右.
样品4-1:岩石结构及构造特征主要是颗粒结构.矿物组分特征:岩石中矿物成分主要是白云石99%,硅质物1%.结构组分特征:颗粒中藻类70%,由云泥组成,大小不等,多在0.2~0.5 mm,最大可达2 mm,呈藻团块.填隙物主要是由亮晶白云石胶结物和云泥组成,亮晶白云石25%,可明显观察到呈马牙状的第一世代,呈嵌晶粒状的第二世代现象微弱.云泥5%,较污浊,少量.镜下定名为亮晶藻白云岩.
孔隙类型为晶间孔与微裂隙共存,见一条贯穿岩石的微裂缝,面缝率 1%.
样品4-2:岩石结构及构造特征主要是颗粒结构.矿物组分特征:岩石中矿物成分主要是白云石98%,硅质物2%.结构组分特征:颗粒中藻类60%,由云泥组成,大小不等,多在0.2~0.5 mm,最大可达2 mm,呈藻团块.填隙物:由亮晶白云石胶结物和云泥组成,亮晶白云石35%,可明显观察到呈马牙状的第一世代,呈嵌晶粒状的第二世代现象较弱.云泥5%,较污浊,少量.镜下定名为亮晶藻白云岩.
孔隙类型为晶间孔与微裂隙共存,见一条断续的微裂缝,面缝率 < 1%.
样品5:岩石结构及构造特征为含藻泥-粉晶结构.矿物组分特征:岩石中矿物成分主要是白云石95%,硅质物1%,黑色有机质物4%.白云石晶体粒径多在0.05~0.1 mm,达粉晶含量多于泥晶,可见少量由泥晶白云石组成的藻类团块.镜下定名为含藻泥-粉晶白云岩.
Agersborg R, Johansen T A, Jakobsen M, et al. 2008. Effects of fluids and dual-pore systems on pressure-dependent velocities and attenuations in carbonates. Geophysics, 73(5): N35-N47. DOI:10.1190/1.2969774 |
Anselmetti F S, Eberli G P, et al. 1993. Controls on sonic velocity in carbonates. Pure and Applied Geophysics, 141(2): 287-323. DOI:10.1007/BF00998333 |
Anselmetti F S, Eberli G P. 1999. The velocity-deviation log:a tool to predict pore type and permeability trends in carbonate drill holes from sonic and porosity or density logs. AAPG Bulletin, 83(3): 450-466. |
Baechle G, Al-Kharusi L, Eberli G, et al. 2007. Effect of spherical pore shapes on acoustic properties in carbonates. AAPG Annual Convention. California, USA: American Association of Petroleum Geologists.
|
Baechle G T, Colpaert A, Eberli G P, et al. 2008. Effects of microporosity on sonic velocity in carbonate rocks. The Leading Edge, 27(8): 1012-1018. DOI:10.1190/1.2967554 |
Berryman J G. 1992. Single-scattering approximations for coefficients in Biot's equations of poroelasticity. The Journal of the Acoustical Society of America, 91(2): 551-571. DOI:10.1121/1.402518 |
Dou Q F, Sun Y F, Sullivan C. 2011. Rock-physics-based carbonate pore type characterization and reservoir permeability heterogeneity evaluation, Upper San Andres reservoir, Permian Basin, west Texas. Journal of Applied Geophysics, 74(1): 8-18. DOI:10.1016/j.jappgeo.2011.02.010 |
Hampson D P, Schuelke J S, Quirein J A. 2001. Use of multiattribute transforms to predict log properties from seismic data. Geophysics, 66(1): 220-236. DOI:10.1190/1.1444899 |
Kumar M, Han D H. 2005. Pore shape effect on elastic properties of carbonate rocks.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, doi: 10.1190/1.2147969.
|
Li H B, Zhang J J, Cai S J, et al. 2019. 3D rock physics template for reservoirs with complex pore structure. Chinese Journal of Geophysics (in Chinese), 62(7): 2711-2723. DOI:10.6038/cjg2019K0672 |
Reuss A. 1929. Berechnung der fließgrenzen von mischkristallen auf grund der Plastizitätsbedingung für einkristalle. Zamm-Zeitschrift für Angewandte Mathematik und Mechanik, 9(1): 49-58. DOI:10.1002/zamm.19290090104 |
Sharma R, Prasad M, Batzle M, et al. 2013. Sensitivity of flow and elastic properties to fabric heterogeneity in carbonates. Geophysical Prospecting, 61(2): 270-286. |
Sun Y F. 2000. Core-log-seismic integration in hemipelagic marine sediments on the eastern flank of the Juan De Fuca Ridge. ODP Scientific Results, 168: 21-35. DOI:10.2973/odp.proc.sr.168.009.2000 |
Sun Y F. 2004. Pore structure effects on elastic wave propagation in rocks:AVO modelling. Journal of Geophysics and Engineering, 1(4): 268-276. DOI:10.1088/1742-2132/1/4/005 |
Verwer K, Eberli G, Baechle G, et al. 2010. Effect of carbonate pore structure on dynamic shear moduli. Geophysics, 75(1): E1-E8. DOI:10.1190/1.3280225 |
Weger R J, Baechle G T, Masaferro J L, et al. 2004. Effects ofpore structure on sonic velocity in carbonates.//74th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1774.
|
Xu S, White R E. 2010. A new velocity model for clay-sand mixtures. Geophysical Prospecting, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
Xu S Y, Payne M A. 2009. Modeling elastic properties in carbonate rocks. The Leading Edge, 28(1): 66-74. DOI:10.1190/1.3064148 |
Zhang T T, Sun Y F, Dou Q F, et al. 2015. Improving porosity-velocity relationships using carbonate pore types. Journal of Computational Acoustics, 23(4): 1540006. DOI:10.1142/S0218396X15400068 |
Zhao L X, Nasser M, Han D H. 2013. Quantitative geophysical pore-type characterization and its geological implication in carbonate reservoirs. Geophysical Prospecting, 61(4): 827-841. DOI:10.1111/1365-2478.12043 |
李宏兵, 张佳佳, 蔡生娟, 等. 2019. 复杂孔隙储层三维岩石物理模版. 地球物理学报, 62(7): 2711-2723. DOI:10.6038/cjg2019K0672 |
 2021, Vol. 64
2021, Vol. 64

