2. 浙江大学海洋学院, 浙江舟山 316021;
3. 大地测量与地球动力学国家重点实验室, 中科院精密测量科学与技术创新研究院, 武汉 430071
2. Ocean College, Zhejiang University, Zhoushan Zhejiang 316021, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China
每逢夏秋,我国东南沿海地区经常遭受西北太平洋台风灾害的侵扰,蒙受巨大的经济损失和人民生命安全威胁.近年来,随着海洋和大气领域科学的发展和技术的革新,台风研究与数值预报均取得了长足的进步,但仍无法满足防灾减灾的切实需求(陈联寿,2006;端义宏等,2020).台风过境时现场观测资料的缺乏是目前台风研究的主要短板,其主要原因在于传统海洋观测仪器布设困难,很难做到大范围布阵或提前布设于台风行经海域;而且,台风这种极端天气情况下,海洋仪器的正常工作、观测数据的获取与质量保障等都会受到严重干扰;此外,由于操作技术难度高、风险大、成本高等因素,目前国内如气象飞机观测等先进台风观测技术应用相对较少,也是导致直接观测数据相对缺乏的重要原因.因此,目前台风监测主要采用卫星遥感的方式.以合成孔径雷达为代表的卫星遥感技术可以获得准确的中低风速下海面风场,但台风高风速区域往往伴随着降雨,会对其回波信号造成一定的影响,导致风速反演误差最高可达10 m·s-1(Uhlhorn and Black, 2003;Klotz and Uhlhorn, 2014;Zhang et al., 2014).综合多学科研究方法与观测数据,发展新的台风监测方法,对传统方法进行必要的补充和相互印证,将有助于我们提高台风监测能力.
近年来,基于台风激发的地震背景噪声、极低频海洋噪声进行台风定位追踪与强度反演的研究逐渐兴起(Gerstoft et al., 2006;Chi et al., 2010;夏英杰等,2011;Sun et al., 2013;Davy et al., 2014;Sufri et al., 2014;Wang and Li, 2015;李风华等,2016;Lin et al., 2018;Fang et al., 2020).海洋已被证明是地震背景噪声的最主要源区,广袤海洋上的波浪每时每刻作用于固体地球,从而源源不断地激发低频背景噪声(Nishida, 2013, 2017).台风作为北半球逆时针旋转的热带气旋,是天然的大尺度“搅拌机”,能够显著加剧海-气相互作用、海浪-海底相互作用及能量耦合,从而使得期间的地震背景噪声显著增强并携带着台风过程物理信息被远处地震台所接收, 这为地震学家利用地震背景噪声研究台风提供了可能.
台风引起的地震背景噪声根据激发机理及优势频段,一般分为“地球嗡鸣”(Hum, 约0.003~0.02 Hz;Rhie and Romanowicz, 2004,2006;Maurya et al., 2019)和“地脉动”(Microseism, 约0.05~0.5 Hz;Longuet-Higgins,1950;Hasselmann,1963;Gerstoft et al., 2006;Bromirski,2009;Ardhuin et al., 2015).地球嗡鸣产生自次重力波与沿岸海底的能量耦合,其强度与海上风暴的影响范围密切相关(Maurya et al., 2019).近期有研究发现,地球嗡鸣频段之上还存在着噪声级相对较低的“风暴地震”(Stormquake, 约0.02~0.05 Hz),起源于风暴激发长周期海浪与陆架特征结构的能量耦合,能量强度可相当于3.5级地震(Fan et al., 2019).地脉动则是地震背景噪声中能量最强的分量,又分为单频和倍频地脉动.单频地脉动由海浪产生的压力扰动直接作用于海底或海岸产生,其频率与波浪频率一致.由于海浪产生的垂向压力扰动随水深呈指数衰减,所以,一般认为单频地脉动源区主要分布在浅海或近岸海区(Hasselmann,1963).而倍频地脉动则是地脉动信号中的主导者,由相向传播的两列同频率海浪非线性相干形成驻波后产生的垂向压力扰动作用于海底而激发,其源区可分布于沿岸、台风中心附近或两个台风之间(Cessaro,1994;Bromirski et al., 2005;Ardhuin et al., 2011;Ardhuin and Herbers, 2013;Ardhuin et al., 2015;Lin et al., 2017;郑露露等,2017;陈栋炉等,2018).一般认为,倍频地脉动主要以Rayleigh波和P波形式传播.早在20世纪中叶,远海台风激发的P波倍频地脉动就已被学者观测发现(Ramirez,1940;Gilmore,1946).近年来,得益于现代化的地震台阵部署和技术发展,Love波及S波形式的倍频地脉动也已被发现并确认(Gerstoft et al., 2008;Tanimoto et al., 2015;Liu et al., 2016).
近些年来,P波倍频地脉动被地震学家初步成功应用于近实时监测定位台风.自Gerstoft等(2006)利用南加利福尼亚地震台网(Southern California Seismic Network,SCSN)成功监测到2000多公里外墨西哥湾2005年超强飓风“卡特丽娜”(Katrina)后,利用地震台阵定位追踪台风的研究逐渐兴起.Zhang等(2010)分别基于SCSN以及日本高灵敏度地震台网(High Sensitivity Seismograph Network,Hi-net)记录的倍频地脉动信号,对2006年超强台风“伊欧凯”(Ioke)进行定位追踪,得到与美国国家飓风中心(National Hurricane Center)公布的台风最佳路径吻合良好的定位结果.Lin等(2018)利用布置于中国东北的NECESSArray地震台阵(NorthEast China Extended SeiSmic Array)监测定位2009年超强台风“卢碧”(Lupit),结果与日本区域专业气象中心(Regional Specialized Meteorological Center,RSMC)公布的台风轨迹及MODIS卫星遥感结果相印证一致.以上基于地震学的台风定位研究未来有望为传统台风监测与研究提供跨学科的数据支持、协助大气和海洋相关数值模型的校正(Zhang et al., 2010;Ardhuin et al., 2012;Lin et al., 2018;Ward Neale et al., 2018).然而,这些应用前景须以对P波倍频地脉动源区精确定位为基础,如何切实提高台风激发P波地脉动源区的定位精度是亟待解决的关键任务.
目前,P波倍频地脉动源区定位主要采用频率域聚束(Frequency-domain Beamforming,FB)方法(Gerstoft et al., 2006;Zhang et al., 2010;Lin et al., 2018;Fang et al., 2020).FB方法作为常用的地震台阵技术之一,主要基于台阵记录的台风激发地脉动波场的相干性,利用理论P波走时追溯反演相应源区.受限于单台阵的空间分辨能力(主要取决于台站数目、台阵孔径和结构等),基于单台阵的FB方法搜索目标海域范围及定位精度通常具有一定的局限性(Euler et al., 2014;Ward Neale et al., 2018).利用多个地震台阵进行联合定位则可以一定程度上弥补这些缺陷.如地震学领域经常使用多个地震台阵对地震源区进行联合定位,以提高定位精度(Roessler et al., 2010;Stipevic′ et al., 2017).然而,在P波地脉动源区定位方面,多台阵联合应用则大多针对月或季节尺度的地脉动源区变化研究(Landès et al., 2010;Hillers et al., 2012),鲜有应用于定位探测台风激发的P波地脉动源这类相对短持续时间的非常定源区.本文提出了将台阵至目标源区网格的距离作为归一化权重因子、结合反卷积技术的双台阵联合FB定位方法,并结合中国喜马拉雅二期台阵(ChinArray Ⅱ)和日本Hi-net(图 1)的连续波形数据,对2014年西北太平洋强台风“海鸥” (Kalmaegi)所激发的P波地脉动源区进行了定位追踪.研究结果表明本文所提出方法不仅有效提高了定位精度及空间分辨能力,并且一定程度上实现了对“海鸥”激发P波地脉动源区的全程、稳定的连续定位与追踪.
1 数据本文选择2014年登陆我国广东省南部沿岸的第15号台风“海鸥”作为研究对象,并以RSMC公布的台风最佳路径数据为参考轨迹(数据时间间隔为6 h,http://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/besttrack.html).“海鸥”起源于关岛东部海域的热带低压,于世界协调时(Universal Time Coordinated,UTC)2014年9月12日成长为热带风暴,并在次日增强为1级台风;14至15日期间,“海鸥”横穿吕宋岛进入我国南海,并在登陆海南岛前成长至巅峰(最大持续风速达38.6 m·s-1),最终在广东湛江沿岸第三次登陆后快速减弱,直至消散于我国内陆(图 1).“海鸥”在其生命周期内,径直穿越于开阔的菲律宾海和相对较为封闭的南海,并具有三次登陆过程,为激发地脉动提供了较为丰富的场景,是理想的研究对象.
本文收集了台风“海鸥”期间(2014年09月13日至16日)地震台阵ChinArray Ⅱ和Hi-net的垂向连续波形数据,分别下载自中国地震科学探测台阵数据中心(http://www.chinarraydmc.cn)和日本Hi-net台网网站(http://www.hinet.bosai.go.jp).除去存在数据质量问题(数据异常、缺失等)的台站,两个台阵分别具有437和747个有效台站用于本文研究.文中使用的总涌浪平均周期数据,属于欧洲中期气象预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)第五代再分析数据集(ECMWF Reanalysis v5,ERA5),网格分辨率为0.5°×0.5°,下载自哥白尼气候变化服务(Copernicus Climate Change Service,C3S,https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form).文中P波地脉动源区海表等效压力谱数据,网格分辨率为0.5°×0.5°,下载自法国海洋开发研究院数据库(the French Research Institute for the Exploitation of the Sea,IFREMER,ftp://ftp.ifremer.fr/ifremer/ww3/HINDCAST/SISMO/).
2 方法 2.1 双台阵联合FB定位方法不同于传统的频率-波数(Frequency-Wave number,f-k)方法,本文采用的FB定位方法基于地震台阵中不同台站记录的P波地脉动信号的相干性并结合相应走时预测,反演其源区.首先,地震台站记录数据均按以下步骤进行预处理:1)去除仪器响应;2)去均值、去趋势;3)降采样至1 Hz;4)0.05~0.45 Hz带通滤波;5)连续记录数据分割成时长为6 h的小段,计算每段数据的标准差,并截去振幅大于1倍标准差的部分,以去除由地震或异常仪器响应等造成的瞬时振幅异常;6)将各段记录数据进行窗口长度为10 min、50%重叠的短时傅里叶变换(Short-Time Fourier Transform,STFT)获得连续频谱S(ω),再除以振幅值以只保留相位信息,避免振幅放大效应并消除局地噪声的影响.

|
图 1 地震台阵ChinArray Ⅱ和Hi-net的地理分布及台风“海鸥”(Kalmaegi)和“风神”(Fengshen)最佳路径轨迹示意图 红色实心小圆点表示地震台站;不同颜色的实心圆表示不同时刻台风中心位置,时间间隔为6 h,近台风中心最大持续风速(Max sustained wind speed)与圆圈内不同颜色相对应,并与圆圈半径成正比.背景地形图下载自https://visibleearth.nasa.gov/images/147190/explorer-base-map/147192l. Fig. 1 Scheme of the deployment of ChinArray Ⅱ and Hi-net, and the best-tracks of Typhoon Kalmaegi and Fengshen The seismic stations are represented by solid red dots, and the typhoon track is indicated by color-coded circles, which are spaced at a 6 h time interval, with the circle sizes proportional to the max sustained wind speed. The background raster map is from https://visibleearth.nasa.gov/images/147190/explorer-base-map/147192l. |
根据预处理数据,构建互谱密度矩阵(Cross-Spectral Density Matrix,CDSM)C,它由N个台站的频谱S(ω)计算得到,即为N×N的矩阵,其第i行和第j列的元素包含台站i和台站j之间的相位延迟,表示为

|
(1) |
其中ω为角频率,t为数据段(t-3h, t+3h)的中值时刻,†为Hermitian转置运算符,〈〉表示对连续10-min窗口频谱的集合平均.
基于网格搜索法,本文将目标海域(100°E—140°E, 5°N—25°N)划分为0.2°×0.2°的网格.当频率为ω时,网格点(lat, lon)处t时刻的波束Bt(ω, lat, lon)可表示为
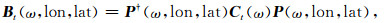
|
(2) |
其中指向各网格点的台阵导向矢量P为
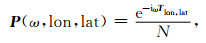
|
(3) |
其中Tlon, lat指从目标源区网格点(lon, lat)到地震台阵的P波走时向量,即Tlon, lat=(tp1, …, tpN)†.本文采用LLNL-G3Dv3三维地球速度模型(Myers et al., 2015)预测各台站对应的P波走时tpi(i=1, 2, 3…N),相对于PREM等一维地球介质模型在一定程度上可以减少浅层介质复杂地质结构对P波走时预测的干扰而提高走时预测精度(Fang et al., 2020).
鉴于单台阵FB定位结果通常受空间分辨能力的限制,本文进而提出双台阵联合FB定位方法,以提升定位精度.根据以往工作研究(Fang et al., 2020),当台风激发的P波地脉动源区至地震台阵距离小于~26°时,FB定位结果将受到上地幔三重震相(Triplication)的严重干扰.因此,本文选择台阵至目标源区网格点的距离作为双台阵联合FB定位方法的归一化因子(Ward Neale et al., 2018),通过降低近源台阵的权重占比以削弱上地幔三重震相的干扰,定义联合台阵(Combined array)导向矢量为
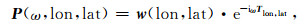
|
(4) |
其中,w(lon, lat)为距离权重归一化向量:
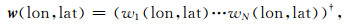
|
(5) |
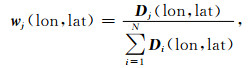
|
(6) |
Dj(lon, lat)为当前所搜索网格点(lon, lat)与台站j之间的距离.
然而,如后文“3.3台阵属性影响分析”所述,地震台阵的组合可能导致联合台阵的台阵响应出现显著的波纹状割裂,严重干扰FB定位结果.因此,本文在上述联合台阵FB方法的基础上,进一步采用反卷积技术CLEAN-SC(CLEAN based on spatial Source Coherence;Sijtsma, 2007),以抑制台阵响应对联合定位结果的负面影响.CLEAN-SC技术本质上是一种迭代“去噪”技术,我们将由式(1)、式(2)得到的Ct(ω)和Bt(ω, lon, lat)作为初始输入C(0)(ω)和B(0)(ω, lon, lat),后续迭代过程如下:
当i≥1时,首先计算i-1时波束能量分布图中的峰值B(i-1)(ω, lonmax, latmax),其中(lonmax, latmax)为该峰值对应的经纬度,其对应的源我们称之为峰值源,它在地震台阵引起的CDSM G(i)(ω)可表示为
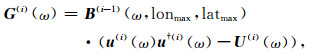
|
(7) |
其中u(i)(ω)为峰值源相干分量(即为N×1的矩阵),U(i)(ω)为u(i)(ω)u(i)(ω)的对角线元素(即为N×N的矩阵).u(i)(ω)可设置初值为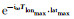
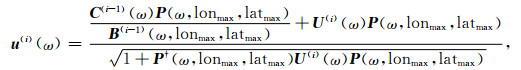
|
(8) |
一般几十次的迭代就可得到较为收敛的u(i)(ω).其中,我们通过去除波束能量分布图中峰值源相干能量来减少台阵响应的干扰,即
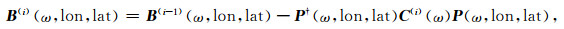
|
(9) |
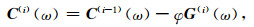
|
(10) |
其中φ为安全因子,取值范围为(0, 1].同时,为弥补波束能量的缺失,须以“洁净”的波束取代该峰值源:
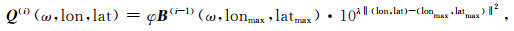
|
(11) |
其中λ为带宽系数,决定“洁净”波束的带宽;‖ ‖表示模长计算.
当迭代I次,满足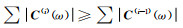

|
(12) |
基于上述结合反卷积技术的联合FB定位方法,本文利用ChinArray Ⅱ和Hi-net对台风“海鸥”期间目标海域(100°E—140°E,5°N—25°N)上的P波地脉动源区进行双台阵联合定位.
2.2 台风激发P波地脉动源区数值模拟理论上,台风激发的P波倍频地脉动源区可表达为相向传播的同频率波列发生非线性相互作用后产生的海表等效压力场.根据Ardhuin和Herbers(2013)和Farra等(2016)的方法,该等效压力场的功率谱FP可写为:
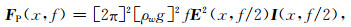
|
(13) |
其中f为P波地脉动信号频率;x表示空间位置;ρw为海水密度(= 1.020 kg·m-3);g为重力加速度;E(x, f/2)为海浪频率谱;无量纲量I(x, f/2)则与海浪能量随方向θ的分布特征,即方向谱M(x, f/2, θ),有关:

|
(14) |
基于上述原理,IFREMER采用美国国家海洋和大气管理局(the National Oceanic and Atmospheric Administration, NOAA)的国家环境预报中心(the National Centers for Environmental Prediction, NCEP)开发的第三代海浪模式WAVEWATCH-Ⅲ (WW3;The WAVEWATCH ⅢⓇ Development Group (WW3DG),2019)计算并发布了相应等效压力谱数据,水平空间分辨率为0.5°×0.5°(Ardhuin and Herbers, 2013).
考虑到场地放大效应,我们进一步引入P波场地放大系数CP (Gualtieri et al., 2014;Farra et al., 2016):
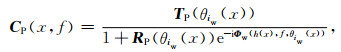
|
(15) |
其中θiw(x)为自源区位置x处传向地震台阵的P波射线出射角,取决于x点与地震台阵之间的距离;h(x)为x处水深,取自ETOPO1测深数据(Amante and Eakins, 2009);TP(θiw(x))和RP(θiw(x))分别为海底P波透射和反射系数:

|
(16) |

|
(17) |
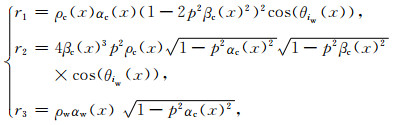
|
(18) |
其中ρc(x)表示x点海底地壳密度,αw(x)和αc(x)分别为x点海水及海底地壳中P波传播速度,βc(x)则为x点海底地壳中S波传播速度,均取值自全球地壳模型CRUST1.0(http://igppweb.uscd.edu/~gabi/rem.html);p表示基于Snell定律的射线参数.Φw(h(x), f, θiw(x))则是P波在水层中传播引起的相移,可表示为

|
(19) |
因此,最终P波地脉动理论源区可表示为
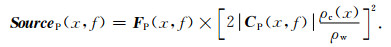
|
(20) |
根据上述方法,本文同时给出了台风“海鸥”期间目标海域上的P波地脉动理论源区.由于目标海域至ChinArray Ⅱ和Hi-net的P波出射角θiw(x)不同,使得二者的CP存在细微差异,本文取二者CP的均值进行计算.
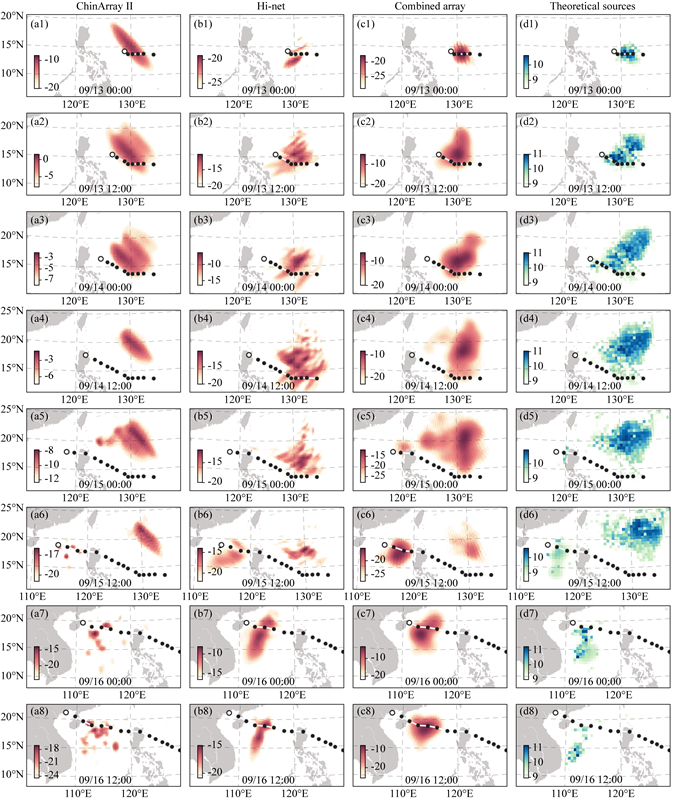
3 结果与讨论 3.1 双台阵联合定位结果基于上述双台阵联合FB定位方法,本文利用ChinArray Ⅱ和Hi-net组成的联合台阵对台风“海鸥”生命周期范围内连续16个时刻(UTC 2014/09/13 00∶00至09/16 18∶00,间隔为6 h)的P波地脉动源区进行了定位,图 2c1—c8按12 h为时间间隔对定位结果进行了显示,对应频率为~0.2 Hz(即台风激发的P波地脉动信号的峰值频率;Lin et al., 2018).同时,为评估双台阵联合FB定位效果,本文对“海鸥”期间的P波地脉动理论源区进行了计算(图 2d1—d8),以作对比验证.双台阵联合FB定位成功探测到“海鸥”激发的P波地脉动源区,且定位所得源区分布与理论计算结果具有相当的一致性:在9月15日“海鸥”穿越吕宋岛进入南海之前,其激发的P波地脉动源区主要分布于菲律宾海之上(图 2c1—c4,d1—d4);在“海鸥”深入南海之后,P波地脉动源区主要分布于南海并紧随台风中心而移动,而菲律宾海上的地脉动源区逐渐衰退(图 2c5—c8,d5—d8).南海海域上定位结果与理论源区的一致性相对菲律宾海域较差:定位源区较为聚焦地分布于台风中心后方,而理论源区则相对离散地向南漂移.这可能与南海较为封闭的海域环境有关,其四周的复杂海岸环境使得理论源区的模拟难度增大.上述结果表明,本文基于距离权重的双台阵联合FB定位方法在一定程度上实现了对“海鸥”激发的P波地脉动源区的全程有效定位与追踪.
|
图 2 台风“海鸥”期间(9月13日至16日)时间间隔为12 h的连续8个时刻的基于(a1—a8)ChinArray Ⅱ、(b1—b8)Hi-net和(c1—c8)联合台阵(Combined array)的FB定位结果(对应频率~0.2 Hz)以及(d1—d8)相应时刻“海鸥”激发P波地脉动理论源区(单位为log10(Pa2·m2·s)).黑色空心圆圈表示当前时刻台风中心位置,黑色实心圆点表示此前不同时刻台风中心轨迹,时间间隔为6 h Fig. 2 Localized P-wave microseism source regions (at ~0.2 Hz) by FB method with ChinArray Ⅱ (a1—a8), Hi-net (b1—b8) and Combined array (c1—c8), and corresponding theoretical source regions (d1—d8, in log10(Pa2·m2·s)) at successive 8 time-points during the lifecycle of Typhoon Kalmaegi (09/13—09/16) with 12 h time intervals. The black circles represent the current typhoon center, with the black solid dots indicating the typhoon locations at 6 h time intervals along the typhoon track |
同时,比较有趣的是,双台阵联合定位结果以及理论源区显示,台风“海鸥”行经菲律宾海期间(09/13 12∶00至09/15 12∶00),其激发的P波地脉动源区较为稳定地分布于其轨迹的右上方,并未随台风中心移动,甚至出现向东北漂移远离的趋势.这表明该P波地脉动源区可能并非单纯由台风“海鸥”产生的波浪场激发.鉴于台风“海鸥”的生成稍晚于台风“风神”的消散,且二者均起源于菲律宾海(图 1),“风神”遗留的波浪场很可能传播至“海鸥”行经海域并与其产生的波浪场相互作用,从而激发出不随“海鸥”移动的P波地脉动源区.为验证这一猜想,本文选用“风神”和“海鸥”交替前后连续12个时刻(UTC 2014/09/09 12∶00至09/15 00∶00,间隔为12 h)的ERA5总涌浪平均周期数据(图 3a—f,m—r)以及相应时刻的海表等效压力谱数据(图 3g—l,s—x)进行对比分析.当“风神”沿日本岛弧向东北移动,分布于其台风中心附近的波浪场及海表等效压力场也随之移动(09/09 12∶00后,图 3a—d,g—j),但有部分风生涌浪群却逐步背向远离,向菲律宾群岛传播(图 3a—f);当这些涌浪群入射菲律宾群岛沿岸时,“风神”消散而“海鸥”逐渐生成壮大(09/11 12∶00至09/12 00∶00,图 3e—f);当台风“海鸥”开始向西北移动,其产生的波浪场与菲律宾沿岸反射的涌浪群非线性相互作用而激发海表等效压力场,且该海表压力场随涌浪群传播而向东北扩散漂移(09/13 00∶00后,图 3n—r,t—x).由于场地放大效应的存在,源自该海表等效压力场的P波地脉动源区较稳定地分布于“海鸥”轨迹的右上方,并呈现向东北漂移趋势.上述分析表明,菲律宾海上不随台风“海鸥”移动的P波地脉动源区,是由“风神”产生的涌浪群与“海鸥”产生的波浪场相互作用而产生.
为了评价本文所提出的基于距离权重的双台阵联合FB定位方法,以下我们进一步通过与单台阵定位结果的对比、联合台阵的台阵属性影响等方面进行了分析与讨论.
3.2 相对单台阵的定位优势分析为评估上述双台阵联合FB技术对定位精度的提升,本文分别利用ChinArray Ⅱ和Hi-net的单台阵数据对台风“海鸥”激发的P波地脉动源区进行了定位.图 2a1—a8和图 2b1—b8分别给出了两个台阵在“海鸥”生命周期范围内连续8个时刻(UTC 2014/09/13 00∶00至09/16 12∶00,间隔为12 h)的定位结果,对应频率为~0.2 Hz.单台阵定位亦均成功探测到“海鸥”激发的P波地脉动源区,但与理论源区(图 2d1—d8)相比,单台阵的定位结果均存在一定缺陷:当P波地脉动源区位于菲律宾海之上时(即09/15 12∶00之前),ChinArray Ⅱ的定位结果虽然未能足够刻画相对较弱源区的分布但却十分聚焦(图 2a1—a6),而Hi-net的定位结果则显得相对散乱且向南漂移(图 2b1—b6);当“海鸥”迁移至南海时(即09/15 00∶00之后),ChinArray Ⅱ的定位结果就变得相当零散(图 2a6—a8),而Hi-net的定位结果虽然略向北漂移但开始变得相对聚焦(图 2b6—b8).
对比上述两个单台阵的定位结果,我们发现一个有趣的现象:ChinArray Ⅱ在菲律宾海上的定位结果比较聚焦,而在南海定位则相对涣散(图 2a1—a8);相反,Hi-net在菲律宾海上的定位结果则比较涣散,而在南海定位相对聚焦(图 2b1—b8).这可能与地震台阵至地脉动源区的距离有关:当台阵距离目标源区较近时,射线路径分布较浅而受地球浅层介质横向非均匀性的影响较大,致使基于理想地球模型的理论预测走时与实际走时之间存在相对较大的偏差,导致台阵的聚束定位结果不稳定、定位能力变差(Fang et al., 2020).当然,地震波传播的“三重震相”(Triplication)也可能是干扰因素之一.P波在固体地球中传播时,会在上地幔的两个主要间断面(约410和660 km)发生反射,产生不同相位的P波.在15°~26°距离范围内,这些不同相位的P波可能近乎同时传播到地震台站,造成台站记录的相位信息混杂,这种现象被称为上地幔三重震相(Chu et al., 2019).当“海鸥”激发的P波地脉动源区与ChinArray Ⅱ和Hi-net的距离在26°以内时,两个台阵的FB定位结果可能因上地幔三重震相干扰而产生额外偏差.而得益于本文引入的距离权重,降低了联合台阵定位中近源台阵的贡献比,双台阵联合FB定位结果很大程度上削弱了上述P波走时预测偏差及上地幔三重震相的干扰,为对“海鸥”激发的P波地脉动源区进行持续、有效定位与追踪奠定了基础.

|
图 3 台风“风神”和“海鸥”交替前后(9月9日至15日)时间间隔为12 h的连续12个时刻的(a—f,m—r)ERA5总涌浪平均周期(单位s),和(g—l,s—x)相应时刻海表等效压力谱(单位为Pa2·m2·s)的空间分布图.黑色空心圆圈表示当前时刻台风中心位置,黑色实心圆点表示此前不同时刻台风中心轨迹,时间间隔为6 h Fig. 3 Spatial distributions of the mean periods of total swell of ERA5 (a—f, m—r; in s) and calculated equivalent surface pressure spectra (g—l, s—x; in Pa2·m2·s) at successive 12 time-points before and after the alternation of Typhoon Fengshen and Kalmaegi (09/09—09/15) with 12 h time intervals. The black circle represents the current typhoon center, with the black solid dots indicating the typhoon locations at 6 h time intervals along the typhoon track |
理论上,地震台阵的空间分辨率R取决于其孔径Φ、地震波波长λ以及与源区的距离D,可用R=λD/Φ表示(Rost and Thomas, 2002;Ward Neale et al., 2018).例如,对于3000 km外的P波地脉动源区,假设其传播速度为6 km·s-1(0.2 Hz频率对应的波长约为30 km),则ChinArray Ⅱ的空间分辨率约为62.4 km,而Hi-net则为47.1 km,即Hi-net的理论分辨能力优于ChinArray Ⅱ.该分辨率R一定程度上反映了地震台阵对相邻源区的探测和分辨能力.虽然,实际应用中,基于FB技术的地震台阵定位空间分辨率通常远不及理论值(Hillers et al., 2012;Ward Neale et al., 2018),但双台阵联合的空间分辨率仍相对单台阵有了较大提升.例如,联合定位结果清晰地显示出“海鸥”穿越吕宋岛后在其北部沿岸激发的较弱的近岸P波地脉动源区(图 2c5和2d5),而ChinArray Ⅱ和Hi-net则无法单独探测到(图 2a5和2b5).这进一步体现了联合台阵相对单台阵的空间分辨能力优势.
此外,由于台风“海鸥”路径轨迹在空间上具有相当大的跨度,在纬向跨越~30°、经向跨越~10°(图 1),上述结果分析表明,单独采用Hi-net或ChinArray Ⅱ均无法对“海鸥”激发P波地脉动源区进行全程有效定位与追踪.鉴于ChinArray Ⅱ和Hi-net的单台阵FB定位结果在空间域上具有一定的互补性,本文采用基于距离权重的双台阵联合FB定位方法在一定程度上综合了两个台阵的定位优势,提升了定位源区的稳定性与精度,实现了对“海鸥”激发的P波地脉动源区的全程、稳定定位追踪.
3.3 台阵属性影响分析地震台阵的固有属性,包括其孔径、几何形状、台站数量及间距等,都会对台阵定位的空间分辨率产生显著的影响.由于台阵可探测信号的最大波长大致近似于其孔径(Schweitzer et al., 2012),能够有效探测台风激发的P波地脉动信号的台阵孔径至少为30 km(假设P波波速为6 km/s);而台阵的几何形状则决定了定位结果的优势空间分辨方向.这种台阵固有属性造成的影响可通过台阵响应函数(Array Response Function, ARF)进行表征(Lin et al., 2018):
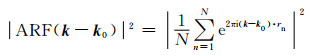
|
(21) |
其中k为波数矢量,k0为参考波数矢量,rn则表示地震台站的位置,N为台站数量.
图 4a和4b分别给出了ChinArray Ⅱ和Hi-net的ARF.得益于两个台阵的大孔径(ChinArray Ⅱ的孔径约为1443 km,Hi-net的孔径约为1910 km),二者的ARF主瓣都较为聚焦,将对目标源区具有较强的定位分辨能力.受台阵几何形状影响,ChinArray Ⅱ的ARF主瓣较为规整,略微沿西南-东北向拉伸,表明其对西北-东南方向的空间分辨能力略优;而Hi-net的ARF主瓣呈西北-东南向的梭形,其对西南-东北方向的空间分辨能力相对更强.因此,台风“海鸥”在菲律宾海和南海产生的P波地脉动源区正好总体大致处于这两个台阵的空间分辨优势方位角方向,即位于ChinArray Ⅱ的东南方向和Hi-net的西南方向,这为联合这两个台阵进行有效定位提供了一定保障.联合台阵由ChinArray Ⅱ和Hi-net组合而成,由于ChinArray Ⅱ的台站数目仅为Hi-net的58.5%(图 1),联合台阵的ARF总体呈近似Hi-net的ARF分布,而ChinArray Ⅱ台站的加入一定程度上削弱了Hi-net的ARF旁瓣(图 4d).遗憾的是,联合台阵的ARF呈现竖向波纹状割裂,将使FB定位结果出现类似的波纹干扰.初步判断,该现象可能与ChinArray Ⅱ和Hi-net的台站数目差异及空间距离有关.为探究该现象的成因,本文进行了联合台阵组合测试.
如图 4j所示,我们在Hi-net中部截取了与ChinArray Ⅱ台站数目相同的台阵,记为Array 1,并将其复制并移动[-18°E, -20°N]得到Array 2,由于台阵几何结构相同,二者的台阵响应如图 4c所示;同时,我们将ChinArray Ⅱ分别复制移动[+15°E, 0°N]和[-15°E, 0°N]得到Array 3和Array 4.我们分别计算这些台阵的联合台阵响应并进行分析:由ChinArray Ⅱ和Array 1的联合台阵响应(图 4e)与图 4d比较可知, 台站数目并非造成波纹状割裂的原因;Array 1和Array 3(图 4f)以及Array 1和Array 4(图 4g)的联合台阵响应差异则表明,台阵间距是造成波纹状割裂现象的主要原因之一,且波纹割裂的密集程度与距离成正相关;而从Array 2和Array 3(图 4h)以及Array 2和Array 4(图 4i)的联合台阵响应差异可见,台阵的相对空间方位决定了波纹状割裂的分布方向.上述分析表明,联合台阵的竖向波纹状割裂由ChinArray Ⅱ和Hi-net的近纬向间距导致.
由于常规FB技术本身无法消除由地震台阵固有属性(如台阵ARF所表征)的影响,本文在双台阵联合FB定位技术的基础上进一步结合反卷积技术CLEAN-SC,尽可能地避免联合定位结果出现波纹状干扰.最终联合定位结果符合预期,只有少数时刻存在淡淡的“波纹”(图 2c1、2c5和2c6),且并不影响定位结果的精度,这体现了本文双台阵联合FB定位技术的可靠性与优势.

|
图 4 地震台阵(a)ChinArray Ⅱ、(b)Hi-net、(c)Array 1、(d)联合台阵(Combined array)、(e)ChinArray Ⅱ+Array 1联合、(f)Array 1+Array 3联合、(g)Array 1+Array 4联合、(h)Array 2+Array 3联合及(i)Array 2+Array 4联合的响应函数ARFs以及(j)相应地理分布 Fig. 4 Array Response Functions (ARFs) of (a) ChinArray Ⅱ, (b) Hi-net, (c) Array 1, (d) Combined array, (e) ChinArray Ⅱ+Array 1, (f) Array 1+Array 3, (g) Array 1+Array 4, (h) Array 2+Array 3 and (i) Array 2+Array 4, and (j) corresponding geographical distribution |
本文基于ChinArray Ⅱ和Hi-net的连续波形数据,对2014年西北太平洋强台风“海鸥”激发的P波地脉动源区进行定位研究.我们发现,台风“海鸥”在菲律宾海激发的P波地脉动主要源自其激发海浪与台风“风神”遗留涌浪的相互作用,而其本身在不同时刻激发海浪之间相互作用而激发的地脉动能量相对较弱,这导致主要源区逐渐偏离“海鸥”移动轨迹.该现象表明由其他风暴引起的涌浪可能“干扰”对特定台风的定位追踪,值得后续深入研究;同时,南海作为“相对封闭”的边缘海,东部岛链的存在能有效“拦截”来自西太平洋风暴引起的涌浪的影响,不失为难得“干净”的台风激发地脉动观测、研究环境.
由于ChinArray Ⅱ、Hi-net单台阵定位结果受多重因素的影响,包括:(1)ARF强旁瓣导致定位结果出现“伪影”、不聚焦;(2)近距离时(即台阵至源区距离小于26°)基于理论地球模型的P波走时估计与实际走时之间的偏差以及(3)上地幔三重震相产生的干扰等,本文提出了将台阵至源区的距离作为归一化因子、结合反卷积技术CLEAN-SC的双台阵联合FB定位方法.该方法能够削弱单台阵定位应用中以上方面的影响,有效提升定位结果的聚焦性与稳定性,实现了对台风“海鸥”在菲律宾海、南海激发的P波地脉动源区的全程、稳定有效定位与追踪.
然而,本文的双台阵联合FB定位研究仍存在一些不足之处.本文的联合定位结果与理论源区在南海海域的差异较大,暂无法判别优劣与原因,亟待后续进一步研究.另外,虽然本文利用3-D地球介质速度模型提高了P波走时估计精度,并且能够通过双台阵联合优化近场源区定位效果,但未能彻底避免上地幔三重震相及近源P波走时估计偏差对定位结果的影响.上述问题的存在仍会对双台阵联合定位的精确性和可靠性造成影响,有待后续进一步研究.
致谢 谨此祝贺陈颙先生从事地球物理教学科研工作60周年.感谢中国地震科学探测台阵数据中心和日本Hi-net台网为本研究提供连续地震记录数据.感谢日本气象厅提供台风最佳路径数据,欧洲中期气象预报中心提供波浪场数据,法国海洋开发研究院提供的P波地脉动源区海表等效压力谱数据.
Amante C, Eakins B W. 2009. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24. Silver Spring: National Geophysical Data Center, doi: 10.7289/V5C8276M.
|
Ardhuin F, Stutzmann E, Schimmel M, et al. 2011. Ocean wave sources of seismic noise. Journal of Geophysical Research: Oceans, 116(C9): C09004. DOI:10.1029/2011JC006952 |
Ardhuin F, Balanche A, Stutzmann E, et al. 2012. From seismic noise to ocean wave parameters: General methods and validation. Journal of Geophysical Research: Oceans, 117(C5): C05002. DOI:10.1029/2011JC007449 |
Ardhuin F, Herbers T H C. 2013. Noise generation in the solid Earth, oceans and atmosphere, from nonlinear interacting surface gravity waves in finite depth. Journal of Fluid Mechanics, 716: 316-348. DOI:10.1017/jfm.2012.548 |
Ardhuin F, Gualtieri L, Stutzmann E. 2015. How ocean waves rock the Earth: Two mechanisms explain microseisms with periods 3 to 300 s. Geophysical Research Letters, 42(3): 765-772. DOI:10.1002/2014GL062782 |
Bromirski P D, Duennebier F K, Stephen R A. 2005. Mid-ocean microseisms. Geochemistry, Geophysics, Geosystems, 6(4): Q04009. DOI:10.1029/2004GC000768 |
Bromirski P D. 2009. Geophysics. Earth vibrations. Science, 324(5930): 1026-1027. DOI:10.1126/science.1171839 |
Cessaro R K. 1994. Sources of primary and secondary microseisms. Bulletin of the Seismological Society of America, 84(1): 142-148. DOI:10.1785/BSSA0840010142 |
Chen D L, Lin J M, Ni S D, et al. 2018. Characteristics of seismic noise on ocean islands in Northwest Pacific and its oceanographic interpretation. Chinese Journal of Geophysics (in Chinese), 61(1): 230-241. DOI:10.6038/cjg2018L0047 |
Chen L S. 2006. The evolution on research and operational forecasting techniques of tropical cyclones. Journal of Applied Meteorological Science (in Chinese), 17(6): 672-681. |
Chi W C, Chen W J, Kuo B Y, et al. 2010. Seismic monitoring of western Pacific typhoons. Marine Geophysical Researches, 31(4): 239-251. DOI:10.1007/s11001-010-9105-x |
Chu R S, Zhu L P, Ding Z F. 2019. Upper-mantle velocity structures beneath the Tibetan Plateau and surrounding areas inferred from triplicated P waveforms. Earth and Planetary Physics, 3(5): 445-458. DOI:10.26464/epp2019045 |
Davy C, Barruol G, Fontaine F R, et al. 2014. Tracking major storms from microseismic and hydroacoustic observations on the seafloor. Geophysical Research Letters, 41(24): 8825-8831. DOI:10.1002/2014GL062319 |
Duan Y H, Fang J, Cheng Z Q, et al. 2020. Advances and trends in tropical cyclone research and forecasting: An overview of the ninth World Meteorological Organization International Workshop on Tropical Cyclones (IWTC-9). Acta Meteorologica Sinica (in Chinese), 78(3): 537-550. DOI:10.11676/qxxb2020.050 |
Euler GG, Wiens D A, Nyblade A A. 2014. Evidence for bathymetric control on the distribution of body wave microseism sources from temporary seismic arrays in Africa. Geophysical Journal International, 197(3): 1869-1883. DOI:10.1093/gji/ggu105 |
Fan W Y, McGuire J J, de Groot-Hedlin C D, et al. 2019. Stormquakes. Geophysical Research Letters, 46(22): 12909-12918. DOI:10.1029/2019GL084217 |
Fang S K, Lin J M, Ni S D, et al. 2020. Improving seismic remote sensing of typhoon with a three-dimensional Earth model. The Journal of the Acoustical Society of America, 148(2): 478-491. DOI:10.1121/10.0001624 |
Farra V, Stutzmann E, Gualtieri L, et al. 2016. Ray-theoretical modeling of secondary microseism P waves. Geophysical Journal International, 206(3): 1730-1739. DOI:10.1093/gji/ggw242 |
Gerstoft P, Fehler M C, Sabra K G. 2006. When Katrina hit California. Geophysical Research Letters, 33(17): L17308. DOI:10.1029/2006GL027270 |
Gerstoft P, Shearer P M, Harmon N, et al. 2008. Global P, PP, and PKP wave microseisms observed from distant storms. Geophysical Research Letters, 35(23): L23306. DOI:10.1029/2008GL036111 |
Gilmore M H. 1946. Microseisms and ocean storms. Bulletin of the Seismological Society of America, 36(2): 89-119. |
Gualtieri L, Stutzmann E, Farra V, et al. 2014. Modelling the ocean site effect on seismic noise body waves. Geophysical Journal International, 197(2): 1096-1106. DOI:10.1093/gji/ggu042 |
Hasselmann K. 1963. A statistical analysis of the generation of microseisms. Reviews of Geophysics, 1(2): 177-210. DOI:10.1029/RG001i002p00177 |
Hillers G, Graham N, Campillo M, et al. 2012. Global oceanic microseism sources as seen by seismic arrays and predicted by wave action models. Geochemistry, Geophysics, Geosystems, 13(1): Q01021. DOI:10.1029/2011GC003875 |
Klotz B W, Uhlhorn E W. 2014. Improved stepped frequency microwave radiometer tropical cyclone surface winds in heavy precipitation. Journal of Atmospheric and Oceanic Technology, 31(11): 2392-2408. DOI:10.1175/JTECH-D-14-00028.1 |
Landès M, Hubans F, Shapiro N M, et al. 2010. Origin of deep ocean microseisms by using teleseismic body waves. Journal of Geophysical Research: Solid Earth, 115(B5): B05302. DOI:10.1029/2009JB006918 |
Li F H, Liu S Q, Wang J Y. 2016. A numerical model of underwater ambient noise generated by typhoons and application in estimation of typhoon wind speed. Acta Acustica (in Chinese), 41(5): 750-757. DOI:10.15949/j.cnki.0371-0025.2016.05.027 |
Lin J M, Lin J, Xu M. 2017. Microseisms generated by Super Typhoon Megi in the Western Pacific Ocean. Journal of Geophysical Research: Oceans, 122(12): 9518-9529. DOI:10.1002/2017JC013310 |
Lin J M, Wang Y T, Wang W T, et al. 2018. Seismic remote sensing of Super Typhoon Lupit (2009) with seismological array observation in NE China. Remote Sensing, 10(2): 235. DOI:10.3390/rs10020235 |
Liu Q X, Koper K D, Burlacu R, et al. 2016. Source locations of teleseismic P, SV, and SH waves observed in microseisms recorded by a large aperture seismic array in China. Earth and Planetary Science Letters, 449: 39-47. DOI:10.1016/j.epsl.2016.05.035 |
Longuet-Higgins M S. 1950. A theory of the origin of microseisms. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 243(857): 1-35. DOI:10.1098/rsta.1950.0012 |
Maurya S, Taira T, Romanowicz B. 2019. Location of seismic "hum" sources following storms in the North Pacific Ocean. Geochemistry, Geophysics, Geosystems, 20(3): 1454-1467. DOI:10.1029/2018GC008112 |
Myers S C, Simmons N A, Johannesson G, et al. 2015. Improved regional and teleseismic P-wave travel-time prediction and event location using a global 3D velocity model. Bulletin of the Seismological Society of America, 105(3): 1642-1660. DOI:10.1785/0120140272 |
Nishida K. 2013. Earth's background free oscillations. Annual Review of Earth and Planetary Sciences, 41(1): 719-740. DOI:10.1146/annurev-earth-050212-124020 |
Nishida K. 2017. Ambient seismic wave field. Proceedings of the Japan Academy, Series B, 93(7): 423-448. DOI:10.2183/pjab.93.026 |
Ramirez J E. 1940. An experimental investigation of the nature and origin of microseisms at St. Louis, Missouri: Part one. Bulletin of the Seismological Society of America, 30(1): 35-84. DOI:10.1785/BSSA0300010035 |
Rhie J, Romanowicz B. 2004. Excitation of Earth's continuous free oscillations by atmosphere-ocean-seafloor coupling. Nature, 431(7008): 552-556. DOI:10.1038/nature02942 |
Rhie J, Romanowicz B. 2006. A study of the relation between ocean storms and the Earth's hum. Geochemistry, Geophysics, Geosystems, 7(10). DOI:10.1029/2006GC001274 |
Roessler D, Krueger F, Ohrnberger M, et al. 2010. Rapid characterisation of large earthquakes by multiple seismic broadband arrays. Natural Hazards and Earth System Sciences, 10(4): 923-932. DOI:10.5194/nhess-10-923-2010 |
Rost S, Thomas C. 2002. Array seismology: Methods and applications. Reviews of Geophysics, 40(3): 2-1. DOI:10.1029/2000RG000100 |
Schweitzer J, Fyen J, Mykkeltveit S, et al. 2012. Seismic arrays. //Bormann P ed. New Manual of Seismological Observatory Practice 2 (NMSOP-2). Potsdam: Deutsches GeoForschungs Zentrum GFZ, 1-80, doi: 10.2312/GFZ.NMSOP-2_ch9.
|
Sijtsma P. 2007. CLEAN based on spatial source coherence. International Journal of Aeroacoustics, 6(4): 357-374. DOI:10.1260/147547207783359459 |
Stipčević J, Kennett B L N, Tkalčić H. 2017. Simultaneous use of multiple seismic arrays. Geophysical Journal International, 209(2): 770-783. DOI:10.1093/gji/ggx027 |
Sufri O, Koper K D, Burlacu R, et al. 2014. Microseisms from Superstorm Sandy. Earth and Planetary Science Letters, 402: 324-336. DOI:10.1016/j.epsl.2013.10.015 |
Sun T H Z, Xue M, Le K P, et al. 2013. Signatures of ocean storms on seismic records in South China Sea and East China Sea. Marine Geophysical Research, 34(3-4): 431-448. DOI:10.1007/s11001-013-9204-6 |
Tanimoto T, Hadziioannou C, Igel H, et al. 2015. Estimate of Rayleigh-to-Love wave ratio in the secondary microseism by colocated ring laser and seismograph. Geophysical Research Letters, 42(8): 2650-2655. DOI:10.1002/2015GL063637 |
The WAVEWATCH Ⅲ® Development Group (WW3DG). 2019. User manual and system documentation of WAVEWATCH Ⅲ® version 6.07. Technical Note 333. College Park: NOAA/NWS/NCEP/MMAB.
|
Uhlhorn E W, Black P G. 2003. Verification of remotely sensed sea surface winds in hurricanes. Journal of Atmospheric and Oceanic Technology, 20(1): 99-116. DOI:10.1175/1520-0426(2003)020〈0099:VORSSS〉2.0.CO;2 |
Wang J Y, Li F H. 2015. Preliminary study on underwater ambient noise generated by typhoons. Chinese Physics Letters, 32(4): 044301. DOI:10.1088/0256-307x/32/4/044301 |
Ward Neale J, Harmon N, Srokosz M. 2018. Improving microseismic P wave source location with multiple seismic arrays. Journal of Geophysical Research: Solid Earth, 123(1): 476-492. DOI:10.1002/2017JB015015 |
Xia Y J, Ni S D, Zeng X F. 2011. Polarization research on seismic noise before Wenchuan Earthquake. Chinese Journal of Geophysics (in Chinese), 54(10): 2590-2596. DOI:10.3969/j.issn.0001-5733.2011.10.016 |
Zhang B, Perrie W, Zhang J A, et al. 2014. High-resolution hurricanevector winds from C-band dual-polarization SAR observations. Journal of Atmospheric and Oceanic Technology, 31(2): 272-286. DOI:10.1175/JTECH-D-13-00006.1 |
Zheng L L, Lin J M, Ni S D, et al. 2017. Characteristics and generation mechanisms of double frequency microseisms generated by typhoons. Chinese Journal of Geophysics (in Chinese), 60(1): 187-197. DOI:10.6038/cjg20170116 |
Zhang J, Gerstoft P, Bromirski P D. 2010. Pelagic and coastal sources of P-wave microseisms: Generation under tropical cyclones. Geophysical Research Letters, 37(15): L15301. DOI:10.1029/2010GL044288 |
陈栋炉, 林建民, 倪四道, 等. 2018. 西北太平洋海岛地区地震背景噪声特征及海洋学解释. 地球物理学报, 61(1): 230-241. DOI:10.6038/cjg2018L0047 |
陈联寿. 2006. 热带气旋研究和业务预报技术的发展. 应用气象学报, 17(6): 672-681. DOI:10.3969/j.issn.1001-7313.2006.06.005 |
端义宏, 方娟, 程正泉, 等. 2020. 热带气旋研究和业务预报进展——第九届世界气象组织热带气旋国际研讨会(IWTC-9)综述. 气象学报, 78(3): 537-550. DOI:10.11676/qxxb2020.050 |
李风华, 刘珊琪, 王璟琰. 2016. 台风激发水下噪声场的建模及其在台风风速反演中的应用. 声学学报, 41(5): 750-757. DOI:10.15949/j.cnki.0371-0025.2016.05.027 |
夏英杰, 倪四道, 曾祥方. 2011. 汶川地震前地脉动信号的单台法研究. 地球物理学报, 54(10): 2590-2596. DOI:10.3969/j.issn.0001-5733.2011.10.016 |
郑露露, 林建民, 倪四道, 等. 2017. 台风激发的第二类地脉动特征及激发模式分析. 地球物理学报, 60(1): 187-197. DOI:10.6038/cjg20170116 |
 2021, Vol. 64
2021, Vol. 64

