利用地震台站所记录到的背景噪声进行互相关计算，获得的噪声互相关函数(Noise Cross-correlation Function, NCF)可在一定程度上近似台站间的格林函数(Shapiro & Campillo, 2004; Sabra et al., 2005; Campillo, 2006).NCF中的信号，可视为在台站间传播的地震波，能够用于不同尺度的地下速度结构成像(Shapiro et al., 2005; Yao et al., 2006; Nishida et al., 2009; Li et al., 2010; Li et al., 2014)和地下介质的波速变化监测(Brenguier et al., 2008a, b; 刘志坤等，2010)等研究.背景噪声互相关方法可在任意两个台站间获取传播的地震信号，因此被广泛应用于地震学研究中，NCF也逐渐成为一种新型的地震观测数据.

背景噪声互相关函数收敛于台站间格林函数的理论假设是背景噪声能量在三维空间内均匀分布的，即满足能量均分条件(Campillo et al., 2003; Snieder et al., 2004; Roux et al., 2005).然而，地球上实际的噪声源并不满足这一理论假设.首先，大部分的噪声源都位于地球表面.虽然地下介质的散射也可被视为噪声源，但是主要的噪声能量仍以在地球表面传播的面波能量为主(Friedrich et al., 1998; Ekstrom, 2001).再者，即使面波类型的噪声源也不满足在地表均匀分布的假设，其在空间和能量强弱上均具有不均匀性.地球背景噪声的能量主要与海洋活动和大气扰动有关，其振幅谱上存在两个明显的峰值，表征两类主要的噪声源.其中周期10~20 s的噪声为第一类地脉动(Primary Microseisms)，主要与海浪和固体地球的直接作用有关.而周期3~10 s的为第二类地脉动(Secondary Microseisms)，其能量相对第一类地脉动较强，是由两列频率相同，方向相反的波干涉而成(Longuet-Higgins, 1950; Hasselmann, 1963)，如海浪在海岸线的反射以及深海风暴的相互作用(Ardhuin et al., 2011).

海洋活动具有明显的季节性变化，且在南半球和北半球的变化特征不同.一般在所在半球的冬季，海洋活动较强，而夏季较弱.受此影响，背景噪声的能量也呈现出明显的季节性变化.由背景噪声互相关获得的NCF中的信号，也会受到噪声源分布的影响.对于以面波信号为主的NCF而言，提取到的面波信号的强弱和细节形态与噪声能量的方位分布有关，对后续成像的精度有一定的影响(Tsai, 2009; Yao & Van der Hist, 2009).同时，在地球表面还存在一些持续、稳定的噪声源(Shapiro et al., 2006; 王伟涛等，2012；Zeng et al., 2010; Retailleau et al., 2017)，这些噪声源所产生的信号并不能通过长时间的叠加进行消除，在进行后续分析时需要进行对应处理(Zheng et al., 2011).背景噪声中也存在一定比例的P波、S波类型的体波信号(Liu et al., 2016)，这些信号通过互相关产生干涉，会在NCF中产生对应的信号(Wang et al., 2018).真实噪声源的时空变化特征与理论均匀分布假设之间的差异，使得NCF中提取到的信号与实际格林函数有所差异.对这些信号进行精细分析，需要对噪声源进行相应的研究.

背景噪声在台站记录中表现为持续的、振幅很小的信号.利用连续记录，可分析噪声能量随频率的分布，结合三分量偏振分析方法可对噪声能量的来源方向进行分析(Koper et al., 2010; Koper et al., 2015; Takagi et al., 2018).自噪声互相关技术出现之后，很多学者基于NCF中的信号对相干噪声的特征进行了分析.Stehly等(2006)提出了背景噪声能量流方法(Normalized Background Energy Flux，NBEF)，利用NCF中正负半轴的信号强度差异对噪声源的空间分布和季节变化进行了研究.Yang等(2008)基于垂直分量NCF中面波信号的信噪比，利用全球分布的多个台阵和地震台网对不同周期噪声的优势方向和季节变化进行了分析，并通过交切方法对噪声源的空间分布进行了研究.Tian和Ritzwoller(2015)也利用信噪比对Juan de Fuca板块和美国西部海岸台站记录到的噪声进行了分析，加深了对北太平洋地区不同频段噪声源的认识.背景噪声在地震台站上的振幅较小，但相干的背景噪声在NCF中可以产生较强的信号.基于NCF的相关分析方法，为研究噪声源的时空分布提供了新的手段.

利用NCF中的信号，可对一些较为持续、稳定的噪声源进行定位分析.Shapiro等(2006)利用NCF中的非面波信号对几内亚湾周期26 s的噪声源进行了定位研究.Zeng和Ni(2010)，以及Wang等(2012)利用国际及中国的地震台站对日本九州岛的非海洋性噪声源进行了研究.Retailleau(2017)选取单个台站同密集台阵之间进行互相关运算，利用NCF中的信号对大西洋北部的一个强噪声源进行了定位分析.Xia等(2013)以及Zeng和Ni等(2014)也利用类似方法对几内亚湾的噪声源进行了多项研究.上述研究表明，利用NCF中的各种信号，可以对噪声源的特征进行分析.同时，所获取的噪声源的时空分布特征，也有助于了解NCF中各种信号的产生机制，利于后续对NCF中各种信号的分析和利用.

已有研究表明，在5~20 s的地脉动周期内，地表噪声源的分布主要受全球海洋活动的控制.噪声源的时空分布，是一个全球尺度的问题.全球性的噪声源分布对台站间NCF的影响，则与所用台站的空间位置和观测周期有关.NCF的波形特征，受控于对其起主要影响的噪声源分布.因此，利用不同地区获得的NCF，可以分析噪声源分布对NCF提取的影响，亦有助于对全球噪声源时空特征的完整描述.

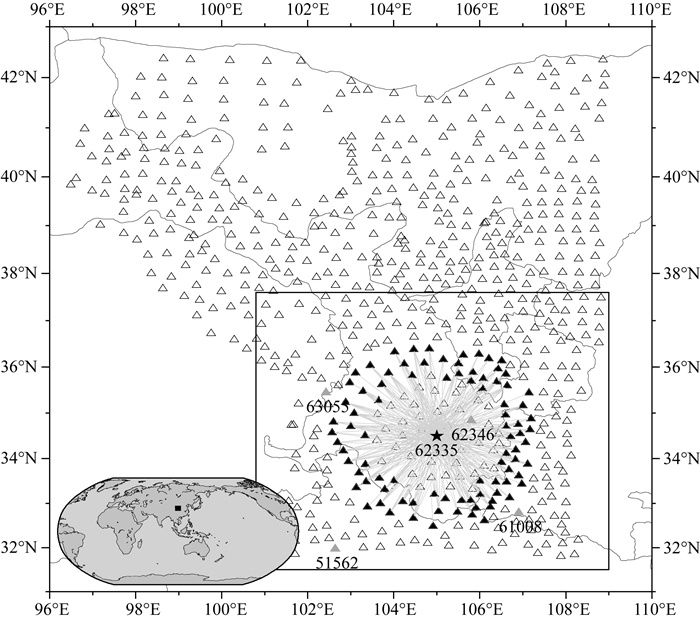
中国地震局地球物理研究所牵头开展的“中国地震科学探测台阵-南北地震带北段”于2013至2016年在南北地震带北段开展了ChinArray二期的密集台阵观测.在观测区域内共布设有678个宽频带地震台站，连续观测时间约为2年(图 1).大尺度密集台阵的长时间记录，为分析噪声源的特征提供了优良的数据支持.本文利用ChinArray二期数据中南部区域的322个地震台站，计算了台站间垂直分量的NCF.之后利用Stehly等(2006)提出的背景能量流方法分析了不同周期噪声能量的优势方位和季节变化，并对噪声源的时空分布对NCF中信号的影响进行了研究.

图 1

Fig. 1

图 1 ChinArray二期台站分布图 三角表示ChinArray二期的678个宽频带台站，其中正方形区域为本研究使用的322个台站分布.五角星为62335台，周边黑色实心三角表示台站间距为500~550 km，路径中心接近62335台的台站分布.灰色台站51562、62346、63055和61008为后文分析采用的台站. Fig. 1 Station map of ChinArray Phase II The triangles represent the 678 broad-band stations of ChinArray Phase II, while the square indicates the 322 stations used in current study. The station 62335 is shown as black star and the black triangles represent a circular distributed array with the center near 62335, with a distance of about 500~550 km from the center near 62335. The labeled stations (51562, 62346, 63055 and 61008) are used in the later analysis.

利用Stehly等(2006)提出的NBEF方法对研究区域内噪声源的方位分布和季节变化进行了分析.其原理简述如下：

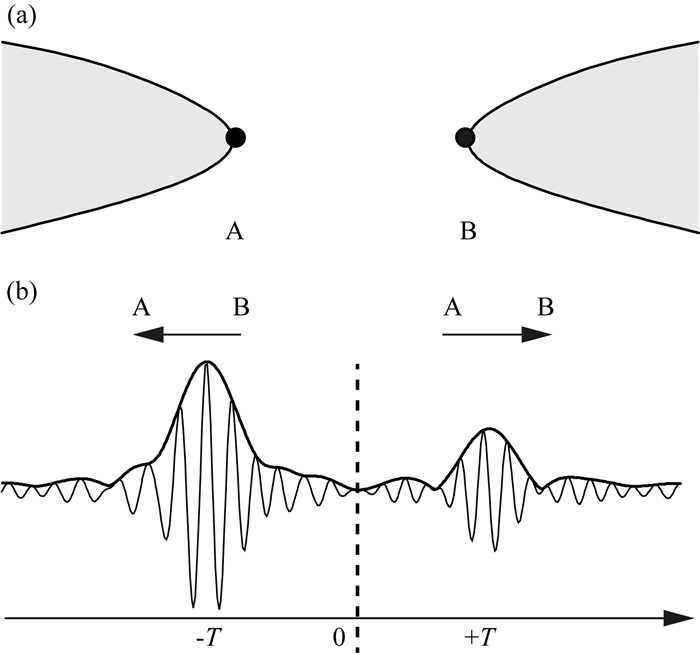
对任意两个台站的连续记录进行互相关可得台站间的NCF，NCF的正负分支分别代表台站间沿相反方向传播的波，反映了台站连线延长线的相干区域(图 2a灰色区域)内的噪声源信息.当台站两侧的噪声源在空间上均匀分布时，NCF的正负分支在振幅和到时上都是对称的，但当台站两侧噪声源的分布不均匀时，NCF的振幅将会出现很大的不同(Lobkis and Weaver, 2001; Snieder, 2004; Stehly et al., 2006).振幅的强弱和从其中一个台站传播至另一个台站的地震波的能量流有关，且主要受位于台站连线延长线的相干区域影响(Snieder et al., 2004; Stehly et al., 2006).因此，NCF波形振幅的强弱可表征该台站对连线上噪声源的强弱.基于此原理，利用路径方位角分布较好的台阵可对台站布设区域的主要噪声能量来源方向进行研究.利用不同方位角路径在不同时段的NCF的正负半轴振幅进行分析，可以获得背景噪声源的优势分布方向和强度随时间的演化信息.

图 2

Fig. 2

图 2 噪声背景能量流方法原理图(据Stehly等(2006)修改) (a) 台站A、B及其路径上面波的相干区域; (b) 噪声源非均匀分布时，台站对AB间互相关函数的正负分支.波形上方黑色实线为其包络 Fig. 2 Schematic illustration of the NBEF method proposed by Stehly et al.(2006) (a) Two stations A and B are shown as black dots while the coherent zone is filled in gray; (b) The NCF for uneven distribution of noise source. The positive and negative parts are for signals traveling from A to B and B to A, respectively. The black line above shows the envelope.

该方法具体流程为，假设有任意两台站A和B(如图 2a)，本文约定将台站A视为虚拟震源，台站B视为虚拟接收器，NCF的正分支波形表征由A传到B的信号，其主要体现的是相应的反方位角θ方向上噪声源的贡献.对台站AB做互相关计算，并在特定时间段(t₁, t₂)内进行叠加得到叠加后的互相关函数NCF(A，B，t₁，t₂)，其中t₁和t₂为此叠加的开始和结束时间.对叠加后所得的NCF(A，B，t₁，t₂)的正分支面波信号求取包络的最大值得ENV_max(A，B，t₁，t₂)，并乘以其台间距的平方根(为台站间距)，来进行面波几何衰减的校正.用校正后的NCF正分支包络的最大值来表示由台站A传至台站B的背景能量流E(A，B，t₁，t₂，θ)，即：

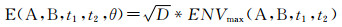
对于台站A和B垂直分量间的NCF，将其波形以零时刻进行时间反转，反转之后的正半轴波形表征由B传向A的信号.交换两个台站的位置信息，将台站B作为虚拟震源，A作为虚拟台站，重新计算反方位角，利用反转之后NCF正半轴的面波最大值，可以获取由B传到A的噪声能量.上式中包含基于距离的加权，因此被称为归一化的噪声背景能量流方法(Stehly et al., 2006).

对密集均匀台阵内的所有台站对计算背景能量流，再综合求和可分析得(t₁, t₂)时间段内整个区域的噪声能量在不同方位角的分布：

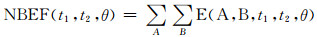
基于上式得到(t₁, t₂)时间段能量流的优势方向，综合不同时段计算所得到的NBEF，便可获取背景噪声能量的主要来源方向及其随时间的变化特征.

噪声背景能量流方法是利用噪声互相关函数研究面波类型噪声源的时空分布的经典方法，相比基于三分量连续数据的偏振分析以及反投影方法(Koper et al., 2010; Liu et al., 2016), 该方法计算速度较快，易于应用于大规模台阵数据的处理.因此，本文利用了该方法对台阵数据进行了处理和分析.

本文使用数据为ChinArray二期所布设的678个宽频带台站南部的一个子台阵，位于图 1中黑色正方形区域内.该子台阵包含322个宽频带台站，平均台间距约为50 km，观测时间为2013年9月至2016年6月，大多超过两年.利用此322个台站的垂直分量记录，计算了51681条路径上的噪声互相关函数(NCF).

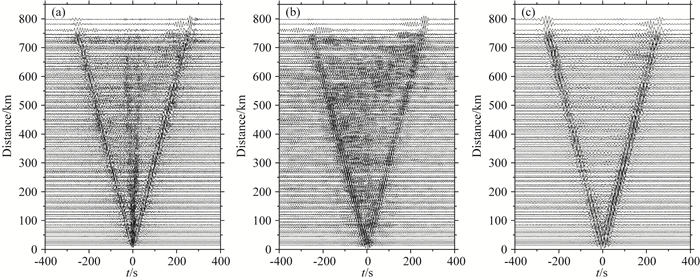
根据Bensen等(2007)的数据处理流程，首先对各台站单天数据的垂直分量进行去均值、去趋势、去除仪器响应、并抽样至1 Hz，然后选取长度为120 s的滑动时窗，计算权重，使用滑动绝对平均方法进行时间域的归一化.时域归一化后，将每天数据进行傅里叶变换至频率域，进行0.008~0.45 Hz的谱白化，以拓宽NCF信号的频谱.在完成单台数据预处理后，对频谱数据进行频率域的互相关，再经由傅里叶反变换获取每个路径上单天的NCF.为对更长时段的数据进行分析，单天NCF的时间范围为±3600 s.获取单天NCF之后，按照不同的时间窗对其进行叠加以获取高信噪比的NCF.对2013年9月至2016年6月所有的单天NCF进行叠加可获取各个路径上的参考波形.图 3显示了多年叠加的NCF在4~8 s，8~12 s和12~20 s三个频段的波形.从中可以看出，三个频段都有较为明显的视速度约为3 km·s^-1的瑞利面波信号.同时，不同频段NCF中含有的信号也存在明显差异.在4~8 s，面波信号之前有一视速度约为24 km·s^-1的较强信号(图 3a)，前人研究认为这个较强信号为高入射角的远震体波干涉而成(Landès et al., 2010; Wang et al., 2018)，其到时趋近于零，在台站间距较近时会与面波信号发生混叠.除此之外，在周期为4~8 s和8~12 s的频段上，还存在一些杂乱的信号(图 3a, 3b)，可能是其他干扰所致.

图 3

Fig. 3

图 3 由2013年9月至2016年6月数据叠加获得的NCF波形 (a) 滤波至4~8 s的NCF；(b) 滤波至8~12 s的NCF；(c) 滤波至12~20 s的NCF. Fig. 3 The waveforms of reference NCFs at different period range The NCFs are stacked from September 2013 to June 2016 and band-pass filtered for period (a) 4~8 s, (b) 8~12 s and (c) 12~20 s respectively.

每个路径上，单天NCF每30天叠加一次，作为该时段内的叠加NCF，之后将叠加时窗滑动5天，获取下一个时段内的叠加NCF.这种滑动叠加方式可确保NCF中面波信号具有一定信噪比，同时可反映NCF中波形随时间的变化.为减小路径分布和数据连续率对后续NBEF分析的干扰，本文选择了在所有时段内单天叠加数目均超过15天的数据进行了分析.同时，依据台站路径的长度和方位分布对数据进行了进一步的筛选.由图 4观察可得，台站路径随距离和方位的分布并不均匀.在后续分析中，本文选择了台站间距大于150 km且小于600 km的路径进行分析.在此范围内，面波信号易于区分，并且路径的方位分布相对较好(图 4b).

图 4

Fig. 4

图 4 研究区域路径的距离和方位分布 (a) NCF随台间距的分布图；(b) NCF随方位角的分布图. Fig. 4 The statistics on inter-stations distance and back-azimuth for all paths (a) Distance distribution of all inter-station paths; (b) Azimuth distribution of all inter-station paths.

利用滑动叠加的NCF数据，可以获得各个路径上噪声能量在两个反方位角上的优势分布.综合所有路径，可获取该时段内台阵区域接收到的背景噪声能量随方向的分布.将所有时段噪声能量和方向分布进行综合分析，可获得研究区域在约2年时间段内接收到的背景噪声能量的方向和季节性变化规律.

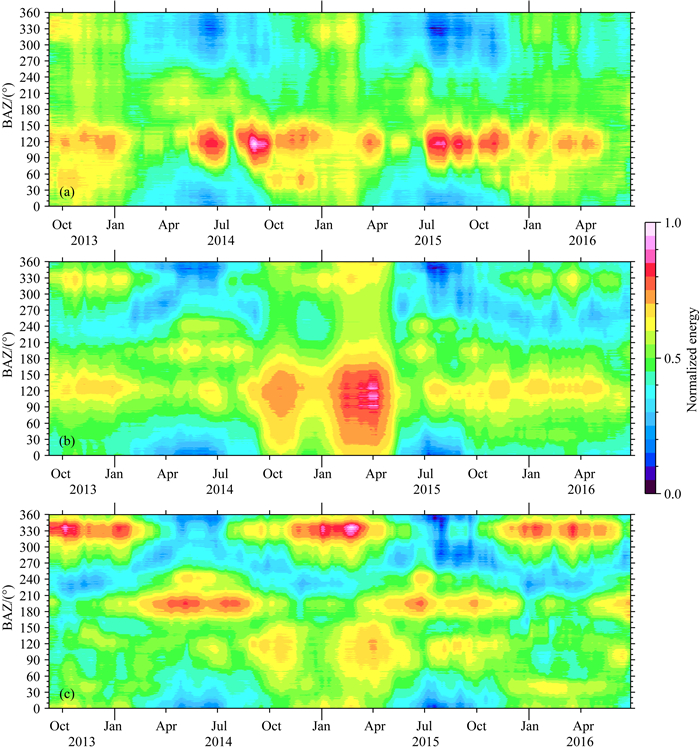
利用该方法，图 5显示了4~8 s，8~12 s和12~20 s三个周期频段内噪声能量的变化规律.总体而言，不同周期的噪声均具有明显的季节性变化，在不同年份的同一季节内具有较为类似的能量分布特征.已有研究表明，在5~20 s的地脉动周期内，地球背景噪声与全球的海洋活动相关(Stehly et al., 2006；Yang et al., 2008).同时，全球海洋活动具有明显的季节变化，且南北半球变化趋势不同.一般而言，在所在半球的冬季，海洋活动较为剧烈，夏季较弱(Hillers et al., 2012).为便于讨论，本文冬季指代北半球冬季，包含每年的11月至次年的3月，夏季指代北半球的夏季，包含每年的5月至8月.

图 5

Fig. 5

图 5 背景噪声能量的优势方向及其随时间的演化图 (a) NCF信号滤波到4~8 s；(b) NCF信号滤波到8~12 s；(c) NCF信号滤波到12~20 s. Fig. 5 Variation of the strength and the direction of the NBEF from September 2013 to June 2016 and band-pass filtered for period (a) 4~8 s, (b) 8~12 s and (c) 12~20 s respectively

在不同的周期频段，噪声能量的优势来源方向不同.其中周期为4~8 s时，噪声能量优势方向为30°~70°和90°~150°，其中90°~150°区域内的噪声能量最强，来自于东侧的北太平洋区域；周期为8~12 s时，噪声的主要优势方向分为三个区域，分别为90°~150°，170°~210°和300°~350°，其中90°~150°能量最强.周期为12~20 s时，能量的主要优势区域为90°~150°，170°~250°，300°~350°，其中300°~350°来源方向的噪声源能量最强，对应大西洋北部区域，170°~250°的能量次之，其能量主要来源对应于南部的印度洋及南大洋区域(图 5).

在不同的周期频段，噪声的能量强度存在明显的季节变化.噪声能量呈现出冬季较强，夏季较弱的反方位角区间包含4~8 s频段的30°~70°，8~12 s频段的90°~150°和300°~350°，12~20 s频段的90°~150°范围也呈现类似特征.噪声的能量强度呈现出夏季较强而冬季较弱的主要包含8~12 s周期的170°~210°及12~20 s周期的170°~250°优势方向.综合来看，整体噪声强度优势方向指向北半球的能量在冬季较强，夏季较弱，指向南半球的变化趋势则与之相反，这与全球海洋活动的变化规律较为一致(Hillers et al., 2012).对8~12 s及12~20 s频段，2014年9月至2015年5月期间相继出现了两个方位角覆盖较广的强异常能量，推测其形成原因可能与短期的海洋活动有关，具体机制仍有待于进一步研究.

为分析噪声源的季节变化对NCF中波形的影响，本文选取了台站路径51562-62346提取到的NCF进行了分析，其台站位置如图 1所示.将该路径上在2014年1月1日至2016年4月4日的单天NCF以15天为间隔进行叠加，共得到55个分时段叠加的NCF，其12~20 s频段的波形如图 6f所示.其中正半轴的波形表示由51562台传往62346台的信号，负半轴表示62346台传往51562台的信号.该路径的反方位角为224°，其对应的地表大圆路径如图 6a黑色实线所示.由图 6a可知，正半轴信号的噪声能量主要来自南半球大洋，而负半轴信号的噪声能量主要来自于太平洋北部.

图 6

Fig. 6

图 6 NCF中波形、信噪比的季节变化以及同平均海浪波高的关系(示例台站为51562和62346) (a) 穿过两个台站的大圆路径及近似的面波噪声源相干区域，黑色网状绘出区域为覆盖路径相干区域的海洋区域，底图为2013—2016平均海洋波高；(b) 北太平洋选定区域的海浪波高随时间的变化规律；(c) NCF负分支的SNR变化图；(d) 印度洋选定区域的海浪波高随时间的变化规律；(e) NCF正分支的SNR变化图；(f) 周期为12~20 s时，NCF信号随时间的变化. Fig. 6 Analysis of the NCF signals between the station 51562 and 62346 (a) The great circle passing through the two stations 51562 and 62346 is shown as a black line. The possible ocean regions contribute to the NCF is marked with shadow; (b) Variation of the averaged wave height over time in the North Pacific Ocean; (c) SNR of the negative time of the correlation functions; (d) Variation of the averaged wave height over time in the Indian Ocean; (e) SNR of the positive time of the correlation functions; (f) NCFs stacked in 15 days for the path 51562-62346 are band-passed for period 12~20 s.

选取分别位于正负半轴100~200 s内的NCF面波信号，计算其信噪比(SNR))，表示来自两个方向的相干能量随着时间的变化，如图 6c和图 6e所示.以与大圆路径偏角为30°的两个大圆路径所形成的区域近似面波的相干区域，计算对应相干区域的全球海浪波高的平均值，可表征两个相干区域内的海洋活动强度.计算平均海浪波高的区域如图 6a中填充区域.为与NCF的信噪比保持一致，在计算海浪波高时，也采用了15天等间隔平均，海浪波高数据来源于WW3的数值模拟数据(Tolman，2005).

为表征面波信号强度随时间的变化，对于15天叠加得到的NCF，分别计算了其正负半轴面波信号的信噪比.根据信号的波形到时，在正半轴上信号窗口选为100~200 s，噪声窗口选为200~300 s，信噪比定义为信号波形绝对值的平均值与噪声波形绝对值的平均值的比值.在负半轴上，相应时间窗口亦沿零时刻进行反转选取.得到55个NCF的正负半轴SNR之后，分别依据相应的正负半轴SNR最大值进行了归一化.从图 6中可以看出，NCF的波形和正负半轴的信噪比均表现出明显的季节性变化，并且正负半轴的变化规律不同.正半轴的信噪比在每年的夏季较高，冬季较低.而负半轴的信噪比则在夏季较低，冬季较高.对比信噪比曲线和海浪波高曲线可知，正负半轴的信噪比与对应区域的海洋活动呈现正相关.这表明该路径上NCF的信号在正负半轴分别受到不同海洋活动性的影响，这同整个台阵由NBEF方法得到的规律一致，亦与前人对噪声源的分析相符(Stehly，2006；Wang et al，2018；Tian and Ritzwoller, 2015).

由图 6f也可以看出，在瑞利面波之前存在一些较强的信号.当噪声源的空间分布不均匀，特别是一些局部地区存在持续、稳定的强噪声源时，NCF中会出现一些台站间格林函数中不存在的异常信号(Zeng and Ni, 2010; Zheng et al., 2011; 王伟涛等，2012; Retailleau et al., 2017；Shapiro et al., 2006).这些信号并不属于两个台站间的格林函数，而是由特定的噪声源分布在互相关计算中干涉产生的.本文将其归为非物理信号，以区别于台站间格林函数中应有的体波、面波等正常信号和震相.

认识此类非物理信号，需要对相应噪声源进行定位分析.对于面波类型的噪声源，传统定位方法需要位置分布较好的多个台阵进行反投影的交切定位.当存在较强的面波噪声源时，其在NCF中产生的非物理信号到时为该噪声源传播至两个台站的走时差(Shaprio et al., 2006；Zeng and Ni, 2010；王伟涛等，2012).基于该原理，Retailleau等(2017)利用单个台站和密集台阵进行互相关，将得到的NCF中的非物理信号进行偏移叠加，对位于大西洋北部的强噪声源进行了定位分析.

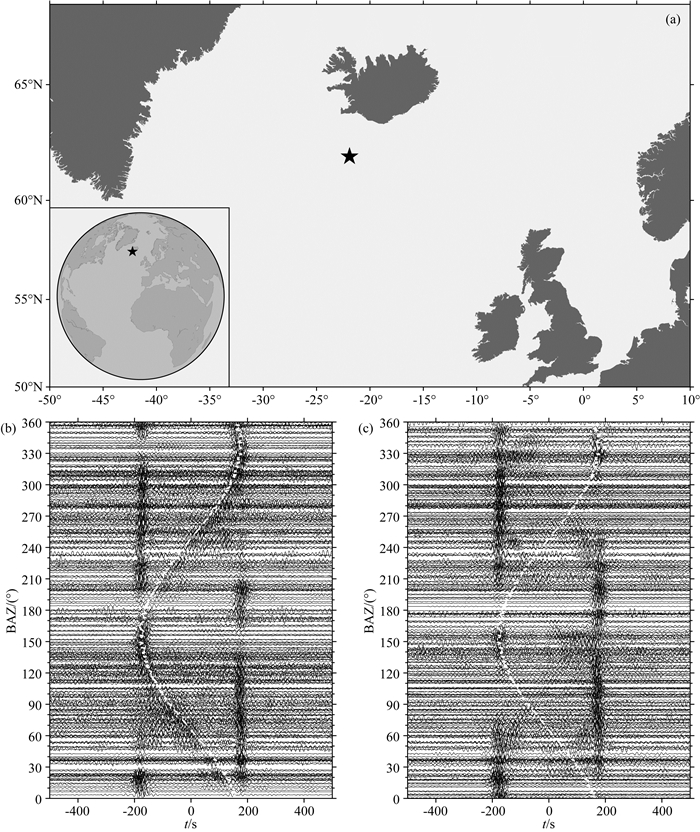
NCF中的信号以面波为主，而面波类型噪声源对NCF的影响可视为一个二维分布.为了描述NCF中信号随方位角的变化，本文选取了台站间距为500~550 km，路径中心接近台站62335的环状分布的300多个路径进行了分析，相关台站分布如图 1所示.如前文所述，噪声源的分布具有明显的季节性变化.因此，我们将2013—2016年每年5—8月份的NCF进行了叠加，作为北半球夏季NCF的叠加波形，而每年的1—3月及10—12月的NCF叠加作为冬季NCF的叠加波形.叠加NCF在周期12~20 s的波形如图 7b和图 7c所示，而图 7a显示了Retailleau等(2017)定位得到位于北大西洋的15~25 s强噪声源的位置.

图 7

Fig. 7

图 7 强噪声源对NCF中信号的影响 (a) 位于大西洋北部的稳定持续噪声源，位置自(Retailleau et al., 2017)；(b) 周期12~20 s时，在距离为500~550 km方位角不同的台站上，冬季叠加的NCF信号随方位角的变化规律，白色曲线为该噪声源产生非物理信号的预测到时；(c)同(b)，夏季叠加的NCF信号. Fig. 7 The influence of strong noise source on signals in NCFs (a) The persistent localized microseism source for 15~25 s in the North Atlantic Ocean (Retailleau et al., 2017); (b) Variation of the signals with back-azimuth for stacked NCFs in winter. The waveforms are band-passed for 12~20 s. The white dashed curve represents the predicted arrival time of the interference signals caused by the microseismic source in (a); (c) Similar to (b) but for stacked NCFs in summer.

由图 7可以看出，由于选取的台站路径长度比较接近，其瑞利面波到时基本在±180 s附件出现.除去瑞利面波之外，图 7b中还存在一组较强的信号.该信号随着方位角呈现规律变化，在反方位角330°及150°时分别接近相应的瑞利面波信号.由其随方位角变化的规律可知，该信号可能是由来自北大西洋的某个强噪声源产生的.利用Retailleau等(2017)确定的噪声源位置，采用面波传播速度3.4 km·s^-1计算了该噪声源至每个路径上两个台站的到时差，作为可能的非物理信号的到时，其到时如图 7b中白色虚线所示.由图 7b可以看出，该预测到时与环形台站分布中出现的信号较为吻合.将该预测到时与夏季叠加的NCF相比，在相关预测时间并无较强信号出现，说明该信号主要在冬季产生.综合以上信息，这些随路径方位规律变化的信号应为大西洋北部的强噪声源产生的非物理信号.

噪声互相关计算主要基于信号的相位相干性，在距离噪声源较远的台站上的噪声信号在经过长时间叠加之后，也可以在NCF中干涉产生可见信号.如Shapiro等(2006)发现的位于几内亚湾的周期26 s的噪声源，其在几千公里间距的台站上也可以被明确观测到.大西洋北部的噪声源在经过较长距离的传播之后，仍保持有一定的相干性，因此在NCF中可以产生相应信号.能量较强的信号更易保持较强的相干性，因此图 7中的异常信号在冬季较为明显，这与大西洋北部噪声源在冬季强度较高的特征相符.同时，在图 7c中可以看出，在夏季叠加NCF中也存在一些相对较弱的信号，且其出现规律相对于冬季(图 7b)更为复杂，推测也可能是由类似机制产生的非物理信号.

根据此类信号的产生机制，到时为该噪声源传播至两个台站的走时差.在均一速度假设下，该源应近似位于以两个台站为焦点的一条双曲线上，曲线形态由其到时决定.如果噪声源的位置在多数路径上的预测走时与实际信号一致，可认为该位置较为可信.通过偏移叠加方式，可以对此类噪声源进行定位.然而，利用NCF中的非物理信号定位相应噪声源位置对台站的布局具有一定要求.如Retailleau等(2017)使用的单台-台阵的定位方式，对于单台至台阵连线中间区域的定位分辨率较好，而对其余区域分辨率不高.利用ChinArray数据来对相关噪声源进行定位，仍有待新的数据支持和详细分析.

为了验证上述结果，本文以台站62335为中心，选择了距其150~350 km的224个台站所形成的台站对，利用NBEF方法计算了12~20 s背景能量流.在获取背景能量流之后，将其以2°的角度进行平均，并进行方位反投影，结果如图 8所示.

图 8

Fig. 8

图 8 (a) 以台站62335为台阵中心，与之台间距为150~350 km的224个台的台站分布图；(b) 2013年9月至2016年6月叠加得到的NCF的背景噪声能量流反投影结果；(c) 夏季月叠加NCF的背景噪声能量流反投影结果；(d) 冬季月叠加NCF的背景噪声能量流反投影结果 Fig. 8 (a) Map of the distribution of 224 stations used in this study. The black triangles indicate the station that the distance with station 62335 is 150~350 km; (b) The back-projection of the NBEF of the NCF stacked from September 2013 to June 2016; (c) The back-projection of the NBEF of the monthly stacked NCF in summer; (d) The back-projection of the NBEF of the monthly stacked NCF in winter

图 8b对全部的单天NCF进行了叠加，投影结果中显示有两个较为明显的方位，分别指向印度洋和大西洋北部.图 8c为夏季叠加结果，显示在西南方向也存在较强的10~20 s的信号.图 8d使用了冬季的叠加数据进行反投影，结果显示信号能量主要分布在大西洋北部，并且其投影的大圆路径与Retailleau等(2017)所获得的强噪声源位置相符.这再次印证了对图 7c中非物理信号的预测结果.受台站分布限制，在夏季及冬季可能的强噪声源位置，仍需要进一步的工作进行确认.

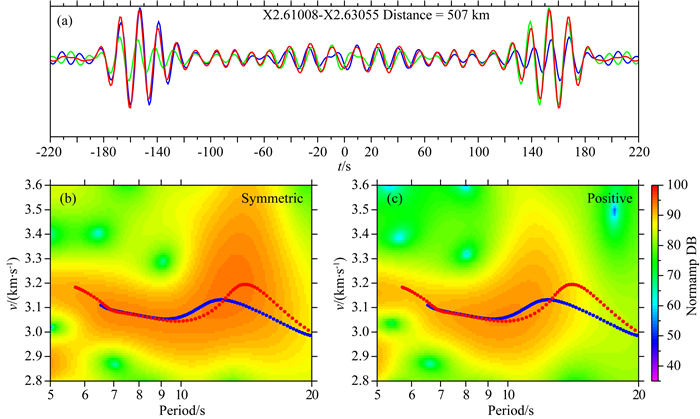
如上分析，噪声源的空间分布对NCF的提取的信号具有较大的影响.特别当持续稳定的强噪声源接近台站路径连线时，在NCF的面波信号之前会出现一些强的非物理信号.此类信号在部分NCF路径上到时接近于常规的瑞利面波信号，甚至可能发生信号的混叠，从而影响后续频散曲线测量的准确性(Zheng et al., 2011).图 9a中蓝色曲线显示了图 7中的台站对61008-63055在观测时段内长时间叠加的NCF波形.该路径台站间距为507 km，对应反方位角为124°，图中显示了其在-220 s至220 s的正负半轴经过12~20 s滤波后的波形.其中到时160 s左右是常规的瑞利面波信号，而由大西洋噪声源产生的信号在负半轴接近瑞利面波的时间出现(图 7b).绿色曲线为该NCF按零时刻时间反转之后的波形，红色曲线是将正负分支叠加之后得到的波形(图 9a).从时间反转后的绿色波形中可以看出，由强噪声源产生的信号走时稍早于瑞利面波.分别利用原始NCF的正分支和正负分支叠加后的面波信号提取频散曲线，得到的曲线如图 9b和图 9c中蓝色和红色曲线所示.可以看出，在6~9 s周期内，二者的频散曲线较为类似.而在12~20 s周期，由于非物理信号的强度较高，在经过正负叠加之后仍起主要作用，导致提取到的群速度相比原始NCF正分支所提取的偏高.针对与瑞利面波时间偏差较大的干扰信号，可以在提取频散曲线时通过细化分析时窗来祛除，但当二者偏差较小时，较难祛除.Zheng等(2011)对日本九州岛噪声源产生的干扰信号进行了分析，发现如果了解强噪声源的位置及其产生机制，便可通过相应无干扰的半轴来进行频散曲线提取，这对相关成像研究中获取可信赖的频散曲线具有重要意义.

图 9

Fig. 9

图 9 噪声源分布非均匀性对频散曲线提取的影响 (a) 滤波至12~20 s的台站61008与63055之间的NCF波形，蓝色是NCF原始波形，绿色为NCF按零时刻时间反转得出的波形，红色的是NCF正负分支叠加得出的波形；(b)和(c)是分别对(a)中所述波形的正半轴提取的频散曲线，颜色与前对应. Fig. 9 The effect of the uniform distribution of the ambient noise source for dispersion (a) The waveform between stations 61028 and 62335 for the period band 12~20 s. The blue curve is the original NCF, the green one is the waveform of NCF by time reversal at zero time, and the red one is symmetric stacked with respect to zero time. (b) and (c) show the dispersion curves measured using positive part of the two stacked NCFs. The color of dispersion curve is consistent with that of corresponding waveforms in (a).

本文采用背景能量流方法，获取了ChinaArray二期台阵南部子台阵记录到的背景噪声能量随时间和空间的演化规律，并分析了噪声源分布不均匀性对NCF中信号的影响，取得了以下认识：

(1) 不同周期频段，噪声能量的主要优势来源方向不同.其中周期为4~8 s和8~12 s时，噪声主要来源方向为90°~150°，源于太平洋北部；周期为12~20 s时，噪声能量的优势方向为170°~250°和300°~350°，分别对应于南半球大洋以及北大西洋.

(2) 背景能量流结果显示噪声能量呈现出明显的季节变化性，来自北半球的噪声能量呈现出冬季较强，夏季较弱的强度变化，而来自南半球的能量强度变化趋势与之相反，这与全球海洋活动相符.

(3) 一些较强的持续稳定的噪声源会对NCF中的信号产生影响，导致在台站格林函数中产生不存在的非物理信号.这些信号在部分路径上会干扰频散曲线的准确提取，影响后续成像精度.

本文研究表明，对噪声源的分析有助于理解NCF中各类信号的产生机制和表现形式，利于对NCF中全波形信息的分析和利用.