随着全球城市化进程的不断加快,城市地质环境越来越受到关注.大多数基础建设和市政公共设施都位于市区地表及浅层地下空间,了解不同地区地层的岩土特性对于场地评价、监测城市地表下沉及维护地下管网运行等至关重要(Mei et al., 2015).同时地下空间的探测和开发对于推动城市由外延扩张式向内涵提升式转变,改善城市环境,建设宜居城市具有重要意义(杨文采等,2019).然而城市的发展给城市地区地球物理数据采集带来了诸多困难,而传统密集接收器的部署及维护又需要短时大量人力物力的支撑.
近年来,分布式声波传感(DAS,Distributed Acoustic Sensing)技术得到迅猛发展,为实现便捷低成本城市地下空间探测提供了可能(王宝善等,2021).DAS通过测量光纤中激光脉冲产生的Rayleigh后向散射信号的相位变化来获得地震波在光纤上引起的轴向应变(Lindsey et al., 2020).整条光纤可以等效成等间距排列的若干个水平分量应变计,相比于传统地震仪,DAS可以实现低成本、多尺度、可重复的超密集地震观测.
与传统速度或加速度地震仪不同,DAS信号是地震波在光纤轴向上引起的应变或应变率响应(Blum et al., 2008),应变与地表速度或位移存在数值关系(Paitz et al., 2021; Lior et al., 2021),同样可以反映径向分量的波场信息.已经在主、被动源速度结构成像(Luo et al., 2020; 宋政宏等, 2020; 林融冰等, 2020),垂直测深剖面(Mateeva et al., 2014; Lindsey et al., 2019),接收函数(Yu et al., 2019),地震监测及预警(Lior et al., 2021; Nayak and Ajo-Franklin, 2021)等方面得到了广泛有效的应用.
利用DAS进行浅地表面波结构成像中,提取频散曲线是其中最为关键的环节之一,获得高分辨率、高信噪的频谱图像对于提取频散曲线及后续压制反演结果的多解性至关重要.近年来,大量研究表明高模式频散曲线的加入可以显著提高反演地层的置信度及深度(Xia et al., 2003; 罗银河等, 2008; Pan et al., 2019),而且高阶频散对于异常夹层的响应更为显著(Arai and Tokimatsu, 2004; Pan et al., 2019).因为面波信号具有显著的时频特性,常规频率-波数变换法(F-K)、倾斜叠加法(τ-p)及相移法等经典Radon变换在某一频率或时刻存在多模式相速度的混叠严重影响了高阶面波的分辨率,而Serdyukov等(2019)对经过S变换的拟炮记录进行的倾斜叠加说明传统的波场变换也可以获得高分辨率的多模式相速度曲线.
Wang等(2019)首先利用频率-贝塞尔变换(F-J)从USAarry记录的背景噪声中提取到了高分辨率的多模式瑞雷波频散曲线;基于该方法提取的多模式面波反演得到了北美大陆更高分辨率的三维速度模型,展示了其在大尺度地壳、岩石圈结构探测方面卓有成效的结果(Wu et al., 2020);该方法不仅适用于天然地震记录中高阶面波相速度的提取(Li and Chen, 2020),在浅地表结构成像中也进行了多次实例性研究(杨振涛等, 2019; 吴华礼等, 2019; 李雪燕等, 2020).Hu等(2020)进一步推导出多分量瑞雷波和勒夫波F-J频谱计算公式并进行了实例验证,Xi等(2021)提出改进的频率-贝塞尔变换(MF-J)以消除垂直分量F-J变换造成的交叉假频(cross artifact)现象.
与传统地震仪不同,DAS记录主要反映了沿光缆方向的应变信号.为探索如何在光纤观测数据中提取高阶面波频散,本文推导了适用于DAS系统地震记录中提取多模式面波频散曲线的MF-J变换公式并应用于实际数据.希望通过本文的研究为利用城市通信光缆进行低成本高分辨率地下结构探测奠定基础.
1 方法原理 1.1 DAS面波记录MF-J方法原理本节简单回顾了F-J方法,并针对DAS记录水平分量的面波信号,推导出改进的F-J(MF-J)频散能量谱计算公式.在假设的水平层状各向同性均匀介质地层中,地表距离震源r处的地震波垂直分量记录uz(r, t)在频率域可以表示为:
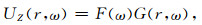
|
(1) |
式中,ω是频率,F(ω)是地震子波,G(r, ω)为震源到检波器之间的格林函数.
对(1)式波场记录进行矢量波数变换,利用贝塞尔函数的正交性(沈永欢等, 1992),最终可以得到Z分量F-J谱计算公式(Wang et al., 2019):
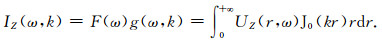
|
(2) |
DAS的地震信号反映了沿光纤轴向上的地震动,所以理论上记录的是径向分量(RR),因为与速度存在数值关系(Paitz et al., 2021; Lior et al., 2021),可以用来表示经验格林函数.根据Hu等(2020)的研究,我们将DAS地震记录的F-J谱表示为:
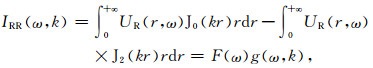
|
(3) |
而贝塞尔函数可以表示成第一类和第二类汉克儿函数Hν(1)和Hν(2)的平均值:
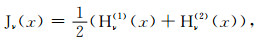
|
(4) |
故式(3)可以重写成:
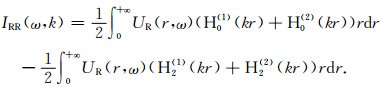
|
(5) |
Forbriger(2003)证明Hν(1)(kr)和Hν(2)(kr)分别代表反向(-k)及正向(+k)的速度扫描,所以根据式(2)计算F-J谱存在的交叉假频会对高频相速度的拾取造成干扰(比如:Wang et al., 2019).Xi等(2021)将出射波的正传、入射波的反传以及入射波的正传、出射波的反传部分进行了独立计算,从而分离出只包含面波相速度和只包含“交叉”假频的修正F-J谱(MF-J).综上,DAS地震记录修正的F-J谱计算公式可以表示如下:
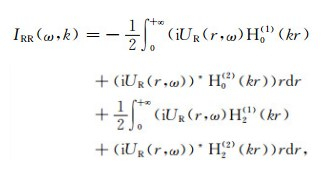
|
(6) |
式中,*表示复共轭,I(ω, k)为MF-J频散能量谱.
数值计算表明式(6)中对Hν(1)及Hν(2)项的积分是等效的,所以为了节省计算时间,我们采用以下公式计算DAS地震记录下MF-J频散能量谱:

|
(7) |
I(ω, c)近似离散积分参照Wang等(2019)中的式(A7)进行计算.
1.2 反演方法根据式(7)计算得到DAS面波MF-J频谱图后,对能量峰值进行识别获得瑞雷波相速度,然后进行反演以构建地层S波速度VS模型.
由于瑞雷波频散曲线主要受地层VS及层厚度(h)的影响(见Xia et al., 1999),故一般将纵波速度(VP)、密度(ρ)通过经验公式表示成VS的函数(例如Gardner et al., 1974; Broche, 2005, 2008),反演过程只优化VS、h对频散曲线进行拟合.本文通过遗传算法与阻尼最小二乘法联合反演提取的多模式瑞雷波频散曲线(Lei et al., 2019),该算法在数值模型及实际资料处理中都表现出良好的稳定性及准确性.这里我们将目标函数定义为:
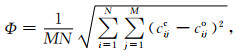
|
(8) |
式中,Φ是评价函数,N是参与反演的阶数,M是第i阶模式下实测相速度的个数,cc是理论频散曲线,co是观测频散曲线.
为了衡量反演结果的稳定性,定义了群体的不确定度:

|
(9) |
式中,σk是第k个模型的不确定度,mk是第k个模型,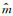
我们设计了一个含低速夹层三层水平层状模型进行数值测试.该模型地层参数如表 1所示,采用爆炸源激发信号,地震信号通过布设在地表的90个检波器接收,道间距为5 m,最小偏移距为10 m,采样率为500 Hz,模拟炮记录为水平分量地震信号,记录时长3 s.
|
|
表 1 三层模型地层参数 Table 1 Parameter of the horizontally layered stratum model |
图 1是通过F-J变换及MF-J变换得到的水平分量面波频谱.根据F-J变换计算的频谱在30 Hz以上可以看到三条明显的交叉假频(图 1a)(Wang et al., 2019),严重污染到高频高阶模式相速度的识别和提取.而根据式(7)计算的MFJ频谱消除了上述交叉假频,真实频散能量并没有受此影响且与理论频散曲线重合,证明式(7)推导的水平分量MF-J谱的计算是正确的.
|
图 1 模拟地层地震记录计算的频散能量谱 (a) F-J频散能量图; (b) MF-J频散能量图,黑色点线是正演的理论频散曲线. Fig. 1 Dispersion energy spectrograms of simulated model seismic record (a) The F-J spectrogram; (b) The MF-J spectrogram, and the black dotted line represents the forward theoretical dispersion curve. |
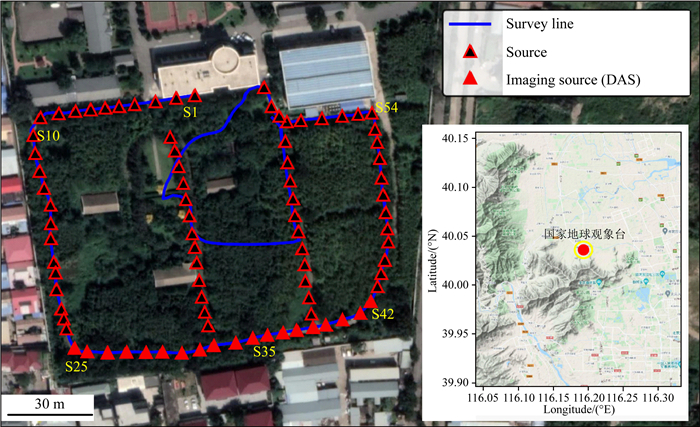
本次实验场地位于北京市海淀区西北部白家疃台地上(北京国家地球观象台),观测实验于2020年9月30日到10月8日间进行.场地地形、光纤布置及成像区域如图 2所示.钻井资料表明实验区下方50 m以浅主要为洪积砾岩及风化土层,更深处为奥陶纪灰岩.
|
图 2 白家疃实验场地地形图及DAS观测系统 蓝色实线为埋置的光纤,红色三角形为主动源炮点位置(纯色三角形为本文研究成像区域),光纤拐角及示例炮点位置通过金色序号标记. Fig. 2 Baijia Tuan Experiment Field topographic map and DAS array The blue line is the embedded fiber, all active source positions are indicated by red triangles (the pure color triangles are located in the imaging area in this study), the golden numbers are corners and examples of source location. |
本次实验采用了与宋政宏等(2020)和林融冰等(2020)研究相同的光纤,该光纤在实验前增加了一段大约400 m长的内圈路径.光纤实际有效记录长度为1040 m,道间距设置为4 m,通道数为260,数据采样率为500 Hz.为了避免平均应变的测量结果出现较大偏差,我们实验中所考虑的最小视波长大约为6 m,明显大于DAS系统2 m的标距,故平均效应基本可以忽略(Paitz et al., 2021).
主动源地震通过70 kg的落锤激发,炮间距10 m,最小偏移距在1 m左右,本文选取了光纤南面近直线上19炮的地震数据(图 2纯色三角形区域),利用提取的多模式频散曲线反演构建浅地表地层VS模型.落锤震源可以近似为垂直的单力源,光纤沿震源径向分布,所以DAS记录数据以瑞雷波为主.
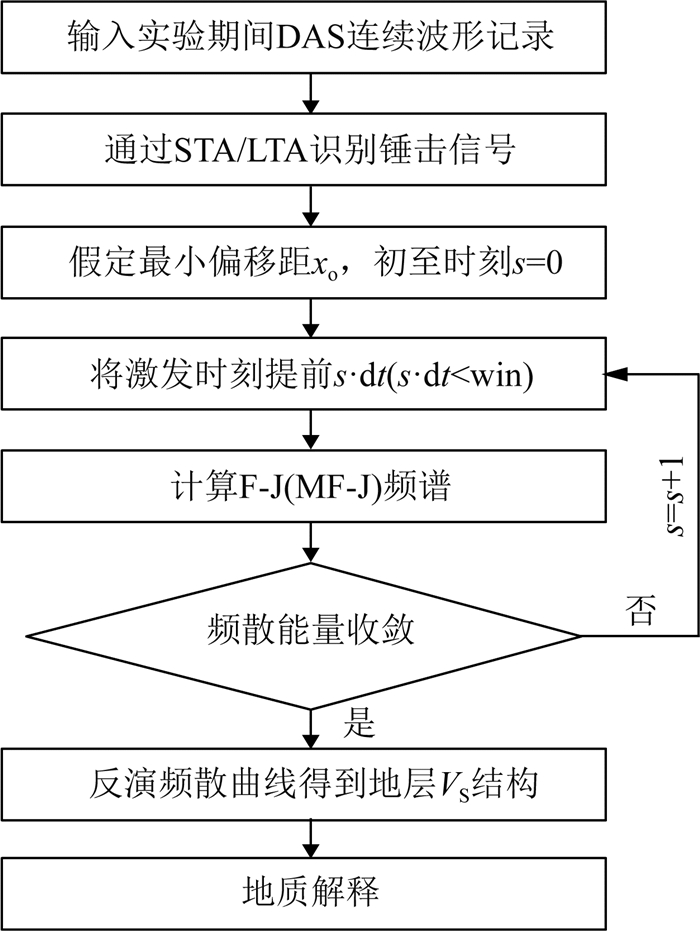
3.2 数据处理及分析与其他面波成像方法(比如多道瞬态面波分析,空间自相关及密集台阵法等)类似,利用DAS观测面波浅地表成像时,同样需要经过数据采集、频谱成像及频散反演三个主要环节.虽然DAS光纤沿线空间间隔提前设定,真实的地理位置需要通过锤击实验确定.但锤击确定的炮点位置会存在一个道间距之内的误差.本次实验DAS数据是连续采集的,没有采用触发计时与主动源联动.这为直接进行F-J频谱的计算造成了困难.考虑到时间和空间的不精确性,本文设计了一套适用于DAS观测面波浅地表成像的处理流程(图 3).
|
图 3 DAS观测面波浅地表成像处理流程 Fig. 3 Shallow structure imaging flowchart using DAS records |
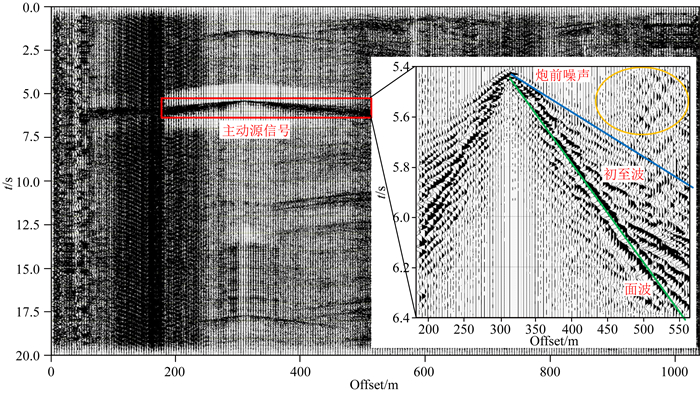
主动源数据采集于10月4日进行,震源初步激发时刻通过手机秒表计时得到,所以图 3中的输入是以上估测时间基础上向前、向后共截取20 s的连续波形记录(图 4),主动源信号通过类似STA/LTA方法(Trnkoczy, 2009)识别并截取,设置短窗时长(STA)为0.1 s,长窗时长(LTA)根据单炮最大偏移距及信噪比人为调节在1 s左右,滑动步长为0.1 s,并依此设定图 3中win为0.1 s.
|
图 4 DAS实验部分连续地震记录及截取的单炮主动源信号 右下角子图是截取窗长1s红色框线内的地震记录. Fig. 4 DAS experiment continuous seismic record and the single shot signal intercepted from it The subgraph in the right is the active seismic record within the red frame of the intercept window length of 1 s. |
但STA/LTA获取的时刻t与震源激发时刻并不对应.而在频谱分析环节,如果缺少准确的发震时刻及最小偏移距信息,F-J变换会对不同频率波数进行累积,导致计算的频谱能量发散严重甚至错误,这与传统波场变换方法仅利用不同道之间的相位及走时差的叠加不同.针对这一问题,我们在计算F-J频谱能量图时,假定最小偏移距为1 m,在时间上以一定步长(s·dt)整体滑动(等同于激发时刻提前或延后)炮记录,dt是采样间隔.当假设的最小偏移距xo与滑动炮记录相匹配时,F-J谱中的相速度能量峰值会通过叠加收敛达到极值(如图 5b和图 5e).
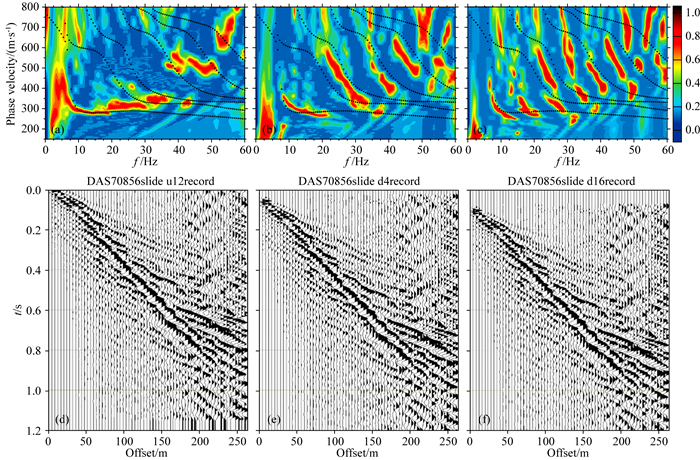
|
图 5 S25炮滑动不同步长地震记录及对应的F-J频谱能量图 黑色点线是预测的理论频散曲线, (d)、(e)、(f)分别是向上滑动12、向下滑动4、向下滑动12个采样点的地震记录,(a)、(b)、(c)分别是对应的F-J谱. Fig. 5 Seismic records and corresponding F-J energy spectrums by sliding different step length of the shot S25 The black dotted line represents the predicted theoretical dispersion curve, and (d), (e), (f) are the seismic records of sliding up 12, sliding down 4, and sliding down 12 sampling points, respectively, (a), (b), (c) are the corresponding F-J energy spectrums, respectively. |
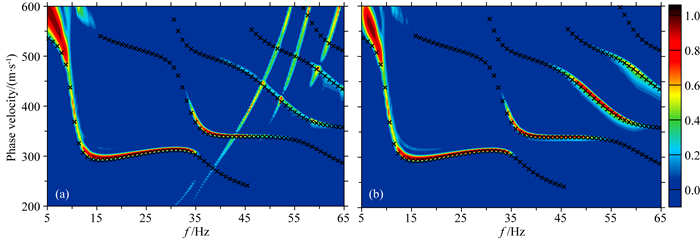
图 6是选取的其中两个单炮地震记录及计算的F-J频谱能量图(S25, S35).图 6b和图 6e(依据式(2)J0项积分)可以看出在高频部分(20~60 Hz)至少存在3个明显的交叉假频,这种假频尤其使得高阶频散受损严重,基于此提取的频散曲线会影响到后续反演结果的稳定性.而通过MF-J计算的频谱(式(7)),交叉假频得到显著压制(图 6c, 6f),增加了频谱的信噪比及分辨率.在S25记录中,可以明显地分辨出基阶、第2、第3及第4高阶频散曲线.尽管S35炮测线更短,分辨率稍差,但仍可以明显地分辨出基阶、第2及第3高阶频散曲线.理论上MF-J变换只是去除了F-J计算频谱中存在的“交叉”假频而不会对信号频散形态产生影响(Wang et al., 2019; Xi et al., 2021),但本文依此计算的F-J(图 6b, 6c)和MF-J的频散(图 6e, 6f)存在明显差异,关于该问题会在讨论部分进行详细分析.
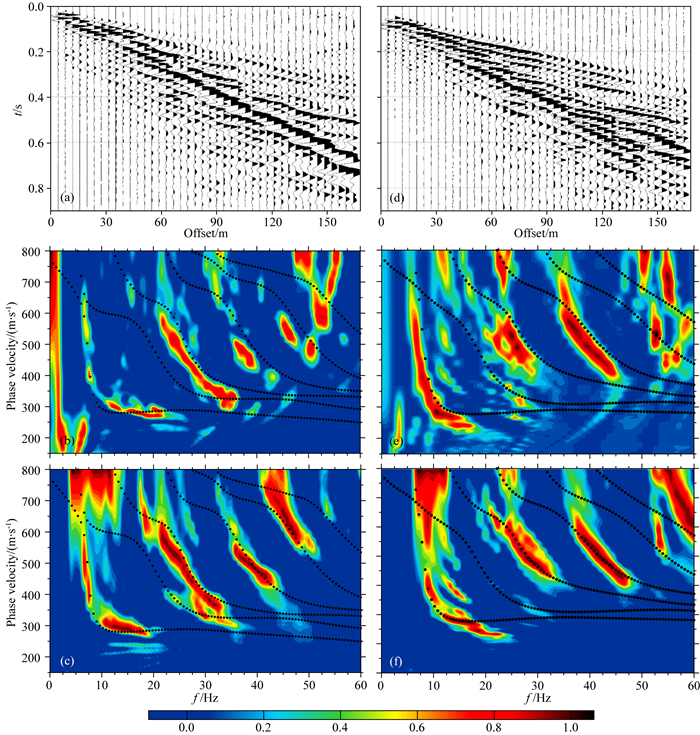
|
图 6 S25(左侧)及S35(右侧)原始炮记录及计算的F-J(MF-J)频谱能量图 黑色点线是预测的理论频散曲线,(a)和(d)是DAS主动源地震记录,(b)和(e)、(c)和(f)分别是J0项积分的F-J谱、H0项积分的MF-J谱. Fig. 6 S25 (left) and S35 (right) are seismic records and calculated F-J (MF-J) energy spectrum The black dotted line represents the predicted theoretical dispersion curve, (a) and (d) are the DAS active seismic records, (b) and (e), (c) and (f) are the F-J spectrum of the J0 integrated and the MF-J spectrum of the H0 integrated, respectively. |
与常规使用垂直分量的瑞雷波不同,水平分量的各高阶模态在某些条件下会更发育(Ikeda et al., 2015; Hu et al., 2020),反映了瑞雷波垂直、水平分量能量衰减上的差异.故DAS的频谱记录有助于瑞雷波各高阶模态的分离及提取,也为反演深部地层参数时提供了更精确约束.可以看出,不同高阶频散明显地在不同频段相继占据主导,整体上呈现出“波浪”式频谱(图 6).Mi等(2018)通过数值模拟证明频谱能量上的不连续或“跳跃”是由于低速层导波无法穿透地表引起的.反演该区域速度剖面(图 7,图 9)存在明显的异常速度夹层也证实了这一观点,而钻孔结果也表明地下的确存在洪积砾岩及风化土层的堆积.
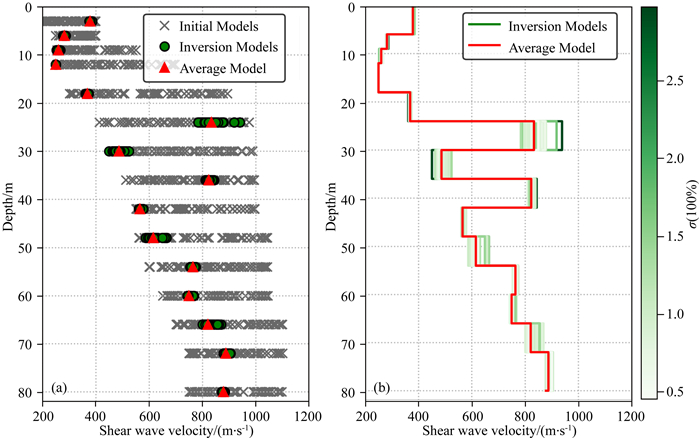
|
图 7 S25炮初始模型及反演结果 (a) 初始群体、反演群体及平均模型的横波速度分布;(b) 最终反演地层结构及群体基于平均模型不确定度分析. Fig. 7 Shot S25 initial model and inversion results (a) The shear wave velocity distribution of the initial group, the inversion group and the average model, (b) The final inversion of the stratigraphic structure and the uncertainty analysis of the group based on the average model. |

|
图 8 S25基阶模态频散曲线反演结果 (a) 只用基阶(黑色)和使用所有阶(红色)获得的地层模型结构及基于基阶平均模型的不确定度分析(绿色);(b) 观测的频散能量图,黑色及红色点划线分别是由图(a)中的黑色及红色地层模型正演的频散曲线. Fig. 8 Shot S25 inversion result of fundamental mode dispersion curve (a) The shear wave velocity model obtained by using only the fundamental (black) and using all modes (red), and the uncertainty analysis based on the fundamental average model (green); (b) F-J spectrum observed and the dispersion curves forwarded according to the fundamental (black) and multimode (red) inversion model in (a). |

|
图 9 研究区南面沿光纤测线反演地层剖面 Fig. 9 Inversion of stratum profile along the optical fiber in the south of the study area |
本文使用GADLS方法(Lei et al., 2019)反演频散曲线,设置的反演初始模型包含15个薄层(前4层厚度h为3 m,后11层厚度为6 m),群体规模60,迭代次数20,每次迭代过程中均选取了残差最小的前20个优势个体进行局部线性优化以引导群体进化方向.
图 7是S25炮记录的反演结果,随机产生的初始模型较好地均匀分布在可能存在的速度空间.平均模型(红色三角形)总体上表现出速度递增的特征,前4层出现的负速度梯度除了因为本次激发震源位于硬化道路上.由于缺少高频相速度的约束,在各炮反演结果中出现了一定范围的数值波动.图 7b是依据式(9)计算的关于平均模型的不确定度分析.因为增加了5个高阶相速度的约束,群体收敛结果较好,群体距平均模型偏差在4%以内.第6层出现了一个明显的高速异常夹层,收敛效果也较其他层更差,虽然该层群体速度收敛效果较差,可能会大于真实地层速度,但从最后的测线剖面来看也是准确反映了高速夹层的存在位置(图 9).
基于上文同样的反演方法及参数设定,仅对基阶频散曲线进行反演结果如图 8所示.由于缺少高模态相速度约束,反演各层速度均与多模态反演结果(图 7)出现较大差异,多数层不确定度分析达到6%左右,反映了基阶反演群体的稳定性较差.同时基于基阶频散反演的结果能很好地拟合观测的基阶频散但是无法拟合高阶面波的频散特征(图 7b).所以高阶模态对于压制反演多解性,提高地下结构成像的准确性及分辨率至关重要.
图 9是光纤测线南面(图 2纯色三角形区域)近直线上19炮记录反演得到的VS速度剖面,与宋政宏等(2020)和林融冰等(2020)结果大约150~260号通道之间的区域重合.由于采集时间、解调设备存在差异,以及本文增加了高模态频散曲线约束等原因,反演结果与前人研究尤其是深部地层VS存在些许差异.因为光纤呈方形分布及炮间距较大(10 m),不同于常规多道面波分析方法,本文将单炮反演结果近似为炮点处地层结构.因而,得到的图 9地层剖面可能会沿着东西方向有压缩效果,且坐标较真实位置偏西一些.增加了高阶面波相速度约束之后,本次实验主动源面波成像的深度可以达到80 m.结合钻孔信息做出如下解释:0~3 m是硬化或夯实的路基,速度接近400 m·s-1,但横向波动较大;3~22 m为低速潜水面,岩性为淤泥质或粉质黏土层,表现出负速度梯度特征;20~30 m之间是一个水平分布的等厚高速夹层,速度大于760 m·s-1,可能是快速堆积的洪积砾岩层;30~50 m之间的速度变化较为剧烈,在300~900 m·s-1均有分布,而且左半部存在一个宽度70 m左右的碗状凹陷,可能经历了不同的沉积过程.
4 讨论 4.1 F-J与MF-J频谱差异Xi等(2021)利用MF-J变换对背景噪声提取高阶面波的研究表明,H0(1)取代J0对格林函数的积分只是去除了频谱中的“交叉”假频,并不影响计算相速度的数值大小.但本文计算的DAS主动源记录MF-J及F-J谱却存在明显的差异(图 6).主动源与背景噪声数据的主要区别在于地震记录U(r, ω)中包含地震子波F(ω),这可能导致了H0(1)与J0的不同响应.基于此假设,我们对由炸药激发(混合相位子波)的一个炮记录进行了试算(图 10),该数据于伊利盆地采集,通过包含96道接收器的直线排列记录,道间距10 m,采样率500 Hz.黑色的点划线是根据图 10b提取频散曲线反演的理论值,反演初始模型设置为一个速度递增的等厚薄层模型,反演地层模型与测井结果吻合良好.从图 10可以看出MF-J变换消除了F-J谱中存在的交叉假频干扰,同时由F-J变换提取的面波相速度明显小于由MF-J变换提取的,这一特征与DAS主动源频谱相对应(图 6),所以本文推测是地震子波F(ω)的存在导致了主动源地震记录F-J与MF-J变换提取频散曲线的差异,但也不能排除可能是由DAS存在仪器响应或因为本次实验DAS通道真实物理位置存在偏差导致,关于此还需要进行深一步研究.

|
图 10 炸药激发炮记录F-J (MF-J)频谱 (a) F-J频谱;(b) MF-J频谱. Fig. 10 F-J (MF-J) energy spectrum of seismic record generated by explosive sources (a) F-J energy spectrum; (b) MF-J energy spectrum. |
可能由于相同的原因,依据式(7)计算的S25炮MF-J频谱IRR(H0(1)+H2(1)项积分)(图 11b)与MF-J频谱IZZ(H0(1)项积分)(图 11a)也存在显著差异.虽然IRR第2及第3高阶的频散曲线可能会更准确,但在计算的其他炮中更多时候MF-J谱IRR分辨率可能更差,比如图 11d,所以为了计算结果的稳定性,本文仅针对MF-J谱IZZ进行计算及反演.
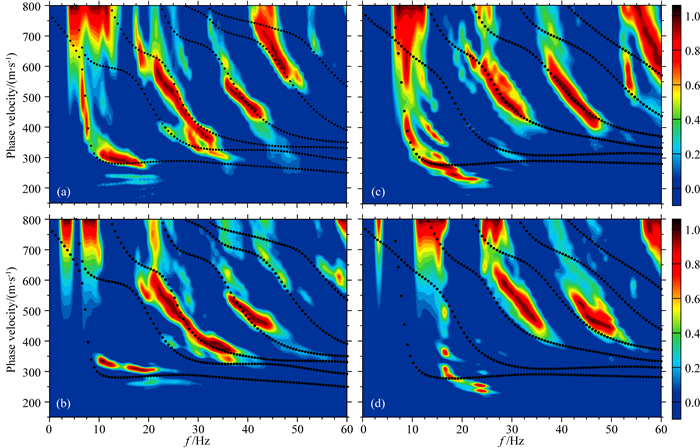
|
图 11 S25(左侧)及S35(右侧)MF-J频谱能量图 黑色点线是预测的理论频散曲线,(a)和(b)、(c)和(d)分别是H0项积分的MF-J谱及H0+H2项积分的MF-J谱. Fig. 11 S25 (left) and S35 (right) MF-J energy spectrum The black dotted line represents the predicted theoretical dispersion curve, (a) and (b), (c) and (d) are the MF-J spectrum of the H0 integrated and the MF-J spectrum of the H0+H2 integrated, respectively. |
在之前Sladen等(2019)、Lior等(2021)等人利用DAS技术对水下光缆进行的研究表明不均匀的光缆-地面耦合及水土相互作用极大地影响了对地震动的敏感性,从而限制了其进行地震监测的可靠性.与之类似,陆上通信光缆通常穿插在地下PVC (Polyvinyl chloride, 聚氯乙烯材料)管道中,对地耦合条件可能更差,而且通信光缆中间分布的光交机(通常盘留不等长度的光缆)也增大了地震监测的不确定性(王宝善等,2021),这可能是利用通信光缆进行地震监测研究面临最大的非技术性挑战之一,而本文实验所用的是专门布设在地下约30 cm的光纤,对地耦合条件较好,所以不会受此困扰.
由于DAS只能探测到沿光纤轴向上的地震动信号,而当城市地质条件或街道规划复杂时(光纤一般沿街道铺设),单分量的坐标旋转、仪器响应的去除等都需要就近布设的地震仪的配合,但也会影响到最终结果的准确性(Spica et al., 2020; Paitz et al., 2021; Lior et al., 2021).
5 结论本文基于推导的水平分量MF-J变换从DAS系统记录的主动源地震信号中提取了高分辨率的多模式瑞雷波相速度,并用于实际资料浅地表结构成像.基于上述研究,得出以下结论:
F-J(MF-J)变换可以从DAS系统的地震记录中提取到多模式面波频散曲线,加入的高阶面波信息约束很大程度上提高了仅依靠基阶频散时的探测深度,并进一步提高了反演地层模型的稳定性及分辨率.
在利用DAS系统进行主动源面波探测时,需要确定准确的震源激发时刻及最小偏移距,否则会影响F-J(MF-J)频散能量谱的分辨率,甚至导致频散曲线出现较大偏差.
致谢 谨此祝贺陈颙先生从事地球物理教学科研工作60周年.感谢上海朴牛科技有限公司提供DAS解调设备,感谢杨微、徐善辉、胡久鹏、冀战波、乔宝平等同志在实验中给予的帮助.
Arai H, Tokimatsu K. 2004. S-wave velocity profiling by inversion of microtremor H/V spectrum. Bulletin of the Seismological Society of America, 94(1): 53-63. DOI:10.1785/0120030028 |
Blum J A, Nooner S L, Zumberge M A. 2008. Recording Earth strain with optical fibers. IEEE Sensors Journal, 8(7): 1152-1160. DOI:10.1109/JSEN.2008.926882 |
Brocher T M. 2005. Empirical relations between elastic wavespeeds and density in the Earth's crust. Bulletin of the Seismological Society of America, 95(6): 2081-2092. DOI:10.1785/0120050077 |
Brocher T M. 2008. Key elements of regional seismic velocity models for long period ground motion simulations. Journal of Seismology, 12(2): 217-221. DOI:10.1007/s10950-007-9061-3 |
Forbriger T. 2003. Inversion of shallow-seismic wavefields: I. Wavefield transformation. Geophysical Journal International, 153(3): 719-734. DOI:10.1046/j.1365-246X.2003.01929.x |
Gardner G H F, Gardner L W, Gregory A R. 1974. Formation velocity and density-the diagnostic basics for stratigraphic traps. Geophysics, 39(6): 770-780. DOI:10.1190/1.1440465 |
Hu S Q, Luo S, Yao H J. 2020. The Frequency-Bessel Spectrograms of multicomponent cross-correlation functions from seismic ambient noise. Journal of Geophysical Research: Solid Earth, 125(8): e2020JB019630. DOI:10.1029/2020JB019630 |
Ikeda T, Matsuoka T, Tsuji T, et al. 2015. Characteristics of the horizontal component of Rayleigh waves in multimode analysis of surface waves. Geophysics, 80(1): EN1-EN11. |
Lei Y H, Shen H Y, Li X X, et al. 2019. Inversion of Rayleigh wave dispersion curves via adaptive GA and nested DLS. Geophysical Journal International, 218(1): 547-559. DOI:10.1093/gji/ggz171 |
Li X Y, Chen X F, Yang Z T, et al. 2020. Application of high-order surface waves in shallow exploration: An example of the Suzhou River, Shanghai. Chinese Journal of Geophysics (in Chinese), 63(1): 247-255. DOI:10.6038/cjg2020N0202 |
Li Z B, Chen X F. 2020. An effective method to extract overtones of surface wave from array seismic records of earthquake events. Journal of Geophysical Research: Solid Earth, 125(3): e2019JB018511. DOI:10.1029/2019JB018511 |
Lin R B, Zeng X F, Song Z H, et al. 2020. Distributed acoustic sensing for imaging shallow structure Ⅱ: Ambient noise tomography. Chinese Journal of Geophysics (in Chinese), 63(4): 1622-1629. DOI:10.6038/cjg2020N0272 |
Lindsey N J, Dawe T C, Ajo-Franklin J B. 2019. Illuminating seafloor faults and ocean dynamics with dark fiber distributed acoustic sensing. Science, 366(6469): 1103-1107. DOI:10.1126/science.aay5881 |
Lindsey N J, Rademacher H, Ajo-Franklin J B. 2020. On the broadband instrument response of fiber-optic DAS arrays. Journal of Geophysical Research: Solid Earth, 125(2): e2019JB018145. DOI:10.1029/2019JB018145 |
Lior I, Sladen A, Rivet D, et al. 2021. On the detection capabilities of underwater distributed acoustic sensing. Journal of Geophysical Research: Solid Earth, 126(3): e2020JB020925. DOI:10.1029/2020JB020925 |
Luo B, Trainor-Guitton W, Bozdaǧ E, et al. 2020. Horizontally orthogonal distributed acoustic sensing array for earthquake- and ambient-noise-based multichannel analysis of surface waves. Geophysical Journal International, 222(3): 2147-2161. DOI:10.1093/gji/ggaa293 |
Luo Y H, Xia J H, Liu J P, et al. 2008. Joint inversion of fundamental and higher mode Rayleigh waves. Chinese Journal of Geophysics (in Chinese), 51(1): 242-249. |
Mateeva A, Lopez J, Potters H, et al. 2014. Distributed acoustic sensing for reservoir monitoring with vertical seismic profiling. Geophysical Prospecting, 62(4): 679-692. DOI:10.1111/1365-2478.12116 |
Mei D, Neukum C, Hui H, et al. 2015. Developing an adequate approach to model the geotechnical parameters for reducing the ventures of underground city development. Engineering Geology for Society and Territory, 5: 639-642. DOI:10.1007/978-3-319-09048-1_124 |
Mi B B, Xia J H, Shen C, et al. 2018. Dispersion energy analysis of Rayleigh and Love waves in the presence of low-velocity layers in near-surface seismic surveys. Surveys in Geophysics, 39(2): 271-288. DOI:10.1007/s10712-017-9440-4 |
Nayak A, Ajo-Franklin J. 2021. Distributed acoustic sensing using dark fiber for array detection of regional earthquakes. Seismological Research Letters, 92(4): 2441-2452. DOI:10.1785/0220200416 |
Paitz P, Edme P, Gräff D, et al. 2021. Empirical Investigations of the Instrument Response for Distributed Acoustic Sensing (DAS) across 17 Octaves. Bulletin of the Seismological Society of America, 111(1): 1-10. DOI:10.1785/0120200185 |
Pan L, Chen X F, Wang J N, et al. 2019. Sensitivity analysis of dispersion curves of Rayleigh waves with fundamental and higher modes. Geophysical Journal International, 216(2): 1276-1303. DOI:10.1093/gji/ggy479 |
Serdyukov A S, Yablokov A V, Duchkov A A, et al. 2019. Slant f-k transform of multichannel seismic surface wave data. Geophysics, 84(1): A19-A24. DOI:10.1190/geo2018-0430.1 |
Shen Y H, Liang Z Z, Xu L H, et al. 1992. Practical Mathematics Manual (in Chinese). Beijing: Science Press.
|
Sladen A, Rivet D, Ampuero J P, et al. 2019. Distributed sensing of earthquakes and ocean-solid Earth interactions on seafloor telecom cables. Nature Communications, 10(1): 5777. DOI:10.1038/s41467-019-13793-z |
Song Z H, Zeng X F, Xu S H, et al. 2020. Distributed Acoustic Sensing for imaging shallow structure I: active source survey. Chinese Journal of Geophysics (in Chinese), 63(2): 532-540. DOI:10.6038/cjg2020N0184 |
Spica Z J, Perton M, Martin E R, et al. 2020. Urban seismic site characterization by fiber-optic seismology. Journal of Geophysical Research: Solid Earth, 125(3): e2019JB018656. DOI:10.1029/2019JB018656 |
Stell W, Marshak D, Yamada T, et al. 1980. Peptides are in the eye of the beholder. Trends in Neurosciences, 3(12): 292-295. DOI:10.1016/S0166-2236(80)80174-3 |
Trnkoczy A. 2009. Understanding and parameter setting of STA/LTA trigger algorithm. //New Manual of Seismological Observatory Practice. Deutsches GeoForschungsZentrum GFZ, Potsdam, Germany, 965-984.
|
Wang B S, Zeng X F, Song Z H, et al. 2021. Seismic observation and subsurface imaging using an urban telecommunication optic-fiber cable. Chinese Science Bulletin (in Chinese), 66(20): 2590-2595. DOI:10.1360/TB-2020-1427 |
Wang J N, Wu G X, Chen X F. 2019. Frequency-Bessel transform method for effective imaging of higher-mode Rayleigh dispersion curves from ambient seismic noise data. Journal of Geophysical Research: Solid Earth, 124(4): 3708-3723. DOI:10.1029/2018JB016595 |
Wu G X, Pan L, Wang J N, et al. 2020. Shear velocity inversion using multimodal dispersion curves from ambient seismic noise data of USArray transportable array. Journal of Geophysical Research: Solid Earth, 125(1): e2019JB018213. DOI:10.1029/2019JB018213 |
Wu H L, Chen X F, Pan L. 2019. S-wave velocity imaging of theKanto basin in Japan using the frequency-Bessel transformation method. Chinese Journal of Geophysics (in Chinese), 62(9): 3400-3407. DOI:10.6038/cjg2019N0205 |
Xi C Q, Xia J H, Mi B B, et al. 2021. Modified frequency-Bessel transform method for dispersion imaging of Rayleigh waves from ambient seismic noise. Geophysical Journal International, 225(2): 1271-1280. DOI:10.1093/gji/ggab008 |
Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics, 64(3): 691-700. DOI:10.1190/1.1444578 |
Xia J H, Miller R D, Park C B, et al. 2003. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 52(1): 45-57. DOI:10.1016/S0926-9851(02)00239-2 |
Yang W C, Tian G, Xia J H, et al. 2019. The prospect of exploitation and utilization of urban underground space in hilly areas of South China. Geology in China (in Chinese), 46(3): 447-454. |
Yang Z T, Chen X F, Pan L, et al. 2019. Multi-channel analysis of Rayleigh waves based on the Vector Wavenumber Transformation Method (VWTM). Chinese Journal of Geophysics (in Chinese), 62(1): 298-305. DOI:10.6038/cjg2019M0641 |
Yu C Q, Zhan Z W, Lindsey N J, et al. 2019. The potential of DAS in teleseismic studies: insights from the Goldstone experiment. Geophysical Research Letters, 46(3): 1320-1328. DOI:10.1029/2018GL081195 |
李雪燕, 陈晓非, 杨振涛, 等. 2020. 城市微动高阶面波在浅层勘探中的应用: 以苏州河地区为例. 地球物理学报, 63(1): 247-255. DOI:10.6038/cjg2020N0202 |
林融冰, 曾祥方, 宋政宏, 等. 2020. 分布式光纤声波传感系统在近地表成像中的应用Ⅱ: 背景噪声成像. 地球物理学报, 63(4): 1622-1629. DOI:10.6038/cjg2020N0272 |
罗银河, 夏江海, 刘江平, 等. 2008. 基阶与高阶瑞利波联合反演研究. 地球物理学报, 51(1): 242-249. DOI:10.3321/j.issn:0001-5733.2008.01.030 |
沈永欢, 梁在中, 许履瑚, 等. 1992. 实用数学手册. 北京: 科学出版社.
|
宋政宏, 曾祥方, 徐善辉, 等. 2020. 分布式光纤声波传感系统在近地表成像中的应用Ⅰ: 主动源高频面波. 地球物理学报, 63(2): 532-540. DOI:10.6038/cjg2020N0184 |
王宝善, 曾祥方, 宋政宏, 等. 2021. 利用城市通信光缆进行地震观测和地下结构探测. 科学通报, 66(20): 2590-2595. |
吴华礼, 陈晓非, 潘磊. 2019. 基于频率-贝塞尔变换法的关东盆地S波速度成像. 地球物理学报, 62(9): 3400-3407. DOI:10.6038/cjg2019N0205 |
杨文采, 田钢, 夏江海, 等. 2019. 华南丘陵地区城市地下空间开发利用前景. 中国地质, 46(3): 447-454. |
杨振涛, 陈晓非, 潘磊, 等. 2019. 基于矢量波数变换法(VWTM)的多道Rayleigh波分析方法. 地球物理学报, 62(1): 298-305. DOI:10.6038/cjg2019M0641 |
 2021, Vol. 64
2021, Vol. 64


