2. 南京工业大学岩土工程研究所, 南京 210009;
3. 西安邮电大学自动化学院, 西安 710121
2. Institute of Geotechnical Engineering, Nanjing University of Technology, Nanjing 210009, China;
3. College of Automation, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
有限差分法计算量小、容易实现,是地球物理学和地震学领域最常用的波动方程数值解法,也被广泛应用于逆时偏移和全波形反演中进行波场正反向延拓.但由于时间和空间离散,有限差分法会产生数值频散,不可避免地降低正演、成像和反演的精度.为改善其精度,不同学者先后提出规则网格和交错网格(Virieux,1986;Luo and Schuster, 1990;董良国等,2000)、显式和隐式(Liu and Sen, 2009a;Kosloff et al.,2010;Chu and Stoffa, 2012)、空间域和时空域(Liu and Sen, 2019b;Ren and Liu, 2015;蔡晓慧等,2015)、非规则网格和无网格(裴正林,2004;孙辉和张剑锋,2019;Li et al.,2017;Liu et al.,2019;刘立彬等,2020;姜占东等,2021)有限差分.有限差分法在勘探地球物理和计算地震学的详细进展请参考Carcione等(2002)、刘洋(2014)和Moczo等(2014),这里不再赘述.
有限差分法的模拟精度由时间和空间导数的离散方式决定.提高空间精度的方法主要包括:增大空间差分算子的长度;优化空间差分系数(Zhang and Yao, 2013;Liu,2014;Yang et al.,2017);伪谱法(Kosloff and Baysal, 1982;Fornberg,1987;Liu and Wei, 2005;刘财等,2013;李青阳等,2018).采用长的差分算子逼近空间偏导数会增加计算量,且存在饱和效应(即算子长度继续增大对模拟精度的改善非常小).常规有限差分法的差分系数是基于泰勒级数展开得到的,只能保证低波数区域的模拟精度.优化有限差分法采用优化算法(如最小二乘、模拟退火等)逼近频散关系求取差分系数,可以大幅提高中-高波数区域的模拟精度.伪谱法通过正反傅里叶变换求取空间偏导数,理论上具有无穷阶/谱精度,但需要更多的计算时间.提高有限差分时间精度的方法包括:Lax-Wendroff法(Dablain,1986;Chen,2009;Amundsen and Pedersen, 2017);新差分模板法(Liu and Sen, 2013;Wang et al.,2016;Tang and Huang, 2014;张保庆等,2016;Ren et al.,2017);时间频散校正法(Stork,2013;Wang and Xu, 2015;Koene et al.,2018).Lax-Wendroff法通过空间偏导数替换高阶时间偏导数来改善时间精度.新差分模板法采用非“十字”或“正交”模板逼近空间偏导数.Liu和Sen(2013)给出一种“菱形”差分模板,新方法可以获得任意偶数阶时间精度,但计算量较大.为平衡精度与效率,Wang等(2016)提出基于“十字+菱形”模板的有限差分法.Tang和Huang(2014)和Ren等(2017)发展了时间4~6阶和任意偶数阶交错网格有限差分法.新差分模板法的差分系数随速度变化,相对比较复杂.时间频散校正法通过正反时间频散变换向观测记录中增加或消除时间频散.Wang和Xu(2015)介绍了有限差分的正反时间频散变换对,并将其应用于逆时偏移中消除时间频散对成像的影响.Koene等(2018)指出采用共轭算子代替逆算子的不足,推导了更精确的正时间频散算子,使得输入信号经过正反变换后能够被精确重建.与其他方法相比,时间频散校正法的效率更高,且可以彻底消除波场中的时间频散误差.
波动方程正演是逆时偏移和全波形反演的基本单元,成像和反演的精度依赖于所采用的数值模拟算法.到目前为止,单独研究有限差分的时间和空间频散特性及其对逆时偏移和全波形反演的影响的文献相对较少.本文采用时间有限差分+空间伪谱法和时间频散校正+空间有限差分分离时间频散和空间频散;详细分析了有限差分的时间和空间频散特性及其对成像和反演精度的影响;发展了抗时间频散、抗空间频散、抗时间+空间频散的逆时偏移和全波形反演方法;通过理论数据和实际资料对提出的成像和反演方法进行了测试.
1 有限差分的时间和空间频散二阶常密度声波方程形式如下(Dablain,1986;Liu and Sen, 2009b):

|
(1) |
式中,L=∂2/∂x2+∂2/∂z2,v为传播速度,p为压强,s为震源项.常规有限差分时间和空间偏导数离散格式为:
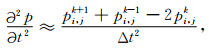
|
(2) |
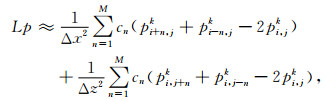
|
(3) |
其中,cn为差分系数,M为空间算子长度参数,Δt为时间步长,Δx和Δz为空间采样间隔.方程(2)和(3)两边进行傅里叶变换并化解可得:
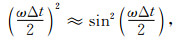
|
(4) |
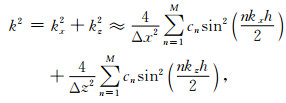
|
(5) |
其中,ω为角频率,k为波数,kx和kz分别为水平与垂直方向的波数.
方程(4)和(5)表示有限差分离散前后频率和波数的变化规律.为便于区分,将不等式右端(离散后)的频率和波数用ωFD、kxFD和kzFD表示,再化简可得:
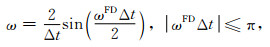
|
(6) |
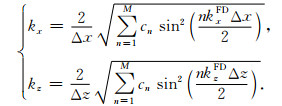
|
(7) |
方程(6)和(7)分别决定有限差分法的时间和空间模拟精度.当ω与ωFD接近时,时间频散较小,反之时间频散较大;当kx和kz与kxFD和kzFD接近时,空间频散较小,反之空间频散较大.基于方程(6)和(7)及原函数与反函数的对称性(关于y=x轴对称),图 1给出常规有限差分法的频率和波数(以kx为例)变化曲线.由图 1可见:随着空间算子长度M增大,kxFD逐渐靠近kx,空间频散减弱;随着波数kx或网格大小Δx增大,kxFD逐渐偏离kx,空间频散增强;随着频率ω或时间步长Δt增大,ωFD逐渐偏离ω,时间频散增强;ωFD≥ω和kxFD≥kx.有限差分法的相速度公式为:
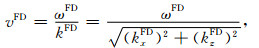
|
(8) |

|
图 1 常规有限差分法离散前后的频率(a)和波数(b)变化曲线 Fig. 1 Variation curves of frequency (a) and wavenumber (b) before and after the discretization in the conventional finite difference method |
有限差分法中时间离散导致ωFD≥ω,vFD≥v,产生时间频散;空间离散导致kxFD≥kx和kzFD≥kz,vFD≤v,产生空间频散.时间和空间频散分别以大于和小于真实速度的速度传播,分别出现在正常波前面的首波和尾部.
有限差分法的空间精度随M的增加而增大.当M趋向于无穷大时,有限差分法变为伪谱法,空间偏导数通过式(9)求解(Kosloff and Baysal, 1982):

|
(9) |
其中,F和F-1分别表示二维正反傅里叶变换.与空间频散不同,时间频散是可预测的,与传播路径和速度等因素无关(Koene et al.,2018).有限差分的时间频散是由于数值离散引起的频率移动(从ω到ωFD)而产生的.将具有频散的数据从ωFD校回到真实频率ω处即可实现时间频散校正,得到原始的无频散数据.由方程(6)可得:

|
(10) |
方程(10)定量表示离散前后的频率变化关系.时间频散校正步骤为(Wang and Xu, 2015):
(1) 通过方程(10)计算不同ω对应的ωFD;
(2) 正变换:
(3) 傅里叶逆变换:
常规有限差分具有时间2阶和空间2M阶精度,同时产生时间和空间频散.伪谱法的空间模拟精度为无穷阶.采用时间有限差分和伪谱法(方程(2)和(9))求解波动方程,可以得到只包含时间频散的数据.时间频散校正法能够消除常规时间二阶有限差分引入的时间频散.采用时间频散校正和空间有限差分(方程(3)和(10))可以得到只包含空间频散的数据.将时间频散校正和伪谱法(方程(9)和(10))相结合可获取不含时间和空间频散的数据.为了书写方便,下文中将有限差分、伪谱法和时间频散校正分别记为FD、PS和TDC.因此,FD、PS、FD+TDC和PS+TDC分别表示全频散、只有时间频散、只有空间频散和无频散数据或者对应的方法.
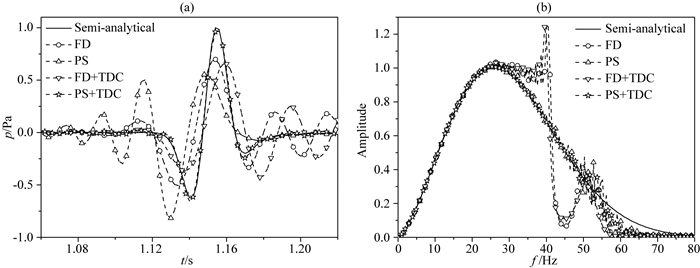
这里采用一个均匀介质模型研究有限差分的时间和空间频散特性.介质速度为2000 m·s-1,网格点数为301×301,空间网格大小为10 m×10 m,时间步长为2.0 ms,最大记录时间为2.0 s.震源为30 Hz的雷克子波,位于点(1000 m, 1000 m)处.图 2给出不同方法得到的点(3000 m, 2000 m)处的波形图及频谱.其中,Semi-analytical为由Cagniard-De Hoop方法(De Hoop,1960)得到的半解析波场.FD表示时间2阶空间10阶精度的有限差分.由图 2可见:时间频散(PS)会引起波场相移,空间频散(FD+TDC)导致波形震荡;时间和空间频散分别出现在正常波前的前部和尾部;PS+TDC可以有效压制时间和空间频散,获得与解析解相近的模拟结果;空间频散引起频谱畸变,时间频散对频谱的影响相对较小.
|
图 2 均匀介质模型(3000 m, 2000 m)处不同方法的波形图(a)及频谱(b) Fig. 2 Waveforms (a) and spectra (b) at the point (3000 m, 2000 m) by different methods on a homogeneous model |
逆时偏移包括震源波场正向传播、检波点波场反向传播和正反向波场互相关成像.将FD、PS、FD+TDC和PS+TDC应用于波场正传和反传中,即可研究时间和空间频散对逆时偏移的影响.但直接进行时间频散校正,需要存储所有网格点所有时刻的正反向波场,并进行大量的正反傅里叶变换,计算和存储需求巨大.为了提高计算效率,Koene等(2018)介绍了一种实用的抗时间频散逆时偏移(FD+TDC)方法:震源s中加入时间频散,源波场正向传播;观测波场中加入时间频散,检波点波场反向传播;正反向波场互相关成像.向无频散数据中添加时间频散就是实现从ω到ωFD的过程,具体步骤为(Koene et al.,2018):
(1) 通过方程(6)计算不同ωFD对应的ω;
(2) 正变换: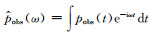
(3) 傅里叶逆变换:
震源波场中只包含源-反射点路径上的时间频散.观测波场中加入时间频散后包含源-反射点-检波点整个路径的时间频散.由于波场正向和反向传播沿不同的时间方向积累时间频散,检波点波场反向传播会抵消掉反射点-检波点路径上积累的时间频散.因此,震源波场和检波点波场具有相同的时间频散(相移),仍可以实现零延迟互相关成像.
伪谱法具有空间无穷阶精度,采用伪谱法进行波场正反向延拓得到抗空间频散逆时偏移(PS)方法.将时间频散校正和伪谱法结合得到抗时间+空间频散逆时偏移(PS+TDC)方法:震源s中加入时间频散,伪谱法源波场正向传播;观测波场中加入时间频散,伪谱法检波点波场反向传播;正反向波场互相关成像.
3 抗频散全波形反演方法全波形反演包括震源波场正向传播、残差波场反向传播、模型参数梯度计算和迭代更新.将FD、PS、FD+TDC和PS+TDC应用于波场正传和反传中,同样可以研究时间和空间频散对全波形反演的影响.抗时间频散全波形反演(FD+TDC)方法为:震源s中加入时间频散,源波场正向传播;观测波场中加入时间频散,残差波场反向传播;模型参数梯度计算;反演迭代(如共轭梯度法)直至满足收敛条件.
与逆时偏移类似,震源波场和伴随波场具有相同的时间频散(源-反射点路径),能够缓解频散误差对模型参数梯度的影响.同时,检波点处的模拟波场和观测波场都包含源-反射点-检波点整个路径的时间频散.导致模拟和观测波场的不匹配主要由模型不精确决定,有利于反演逐渐收敛于真实模型.
采用伪谱法或时间频散校正+伪谱法可以得到抗空间频散(PS)或抗时间+空间频散全波形反演(PS+TDC)方法.
由于震源波场和伴随波场中残留有源-反射点路径的时间频散,导致得到的模型参数梯度与无频散情况仍有差异.模拟波场和观测波场包含源-反射点-检波点路径的时间频散引起波形震荡、频谱改变,也会增加反演的多解性.因此,抗空间频散(PS)和抗时间+空间频散(PS+TDC)全波形反演方法仍无法彻底消除时间频散的影响.与波场延拓相比,观测波场中添加时间频散的计算量可忽略不计(且可在偏移和反演之前完成).抗时间+空间频散(PS+TDC)逆时偏移和全波形反演方法的计算效率与空间频散校正(PS)方法相近.
4 数值算例采用salt模型、Sigsbee2A模型、实际资料对抗频散逆时偏移和全波形反演方法进行测试.通过对比抗空间频散和抗时间+空间频散方法的结果研究时间频散对成像和反演的影响;对比抗时间频散和抗时间+空间频散方法的结果研究空间频散对成像和反演的影响.基于不同方法与参考解的接近程度验证抗时间+空间频散方法的有效性.
4.1 逆时偏移SEG/EAGEsalt模型如图 3所示.空间网格大小为20 m×20 m,时间步长为2.0 ms,最大记录时间为4.0 s.震源采用主频为30 Hz的Ricker子波.31个震源和601个检波点均匀分布于地表.采用伪谱法和小时间步长(Δt=0.5 ms)模拟无频散观测记录.FD表示时间2阶空间16阶精度的有限差分.常规(FD)和抗空间频散(PS)逆时偏移中直接对无频散观测记录进行反传,而抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法中先在观测记录中加入时间频散后再反传.图 4为第16炮(7800 m, 2160 m)处不同偏移方法的正反向传播波场和频谱.为便于比较,采用伪谱法和小时间步长(Δt=0.5 ms)进行波场正反向延拓并成像作为参考解(Ref).由图 4可见,正传和反传波场的时间频散分别引起波形向负时间和正时间方向移动,正传和反传波场的空间频散分别出现在正常波前时间增大和减小的方向;常规(FD)和抗时间频散(FD+TDC)方法的正传波场同时包含时间和空间频散(相移和震荡),而抗空间频散(PS)和抗时间+空间频散(PS+TDC)方法的正传波场中只积累了源-反射点路径的时间频散(相移);常规(FD)和抗空间频散(PS)方法的反传波场包含检波点-反射点路径的时间频散,而抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法的反传波场中积累了源-反射点路径的时间频散,常规(FD)和抗时间频散(FD+TDC) 方法的反传波场空间频散较强;常规(FD)和抗时间频散(FD+TDC)方法的正传波场频谱变形严重,抗空间频散(PS)和抗时间+空间频散(PS+TDC)方法的正反传波场频谱与参考解的差异较小.图 5给出不同方法的正反向传播波场匹配图.常规(FD)和抗空间频散(PS)方法正反传波场中分别积累了源-反射点和检波点-反射点路径的时间频散,波形沿相反的方向移动,导致正反传波场无法匹配;抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法的正反传波场中包含相同的源-反射点路径时间频散,波形都沿时间负方向移动,正反传波场相位相同,仍然能进行互相关条件成像;采用伪谱法(PS)进行正反向波场延拓,可以有效压制空间频散,减小波形震荡对成像精度的影响.

|
图 3 盐丘模型 Fig. 3 Salt dome model |
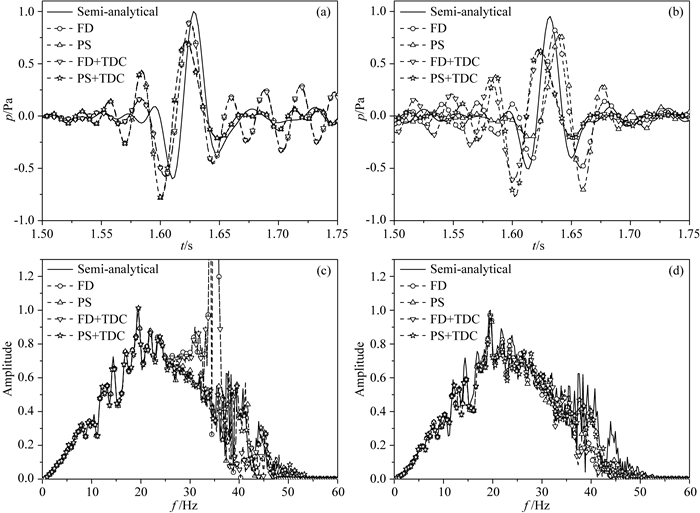
|
图 4 盐丘模型(7800 m, 2160 m)处不同方法的正反向波场及频谱 (a) 正向波场;(b) 反向波场;(c) 正向波场频谱;(d) 反向波场频谱. Fig. 4 Wavefields and spectra at the point (7800 m, 2160 m) by different methods on salt dome model (a) Forward wavefield; (b) Backward wavefield; (c) Spectrum of (a); (d) Spectrum of (b). |

|
图 5 盐丘模型不同方法的正反向波场匹配图 (a) Ref; (b) FD; (c) PS; (d) FD+TDC; (e) PS+TDC. Fig. 5 Matching diagrams of forward- and backward-propagated wavefields by different methods for the salt dome model |
图 6为不同偏移方法得到的成像剖面.由图 6可知,常规(FD)方法同时受时间和空间频散影响,无法准确成像;抗空间频散(PS)方法只与时间频散有关,出现同相轴不聚焦、分辨率降低、反射界面偏离真实位置等现象;抗时间频散(FD+TDC)方法只受空间频散影响,产生了许多高频噪声(如黑色箭头所示)和虚假反射界面(如白色箭头所示);抗时间+空间频散(PS+TDC)方法几乎不受频散影响,得到了与参考解相近的结果.图 7给出不同方法像的波数谱.抗空间频散(PS)方法的谱中包含垂直方向的线条(如黑色箭头所示),对应于空间域的周期性虚假水平同相轴;抗时间频散(FD+TDC)方法的谱中出现了一些高波数成分(如黑色箭头所示),对应于空间域的高频成像噪声;抗时间频散(FD+TDC)方法的波数谱与参考解能够较好地吻合.
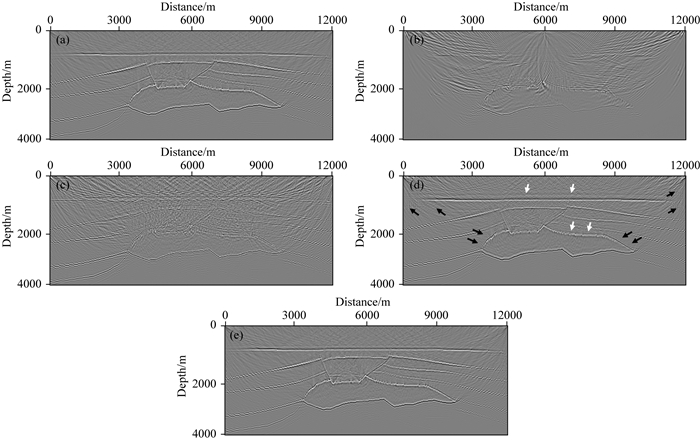
|
图 6 盐丘模型不同方法的成像结果 (a) Ref; (b) FD; (c) PS; (d) FD+TDC; (e) PS+TDC. Fig. 6 Images by different methods for the salt dome model |
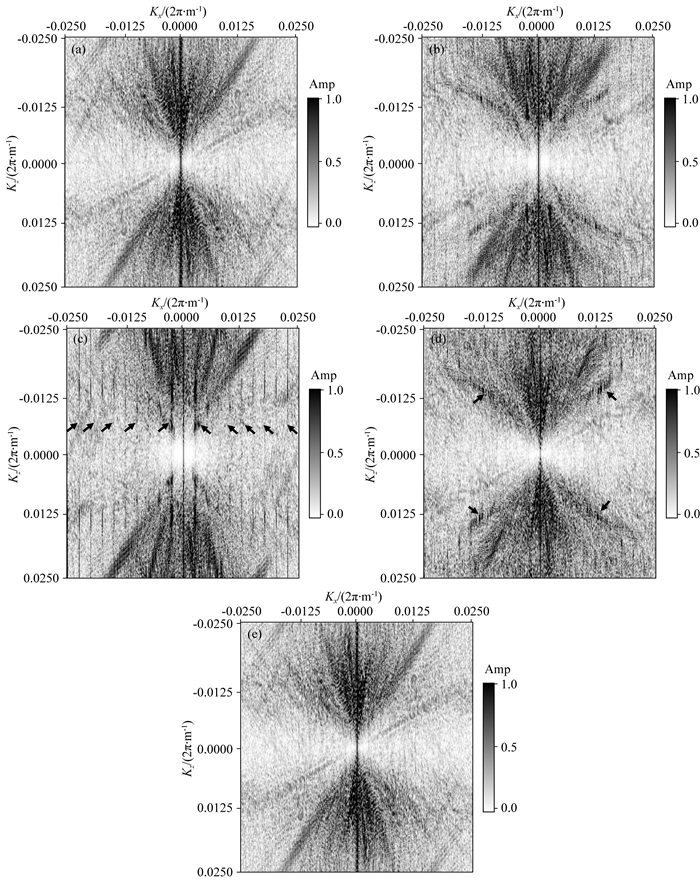
|
图 7 盐丘模型不同方法成像结果的波数谱 (a) Ref; (b) FD; (c) PS; (d) FD+TDC; (e) PS+TDC. Fig. 7 Spectra of images by different methods for the salt dome model |
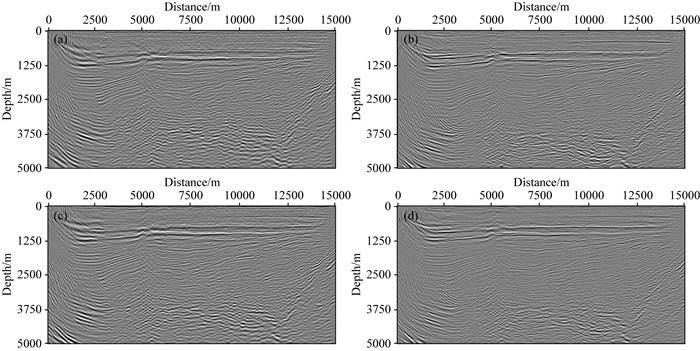
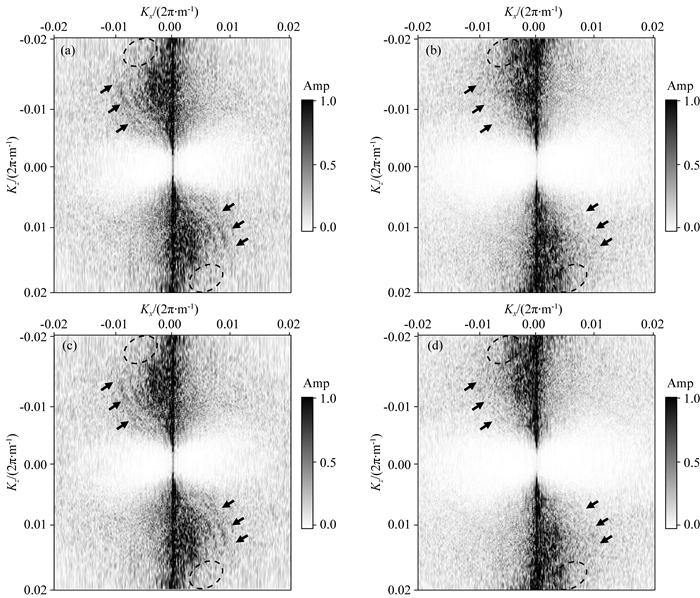
下面采用海上某工区实际地震资料对不同的偏移方法进行测试.该数据包含240炮,每炮120道,炮间距50 m,道间距25 m.网格大小为25 m×25 m,时间步长为2.0 ms,最大记录时间为4.0 s.图 8给出其中5炮的地震记录.图 9为偏移速度模型.震源子波是通过软件提取的最小相位子波.FD表示时间2阶空间10阶精度的有限差分.图 10展示了不同偏移方法的成像结果.由图 10可见:常规(FD)和抗时间频散(FD+TDC)方法偏移剖面中存在较强的成像噪声;抗空间频散(PS)方法偏移剖面同相轴的连续性较差;抗时间+空间频散(FD+TDC)方法不受时间和空间频散的影响,得到同相轴连续性更好、噪声少、分辨率更高的像.图 11给出不同方法成像结果的波数谱.通过时间频散校正和伪谱法压制时间和空间频散,可有效恢复出缺失的波数成分并削弱成像噪声(如虚线框和箭头所示).但实际应用中速度模型和震源子波未知,成像结果同时受速度和震源精度以及数值频散的影响,导致不同方法的偏移效果差异不明显.只有消除其他不利因素(如速度误差、震源误差、照明不均等)影响,本文发展的抗频散逆时偏移方法才更加有效.

|
图 8 实际地震记录 Fig. 8 Real seismic record |

|
图 9 实际资料偏移速度模型 Fig. 9 Migration velocity model for real data |
|
图 10 实际资料不同方法的成像结果 (a) FD; (b) PS; (c FD+TDC; (d) PS+TDC. Fig. 10 Images by different methods for real data |
|
图 11 实际资料不同方法的成像结果波数谱 (a) FD; (b) PS; (c) FD+TDC; (d) PS+TDC. Fig. 11 Spectra of images by different methods for real data |
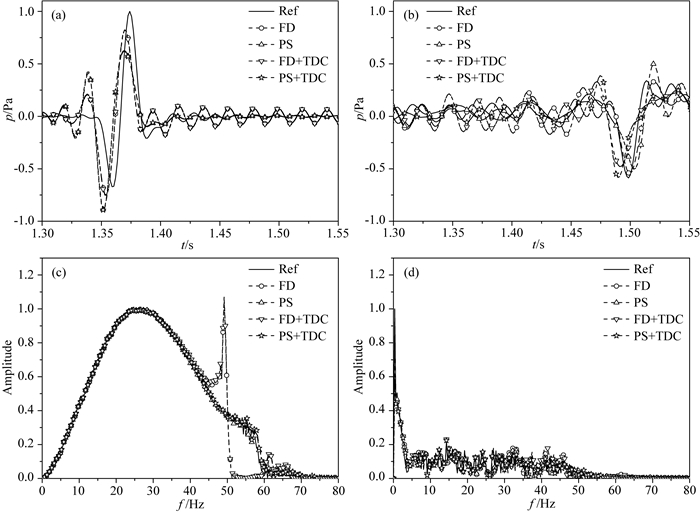
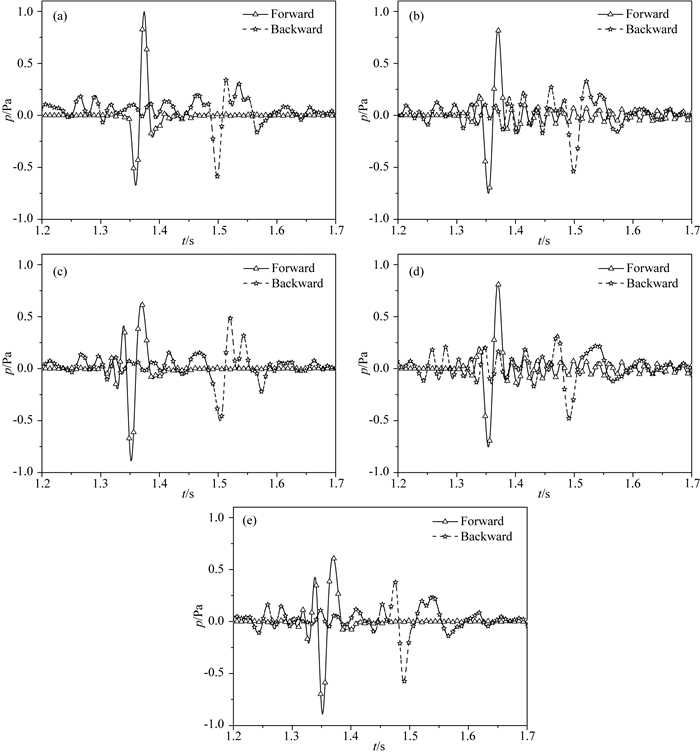
Sigsbee2A模型如图 12所示.计算区域为5600 m ×2960 m,网格大小为16 m×16 m,时间步长为1.5 ms,最大记录长度为3.0 s.震源采用主频为30 Hz的Ricker子波.36个震源和351个检波点均匀分布于地表.初始速度模型为真实模型的平滑结果,如图 13所示.由于初始模型与真实模型相近,我们进行单尺度反演,不同方法迭代10次.采用伪谱法和小时间步长(Δt=0.375 ms)模拟无频散观测记录.抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法中先在观测记录中加入时间频散再计算残差并进行波场反向延拓.图 14为第18炮(4000 m, 2240 m) 处不同方法第一次迭代时的正反向传播波场和频谱.FD表示时间2阶空间12阶精度的有限差分.采用伪谱法和小时间步长(Δt=0.375 ms)进行波场正反向延拓并反演作为参考解(Ref).由图 14可见:常规(FD)、抗空间频散(PS)、抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法的正传波场相对于参考解向时间负方向发生相移;常规(FD)和抗空间频散(PS)的反传波场相对于参考解向时间正方向发生相移,而抗时间频散(FD+TDC)和抗时间+空间频散PS+TDC)方法的反传波场仍向时间负方向移动;正反向波场的空间频散分别出现在正常波前时间增大和减小的方向,伪谱法(PS)可以有效压制空间频散.图 15给出不同反演方法第一次迭代时的正反传波场匹配图.时间频散校正可以保证正反向波场中包含等量的(源-反射点路径)时间频散.抗时间频散(FD+TDC)和抗时间+空间频散(PS+TDC)方法的正反传波场的时移量与参考解正反传波场的时移量大致相同.正反传波场的不匹配主要是由于速度存在误差导致的.

|
图 12 Sigsbee2A模型 Fig. 12 Sigsbee2A model |

|
图 13 Sigsbee2A模型初始模型 Fig. 13 Initial model for the Sigsbee2A model |
|
图 14 Sigsbee2A模型(4000 m, 2240 m)处不同方法的正反向波场及频谱 (a) 正向波场;(b) 反向波场;(c) 正向波场频谱;(d) 反向波场频谱. Fig. 14 Forward and backward wavefields and frequency spectra at the point (4000 m, 2240 m) by different methods for the Sigsbee2A model (a) Forward wavefield; (b) Backward wavefield; (c) Spectrum of (a); (d)Spectrum of (b). |
|
图 15 Sigsbee2A模型不同方法的正反向波场匹配图 (a) Ref; (b) FD; (c) PS; (d) FD+TDC; (e) PS+TDC. Fig. 15 Matching diagrams of forward- and backward-propagated wavefields by different methods for the Sigsbee2A model |
图 16为不同反演方法得到的速度模型.由图 16可知,常规(FD)和抗时间频散(FD+TDC)方法受空间频散影响严重,无法得到满意的结果;抗空间频散(PS)和抗时间+空间频散(PS+TDC)方法反演的速度模型有一定改善.为进一步比较,图 17给出Distance = 2720 m处不同方法的反演结果.抗空间频散(PS)方法受时间频散影响,反演精度较低;抗时间+空间频散(PS+TDC)方法可以缓解时间和空间频散对反演的影响,获得了与参考解更接近的结果.图 18展示了不同方法的收敛曲线.强的空间频散导致常规(FD)和抗时间频散(FD+TDC)方法无法收敛;抗时间+空间频散(PS+TDC)方法受时间频散影响较小,比抗空间频散(PS)方法的收敛速度快.抗时间+空间频散(PS+TDC)方法中震源和伴随波场中残留有源-反射点路径的时间频散,模拟和观测波场也包含源-反射点-检波点路径的时间频散.因此,抗频散(PS+TDC)全波形反演方法仍无法彻底消除时间频散的影响,其反演结果和收敛性与参考解仍有一定距离.

|
图 16 Sigsbee2A模型不同方法的反演结果 (a) Ref; (b) FD; (c) PS; (d) FD+TDC; (e) PS+TDC. Fig. 16 Inversion results by different methods for the Sigsbee2A model |
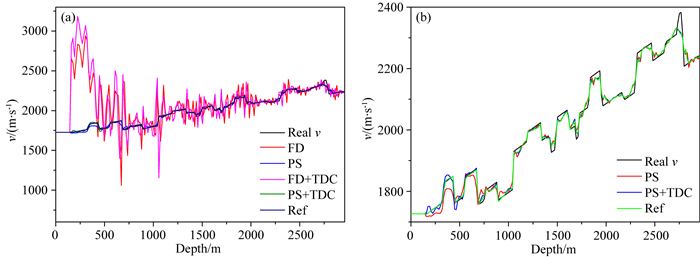
|
图 17 Sigsbee2A模型Distance=2720 m处不同方法的反演结果 Fig. 17 Inversion results at distance 2720 m by different methods for the Sigsbee2A model |

|
图 18 Sigsbee2A模型不同方法的收敛曲线 Fig. 18 Convergence curves by different methods for the Sigsbee2A model |
下面采用一维初始模型(如图 19所示)对不同的反演方法进行测试.由于初始模拟与真实模型相差较远,我们进行多尺度反演:0~5 Hz、0~10 Hz和0~15 Hz,每个尺度迭代10次.图 20给出Distance=2720 m处不同方法的反演结果.在大尺度低频反演中,时间和空间频散相对较弱,对全波形反演的影响非常小;通过时间频散校正(TDC)减小时间频散的影响,可以微弱改善反演精度.

|
图 19 Sigsbee2A模型一维初始模型 Fig. 19 1D initial model for the Sigsbee2A model |
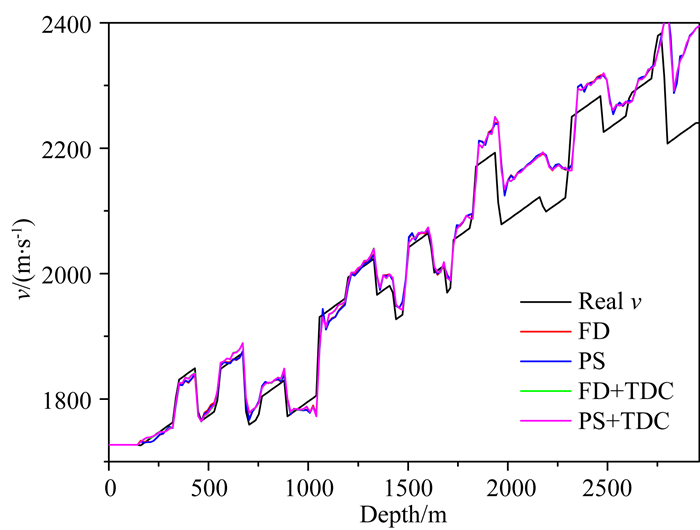
|
图 20 一维初始模型时Sigsbee2A模型Distance= 2720 m处不同方法的反演结果 Fig. 20 Inversion results at distance 2720 m by different methods with the 1D initial model for the Sigsbee2A model |
本文详细研究了有限差分的时间和空间频散特性及其对逆时偏移和全波形反演的影响.通过时间有限差分+伪谱法和时间频散校正+空间有限差分分离出时间和空间频散,进而发展了抗时间频散、抗空间频散、抗时间+空间频散的逆时偏移和全波形反演方法.模型算例和实际资料应用表明:逆时偏移同时受时间和空间频散影响,时间频散导致同相轴连续性变差、成像位置偏离,空间频散产生高频噪声和虚假反射界面;全波形反演在低频大尺度反演中几乎不受时间和空间频散影响,高频精细反演中时间频散会降低反演精度,空间频散可能导致不收敛;抗频散方法可以有效缓解时间和空间频散影响,获得满意的偏移剖面和反演结果.
时间频散校正和伪谱法不依赖于差分网格和波动方程,本文的抗频散方法可以直接推广到复杂介质(如变密度声波、弹性、各向异性等)逆时偏移和全波形反演中.当模型复杂且存在速度剧烈变化界面时,伪谱法的模拟精度变差.通过对速度进行平滑或者采用谱元法可以缓解上述问题.时间频散校正+优化空间有限差分也是一种兼顾精度和计算效率的方法.为彻底消除时间频散对全波形反演的影响,需要进一步研究基于高阶时间有限差分的抗频散方法.
Amundsen L, Pedersen Ø. 2017. Time step n-tupling for wave equations. Geophysics, 82(6): T249-T254. DOI:10.1190/geo2017-0377.1 |
Cai X H, Liu Y, Wang J M, et al. 2015. Full-wavefield VSP reverse-time migration based on the adaptive optimal finite-difference scheme. Chinese Journal of Geophysics (in Chinese), 58(9): 3317-3334. DOI:10.6038/cjg20150925 |
Carcione J M, Herman G C, Ten Kroode A P E. 2002. Seismic modeling. Geophysics, 67(4): 1304-1325. DOI:10.1190/1.1500393 |
Chen J B. 2009. Lax-Wendroff and Nyström methods for seismic modelling. Geophysical Prospecting, 57(6): 931-941. DOI:10.1111/j.1365-2478.2009.00802.x |
Chu C L, Stoffa P L. 2012. An implicit finite-difference operator for the Helmholtz equation. Geophysics, 77(4): T97-T107. DOI:10.1190/geo2011-0314.1 |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
De Hoop A T. 1960. A modification of Cagniard's method for solving seismic pulse problems. Applied Scientific Research, Section B, 8(1): 349-356. DOI:10.1007/BF02920068 |
Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419. |
Fornberg B. 1987. The pseudospectral method: Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501. DOI:10.1190/1.1442319 |
Jiang Z D, Fan C W, Li X Z, et al. 2021. Numerical simulation of marine ghost wave based on high order finite difference method with variable grids. Progress in Geophysics (in Chinese), 36(1): 365-373. DOI:10.6038/pg2021DD0485 |
Koene E F M, Robertsson J O A, Broggini F, et al. 2018. Eliminating time dispersion from seismic wave modeling. Geophysical Journal International, 213(1): 169-180. DOI:10.1093/gji/ggx563 |
Kosloff D, Pestana R C, Tal-Ezer H. 2010. Acoustic and elastic numerical wave simulations by recursive spatial derivative operators. Geophysics, 75(6): T167--T174. DOI:10.1190/1.3485217 |
Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
Li B, Liu Y, Sen M K, et al. 2017. Time-space-domain mesh-free finite difference based on least squares for 2D acoustic-wave modeling. Geophysics, 82(4): T143-T157. DOI:10.1190/geo2016-0464.1 |
Li Q Y, Wu G C, Liang Z Y. 2018. Time domain high-order pseudo spectral method based on PML boundary for elastic wavefield simulation. Progress in Geophysics (in Chinese), 33(1): 228-235. DOI:10.6038/pg2018BB0014 |
Liu C, Lan H T, Guo Z Q, et al. 2013. Pseudo-spectral modeling and feature analysis of wave propagation in two-phase HTI medium based on reformulated BISQ mechanism. Chinese Journal of Geophysics (in Chinese), 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
Liu L B, Duan P R, Zhang Y Y, et al. 2020. Overview of mesh-free method of seismic forward numerical simulation. Progress in Geophysics (in Chinese), 35(5): 1815-1825. DOI:10.6038/pg2020DD0117 |
Liu X, Liu Y, Ren Z M, et al. 2019. Perfectly matched layer boundary conditions for frequency-domain acoustic wave simulation in the mesh-free discretization. Geophysical Prospecting, 67(7): 1732-1744. DOI:10.1111/1365-2478.12788 |
Liu Y. 2014. Research progress on time-space domain finitedifference numerical solution and absorption boundary conditions of wave equation. Oil Geophysical Prospecting (in Chinese), 49(1): 35-46. |
Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
Liu Y, Sen M K. 2009a. An implicit staggered-grid finite-difference method for seismic modelling. Geophysical Journal International, 179(1): 459-474. DOI:10.1111/j.1365-246X.2009.04305.x |
Liu Y, Sen M K. 2009b. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
Liu Y, Sen M K. 2013. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation. Journal of Computational Physics, 232(1): 327-345. DOI:10.1016/j.jcp.2012.08.025 |
Liu Y, Wei X C. 2005. A stability criterion of elastic wave modelling by the Fourier method. Journal of Geophysics and Engineering, 2(2): 153-157. DOI:10.1088/1742-2132/2/2/010 |
Luo Y, Schuster G. 1990. Parsimonious staggered grid finite-differencing of the wave equation. Geophysical Research Letters, 17(2): 155-158. DOI:10.1029/GL017i002p00155 |
Moczo P, Kristek J, Galis M. 2014. The Finite-Difference Modelling of Earthquake Motions: Waves and Ruptures. Cambridge: Cambridge University Press.
|
Pei Z L. 2004. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface. Oil Geophysical Prospecting (in Chinese), 39(6): 629-634. |
Ren Z M, Li Z C, Liu Y, et al. 2017. Modeling of the acoustic wave equation by staggered-grid finite-difference schemes with high-order temporal and spatial accuracy. Bulletin of the Seismological Society of America, 107(5): 2160-2182. DOI:10.1785/0120170068 |
Ren Z M, Liu Y. 2015. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes. Geophysics, 80(1): T17-T40. DOI:10.1190/geo2014-0269.1 |
Stork C. 2013. Eliminating nearly all dispersion error from FD modeling and RTM with minimal cost increase. //75th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Sun H, Zhang J F. 2019. 3D acoustic wave modeling based on irregular grid method with double-mesh implementation. Chinese Journal of Geophysics (in Chinese), 62(9): 3534-3544. DOI:10.6038/cjg2019N0059 |
Tan S R, Huang L J. 2014. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation. Geophysical Journal International, 197(2): 1250-1267. DOI:10.1093/gji/ggu077 |
Virieux J. 1986. P-SV wave propagation in heterogeneous media; Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 |
Wang E J, Liu Y, Sen M K. 2016. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils. Geophysical Journal International, 206(3): 1933-1958. DOI:10.1093/gji/ggw250 |
Wang M X, Xu S. 2015. Finite-difference time dispersion transforms for wave propagation. Geophysics, 80(6): WD19-WD25. DOI:10.1190/geo2015-0059.1 |
Yang L, Yan H Y, Liu H. 2017. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm. Geophysics, 82(1): T27-T42. DOI:10.1190/geo2016-0171.1 |
Zhang B Q, Zhou H, Chen H M, et al. 2016. Time-space domain high-order finite-difference methods for seismic wave numerical simulation based on new stencils. Chinese Journal of Geophysics (in Chinese), 59(5): 1804-1814. DOI:10.6038/cjg20160523 |
Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
蔡晓慧, 刘洋, 王建民, 等. 2015. 基于自适应优化有限差分方法的全波VSP逆时偏移. 地球物理学报, 58(9): 3317-3334. DOI:10.6038/cjg20150925 |
董良国, 马在田, 曹景忠, 等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
姜占东, 范彩伟, 黎孝璋, 等. 2021. 基于变网格高阶有限差分的鬼波数值模拟研究. 地球物理学进展, 36(1): 365-373. DOI:10.6038/pg2021DD0485 |
李青阳, 吴国忱, 梁展源. 2018. 基于PML边界的时间高阶伪谱法弹性波场模拟. 地球物理学进展, 33(1): 228-235. DOI:10.6038/pg2018BB0014 |
刘财, 兰慧田, 郭智奇, 等. 2013. 基于改进BISQ机制的双相HTI介质波传播伪谱法模拟与特征分析. 地球物理学报, 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
刘立彬, 段沛然, 张云银, 等. 2020. 基于无网格的地震波场数值模拟方法综述. 地球物理学进展, 35(5): 1815-1825. DOI:10.6038/pg2020DD0117 |
刘洋. 2014. 波动方程时空域有限差分数值解及吸收边界条件研究进展. 石油地球物理勘探, 49(1): 35-46. |
裴正林. 2004. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟. 石油地球物理勘探, 39(6): 629-634. DOI:10.3321/j.issn:1000-7210.2004.06.002 |
孙辉, 张剑锋. 2019. 基于非规则双重网格的三维声波方程模拟. 地球物理学报, 62(9): 3534-3544. DOI:10.6038/cjg2019N0059 |
张保庆, 周辉, 陈汉明, 等. 2016. 基于新的差分结构的时-空域高阶有限差分波动方程数值模拟方法. 地球物理学报, 59(5): 1804-1814. DOI:10.6038/cjg20160523 |
 2021, Vol. 64
2021, Vol. 64

